6.3: Обсяги обертання - циліндричні оболонки

Last updated
Save as PDF

Page ID: 61647

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Обчислити обсяг твердого тіла обертання можна за допомогою методу циліндричних оболонок.
Порівняйте різні методи розрахунку обсягу обороту.

У цьому розділі ми розглянемо метод циліндричних оболонок, кінцевий метод знаходження обсягу твердого тіла обертання. Ми можемо використовувати цей метод на тих же видах твердих тіл, що і метод диска або метод шайби; однак, з методами диска та шайби ми інтегруємо вздовж осі координат паралельно осі обертання. За допомогою методу циліндричних оболонок інтегруємо по осі координат перпендикулярно осі обертання. Можливість вибрати, яку змінну інтеграції ми хочемо використовувати, може бути значною перевагою при більш складних функціях. Також специфічна геометрія твердого тіла іноді робить метод використання циліндричних оболонок більш привабливим, ніж при використанні методу шайби. В останній частині цього розділу ми розглянемо всі методи пошуку обсягу, які ми вивчили, і викладемо деякі рекомендації, які допоможуть вам визначити, який метод використовувати в тій чи іншій ситуації.

Метод циліндричних оболонок

Знову ж таки, ми працюємо з твердою революцією. Як і раніше, визначаємо область$R$, обмежену вище графіком функції$y=f(x)$, знизу $x$- віссю, а зліва і справа лініями$x=a$ і$x=b$, відповідно, як показано на малюнку$\PageIndex{1a}$. Потім ми обертаємо цю область навколо$y$ -осі, як показано на малюнку$\PageIndex{1b}$. Зверніть увагу, що це відрізняється від того, що ми робили раніше. Раніше області, визначені з точки зору функцій,$x$ оберталися навколо $x$-осі або паралельної їй лінії.

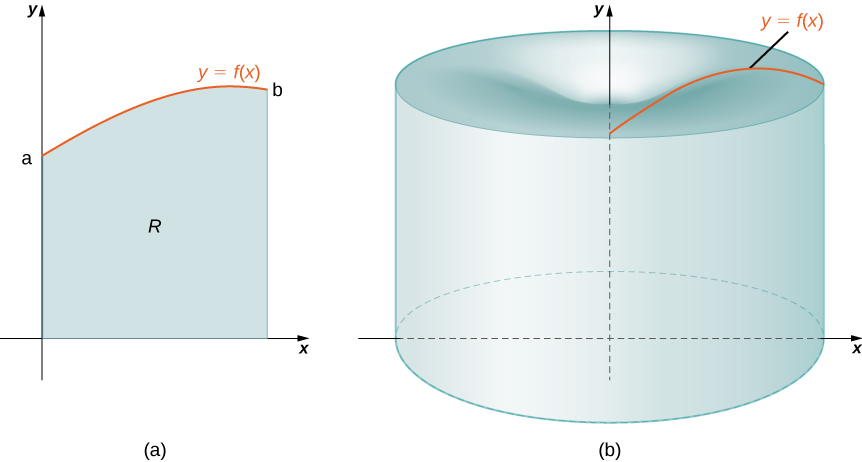
Ця цифра має два графіки. Перший графік позначений як «a» і є зростаючою кривою в першому квадранті. Крива позначена «y=f (x)». Крива починається на осі y в y = a, під кривою над віссю x знаходиться затінена область з міткою «R». Затінена область обмежена праворуч лінією x=b, другий графік — тривимірне тверде тіло. Він був створений шляхом обертання затіненої області від «a» навколо осі y. — Рисунок$\PageIndex{1}$: (a) Область, обмежена графіком функції$x$. (b) Тверда речовина обертання, що утворюється, коли область обертається навколо **$y$-осі.**

Як ми вже багато разів робили раніше, розділіть інтервал$[a,b]$ за допомогою звичайного розділу,$P={x_0,x_1,…,x_n}$ і, для$i=1,2,…,n$, вибирайте точку$x^∗_i∈[x_{i−1},x_i]$. Потім побудуйте прямокутник через інтервал$[x_{i−1},x_i]$ висоти$f(x^∗_i)$ і ширини$Δx$. Представницький прямокутник зображений на малюнку$\PageIndex{2a}$. Коли цей прямокутник обертається навколо$y$ -осі, замість диска або шайби ми отримуємо циліндричну оболонку, як показано на малюнку$\PageIndex{2}$.

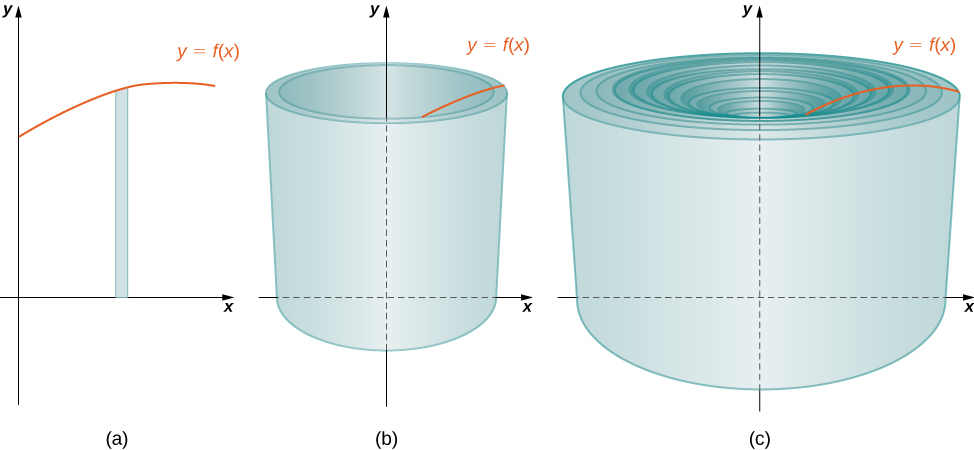
Ця цифра має два зображення. Перший являє собою циліндричну оболонку, порожнисту посередині. Вона має вертикальну вісь в центрі. Існує також крива, яка відповідає вершині циліндра. Друге зображення являє собою набір концентричних циліндрів, один всередині іншого утворюють вкладеність циліндрів. — Малюнок$\PageIndex{2}$: (а) Представницький прямокутник. (b) Коли цей прямокутник обертається навколо **$y$-осі**, результатом є циліндрична оболонка. (c) Коли ми складемо всі оболонки разом, ми отримуємо наближення вихідного твердого тіла.

Щоб розрахувати обсяг цієї раковини, розглянемо рис$\PageIndex{3}$.

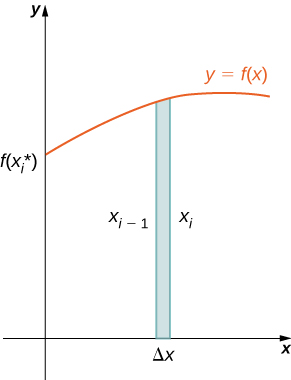
Ця цифра являє собою графік в першому квадранті. Крива збільшується і позначена «y=f (x)». Крива починається на осі y з f (x*). Нижче кривої знаходиться затінений прямокутник. Прямокутник починається з осі x. Ширина прямокутника дорівнює дельті x, дві сторони прямокутника позначені як «xsub (i-1)» та «xsubi». — Малюнок$\PageIndex{3}$: Розрахунок обсягу раковини.

Оболонка являє собою циліндр, тому її обсяг - площа поперечного перерізу, помножена на висоту циліндра. Поперечні перерізи аннулі (кільцеподібні області - по суті, кола з отвором у центрі), з зовнішнім радіусом$x_i$ і внутрішнім радіусом$x_{i−1}$. Таким чином, площа поперечного перерізу дорівнює$πx^2_i−πx^2_{i−1}$. Висота циліндра дорівнює$f(x^∗_i).$ Тоді обсяг оболонки дорівнює

\[ \begin{align*} V_{shell} =f(x^∗_i)(π\,x^2_{i}−π\,x^2_{i−1}) \\[4pt] =π\,f(x^∗_i)(x^2_i−x^2_{i−1}) \\[4pt] =π\,f(x^∗_i)(x_i+x_{i−1})(x_i−x_{i−1}) \\[4pt] =2π\,f(x^∗_i)\left(\dfrac {x_i+x_{i−1}}{2}\right)(x_i−x_{i−1}). \end{align*}\]

Зверніть увагу, що$x_i−x_{i−1}=Δx,$ так у нас є

\[V_{shell}=2π\,f(x^∗_i)\left(\dfrac {x_i+x_{i−1}}{2}\right)\,Δx. \nonumber \]

Крім того,$\dfrac {x_i+x_{i−1}}{2}$ це як середина інтервалу, так$[x_{i−1},x_i]$ і середній радіус оболонки, і ми можемо наблизити це по$x^∗_i$. У нас тоді є

\[V_{shell}≈2π\,f(x^∗_i)x^∗_i\,Δx. \nonumber \]

Інший спосіб думати про це - подумати про те, щоб зробити вертикальний розріз в оболонці, а потім відкрити його, щоб сформувати плоску пластину (рис.$\PageIndex{4}$).

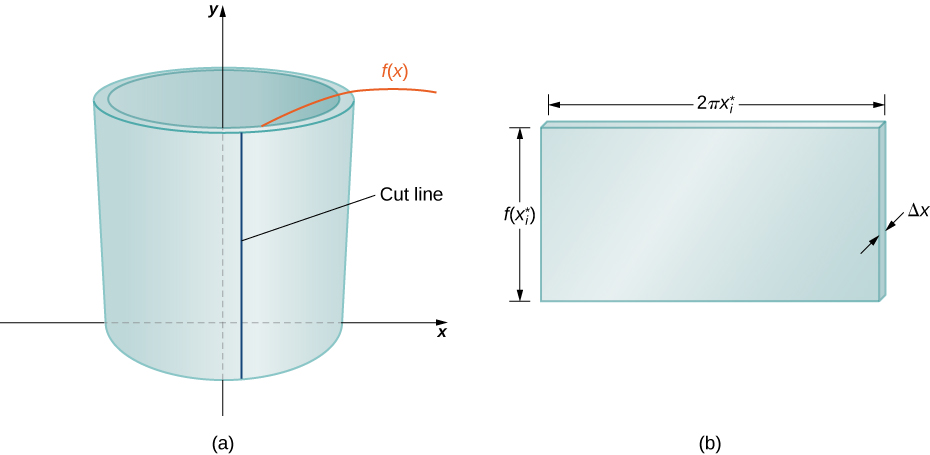
Ця цифра має два зображення. Перший має маркування «a» і являє собою порожнистий циліндр навколо осі y. На передній частині цього циліндра розташована вертикальна лінія з написом «лінія розрізу». Висота циліндра дорівнює «y=f (x)». Друга цифра має маркування «b» і являє собою заштрихований прямокутний блок. Висота прямокутника дорівнює «f (x*), ширина прямокутника - «2pix*», а товщина прямокутника - «дельта х». — Малюнок$\PageIndex{4}$: (а) Зробіть вертикальний розріз в представницькій оболонці. (b) Відкрийте оболонку вгору, щоб сформувати плоску пластину.

В реальності зовнішній радіус раковини більше внутрішнього радіуса, а значить задній край пластини був би трохи довше переднього краю пластини. Однак ми можемо наблизити сплющену оболонку плоскою пластиною висоти$f(x^∗_i)$$2πx^∗_i$, ширини і товщини$Δx$ (рис.). Обсяг шкаралупи, значить, приблизно дорівнює обсягу плоскої пластини. Помноживши висоту, ширину і глибину плити, отримуємо

\[V_{shell}≈f(x^∗_i)(2π\,x^∗_i)\,Δx, \nonumber \]

яка є тією ж формулою, яку ми мали раніше.

Щоб розрахувати обсяг всього твердого тіла, потім складаємо обсяги всіх оболонок і отримуємо

\[V≈\sum_{i=1}^n(2π\,x^∗_if(x^∗_i)\,Δx). \nonumber \]

Тут у нас є ще одна сума Рімана, цього разу для функції$2π\,x\,f(x).$ Беручи межу, як$n→∞$ дає нам

\[V=\lim_{n→∞}\sum_{i=1}^n(2π\,x^∗_if(x^∗_i)\,Δx)=\int ^b_a(2π\,x\,f(x))\,dx. \nonumber \]

Це призводить до наступного правила способу циліндричних оболонок.

Правило: Метод циліндричних оболонок

$f(x)$Дозволяти бути безперервним і невід'ємним. Визначте$R$ як область, обмежену вище графіком$f(x)$, нижче $x$- віссю, зліва від лінії$x=a$, а праворуч - лінією$x=b$. Тоді обсяг твердого тіла обертання, утвореного обертанням$R$ навколо$y$ -осі, задається

\[V=\int ^b_a(2π\,x\,f(x))\,dx. \nonumber \]

Тепер розглянемо приклад.

Приклад$\PageIndex{1}$: The Method of Cylindrical Shells I

Визначте$R$ як область, обмежену вище графіком$f(x)=1/x$ і нижче по $x$осі -над інтервалом$[1,3]$. Знайдіть об'єм твердого тіла обертання, утвореного$R$ обертанням навколо$y$ -осі.

Рішення

Спочатку ми повинні графікувати область$R$ та пов'язане з ним тверде тіло обертання, як показано на малюнку$\PageIndex{5}$.

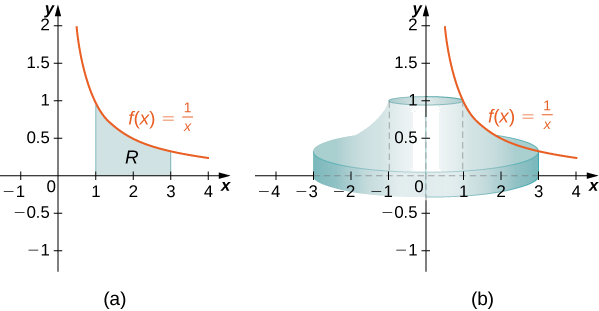
Ця цифра має три зображення. Перший - це тверде тіло, яке було утворено обертанням кривої y = 1/x навколо осі y. Тверде тіло починається на осі x і зупиняється там, де y = 1. Друге зображення має позначення «a» і є графіком y=1/x у першому квадранті. Під кривою знаходиться затінена область з позначкою «R». Область обмежена кривою, віссю x, ліворуч на x = 1 і праворуч при x = 3. Третє зображення має позначення «b» і являє собою половину твердого тіла, утвореного обертанням затіненої області навколо осі y. — Малюнок$\PageIndex{5}$: (а) Область$R$ під графіком$f(x)=1/x$ над інтервалом$[1,3]$. (b) Тверда речовина обертання, породжена$R$ обертанням навколо$y$ -осі.

Рисунок$\PageIndex{5}$ (c) Візуалізація твердого тіла обертання за допомогою CalcPlot3D.

Тоді обсяг твердого тіла задається

\[ \begin{align*} V =\int ^b_a(2π\,x\,f(x))\,dx \\ =\int ^3_1\left(2π\,x\left(\dfrac {1}{x}\right)\right)\,dx \\ =\int ^3_12π\,dx\\ =2π\,x\bigg|^3_1=4π\,\text{units}^3. \end{align*}\]

Вправа$\PageIndex{1}$

Визначте R як область, обмежену вище графіком$f(x)=x^2$ і нижче по$x$ осі -над інтервалом$[1,2]$. Знайдіть об'єм твердого тіла обертання, утвореного$R$ обертанням навколо$y$ -осі.

Підказка: Скористайтеся процедурою з Прикладу$\PageIndex{1}$.

Відповідь: $\dfrac{15π}{2} \, \text{units}^3 $

Приклад$\PageIndex{2}$: The Method of Cylindrical Shells II

Визначте$R$ як область, обмежену вище графіком$f(x)=2x−x^2$ і нижче по$x$ осі -над інтервалом$[0,2]$. Знайдіть об'єм твердого тіла обертання, утвореного$R$ обертанням навколо $y$-осі.

Рішення

Спочатку графуйте область$R$ і пов'язане з ним тверде тіло обертання, як показано на малюнку$\PageIndex{6}$.

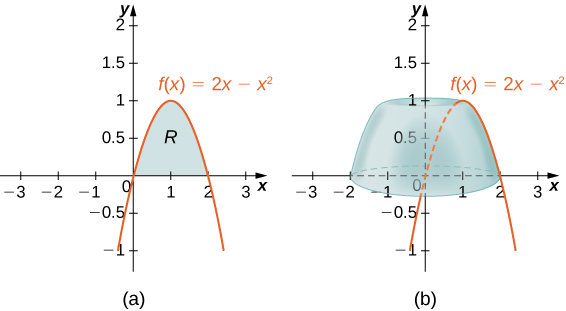
Ця цифра має два графіки. Перший графік позначений як «a» і є кривою f (x) =2x-x^2. Це перевернута парабола, що перетинає вісь x біля мурахи походження при x = 2. Під кривою область в першому квадранті затінена і позначена «R». Друга цифра - це графік тієї ж кривої. На графіку знаходиться тверде тіло, яке утворюється обертанням області від «a» щодо осі y. — Малюнок$\PageIndex{6}$: (а) Область$R$ *під графіком$f(x)=2x−x^2$* *над інтервалом$[0,2].$* *(б) Обсяг обертання, отриманий при обертанні* $R$*про$y$* *-осі.*

Тоді обсяг твердого тіла задається

\[\begin{align*} V =\int ^b_a(2π\,x\,f(x))\,dx \\ =\int ^2_0(2π\,x(2x−x^2))\,dx \\ = 2π\int ^2_0(2x^2−x^3)\,dx \\ =2π \left. \left[\dfrac {2x^3}{3}−\dfrac {x^4}{4}\right]\right|^2_0 \\ =\dfrac {8π}{3}\,\text{units}^3 \end{align*}\]

Вправа$\PageIndex{2}$

Визначте$R$ як область, обмежену вище графіком$f(x)=3x−x^2$ і нижче по$x$ осі -над інтервалом$[0,2]$. Знайдіть об'єм твердого тіла обертання, утвореного$R$ обертанням навколо$y$ -осі.

Підказка

Скористайтеся процесом з Прикладу$\PageIndex{2}$.

Відповідь

$8π \, \text{units}^3 $

Як і у випадку з дисковим методом і методом шайби, ми можемо використовувати метод циліндричних оболонок з твердими частинами обертання, обертаються навколо$x$ -осі, коли ми хочемо інтегруватися щодо$y$. Аналогічне правило для цього виду твердих тіл наведено тут.

Правило: Метод циліндричних оболонок для твердих тіл обертання навколо$x$-axis

$g(y)$Дозволяти бути безперервним і невід'ємним. Визначте$Q$ як область, обмежену праворуч графіком$g(y)$, ліворуч$y$ - віссю, нижче лінією$y=c$ і вище лінією$y=d$. Потім обсяг твердого тіла обертання, утвореного обертанням$Q$ навколо$x$ -осі, задається

\[V=\int ^d_c(2π\,y\,g(y))\,dy. \nonumber \]

Приклад$\PageIndex{3}$: The Method of Cylindrical Shells for a Solid Revolved around the $x$-axis

Визначте$Q$ як область, обмежену праворуч графіком,$g(y)=2\sqrt{y}$ а ліворуч$y$ - віссю для$y∈[0,4]$. Знайдіть об'єм твердого тіла обертання, утвореного$Q$ обертанням навколо$x$ -осі.

Рішення

Спочатку нам потрібно скласти графік області$Q$ та пов'язаного з ним твердого тіла обертання, як показано на малюнку$\PageIndex{7}$.

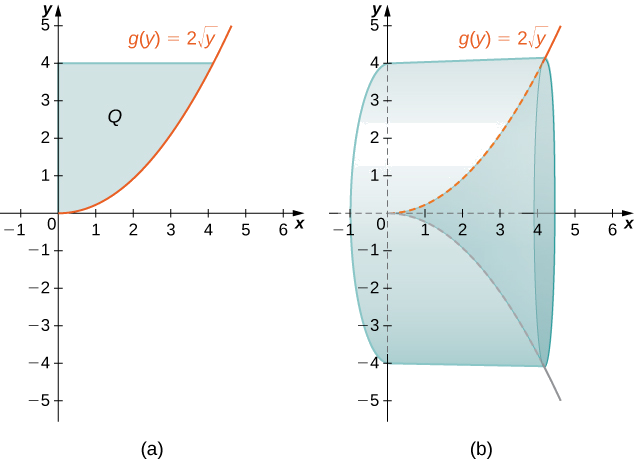
$Ця цифра має два графіки. Перший граф позначений як «a» і являє собою криву g (y) =2squareroot (y). Це зростаюча крива в першому квадранті, що починається на початку. Між віссю Y та кривою є затінена область з позначкою «Q». Затінена область обмежена вище лінією y=4. Другий графік - це та сама крива в «a» і позначена «b». Він також має тверду область, яка була утворена обертанням кривої в «a» навколо осі x. Тверде тіло починається з осі y і зупиняється на x = 4.$
Рисунок$\PageIndex{7}$: (a) Область$Q$ зліва від функції$g(y)$ за інтервалом$[0,4]$. (b) Тверда речовина обертання, породжена$Q$ обертанням навколо$x$ -осі.

Позначте затінену область$Q$. Тоді обсяг твердого тіла задається

\[ \begin{align*} V =\int ^d_c(2π\,y\,g(y))\,dy \\ =\int ^4_0(2π\,y(2\sqrt{y}))\,dy \\ =4π\int ^4_0y^{3/2}\,dy \\ =4π\left[\dfrac {2y^{5/2}}{5}\right]∣^4_0 \\ =\dfrac {256π}{5}\, \text{units}^3 \end{align*}\]

Вправа$\PageIndex{3}$

Визначте$Q$ як область, обмежену праворуч графіком,$g(y)=3/y$ а ліворуч$y$ - віссю для$y∈[1,3]$. Знайдіть об'єм твердого тіла обертання, утвореного$Q$ обертанням навколо$x$ -осі.

Підказка

Скористайтеся процесом з Прикладу$\PageIndex{3}$.

Відповідь

$12π$одиниць ³

Для наступного прикладу ми розглянемо тверде тіло обертання, для якого графік функції обертається навколо прямої, відмінної від однієї з двох осей координат. Щоб налаштувати це, нам потрібно переглянути розробку методу циліндричних оболонок. Нагадаємо, що ми знайшли обсяг однієї з оболонок, який потрібно надати

\[\begin{align*} V_{shell} =f(x^∗_i)(π\,x^2_i−π\,x^2_{i−1}) \\[4pt] =π\,f(x^∗_i)(x^2_i−x^2_{i−1}) \\[4pt] =π\,f(x^∗_i)(x_i+x_{i−1})(x_i−x_{i−1}) \\[4pt] =2π\,f(x^∗_i)\left(\dfrac {x_i+x_{i−1}}{2}\right)(x_i−x_{i−1}).\end{align*}\]

Це було засновано на оболонці з зовнішнім радіусом$x_i$ і внутрішнім радіусом$x_{i−1}$. Якщо, однак, ми обертаємо область навколо лінії, відмінної від$y$ -осі, у нас є інший зовнішній і внутрішній радіус. Припустимо, наприклад, що ми обертаємо область навколо лінії,$x=−k,$ де$k$ є якась позитивна константа. Потім зовнішній радіус оболонки дорівнює$x_i+k$ і внутрішній радіус оболонки$x_{i−1}+k$. Підставляючи ці терміни в вираз для обсягу, ми бачимо, що при обертанні площини навколо лінії$x=−k,$ обсяг оболонки задається

\[\begin{align*} V_{shell} =2π\,f(x^∗_i)(\dfrac {(x_i+k)+(x_{i−1}+k)}{2})((x_i+k)−(x_{i−1}+k)) \\[4pt] =2π\,f(x^∗_i)\left(\left(\dfrac {x_i+x_{i−2}}{2}\right)+k\right)Δx.\end{align*}\]

Як і раніше, ми помічаємо, що$\dfrac {x_i+x_{i−1}}{2}$ це середина інтервалу$[x_{i−1},x_i]$ і може бути наближена$x^∗_i$. Потім приблизний обсяг оболонки дорівнює

\[V_{shell}≈2π(x^∗_i+k)f(x^∗_i)Δx. \nonumber \]

Решта розвитку триває, як і раніше, і ми бачимо, що

\[V=\int ^b_a(2π(x+k)f(x))dx. \nonumber \]

Ми також могли б обертати область навколо інших горизонтальних або вертикальних ліній, таких як вертикальна лінія в правій половині площини. У кожному конкретному випадку формулу обсягу потрібно коригувати відповідним чином. Зокрема,$x$ -термін в інтегралі повинен бути замінений виразом, що представляє радіус оболонки. Щоб побачити, як це працює, розглянемо наступний приклад.

Приклад$\PageIndex{4}$: A Region of Revolution Revolved around a Line

Визначте$R$ як область, обмежену вище графіком$f(x)=x$ і нижче по$x$ осі -над інтервалом$[1,2]$. Знайти об'єм твердого тіла обертання, утвореного$R$ обертанням навколо лінії$x=−1.$

Рішення

Спочатку намалюйте область$R$ і пов'язане з ним тверде тіло обертання, як показано на малюнку$\PageIndex{8}$.

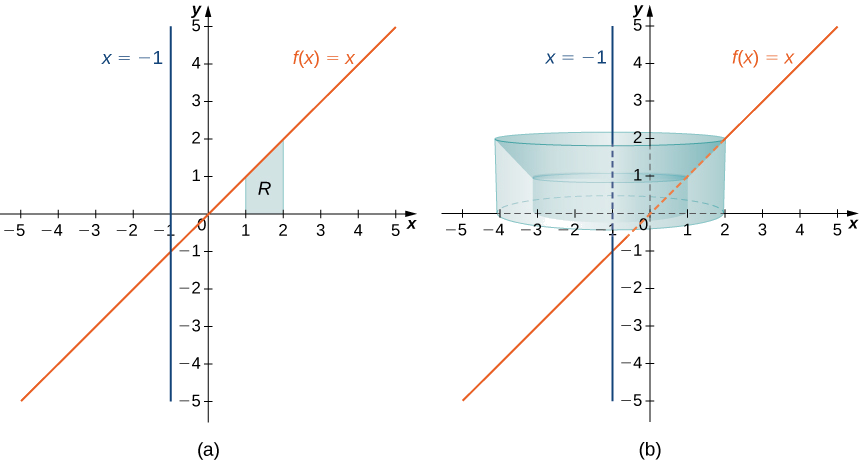
$Ця цифра має два графіки. Перший графік позначений як «a» і є лінією f (x) =x, діагональною лінією через початок. Існує затінена область над віссю x під лінією з позначкою «R». Ця область обмежена ліворуч лінією x=1, а праворуч лінією x=2. На графіку також є вертикальна лінія x = -1. Друга цифра має ті ж графіки, що і «a» і має маркування «b». Також на графіку знаходиться тверде тіло, утворене обертанням області «R» з першого графіка навколо прямої x=-1.$
Рисунок$\PageIndex{8}$: (а) Область$R$ між графіком$f(x)$ і$x$ -віссю над інтервалом$[1,2]$. (b) Тверда речовина обертання, породжена$R$ обертанням навколо лінії$x=−1.$

Зауважте, що радіус оболонки задається за допомогою$x+1$. Тоді обсяг твердого тіла задається

\[\begin{align*} V =\int ^2_1 2π(x+1)f(x)\, dx \\ =\int ^2_1 2π(x+1)x \, dx=2π\int ^2_1 x^2+x \, dx \\ =2π \left[\dfrac{x^3}{3}+\dfrac{x^2}{2}\right]\bigg|^2_1 \\ =\dfrac{23π}{3} \, \text{units}^3 \end{align*}\]

Вправа$\PageIndex{4}$

Визначте$R$ як область, обмежену вище графіком$f(x)=x^2$ і нижче по$x$ осі -над інтервалом$[0,1]$. Знайдіть об'єм твердого тіла обертання, утвореного$R$ обертанням навколо лінії$x=−2$.

Підказка

Скористайтеся процесом з Прикладу$\PageIndex{4}$.

Відповідь

$\dfrac {11π}{6}$одиниць ³

Для нашого остаточного прикладу в цьому розділі розглянемо обсяг твердого тіла обертання, для якого область обертання обмежена графами двох функцій.

Приклад$\PageIndex{5}$: A Region of Revolution Bounded by the Graphs of Two Functions

Визначте$R$ як область, обмежену вище графіком функції,$f(x)=\sqrt{x}$ а нижче - графіком функції$g(x)=1/x$ за інтервалом$[1,4]$. Знайдіть об'єм твердого тіла обертання, породженого$R$ обертанням навколо$y$ -осі.

Рішення

Спочатку намалюйте область$R$ і пов'язане з ним тверде тіло обертання, як показано на малюнку$\PageIndex{9}$.

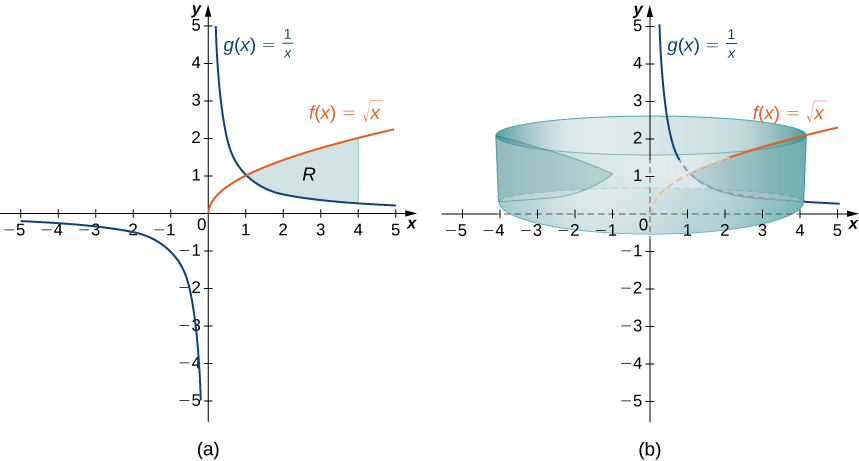
$Ця цифра має два графіки. Перший граф має позначення «a» і має дві криві. Криві є графіками f (x) =squareroot (x) та g (x) =1/x. У першому квадранті криві перетинаються на (1,1). Між кривими в першому квадранті є затінена область з міткою «R», обмежена праворуч лінією x=4. Другий графік позначений «b» і є таким же, як і графіки в «a». Також на цьому графіку знаходиться тверде тіло, яке утворилося обертанням області «R» від фігури «a» навколо осі y.$
Малюнок$\PageIndex{9}$: (а) Область$R$ між графіком$f(x)$ і графіком$g(x)$ над інтервалом$[1,4]$. (b) Тверда речовина обертання, породжена$R$ обертанням навколо$y$ -осі.

Зверніть увагу, що віссю обертання є$y$ -вісь, тому радіус оболонки задається просто$x$. Нам не потрібно вносити жодних коригувань у x-термін нашого integrand. Висота оболонки, однак, задається$f(x)−g(x)$, тому в цьому випадку нам потрібно відрегулювати$f(x)$ термін integrand. Тоді обсяг твердого тіла задається

\[\begin{align*} V =\int ^4_1(2π\,x(f(x)−g(x)))\,dx \\[4pt] = \int ^4_1(2π\,x(\sqrt{x}−\dfrac {1}{x}))\,dx=2π\int ^4_1(x^{3/2}−1)dx \\[4pt] = 2π\left[\dfrac {2x^{5/2}}{5}−x\right]\bigg|^4_1=\dfrac {94π}{5} \, \text{units}^3. \end{align*}\]

Вправа$\PageIndex{5}$

Визначте$R$ як область, обмежену вище графіком$f(x)=x$ і нижче графіком$g(x)=x^2$ за інтервалом$[0,1]$. Знайдіть об'єм твердого тіла обертання, утвореного$R$ обертанням навколо$y$ -осі.

Підказка

Підказка: Скористайтеся процесом з Прикладу$\PageIndex{5}$.

Відповідь

$\dfrac {π}{6}$одиниць ³

Який метод ми повинні використовувати?

Ми вивчили кілька методів знаходження обсягу твердої речовини обертання, але як дізнатися, який метод використовувати? Це часто зводиться до вибору того, який інтеграл найпростіше оцінити. Рисунок$\PageIndex{10}$ описує різні підходи до твердих тіл обертання навколо$x$ -осі. Вам належить розробити аналогічну таблицю для твердих тіл обертання навколо$y$ -осі.

$Ця цифра являє собою таблицю порівняння різних методів знаходження обсягів твердих тіл обертання. Стовпці в таблиці мають позначення «порівняння», «метод диска», «метод шайби» та «метод оболонки». Рядки позначені як «формула об'єму», «суцільний», «інтервал до розділу», «прямокутники», «типова область» та «прямокутник». У стовпці дискового методу формула задається як певний інтеграл від a до b pi раз [f (x)] ^2. Тверда речовина не має порожнини в центрі, перегородка - [a, b], прямокутники вертикальні, а типова область - затінена область над віссю x і нижче кривої f (x). У стовпці методу шайби формула дається як певний інтеграл від a до b pi разів [f (x)] ^2- [g (x)] ^2- [g (x)] ^2. Тверда речовина має порожнину в центрі, перегородка - [a, b], прямокутники вертикальні, а типова область - затінена область над кривою g (x) і нижче кривої f (x). У стовпці методу оболонки формула задана як певний інтеграл від c до d 2pi раз yg (y). Тверде тіло з порожниною або без неї в центрі, перегородка - це [c, d] прямокутники горизонтальні, а типова область - затінена область над віссю x і нижче кривої g (y).$
Малюнок$\PageIndex{10}$

Давайте розглянемо пару додаткових проблем і визначимося з найкращим підходом для їх вирішення.

Приклад$\PageIndex{6}$: Selecting the Best Method

Для кожної з наступних задач виберіть найкращий спосіб знайти об'єм твердого тіла обертання, породженого обертанням даної області навколо$x$ -осі, і встановіть інтеграл, щоб знайти об'єм (не оцінюйте інтеграл).

Область, обмежена графіками$y=x, y=2−x,$ і$x$ -віссю.

Область, обмежена графіками$y=4x−x^2$ і$x$ -віссю.

Рішення

а.

Спочатку намалюйте регіон та тверду революцію, як показано на малюнку.

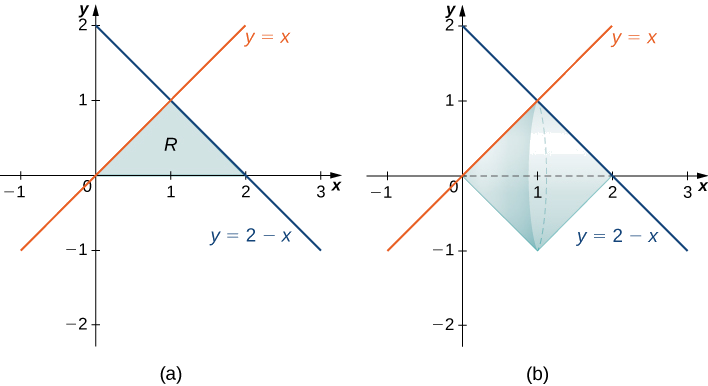
$Ця цифра має два графіки. Перший граф має позначення «a» і має дві лінії y=x та y=2-x, намальовані у першому квадранті. Лінії перетинаються в (1,1) і утворюють трикутник над віссю х. Область, яка є трикутником, затінена. Другий граф позначений «b» і являє собою ті ж графіки, що і «a». Затінена трикутна область в «a» була повернута навколо осі x, утворюючи тверде тіло на другому графіку.$
Рисунок$\PageIndex{11}$: (a) Область,$R$ обмежена двома лініями та$x$ віссю -. (b) Тверда речовина обертання, породжена$R$ обертанням навколо$x$ -осі.

Дивлячись на регіон, якщо ми хочемо інтегруватися стосовно$x$, нам доведеться розбити інтеграл на дві частини, тому що у нас є різні функції, що обмежують область над$[0,1]$ і$[1,2]$. У цьому випадку, використовуючи метод диска, ми б

\[V=\int ^1_0 π\,x^2\,dx+\int ^2_1 π(2−x)^2\,dx. \nonumber \]

Якби ми використовували метод оболонки замість цього, ми б використовували функції y для представлення кривих, виробляючи

\[V=\int ^1_0 2π\,y[(2−y)−y] \,dy=\int ^1_0 2π\,y[2−2y]\,dy. \nonumber \]

Жоден з цих інтегралів не є особливо обтяжливим, але оскільки метод оболонки вимагає лише одного інтеграла, а integrand вимагає меншого спрощення, ми, ймовірно, повинні піти з методом оболонки в цьому випадку.

б.

Спочатку намалюйте регіон та тверду революцію, як показано на малюнку.

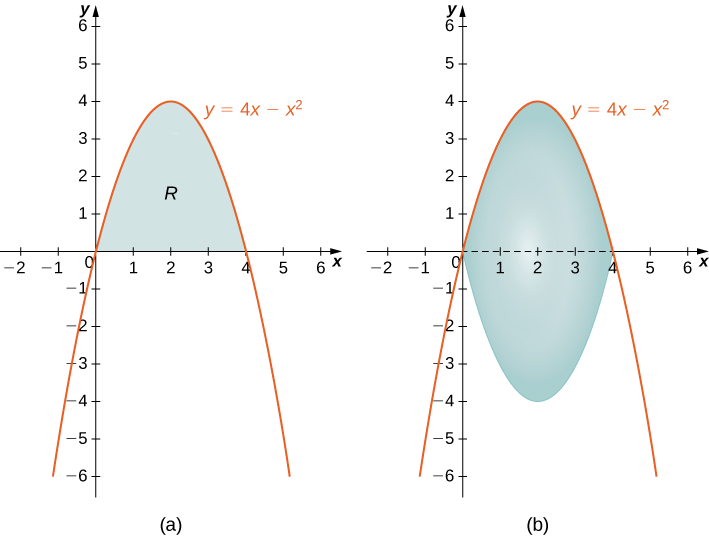
$Ця цифра має два графіки. Перший графік позначений як «a» і є кривою y=4x-x^2. Це перевернута парабола, що перетинає вісь x біля початку та в x = 4. Область над віссю x і нижче кривої затінюється і позначена «R». Другий граф з позначкою «b» такий же, як і в «a». На цьому графіку затінена область «R» була повернута навколо осі x, утворюючи тверде тіло.$
Малюнок$\PageIndex{12}$: (a) Область$R$ між кривою та$x$ віссю. (b) Тверда речовина обертання, породжена$R$ обертанням навколо$x$ -осі.

Дивлячись на область, було б проблематично визначити горизонтальний прямокутник; область обмежена ліворуч і праворуч тією ж функцією. Тому можна відкинути метод снарядів. Тверде тіло не має порожнини посередині, тому ми можемо використовувати метод дисків. Тоді

\[V=\int ^4_0π\left(4x−x^2\right)^2\,dx \nonumber \]

Вправа$\PageIndex{6}$

Виберіть найкращий метод, щоб знайти об'єм твердого тіла обертання, породженого обертанням даної області навколо$x$ -осі, і встановіть інтеграл для знаходження об'єму (не оцінюйте інтеграл): область, обмежену графами$y=2−x^2$ і$y=x^2$.

Підказка

Намалюйте область та скористайтеся Figure,$\PageIndex{12}$ щоб вирішити, який інтеграл найпростіше оцінити.

Відповідь

Використовувати метод шайб;\[V=\int ^1_{−1}π\left[\left(2−x^2\right)^2−\left(x^2\right)^2\right]\,dx \nonumber \]

Ключові концепції

Метод циліндричних оболонок - ще один метод використання певного інтеграла для розрахунку обсягу твердого тіла обертання. Цей метод іноді є кращим або методом дисків, або методом шайб, оскільки ми інтегруємо щодо іншої змінної. У деяких випадках один інтеграл істотно складніше іншого.

Геометрія функцій та складність інтеграції є основними факторами при вирішенні того, який метод інтеграції використовувати.

Ключові рівняння

Метод циліндричних оболонок

$\displaystyle V=\int ^b_a\left(2π\,x\,f(x)\right)\,dx$

Глосарій

метод циліндричних оболонок

метод обчислення обсягу твердого тіла обертання шляхом ділення твердого тіла на вкладені циліндричні оболонки; цей метод відрізняється від методів дисків або шайб тим, що ми інтегруємо щодо протилежної змінної

Правило: Метод циліндричних оболонок

Приклад\(\PageIndex{1}\): The Method of Cylindrical Shells I

Вправа\(\PageIndex{1}\)

Приклад\(\PageIndex{2}\): The Method of Cylindrical Shells II

Вправа\(\PageIndex{2}\)

Правило: Метод циліндричних оболонок для твердих тіл обертання навколо\(x\)-axis

Приклад\(\PageIndex{3}\): The Method of Cylindrical Shells for a Solid Revolved around the \(x\)-axis

Вправа\(\PageIndex{3}\)

Приклад\(\PageIndex{4}\): A Region of Revolution Revolved around a Line

Вправа\(\PageIndex{4}\)

Приклад\(\PageIndex{5}\): A Region of Revolution Bounded by the Graphs of Two Functions

Вправа\(\PageIndex{5}\)

Приклад\(\PageIndex{6}\): Selecting the Best Method

Вправа\(\PageIndex{6}\)

Ключові рівняння