7.3: Метод оболонки

Last updated
Save as PDF

Page ID: 60714

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Часто дану проблему можна вирішити не одним способом. Конкретний метод може бути обраний з огляду на зручність, особисті переваги або, можливо, необхідність. Зрештою, добре мати варіанти.

У попередньому розділі були введені методи диска та шайби, які обчислювали об'єм тіл обертання шляхом інтеграції площі поперечного перерізу твердого тіла. У цьому розділі розробляється ще один метод обчислення обсягу, метод оболонки. Замість того, щоб нарізати тверде тіло перпендикулярно осі обертання, створюючи поперечні перерізи, ми тепер нарізаємо його паралельно осі обертання, створюючи «оболонки».

Розглянемо малюнок$\PageIndex{1}$, де область, показана в (а), обертається навколо$y$ -осі, утворюючи тверде тіло, показане в (b). Невеликий зріз області малюється в (а), паралельно осі обертання. При обертанні області цей тонкий зріз утворює циліндричну оболонку, як зображено в частині (в) малюнка. Попередній розділ наближався до твердого тіла з великою кількістю тонких дисків (або шайб); тепер ми наближаємо тверду речовину з багатьма тонкими циліндричними оболонками.

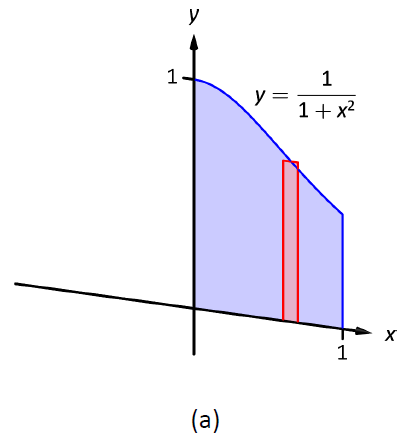
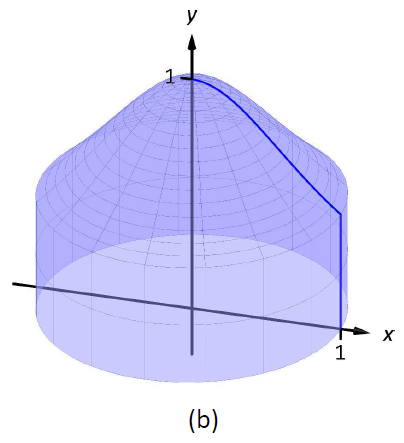
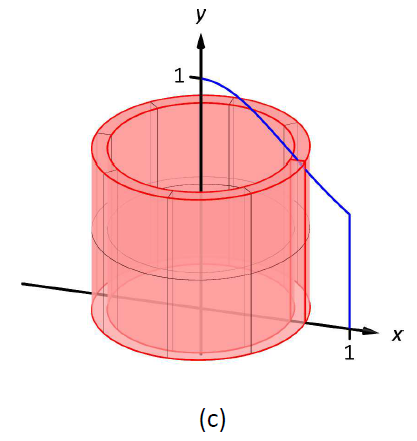
$7.3.1a.png$ $7.3.1 б.пнг$ $7.3.1 к.пнг$

Малюнок$\PageIndex{1}$: Представляємо метод оболонки.

Рисунок$\PageIndex{1}$ (d): Динамічна версія цього малюнка, створена за допомогою CalcPlot3D.

Щоб обчислити обсяг однієї оболонки, спочатку розглянемо паперову етикетку на банку супу з радіусом$r$ і висотою$h$. Яка площа цієї етикетки? Простий спосіб визначення цього - вирізати етикетку і викласти її рівно, утворюючи прямокутник з висотою$h$ і довжиною$2\pi r$. Таким чином площа є$A = 2\pi rh$; див$\PageIndex{2a}$. Рис.

Аналогічний процес виконайте з циліндричною оболонкою, з висотою$h$$\Delta x$, товщиною і приблизним радіусом$r$. Різання раковини і укладання її плоско утворює прямокутне суцільне тіло з довжиною$2\pi r$, висотою$h$ і глибиною$dx$. Таким чином обсяг є$V \approx 2\pi rh\ dx$; див$\PageIndex{2c}$. Рис. (Ми говоримо «приблизно», оскільки наш радіус був наближенням.)

Розбиваючи тверде тіло на$n$ циліндричні оболонки, ми можемо наблизити обсяг твердого тіла як

$ $ V =\ сума_ {i = 1} ^n 2\ пі r_ih_i\ dx_i,\]

де$r_i$,$h_i$ і$dx_i$ - радіус, висота і товщина$i\,^\text{th}$ раковини відповідно.

Це сума Рімана. Прийняття межі, коли товщина оболонок наближається до 0, призводить до певного інтегралу.

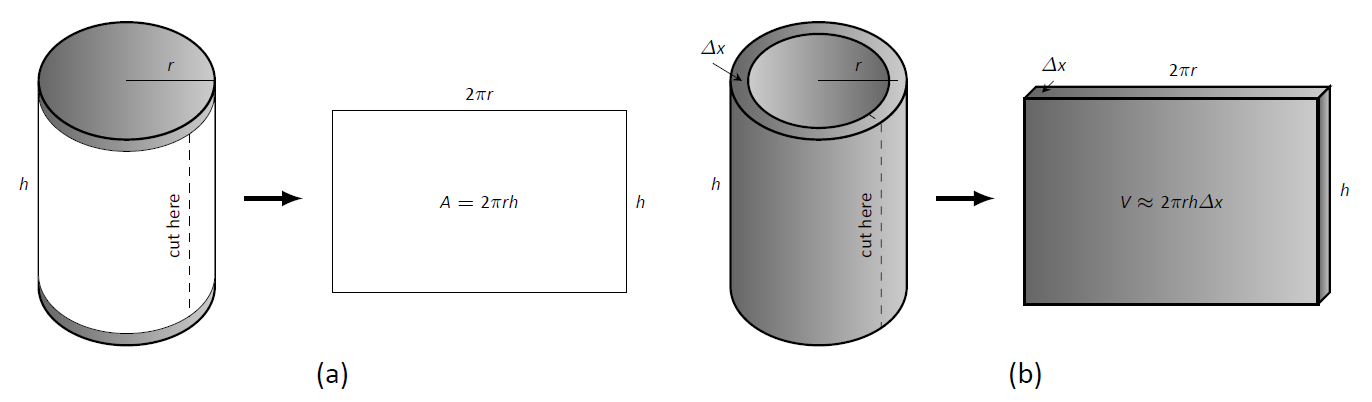
$7.3.2.png$

Рисунок$\PageIndex{2}$: Визначення обсягу тонкої циліндричної оболонки.} \ label {рис.: супкан}

Ключова ідея 25: Метод оболонки

Нехай тверде тіло утворюється шляхом обертання області$R$, обмеженої$x=a$ і$x=b$, навколо вертикальної осі. $r(x)$Дозволяти представляти відстань від осі обертання до$x$ (тобто радіус оболонки зразка) і нехай$h(x)$ представляють висоту твердого тіла на$x$ (тобто висоту оболонки). Обсяг твердого тіла дорівнює

\[V = 2\pi\int_a^b r(x)h(x)\ dx.\]

Особливі випадки:

Коли область$R$ обмежена вище$y=f(x)$ і нижче по$y=g(x)$, то$h(x) = f(x)-g(x)$.
Коли віссю обертання є$y$ -вісь (тобто$x=0$) то$r(x) = x$.

Давайте потренуємося, використовуючи метод оболонки.

Приклад$\PageIndex{1}$: Finding volume using the Shell Method

Знайти об'єм твердого тіла, утвореного обертанням області,$y=1/(1+x^2)$ обмеженої$y=0$,$x=0$ і$x=1$ навколо$y$ -осі.

Рішення

Це область, яка використовується для введення методу оболонки на малюнку$\PageIndex{1}$, але знову намальована$\PageIndex{3}$ на малюнку для більш детальної довідки. Лінія проводиться в області, паралельної осі обертання, що представляє оболонку, яка буде вирізана, коли область обертається навколо$y$ -осі. (Це диференціальний елемент.)

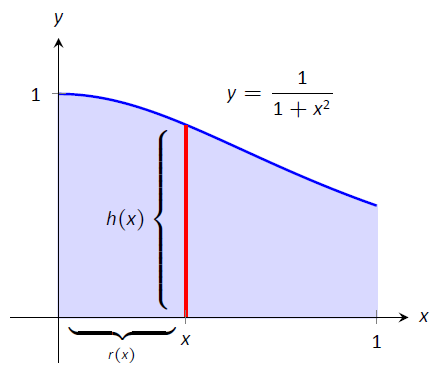
$7.3.3.png$

Малюнок$\PageIndex{3}$: Графік області в прикладі$\PageIndex{1}$.

Відстань ця лінія від осі обертання визначає$r(x)$; оскільки відстань від$x$ до$y$ -осі є$x$, ми маємо$r(x)=x$. Висота цього рядка визначає$h(x)$; верхня частина рядка знаходиться в$y=1/(1+x^2)$, тоді як нижня частина рядка знаходиться в$y=0$. Таким чином$h(x) = 1/(1+x^2)-0 = 1/(1+x^2)$. Область обмежена від$x=0$ до$x=1$, тому обсяг дорівнює

\[V = 2\pi\int_0^1 \dfrac{x}{1+x^2}\ dx.\]

Для цього потрібна заміна. Нехай$u=1+x^2$, так$du = 2x\ dx$. Також міняємо межі:$u(0) = 1$ і$u(1) = 2$. Таким чином, ми маємо:

\[\begin{align*} &= \pi\int_1^2 \dfrac{1}{u}\ du \\[4pt] &= \pi\ln u\Big|_1^2\\[4pt] &= \pi\ln 2 - \pi\ln 1\\[4pt] &= \pi\ln 2 \approx 2.178 \ \text{units}^3.\end{align*}\]

Примітка: для того, щоб знайти цей том за допомогою методу диска, потрібно було б два інтеграли для обліку регіонів вище і нижче$y=1/2$.

За допомогою методу оболонки нічого особливого не потрібно враховувати, щоб обчислити об'єм твердого тіла, який має отвір посередині, як показано далі.

Приклад$\PageIndex{2}$: Finding volume using the Shell Method

Знайдіть обсяг твердого тіла, утвореного обертанням трикутної області, визначеної точками$(0,1)$,$(1,1)$ і$(1,3)$ близько лінії$x=3$.

Рішення

Область намальована на малюнку$\PageIndex{4a}$ разом з диференціальним елементом, лінією в межах області, паралельною осі обертання. У частині (b) фігури ми бачимо оболонку, промальовану диференціальним елементом, а в частині (c) показано все тверде тіло.

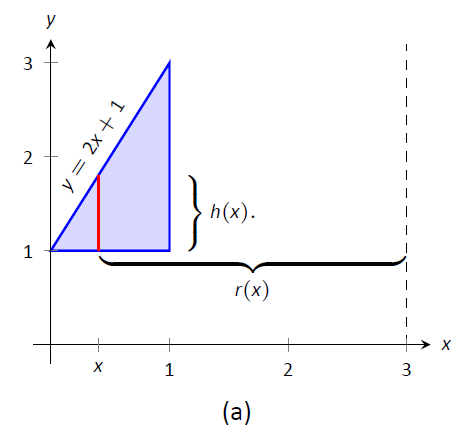
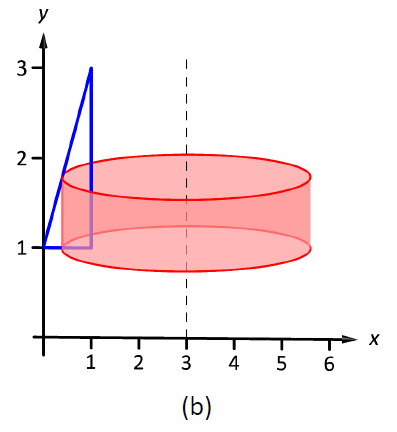
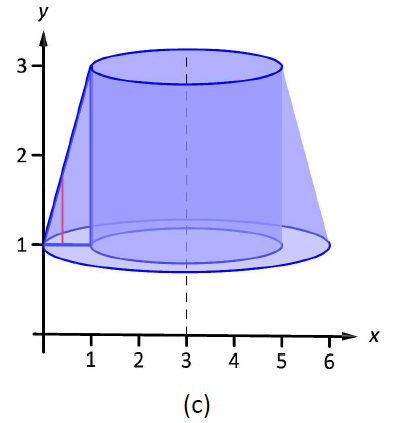
$7.3.4a.png$ $7.3.4 б.пнг$ $7.3.4 к.пнг$

Малюнок$\PageIndex{4}$: Графік області в прикладі$\PageIndex{2}$

Висота диференціального елемента - це відстань від$y=1$ до$y=2x+1$, лінія, яка з'єднує точки$(0,1)$ і$(1,3)$. Таким чином$h(x) = 2x+1-1 = 2x$. Радіус оболонки, утвореної диференціальним елементом, - це відстань від$x$ до$x=3$; тобто воно є$r(x)=3-x$. $x$Межі регіону,$x=0$ щоб$x=1$, даючи

\[\begin{align*} V &= 2\pi\int_0^1 (3-x)(2x)\ dx \\[4pt] &= 2\pi\int_0^1 \big(6x-2x^2)\ dx \\[4pt] &= 2\pi\left(3x^2-\dfrac23x^3\right)\Big|_0^1\\[4pt] &= \dfrac{14}{3}\pi\approx 14.66 \ \text{units}^3.\end{align*}\]

При обертанні області навколо горизонтальної осі ми повинні враховувати функції радіуса та висоти з точки зору$y$, а не$x$.

Приклад$\PageIndex{3}$: Finding volume using the Shell Method

Знайти об'єм твердого тіла, утвореного обертанням області, наведеної в прикладі$\PageIndex{2}$ про$x$ -вісь.

Рішення

Область намальована на малюнку$\PageIndex{5a}$ з зразком диференціального елемента. У частині (b) фігури малюється оболонка, утворена диференціальним елементом, а тверде тіло намальовано в (с). (Зверніть увагу, що трикутна область тут виглядає «короткою і широкою», тоді як в попередньому прикладі ця ж область виглядала «високою і вузькою». Це тому, що межі на графіках різні.)

Висота диференціального елемента - a$x$ -відстань, між$x=\dfrac12y-\dfrac12$ і$x=1$. Таким$h(y) = 1-(\dfrac12y-\dfrac12) = -\dfrac12y+\dfrac32.$ чином Радіус - це відстань від$y$ до$x$ -осі, так$r(y) =y$. Межами$y$ області є$y=1$ і$y=3$, що ведуть до інтегральної

\[\begin{align*}V &= 2\pi\int_1^3\left[y\left(-\dfrac12y+\dfrac32\right)\right]\ dy \\[4pt]&= 2\pi\int_1^3\left[-\dfrac12y^2+\dfrac32y\right]\ dy \\[4pt] &= 2\pi\left[-\dfrac16y^3+\dfrac34y^2\right]\Big|_1^3 \\[4pt] &= 2\pi\left[\dfrac94-\dfrac7{12}\right]\\[4pt] &= \dfrac{10}{3}\pi \approx 10.472\ \text{units}^3.\end{align*}\]

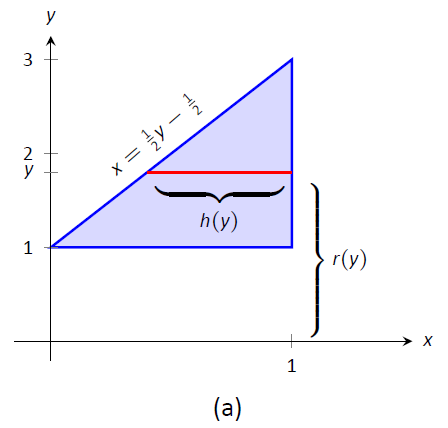
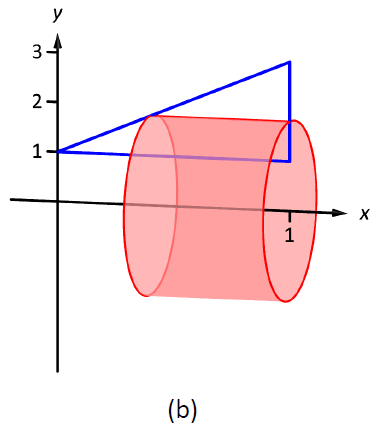
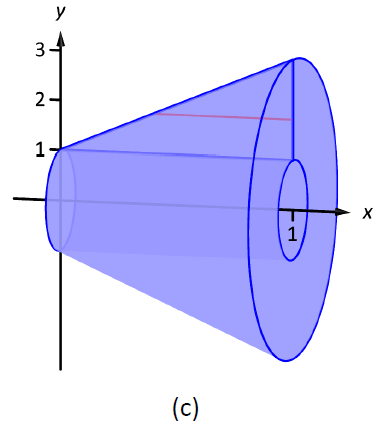
$7.3.5a.png$ $7.3.5 б.пнг$ $7.3.5 к.пнг$

Малюнок$\PageIndex{5}$: Графік області в прикладі$\PageIndex{3}$

На початку цього розділу було заявлено, що «добре мати варіанти». Наступний приклад досить легко знаходить обсяг твердого тіла за допомогою методу оболонки, але використання методу шайби було б досить важкою справою.

Приклад$\PageIndex{4}$: Finding volume using the Shell Method

Знайдіть об'єм твердого тіла, утвореного обертанням області, обмеженої$y= \sin x$ та$x$ -віссю від$x=0$ до$x=\pi$ приблизно$y$ -осі.

Рішення

Область і диференціальний елемент, оболонка, утворена цим диференціальним елементом, і отримане тверде тіло наведені на рис$\PageIndex{6}$.

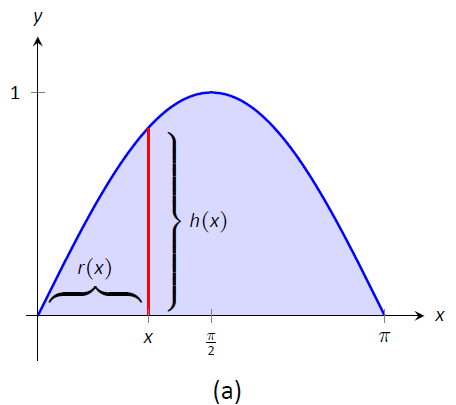
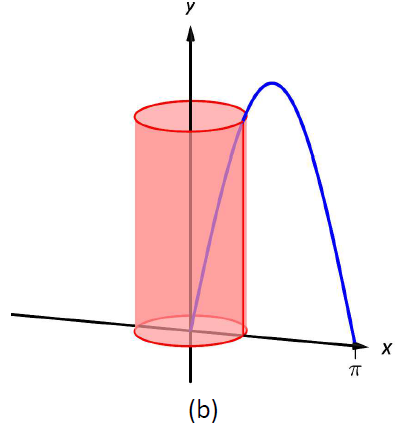
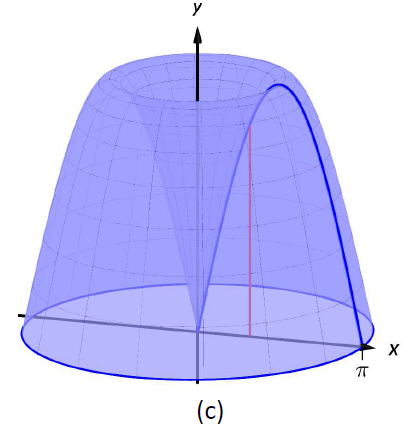
$7.3.6a.png$ $7.3.6 б.пнг$ $7.3.6 к.пнг$

Малюнок$\PageIndex{6}$: Графік області в прикладі$\PageIndex{4}$

Радіус оболонки зразка дорівнює$r(x) = x$; висота оболонки зразка становить$h(x) = \sin x$, кожен від$x=0$ до$x=\pi$. Таким чином, обсяг твердого тіла дорівнює

\[V = 2\pi\int_0^{\pi} x\sin x\ dx.\]

Для цього потрібна інтеграція по частинам. Встановіть$u=x$ і$dv=\sin x\ dx$; ми залишаємо його читачеві, щоб заповнити решту. У нас є:

\ [\ почати {align*} &= 2\ пі\ Великий [-х\ cos x\ Big|_0^ {\ pi} +\ int_0^ {\ pi}\ cos x\ dx\ Big]\\ [4pt]
&= 2\ pi\ Big [\ pi +\ sin x\ Big|_0^ {\ pi}\\ Big]\\ [4pt]
&= 2\ pi\\ Великий [\ pi + 0\ Великий]\\ [4pt]
&= 2\ pi ^ 2\ приблизно 19,74\\ текст {одиниці} ^3. \ end {вирівнювати*}\]

Зверніть увагу, що для того, щоб використовувати метод шайби, нам потрібно буде вирішити$y=\sin x$ для$x$, що вимагає використання функції arcsine. Ми залишаємо це читачеві, щоб переконатися, що функція зовнішнього радіуса є,$R(y) = \pi-\arcsin y$ а функція внутрішнього радіуса є$r(y)=\arcsin y$. Таким чином, обсяг можна обчислити як

$$\ pi\ int_0^1\ Великий [(\ pi-\ arcsin y) ^2- (\ arcsin y) ^2\ Big]\ dy.\]

Цей інтеграл не страшний, враховуючи, що$\arcsin^2 y$ терміни скасовують, але він є більш обтяжливим, ніж інтеграл, створений методом оболонки.

Ми закінчуємо цей розділ таблицею, яка підсумовує використання методів шайби та оболонки.

Ключова ідея 26: Короткий зміст методів шайби та оболонки

Нехай область$R$ задається з$x$ -bounds$x=a$ і$x=b$ і$y$ -bounds$y=c$ і$y=d$.

\[\begin{align*} & \text{Washer Method} & & \text{Shell Method} \\[4pt] \text{Horizontal Axis} \quad & \pi\int_a^b \big(R(x)^2-r(x)^2\big)\ dx & & 2\pi\int_c^d r(y)h(y)\ dy \\[4pt] \\[4pt] \text{Vertical Axis} \quad & \pi \int_c^d\big(R(y)^2-r(y)^2\big)\ dy & & 2\pi\int_a^b r(x)h(x)\ dx \end{align*}\]

Як і в попередньому розділі, реальна мета цього розділу - не мати можливості обчислювати обсяги певних твердих тіл. Швидше за все, це мати можливість вирішити проблему, спочатку наближаючись, а потім використовуючи межі для уточнення наближення, щоб дати точне значення. У цьому розділі ми наближаємо обсяг твердого тіла, розрізавши його на тонкі циліндричні оболонки. Підсумовуючи обсяги кожної оболонки, отримуємо наближення обсягу. Приймаючи межу, оскільки кількість однаково розташованих оболонок переходить до нескінченності, наше підсумовування можна оцінити як певний інтеграл, даючи точне значення.

Цей же принцип ми знову використовуємо в наступному розділі, де знаходимо довжину кривих в площині.