3.4: Увігнутість і друга похідна

Last updated
Save as PDF

Page ID: 60703

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Продовжується наше вивчення «приємних» функцій. Попередній розділ показав, як перша похідна функції$f'$, може передавати важливу інформацію про$f$. Ми тепер застосуємо цю ж техніку до$f'$ себе, і дізнаємося, про що це говорить нам$f$. Ключ до вивчення$f'$ полягає в розгляді його похідної, а саме$f''$, яка є другою похідною від$f$. Коли$f''>0$,$f'$ збільшується. Коли$f''<0$,$f'$ зменшується. $f'$має відносні максимуми та мінімуми, де$f''=0$ або не визначено. Цей розділ досліджує, як знання інформації про$f''$ дає інформацію про$f$.

Увігнутість

Починаємо з визначення, потім досліджуємо його значення.

Визначення увігнуті вгору і увігнуті вниз

$f$Дозволяти диференціюватися на проміжку$I$. Графік$f$ увігнутий вгору,$I$ якщо$f'$ збільшується. Графік$f$ увігнутий вниз,$I$ якщо$f'$ зменшується. Якщо$f'$ постійний, то граф,$f$ як кажуть, не має увігнутості.

Примітка: Ми часто заявляємо,$f$ що "увігнутий вгору» замість «граф$f$ увігнутий вгору» для простоти.

Графік функції$f$ увігнутий вгору при$f'$ збільшенні. Це означає, що коли хтось дивиться на увігнутий вгору графік зліва направо, нахили дотичних ліній будуть збільшуватися. Розглянемо малюнок$\PageIndex{1}$, де увігнутий вгору графік показаний разом з деякими дотичними лініями. Зверніть увагу, як дотична лінія зліва крута, вниз, що відповідає невеликому значенню$f'$. Праворуч дотична лінія крута, вгору, що відповідає великому значенню$f'$.

$альт$

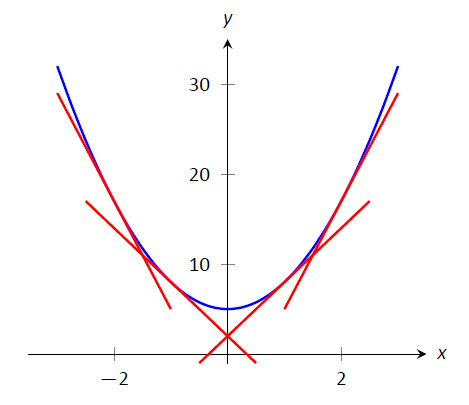
Малюнок$\PageIndex{1}$: Функція$f$ з увігнутим вгору графіком. Зверніть увагу, як нахили дотичних ліній, дивлячись зліва направо, збільшуються.

Якщо функція зменшується і увігнута вгору, то її швидкість зниження сповільнюється; це «вирівнювання». Якщо функція збільшується і увігнута вгору, то швидкість збільшення збільшується. Функція збільшується з більш швидкою і швидкою швидкістю.

Тепер розглянемо функцію, яка увігнута вниз. Ми по суті повторюємо наведені вище пункти з невеликою варіацією.

Графік функції$f$ увігнутий вниз, коли$f'$ зменшується. Це означає, що коли хтось дивиться на увігнутий вниз графік зліва направо, нахили дотичних ліній будуть зменшуватися. Розглянемо малюнок$\PageIndex{2}$, де увігнутий вниз графік показаний разом з деякими дотичними лініями. Зверніть увагу, як дотична лінія зліва крута, вгору, що відповідає великому значенню$f'$. Праворуч дотична лінія крута, вниз, що відповідає невеликому значенню$f'$.

$альт$

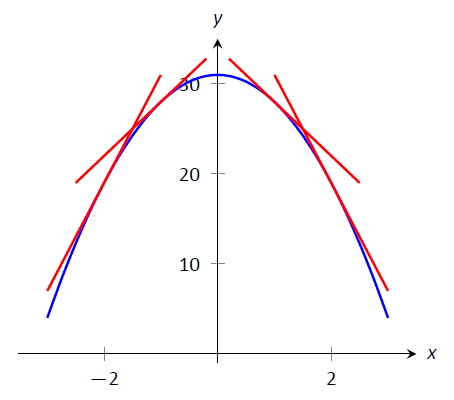
Малюнок$\PageIndex{2}$: Функція$f$ з увігнутим вниз графіком. Зверніть увагу, як нахили дотичних ліній, дивлячись зліва направо, зменшуються.

Якщо функція збільшується і увігнута вниз, то її швидкість збільшення сповільнюється; це «вирівнювання». Якщо функція зменшується і увігнута вниз, то швидкість зменшення зменшується. Функція зменшується з більш швидкою і швидкою швидкістю.

Примітка: Мнемоніка для запам'ятовування того, що означає увігнута вгору/вниз: «Увігнута вгору - це як чашка; увігнутий вниз - як хмурий». Це, правда, жахливо, але працює.

Наше визначення увігнутого вгору і увігнутого вниз дається в терміні, коли перша похідна збільшується або зменшується. Ми можемо застосувати результати попереднього розділу та знайти інтервали, на яких графік увігнутий вгору або вниз. Тобто ми визнаємо, що$f'$ збільшується$f''>0$, коли і т.д.

Теорема$\PageIndex{1}$: Test for Concavity

$f$Дозволяти бути двічі диференційовані на проміжку$I$. Графік$f$ увігнутий вгору, якщо$f''>0$ увімкнено$I$, і увігнутий вниз, якщо$f''<0$ увімкнено$I$.

$альт$

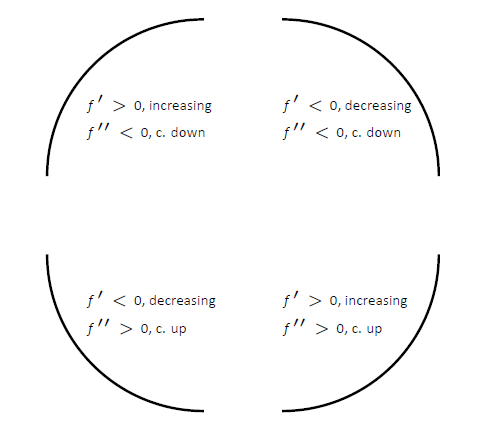
Малюнок$\PageIndex{3}$: Демонстрація 4 способів взаємодії увігнутості зі збільшенням/зменшенням разом із взаємозв'язками з першою та другою похідними.

Примітка: Геометрично кажучи, функція увігнута вгору, якщо її графік лежить над дотичними лініями. Функція увігнута вниз, якщо її графік лежить нижче дотичних ліній.

Якщо важливо знати, де граф увігнутий вгору/вниз, має сенс, що місця, де графік змінюється від одного до іншого, також важливі. Це призводить нас до визначення.

Визначення: Точка перегину

Точка перегину - це точка на графіку,$f$ в якій$f$ змінюється увігнутість.

На малюнку$\PageIndex{4}$ показаний графік функції з позначеними точками перегину.

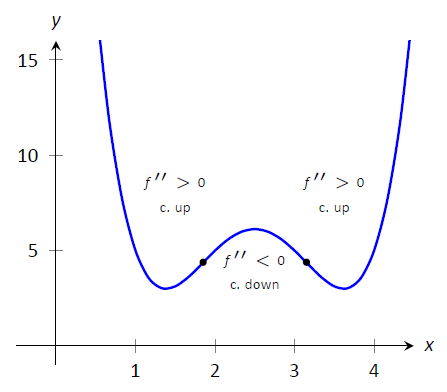
$функцією для цього зображення є x^5-3x^3+2x+1$

Малюнок$\PageIndex{4}$: Графік функції з позначеними точками її перегину. Також вказуються інтервали, де увігнуті вгору/вниз.

Якщо увігнутість$f$ змінюється в точці$(c,f(c))$,$f'$ то змінюється від збільшення до зменшення (або, зменшуючи до збільшення) при$x=c$. Це означає, що ознака$f''$ змінюється від позитивного до негативного (або, негативного на позитивний) при$x=c$. Це призводить до наступної теореми.

Теорема$\PageIndex{2}$: Points of Inflection

Якщо$(c,f(c))$ є точкою перегину на графіку$f$, то або$f''=0$ або не$f''$ визначається в$c$.

Ми виділили поняття увігнутості і точок перегину. Зараз настав час практикувати використання цих понять; враховуючи функцію, ми повинні мати можливість знайти її точки перегину та визначити інтервали, на яких вона увігнута вгору або вниз. Ми робимо це в наступних прикладах.

Приклад$\PageIndex{1}$: Finding intervals of concave up/down, inflection points

Нехай$f(x)=x^3-3x+1$. Знайдіть точки перегину$f$ і проміжки, на яких вона увігнута вгору/вниз.

Рішення

Починаємо з пошуку$f'(x)=3x^2-3$ і$f''(x)=6x$. Щоб знайти точки перегину, скористаємося теоремою$\PageIndex{2}$ і знаходимо де$f''(x)=0$ або де$f''$ невизначено. Ми знаходимо$f''$ завжди визначено, і дорівнює 0 тільки тоді, коли$x=0$. Так що точка$(0,1)$ є єдино можливою точкою перегину.

Ця можлива точка перегину ділить дійсну пряму на два інтервали,$(-\infty,0)$ і$(0,\infty)$. Ми використовуємо процес, подібний до того, який використовувався в попередньому розділі, щоб визначити збільшення/зменшення. Виберіть будь-який$c<0$;$f''(c)<0$$f$ так увігнутий вниз на$(-\infty,0)$. Виберіть будь-який$c>0$;$f''(c)>0$$f$ так увігнуті вгору на$(0,\infty)$. Оскільки увігнутість змінюється на$x=0$, точка$(0,1)$ є точкою перегину.

$альт$

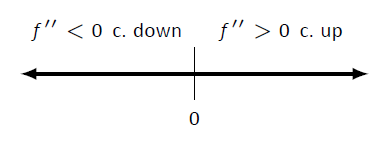
Малюнок$\PageIndex{5}$: Числовий рядок, що визначає увігнутість$f$ у прикладі$\PageIndex{1}$.

Числовий рядок на малюнку$\PageIndex{5}$ ілюструє процес визначення увігнутості; на малюнку$\PageIndex{6}$ показаний графік$f$ і$f''$, підтверджуючи наші результати. Зверніть увагу$f$, як увігнутий вниз точно, коли$f''(x)<0$ і увігнуті вгору, коли$f''(x)>0$.

$альт$

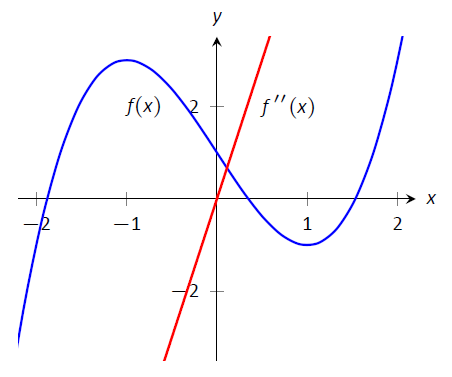
Малюнок$\PageIndex{6}$: Графік$f(x)$ використаного в прикладі$\PageIndex{1}$

Приклад$\PageIndex{2}$: Finding intervals of concave up/down, inflection points

Нехай$f(x)=x/(x^2-1)$. Знайдіть точки перегину$f$ і проміжки, на яких вона увігнута вгору/вниз.

Рішення

Нам потрібно знайти$f'$ і$f''$. Використовуючи правило частки і спрощуючи, знаходимо

\[f'(x)=\frac{-(1+x^2)}{(x^2-1)^2} \quad \text{and}\quad f''(x) = \frac{2x(x^2+3)}{(x^2-1)^3}.\]

Щоб знайти можливі точки перегину, ми прагнемо знайти, де$f''(x)=0$ і де$f''$ не визначено. Рішення$f''x)=0$ зводиться до розв'язання$2x(x^2+3)=0$; знаходимо$x=0$. Ми знаходимо,$f''$ що не визначено$x=\pm 1$, коли, бо тоді знаменник$f''$ дорівнює 0. Відзначимо також, що$f$ сам по собі не визначається при$x=\pm1$, маючи домен$(-\infty,-1)\cup(-1,1)\cup(1,\infty)$. Оскільки область об'єднання трьох інтервалів, має сенс, що увігнутість$f$ може перемикатися через інтервали.$f$ Технічно ми не можемо сказати, що$f$ має точку перегину,$x=\pm1$ оскільки вони не є частиною домену, але ми все одно повинні вважати ці$x$ -значення важливими і буде включати їх у наш номер рядка.

Важливими$x$ -значеннями, при яких увігнутість може перемикатися$x=-1$, є$x=0$ і$x=1$, які розділяють числовий рядок на чотири інтервали, як показано на малюнку$\PageIndex{7}$. Визначаємо увігнутість на кожній. Майте на увазі, що все, що нас турбує, - це знак$f''$ на інтервалі.

Інтервал 1,$(-\infty,-1)$: Виберіть число$c$ в цьому інтервалі з великою величиною (наприклад,$c=-100$). Знаменник$f''(x)$ буде позитивним. У чисельнику$(c^2+3)$ буде позитивним, а$2c$ термін - негативним. При цьому чисельник негативний і$f''(c)$ негативний. $f$Робимо висновок увігнутим вниз$(-\infty,-1)$.

Інтервал 2,$(-1,0)$: Для будь-якого числа$c$ в цьому інтервалі термін$2c$ в чисельнику буде від'ємним, термін$(c^2+3)$ в чисельнику - додатним, а термін$(c^2-1)^3$ в знаменнику - від'ємним. Таким чином$f''(c)>0$ і$f$ увігнутий вгору на цьому проміжку.

Інтервал 3,$(0,1)$: Будь-яке число$c$ в цьому інтервалі буде позитивним і «малим». Таким чином, чисельник є додатним, а знаменник негативний. Таким чином$f''(c)<0$ і$f$ увігнутий вниз на цьому проміжку.

Інтервал 4$(1,\infty)$: Виберіть велике значення для$c$. Очевидно$f''(c)>0$, що, тому ми робимо висновок,$f$ що увігнутий вгору$(1,\infty)$.

$альт$

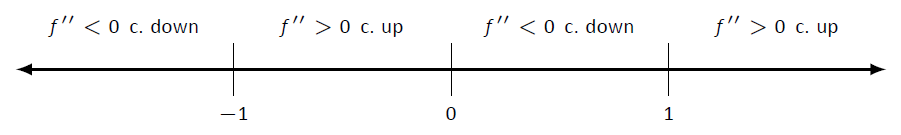
Малюнок$\PageIndex{7}$: Номер рядка для$f$ у прикладі$\PageIndex{2}$

Ми робимо висновок,$f$ що увігнута вгору$(-1,0)\cup(1,\infty)$ і увігнута вниз$(-\infty,-1)\cup(0,1)$. Існує тільки одна точка перегину$(0,0)$, як$f$ не визначено в$x=\pm 1$. Наша робота підтверджена графіком$f$ на рис$\PageIndex{8}$. Зверніть увагу$f$, як увігнутий вгору,$f''$ коли позитивний, і увігнутий вниз, коли$f''$ негативний.

$альт$

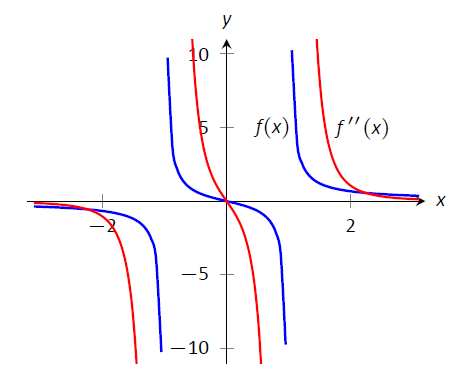
Малюнок$\PageIndex{8}$: Графік$f(x)$ і$f''(x)$ в прикладі$\PageIndex{2}$

Нагадаємо, що$f$ відносні максимуми і мінімуми знаходять в критичних точках$f$; тобто вони знаходять, коли$f'(x)=0$ або коли$f'$ не визначено. Так само відносні максимуми та мінімуми$f'$ знаходять, коли$f''(x)=0$ або$f''$ коли не визначено; зверніть увагу, що це точки перегину$f$.

Що означає «відносний максимум$f'$»? Похідна вимірює швидкість зміни$f$; максимізація$f'$ означає знаходження місця, де$f$ збільшується найбільше - де$f$ має найкрутішу дотичну лінію. Аналогічний оператор може бути зроблений для мінімізації$f'$; він відповідає де$f$ має найкрутішу негативно-похилу дотичну лінію.

Ми використовуємо цю концепцію в наступному прикладі.

Приклад$\PageIndex{3}$: Understanding inflection points

Продажі певного товару протягом трирічного проміжку моделюються$S(t)= t^4-8t^2+20$, де$t$ знаходиться час в роках, показаний на малюнку$\PageIndex{9}$. Протягом перших двох років продажі знижуються. Знайдіть точку, в якій продажі знижуються найбільшими темпами.

$альт$

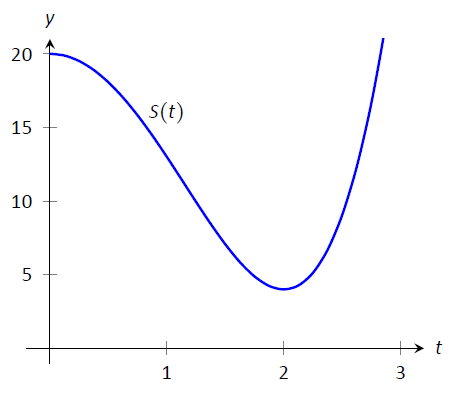
Малюнок$\PageIndex{9}$: Графік$S(t)$ в прикладі$\PageIndex{3}$, моделювання продажу товару з плином часу.

Ми хочемо максимізувати темп зниження, тобто ми хочемо знайти там, де$S'$ є мінімум. Для цього знаходимо$S''$ де 0. Знаходимо$S'(t)=4t^3-16t$ і$S''(t)=12t^2-16$. Встановлюючи$S''(t)=0$ і вирішуючи, отримуємо$t=\sqrt{4/3}\approx 1.16$ (ми ігноруємо негативне значення,$t$ так як воно не лежить в області нашої функції$S$).

Це і точка перегину, і точка максимального зменшення. Це момент, коли речі спочатку починають шукати компанію. Після точки перегину все ще знадобиться деякий час, перш ніж продажі почнуть збільшуватися, але принаймні продажі не зменшуються так швидко, як це було.

Графік$S(t)$ і$S'(t)$ наведено на рис$\PageIndex{10}$. Коли$S'(t)<0$, продажі знижуються; зверніть увагу, як при$t\approx 1.16$,$S'(t)$ зводиться до мінімуму. Тобто продажі знижуються найшвидшими темпами на$t\approx 1.16$. На проміжку$(1.16,2)$,$S$ зменшується, але увігнута вгору, тому зниження продажів «нівелюється».

$альт$

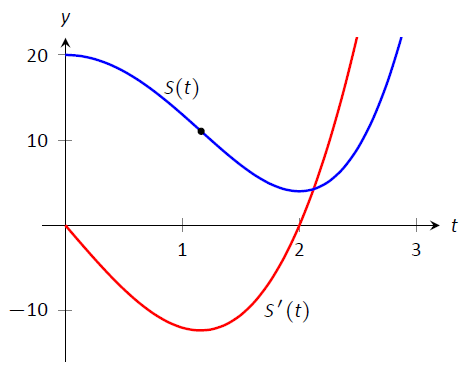
Малюнок$\PageIndex{10}$: Графік$S(t)$ у прикладі$\PageIndex{3}$ разом з$S'(t)$.

Не кожна критична точка відповідає відносній крайності;$f(x)=x^3$ має критичну точку,$(0,0)$ але не має відносного максимуму або мінімуму. Так само, тільки тому, що$f''(x)=0$ ми не можемо зробити висновок про зміни увігнутості в цей момент. Ми були обережні, перш ніж використовувати термінологію "можлива точка перегину», оскільки нам потрібно було перевірити, чи змінилася увігнутість. Канонічним прикладом зміни$f''(x)=0$ без увігнутості є$f(x)=x^4$. При$x=0$,$f''(x)=0$ але$f$ завжди увігнута вгору, як показано на малюнку$\PageIndex{11}$.

$альт$

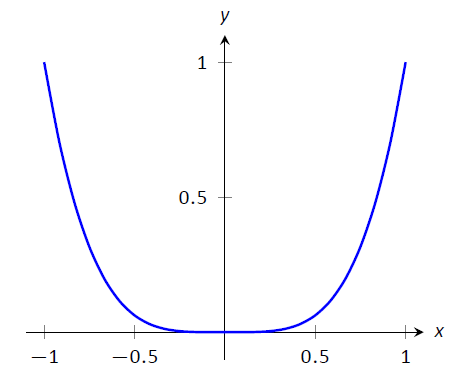
Малюнок$\PageIndex{11}$: Графік$f(x) = x^4$. $f$Ясно завжди увігнуті вгору, незважаючи на те, що$f''(x) = 0$ коли$x=0$. Саме в даному прикладі можлива точка перегину не$(0,0)$ є точкою перегину.

Примітка: Примітка про увігнутість:

Взагалі увігнутість може змінюватися тільки там, де або друга похідна дорівнює 0, де є вертикальна асимптота, або (рідко на практиці), де друга похідна невизначена. Але увігнутість не\ emph {have} для зміни в цих місцях. Наприклад, якщо$f(x)=x^4$, то$f''(0)=0$, але немає зміни увігнутості при 0, а також немає точки перегину там. Причому якщо$f(x)=1/x^2$, то$f$ має вертикальну асимптоту на 0, але зміни увігнутості при 0 немає.

Другий похідний тест

Перша похідна функції дала нам тест, щоб знайти, чи відповідає критичне значення відносному максимуму, мінімуму чи ні. Друга похідна дає нам ще один спосіб перевірити, чи є критична точка локальним максимумом або мінімумом. Наступна теорема офіційно стверджує щось інтуїтивне: якщо критичне значення виникає в області, де функція увігнута вгору, то$f$ це критичне значення повинно відповідати відносному мінімуму$f$ тощо Див. Рисунок$\PageIndex{12}$ для візуалізації цього.

$альт$

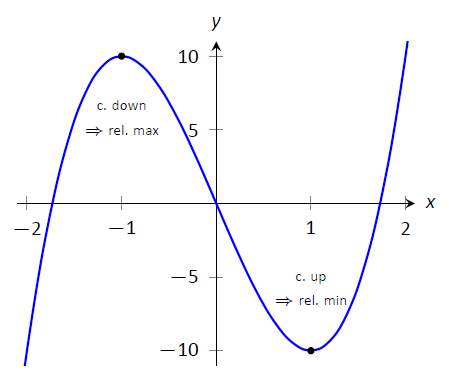
Малюнок$\PageIndex{12}$: Демонстрація того факту, що відносні максимуми виникають, коли граф увігнутий вниз і відносні мінімуми виникають, коли граф увігнутий вгору.

Теорема$\PageIndex{3}$: The Second Derivative Test

$c$Дозволяти критичне значення$f$ де$f''(c)$ визначено.

Якщо$f''(c)>0$, то$f$ має локальний мінімум при$(c,f(c))$.
Якщо$f''(c)<0$, то$f$ має локальний максимум при$(c,f(c))$.

Другий тест похідних відноситься до першого тесту похідних наступним чином. Якщо$f''(c)>0$, то граф увігнутий вгору в критичній точці$c$ і$f'$ сам зростає. Так як$f'(c)=0$ і$f'$ зростає на$c$, то він повинен перейти від негативного до позитивного при$c$. Це означає, що функція переходить від зменшення до збільшення, вказуючи локальний мінімум при$c$.

Приклад$\PageIndex{4}$: Using the Second Derivative Test

Нехай$f(x)=100/x + x$. Знайдіть критичні точки$f$ і використовуйте Другий тест похідних, щоб позначити їх як відносні максимуми або мінімуми.

Рішення

Ми знаходимо$f'(x)=-100/x^2+1$ і$f''(x) = 200/x^3.$ встановлюємо$f'(x)=0$ і вирішуємо$x$ для пошуку критичних значень (зверніть увагу, що f'\ не визначено в$x=0$, але ні$f$ так це не є критичним значенням.) Знаходимо критичні значення є$x=\pm 10$. Оцінюючи$f''$ при$x=10$ дає$0.1>0$, тому є локальний мінімум при$x=10$. Оцінюючи$f''(-10)=-0.1<0$, визначаючи відносний максимум при$x=-10$. Ці результати підтверджені на рис$\PageIndex{13}$.

$альт$

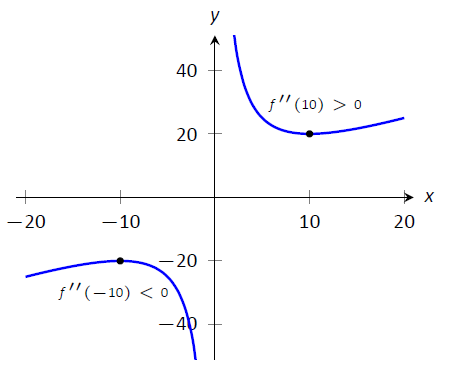
Малюнок$\PageIndex{13}$: Графік$f(x)$ у прикладі$\PageIndex{4}$. Друга похідна оцінюється в кожній критичній точці. Коли графік увігнутий вгору, критична точка являє собою локальний мінімум; коли графік увігнутий вниз, критична точка являє собою локальний максимум.

Ми вивчали, як перша та друга похідні функції пов'язують інформацію про графік цієї функції. Ми знайшли інтервали збільшення і зменшення, інтервали, де граф увігнутий вгору і вниз, а також місця відносних екстрем і точок перегину. У главі 1 ми побачили, як межі пояснювали асимптотичну поведінку. У наступному розділі ми об'єднаємо всю цю інформацію для отримання точних ескізів функцій.