3.3: Збільшення та зменшення функцій

Last updated
Save as PDF

Page ID: 60704

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Наше вивчення «приємних» функцій$f$ у цьому розділі досі зосереджено на окремих точках: точках, де$f$ максимальна/мінімальна, точок, де$f'(x) = 0$ або$f'$ не існує, і точок,$c$ де$f'(c)$ середня швидкість зміни$f$ на якомусь інтервалі.

У цьому розділі ми починаємо вивчати, як поводяться функції між спеціальними точками; починаємо більш детально вивчати форму їх графіків.

Почнемо з інтуїтивної концепції. Враховуючи графік на малюнку$\PageIndex{1}$, де б ви сказали, що функція збільшується? Зниження?

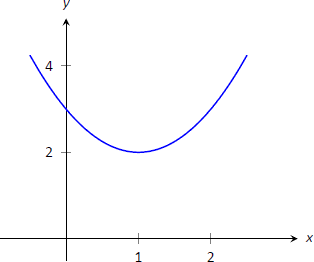
$imageedit_45_5770400714.png$

Рисунок$\PageIndex{1}$: Графік функції, що$f$ використовується для ілюстрації понять збільшення та зменшення.

Незважаючи на те, що ми не визначили ці терміни математично, один, ймовірно, відповів, що$f$ збільшується, коли$x>1$ і зменшується, коли$x<1$. Ми формально визначаємо ці терміни тут.

Визначення: Збільшення та зменшення функцій

$f$Дозволяти функція, визначена на інтервалі$I$. \ index {функція збільшення}\ index {функція зменшення}\ index {зростаюча функція! строго}\ index {спадна функція! строго}

$f$збільшується,$I$ якщо для кожного$a<b$ в$I$,$f(a) \leq f(b)$.
$f$зменшується,$I$ якщо для кожного$a<b$ в$I$,$f(a) \geq f(b)$.

Функція суворо збільшується, коли$a<b$ в$I$ має на увазі$f(a) < f(b)$, з подібним визначенням, що тримає на увазі суворо зменшення.

Неофіційно функція збільшується, якщо$x$ стає більшою (тобто, дивлячись зліва направо)$f(x)$ стає більшою.

Наш інтерес полягає в пошуку інтервалів, в області яких або$f$ збільшується, або зменшується.$f$ Така інформація повинна здатися корисною. Наприклад, якщо$f$ описує швидкість об'єкта, ми можемо знати, коли швидкість збільшувалася або зменшувалася (тобто коли об'єкт прискорювався проти уповільнення). Якщо$f$ описується населення міста, ми повинні бути зацікавлені в тому, коли чисельність населення зростає або скорочується.

Щоб знайти такі інтервали, знову розглянемо січні лінії. $f$Дозволяти бути зростаюча, диференційовна функція на відкритому інтервалі$I$, наприклад, показана на малюнку$\PageIndex{2}$, і нехай$a<b$ буде дано в$I$. Проводиться січна лінія на графіку$f$ від$x=a$ до$x=b$; вона має нахил$(f(b)-f(a))/(b-a)$. Але зверніть увагу:

\[\dfrac{f(b)-f(a)}{b-a} \Rightarrow \dfrac{\text{numerator }>0}{\text{denominator } >0} \Rightarrow \text{slope of the secent line} >0 \Rightarrow \text{Average rate of chjange of $f$ on $[a,b]$ is $>0$.} \]

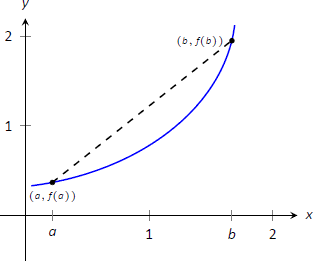
$imageedit_41_5771764490.png$

Малюнок$\PageIndex{2}$: Вивчення січної лінії зростаючої функції.

Ми математично показали, що вже могло бути очевидним: коли$f$ збільшується, його січні лінії матимуть позитивний нахил. Тепер нагадаємо Теорема про середнє значення гарантує, що існує число$c$, де$a<c<b$, таке що

\[f'(c) = \frac{f(b)-f(a)}{b-a}>0.\]

Розглядаючи всі такі січні лінії в$I$, ми настійно маємо на увазі, що$f'(x) \geq 0$ далі$I$. Аналогічне твердження можна зробити і для спадних функцій.

Нашу вище логіку можна підсумувати як «Якщо$f$ збільшується, то,$f'$ ймовірно, позитивна». Теорема$\PageIndex{1}$ нижче повертає це, заявляючи: «Якщо$f'$ позитивний,$f$ то збільшується». Це призводить нас до методу знаходження, коли функції збільшуються і зменшуються.

Теорема$\PageIndex{1}$: Test For Increasing/Decreasing Functions

$f$Дозволяти бути безперервна функція на$[a,b]$ і диференційована на$(a,b)$.

Якщо$f'(c) > 0$ для всіх$c$ в$(a,b)$,$f$ то збільшується на$[a,b]$.
Якщо$f'(c) <0$ для всіх$c$ в$(a,b)$, то$f$ зменшується на$[a,b]$.
Якщо$f'(c) =0$ для всіх$c$ в$(a,b)$, то$f$ постійний на$[a,b]$.

Примітка: Теорема$\PageIndex{1}$ також має значення, якщо$f'(c) = 0$ для кінцевої кількості значень$c$ in$I$.

Нехай$a$ і$b$ бути в$I$ де$f'(a)>0$ і$f'(b)<0$. З теореми проміжних значень випливає, що$c$ між$a$ і$b$ де має бути деяке значення$f'(c) = 0$. Це призводить нас до наступного методу знаходження інтервалів, на яких функція збільшується або зменшується.

Ключова ідея 3: Пошук інтервалів, на яких$f$ is Increasing or Decreasing

$f$Дозволяти диференційовну функцію на проміжку I. Знайти інтервали, на яких$f$ відбувається збільшення і зменшення:

Знайдіть критичні значення$f$. Тобто знайти все там,$c$$I$ де$f'(c) = 0$ або$f'$ не визначено.
Використовуйте критичні значення для$I$ поділу на субінтервали.
Виберіть будь-яку точку$p$ в кожному підінтервалі, і знайдіть знак$f'(p)$.
1. Якщо$f'(p)>0$, то$f$ збільшується на цьому субінтервалі.
2. Якщо$f'(p)<0$, то$f$ зменшується на цьому субінтервалі.

Ми демонструємо використання цього процесу в наступному прикладі.

Приклад$\PageIndex{1}$: Finding intervals of increasing/decreasing

Нехай$f(x) = x^3+x^2-x+1$. Знайти інтервали, на яких$f$ відбувається збільшення або зменшення.

Рішення

Використовуючи Key Idea 3, ми спочатку знаходимо критичні значення$f$. У нас є$f'(x) = 3x^2+2x-1 = (3x-1)(x+1)$, так$f'(x) = 0$ коли$x=-1$ і коли$x=1/3$. $f'$ніколи не є невизначеною.

Оскільки інтервал для розгляду нам не був вказаний, розглянемо весь домен$f$ якого є$(-\infty,\infty)$. Таким чином, ми розбиваємо всю реальну лінію на три підінтервали на основі двох критичних значень, які ми щойно знайшли:$(-\infty,-1)$,$(-1,1/3)$ і$(1/3,\infty)$. Це показано на малюнку$\PageIndex{3}$.

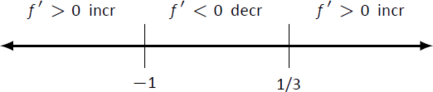
$imageedit_37_7206637863.png$

Малюнок$\PageIndex{3}$: Числовий рядок для$f$ у прикладі$\PageIndex{1}$

Тепер ми вибираємо значення$p$ в кожному підінтервалі і знаходимо знак$f'(p)$. Все, що нас хвилює, - це знак, тому нам насправді не потрібно повністю обчислювати$f'(p)$; вибрати «приємні» значення, які роблять це простим.

Субаінтервал 1,$(-\infty,-1)$: Ми (довільно) вибираємо$p=-2$. Ми можемо обчислити$f'(-2)$ безпосередньо:$f'(-2) = 3(-2)^2+2(-2)-1=7>0$. Робимо висновок,$f$ що збільшується на$(-\infty,-1)$.

Зверніть увагу, що ми можемо прийти до такого ж висновку без обчислень. Наприклад, ми могли б вибрати$p=-100$. Перший термін в$f'(-100)$,$3(-100)^2$ тобто явно позитивний і дуже великий. Інші терміни невеликі в порівнянні, тому ми знаємо$f'(-100)>0$. Все, що нам потрібно, це знак.

Subinterval 2,$(-1,1/3)$: Ми вибираємо,$p=0$ оскільки це значення здається легко мати справу. $f'(0) = -1<0$. Робимо висновок$f$, що зменшується далі$(-1,1/3)$.

Subinterval 3,$(1/3,\infty)$: Виберіть довільно велике значення для$p>1/3$ і зверніть увагу, що$f'(p) =3p^2+2p-1 >0$. Робимо висновок,$f$ що збільшується на$(1/3,\infty)$.

Ми можемо перевірити наші розрахунки, розглянувши Рисунок$\PageIndex{4}$, де$f$ зображено графіки. Графік також представлений$f'$; зверніть увагу, як$f'>0$ коли$f$ збільшується, а$f'<0$ коли$f$ зменшується.

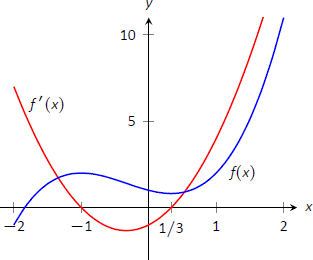
$imageedit_32_8933645687.png$

Малюнок$\PageIndex{4}$: Графік$f(x)$ у прикладі$\PageIndex{1}$, що показує, де$f$ відбувається збільшення і зменшення.

Один виправданий, задаючись питанням, чому так багато роботи робиться, коли графік, здається, робить інтервали дуже чіткими. Наведемо три причини, за якими вищевказана робота стоїть.

По-перше, точки, в яких$f$ переходить від збільшення до зменшення, точно не відомі з урахуванням графіка. Графік показує нам щось значне, що відбувається поруч$x=-1$ і$x=0.3$, але ми не можемо точно визначити, звідки з графіка.

Можна стверджувати, що просто пошук критичних значень є важливим; як тільки ми знаємо, що значні точки є$x=1/3$,$x=-1$ і графік показує зростаючі/зменшуються риси просто добре. Це правда. Однак методика, прописана тут, допомагає посилити взаємозв'язок між збільшенням/зменшенням та ознакою$f'$. Після того, як оволодіння цією концепцією (та кількома іншими) отримано, можна виявити, що або (а) обчислюються лише критичні точки, а графік показує все інше, що бажано, або (б) графік ніколи не виробляється, оскільки визначення збільшення/зменшення використання$f'$ є простим, а графік непотрібний .

Тож наша друга причина, чому вищевказана робота варта, полягає в наступному: як тільки оволодіння предметом буде напрацьовано, у нас є варіанти пошуку потрібної інформації. Ми працюємо над розвитком майстерності.

Нарешті, наша третя причина: багато проблем, з якими ми стикаємося «в реальному світі», дуже складні. Рішення можна проаналізувати лише за допомогою комп'ютерів, щоб зробити багато обчислень для нас. Однак комп'ютери не вирішують проблеми «самостійно»; їх потрібно навчити (тобто запрограмувати) робити правильні речі. Було б вигідно дати функцію комп'ютеру і змусити її повернути максимальне і мінімальне значення, інтервали, на яких функція збільшується і зменшується, розташування відносних максимумів тощо Робота, яку ми робимо тут, легко програмується. Важко навчити комп'ютер «дивитися на графік і бачити, чи йде він вгору або вниз». Легко навчити комп'ютер «визначити, чи є число більше або менше 0».

У розділі 3.1 ми дізналися визначення відносних максимумів і мінімумів і виявили, що вони відбуваються в критичних точках. Зараз ми дізнаємося, що функції можуть переходити від збільшення до зменшення (і навпаки) у критичних точках. Це нове розуміння збільшення та зменшення створює чудовий метод визначення того, чи відповідає критична точка максимуму, мінімуму чи ні. Уявіть собі функцію, що збільшується до критичної точки в$x=c$, після чого вона зменшується. Швидкий ескіз допомагає підтвердити, що$f(c)$ повинен бути відносним максимумом. Аналогічне твердження можна зробити і для відносних мінімумів. Формалізуємо це поняття в теоремі.

Теорема$\PageIndex{2}$: First Derivative Test

$f$Дозволяти диференціюватися$I$ і нехай$c$ буде критичне число в$I$.

Якщо ознака$f'$ перемикається з позитивного на негативний при$c$, то$f(c)$ є відносним максимумом$f$.
Якщо знак$f'$ перемикається з негативного на позитивний при$c$, то$f(c)$ є відносним мінімумом$f$.
Якщо ознака$f'$ не змінюється при$c$, то не$f(c)$ є відносною крайністю$f$.

Приклад$\PageIndex{2}$: Using the First Derivative Test

Знайдіть інтервали, на яких$f$ збільшується і зменшується, і використовуйте перший тест похідної для визначення відносної крайності$f$, де

\[f(x) = \frac{x^2+3}{x-1}.\]

Рішення

Почнемо з того, що відзначаємо домен$f$:$(-\infty,1)\cup(1,\infty)$. $f$Ключова ідея 3 описує, як знайти інтервали, де збільшується і зменшується, коли область$f$ є інтервалом. Оскільки область$f$ в цьому прикладі - об'єднання двох інтервалів, ми застосовуємо прийоми Key Idea 3 до обох інтервалів області$f$.

Оскільки$f$ не визначено при$x=1$, приростаючий/зменшувальний характер$f$ може перемикатися при цьому значенні. Ми формально не$x=1$ вважаємо критичним значенням$f$, але ми включимо його в наш список критичних значень, які ми знаходимо далі.

Використовуючи правило частки, знаходимо

\[f'(x) = \frac{x^2-2x-3}{(x-1)^2}.\]

Нам потрібно знайти критичні значення$f$; ми хочемо знати, коли$f'(x)=0$ і коли$f'$ не визначено. Останнє є простим: коли знаменник$f'(x)$ дорівнює 0,$f'$ не визначено. Це відбувається коли$x=1$, який ми вже визнали важливою цінністю.

Примітка: Строго кажучи, не$x=1$ є критичним значенням$f$, як$f$ не визначено при$x=1$. Тому ми насправді застосовуємо Key Idea 3 до інтервалів$(-\infty,1)$ і$(1,\infty)$. Ми робимо зауваження$x=1$ на числовому рядку, оскільки ми визнаємо, що поведінка$f$ може змінитися там, оскільки вона там не визначена.

$f'(x)=0$коли чисельник$f'(x)$ дорівнює 0. Це відбувається, коли$x^2-2x-3 = (x-3)(x+1) = 0$; тобто коли$x=-1,3$.

Ми виявили, що$f$ має дві критичні цифри$x=-1,3$, і при цьому може статися$x=1$ щось важливе. Ці три числа ділять дійсний числовий рядок на 4 підінтервали:

\[(-\infty,-1), \quad (-1, 1), \quad (1,3) \quad \text{and} \quad (3,\infty).\]

Виберіть число$p$ з кожного субінтервалу та перевірте знак$f'$ at,$p$ щоб визначити, чи збільшується чи$f$ зменшується на цьому інтервалі. Знову ж таки, ми робимо добре, щоб уникнути складних обчислень; зверніть увагу, що знаменник$f'$ завжди позитивний, тому ми можемо ігнорувати його під час нашої роботи.

Інтервал 1,$(-\infty,-1)$: Вибір дуже маленького числа (тобто від'ємного числа з великою величиною)$p$ повертає$p^2-2p-3$ чисельник$f'$; що буде додатним. $f$Звідси збільшується на$(-\infty,-1)$.

Інтервал 2,$(-1,1)$: Вибір 0 здається простим:$f'(0)=-3<0$. Робимо висновок$f$, що зменшується далі$(-1,1)$.

Інтервал 3,$(1,3)$: Вибір 2 здається простим:$f'(2) = -3<0$. Знову ж таки,$f$ зменшується.

Інтервал 4,$(3,\infty)$: Вибір дуже великого числа$p$ з цього підінтервалу дасть позитивний чисельник і (звичайно) позитивний знаменник. Так$f$ збільшується на$(3,\infty)$.

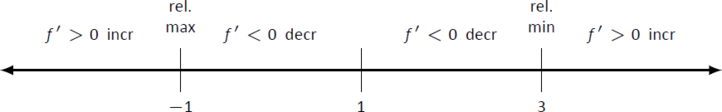
$imageedit_28_3242494758.png$

Малюнок$\PageIndex{5}$: Номер рядка для$f$ у прикладі$\PageIndex{2}$

Підсумовуючи,$f$ збільшується на множині$(-\infty,-1)\cup (3,\infty)$ і зменшується на множині$(-1,1)\cup (1,3)$. Оскільки в$x=-1$, знак f'\ перейшов з позитивного на негативний, Теорема$\PageIndex{2}$ стверджує, що$f(-1)$ є відносним максимумом$f$. В$x=3$, знак f'\ переключився з негативного на позитивний, значення$f(3)$ є відносним мінімумом. При$x=1$,$f$ не визначено, тому немає відносної крайності при$x=1$.

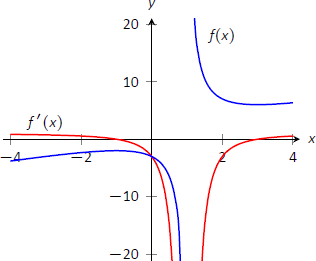
$imageedit_23_4550734806.png$

Малюнок$\PageIndex{6}$: Графік$f(x)$ у прикладі$\PageIndex{2}$, що показує, де$f$ відбувається збільшення і зменшення.

Це підсумовано в числовому рядку, показаному на малюнку$\PageIndex{3}$. Також на малюнку$\PageIndex{4}$ зображений графік$f$, що підтверджує наші розрахунки. Ця цифра також показує$f'$, знову демонструючи, що$f$ збільшується, коли$f'>0$ і зменшується, коли$f'<0$.

Часто виникає спокуса думати, що функції завжди чергуються «збільшення, зменшення, збільшення, зменшення$\ldots$» навколо критичних значень. Наш попередній приклад продемонстрував, що це не завжди так. Хоча технічно не$x=1$ було критичним значенням, це була важлива цінність, яку ми повинні були враховувати. Ми$f$ виявили, що зменшується «по обидва боки$x=1.$»

Розберемо ще один приклад.

Приклад$\PageIndex{3}$: Using the First Derivative Test

Знайдіть інтервали, на яких$f(x) = x^{8/3}-4x^{2/3}$ відбувається збільшення і зменшення, і виявити відносну крайність.

Рішення

Знову починаємо з прийому похідних. Оскільки ми знаємо, що хочемо вирішити$f'(x) = 0$, ми зробимо деяку алгебру після взяття похідних.

\[\begin{align} f(x) &= x^{\frac{8}{3}}-4x^{\frac{2}{3}} \\ f'(x) &= \dfrac{8}{3} x^{\frac{5}{3}} - \dfrac{8}{3}x^{-\frac{1}{3}} \\ &= \dfrac{8}{3}x^{-\frac{1}{3}} \left(x^{\frac{6}{3}}-1 \right)\\ &=\frac{8}{3}x^{-\frac{1}{3}}(x^2-1)\\ &=\frac{8}{3}x^{-\frac{1}{3}}(x-1)(x+1). \end{align}\]

Це виведення$f'$ показує, що$f'(x) = 0$ коли$x=\pm 1$ і не$f'$ визначається коли$x=0$. Таким чином, ми маємо 3 критичних значення, розбиваючи числову лінію на 4 субінтервали, як показано на малюнку$\PageIndex{5}$.

Інтервал 1$(\infty,-1)$: Ми вибираємо$p=-2$; ми можемо легко перевірити це$f'(-2)<0$. Так$f$ зменшується на$(-\infty,-1)$.

Інтервал 2,$(-1,0)$: Виберіть$p=-1/2$. Ще раз практикуємо знаходження знака$f'(p)$ без обчислення фактичного значення. У нас є$$f'(p) = (8/3)p^{-1/3}(p-1)(p+1)$; знайти знак кожного з трьох термінів.

\[f'(p) = \frac 83 \cdot \underbrace{p^{-\frac13}}_{<0}\cdot \underbrace{(p-1)}_{<0}\underbrace{(p+1)}_{>0}.\]

У нас є «негативний$\times$ негативний$\times$ позитив», що дає позитивне число;$f$ збільшується на$(-1,0)$.

Інтервал 3,$(0,1)$: Ми робимо аналогічний аналіз ознак, як і раніше, використовуючи$p$ в$(0,1)$.

\[f'(p) = \frac 83 \cdot \underbrace{p^{-\frac13}}_{>0}\cdot \underbrace{(p-1)}_{<0}\underbrace{(p+1)}_{>0}.\]

У нас є 2 позитивні фактори і один негативний фактор;$f'(p)<0$ і так$f$ зменшується$(0,1)$.

Інтервал 4,$(1,\infty)$: Подібна робота, виконана для інших трьох інтервалів показує, що$f'(x)>0$ на$(1,\infty)$, так$f$ збільшується на цьому інтервалі.

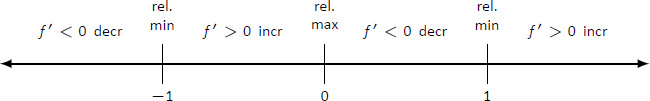
$imageedit_19_2956987507.png$

Малюнок$\PageIndex{7}$: Числовий рядок для$f$ у прикладі$\PageIndex{3}$

Ми робимо висновок, заявивши,$f$ що збільшується$(-1,0) \cup (1,\infty)$ і зменшується на$(-\infty,-1) \cup (0,1)$. Знак$f'$ зміни від негативного до позитивного навколо$x=-1$ і$x=1$, що означає за теоремою$\PageIndex{2}$, що$f(-1)$ і$f(1)$ є відносними мінімумами$f$. Як ознака$f'$ змін від позитивного до негативного при$x=0$, ми маємо відносний максимум при$f(0)$. $\PageIndex{8}$На малюнку зображений графік$f$, що підтверджує наш результат. Ми також графуємо$f'$, виділяючи ще раз,$f$ що збільшується, коли$f'>0$ і зменшується, коли$f'<0$.

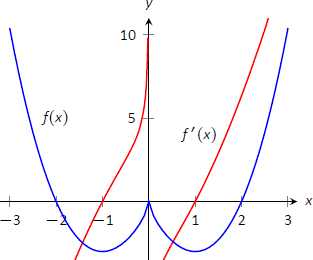
$imageedit_15_4725886460.png$

Малюнок$\PageIndex{8}$: Графік$f(x)$ у прикладі$\PageIndex{3}$, що показує, де$f$ відбувається збільшення і зменшення.

Ми бачили, як перша похідна функції допомагає визначити, коли функція йде «вгору» або «вниз». У наступному розділі ми побачимо, як друга похідна допомагає визначити, як графік кривих функції.