8.3: Аналіз графіків функцій
- Page ID
- 54376
З огляду на набір інформації про ключові властивості функції, можна намалювати графік. Перш ніж ми продовжимо, зробіть спробу підсумувати те, що ви вважаєте ключовими властивостями. Часто ключові властивості функції не всі представлені вам безпосередньо, але повинні бути визначені з наявної інформації.
Аналіз графіків функцій
Спочатку ми узагальнимо інформацію про функції, які ми тепер можемо генерувати на основі наших попередніх концепцій. Потім ми будемо використовувати цю інформацію для аналізу прикладів репрезентативних раціональних, поліноміальних, радикальних і тригонометричних функцій.
Давайте використаємо таблицю, подібну до показаної як шаблон, щоб організувати наші висновки.
| f (х) = | Аналіз |
| Домен і діапазон | |
| Перехоплення і нулі | |
| Асимптоти і межі на нескінченності | |
| Диференційованість | |
| Інтервали, де f збільшується | |
| Інтервали, де f зменшується | |
| відносна крайність | |
| Увігнутість | |
| Точки перегину |
Аналіз раціональних функцій
Розглянемо раціональну функцію\( f(x)=\frac{x^2−4}{x^2−2x−8} \nonumber\).
Нулі, домен та діапазон
Здається, функція має нулі при x = ± 2. Однак, як тільки ми враховуємо вираз, який ми бачимо
\( \frac{x^2−4}{x^2−2x−8}=\frac{(x+2)(x−2)}{(x−4)(x+2)}= \frac{x−2}{x−4} \nonumber\)
Отже, функція має нуль при x=2, є дірка у графі x=−2, область є\( (−∞,−2)∪(−2,4)∪(4,+∞) \nonumber\), а y-перехоплення знаходиться на рівні (0,12).
Асимптоти і межі на нескінченності
З огляду на домен, відзначимо, що існує вертикальна асимптота при x=4. Для визначення інших асимптотів досліджено межу f як x→∞ та x→−∞. У нас є
\[ \lim_{x \to ∞} \frac{x^2−4}{x^2−2x−8}= \lim_{x \to ∞} \frac{ \frac{x^2}{x^2}−\frac{4}{x^2}} {\frac{x^2}{x^2}−\frac{2x}{x^2}−\frac{8}{x^2}}=\lim_{x \to ∞} \frac{1−\frac{4}{x^2}}{1−\frac{2}{x}−\frac{8}{x^2}}=1 \nonumber\].
Точно так само ми бачимо, що\( \lim_{x \to −∞} \frac{x^2−4}{x^2−2x−8}=1 \nonumber\). Ми також зауважимо, що\( y≠\frac{2}{3} \nonumber\) починаючи з x−2.
Отже, у нас є горизонтальна асимптота при y = 1.
Диференційованість
\( f′(x)=\frac{−2x^2−8x−8}{(x2−2x−8)}=\frac{−2}{(x−4)^2}<0 \nonumber\). Отже, функція диференційовна в кожній точці своєї області, і оскільки f′ (x) <0 у своїй області, то f зменшується на своїй області,\( (−∞,−2)∪(−2,4)∪(4,+∞) \nonumber\).
\[ f′′(x)= \frac{4}{(x−4)^3} \nonumber\].
f′′ (x) 0 в області f, отже, немає відносних екстремумів і точок перегину.
Аналогічно, f′′ (x) <0, коли x<4. Отже, граф увігнутий вниз для x<4, x−2.
Давайте підсумуємо наші результати в таблиці, перш ніж накидати графік.
| f (x) =x2−4x2−2x−8 | Аналіз |
| Домен і діапазон |
\( D=(−∞,−2)∪(−2,4)∪(4,+∞) \nonumber\) \ (R= {\ mbox {всі реали} 1або\ frac {2} {3}} |
| Перехоплення і нулі |
Нуль при x = 2, y− перехоплення в (0,\( \frac{1}{2} \nonumber\)) |
| Асимптоти і межі на нескінченності |
ВА при х = 4, ГК при y = 1, Дірка на графіку при x=−2 |
| Диференційованість | Диференційований у кожній точці свого домену |
| Інтервали, де f збільшується | Ніде |
| Інтервали, де f зменшується | \( (−∞,−2)∪(−2,4)∪(4,+∞) \nonumber\) |
| відносна крайність | Жоден |
| Увігнутість |
Увігнуті вгору в (4, +∞), Увігнуті вниз в\( (−∞,−2)∪(−2,4) \nonumber\) |
| Точки перегину |
Жоден |
Нарешті, ми накидаємо графік наступним чином:
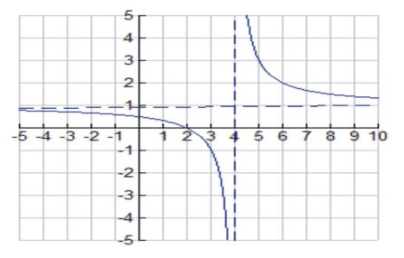
CC ЗА NC-SA
Аналіз радикальних функцій
Тепер, Розглянемо функцію\( f(x)= \sqrt{2x−1} \nonumber\).
Нулі, домен та діапазон
Домен f є\( (\frac{1}{2},+∞) \nonumber\), і він має нуль at\(x=\frac{1}{2} \nonumber\).
Асимптоти і межі на нескінченності
З огляду на область, відзначимо, що вертикальних асимптотів немає. Відзначимо, що\( \lim_{x \to ∞} f(x)=+∞ \nonumber\).
Диференційованість
\( f′(x)=\frac{1}{\sqrt{2x−1}}>0 \nonumber\)для всієї області f. отже f збільшується скрізь у своїй області. f′ (x) не визначено в\( x=\frac{1}{2} \nonumber\), тому\( x=\frac{1}{2} \nonumber\) є критичним значенням.
\( f′′(x)=\frac{−1}{\sqrt{(2x−1)^3}<0 \nonumber\)всюди в\( (\frac{1}{2},+∞) \nonumber\). Отже f увігнута вниз\( (\frac{1}{2},+∞) \nonumber\).
f′ (x) не визначається в\( x=\frac{1}{2} \nonumber\), тому\( x=\frac{1}{2} \nonumber\) є абсолютним мінімумом.
| f (x) = 2x√−1 | Аналіз |
| Домен і діапазон |
\( D=(\frac{1}{2},+∞),R={y≥0} \nonumber\) |
| Перехоплення і нулі |
Нуль при\( x=\frac{1}{2} \nonumber\), Немає y− перехоплення |
| Асимптоти і межі на нескінченності |
Немає асимптотів |
| Диференційованість | Диференційована в (\( \frac{1}{2} \nonumber\), +∞) |
| Інтервали, де f збільшується | Скрізь в D = (\( \frac{1}{2} \nonumber\), +∞) |
| Інтервали, де f зменшується | Ніде |
| відносна крайність | Жоден |
| Увігнутість |
Абсолютний мінімум при x =\( \frac{1}{2} \nonumber\), розташований при (\( \frac{1}{2} \nonumber\),0) Увігнутий вниз в (\( \frac{1}{2} \nonumber\), +∞) |
| Точки перегину |
Жоден |
Ось ескіз графіка:
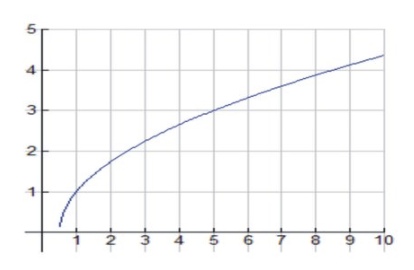
CC ЗА NC-SA
Аналіз тригонометричних функцій
Ми побачимо, що хоча тригонометричні функції можна проаналізувати, використовуючи те, що ми знаємо про похідні, вони нададуть деякі цікаві проблеми, які нам потрібно буде вирішити.
Розглянемо функцію\( f(x)=x−2sinx \nonumber\) на інтервалі\( [−π,π] \nonumber\).
Нулі, домен та діапазон
Відзначимо, що f є безперервною функцією і досягає абсолютного максимуму і мінімуму в\( [−π,π] \nonumber\). Його домен є\( [−π,π] \nonumber\), і його діапазон є\( R={−π≤y≤π} \nonumber\).
Диференційованість
\[ f′(x)=1−2cosx=0 \mbox{ at } x=−\frac{π}{3},\frac{π}{3} \nonumber\].
Зауважте, що\( f′(x)>0 \mbox{ on } (−π,−\frac{π}{3}) \mbox{ and } (\frac{π}{3},π) \nonumber\); отже, функція збільшується в (−π, −π3) та (π3, π).
Зауважте, що f′ (x) <0 на (−π3, π3); отже функція зменшується у (−π3, π3).
f′′ (x) = 2sinx = 0, якщо х = 0, π, −π. Отже, критичні значення мають значення x = −π, −π3, π3 та π.
f′′ (π3) > 0; отже, існує відносний мінімум при x = π3.
f′′ (−π3) <0; отже, існує відносний максимум при x=−π3.
f′′ (х 0 <0 on (−π,0) and f′′ (x) > на (0, π). Звідси графік увігнутий вниз (−π,0) і увігнутий вгору і зменшується на (0, π). Існує точка перегину в x=0, розташована в точці (0, 0).
Нарешті, існує абсолютний мінімум при\( x=−π \nonumber\), розташований на\( (−π,−π) \nonumber\), і абсолютний максимум при\( x=π \nonumber\), розташований за адресою\( (π,π) \nonumber\).
| f (x) = x−2sinx | Аналіз |
| Домен і діапазон |
\( D=[−π,π],R={−π≤y≤π} \nonumber\) |
| Перехоплення і нулі |
\( x=−\frac{π}{3}, \frac{π}{3} \nonumber\) |
| Асимптоти і межі на нескінченності |
Немає асимптотів |
| Диференційованість | Диференційована в\( D=[−π,π] \nonumber\) |
| Інтервали, де f збільшується | \( (\frac{π}{3},π) \mbox{ and } (−π,−\frac{π}{3}) \nonumber\) |
| Інтервали, де f зменшується | \ (−\ frac {π} {3},\ frac {π} {3}) |
| відносна крайність |
Відносний максимум при\( x=−\frac{π}{3} \nonumber\) Відносний мінімум при\( x=\frac{π}{3} \nonumber\) |
| Увігнутість |
Абсолютний максимум при x = π, розташований в (π, π) Абсолютний мінімум при x = −π, розташований на (−π, −π) Увігнутий вгору в (0, π) |
| Точки перегину |
x=0, розташований в точці (0, 0) |
Ось ескіз графіка:
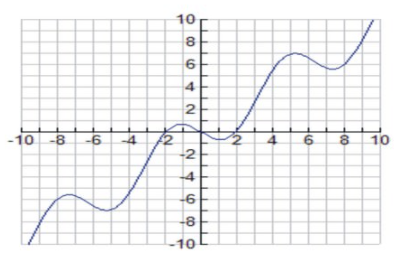
CC ЗА NC-SA
Приклади
Приклад 1
Раніше вам було запропоновано узагальнити ключові властивості функцій. Як ви бачили в цій концепції, ключові властивості функцій включають: область, діапазон, перехоплення, асимптоти (включаючи межі на нескінченності), безперервність і диференційовність, збільшення і зменшення інтервалів, екстремуми, увігнутості та точки перегину.
Приклад 2
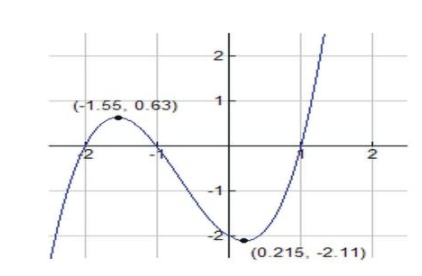
Розглянемо поліноміальну функцію\(f(x)=x^3+2x^2−x−2 \nonumber\).
Нулі, домен та діапазон
Домен f дорівнює (−∞, +∞), а y-перехоплення в (0, -2).
Функція може бути врахована\( f(x)=x^3+2x^2−x−2=x^2(x+2)−1(x+2)=(x^2−1)(x+2)=(x−1)(x+1)(x+2) \nonumber\)
і, таким чином, має нулі при x = ± 1, −2.
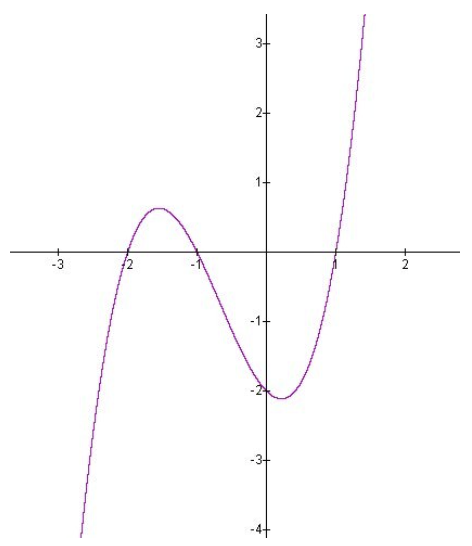
CC ЗА NC-SA
Асимптоти і межі на нескінченності
З огляду на область, відзначимо, що вертикальних асимптотів немає. Відзначимо, що і\( \lim_{x \to ∞} f(x)=+∞ \mbox{ and } \lim_{x \to {−∞}} f(x)=−∞ \nonumber\).
Диференційованість
\( f′(x)=3x^2+4x−1=0 \mbox{ if } x=\frac{−4±\sqrt{28}}{6}=\frac{−2±\sqrt{7}}{3} \nonumber\). Це критичні значення. Зауважимо, що функція диференційовна в кожній точці своєї області.
\( f′(x)>0 \mbox{ on } (−∞,\sqrt{−2−\sqrt{7}}{3}) \mbox{ and } (\frac{−2+\sqrt{7}}{3},+∞) \nonumber\); отже, функція збільшується в цих інтервалах.
Аналогічно,\( f′(x)<0 \mbox{ on } (\frac{−2−\sqrt{7}}{3},\fraac{−2+\sqrt{7}}{3}) \nonumber\) і, таким чином, відбувається зменшення там.
\( f′′(x)=6x+4=0 \mbox{ if } x=−\frac{2}{3} \nonumber\)де є точка перегину.
Крім того,\( f′′(\frac{−2−\sqrt{7}}{3})<0 \nonumber\). Звідси графік має відносний максимум в точці\( x=\frac{−2−\sqrt{7}}{3} \nonumber\) і знаходиться в точці (-1,55, 0,63).
Відзначимо, що\( f′′(x)<0 \mbox{ for } x<−\sqrt{2}{3} \nonumber\). Графік увігнутий вниз\( (−∞,−\frac{2}{3}) \nonumber\).
І ми маємо\( f′′(\frac{−2+\sqrt{7}}{3})>0 \nonumber\); отже, графік має відносний мінімум\( x=\frac{−2+\sqrt{7}}{3} \nonumber\) в точці (0.22, -2.11).
Відзначимо, що\( f′′(x)>0 \mbox{ for } x>−\frac{2}{3} \nonumber\). Графік увігнутий вгору\( (−\frac{2}{3},+∞) \nonumber\).
Підсумок таблиці
| \( f(x)=x^3+2x^2−x−2 \nonumber\) | Аналіз |
| Домен і діапазон |
D= (−∞, +∞), R= {всі реали} |
| Перехоплення і нулі |
Нулі при x = ± 1, −2, y, перехоплює при (0, -2) |
| Асимптоти і межі на нескінченності |
Немає асимптотів |
| Диференційованість | Диференційований у кожній точці свого домену |
| Інтервали, де f збільшується | \( (−∞,\frac{−2−\sqrt{7}}{3}) and (\frac{−2+\frac{7}}{3},+∞) \nonumber\) |
| Інтервали, де f зменшується | \( (\frac{−2−\sqrt{7}}{3},\frac{−2+\sqrt{7}}{3}) \nonumber\) |
| відносна крайність |
Відносний максимум в точці\( x=\frac{−2−\sqrt{7}}{3} \nonumber\) і розташований в точці (-1,55, 0,63); Відносний мінімум в точці\( x=\frac{−2+\sqrt{7}}{3} \nonumber\) і розташований в точці (0,22, -2,11). |
| Увігнутість |
Увігнуті вгору в\( (−\frac{2}{3},+∞) \nonumber\). Увігнуті вниз в\( (−∞,−\frac{2}{3}) \nonumber\). |
| Точки перегину |
\( x=−\frac{2}{3} \nonumber\), що знаходиться в точці\( (−\frac{2}{3},−.74) \nonumber\) |
Ось ескіз графіка:
CC ЗА NC-SA
Рецензія
Для всіх перерахованих нижче функцій узагальнити функції, заповнивши таблицю нижче. Використовуйте інформацію для ескізу графіка функції.
| f (х) = | Аналіз |
| Домен і діапазон | |
| Перехоплення і нулі | |
| Асимптоти і межі на нескінченності | |
| Диференційованість | |
| Інтервали, де f збільшується | |
| Інтервали, де f зменшується | |
| відносна крайність | |
| Увігнутість | |
| Точки перегину |
- \( f(x)=x^3+3x^2−x−3 \nonumber\)
- \( f(x)=−x^4+4x^3−4x^2 \nonumber\)
- \( f(x)=\frac{2x−2}{x^2} \nonumber\)
- \( f(x)=x−x^{\frac{1}{3}} \nonumber\)
- \( f(x)=−\sqrt{2x−6}+3 \nonumber\)
- \( f(x)=x^2−2\sqrt{x} \nonumber\)
- \( f(x)=1+cosx \mbox{ on the interval } [−π,π] \nonumber\)
- \( f(x)=x^2−x+1 \nonumber\)
- \( f(x)=4x^3−6x^2−1 \nonumber\)
- \( f(x)=\frac{x^2}{x−1} \nonumber\)
- \( f(x)=\frac{x^2}{e^{−x}} \nonumber\)
- \( f(x)=cosx−x \nonumber\)
- \( f(x)=e^{−2x}+e^x \nonumber\)
- \( f(x)=5e^{−x}+x^3 \nonumber\)
- \( f(x)=x^5−7x^2+2 \nonumber\)
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 4.8.
Лексика
| Термін | Визначення |
|---|---|
| Асимптоти | Асимптота - це рядок на графіку функції, що представляє значення, до якого функція може наблизитися, але не досягати (за деякими винятками). |
| увігнутість | Увігнутість описує поведінку нахилу дотичної лінії такої функції, що увігнутість є позитивною, якщо нахил збільшується, негативною, якщо нахил зменшується, і нульовою, якщо нахил постійний. |
| зменшується | Функція зменшується протягом інтервалу, якщо її значення y стають меншими за інтервал. Графік буде опускатися зліва направо за інтервал. |
| диференційований | Диференційована функція - це функція, яка має похідну, яку можна обчислити. |
| домену | Домен функції - це множина x-значень, для яких визначена функція. |
| збільшуючи | Функція збільшується протягом інтервалу, якщо її значення y стають більшими за інтервал. Графік буде підніматися зліва направо за інтервал. |
| точка перегину | Точка перегину - це точка в області, де увігнутість змінюється від позитивної до негативної або негативної на позитивну. |
| Діапазон | Діапазон функції - це набір значень y, для яких визначена функція. |
| відносна крайність | Відносним екстремумом функції є точки функції зі значеннями y, які є найвищими або найнижчими з локальної околиці функції. |
Додаткові ресурси
PLIX: Грайте, вчіться, взаємодійте, досліджуйте - аналіз раціональної функції
Відео: Графік з використанням похідних
Реальний світ: Тотальна ліквідація