1.22: Площа поверхні загальних твердих тіл

Last updated
Save as PDF

Page ID: 65820

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Ви можете використовувати калькулятор у цьому модулі.

Тепер ми звернемо свою увагу з двовимірних фігур на тривимірні фігури, які ми часто називаємо твердими частинами, навіть якщо вони порожнисті всередині. У цьому модулі ми розглянемо ділянки поверхні деяких загальних твердих тіл. (Ми розглянемо обсяг в більш пізньому модулі.) Площа поверхні - це те, що звучить як: це сума площ всіх зовнішніх поверхонь твердого тіла. Коли ви намагаєтеся обернути подарунок, тому що ваш аркуш обгорткового паперу не досить великий, ви маєте справу з площею поверхні.

Є два різних види площі поверхні, які важливі: площа бічної поверхні (LSA) і загальна площа поверхні (TSA). Щоб візуалізувати різницю між LSA і TSA, розглянемо баночку супу. Площа бічної поверхні буде використовуватися для вимірювання розміру паперової етикетки навколо банки. Загальна площа поверхні буде використана для вимірювання кількості листового металу, необхідного для виготовлення банки. Іншими словами, загальна площа поверхні включає верх і низ, тоді як площа бічної поверхні не має.

Прямокутні тіла

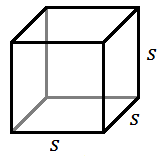
Прямокутний суцільний виглядає як прямокутний короб. Він має три пари прямокутників однакового розміру спереду і ззаду, зліва і справа, а також зверху і знизу. Куб - це спеціальне прямокутне тверде тіло з квадратами однакового розміру для всіх шести граней.

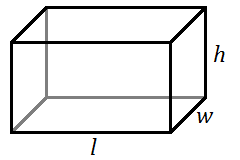
тривимірна прямокутна коробка з нижнім переднім краєм з позначкою l, нижній правий край позначений w, і вертикальний правий край позначений h — Малюнок$\PageIndex{1}$: (ліворуч) Прямокутне тверде тіло і (праворуч) куб.

тривимірна квадратна коробка з нижнім переднім краєм позначені s, нижній правий край позначений s, і вертикальний правий край позначений s — Малюнок$\PageIndex{1}$: (ліворуч) Прямокутне тверде тіло і (праворуч) куб.

Площа бічної поверхні - це об'єднана загальна площа чотирьох вертикальних граней твердого тіла, але не верхньої та нижньої. Якби ви фарбували чотири стіни кімнати, ви б думали про площу бічної поверхні.

Загальна площа поверхні - це об'єднана загальна площа всіх шести граней твердого тіла. Якби ви фарбували чотири стіни, підлогу і стелю кімнати, ви б думали про загальну площу поверхні.

Для прямокутного твердого тіла довжиною$l$$w$, шириною та висотою$h$... ^[1]

$LSA=2lh+2wh$

$TSA=2lh+2wh+2lw$

$TSA=LSA+2lw$

Для куба з довжиною сторони$s$...

$LSA=4s^2$

$TSA=6s^2$

Примітка: Ці розміри іноді називають основою, глибиною та висотою.

Вправи$\PageIndex{1}$

1. Знайдіть площу бічної поверхні цього прямокутного тіла.

2. Знайдіть загальну площу поверхні цього прямокутного тіла.

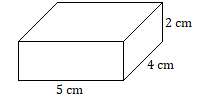
Відповідь

1. $36\text{ cm}^2$

2. $76\text{ cm}^2$

Циліндри

Як уже згадувалося раніше в цьому модулі, площа бічної поверхні банки для супу - це паперова етикетка, яка представляє собою прямокутник. Тому площа бічної поверхні циліндра - це прямокутник; його ширина дорівнює окружності кола$2\pi{r}$, а його висота - висоті циліндра.

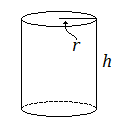
Оскільки циліндр має однакові за розміром кола у верхній і нижній частині, його загальна площа поверхні дорівнює площі бічної поверхні плюс двічі більше площі одного з кіл.

Для циліндра з радіусом$r$ і висотою$h$...

$LSA=2\pi{rh}$
$TSA=2\pi{rh}+2\pi{r^2}$
$TSA=LSA+2\pi{r^2}$

Майте на увазі, що якщо вам дано діаметр циліндра, вам потрібно буде розрізати його навпіл, перш ніж використовувати ці формули.

Вправи$\PageIndex{1}$

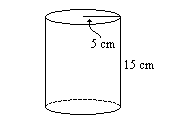
3. Знайдіть площу бічної поверхні цього циліндра.

4. Знайдіть загальну площу поверхні цього циліндра.

Відповідь

3. $471\text{ cm}^2$

4. $628\text{ cm}^2$

Сфери

Кінцевим твердим тілом цього модуля є сфера, яку можна розглядати як коло у трьох вимірах: кожна точка на поверхні сфери знаходиться на однаковій відстані від центру. Через це сфера має лише одне важливе вимірювання: її радіус. Звичайно, його діаметр також може бути важливим, але ідея полягає в тому, що сфера не має різних розмірів, таких як довжина, ширина та висота. Сфера має однаковий радіус (або діаметр) у кожному напрямку.

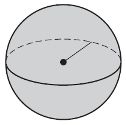
Нам потрібно було б використовувати обчислення, щоб отримати формулу для площі поверхні сфери, тому ми просто припустимо, що це правда і отримати з бізнесом під рукою. Зверніть увагу, що, оскільки сфера не має верхньої або нижньої граней, нам не потрібно турбуватися про пошук області бічної поверхні. Єдина площа поверхні - загальна площа поверхні.

Для сфери з радіусом$r$ або діаметром$d$...

$SA=4\pi{r^2}$або$SA=\pi{d^2}$

За збігом обставин площа поверхні сфери в$4$ рази перевищує площу кола поперечного перерізу в найширшій частині сфери. Можливо, вам буде цікаво спробувати візуалізувати це або відправитися на кухню для демонстрації: якщо ви розрізаєте апельсин на чотири чверті, шкірка на одному з цих чверть апельсинів має ту ж площу, що і коло, утворений першим розрізом.

Вправи$\PageIndex{1}$

5. Знайдіть площу поверхні цієї сфери.

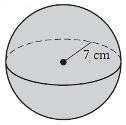
$сфера радіусом 7 см$

6. Знайдіть площу поверхні цієї сфери.

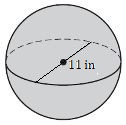
$сфера діаметром 11 дюймів$

Відповідь

5. $616\text{ cm}^2$

6. $380\text{ cm}^2$

Ви можете використовувати великі літери для змінних тут, оскільки мала буква «l» може бути легко прийнята за число «1". ←

Вправи\(\PageIndex{1}\)

Вправи\(\PageIndex{1}\)

Вправи\(\PageIndex{1}\)