1.23: Площа правильних багатокутників

Last updated
Save as PDF

Page ID: 65847

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Ви можете використовувати калькулятор у цьому модулі.

Будівля Пентагону охоплює$28.7$ гектари ($116,000\text{ m}^2$) і включає в себе додаткові$5.1$ гектари ($21,000\text{ m}^2$) як центральний двір. ^[1] П'ятикутник є прикладом правильного багатокутника.

$Будівля Пентагону$

Правильний багатокутник має всі сторони однакової довжини і всі кути однакової міри. Через цю симетрію коло може бути вписано - намальовано всередині багатокутника, торкаючись кожної сторони в одній точці, або описано - намальовано поза багатокутником, що перетинає кожну вершину. Ми зосередимося на вписаному колі в першу чергу.

Назвемо радіус вписаного кола малим$r$ регістрам; це відстань від центру багатокутника перпендикулярно одній зі сторін. ^[2]

коло всередині звичайного п'ятикутника. Коло стосується центру всіх п'яти сторін п'ятикутника. — Малюнок$\PageIndex{1}$: (зліва) вписане коло (праворуч) вписане коло з радіусом.

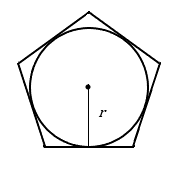
регулярний п'ятикутник з окружністю всередині нього торкаючись центральної точки кожної сторони п'ятикутника, і радіус, проведений від центру прямо вниз до центру нижньої сторони, позначені рядковим r — Малюнок$\PageIndex{1}$: (зліва) вписане коло (праворуч) вписане коло з радіусом.

Площа регулярного багатокутника (з радіусом, накресленим до центру однієї сторони) ^[3]

Для правильного багатокутника зі$n$ сторонами довжини$s$ та вписаним (внутрішнім) радіусом$r$,

\[A=nsr\div2 \nonumber \]

Примітка: Ця формула походить від поділу багатокутника на$n$ трикутники однакового розміру та об'єднання площ цих трикутників.

Вправи$\PageIndex{1}$

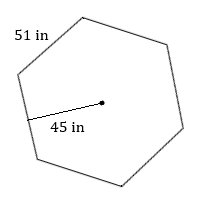
1. Обчисліть площу цього правильного шестикутника.

$правильний шестикутник зі стороною 51 дюйм і радіусом в одну сторону 45 дюймів$

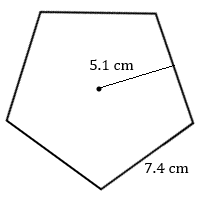
2. Обчисліть площу цього правильного п'ятикутника.

$правильний п'ятикутник зі стороною 7,4 см і радіусом в одну сторону 5,1 см$

3. Знак зупинки має висоту$30$ inches, and each edge measures $12.5$ inches. Find the area of the sign.

$восьмикутний знак зупинки$

Відповідь

1. $6,900\text{ in}^2$

2. $94\text{ cm}^2$

3. $750\text{ in}^2$

Гаразд, але що робити, якщо ми знаємо відстань від центру до одного з кутів замість відстані від центру до краю? Нам потрібно буде уявити собі обведене коло.

Назвемо радіус описаного кола капіталом$R$; це відстань від центру багатокутника до однієї з вершин (кутів).

коло за межами регулярного п'ятикутника. Всі п'ять кутових точок п'ятикутника торкаються кола. — Малюнок$\PageIndex{2}$: (ліворуч) обведене коло і (праворуч) обведені кола з великим колом.

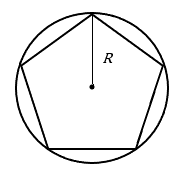
регулярний п'ятикутник всередині кола з усіма п'ятьма кутовими точками на колі, і радіус від центру до однієї кутової точки позначені капітал R — Малюнок$\PageIndex{2}$: (ліворуч) обведене коло і (праворуч) обведені кола з великим колом.

Площа правильного багатокутника (з радіусом, накресленим до вершини) ^[4]

Для правильного багатокутника зі$n$ сторонами довжини та$s$ обмеженим (зовнішнім) радіусом$R$,

\[A=0.25ns\sqrt{4R^2-s^2} \nonumber \]

або

\[A=ns\sqrt{4R^2-s^2}\div4 \nonumber \]

Примітка: Ця формула також походить від поділу багатокутника на$n$ трикутники однакового розміру та об'єднання площ цих трикутників. Ця формула включає квадратний корінь, оскільки вона включає теорему Піфагора.

Вправи$\PageIndex{1}$

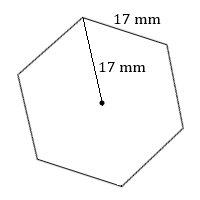
4. Обчисліть площу цього правильного шестикутника.

$правильний шестигранник зі стороною 17 мм і радіусом до однієї вершини 17 дюймів$

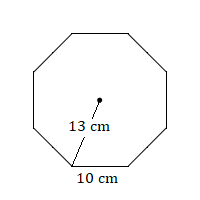
5. Обчисліть площу цього правильного восьмикутника.

$восьмикутник зі стороною 10 см і радіусом до вершини 13 см$

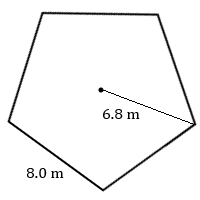
6. Обчисліть площу цього правильного п'ятикутника.

$правильний п'ятикутник зі стороною 8,0 м і радіусом до однієї вершини 6,8 м$

Відповідь

4. $750\text{ mm}^2$

5. $480\text{ cm}^2$

6. $110\text{ m}^2$

Як відомо, складова фігура - це геометрична фігура, яка утворюється шляхом з'єднання двох і більше основних геометричних фігур. Давайте розглянемо складену фігуру, утворену колом і правильним багатокутником.

Вправа$\PageIndex{1}$

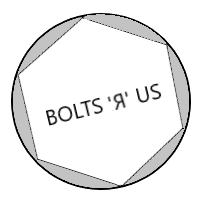
7. Шестигранна головка болта щільно вписується в круглий ковпачок з круглим отвором з внутрішнім діаметром$46\text{ mm}$ as shown in this diagram. Opposite sides of the bolt head are $40\text{ mm}$ apart. Find the total empty area in the hole around the edges of the bolt head.

$шестикутник з позначкою «болти r us», вписаний в коло$

Відповідь: $280\text{ mm}^2$(Площа кола$\approx1,660\text{ mm}^2$ і площа шестикутника дорівнює$1,380\text{ mm}^2$)

https://en.Wikipedia.org/wiki/The_Pentagon :05
Внутрішній радіус частіше називають апофемом і позначено$a$, але ми намагаємося звести жаргон до мінімуму в цьому підручнику. م
Ця формула частіше записується як половина апофему, що помножується на периметр$A=\dfrac{1}{2}ap$:
Ваш автор створив цю формулу, тому що в кожній іншій її версії використовується тригонометрія, яку ми не висвітлюємо в цьому підручнику. م

Вправи\(\PageIndex{1}\)

Вправи\(\PageIndex{1}\)

Вправа\(\PageIndex{1}\)