12.2: Вектори в трьох вимірах
- Page ID
- 61497
- Опишіть тривимірний простір математично.
- Знайдіть точки в просторі за допомогою координат.
- Запишіть формулу відстані в трьох вимірах.
- Напишіть рівняння для простих площин і сфер.
- Виконуйте векторні операції в\(\mathbb{R}^{3}\).
Вектори є корисними інструментами для розв'язання двовимірних задач. Життя, однак, відбувається в трьох вимірах. Щоб розширити використання векторів до більш реалістичних додатків, необхідно створити рамки для опису тривимірного простору. Наприклад, хоча двовимірна карта є корисним інструментом для навігації з одного місця в інше, в деяких випадках важлива топографія землі. Чи проходить ваш запланований маршрут через гори? Вам доведеться перетнути річку? Щоб повністю оцінити вплив цих географічних особливостей, необхідно використовувати три виміри. У цьому розділі представлено природне розширення двовимірної декартової координатної площини на три виміри.
Тривимірні системи координат
Як ми дізналися, двовимірна прямокутна система координат містить дві перпендикулярні осі: горизонтальну\(x\) -вісь і вертикальну \(y\)-вісь. Ми можемо додати третій вимір,\(z\) -вісь, яка перпендикулярна як до\(x\) -осі, так і до\(y\) -осі. Ми називаємо цю систему тривимірною прямокутною системою координат. Він являє собою три виміри, з якими ми стикаємося в реальному житті.
Тривимірна прямокутна система координат складається з трьох перпендикулярних осей:\(y\) -вісь, -вісь та\(z\) -вісь.\(x\) Оскільки кожна вісь є числовим рядком, що представляє всі дійсні числа в\(ℝ\), тривимірна система часто позначається\(ℝ^3\).
На\(\PageIndex{1a}\) малюнку позитивна \(z\)вісь показана над площиною, що містить\(x\) - і\(y\) -осі. Позитивна\(x\) -вісь з'являється ліворуч, а позитивна\(y\) -вісь - праворуч. Природне питання, яке слід задати, полягає в тому, як було визначено цю домовленість? Система, що відображається, слідує правилу праворуч. Якщо ми беремо праву руку і вирівнюємо пальці з позитивною\(x\) -віссю, то скручуємо пальці так, щоб вони вказували в напрямку позитивної \(y\)-осі, наш великий палець вказує в сторону позитивної\(z\) -осі (рис.\(\PageIndex{1b}\)). У цьому тексті ми завжди працюємо з системами координат, налаштованими відповідно до правилом праворуч. Деякі системи дотримуються правила лівої руки, але правило правої руки вважається стандартним представленням.
У двох вимірах опишемо точку в площині з координатами\((x,y)\). Кожна координата описує, як точка вирівнюється з відповідною віссю. У трьох вимірах додається нова координата\(z\), щоб вказати вирівнювання за допомогою\(z\) -осі:\((x,y,z)\). Точка в просторі ідентифікується за всіма трьома координатами (рис.\(\PageIndex{2}\)). Для побудови точки\((x,y,z)\), йти\(x\) одиниці вздовж \(x\)-осі, потім \(y\)одиниці в напрямку\(y\) -осі, потім\(z\) одиниці в напрямку\(z\) -осі.
Намалюйте точку\((1,−2,3)\) в тривимірному просторі.
Рішення
Щоб намалювати точку, почніть з ескізу трьох сторін прямокутної призми вздовж осей координат: одна одиниця в позитивному\(x\) напрямку,\(2\) одиниці в\(y\) негативному напрямку та\(3\) одиниці в позитивному\(z\) напрямку. Завершіть призму для побудови точки (рис.\(\PageIndex{3}\)).
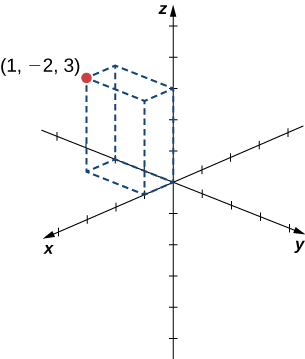
Намалюйте точку\((−2,3,−1)\) в тривимірному просторі.
- Підказка
-
Почніть з ескізу координатних осей. Наприклад, рис\(\PageIndex{3}\). Потім намалюйте прямокутну призму, щоб допомогти знайти точку в просторі.
- Відповідь
-
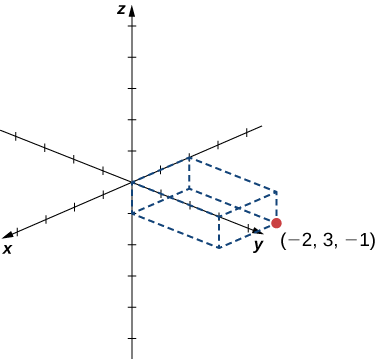
У двовимірному просторі координатна площина визначається парою перпендикулярних осей. Ці осі дозволяють назвати будь-яке місце в площині. У трьох вимірах ми визначаємо координатні площини координатними осями, так само, як у двох вимірах. Зараз три осі, тому є три пари осей, що перетинаються. Кожна пара осей утворює координатну площину:\(xy\) -площину, \(xz\)-площину та\(yz\) -площину (рис.\(\PageIndex{4}\)). Ми визначаємо\(xy\) -plane формально як наступний набір:\(\{(x,y,0):x,y∈ℝ\}.\) Аналогічно, \(xz\)-plane і\(yz\) -plane визначаються як\(\{(x,0,z):x,z∈ℝ\}\) і\(\{(0,y,z):y,z∈ℝ\},\) відповідно.
Щоб уявити це, уявіть, що ви будуєте будинок і стоїте в кімнаті, де закінчено лише дві з чотирьох стін. (Припустимо, що дві готові стіни примикають один до одного.) Якщо ви стоїте спиною до кута, де зустрічаються дві готові стіни, звернені до кімнати, підлога - це\(xy\) площина, стіна праворуч \(xz\)- площина, а стіна зліва від вас \(yz\)- площина.
У двох вимірах координатні осі поділяють площину на чотири квадранта. Аналогічно координатні площини ділять простір між ними на вісім областей про походження, званих октантами. Октанти заповнюють\(ℝ^3\) так само, як заповнюють квадранти\(ℝ^2\), як показано на малюнку\(\PageIndex{5}\).
Більшість робіт в тривимірному просторі є комфортним продовженням відповідних понять в двох вимірах. У цьому розділі ми використовуємо наші знання кіл для опису сфер, а потім розширюємо наше розуміння векторів до трьох вимірів. Для досягнення цих цілей ми починаємо з адаптації формули відстані до тривимірного простору.
Якщо дві точки лежать в одній координатній площині, то розрахувати відстань між ними нескладно. Ми знаємо, що відстань\(d\) між двома точками\((x_1,y_1)\) і\((x_2,y_2)\) в\(xy\) -координатної площині задається за формулою
\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}. \nonumber \]
Формула відстані між двома точками в просторі є природним продовженням цієї формули.
Відстань\(d\) між точками\((x_1,y_1,z_1)\) і\((x_2,y_2,z_2)\) задається за формулою
\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2}. \label{distanceForm} \]
Доказ цієї теореми залишають як вправу. (Підказка: Спочатку знайдіть відстань\(d_1\) між точками\((x_1,y_1,z_1)\) і\((x_2,y_2,z_1)\), як показано на малюнку\(\PageIndex{6}\).)
Знайти відстань між точками\(P_1=(3,−1,5)\) і\(P_2=(2,1,−1).\)
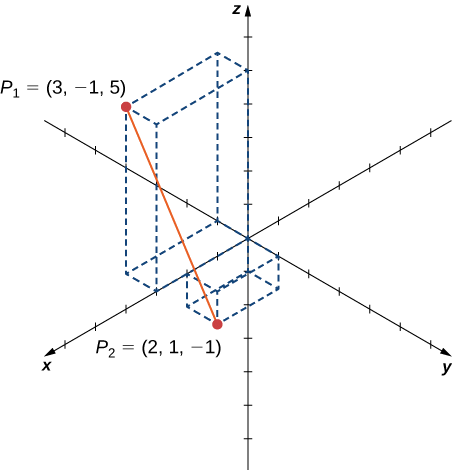
Рішення
Підставляємо значення безпосередньо у формулу відстані (Equation\ ref {distanceForm}):
\[\begin{align*} d(P_1,P_2) &=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2} \\[4pt] &=\sqrt{(2−3)^2+(1−(−1))^2+(−1−5)^2} \\[4pt] &=\sqrt{(-1)^2+2^2+(−6)^2} \\[4pt] &=\sqrt{41}. \end{align*}\]
Знайти відстань між точками\(P_1=(1,−5,4)\) і\(P_2=(4,−1,−1)\).
- Підказка
-
\(d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2}\)
- Відповідь
-
\(5\sqrt{2}\)
Перш ніж перейти до наступного розділу, давайте зрозуміємо, чим\(ℝ^3\) відрізняється від\(ℝ^2\). Наприклад, в, лінії\(ℝ^2\), які не є паралельними, повинні завжди перетинатися. Це не так в\(ℝ^3\). Для прикладу розглянемо лінії, показані на малюнку\(\PageIndex{8}\). Ці дві лінії не паралельні, а також не перетинаються.
Малюнок\(\PageIndex{8}\): Ці дві лінії не паралельні, але все ж не перетинаються.
Ви також можете мати кола, які пов'язані між собою, але не мають спільних точок, як на малюнку\(\PageIndex{9}\).
Малюнок\(\PageIndex{9}\): Ці кола пов'язані між собою, але не мають спільних точок.
Ми маємо набагато більшу гнучкість, працюючи в трьох вимірах, ніж у нас, якщо ми застрягли лише з двома вимірами.
Написання рівнянь в\(ℝ^3\)
Тепер, коли ми можемо представляти точки в просторі та знаходити відстань між ними, ми можемо навчитися писати рівняння геометричних об'єктів, таких як лінії, площини та криволінійні поверхні\(ℝ^3\). Спочатку почнемо з простого рівняння. Порівняйте графіки рівняння\(x=0\) в\(ℝ\)\(ℝ^2\), і\(ℝ^3\) (рис.\(\PageIndex{10}\)). З цих графіків ми бачимо те саме рівняння, яке може описати точку, лінію або площину.
У просторі рівняння\(x=0\) описує всі точки\((0,y,z)\). Це рівняння визначає\(yz\) -площину. Аналогічно,\(xy\) -plane містить всі точки форми\((x,y,0)\). Рівняння\(z=0\) визначає \(xy\)-площину, а рівняння\(y=0\) описує\(xz\) -площину (рис.\(\PageIndex{11}\)).
Розуміння рівнянь координатних площин дозволяє написати рівняння для будь-якої площини, паралельної одній з координатних площин. Коли площина паралельна \(xy\)-площині, наприклад, координата\(z\) - кожної точки на площині має однакову постійну величину. Тільки\(x\) - і \(y\)- координати точок у цій площині змінюються від точки до точки.
- Площина в просторі, яка паралельна\(xy\) -площині і містить точку,\((a,b,c)\) може бути представлена рівнянням\(z=c\).
- Площина в просторі, яка паралельна\(xz\) -площині і містить точку,\((a,b,c)\) може бути представлена рівнянням\(y=b\).
- Площина в просторі, яка паралельна\(yz\) -площині і містить точку,\((a,b,c)\) може бути представлена рівнянням\(x=a\).
- Напишіть рівняння площини\((3,11,7)\), що проходить через точку, паралельну\(yz\) -площині.
- Знайти рівняння площини, що проходить через точки\((6,−2,9), (0,−2,4),\) і\((1,−2,−3).\)
Рішення
- Коли площина паралельна\(yz\) -площині, тільки \(y\)- і\(z\) -координати можуть змінюватися. \(x\)-координата має однакове постійне значення для всіх точок цієї площини, тому ця площина може бути представлена рівнянням\(x=3\).
- Кожна з точок\((1,−2,−3)\) має однакову\((6,−2,9), (0,−2,4),\) і ту ж \(y\)- координату. Цю площину можна представити рівнянням\(y=−2\).
Напишіть рівняння площини\((1,−6,−4)\), що проходить через точку, паралельну\(xy\) -площині.
- Підказка
-
Якщо площина паралельна\(xy\) -площині, z- координати точок у цій площині не змінюються.
- Відповідь
-
\(z=−4\)
Як ми бачили, в\(ℝ^2\) рівнянні\(x=5\) описується вертикальна лінія, що проходить через точку\((5,0)\). Ця лінія паралельна\(y\) -осі. У природному розширенні рівняння\(x=5\) в\(ℝ^3\) описує площину, що проходить через точку\((5,0,0)\), яка паралельна \(yz\)-площині. Ще одне природне продовження знайомого рівняння знаходиться в рівнянні сфери.
Сфера - це сукупність усіх точок у просторі, рівновіддалених від фіксованої точки, центру сфери (рис.\(\PageIndex{12}\)), так само, як множина всіх точок у площині, що знаходяться на рівновіддаленому від центру, являє собою коло. У сфері, як і в колі, відстань від центру до точки на сфері називається радіусом.
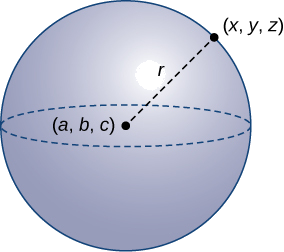
Рівняння кола виводиться за допомогою формули відстані в двох вимірах. Таким же чином рівняння сфери базується на тривимірній формулі відстані.
Сфера з центром\((a,b,c)\) і радіусом\(r\) може бути представлена рівнянням
\[(x−a)^2+(y−b)^2+(z−c)^2=r^2. \nonumber \]
Це рівняння відоме як стандартне рівняння сфери.
Знайдіть стандартне рівняння сфери з центром\((10,7,4)\) і точкою\((−1,3,−2)\), як показано на малюнку\(\PageIndex{13}\).
Малюнок\(\PageIndex{13}\): Сфера з центром у точці\((10,7,4)\), що містить\((−1,3,−2).\)
Рішення
Використовуйте формулу відстані, щоб знайти радіус\(r\) сфери:
\[\begin{align*} r &=\sqrt{(−1−10)^2+(3−7)^2+(−2−4)^2} \\[4pt] &=\sqrt{(−11)^2+(−4)^2+(−6)^2} \\[4pt] &=\sqrt{173} \end{align*} \nonumber \]
Стандартне рівняння сфери
\[(x−10)^2+(y−7)^2+(z−4)^2=173. \nonumber \]
Знайти стандартне рівняння сфери з центром,\((−2,4,−5)\) що містить точку\((4,4,−1).\)
- Підказка
-
Спочатку використовуйте формулу відстані, щоб знайти радіус сфери.
- Відповідь
-
\[(x+2)^2+(y−4)^2+(z+5)^2=52 \nonumber \]
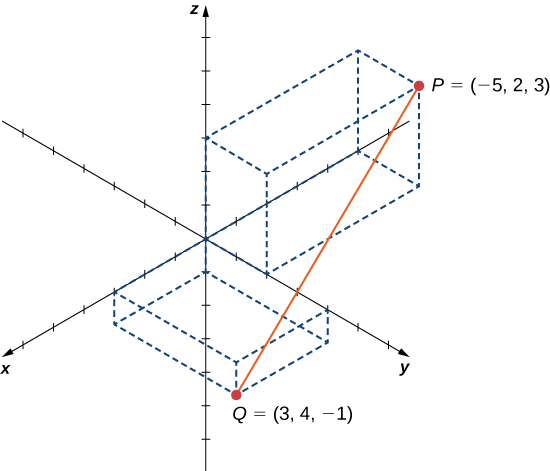
Нехай\(P=(−5,2,3)\) і\(Q=(3,4,−1)\), і припустимо, відрізок лінії\(\overline{PQ}\) утворює діаметр сфери (рис.\(\PageIndex{14}\)). Знайдіть рівняння сфери.
Рішення:
Оскільки\(\overline{PQ}\) це діаметр сфери, ми знаємо, що центр сфери є середньою\(\overline{PQ}\) точкою.Тоді,
\[C=\left(\dfrac{−5+3}{2},\dfrac{2+4}{2},\dfrac{3+(−1)}{2}\right)=(−1,3,1). \nonumber \]
Крім того, ми знаємо, що радіус сфери дорівнює половині довжини діаметра. Це дає
\[\begin{align*} r &=\dfrac{1}{2}\sqrt{(−5−3)^2+(2−4)^2+(3−(−1))^2} \\[4pt] &=\dfrac{1}{2}\sqrt{64+4+16} \\[4pt] &=\sqrt{21} \end{align*}\]
Тоді рівняння сфери\((x+1)^2+(y−3)^2+(z−1)^2=21.\)
Знайти рівняння сфери з діаметром\(\overline{PQ}\), де\(P=(2,−1,−3)\) і\(Q=(−2,5,−1).\)
- Підказка
-
Спочатку знайдіть середину діаметра.
- Відповідь
-
\[x^2+(y−2)^2+(z+2)^2=14 \nonumber \]
Опишіть множину точок, яка задовольняє,\((x−4)(z−2)=0,\) і графік множини.
Рішення
Ми повинні мати або\(x−4=0\) або\(z−2=0\), тому множина точок утворює дві площини\(x=4\) і\(z=2\) (рис.\(\PageIndex{15}\)).
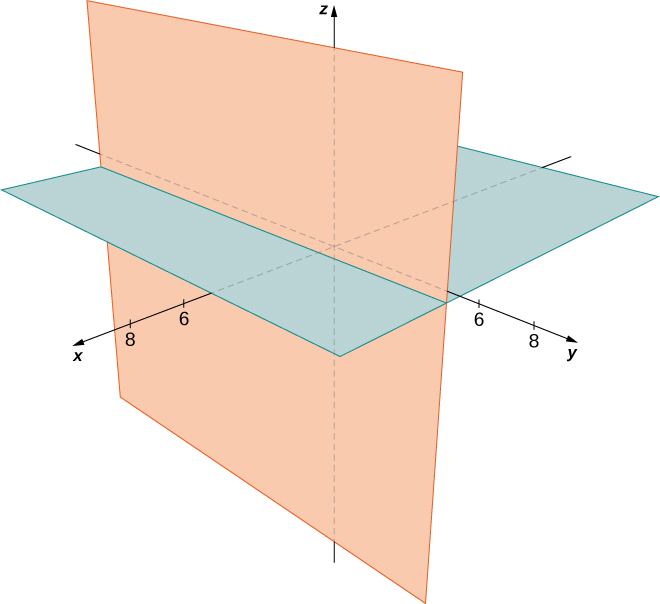
Опишіть множину точок, яка задовольняє,\((y+2)(z−3)=0,\) і графік множини.
- Підказка
-
Один з факторів повинен дорівнювати нулю.
- Відповідь
-
Безліч точок утворює дві площини\(y=−2\) і\(z=3\).
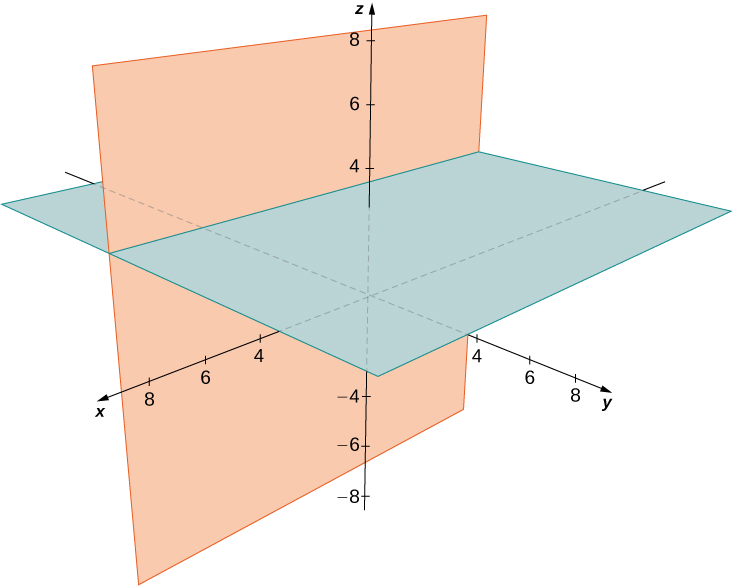
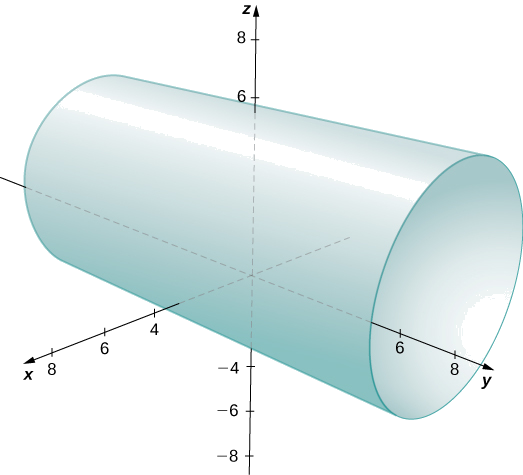
Опишіть множину точок у тривимірному просторі, що задовольняє,\((x−2)^2+(y−1)^2=4,\) і графік множини.
Рішення
The\(x\) - і \(y\)-координати утворюють коло в \(xy\)-площині радіуса\(2\), в центрі\((2,1)\). Оскільки обмеження на \(z\)-координату немає, то тривимірним результатом є круглий циліндр радіуса,\(2\) центрований на лінії з\(x=2\) і\(y=1\). Циліндр простягається на невизначений термін в\(z\) -напрямку (рис.\(\PageIndex{16}\)).
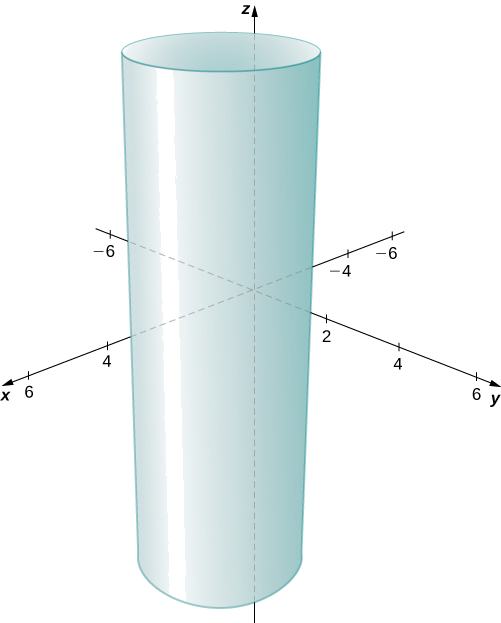
Опишіть множину точок у тривимірному просторі, що задовольняє\(x^2+(z−2)^2=16\), і зробіть графік поверхні.
- Підказка
-
Подумайте, що станеться, якщо ви побудуєте це рівняння у двох вимірах у\(xz\) -площині.
- Відповідь
-
Циліндр радіусом 4 по центру на лінії з\(x=0\) і\(z=2\).
Робота з векторами в\(ℝ^3\)
Так само, як і двовимірні вектори, тривимірні вектори - це величини як з величиною, так і напрямком, і вони представлені спрямованими відрізками ліній (стрілками). При тривимірному векторі використовуємо тривимірну стрілку.
Тривимірні вектори також можуть бути представлені у вигляді компонентів. Позначення\(\vecs{v}=⟨x,y,z⟩\) є природним продовженням двовимірного відмінка, що представляє вектор з початковою точкою в початку\((0,0,0)\), і кінцевою точкою\((x,y,z)\). Нульовим вектором є\(\vecs{0}=⟨0,0,0⟩\). Так, наприклад, тривимірний вектор\(\vecs{v}=⟨2,4,1⟩\) представлений спрямованим відрізком лінії від точки\((0,0,0)\) до точки\((2,4,1)\) (рис.\(\PageIndex{17}\)).
Векторне додавання та скалярне множення визначено аналогічно двовимірному випадку. Якщо\(\vecs{v}=⟨x_1,y_1,z_1⟩\) і\(\vecs{w}=⟨x_2,y_2,z_2⟩\) є векторами, і\(k\) є скалярним, то
\[\vecs{v}+\vecs{w}=⟨x_1+x_2,y_1+y_2,z_1+z_2⟩ \nonumber \]
і
\[k\vecs{v}=⟨kx_1,ky_1,kz_1⟩. \nonumber \]
Якщо\(k=−1,\) потім\(k\vecs{v}=(−1)\vecs{v}\) записується як\(−\vecs{v}\), а векторне віднімання визначається\(\vecs{v}−\vecs{w}=\vecs{v}+(−\vecs{w})=\vecs{v}+(−1)\vecs{w}\).
Стандартні одиничні вектори також легко поширюються на три виміри\(\hat{\mathbf i}=⟨1,0,0⟩\)\(\hat{\mathbf j}=⟨0,1,0⟩\), і\(\hat{\mathbf k}=⟨0,0,1⟩\), і ми використовуємо їх так само, як ми використовували стандартні одиничні вектори в двох вимірах. Таким чином, ми можемо зобразити\(ℝ^3\) вектор наступними способами:
\[\vecs{v}=⟨x,y,z⟩=x\hat{\mathbf i}+y\hat{\mathbf j}+z\hat{\mathbf k} \nonumber \].
\(\vecd{PQ}\)Дозволяти вектор з початковою точкою\(P=(3,12,6)\) та кінцевою точкою\(Q=(−4,−3,2)\), як показано на малюнку\(\PageIndex{18}\). Експрес як\(\vecd{PQ}\) у вигляді компонента, так і за допомогою стандартних одиничних векторів.
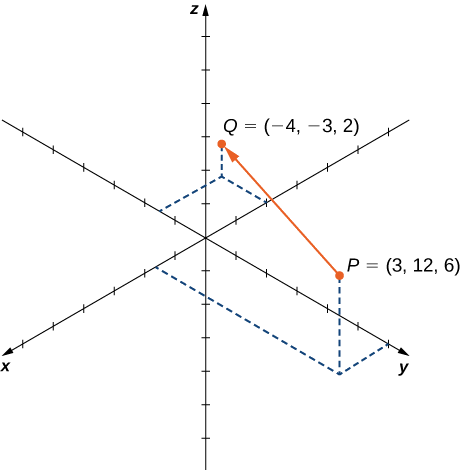
Рішення
У складовій формі
\[\begin{align*} \vecd{PQ} =⟨x_2−x_1,y_2−y_1,z_2−z_1⟩ \\[4pt] =⟨−4−3,−3−12,2−6⟩ \\[4pt] =⟨−7,−15,−4⟩. \end{align*}\]
У стандартній одиничній формі
\[\vecd{PQ}=−7\hat{\mathbf i}−15\hat{\mathbf j}−4\hat{\mathbf k}. \nonumber \]
Нехай\(S=(3,8,2)\) і\(T=(2,−1,3)\). Експрес\(\vec{ST}\) в складовій формі і в стандартній одиничній формі.
- Підказка
-
Напишіть спочатку\(\vecd{ST}\) в складовій формі. \(T\)є кінцевою точкою\(\vecd{ST}\).
- Відповідь
-
\(\vecd{ST}=⟨−1,−9,1⟩=−\hat{\mathbf i}−9\hat{\mathbf j}+\hat{\mathbf k}\)
Як описано раніше, вектори в трьох вимірах поводяться так само, як вектори в площині. Геометрична інтерпретація векторного складання, наприклад, однакова як в дво-, так і в тривимірному просторі (рис.\(\PageIndex{19}\)).
Ми вже бачили, як деякі алгебраїчні властивості векторів, такі як додавання векторів та скалярне множення, можуть бути розширені до трьох вимірів. Інші властивості можуть бути розширені аналогічним чином. Вони узагальнені тут для нашої довідки.
\(\vecs{v}=⟨x_1,y_1,z_1⟩\)\(\vecs{w}=⟨x_2,y_2,z_2⟩\)Дозволяти і бути вектори, і нехай\(k\) бути скалярним.
- Скалярне множення:\[k\vecs{v}=⟨kx_1,ky_1,kz_1⟩ \nonumber \]
- Векторне додавання:\[\vecs{v}+\vecs{w}=⟨x_1,y_1,z_1⟩+⟨x_2,y_2,z_2⟩=⟨x_1+x_2,y_1+y_2,z_1+z_2⟩ \nonumber \]
- Векторне віднімання:\[\vecs{v}−\vecs{w}=⟨x_1,y_1,z_1⟩−⟨x_2,y_2,z_2⟩=⟨x_1−x_2,y_1−y_2,z_1−z_2⟩ \nonumber \]
- Векторна величина:\[\|\vecs{v}\|=\sqrt{x_1^2+y_1^2+z_1^2} \nonumber \]
- Одиничний вектор у напрямку\(\vecs{v}\):\[\dfrac{1}{\|\vecs{v}\|}\vecs{v}=\dfrac{1}{\|\vecs{v}\|}⟨x_1,y_1,z_1⟩=⟨\dfrac{x_1}{\|\vecs{v}\|},\dfrac{y_1}{\|\vecs{v}\|},\dfrac{z_1}{\|\vecs{v}\|}⟩, \quad \text{if} \, \vecs{v}≠\vecs{0} \nonumber \]
Ми бачили, що векторне додавання у двох вимірах задовольняє комутативні, асоціативні та адитивні зворотні властивості. Ці властивості векторних операцій справедливі і для тривимірних векторів. Скалярне множення векторів задовольняє розподільну властивість, а нульовий вектор виступає в ролі адитивної ідентичності. Докази для перевірки цих властивостей у трьох вимірах - це прямі розширення доказів у двох вимірах.
Нехай\(\vecs{v}=⟨−2,9,5⟩\) і\(\vecs{w}=⟨1,−1,0⟩\) (рис.\(\PageIndex{20}\)). Знайдіть наступні вектори.
- \(3\vecs{v}−2\vecs{w}\)
- \(5\|\vecs{w}\|\)
- \(\|5 \vecs{w}\|\)
- Одиничний вектор у напрямку\(\vecs{v}\)
Рішення
а. спочатку використовуйте скалярне множення кожного вектора, потім відніміть:
\[\begin{align*} 3\vecs{v}−2\vecs{w} =3⟨−2,9,5⟩−2⟨1,−1,0⟩ \\[4pt] =⟨−6,27,15⟩−⟨2,−2,0⟩ \\[4pt] =⟨−6−2,27−(−2),15−0⟩ \\[4pt] =⟨−8,29,15⟩. \end{align*}\]
б. запишіть рівняння для величини вектора, потім скористайтеся скалярним множенням:
\[5\|\vecs{w}\|=5\sqrt{1^2+(−1)^2+0^2}=5\sqrt{2}. \nonumber \]
спершу використовуйте скалярне множення, потім знайдіть величину нового вектора. Зверніть увагу, що результат такий же, як і для частини b.:
\[\|5 \vecs{w}\|=∥⟨5,−5,0⟩∥=\sqrt{5^2+(−5)^2+0^2}=\sqrt{50}=5\sqrt{2} \nonumber \]
d Нагадаємо, що для знаходження одиничного вектора в двох вимірах ділимо вектор на його величину. Процедура однакова в трьох вимірах:
\[\begin{align*} \dfrac{\vecs{v}}{\|\vecs{v}\|} =\dfrac{1}{\|\vecs{v}\|}⟨−2,9,5⟩ \\[4pt] =\dfrac{1}{\sqrt{(−2)^2+9^2+5^2}}⟨−2,9,5⟩ \\[4pt] =\dfrac{1}{\sqrt{110}}⟨−2,9,5⟩ \\[4pt] =⟨\dfrac{−2}{\sqrt{110}},\dfrac{9}{\sqrt{110}},\dfrac{5}{\sqrt{110}}⟩ . \end{align*}\]
Нехай\(\vecs{v}=⟨−1,−1,1⟩\) і\(\vecs{w}=⟨2,0,1⟩\). Знайти одиничний вектор у напрямку\(5\vecs{v}+3\vecs{w}.\)
- Підказка
-
Почніть з написання\(5\vecs{v}+3\vecs{w}\) в складовій формі.
- Відповідь
-
\(⟨\dfrac{1}{3\sqrt{10}},−\dfrac{5}{3\sqrt{10}},\dfrac{8}{3\sqrt{10}}⟩\)
Квотербек стоїть на футбольному полі, готуючись кинути пас. Його приймач стоїть 20 ярдів вниз по полю і 15 ярд до захисника 's ліворуч. Квотербек кидає м'яч зі швидкістю 60 миль/год до приймача під кутом вгору\(30°\) (див. Наступний малюнок). Запишіть початковий вектор швидкості кулі\(\vecs{v}\), в складовій формі.
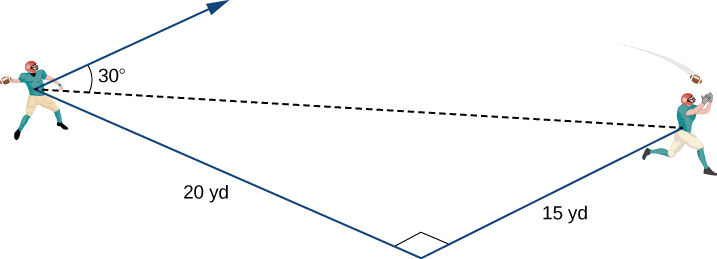
Рішення
Перше, що ми хочемо зробити, це знайти вектор в тому ж напрямку, що і вектор швидкості кулі. Потім ми масштабуємо вектор відповідним чином, щоб він мав правильну величину. Розглянемо вектор\(\vecs{w}\), що проходить від руки захисника до точки безпосередньо над головою приймача під кутом\(30°\) (див. Наступний малюнок). Цей вектор мав би такий же напрямок\(\vecs{v}\), як, але він може не мати потрібної величини.
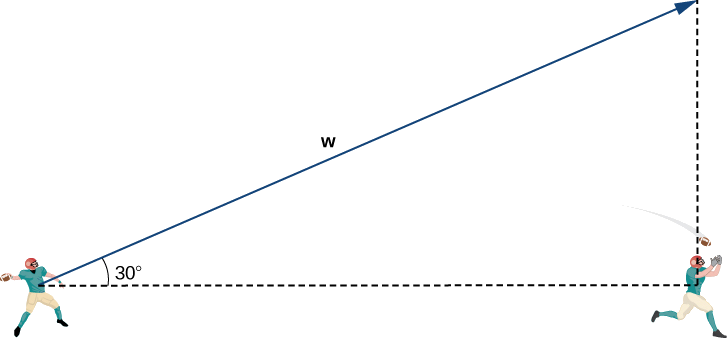
Приймач 20 ярдів вниз по полю і 15 ярд до захисника 's ліворуч. Тому пряма відстань від захисника до приймача становить
Дист від QB до приймача\(=\sqrt{15^2+20^2}=\sqrt{225+400}=\sqrt{625}=25\) yd.
Ми маємо\(\dfrac{25}{\|\vecs{w}\|}=\cos 30°.\) Тоді величина\(\vecs{w}\) задається
\(\|\vecs{w}\|=\dfrac{25}{\cos 30°}=\dfrac{25⋅2}{\sqrt{3}}=\dfrac{50}{\sqrt{3}}\)йд
і вертикальна відстань від приймача до\(\vecs{w}\) кінцевої точки
Vert dist від приймача до кінцевої точки\(\vecs{w}=\|\vecs{w}\| \sin 30°=\dfrac{50}{\sqrt{3}}⋅\dfrac{1}{2}=\dfrac{25}{\sqrt{3}}\) yd.
Потім\(\vecs{w}=⟨20,15,\dfrac{25}{\sqrt{3}}⟩\), і має той же напрямок, що і\(\vecs{v}\).
Нагадаємо, хоча, що ми розрахували величину бути\(\|\vecs{w}\|=\dfrac{50}{\sqrt{3}}\) yd, і\(\vecs{v}\) має величину\(60\) миль/год.\(\vecs{w}\) Отже, нам потрібно помножити вектор\(\vecs{w}\) на відповідну константу,\(k\). Ми хочемо знайти значення\(k\) так, що\(∥k\vecs{w}∥=60\) миль/год *. У нас є
\(\|k \vecs{w}\|=k\|\vecs{w}\|=k\dfrac{50}{\sqrt{3}}\)ярд,
так ми хочемо
\(k \left(\dfrac{50}{\sqrt{3}}\text{ yd}\right) =60\)миль/год
\(k=\dfrac{60\sqrt{3}}{50}\)миль/год/yd
\(k=\dfrac{6\sqrt{3}}{5}\)миль/год/yd.
Тоді
\(\vecs{v}=k\vecs{w}=k⟨20,15,\dfrac{25}{\sqrt{3}}⟩=\dfrac{6\sqrt{3}}{5}\;⟨20,15,\dfrac{25}{\sqrt{3}}⟩=⟨24\sqrt{3},18\sqrt{3},30⟩\).
Давайте ще раз перевіримо, що\(\|\vecs{v}\|=60\) миль/год. У нас є
\(\|\vecs{v}\|=\sqrt{(24\sqrt{3})^2+(18\sqrt{3})^2+(30)^2}=\sqrt{1728+972+900}=\sqrt{3600}=60\)миль/год.
Отже, ми знайшли правильні компоненти для\(\vecs{v}\).
Читачі, які спостерігали за одиницями виміру, може бути цікаво, що саме відбувається в цей момент: чи не ми просто змішували ярди та милі на годину? Ми цього не зробили, але причина тонка. Один із способів зрозуміти це - зрозуміти, що в цій задачі дійсно є дві паралельні системи координат: одна дає позиції вниз по полю, через поле, і вгору в повітря в одиницях ярдів; інший дає швидкість вниз по полю, через поле, і вгору в повітря в одиницях миль на годину. Вектор\(\vecs{w}\) обчислюється в системі координат положення; вектор\(\vecs{v}\) буде в системі швидкостей. Оскільки відповідні осі в кожній системі паралельні, напрямки в двох системах також паралельні, тому твердження, що\(\vecs{w}\) і\(\vecs{v}\) точка в одному напрямку є правильною. Константа\(k\), яку ми шукаємо, є коефіцієнтом перетворення між величинами цих двох векторів, перетворюючись із системи позицій на швидкість у процес. І як видно вище, наш розрахунок\(k\) виробляє потрібні одиниці для такої конверсії, а саме милі на годину на ярд.
Припустимо, захисник і приймач знаходяться в тому ж місці, що і в попередньому прикладі. На цей раз, однак, захисник кидає м'яч зі швидкістю\(40\) миль/год і кутом\(45°\). Запишіть початковий вектор швидкості кулі\(\vecs{v}\), в складовій формі.
- Підказка
-
Дотримуйтесь процесу, використаного в попередньому прикладі.
- Відповідь
-
\(v=⟨16\sqrt{2},12\sqrt{2},20\sqrt{2}⟩\)
Ключові поняття
- Тривимірна система координат будується навколо набору з трьох осей, які перетинаються під прямим кутом в одній точці, початку. \((x,y,z)\)Впорядковані трійки використовуються для опису розташування точки в просторі.
- Відстань\(d\) між точками\((x_1,y_1,z_1)\) і\((x_2,y_2,z_2)\) задається за формулою\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2}.\nonumber \]
- У трьох вимірах рівняння\(z=c\) описують\(x=a,\, y=b,\) і площини, паралельні координатним площинам.
- Стандартне рівняння сфери з центром\((a,b,c)\) і радіусом\(r\) дорівнює\[(x−a)^2+(y−b)^2+(z−c)^2=r^2. \nonumber \]
- У трьох вимірах, як і в двох, вектори зазвичай виражаються в складовій формі\(\vecs v=⟨x,y,z⟩\), або через стандартні одиничні вектори,\(\vecs v= x\,\mathbf{\hat i}+y\,\mathbf{\hat j}+z\,\mathbf{\hat k}.\)
- Властивості векторів у просторі є природним продовженням властивостей векторів у площині. \(\vecs v=⟨x_1,y_1,z_1⟩\)\(\vecs w=⟨x_2,y_2,z_2⟩\)Дозволяти і бути вектори, і нехай\(k\) бути скалярним.
Скалярне множення:
\[k\vecs{v}=⟨kx_1,ky_1,kz_1⟩ \nonumber \]
Векторне додавання:
\[\vecs{v}+\vecs{w}=⟨x_1,y_1,z_1⟩+⟨x_2,y_2,z_2⟩=⟨x_1+x_2,y_1+y_2,z_1+z_2⟩ \nonumber \]
Векторне віднімання:
\[\vecs{v}−\vecs{w}=⟨x_1,y_1,z_1⟩−⟨x_2,y_2,z_2⟩=⟨x_1−x_2,y_1−y_2,z_1−z_2⟩ \nonumber \]
Векторна величина:
\[‖\vecs{v}‖=\sqrt{x_1^2+y_1^2+z_1^2} \nonumber \]
Одиничний вектор у напрямку\(\vecs{v}\):
\[\dfrac{\vecs{v}}{‖\vecs{v}‖}=\dfrac{1}{‖\vecs{v}‖}⟨x_1,y_1,z_1⟩=⟨\dfrac{x_1}{‖\vecs{v}‖},\dfrac{y_1}{‖\vecs{v}‖},\dfrac{z_1}{‖\vecs{v}‖}⟩, \; \vecs{v}≠\vecs{0} \nonumber \]
Ключові рівняння
Відстань між двома точками в просторі:
\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2} \nonumber \]
Сфера з центром\((a,b,c)\) і радіусом\(r\):
\[(x−a)^2+(y−b)^2+(z−c)^2=r^2 \nonumber \]
Глосарій
- координатна площина
- площина, що містить дві з трьох осей координат у тривимірній системі координат, названі осями, які вона містить:\(xy\) -plane,\(xz\) -plane, або\(yz\) -plane
- правилом правої руки
- загальний спосіб визначення орієнтації тривимірної системи координат; коли права рука вигнута навколо\(z\) осі таким чином, що пальці скручуються від позитивної\(x\) -осі до позитивної\(y\) -осі, великий палець вказує у напрямку позитивної\(z\) -осі
- октанти
- вісім областей простору, створених координатними площинами
- сфера
- множина всіх точок, рівновіддалених від заданої точки, відомої як центр
- стандартне рівняння сфери
- \((x−a)^2+(y−b)^2+(z−c)^2=r^2\)описує сферу з центром\((a,b,c)\) і радіусом\(r\)
- тривимірна прямокутна система координат
- система координат, визначена трьома лініями, які перетинаються під прямим кутом; кожна точка в просторі описується впорядкованою трійкою\((x,y,z)\), яка визначає її розташування відносно визначальних осей
Дописувачі
Приклад\(\PageIndex{10}\) був змінений Дугом Болдуіном та Полом Зебургером, щоб уточнити одиниці вимірювання, які він використовує, і як він їх використовує.
Пол Зебургер також створив динамічні версії Figures\(\PageIndex{8}, \PageIndex{9}\) і\(\PageIndex{13}\) за допомогою CalcPlot3D.
