10.1: Вступ до декартових координат у просторі

Last updated
Save as PDF

Page ID: 60751

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

До цього моменту в цьому тексті ми розглядали математику в двовимірному світі. Ми побудували графіки на$y$ площині$x$ - за допомогою прямокутних і полярних координат і знайшли площу областей на площині. Ми розглянули властивості твердих об'єктів, такі як об'єм і площа поверхні, але лише спочатку визначаючи криву в площині, а потім обертаючи її з площини.

Хоча є чудова математика для вивчення в «2D», ми живемо в «3D» світі, і врешті-решт ми захочемо застосувати математику за участю цього третього виміру. У цьому розділі ми вводимо декартові координати в просторі та досліджуємо основні поверхні. Це закладе основу для більшої частини того, що ми робимо в решті тексту.

Кожна точка$P$ в просторі може бути представлена впорядкованою трійкою$P=(a,b,c)$$a$, де,$b$ і$c$ представляти відносне положення$P$ уздовж$x$ -,$y$ - і$z$ -осей відповідно. Кожна вісь перпендикулярна двом іншим.

Візуалізація точок у просторі на папері може бути проблематичною, оскільки ми намагаємося представити тривимірне поняття на двовимірному середовищі. Ми не можемо намалювати три лінії, що представляють три осі, в яких кожна лінія перпендикулярна іншим двом. Незважаючи на це питання, існують стандартні конвенції для побудови фігур у просторі, які ми обговоримо, які є більш ніж адекватними.

Однією з умовностей є те, що осі повинні відповідати правилу правої руки. Це правило стверджує, що коли вказівний палець правої руки витягнутий у напрямку позитивної$x$ -осі, а середній палець (зігнутий «всередину» так перпендикулярно долоні) вказує уздовж позитивної$y$ -осі, то витягнутий великий палець буде вказувати в сторону позитивного $z$-вісь. (Це може зайняти певну думку, щоб перевірити це, але ця система за своєю суттю відрізняється від тієї, яка створена за допомогою «правила лівої руки».). Існує два популярних методу малювання осей, які ми коротко обговоримо.

На малюнку$\PageIndex{1}$ ми бачимо точку,$P=(2,1,3)$ нанесену на набір осей. Основна умова тут полягає в тому, що$y$ площина$x$ - малюється стандартним способом, з$z$ -віссю вниз вліво. Перспектива полягає в тому, що папір представляє$y$ площину$x$ - і позитивна$z$ вісь йде вгору, зі сторінки. Цей спосіб воліють багато інженерів. Оскільки важко сказати, де одна точка лежить по відношенню до всіх осей, були додані пунктирні лінії, щоб побачити, наскільки далеко вздовж кожної осі лежить точка.

Малюнок$\PageIndex{1}$: Побудова точки$P=(2,1,3)$ в просторі.

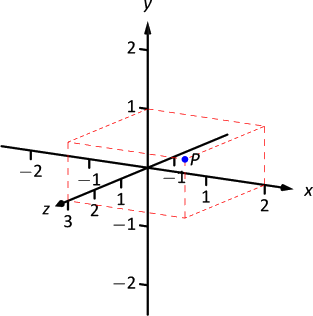
Можна також розглянути$x$ -$y$ площину як горизонтальну площину в, скажімо, кімнаті, де позитивна$z$ -вісь спрямована вгору. Коли один крок назад і дивиться на цю кімнату, можна намалювати осі, як показано на малюнку$\PageIndex{2}$. Цю ж точку$P$ малюють, знову пунктирними лініями. Таку точку зору воліє більшість математиків, і є умовністю, прийнятою цим текстом.

Рисунок$\PageIndex{2}$: Побудова точки$P=(2,1,3)$ в просторі з перспективою, яка використовується в цьому тексті.

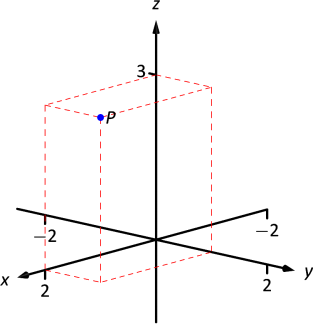
Примітка

Поки осі координат розташовані так, щоб вони слідували правилу правої руки, не має значення, як осі намальовані на папері.

Вимірювання відстані

Дуже важливо знати, як вимірювати відстані між точками в просторі. Формула для цього заснована на вимірюванні відстані в площині і відома (в обох контекстах) як евклідова міра відстані.

Визначення 48: відстань у просторі

Дозволяти$P=(x_1,y_1,z_1)$ і$Q = (x_2,y_2,z_2)$ бути точки в просторі. Відстань$D$ між$P$ і$Q$ становить

\[D = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}.\]

Ми посилаємося на відрізок лінії, який з'єднує точки$P$ і$Q$ в просторі як$\overline{PQ}$, і посилаємося на довжину цього відрізка як$||\overline{PQ}||$. Наведена вище формула відстані дозволяє обчислити довжину цього відрізка.

Приклад$\PageIndex{1}$: Length of a line segment

Нехай$P = (1,4,-1)$ і нехай$Q = (2,1,1)$. Намалюйте відрізок лінії$\overline{PQ}$ і знайдіть його довжину.

Рішення

Точки$P$ і$Q$ нанесені на малюнку$\PageIndex{3}$; особливого розгляду не потрібно робити, щоб намалювати відрізок лінії, що з'єднує ці дві точки; просто з'єднайте їх прямою лінією.

Малюнок$\PageIndex{3}$: Побудова точок$P$ і$Q$ в прикладі$\PageIndex{1}$.

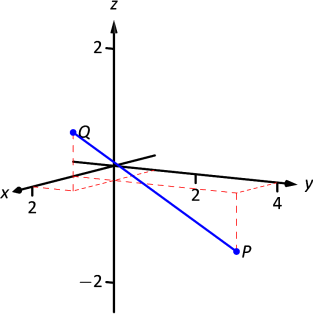
Не можна насправді виміряти цей рядок на сторінці і вивести щось значуще; її справжня довжина повинна вимірюватися аналітично. Застосовуючи визначення 48, ми маємо

\[||\overline{PQ}|| = \sqrt{(2-1)^2+(1-4)^2+(1-(-1))^2} = \sqrt{14}\approx 3.74.\]

Сфери

Подібно до того, як коло - це множина всіх точок на площині, рівновіддаленій від заданої точки (її центру), сфера - це сукупність усіх точок у просторі, які є рівновіддаленими від заданої точки. Визначення 48 дозволяє записати рівняння сфери. Ми починаємо з точки$C = (a,b,c)$, яка повинна бути центром сфери з радіусом$r$. Якщо точка$P=(x,y,z)$ лежить на сфері, то$P$ це$r$ одиниці з$C$; тобто

\[||\overline{PC}|| = \sqrt{(x-a)^2+(y-b)^2+(z-c)^2} = r.\]

Квадратуючи обидві сторони, ми отримуємо стандартне рівняння сфери в просторі з центром в$C=(a,b,c)$ радіусі$r$, як зазначено в наступній ключовій ідеї.

КЛЮЧОВА ІДЕЯ 45: СТАНДАРТНЕ РІВНЯННЯ СФЕРИ У ПРОСТОРІ

Стандартне рівняння сфери з радіусом$r$, центрованим по центру$C=(a,b,c)$, дорівнює\[(x-a)^2+(y-b)^2+(z-c)^2=r^2.\]

Приклад$\PageIndex{2}$: Equation of a sphere

Знайти центр і радіус сфери, визначені$x^2+2x+y^2-4y+z^2-6z=2.$

Рішення

Щоб визначити центр і радіус, треба поставити рівняння в стандартному вигляді. Для цього потрібно виконати квадрат (три рази).

\ [\ почати {вирівнювати*} х
^ 2+2x+y^2-4y+z ^ 2-6z&= 2\\
(x^2+2x+1) + (y^2-4y+4) + (z^2-6z+9) - 14 &= 2\\
(x+1) ^2 + (y-2) ^2 + (z-3) ^2 &= 16
\ кінець {вирівнювати*}]

Сфера зосереджена в центрі$(-1,2,3)$ і має радіус 4.

Рівняння сфери є прикладом неявної функції, що визначає поверхню у просторі. У випадку сфери, змінні$x$,$y$ і всі$z$ використовуються. Зараз ми розглянемо ситуації, коли визначаються поверхні, де одна або дві з цих змінних відсутні.

Вступ до літаків у космосі

Осі координат природно визначають три площини (показано на малюнку$\PageIndex{4}$), координатні площини:$y$ площину$x$ - площину,$z$ площину$y$ - і$z$ площину$x$ -. $x$$y$Площина - характеризується як множина всіх точок у просторі, де$z$ значення -дорівнює 0. Це, власне, дає нам рівняння, яке описує цю площину:$z=0$. Аналогічно,$z$ площина$x$ - це всі точки, де$y$ значення -дорівнює 0, що характеризується$y=0$.

10.4. PNG — Малюнок$\PageIndex{4}$: Координатні площини.

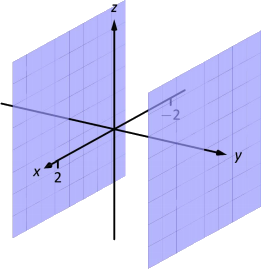
Рівняння$x=2$ описує всі точки в просторі, де$x$ значення -дорівнює 2. Це площина, паралельна$y$ -$z$ координатної площині, зображеної на малюнку$\PageIndex{5}$.

10.5.PNG — Малюнок$\PageIndex{5}$: Літак$x=2$.

Приклад$\PageIndex{3}$: Regions defined by planes

Намалюйте область, визначену нерівностями$-1\leq y\leq 2$.

Рішення

Регіон - це всі точки між площинами$y=-1$ і$y=2$. Ці площини намальовані на малюнку$\PageIndex{6}$, які паралельні$x$ -$z$ площині. Таким чином область поширюється нескінченно в$z$ напрямках$x$ і обмежується площинами в$y$ напрямку.

Рисунок$\PageIndex{6}$: Намальовування меж області у прикладі$\PageIndex{3}$.

Циліндри

Рівняння,$x=1$ очевидно, не вистачає$z$ змінних$y$ і, тобто він визначає точки, де$y$ і$z$ координати можуть приймати будь-яке значення. Тепер розглянемо рівняння$x^2+y^2=1$ в просторі. У площині це рівняння описує коло радіусом 1, центрований у початку. У просторі$z$ координата не вказується, тобто вона може приймати будь-яке значення. На малюнку$\PageIndex{7a}$ ми показуємо частину графіка рівняння,$x^2+y^2=1$ намалювавши 3 кола: нижня має константу$z$ -значення$-1.5$, середня має$z$ -значення 0, а верхнє коло має$z$ -значення 1. Поклавши всі можливі$z$ -значення, отримуємо поверхню, зображену на малюнку$\PageIndex{7b}$.
Ця поверхня виглядає як «трубка», або «циліндр»; математики називають цю поверхню циліндром з зовсім іншої причини.

10.8.ПНГ — Малюнок$\PageIndex{7}$: Ескіз$x^2+y^2=1$.

Визначення 49: ЦИЛІНДР, директриса та постанови

$C$Дозволяти крива в площині і$L$ нехай лінія не паралельна$C$. Циліндр - це сукупність усіх ліній, паралельних до$L$ того, що проходять$C$. Крива$C$ - це директриса циліндра, а лінії - постанови.

У цьому тексті розглядаються криві,$C$ які лежать в площинях, паралельних одній з координатних площин, і лінії,$L$ які перпендикулярні цим площинам, утворюючи правильні циліндри. Таким чином, директриса може бути визначена за допомогою рівнянь, що включають 2 змінні, і правила будуть паралельні осі 3$^\text{rd}$ змінної.

У прикладі, що передує визначенню, крива$x^2+y^2=1$ в$y$ площині$x$ - це директриса, а правила - лінії, паралельні$z$ -осі. (Будь-яке коло, показане на малюнку 10.8, можна вважати директрисою; ми просто вибираємо ту, де$z=0$.) Зразки постанов також можна подивитися в частині (б) малюнка. Більше прикладів допоможуть нам розібратися в цьому визначенні.

Приклад$\PageIndex{4}$: Graphing cylinders

Графік циліндра наступних циліндрів.

$z=y^2$
$x=\sin z$

Рішення

Ми можемо розглядати рівняння$z=y^2$ як параболу в$z$ площині$y$ -, як показано на малюнку$\PageIndex{8a}$. Як$x$ не видно в рівнянні, постанови представляють собою лінії через цю параболу паралельно$x$ -осі, показані на малюнку$\PageIndex{8b}$. Ці постанови дають загальне уявлення про те, як виглядає поверхня, намальована в (с).

Малюнок$\PageIndex{8}$: Ескіз циліндра, визначеного$z=y^2$.

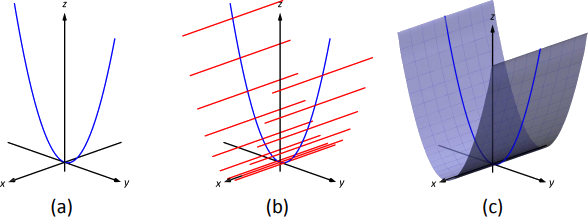
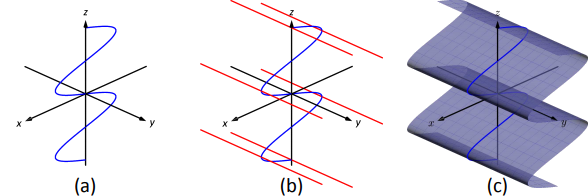
Ми можемо розглядати рівняння$x=\sin z$ як синусоїдальну криву, яка існує в$z$ площині$x$ -, як показано на малюнку$\PageIndex{9a}$. Правила паралельні$y$ осі, оскільки змінна$y$ не відображається в рівнянні$x=\sin z$; деякі з них показані на малюнку$\PageIndex{9b}$. Поверхня показана в частині (с) малюнка.

Малюнок$\PageIndex{9}$: Ескіз циліндра, визначеного$x=\sin z$.

Поверхні революції

Одним із застосувань інтеграції, яке ми дізналися раніше, було знайти об'єм твердих тіл обертання - твердих тіл, утворених обертанням кривої навколо горизонтальної або вертикальної осі. Ми зараз розглянемо, як знайти рівняння поверхні такого твердого тіла.

Розглянемо поверхню, утворену$y=\sqrt{x}$ обертанням навколо$x$ -осі. Поперечні перерізи цієї поверхні паралельні$y$ -$z$ площині є колами, як показано на малюнку$\PageIndex{1a}$. Кожне коло має рівняння форми$y^2+z^2=r^2$ для деякого радіуса$r$. Радіус є функцією$x$; насправді, це$r(x) = \sqrt{x}$. Таким чином, рівняння поверхні, показане на малюнку$\PageIndex{10b}$, є$y^2+z^2=(\sqrt{x})^2.$

10.10.ПНГ — Малюнок$\PageIndex{10}$: Введення поверхонь обертання.

Узагальнюємо наведені вище принципи, щоб дати рівняння поверхонь, утворених обертовими кривими навколо осей координат.

КЛЮЧОВА ІДЕЯ 46: ПОВЕРХНІ ОБЕРТАННЯ, ЧАСТИНА 1

$r$Дозволяти функція радіуса.

Рівняння поверхні, утвореної обертовою$y=r(x)$ або$z=r(x)$ навколо$x$ -осі, є$y^2+z^2=r(x)^2$.
Рівняння поверхні, утвореної обертовою$x=r(y)$ або$z=r(y)$ навколо$y$ -осі, є$x^2+z^2=r(y)^2$.
Рівняння поверхні, утвореної обертовою$x=r(z)$ або$y=r(z)$ навколо$z$ -осі, є$x^2+y^2=r(z)^2$.

Приклад$\PageIndex{5}$: Finding equation of a surface of revolution

Нехай$y=\sin z$ далі$[0,\pi]$. Знайдіть рівняння поверхні обертання, утвореної обертанням$y=\sin z$ навколо$z$ -осі.

Рішення

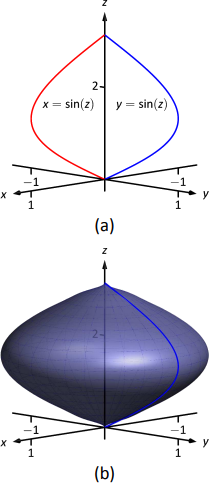
Використовуючи Key Idea 46, ми знаходимо рівняння поверхні має$x^2+y^2=\sin^2z$. Крива намальована на малюнку,$\PageIndex{11a}$ а поверхня намальована на малюнку$\PageIndex{11b}$.

Зверніть увагу, як поверхня (а значить і отримане рівняння) однакова, якщо ми почали з кривої$x=\sin z$, яка також намальована на малюнку$\PageIndex{11a}$.

Малюнок$\PageIndex{11}$: Обертається навколо$y=\sin z$ осі z у прикладі$\PageIndex{5}$.

Цей конкретний спосіб створення поверхонь обертання обмежений. Наприклад, у розділі 7.3 ми знайшли об'єм твердого тіла, утвореного$y=\sin x$ обертанням навколо$y$ -осі. Наш сучасний метод формування поверхонь може обертатися лише$y=\sin x$ навколо$x$ -осі. Спроба переписати$y=\sin x$ як функцію не тривіальна, оскільки просто написання дає$x=\sin^{-1}y$ лише частину регіону,$y$ який ми бажаємо.

Те, що ми хочемо, - це спосіб написання поверхні обертання, утвореної$y=f(x)$ обертанням навколо$y$ -осі. Ми починаємо з того, що спочатку визнаємо, що ця поверхня така ж, як обертається навколо$z=f(x)$$z$ -осі. Це дасть нам більш природний спосіб перегляду поверхні.

Значення of$x$ - це вимірювання відстані від$z$ -осі. На відстані$r$ намічаємо a$z$ -висоту$f(r)$. При обертанні$f(x)$ навколо$z$ -осі, ми хочемо, щоб всі точки на відстані$r$ від$z$ -осі в$y$ площині$x$ - мали$z$ -висоту$f(r)$. Всі такі точки задовольняють$r^2=x^2+y^2$ рівнянню; отже$r=\sqrt{x^2+y^2}$. Заміна$r$$\sqrt{x^2+y^2}$ на in$f(r)$ дає$z=f(\sqrt{x^2+y^2})$. Це рівняння поверхні.

КЛЮЧОВА ІДЕЯ 47: ПОВЕРХНІ РЕВОЛЮЦІЇ, ЧАСТИНА 2

Дозволяти$z=f(x)$$x\geq 0$, бути кривою в$x$ -$z$ площині. Поверхня, утворена обертанням цієї кривої навколо$z$ -осі, має рівняння$z=f \left(\sqrt{x^2+y^2} \right)$.

Приклад$\PageIndex{6}$: Finding equation of surface of revolution

Знайдіть рівняння поверхні, знайденої обертанням$z=\sin x$ навколо$z$ -осі.

Рішення

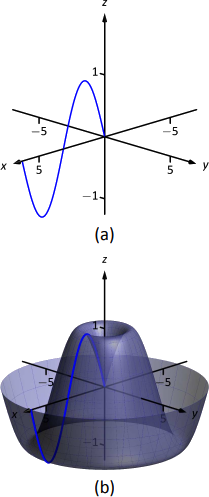
Використовуючи Key Idea 47, поверхня має рівняння$z=\sin \left(\sqrt{x^2+y^2} \right)$. Крива і поверхня зображені на малюнку$\PageIndex{12}$.

Малюнок$\PageIndex{12}$: Обертається навколо$z=\sin x$ осі z у прикладі$\PageIndex{6}$.

Квадричні поверхні

Сфери, площини та циліндри є важливими поверхнями для розуміння. Ми зараз розглянемо один останній тип поверхні, чотирикутну поверхню. Визначення може виглядати залякуючим, але ми покажемо, як проаналізувати ці поверхні освітлюючим способом.

Визначення 50: КВАДРАТНА ПОВЕРХНЯ

Квадрична поверхня - це графік загального рівняння другого ступеня у трьох змінних:

\[Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Iz+J=0.\]

Коли коефіцієнти$D$,$E$ або не$F$ дорівнюють нулю, основні форми квадратних поверхонь обертаються в просторі. Ми зупинимося на квадратних поверхнях, де ці коефіцієнти дорівнюють 0; обертання розглядати не будемо. Існує шість основних квадратичних поверхонь: еліптичний параболоїд, еліптичний конус, еліпсоїд, гіперболоїд одного листа, гіперболоїд двох аркушів і гіперболічний параболоїд.

Вивчаємо кожну форму, розглядаючи сліди, тобто перетину кожної поверхні з площиною, паралельною координатній площині. Наприклад, розглянемо еліптичний параболоїд$z= x^2/4+y^2$, показаний на малюнку 10.13. Якщо ми перетинаємо цю форму з$z=d$ площиною (тобто$z$ замінити на$d$), то маємо рівняння:

\[d = \frac{x^2}4+y^2.\]

Розділіть обидві сторони на$d$:

\[1 = \frac{x^2}{4d} + \frac{y^2}{d}.\]

Це описує еліпс - тому поперечні перерізи, паралельні$x$$y$ координатній площині - це еліпси. Цей еліпс намальований на малюнку$\PageIndex{13}$.

10,1.PNG — Малюнок$\PageIndex{13}$: Еліптичний параболоїд$z=x^2/4+y^2$.

Тепер розглянемо поперечні перерізи, паралельні$x$ -$z$ площині. Наприклад, дозволяючи$y=0$ дає рівняння$z=x^2/4$, явно параболу. Перетин з площиною$x=0$ дає поперечний переріз, який визначається$z=y^2$, інша парабола. Ці параболи також намальовані на малюнку.

Таким чином ми бачимо, звідки еліптичний параболоїд отримує свою назву: одні поперечні перерізи - еліпси, а інші - параболи.

Такий аналіз можна зробити з кожною з квадратних поверхонь. Наведемо зразкове рівняння кожного, надаємо ескіз з репрезентативними слідами, опишемо ці сліди.

еліптичний параболоїд,$z=\frac{x^2}{a^2}+\frac{y^2}{b^2}$

$еліптичний par.PNG$

Одна змінна в рівнянні еліптичного параболоїда буде піднята до першого ступеня; вище, це$z$ змінна. Параболоїд буде «відкриватися» у напрямку осі цієї змінної. Таким чином$x= y^2/a^2+z^2/b^2$, являє собою еліптичний параболоїд, який відкривається вздовж$x$ -осі.

Множення правої сторони на$(-1)$ визначає еліптичний параболоїд, який «відкривається» у зворотному напрямку.

Еліптичний конус,$ z^2=\frac{x^2}{a^2}+\frac{y^2}{b^2}$

$еліптичний cone.PNG$

Можна переписати рівняння як$z^2-x^2/a^2-y^2/{b^2} = 0$. Одна змінна з позитивним коефіцієнтом відповідає осі, по якій «відкриваються» конуси.

еліпсоїд,$ \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$

$ellipsoid.PNG$
Якщо$a=b=c\neq0$, еліпсоїд — це сфера з радіусом$a$; порівняйте з Key Idea 45.

Гіперболоїд одного аркуша,$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$

$гіперболоїд одного sheet.PNG$

Одна змінна з негативним коефіцієнтом відповідає осі, по якій «відкриває» гіперболоїд.

Гіперболоїд двох аркушів,$ \frac{z^2}{c^2}-\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

$гіперболоїд 2 shhet.PNG$

Одна змінна з позитивним коефіцієнтом відповідає осі, по якій «відкриває» гіперболоїд. У ілюстрованому випадку, коли$|d|<|c|$, немає і сліду.

гіперболічний параболоїд,$ z=\frac{x^2}{a^2}-\frac{y^2}{b^2}$

$гіперболічний parab.PNG$

Параболічні сліди відкриються вздовж осі однієї змінної, яка піднята до першої потужності.

Приклад$\PageIndex{7}$: Sketching quadric surfaces

Намалюйте квадратну поверхню, визначену заданим рівнянням.

$y=\frac{x^2}{4}+\frac{z^2}{16}$
$ x^2+\frac{y^2}{9}+\frac{z^2}{4}=1.$
$ z=y^2-x^2$.

Рішення

$ y=\frac{x^2}{4}+\frac{z^2}{16}$: Спочатку

ми ідентифікуємо квадрік за шаблоном - узгодження з рівняннями, наведеними раніше. Лише дві поверхні мають рівняння, де одна змінна піднімається до першого ступеня, еліптичний параболоїд і гіперболічний параболоїд. В останньому випадку інші змінні мають різні ознаки, тому зробимо висновок, що це описує гіперболічний параболоїд. Оскільки змінна з першою потужністю є$y$, відзначимо, що параболоїд відкривається вздовж$y$ -осі.

Щоб зробити пристойний ескіз від руки, нам потрібно лише намалювати кілька слідів. При цьому сліди$x=0$ і$z=0$ утворюють параболи, які окреслюють фігуру.

$x=0$: Слідом є парабола$y=z^2/16$

$z=0$: слід - це парабола$y=x^2/4$.

Графік кожного сліду у відповідній площині створює ескіз, як показано на малюнку$\PageIndex{14a}$. Цього достатньо, щоб дати уявлення про те, як виглядає параболоїд. Поверхня заповнюється на рис$\PageIndex{14b}$.

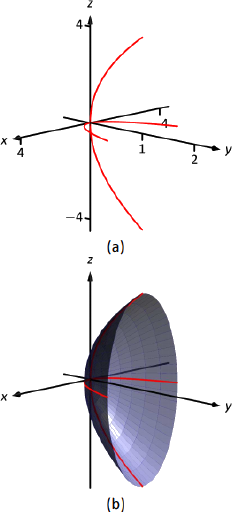
$imageedit_28_3500413797.png$
Малюнок$\PageIndex{14}$: Ескіз еліптичного параболоїда.

$ x^2+\frac{y^2}{9}+\frac{z^2}{4}=1:$

Це еліпсоїд. Ми можемо отримати гарне уявлення про його форму, намалювавши сліди в координатних площинях.

$x=0$: Слідом є еліпс$\frac{y^2}{9}+\frac{z^2}{4}=1$. Велика вісь знаходиться вздовж$y$ —осі довжиною 6 (як$b=3$, довжина осі 6); незначна вісь вздовж$z$ -осі довжиною 4.

$y=0$: трасування - це еліпс$ x^2+\frac{z^2}{4}=1.$ Велика вісь знаходиться вздовж$z$ -осі, а незначна вісь має довжину 2 вздовж$x$ -осі.

$z=0$: Трасування - це$ x^2+\frac{y^2}{9}=1,$ еліпс з великою віссю вздовж$y$ -осі.

Графік кожного сліду у відповідній площині створює ескіз, як показано на малюнку$\PageIndex{15a}$. Заповнення поверхні дає малюнок малюнок$\PageIndex{15b}$.

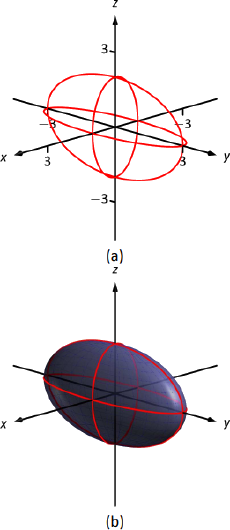
$imageedit_32_7724888216.png$
Малюнок$\PageIndex{15}$: Ескіз еліпсоїда.
$ z=y^2-x^2$:

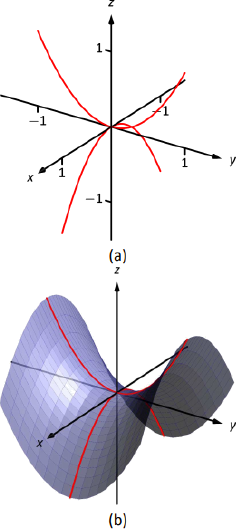
Це визначає гіперболічний параболоїд, дуже схожий на той, що показаний у галереї квадратних розділів. Розглянемо сліди в$x-z$ літаках$y-z$ і

$x=0$:: слід$z=y^2$, парабола відкривається в$y-z$ площині.

$y=0$: Слід$z=-x^2$, парабола відкривається вниз в$x-z$ літаку.

Ескіз цих двох парабол дає ескіз, подібний до того, що на малюнку Рисунок$\PageIndex{16a}$, а заповнення поверхні дає ескіз, як Рисунок$\PageIndex{16b}$.

Малюнок$\PageIndex{16}$: Ескіз гіперболічного параболоїда.

Приклад$\PageIndex{8}$: Identifying quadric surfaces

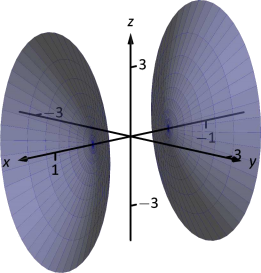
Розглянемо квадратну поверхню, показану на малюнку$\PageIndex{17}$. Яке з наведених нижче рівнянь найкраще підходить для цієї поверхні?

\ [\ nomumber\ begin {вирівнювання}
(a)\, & x^2-y^2-\ frac {z^2} {9} =0\ qquad\ qquad & (c)\, z^2-x^2-y^2=1\\ nonumber
(b)\, & x^2-y^2-z^2=1\ qquad\ qquad & (d\), 4x^2-y^2-\ розрив {z^2} 9=1
\ кінець {вирівняти}\]

Рішення

На зображенні чітко відображається гіперболоїд з двох аркушів. Галерея повідомляє нам, що рівняння матиме форму, подібну до$\frac{z^2}{c^2}-\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$.

Ми можемо відразу виключити варіант (а), оскільки константа в цьому рівнянні не дорівнює 1.

Гіперболоїд «відкривається» уздовж$x$ -осі, тобто$x$ повинна бути єдина змінна з позитивним коефіцієнтом, що виключає (с).

Гіперболоїд ширше в$z$ -напрямку, ніж в$y$ -напрямку, тому нам потрібно рівняння де$c>b$. Це усуває (б), залишаючи нас з (d). Ми повинні переконатися, що рівняння, наведене в (d)$4x^2-y^2-\frac{z^2}9=1$, підходить.

Ми вже встановили, що це рівняння описує гіперболоїд з двох аркушів, який відкривається в$x$ -напрямку і ширше в$z$ -напрямку, ніж в$y$. Тепер зверніть увагу на коефіцієнт$x$ -термін. Рерайтинг$4x^2$ в стандартному вигляді, у нас є:$ 4x^2 = \frac{x^2}{(1/2)^2}$. Таким чином$z=0$, коли$y=0$ і,$x$ повинно бути$1/2$; тобто кожен гіперболоїд «починається» в$x=1/2$. Це відповідає нашій фігурі.

Робимо висновок, що$ 4x^2-y^2-\frac{z^2}9=1$ найкраще підходить графіку.

Цей розділ ввів точки у просторі та показав, як рівняння можуть описувати поверхні. Наступні розділи досліджують вектори, важливий математичний об'єкт, який ми будемо використовувати для вивчення кривих у просторі.

Дописувачі та атрибуція

Template:ContribApexCalc