6.2: Площа паралелограма

У паралелограмі$ABCD$ малюнка сторона$AB$ називається основою$\PageIndex{1}$, а відрізок лінії$DE$ називається висотою або висотою. Основа може бути будь-якою стороною паралелограма, хоча зазвичай вона вибирається як сторона, на якій паралелограм, здається, спирається. Висота являє собою лінію, проведену перпендикулярно підставі з протилежного боку.

Малюнок$\PageIndex{1}$: Паралелограм$ABCD$ з основою$b$ і висотою$h$.

Теорема$\PageIndex{1}$

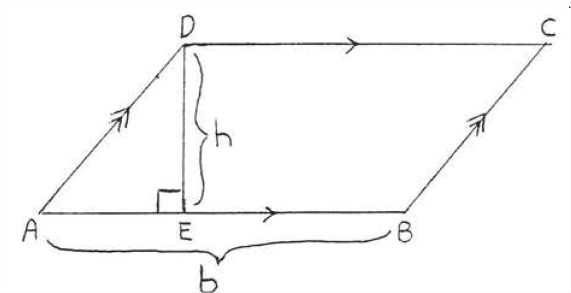
Площа паралелограма дорівнює його основи, що помножується на висоту.

$$A = bh$$

Доказ

Малюємо$BF$ і$CF$ як показано на малюнку$\PageIndex{2}$. $\angle A=\angle CBF$,$\angle AED=\angle F=90^{\circ},$ і$AD=BC$. Тому$\triangle ADE \cong \triangle BCF$ і площа$\triangle ADE$ дорівнює площі$\triangle BCF$. У нас є:

$$\begin{array} {rcl} {\text{Area of parallelogram } ABCD} & = & {\text{Area of } \triangle ADE + \text{ Area of trapezoid } BCDE} \\ {} & = & {\text{Area of } \triangle BCF + \text{ Area of trapezoid } BCDE} \\ {} & = & {\text{Area of rectangle } CDEF} \\ {} & = & {bh.} \end{array}$$

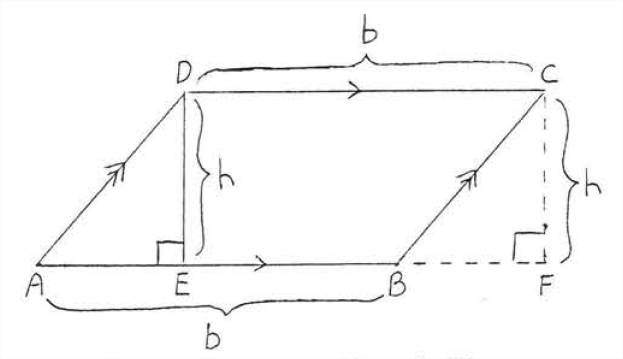
Малюнок$\PageIndex{2}$: Малюємо$BF$ і$CF$.

Приклад$\PageIndex{1}$

Знайдіть площу і периметр$ABCD$:

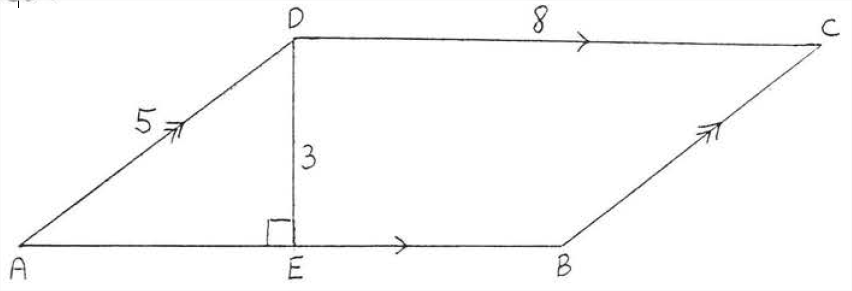
Рішення

$b = AB = CD = 8$,$h = 3$. $\text{Area } = bh = (8)(3) = 24$. $AB = CD=8$. $BC = AD =5$. Периметр = 8 + 8 + 5 + 5 = 26.

Відповідь:

Площа = 24, Периметр = 26.

Приклад$\PageIndex{2}$

Знайдіть площу і периметр$ABCD$:

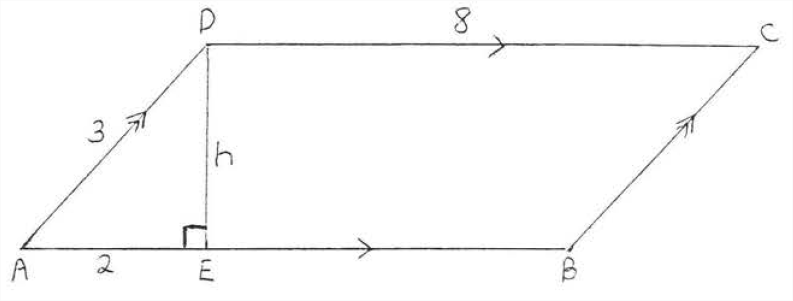
Рішення

Застосуйте теорему Піфагора до прямокутного трикутника$ADE$:

$$\begin{array} {rcl} {\text{AE}^2 + \text{DE}^2} & = & {\text{AD}^2} \\ {2^2 + h^2} & = & {3^2} \\ {4 + h^2} & = & {9} \\ {h^2} & = & {5} \\ {h} & = & {\sqrt{5}} \end{array}$$

Площа =$bh = (8)(\sqrt{5}) = 8\sqrt{5}$

Периметр$=8+8+3+3=22$

Відповідь:$A = 8 \sqrt{5}, P = 22$.

Приклад$\PageIndex{3}$

Знайти площу і периметр до найближчої десятої

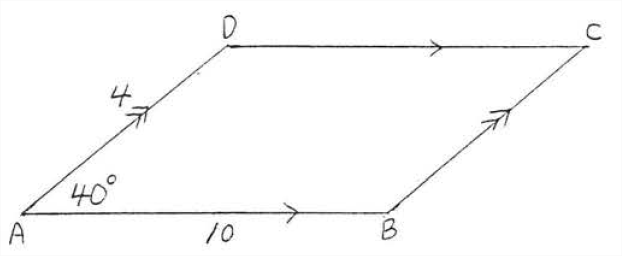
Рішення

Щоб знайти площу, ми повинні спочатку знайти висоту$h$ (рис.$\PageIndex{3}$), Використовуючи тригонометрію

Малюнок$\PageIndex{3}$: Малюємо по висоті$h$.

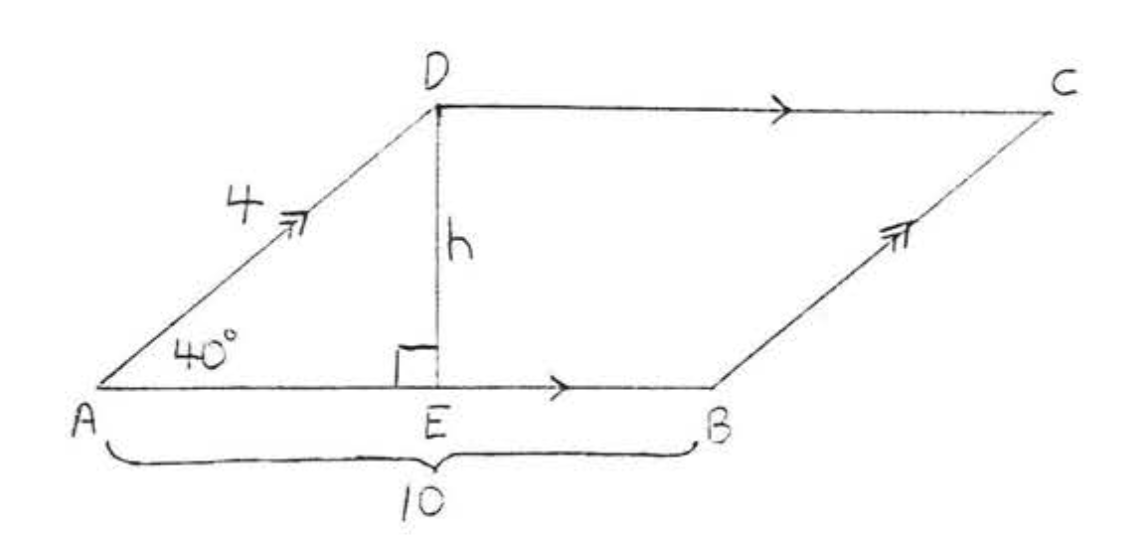
$\begin{array} {rcl} {\sin 40^{\circ}} & = & {\dfrac{h}{4}} \\ {(4) .6428} & = & {\dfrac{h}{\cancel{4}} (\cancel{4})} \\ {2.5712} & = & {h} \end{array}$

Площа =$bh = (10)(2.5712) = 25.712 - 25.7$

Периметр = 10 + 10 + 4 + 4 = 28.

Відповідь

$A = 25.7$,$P = 28$.

Приклад$\PageIndex{4}$

Знайти,$x$ якщо площа 21.

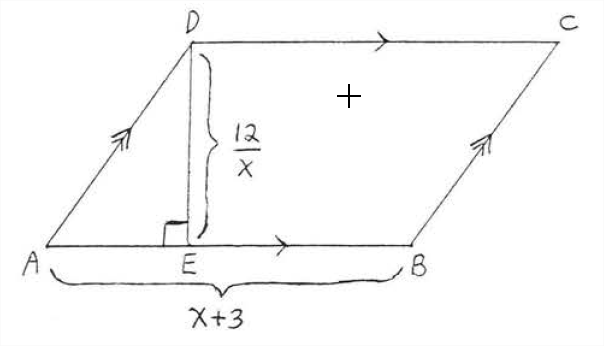
Рішення

$$\begin{array} {rcl} {A} & = & {bh} \\ {21} & = & {(x + 3)(\dfrac{12}{x})} \\ {(x)21} & = & {(x + 3)(\dfrac{12}{\cancel{x}})(\cancel{x})} \\ {21x} & = & {12x + 36} \\ {9x} & = & {36} \\ {x} & = & {4} \end{array}$$

Перевірка:

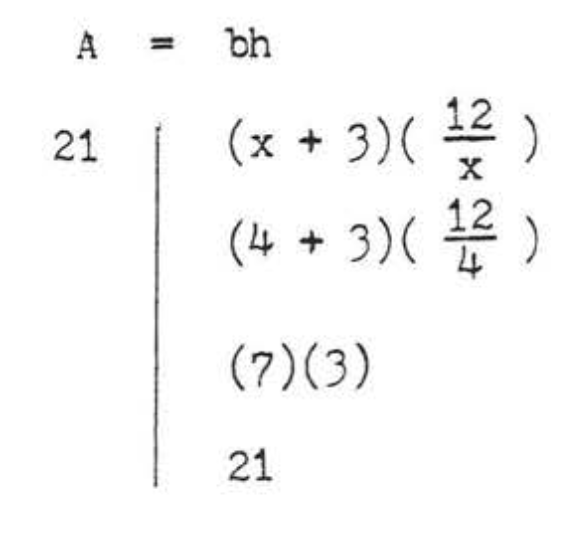
Відповідь

$x = 4$.

Приклад$\PageIndex{5}$

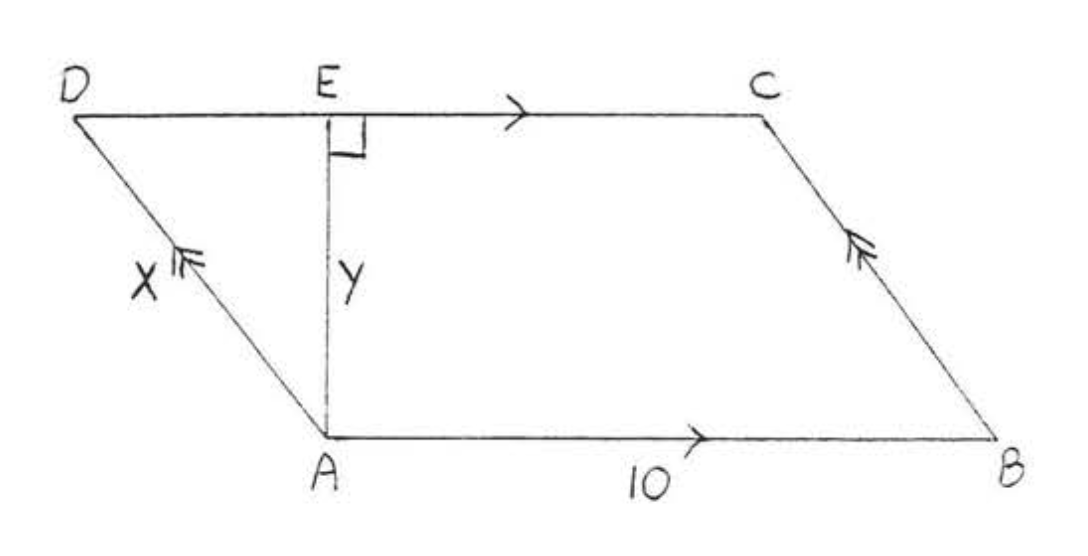
Площа паралелограма$ABCD$ дорівнює 48, а периметр - 34. Знайти$x$ і$y$:

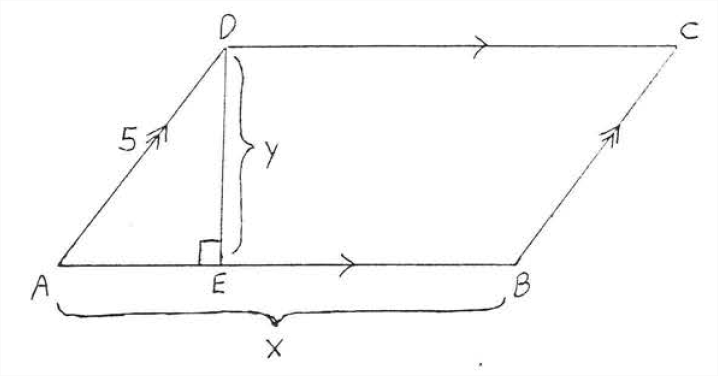
Рішення

$$\begin{array} {rcl} {\text{Perimeter}} & = & {AB +BC+CD+DA} \\ {34} & = & {x + 5 + x+5} \\ {34} & = & {2x+10} \\ {24} & = & {2x} \\ {12} & = & {x} \\ {\text{Area}} & = & {xy} \\ {48} & = & {12y} \\ {4} & = & {y} \end{array}$$

Перевірка:

Відповідь

$x = 12, y = 4$

Проблеми

1 - 4. Знайти площу і периметр$ABCD$

1.

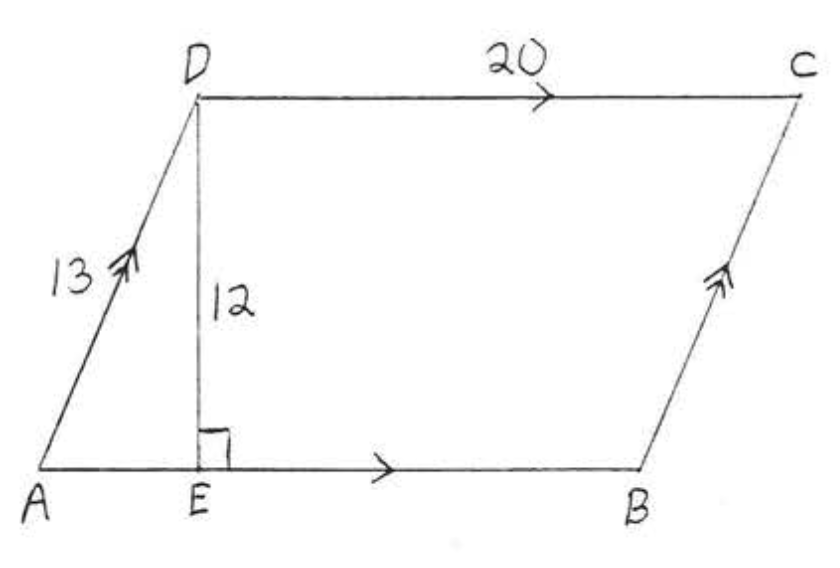
2.

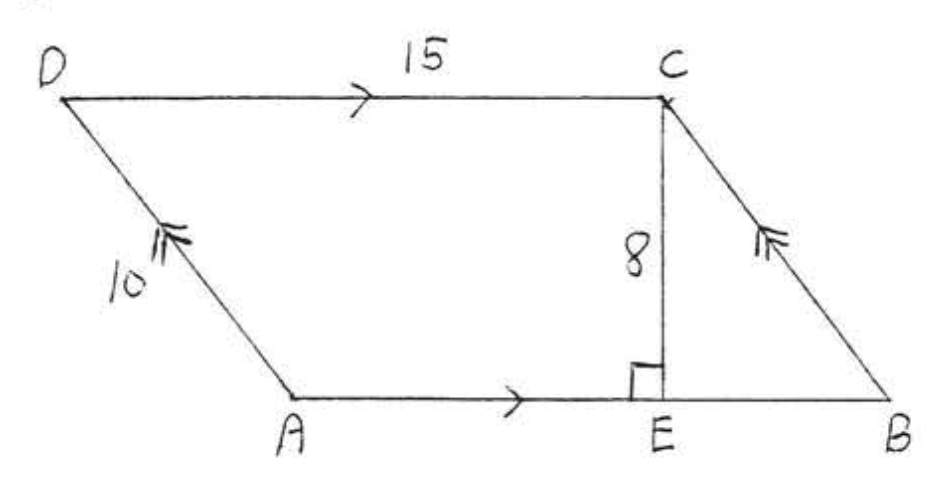
3.

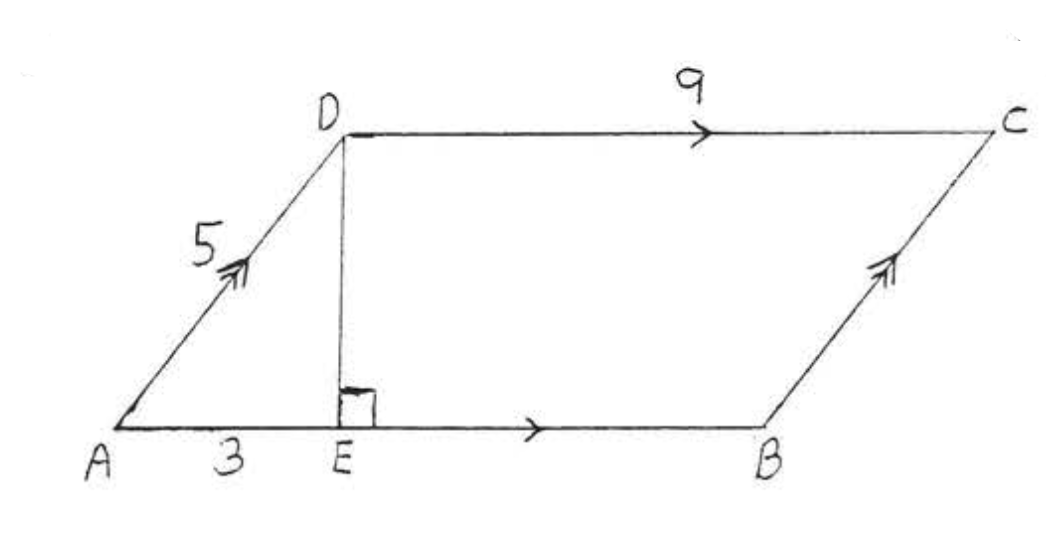
4.

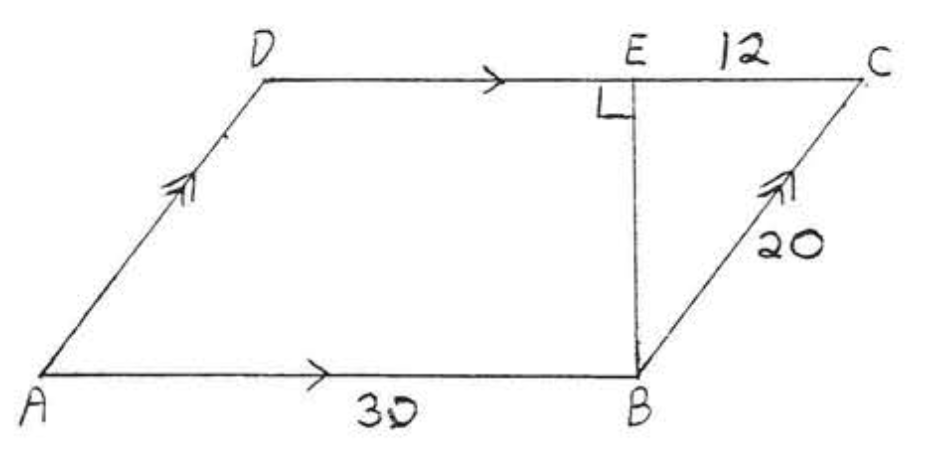
5 - 6. Знайдіть площу і периметр до найближчої десятої:

5.

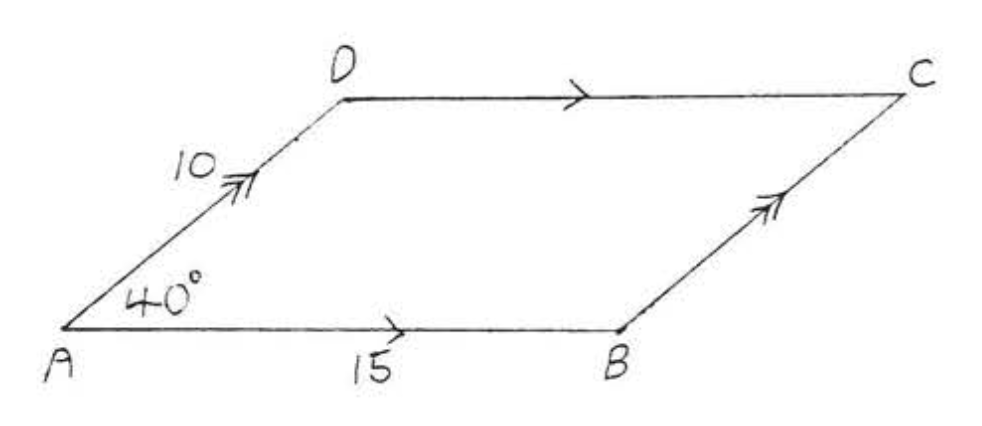
6.

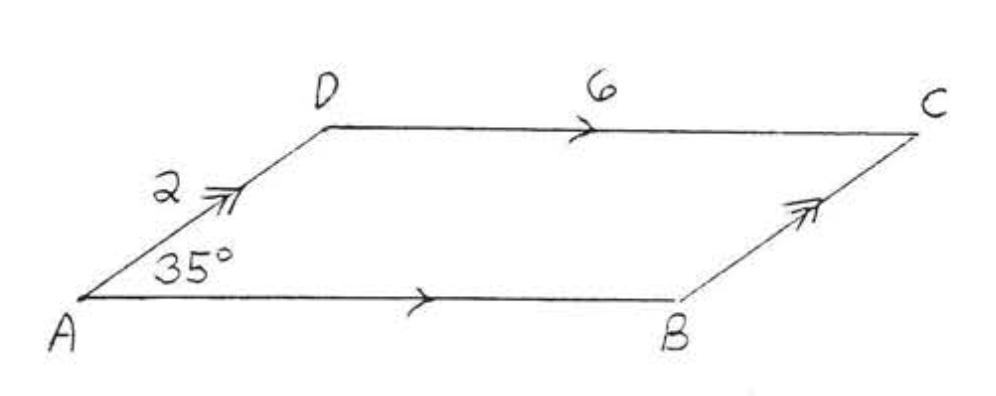
7 - 8. Знайдіть площу і периметр. Залиште відповіді в найпростішій радикальній формі:

7.

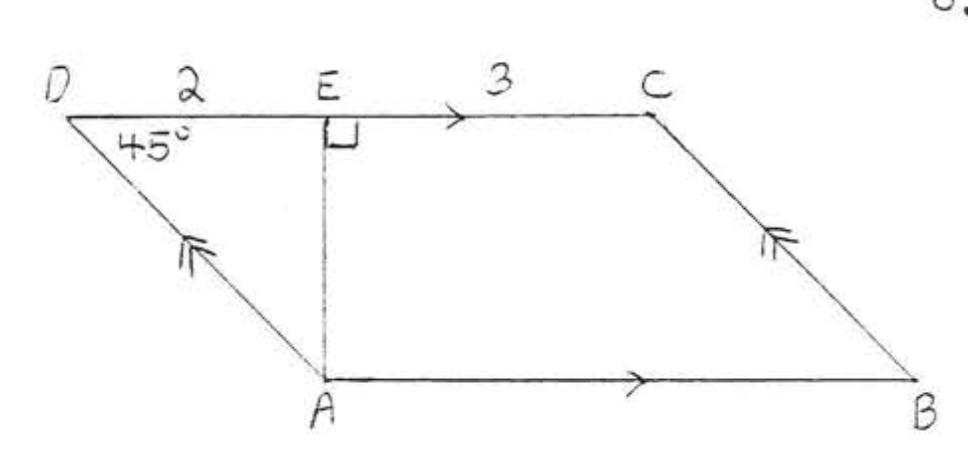
8.

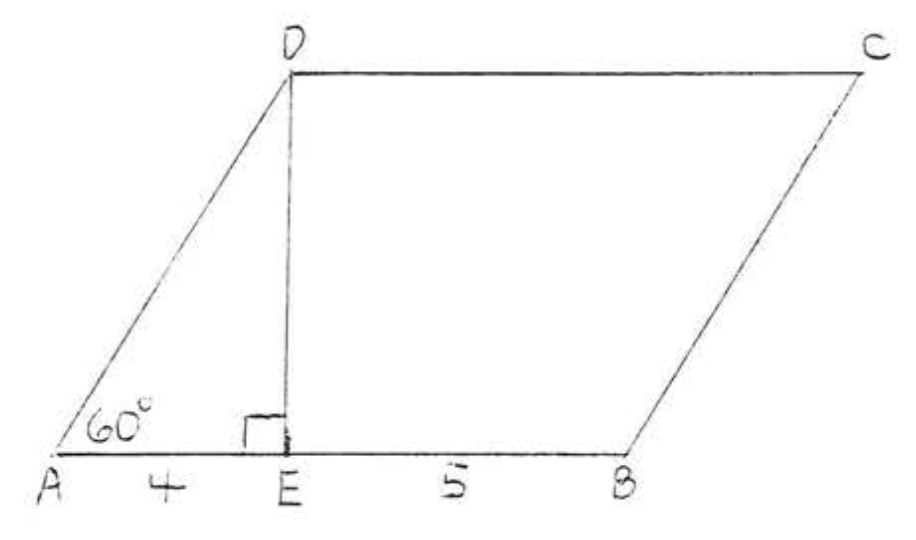
9. Знайти,$x$ якщо площа 36:$ABCD$

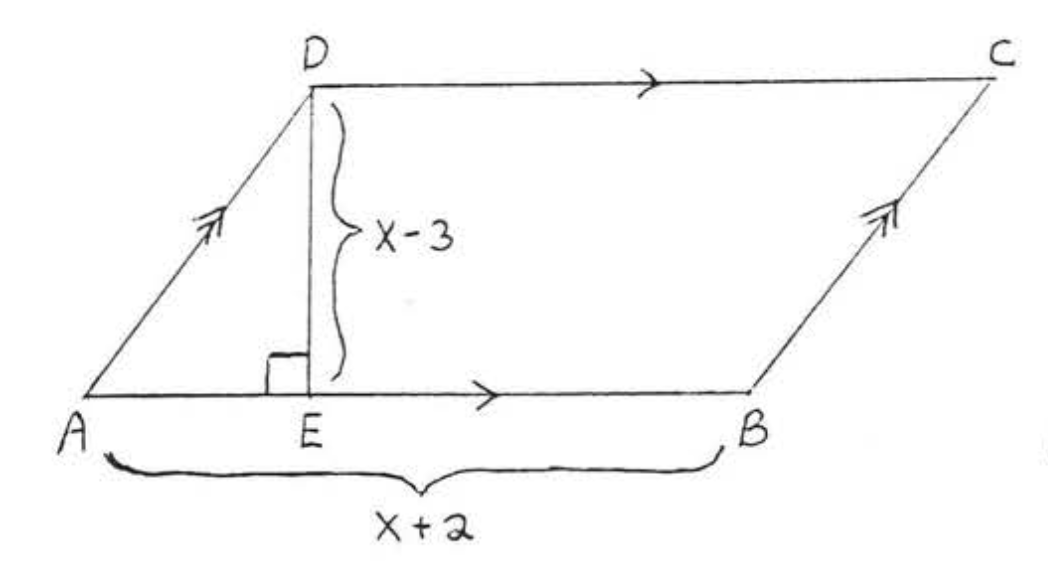
10. Знайти,$x$ якщо площа$ABCD$ дорівнює 72:

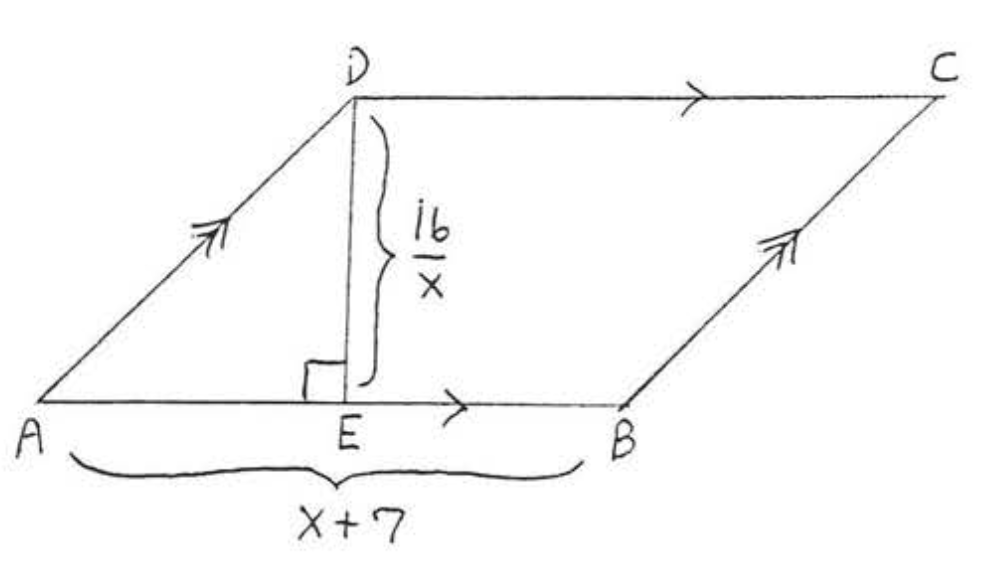
11. Знайдіть,$x$ якщо периметр дорівнює 22:

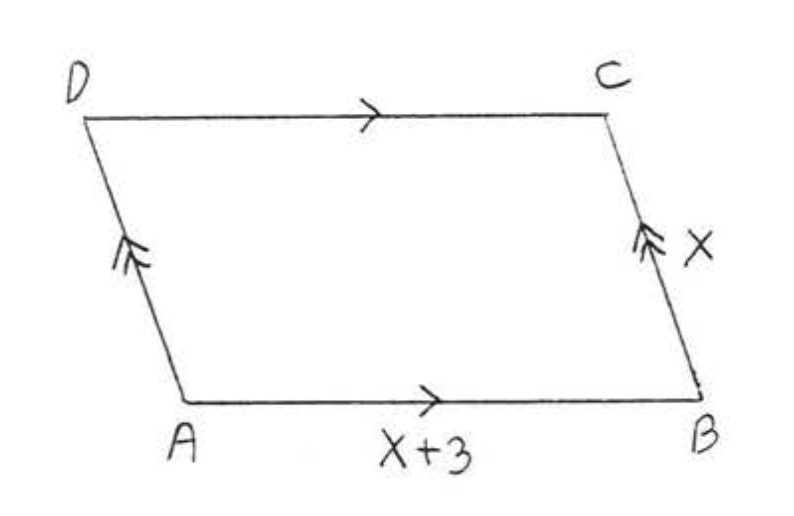
12. Знайдіть,$x$ якщо периметр дорівнює 40:

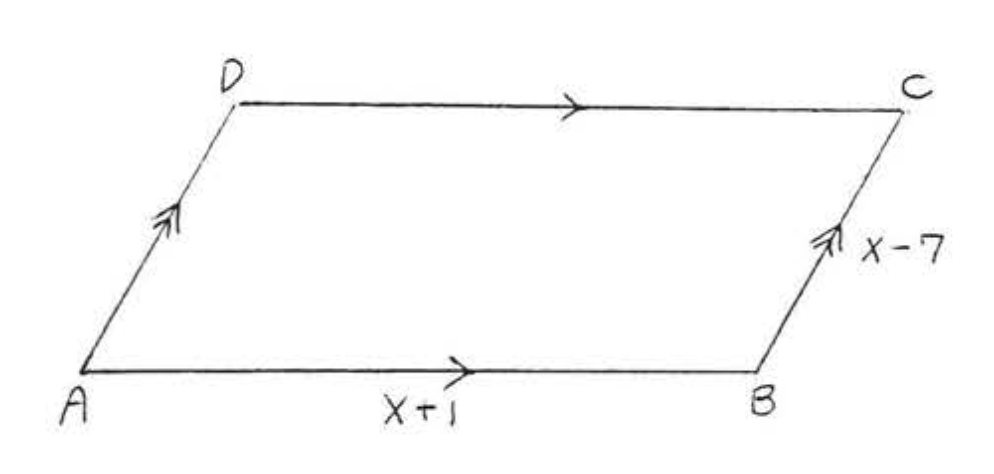
13. Площа$ABCD$ становить 40, а периметр - 28. Знайти$x$ і$y$:

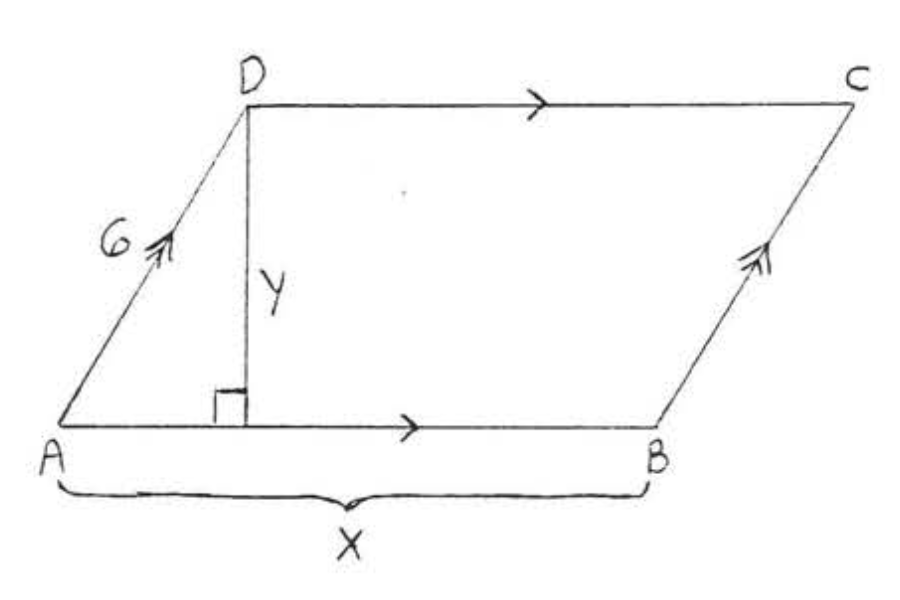
14. Площа$ABCD$ становить 40, а периметр - 30. Знайти$x$ і$y$: