5.9: Паралелограми

Last updated
Save as PDF

Page ID: 54800

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Знайти невідомі вимірювання кута чотирикутників з двома парами паралельних сторін.

Паралелограм - це чотирикутник з двома парами паралельних сторін.

Ф-Д_ФФ6Ф 6СЕ 996БФ 5Ф0Д715А1Ф7816Д66ФД4538Д7589Е5ФА43ДБ6Б87БФ+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

Зверніть увагу, що кожна пара сторін позначена паралельно (для останніх двох фігур пам'ятайте, що коли дві лінії перпендикулярні одній лінії, то вони паралельні). Паралелограми мають масу цікавих властивостей.

Факти про паралелограмах

Теорема протилежних сторін: Якщо чотирикутник є паралелограмом, то обидві пари протилежних сторін конгруентні.

Якщо

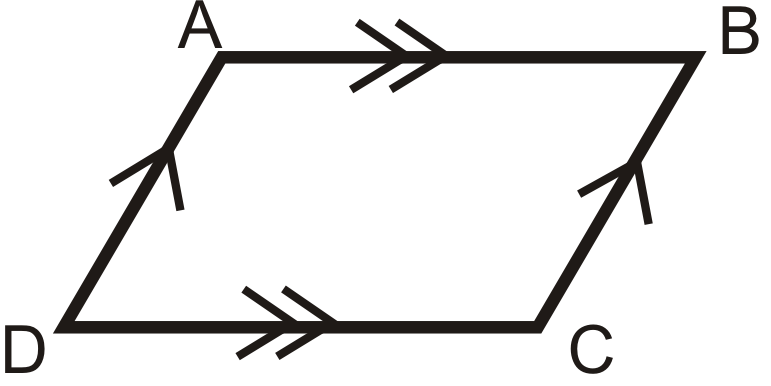
F-D_6CC6F1714D92491 С4ДД1108Ф4513 ДД757386ДДД171С6БК62ДБББ3А+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

потім

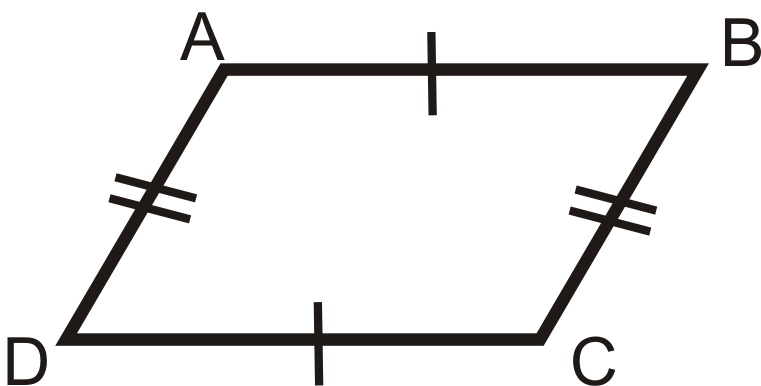
F-D_368D168609Д0Д0459Д5Е70 ФАА 3765Б22ЕКА 0Ф6С4Ф916BE35D17E8AE+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

2. Теорема протилежних кутів: Якщо чотирикутник є паралелограмом, то обидві пари протилежних кутів конгруентні.

Якщо

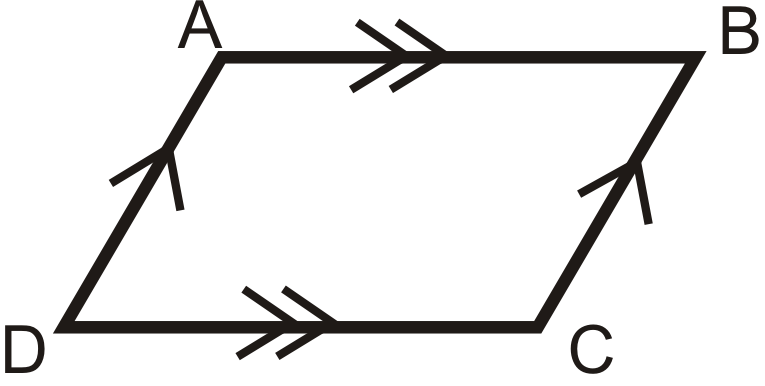
F-д_75Ф9С402DA3 2018 E3A196 бути 527Е867Е32А2Б2732ФДБ6667Б79Е501А7+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{4}\)

потім

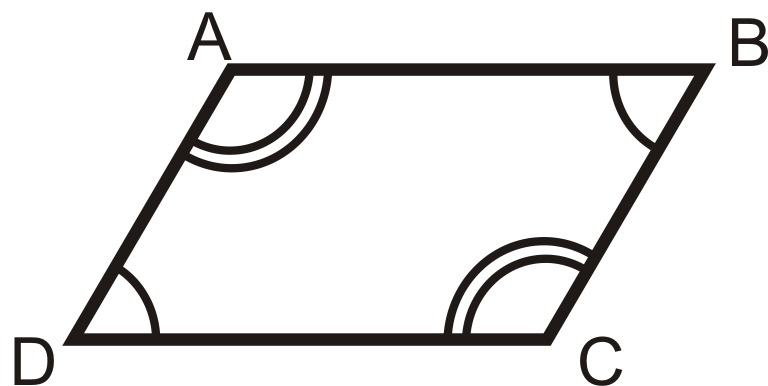
F-д_38А 3А7Е2860БД48А289437Б11С5Д8Д38969C1 Бее 2977Б985FE32989E+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{5}\)

3. Теорема послідовних кутів: Якщо чотирикутник є паралелограмом, то всі пари послідовних кутів є додатковими.

Якщо

потім

\(\begin{aligned} m\angle A+m\angle D&=180^{\circ} \\ m\angle A+m\angle B&=180^{\circ} \\ m\angle B+m\angle C&=180^{\circ} \\ m\angle C+m\angle D&=180^{\circ} \end{aligned}\)

4. Теорема діагоналей паралелограма: Якщо чотирикутник є паралелограмом, то діагоналі розділяють один одного.

Якщо

потім

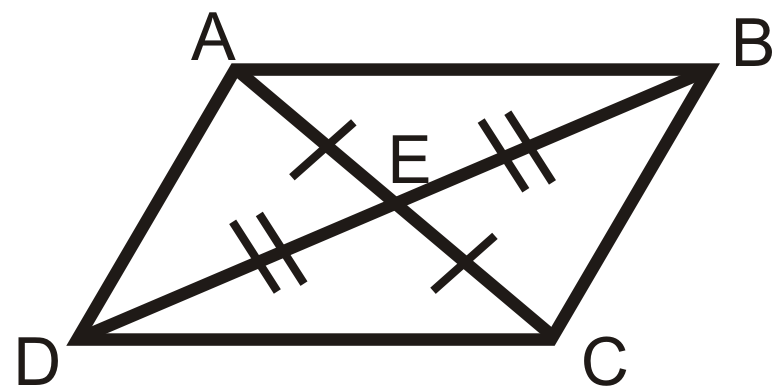
Ф-Д_0Ф402Ф 150856274CE28Е 896 С9006901772509 ЕЕФ 54673 ЕФ6843ЕА6+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{9}\)

Що робити, якщо вам сказали, що\(FGHI\) це паралелограм і вам дається довжина FG\) і міра\(\angle F\)? Що ви можете визначити про\(HI\),\(\angle H\),\(\angle G\), і\(\angle I\)?

Приклад\(\PageIndex{1}\)

Покажіть, що діагоналі\(FGHJ\) розсікають один одного.

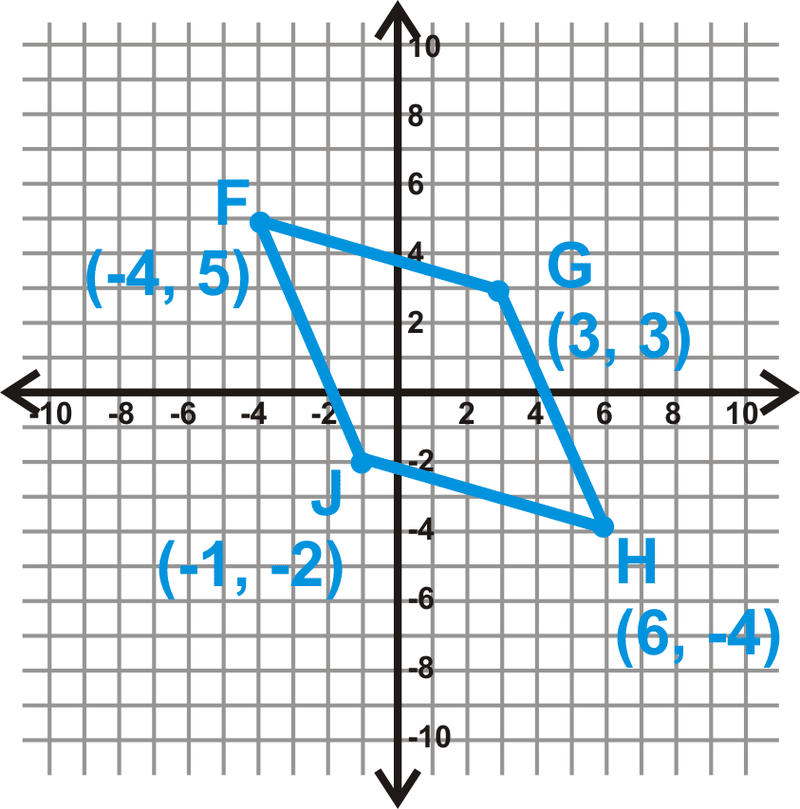
F-д_03А8Е7Д7Д582 БЦД 6Е32549ДА3Б61910 АБД 4АА3983417573F8595+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{10}\)

Рішення

Знайдіть середину кожної діагоналі.

\(\begin{aligned}\text{ Midpoint of } \overline{FH}:& \left(\dfrac{−4+6}{2}, \dfrac{5−4}{2}\right)=(1,0.5) \\ \text{ Midpoint of } of\: \overline{GJ}: & \left(\dfrac{3−1}{2}, \dfrac{3−2}{2}\tight)=(1,0.5)\end{aligned}\)

Оскільки вони є однією точкою, діагоналі перетинаються в середній точці один одного. Це означає, що вони розсікають один одного.

Приклад\(\PageIndex{2}\)

Знайдіть міри a та b в паралелограмі нижче:

F-D_345C1EB74АФ71473E0E2933БА 2798БД8 КС094438Б8Ф45С2ДБД 9989+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{11}\)

Рішення

Послідовні кути є додатковими так\(127^{\circ}+m\angle b=180^{\circ}\), що означає, що\(m\angle b=53^{\circ}\). \(a\)і\(b\) є чергуються внутрішні кути, і оскільки лінії паралельні (оскільки це паралелограм), це означає, що\(m\angle a=m\angle b=53^{\circ}\).

Приклад\(\PageIndex{3}\)

\(ABCD\)є паралелограмом. Якщо\(m\angle A=56^{\circ}\), знайдіть міру інших кутів.

Рішення

Спочатку намалюйте малюнок. При маркуванні вершин букви перераховуються, по порядку.

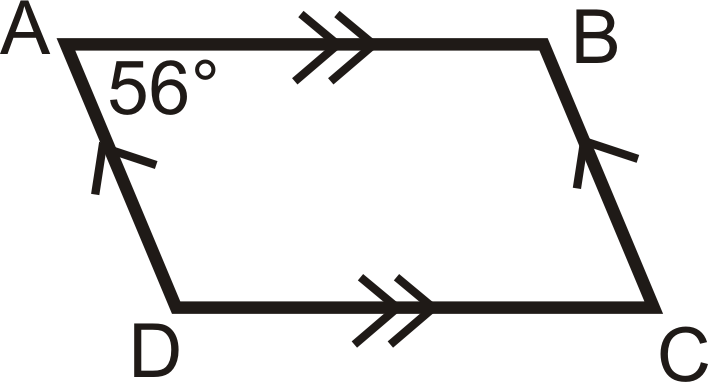
Ф-д_С5ДФ 69650 ЕЦББ0Д4710С414д22Б150 Е9Д7ДДБ1Д0854803ДДД+зображення_крихіткий+зображення_крихіткий_крихіткий.PNG — Малюнок\(\PageIndex{12}\)

Якщо\(m\angle A=56^{\circ}\), то\(m\angle C=56^{\circ}\) по теоремі протилежних кутів.

\ (\ почати {вирівняний}
&м\ кут A+м\ кут B = 180^ {\ circ}\ quad\ text {за теоремою послідовних кутів.}\\
&56^ {\ circ} +м\ кут B = 124^ {\
circ}\ квадратний кут\ D = 124^ {\ circ}\ квадратний кут\ D = 124^ {\ circ}\ text {тому що це протилежний кут}\ кут B
\ end {вирівняний}\)

Приклад\(\PageIndex{4}\)

Знайдіть значення\(x\) і\(y\).

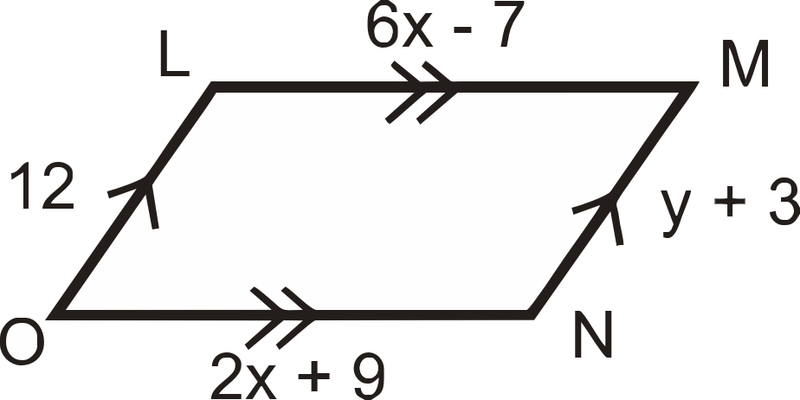
F-д_ББД 796 Е60Ф 9972 ДК 63А286А56789А9500ФБ9Е460Ф1Ф1ФБ 19КБФ 0Ф8Б5+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{13}\)

Рішення

Пам'ятайте, що протилежні сторони паралелограма конгруентні. Налаштуйте рівняння і вирішуйте.

\(\begin{aligned} 6x−7&=2x+9 \\ 4x&=16 \\ x&=4 \\ y+3&=12 \\ y&=9\end{aligned} \)

Приклад\(\PageIndex{5}\)

Доведіть теорему протилежних сторін.

F-д_481247021БД 2921618 ЕДФ 2Ф5Е05543 ФФ7668412А6А797825Б7Б69Ф29+зображення_крихіткий+зображення_крихіткий_png — Малюнок\(\PageIndex{14}\)

Рішення

Задано:\(ABCD\) є паралелограмом з діагоналлю\(\overline{BD}\)

Доведіть:\(\overline{AB}\cong \overline{DC}\),\(\overline{AD}\cong \overline{BC} \)

*Заява*	*Причина*
1. \(ABCD\)являє собою паралелограм з діагоналлю\(\overline{BD}\)	1. Враховується
2. \(\overline{AB}\parallel \overline{DC}\),\(\overline{AD}\parallel \overline{BC}\)	2. Визначення паралелограма
3. \(\angle ABD\cong \angle BDC\),\(\angle ADB\cong \angle DBC\)	3. Теорема про альтернативні внутрішні кути
4. \(\overline{DB}\cong \overline{DB}\)	4. Рефлексивний PoC
5. \(\Delta ABD\cong \Delta CDB\)	5. АСА
6. \(\overline{AB}\cong \overline{DC}\),\(\overline{AD}\cong \overline{BC}\)	6. CPCTC

Доказ теореми протилежних кутів майже ідентичний.

Рецензія

\(ABCD\)є паралелограмом. Заповніть пробіли нижче.

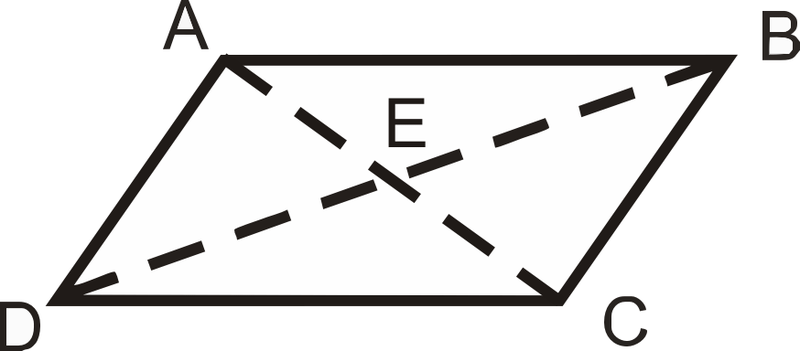
F-д_4С50CDD807989540195FFB2226DF7DC09513FF33267308D9F8F8203CA8+зображення_крихіткий+зображення_крихіткий_png — Малюнок\(\PageIndex{15}\)

Якщо\(AB=6\), то\(CD= \text{______}\).
Якщо\(AE=4\), то\(AC= \text{______}\).
Якщо\(m\angle ADC=80^{\circ}\),\(m\angle DAB = \text{______}\).
Якщо\(m\angle BAC=45^{\circ}\),\(m\angle ACD = \text{______}\).
Якщо\(m\angle CBD=62^{\circ}\),\(m\angle ADB = \text{______}\).
Якщо\(DB=16\), то\(DE = \text{______}\).
Якщо\( m\angle B=72^{\circ}\) в паралелограмі\(ABCD\), знайдіть інші три кути.
Якщо\(m\angle S=143^{\circ}\) в паралелограмі\(PQRS\), знайдіть інші три кути.
Якщо\(\overline{AB}\perp \overline{BC}\) в паралелограмі\(ABCD\), знайдіть міру всіх чотирьох кутів.
Якщо\(m\angle F=x^{\circ}\) в паралелограмі\(EFGH\), знайдіть інші три кути.

Для питань 11-18 знайдіть значення змінної (ів). Всі наведені нижче цифри - паралелограми.

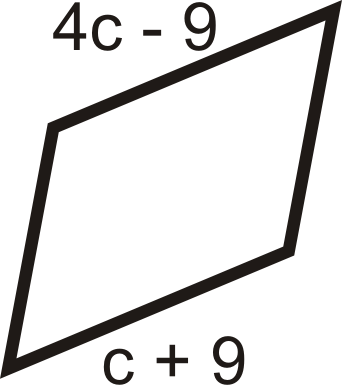
Малюнок\(\PageIndex{16}\)
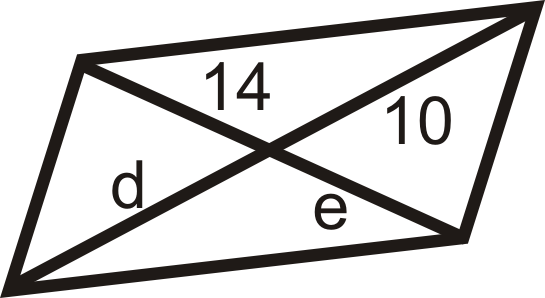
Малюнок\(\PageIndex{17}\)
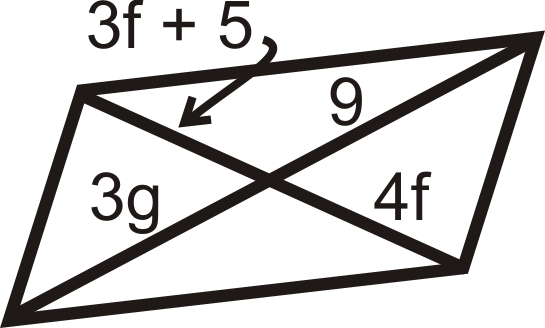
Малюнок\(\PageIndex{18}\)
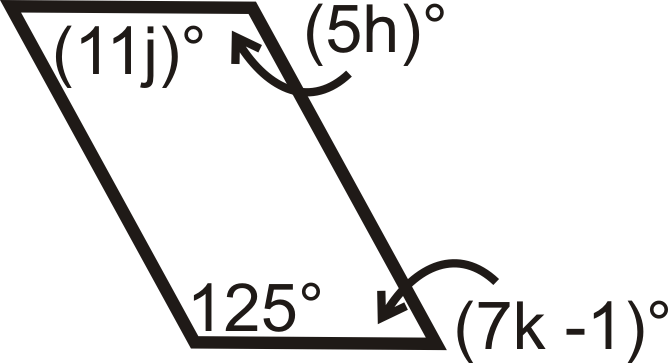
Малюнок\(\PageIndex{19}\)
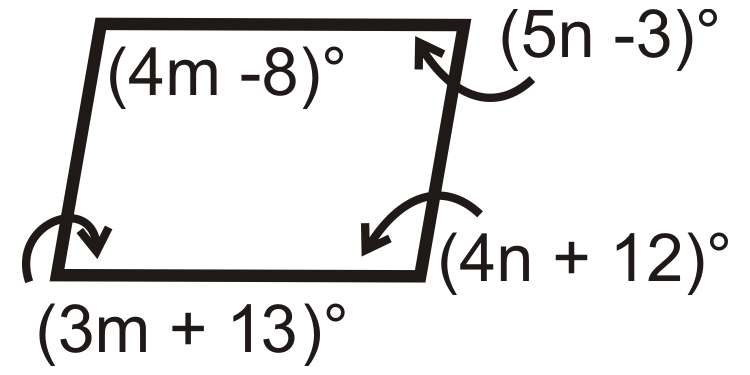
Малюнок\(\PageIndex{20}\)
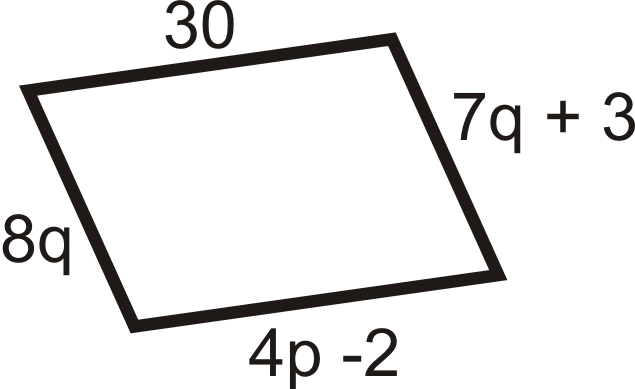
Малюнок\(\PageIndex{21}\)
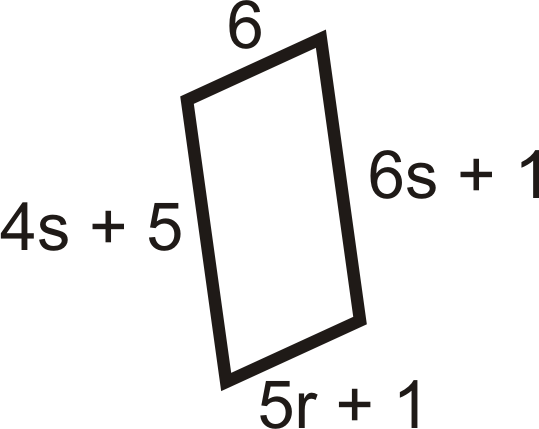
Малюнок\(\PageIndex{22}\)
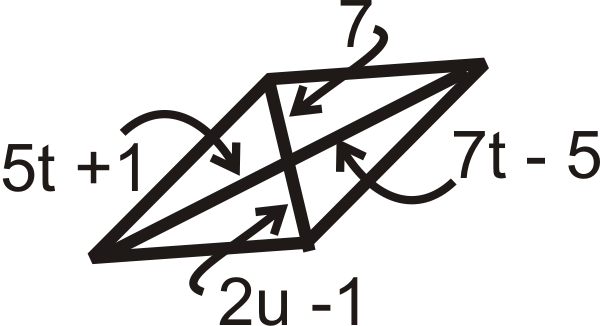
Малюнок\(\PageIndex{23}\)

Використовуйте паралелограм\(WAVE\), щоб знайти:

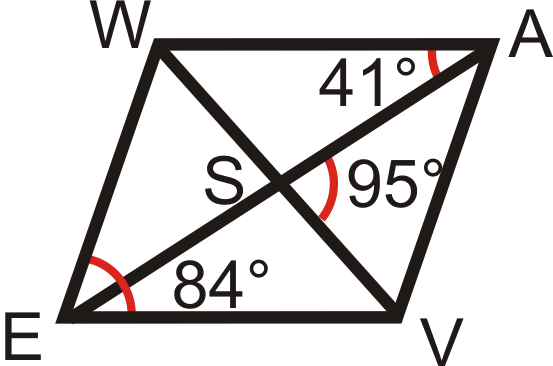
F-D_4Е 8938772296E11Б 4816Б25С00CD47a8E5E0B3A528676C779637A+зображення_крихіткий+зображення_крихіткий_крошечкий.PNG — Малюнок\(\PageIndex{24}\)

\(m\angle AWE\)
\(m\angle ESV\)
\(m\angle WEA\)
\(m\angle AVW\)

Знайдіть точку перетину діагоналей, щоб побачити, чи\(EFGH\) є паралелограмом.

\(E(−1,3), F(3,4), G(5,−1), H(1,−2)\)
\(E(3,−2), F(7,0), G(9,−4), H(5,−4)\)
\(E(−6,3), F(2,5), G(6,−3), H(−4,−5)\)
\(E(−2,−2), F(−4,−6), G(−6,−4), H(−4,0)\)

Заповніть пропуски в докази нижче.

Теорема протилежних кутів

Задано:\(ABCD\) є паралелограмом з діагоналлю\(\overline{BD}\)

Доведіть:\(\angle A\cong \angle C\)

*Заява*	*Причина*
1.	1. Враховується
2. \(\overline{AB}\parallel \overline{DC}\),\(\overline{AD}\parallel \overline{BC}\)	2.
3.	3. Теорема про альтернативні внутрішні кути
4.	4. Рефлексивний PoC
5. \(\Delta ABD\cong \Delta CDB\)	5.
6. \(\angle A\cong \angle C\)	6.

Теорема діагоналей паралелограма

Задано:\(ABCD\) це паралелограм з діагоналями\(\overline{BD}\) і\(\overline{AC}\)

Доведіть:\(\overline{AE}\cong \overline{EC}\),\(\overline{DE}\cong \overline{EB}\)

*Заява*	*Причина*
1.	1.
2.	2. Визначення паралелограма
3.	3. Теорема про альтернативні внутрішні кути
4. \(\overline{AB}\cong \overline{DC}\)	4.
5.	5.
6. \( \overline{AE}\cong \overline{EC}\),\(\overline{DE}\cong \overline{EB}\)	6.

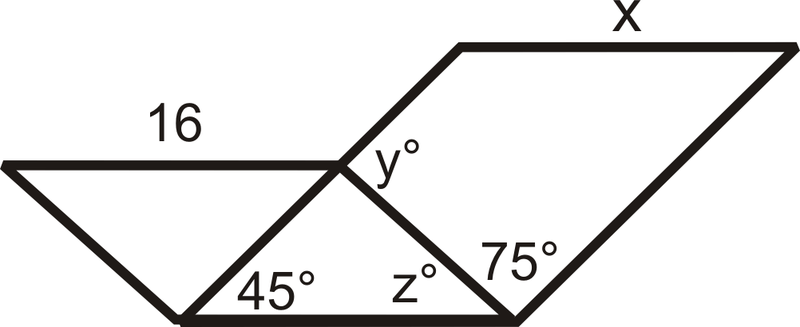
Знайти\(x\),\(y^{\circ}\), і\(z^{\circ}\). (Два чотирикутника з однаковою стороною - паралелограми.)

Ф-д_АФ 556799А2227ААФ Ф 648002Ф19Е53209Б290Е583Ф53366Ф957Ф841E9+зображення_крихіткий+зображення_крихіткий_PNG — Малюнок\(\PageIndex{27}\)

Лексика

Термін	Визначення
паралелограм	Чотирикутник з двома парами паралельних сторін. Паралелограм може бути прямокутником, ромбом або квадратом, але не повинен бути жодним з трьох.

Додаткові ресурси

Інтерактивний елемент

Відео: Принципи паралелограм - Основні

Діяльність: Паралелограми Питання обговорення

Навчальні посібники: паралелограми навчальний посібник

Практика: Паралелограми

Реальний світ: Паралелограми