Skip to main content
LibreTexts - Ukrayinska

1.19: Площа багатокутників і кіл

  1. Last updated
  2. Save as PDF
  • Page ID
    65881

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Ви можете використовувати калькулятор для більшості цього модуля, якщо це необхідно.

    Ми бачили, що периметр багатокутника - це відстань навколо зовнішньої сторони. Периметр - це довжина, яка є одновимірною, і тому вона вимірюється в лінійних одиницях (фути, сантиметри, милі і т.д.). Площа багатокутника - це кількість двовимірного простору всередині багатокутника, і вона вимірюється в квадратних одиницях: квадратні фути, квадратні сантиметри, квадратні милі тощо.

    Ви завжди можете думати про площу як кількість квадратів, необхідних для повного заповнення форми.

    Вправи\(\PageIndex{1}\)

    1. Знайдіть площу цього прямокутника.

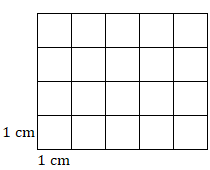
    2. Знайдіть площу цього квадрата.

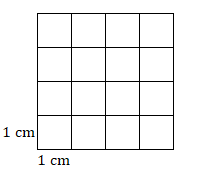
    Відповідь

    1. \(20\text{ cm}^2\)

    2. \(16\text{ cm}^2\)

    Прямокутники і квадрати

    Звичайно, існують формули для пошуку площ прямокутників і квадратів; ми не повинні рахувати маленькі квадрати.

    Площа прямокутника

    \(A=lw\)[1] або\(A=bh\)

    Площа площі

    \[A=s^2 \nonumber \]

    Вправи\(\PageIndex{1}\)

    Знайдіть площу кожної фігури.

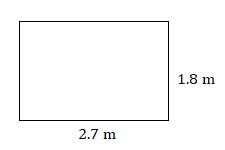
    3.

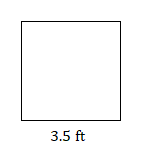
    4.

    Відповідь

    3. \(4.86\text{ m}^2\)

    4. \(12.25\text{ ft}^2\)

    Паралелограми

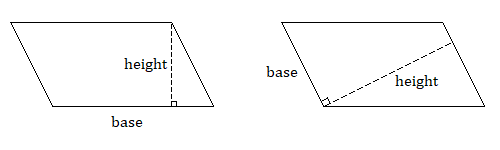
    Ще одним поширеним багатокутником є паралелограм, який виглядає як нахилений прямокутник. Як випливає з назви, пари протилежних сторін паралельні і мають однакову довжину. Зверніть увагу, що, якщо ми позначити одну сторону як основу паралелограма, у нас є перпендикулярна висота, яка не довжина інших сторін.

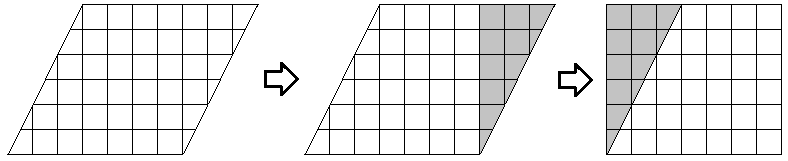
    Наступний набір діаграм показує, що ми можемо відрізати частину паралелограма і переставити частини в прямокутник з тією ж основою і висотою, що і вихідний паралелограм. Паралелограм з основою\(7\) одиниць і вертикальною висотою\(6\) одиниць перетворюється в\(6\) прямокутник, з площею\(42\) квадратних одиниць.\(7\)

    Тому формула площі паралелограма ідентична формулі для площі прямокутника за умови, що ми обережно використовуємо підставу і висоту, яка повинна бути перпендикулярною.

    Площа паралелограма

    \(A=bh\)

    Вправи\(\PageIndex{1}\)

    Знайдіть площу кожного паралелограма.

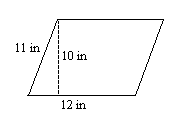
    5.

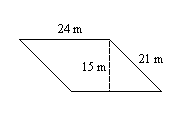
    6.

    Відповідь

    5. \(120\text{ in}^2\)

    6. \(360\text{ m}^2\)

    Трикутники

    Коли нам потрібно знайти площу трикутника, нам потрібно визначити основу і висоту, яка перпендикулярна цій основі. Якщо трикутник тупий, можливо, доведеться уявити висоту поза трикутником і продовжити базову лінію, щоб відповідати їй.

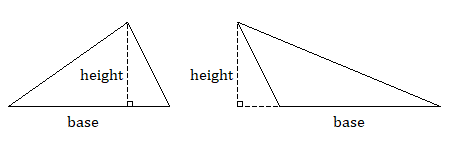
    Як показано нижче, будь-який трикутник можна подвоїти, щоб утворити паралелограм. Тому площа трикутника дорівнює половині площі паралелограма з однаковим підставою і висотою.

    Площа трикутника

    \(A=\dfrac{1}{2}bh\)або\(A=bh\div2\)

    Як і у випадку з паралелограмом, пам'ятайте, що висота повинна бути перпендикулярна підставі.

    Вправи\(\PageIndex{1}\)

    Знайдіть площу кожного трикутника.

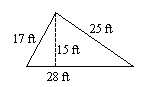
    7.

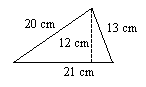
    8.

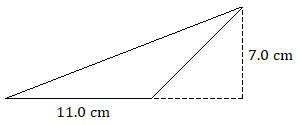
    9.

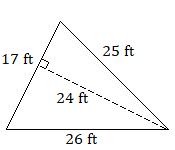
    10.

    Відповідь

    7. \(210\text{ ft}^2\)

    8. \(126\text{ cm}^2\)

    9. \(38.5\text{ cm}^2\)

    10. \(204\text{ ft}^2\)

    Трапеції

    Дещо менш поширеним чотирикутником є трапеція, яка має рівно одну пару паралельних сторін, які ми називаємо підставами. Перший приклад, показаний нижче, називається рівнобедреною трапецією, оскільки, як і рівнобедрений трикутник, дві його непаралельні сторони мають рівні довжини.

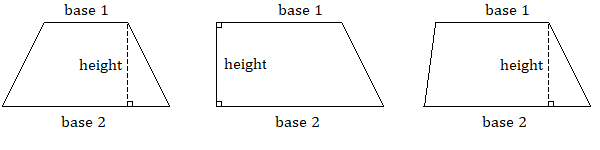
    Існує кілька способів показати, звідки береться формула площі, але пояснення краще у відео, оскільки вони можуть бути анімовані. [2] [3] [4]

    Площа трапеції

    \[A=\dfrac{1}{2}h(b_1+b_2) \nonumber \]

    або

    \[A=(b_1+b_2)h\div2 \nonumber \]

    Не лякайтеся індекси на\(b_1\) і\(b_2\); це просто спосіб назвати два різних вимірювання, використовуючи ту ж букву для змінної. (Багато людей називають бази\(a\) і\(b\) замість цього; не соромтеся писати його будь-яким способом, який ви віддаєте перевагу.) Як би ви не називали їх, ви просто додаєте дві основи, помножуєте на висоту і берете половину цього.

    Вправи\(\PageIndex{1}\)

    Знайдіть площу кожної трапеції.

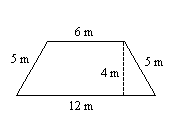
    11.

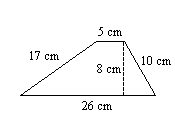
    12.

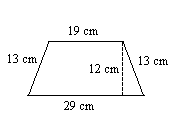
    13.

    Відповідь

    11. \(36\text{ m}^2\)

    12. \(124\text{ cm}^2\)

    13. \(288\text{ cm}^2\)

    Кола

    Площа кола в\(\pi\) рази перевищує квадрат радіуса:\(A=\pi{r^2}\). Одиниці все ще квадратні одиниці, хоча коло кругле. (Подумайте про квадрати на круглої вафлі.) Оскільки ми не можемо вмістити цілу кількість квадратів - або точну частку квадратів - всередині кола, площа кола буде наближенням.

    кругова вафля з квадратною сіткою візерунком

    Площа кола

    \ [A=\ пі {r^2}\)]

    Пам'ятайте про це\(\pi\approx3.1416\).

    Вправи\(\PageIndex{1}\)

    Знайдіть площу кожного кола. Округляйте до найближчої десятої або до трьох значущих цифр, залежно від того, що здається доречним.

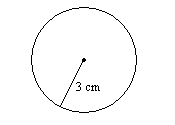
    14. коло з маркуванням радіусом 3 см

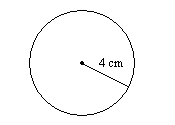
    15. коло з маркуванням радіусом 4 см

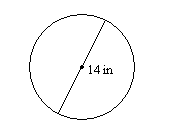
    16. коло діаметром з маркуванням 14 дюймів

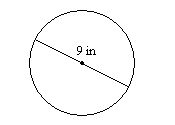
    17. коло діаметром з маркуванням 9 дюймів

    Кожна фігура - це частка кола. Розрахуйте кожну площу.

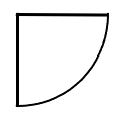
    18. Радіус чверті кола -\(5\) метри.

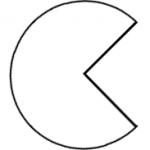
    19. З кола з діаметром\(7\) стопи вилучили чверть кола.

    Відповідь

    14. \(28.3\text{ cm}^2\)

    15. \(50.3\text{ cm}^2\)

    16. \(153.9\text{ in}^2\)

    17. \(63.6\text{ in}^2\)

    18. \(19.6\text{ m}^2\)

    19. \(28.9\text{ ft}^2\)

    1. Ви можете використовувати великі літери для змінних тут, оскільки мала буква «l» може бути легко прийнята за число «1". ←
    2. https://youtu.be/yTnYRpcZA9c :05
    3. https://youtu.be/WZtO3oERges :05
    4. https://youtu.be/uLHc6Br2veg :05