3.1: Паралелограми

Last updated
Save as PDF

Page ID: 58875

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Багатокутник - це фігура, утворена відрізками лінії, які пов'язані частину площини (Рисунок$\PageIndex{1}$), Відрізки обмежувальної лінії називаються сторонами багатокутника, Кути, утворені сторонами, - це кути багатокутника і вершини цих кути - це вершини багатокутника, найпростіший багатокутник - це трикутник, який має 3 сторони, У цій главі ми вивчимо чотирикутник, багатокутник з 4 сторонами (рис.$\PageIndex{2}$). Інші багатокутники - це п'ятикутник (5 сторін), шестикутник (6 сторін), восьмикутник (8 сторін) та декагон (10 сторін).

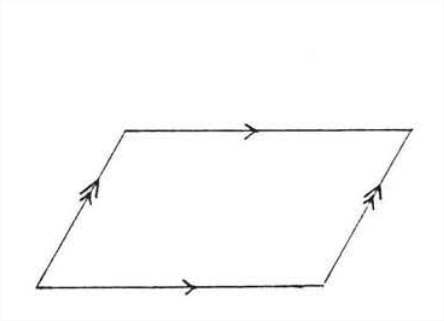
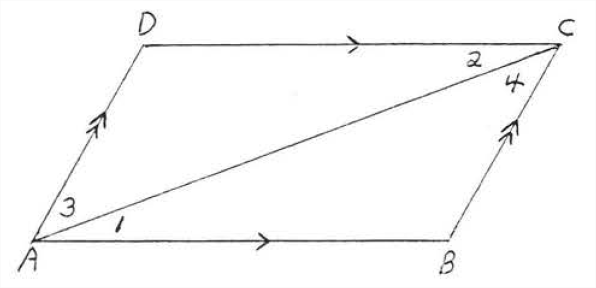
Паралелограм - це чотирикутник, в якому протилежні сторони паралельні (рис.$\PageIndex{3}$). Щоб виявити його властивості, проведемо діагональ, лінію, що з'єднує протилежні вершини паралелограма. На малюнку 4 змінний струм - діагональ паралелограма$ABCD$. Ми зараз доведемо$\Delta ABC \cong \Delta CDA$.

Малюнок$\PageIndex{4}$: Діагональ$AC$ ділить паралелограм$ABCD$ на два конгруентних трикутника.

Заяви	причини
1. $\angle 1 = \angle 2$.	1. Чергуються внутрішні кути паралельних ліній$AB$ і$CD$ рівні.
2. $\angle 3 = \angle 4$.	2. Чергуються внутрішні кути паралельних ліній$BC$ і$AD$ рівні.
3. $AC = AC$.	3. Ідентичність.
4. $\triangle ABC \cong \triangle CDA$.	4. $ASA = ASA$.
5. $AB = CD$,$BC = DA$.	5. Відповідні сторони конгруентних трикутників рівні.
6. $\angle B = \angle D$.	6. Відповідні кути конгруентних трикутників рівні.
7. $\angle A = \angle C$.	7. $\angle A = \angle 1 +\angle 3 = \angle 2 + \angle 4 = \angle C$(Додайте твердження 1 і 2).

Доведено наступну теорему:

Теорема$\PageIndex{1}$

Протилежні сторони і протилежні кути паралелограма рівні.

У$ABCD$ паралелограмі фігури$\PageIndex{5}$,$AB = CD$,$AD = BC$,$\angle A = \angle C$, і$\angle B = \angle D$.

Приклад$\PageIndex{1}$

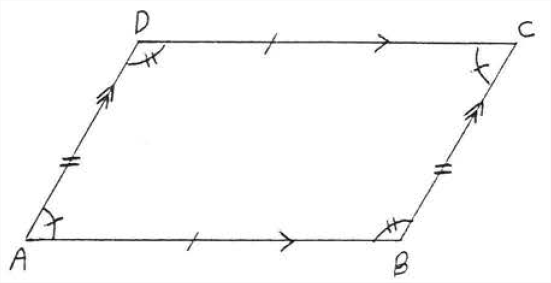
Знайти$x$$y$,$r$ і$s$:

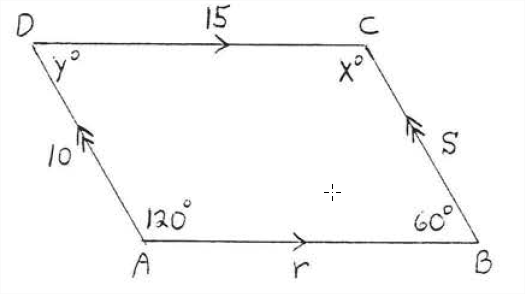
$clipboard_ebff146676a9cb2cf865e63954df141f7.png$

Рішення

За теоремою$\PageIndex{1}$ протилежні сторони і протилежні кути рівні. Значить$x^{\circ} = 120^{\circ}$$y^{\circ} = 60^{\circ}, r = 15$, і$s = 10$.

Відповідь:$x = 120, y = 60, r = 15, s = 10$.

Приклад$\PageIndex{2}$

Знайти$x, y, x$ і$z:$

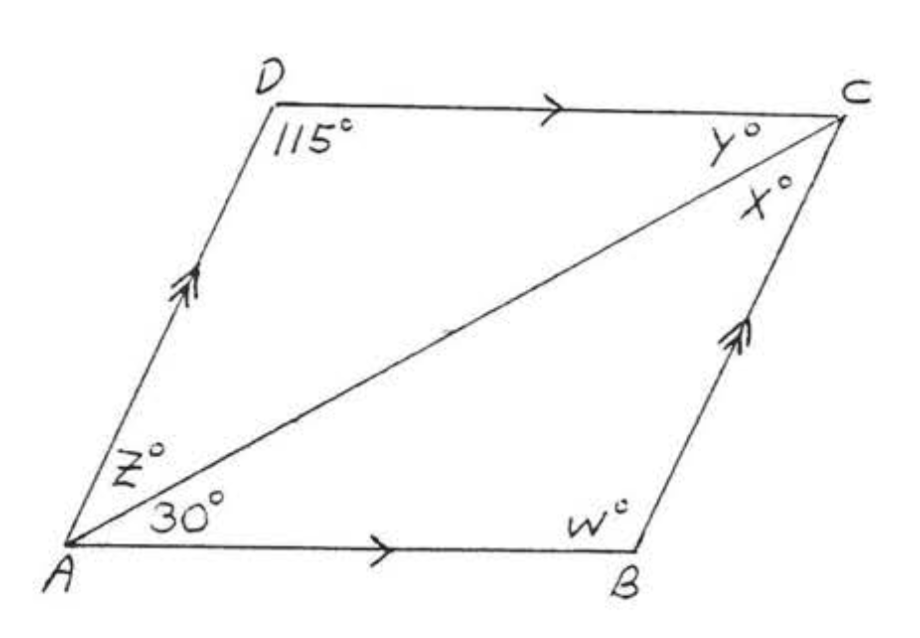
$2020-11-10 8.07.08.пнг$

Рішення

$w^{\circ} = 115^{\circ}$так як протилежні кути паралелограма рівні. $x^{\circ} = 180^{\circ} -(w^{\circ} + 30^{\circ}) = 180^{\circ} - (115^{\circ} + 30^{\circ}) = 180^{\circ} - 145^{\circ} = 35^{\circ}$, Тому що сума кутів$\triangle ABC$ є$180^{\circ}$,$y^{\circ} = 30^{\circ}$ і$x^{\circ} = x^{\circ} = 35^{\circ}$ тому що вони чергуються внутрішні кути паралельних ліній.

Відповідь:$w = 115$,$x = z = 35$,$y = 30$.

Приклад$\PageIndex{3}$

Знайти$x$$y$, і$z$:

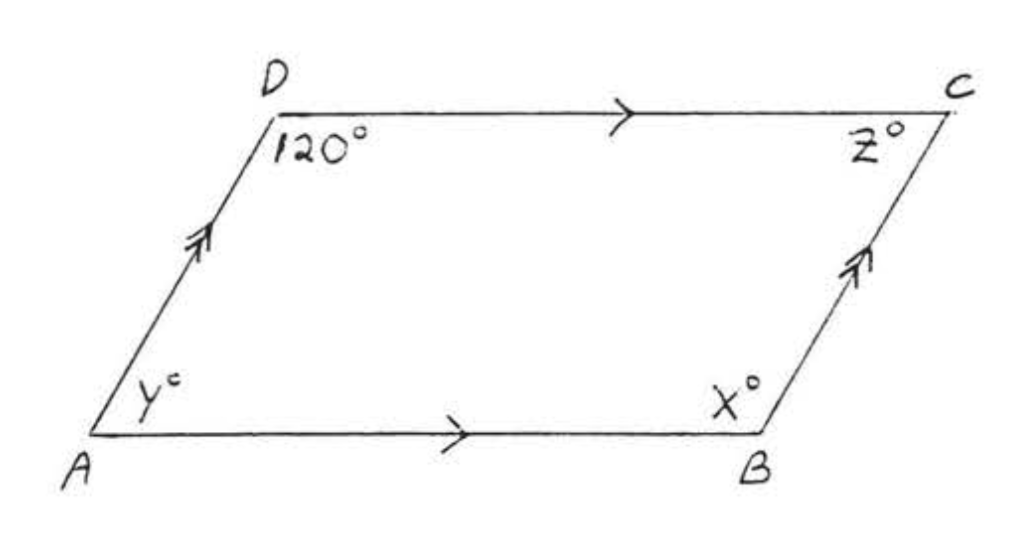
$2020-11-10 8.12.15 пнг$

Рішення

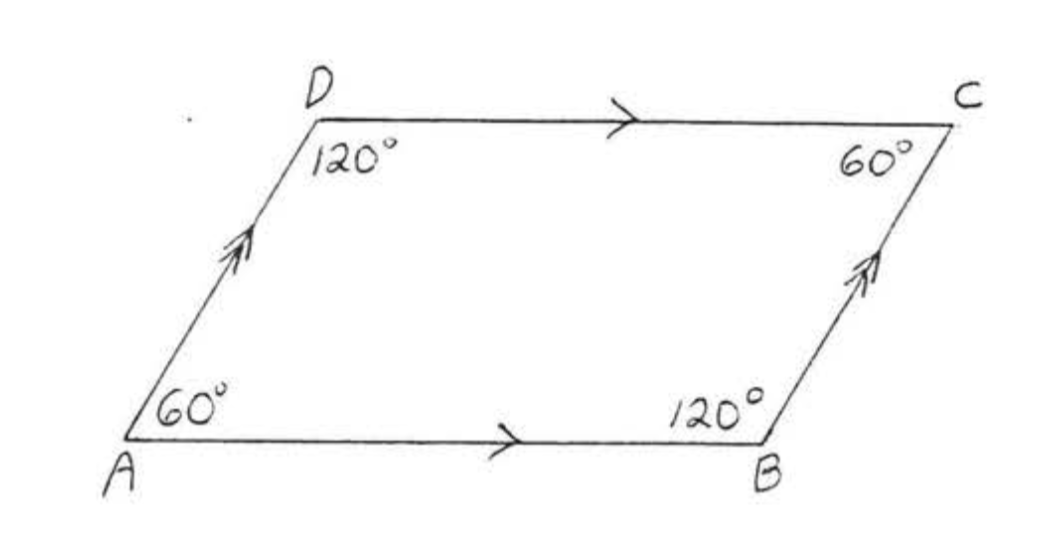
$x = 120$і$y = z$ тому, що протилежні кути рівні,$\angle A$ і$\angle D$ є додатковими J, тому що вони є внутрішніми кутами на тій же стороні поперечної паралельних ліній (вони утворюють букву «C» Теорема$\PageIndex{3}$, розділ 1.4).

Відповідь:$x = 120, y = z = 60$.

У$\angle A$ прикладі і$\PageIndex{3}$$\angle B$,$\angle B$ і$\angle C$,$\angle C$ і$\angle D$, і$\angle D$ і$\angle A$ називаються послідовними кутами паралелограма$ABCD$. Приклад$\PageIndex{3}$ передбачає наступну теорему:

Теорема$\PageIndex{2}$

Послідовні кути паралелограма є додатковими.

На малюнку 6,$\angle A + \angle B = \angle B + \angle C = \angle C + \angle D = \angle D + \angle A = 180^{\circ}$.

2020-11-10 пнг — Малюнок$\PageIndex{6}$, Послідовні кути паралелограма$ABCD$ є додатковими.

Приклад$\PageIndex{4}$

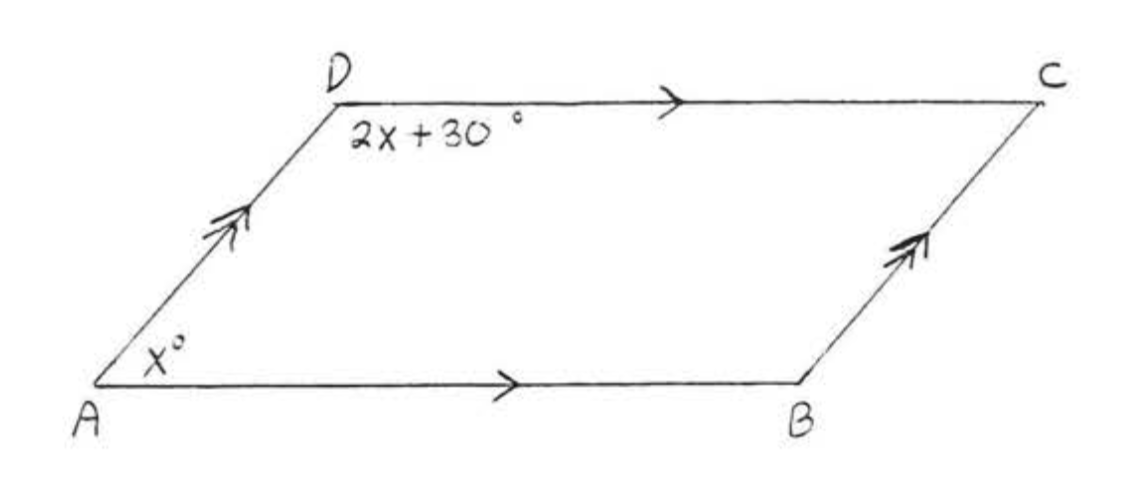
Знайти$x$,$\angle A$,$\angle B$,$\angle C$, і$\angle D$.

$2020-11-10 8.22.16.пнг$

Рішення

$\angle A$і$\angle D$ є додатковими за теоремою$\PageIndex{2}$.

\[\begin{array} {rcl} {\angle A + \angle D} & = & {180^{\circ}} \\ {x + 2x + 30} & = & {180} \\ {3x + 30} & = & {180} \\ {3x} & = & {180 - 30} \\ {3x} & = & {150} \\ {x} & = & {50} \end{array}\]

$\angle A = x^{\circ} = 50^{\circ}$

$\angle C = \angle A = 50^{\circ}$

$\angle D = 2x + 30^{\circ} = 2(50) + 30^{\circ} = 100 + 30^{\circ} = 130^{\circ}$.

$\angle B = \angle D = 130^{\circ}$.

Перевірка:

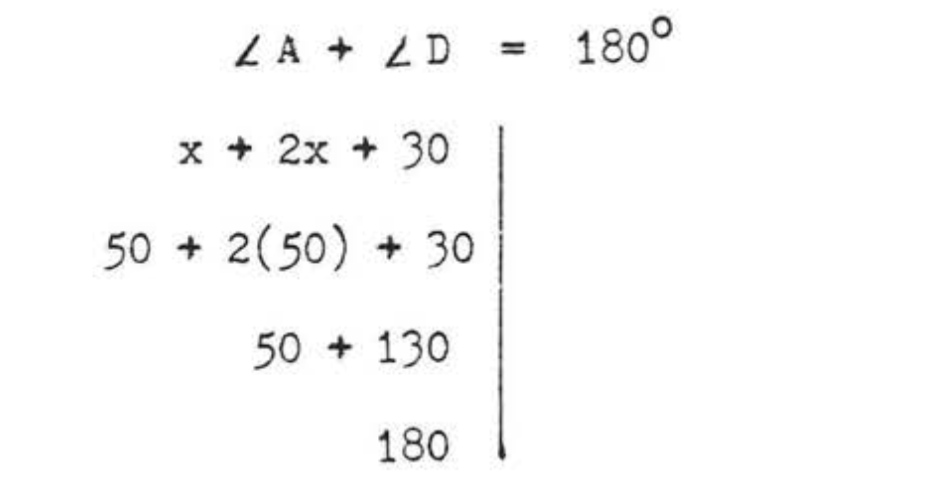
$2020-11-10 8.28.57.png$

Відповідь:$x = 50$,$A = 50^{\circ}$,$B = 130^{\circ}$,$C = 50^{\circ}$,$D = 130^{\circ}$.

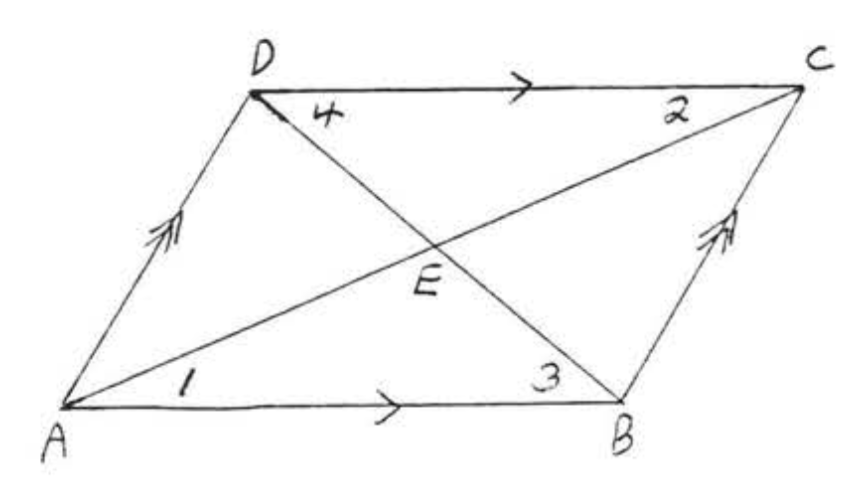
Припустимо тепер, що намальовані обидві діагоналі паралелограма (рис.$\PageIndex{7}$):

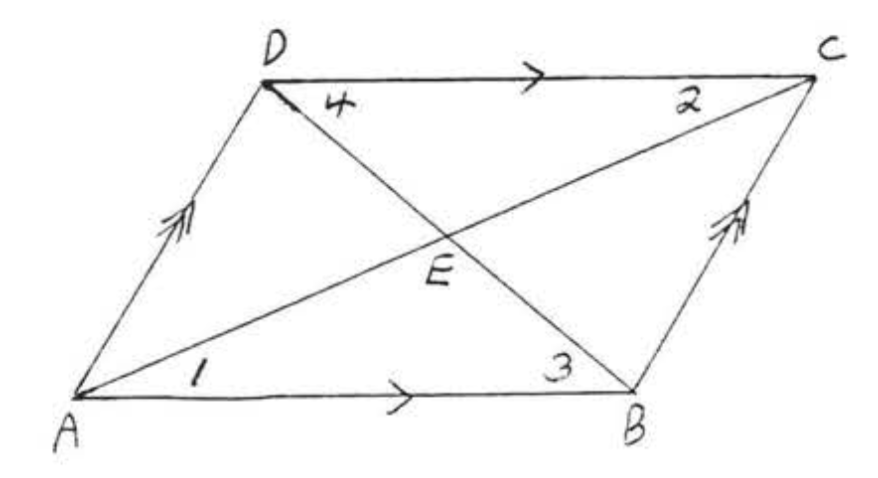
2020-11-10 8.32.56.PNG — Малюнок$\PageIndex{7}$. Parallelogram $ABCD$ with diagonals $AC$ and $BD$.

У нас є$\angle 1 = \angle 2$ and $\angle 3 = \angle 4$ (both pairs of angles are alternate interior angles of parallel lines $AB$ and $CD$. Also $AB = CD$ from Theorem$\PageIndex{1}$. Therefore $\triangle ABE \cong \triangle CDE$ by $ASA = ASA$. Since corresponding sides of congruent triangles are equal, $AE = CE$ and $DE = BE$. We have proven:

Теорема$\PageIndex{3}$

Діагоналі паралелограма розрізають один одного (розрізають один одного навпіл).

2020-11-10 8.40.46 PNG — Малюнок$\PageIndex{8}$. The diagonals of parallelogram $ABCD$ bisect each other.

Приклад$\PageIndex{5}$

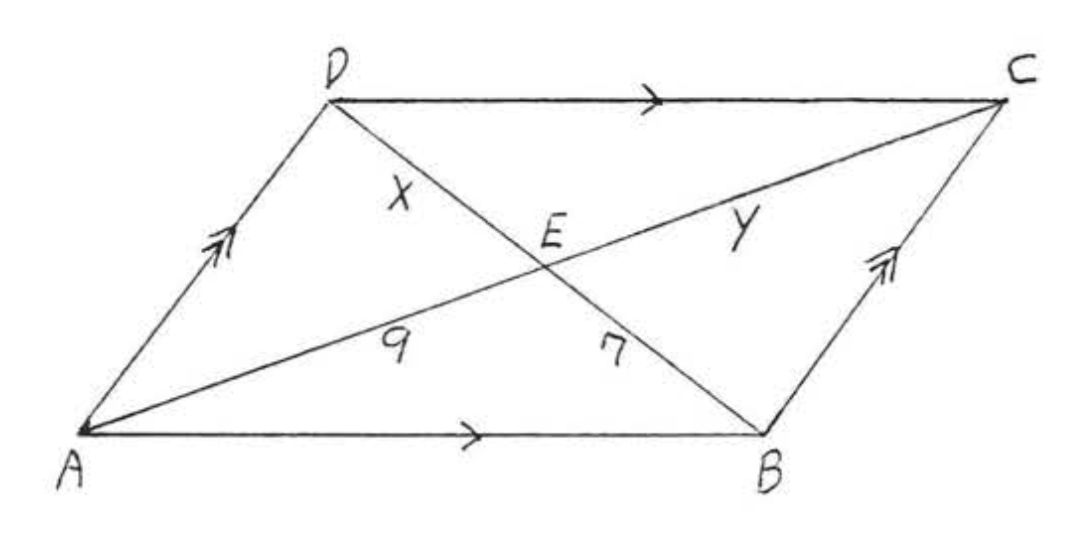
Знайти$x, y, AC$, і$BD$:

$2020-11-10 8.48.png$

Рішення

За теоремою$\PageIndex{3}$ діагоналі розділяють один одного.

\[\begin{array} {rcl} {x} & = & {7} \\ {y} & = & {9} \\ {AC} & = & {9 + 9 = 18} \\ {BD} & = & {7 + 7 = 14} \end{array}\]

Відповідь:$x = 7, y = 9, AC = 18, BD = 14$.

Приклад$\PageIndex{6}$

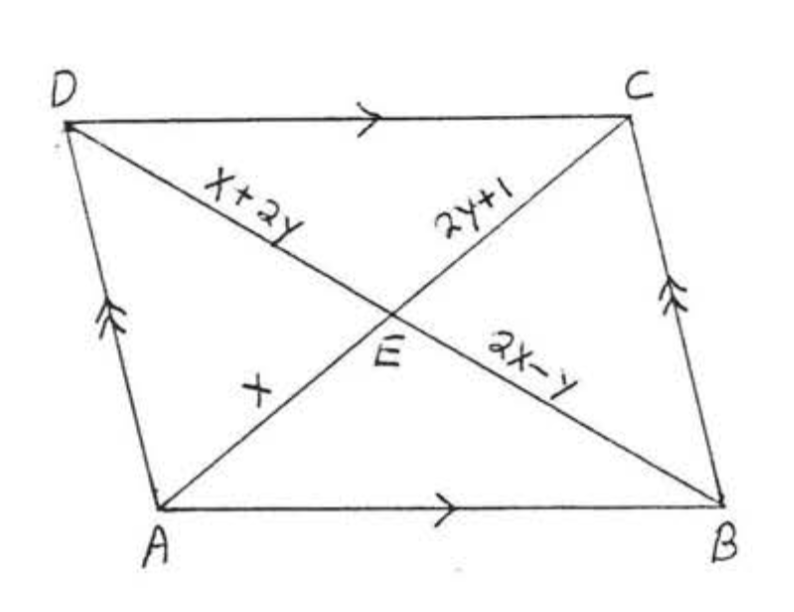
Знайти$x, y, AC$, і$BD$:

$2020-11-10 8.45.49.PNG$

Рішення

За теоремою$\PageIndex{3}$ діагоналі розділяють один одного.

$\begin{array} {rcl} {AE} & = & {CE} \\ {x} & = & {2y + 1} \\ {x - 2y} & = & {1} \end{array}$$\begin{array} {rcl} {BE} & = & {DE} \\ {2x - y} & = & {x + 2y} \\ {2x - y - x - 2y} & = & {0} \\ {x - 3y} & = & {0} \end{array}$

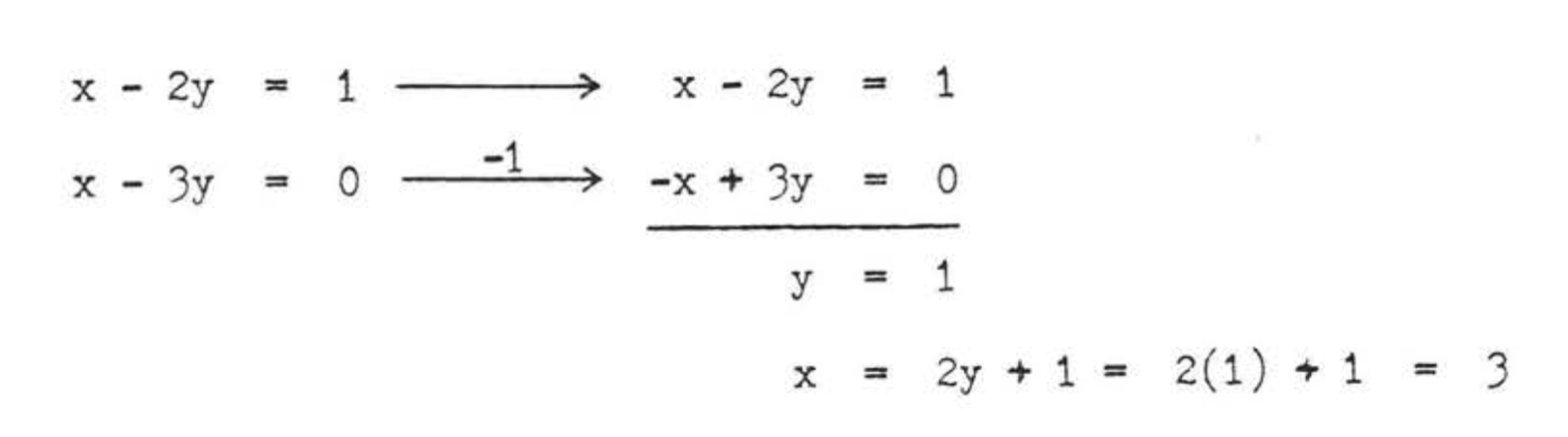
$2020-11-10 пнг$

Перевірка:

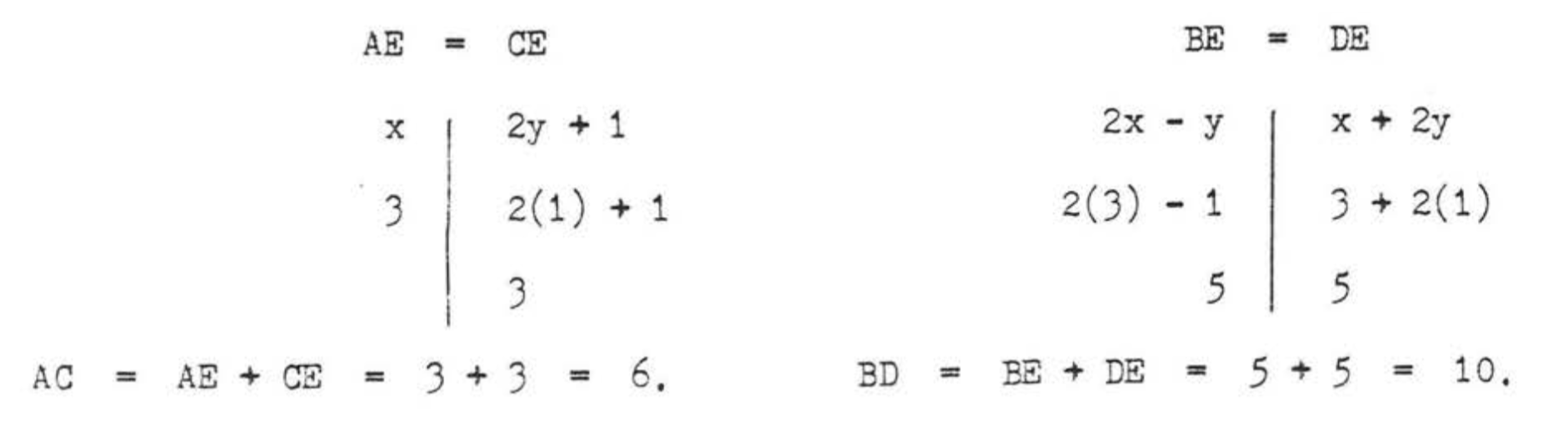
$2020-11-10 8.50.14.PNG$

Відповідь:$x = 3, y = 1, AC = 6, BD = 10$.

Приклад$\PageIndex{7}$

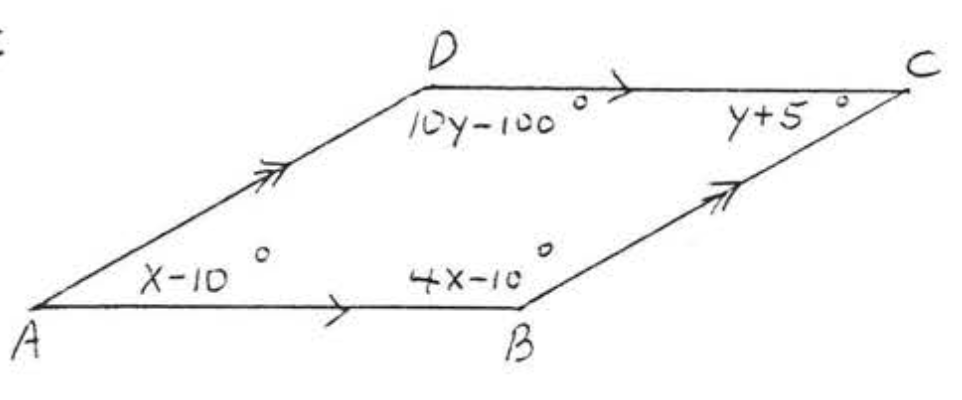
Знайти$x, y, \angle A, \angle B, \angle C$, і$\angle D$:

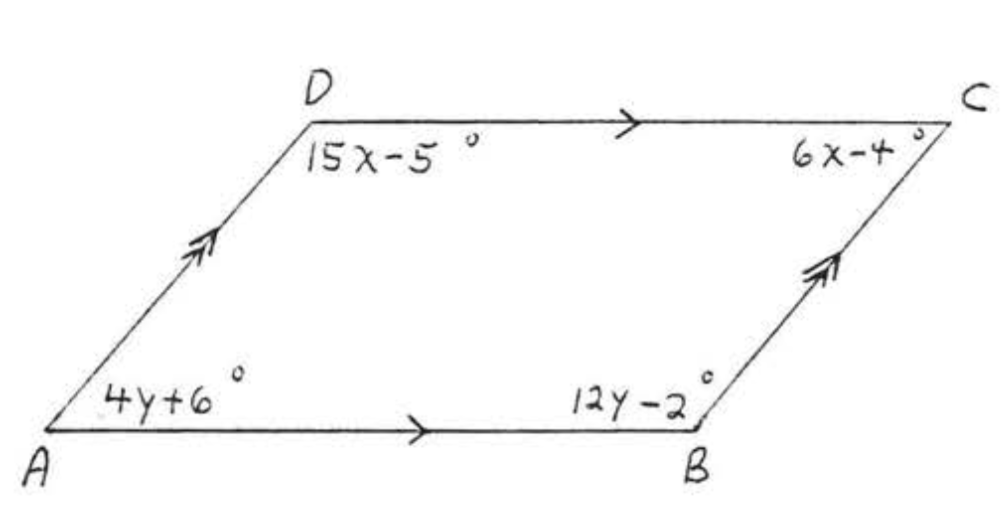
$2020-11-10 8.52.21png$

Рішення

За теоремою$\PageIndex{2}$:

$\begin{array} {rcl} {\angle A + \angle B} & = & {180^{\circ}} \\ {4y + 6 + 12y - 2} & = & {180} \\ {16y + 4} & = & {180} \\ {16y} & = & {180 - 4} \\ {16y} & = & {176} \\ {y} & = & {11} \end{array}$і$\begin{array} {rcl} {\angle C + \angle D} & = & {180^{\circ}} \\ {6x - 4 + 15x - 5} & = & {180} \\ {21x - 9} & = & {180} \\ {21x} & = & {180 + 9} \\ {21x} & = & {189} \\ {x} & = & {9} \end{array}$

Перевірка:

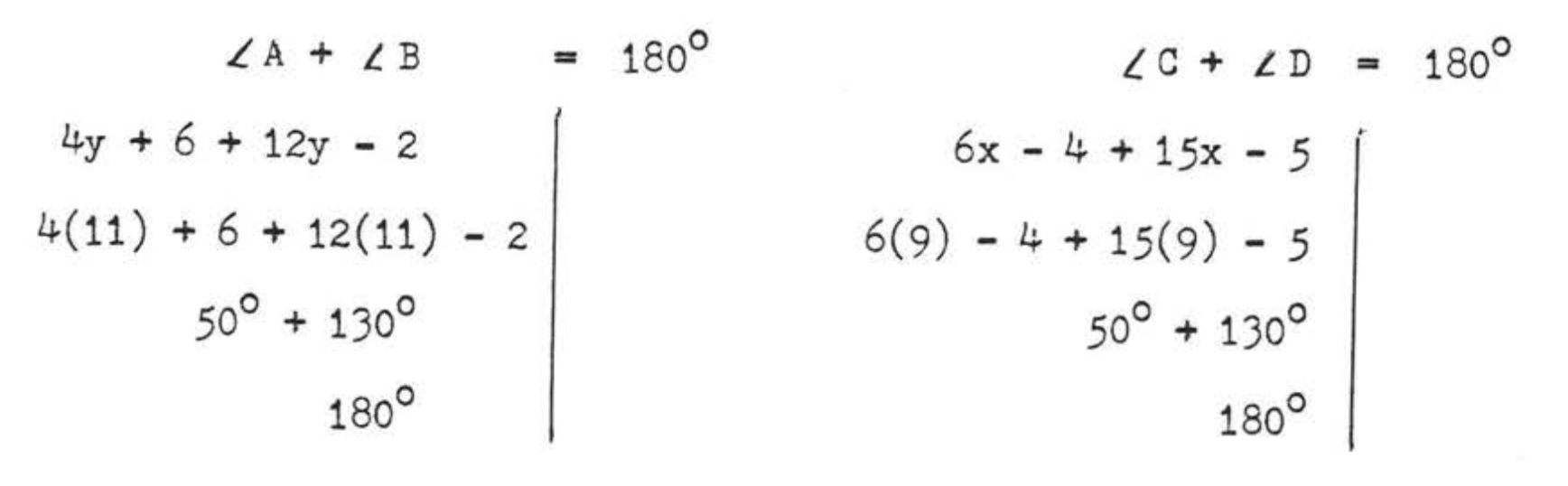
$2020-11-10 9.01.10.пнг$

Відповідь:$x = 9, y = 11, \angle A = \angle C = 50^{\circ}, \angle B = \angle D = 130^{\circ}$.

Проблеми

Для кожного з наступних станів будь-яка теорема, яка використовується для отримання вашої відповіді (-ів):

1. Знайти$x, y, r$, і$s$:

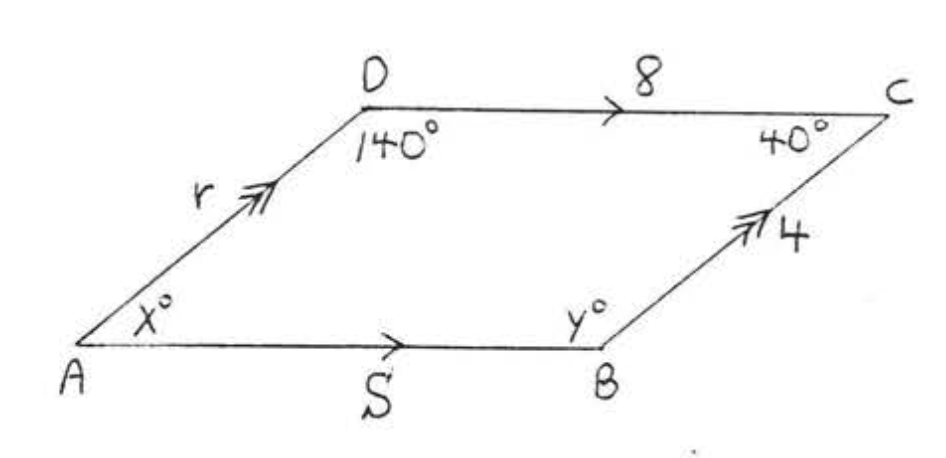
$Знімок екрана 2020-11-10 о 9.12.28 PM.png$

2. Знайти$x, y, r$, і$s$:

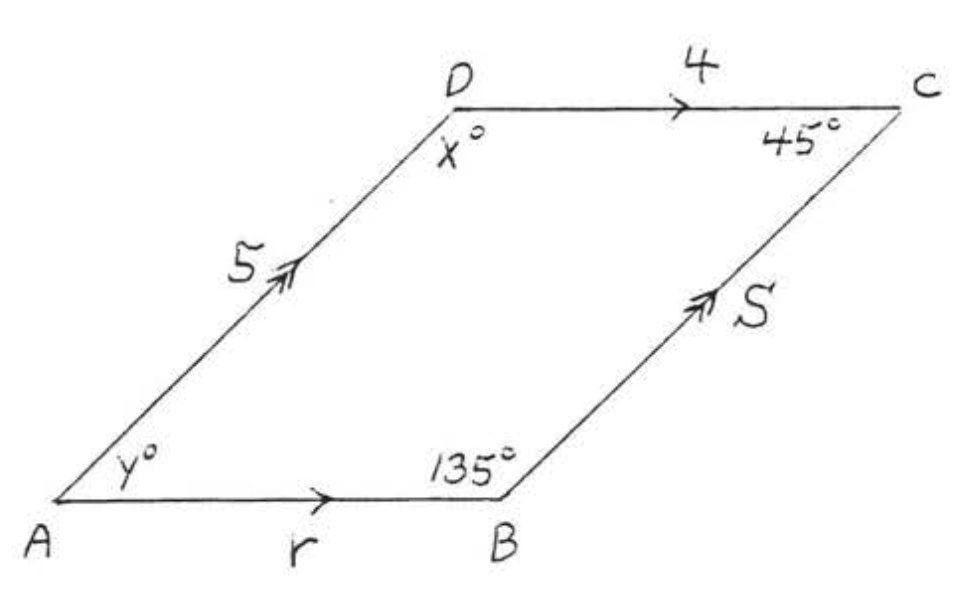
$Знімок екрана 2020-11-10 в 10.57.48 PM.png$

3. Знайти$w, x, y$, і$z$:

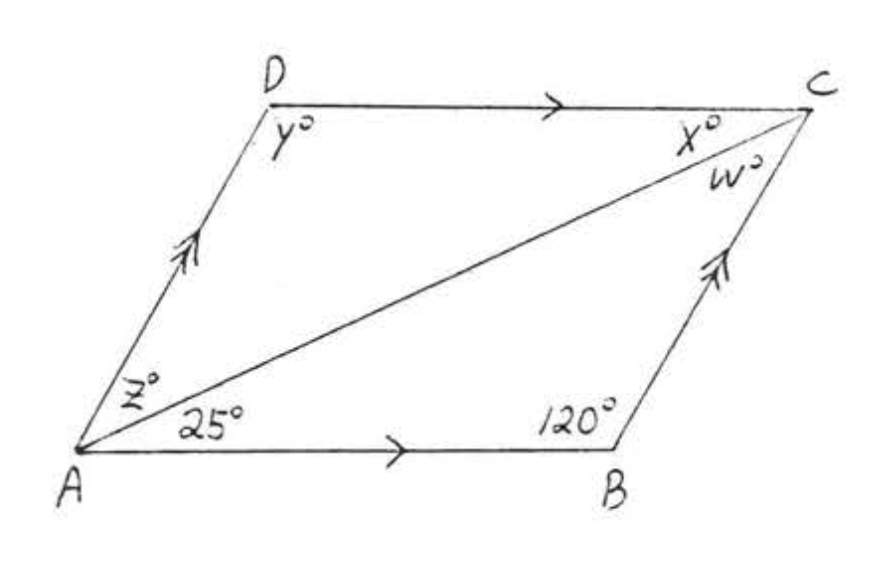
$Знімок екрана 2020-11-10 у 10.58.04 PM.png$

4. Знайти$w, x, y$, і$z$:

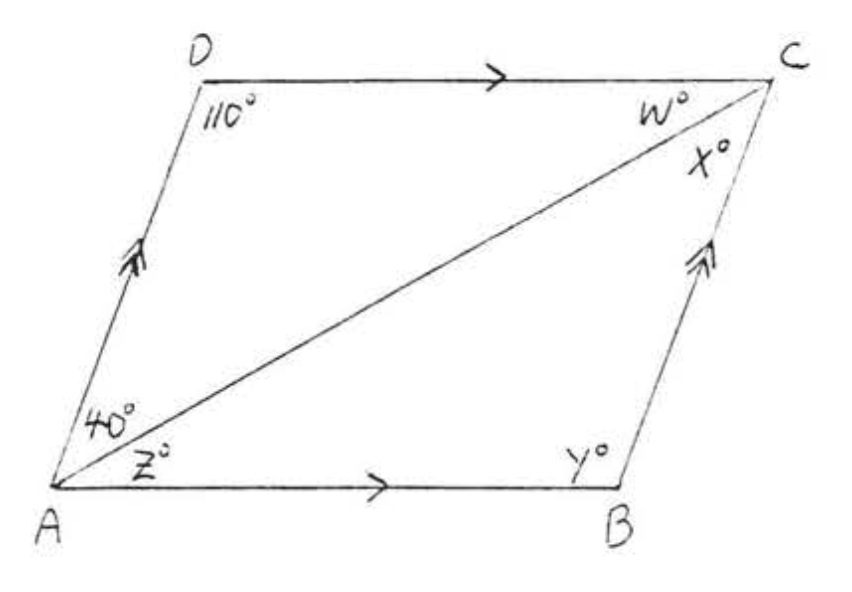
$Знімок екрана 2020-11-10 о 10.58.26 PM.png$

5. Знайти$x, y$, і$z$:

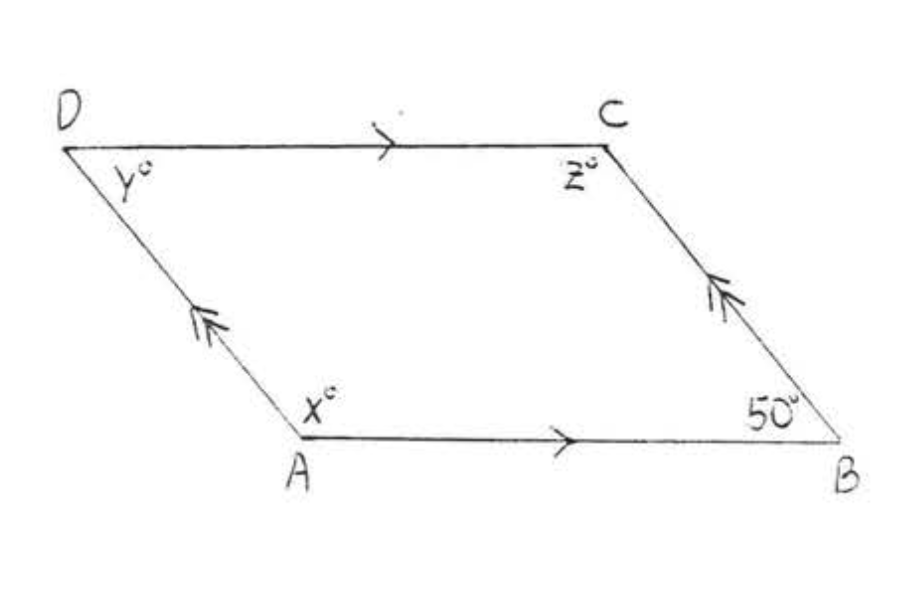
$Знімок екрана 2020-11-10 в 10.58.49 PM.png$

6. Знайти$x, y$, і$z$:

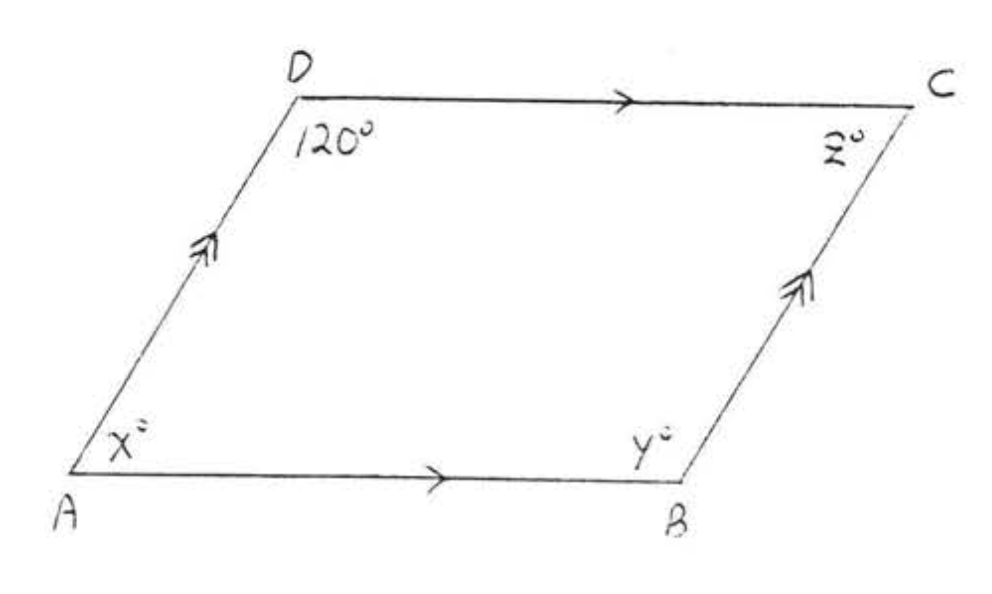
$Знімок екрана 2020-11-10 у 10.59.10 PM.png$

7. Знайти$x, \angle A, \angle B, \angle C$, і$\angle D$:

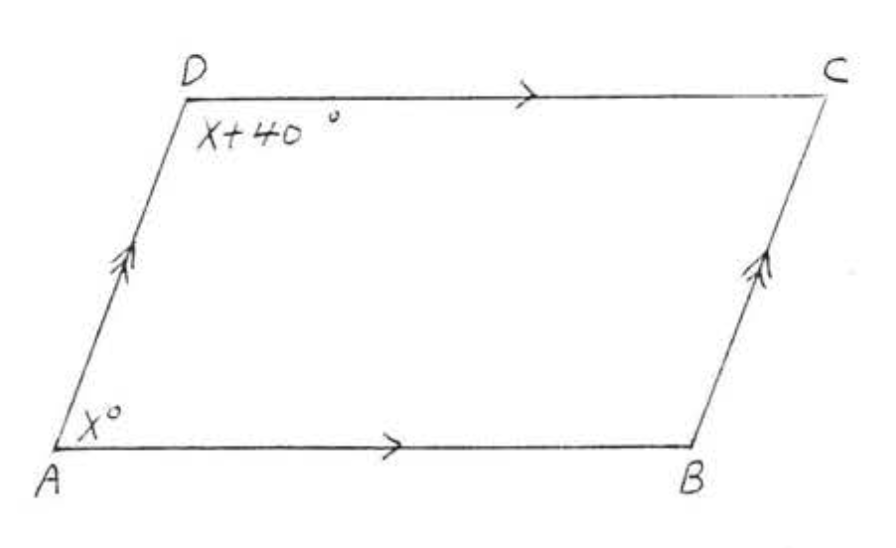
$Знімок екрана 2020-11-10 у 10.59.45 PM.png$

8. Знайти$x, \angle A, \angle B, \angle C$, і$\angle D$:

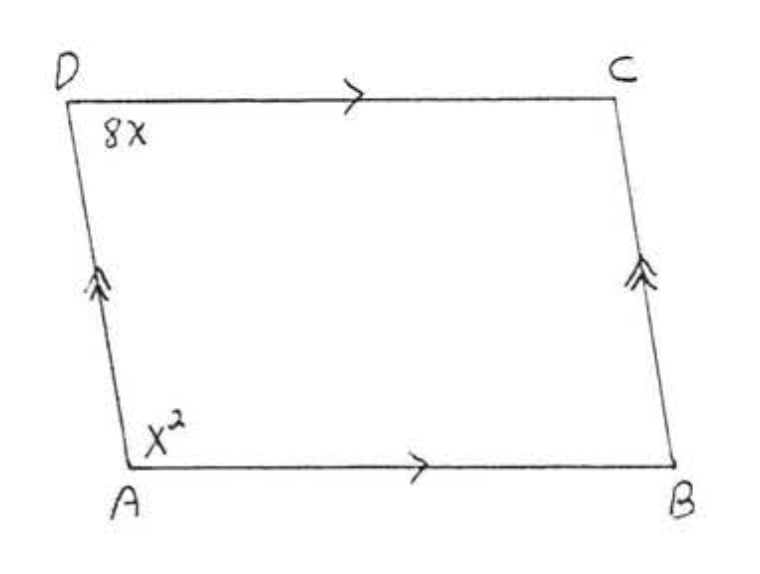
$Знімок екрана 2020-11-10 в 11.00.10 PM.png$

9. Знайти$x, y, AC$, і$BD$:

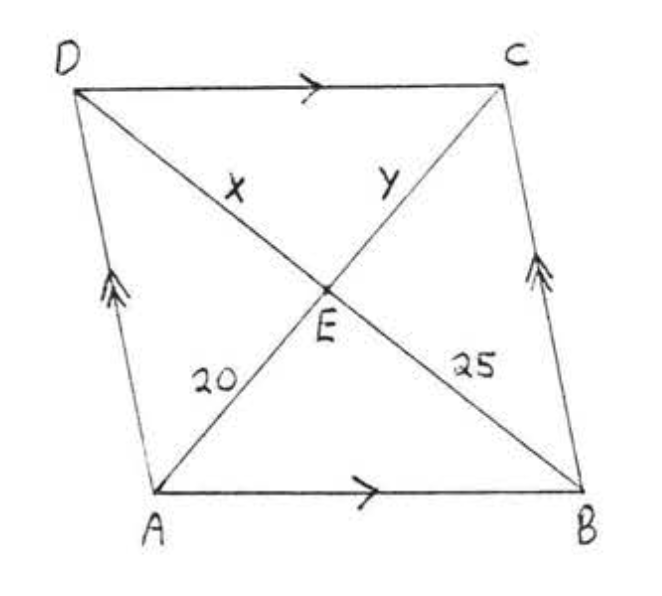
$Знімок екрана 2020-11-10 о 11.00.29 PM.png$

10. Знайти$x, y, AC$, і$BD$:

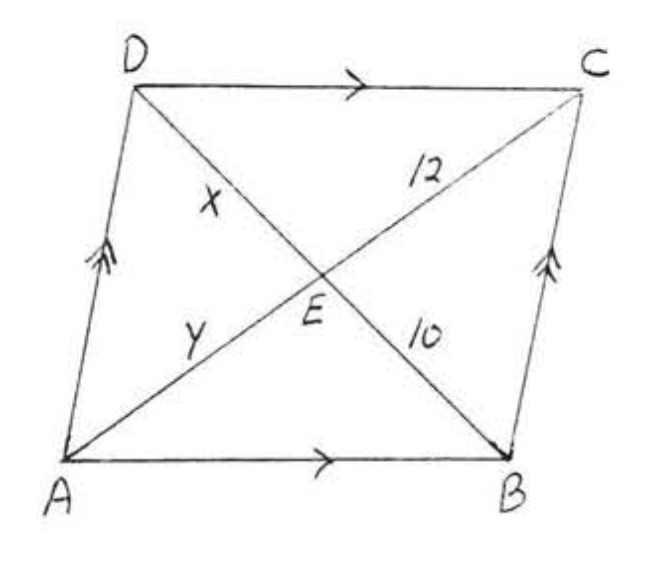
$Знімок екрана 2020-11-10 в 11.00.48 PM.png$

11. Знайти$x, AB$, і$CD$:

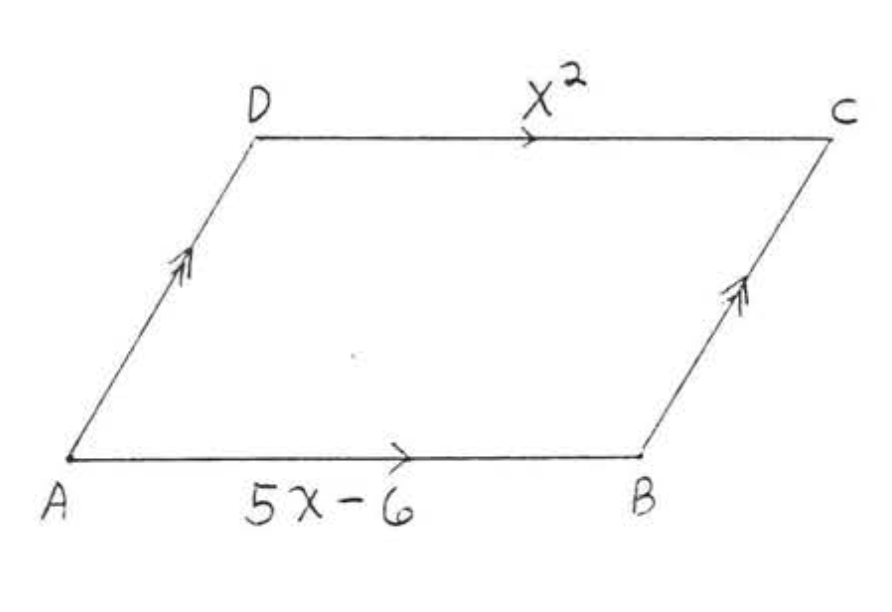
$Знімок екрана 2020-11-10 в 11.01.11 PM.png$

12. Знайти$x, AD$, і$BC$:

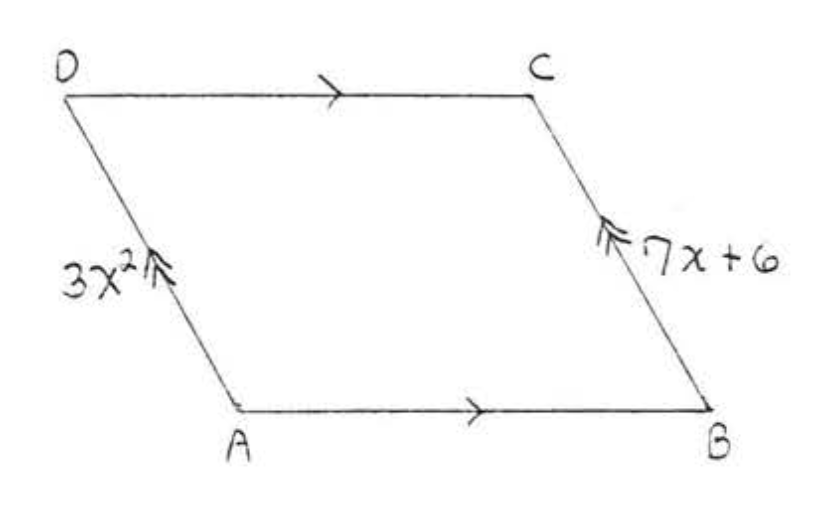
$Знімок екрана 2020-11-10 в 11.01.24 PM.png$

13. Знайти$x, y, AB, BC, CD$, і$AD$:

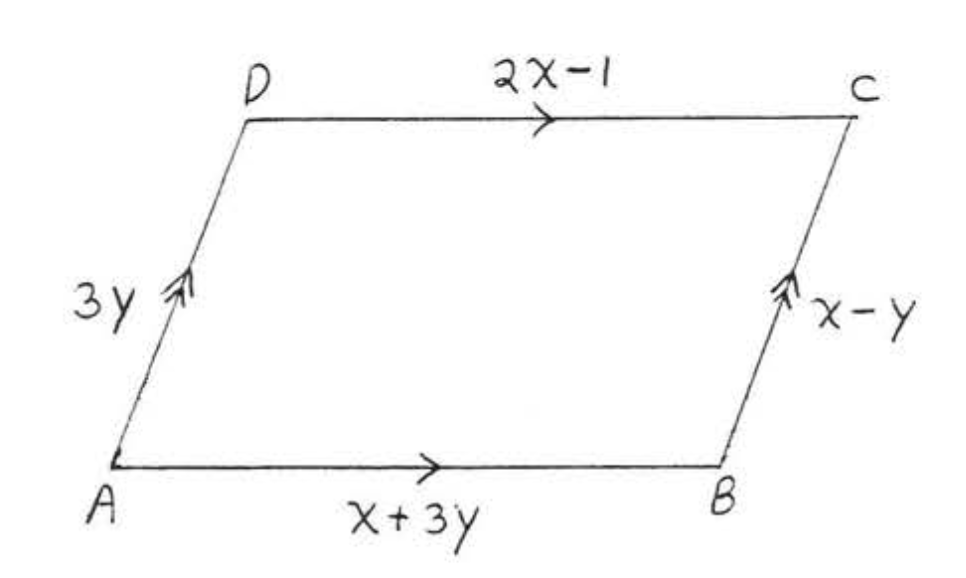
$Знімок екрана 2020-11-10 в 11.01.39 PM.png$

14. Знайти$x, y, AB, BC, CD$, і$AD$:

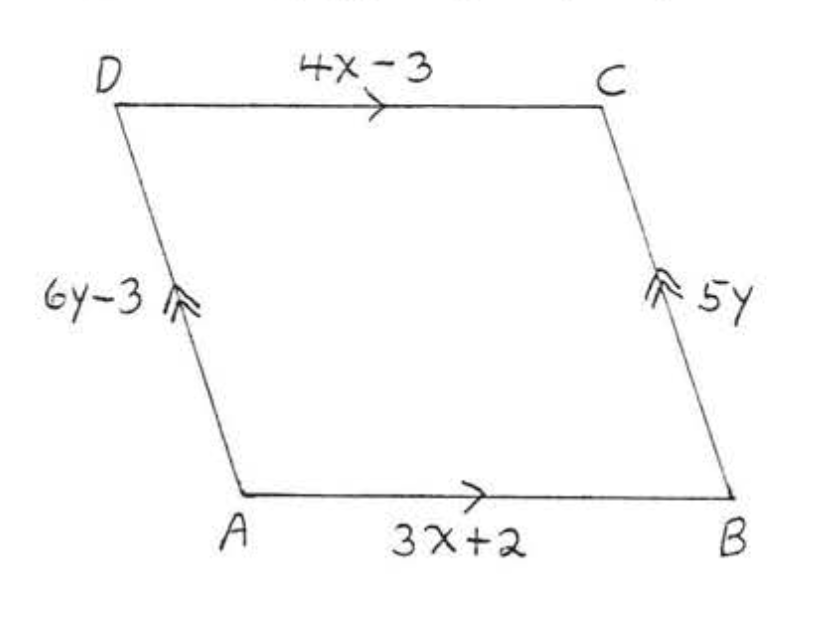
$Знімок екрана 2020-11-10 в 11.01.56 PM.png$

15. Знайти$x, y, AC$, і$BD$:

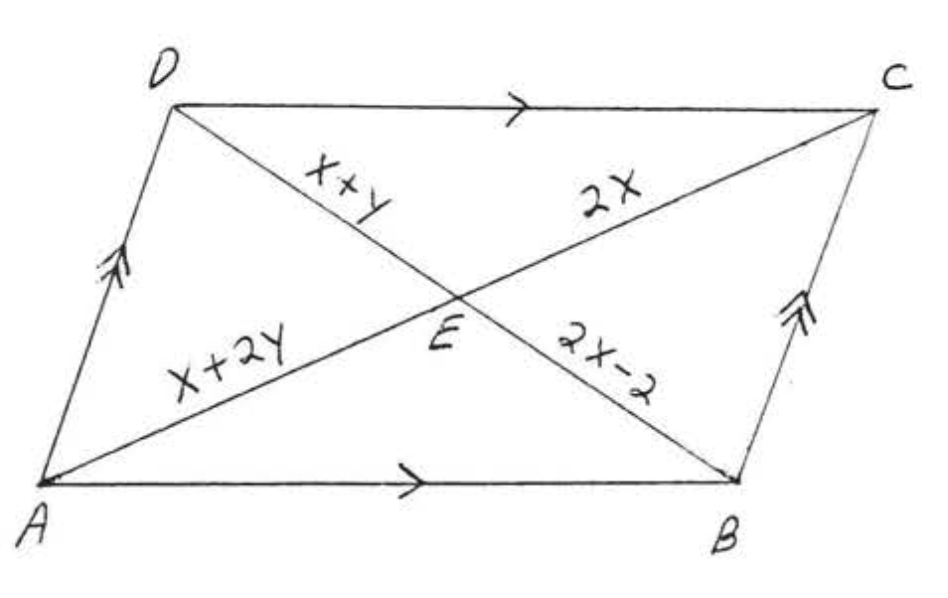
$Знімок екрана 2020-11-10 о 11.03.41 PM.png$

16. Знайти$x, y, AC$, і$BD$:

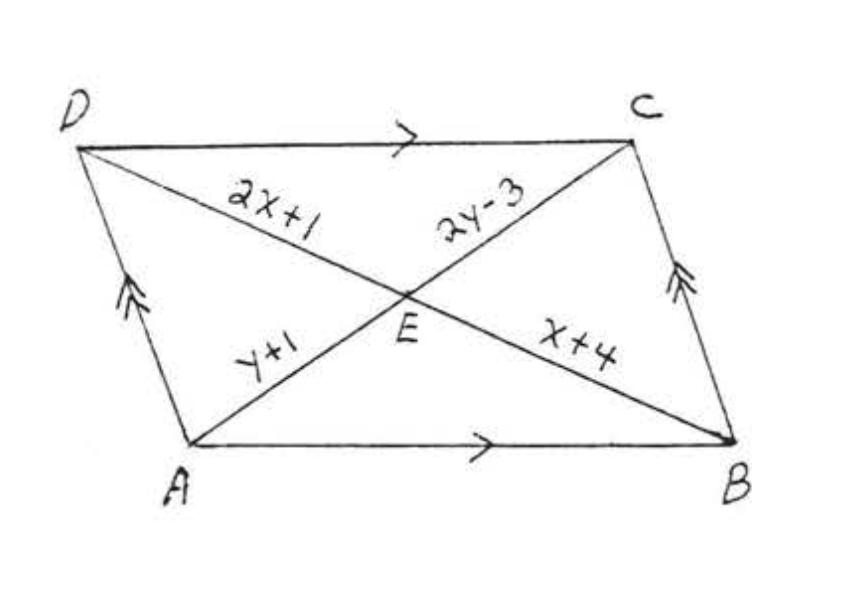
$Знімок екрана 2020-11-10 о 11.03.59 PM.png$

17. Знайти$x, y, \angle A, \angle B, \angle C$, і$\angle D$:

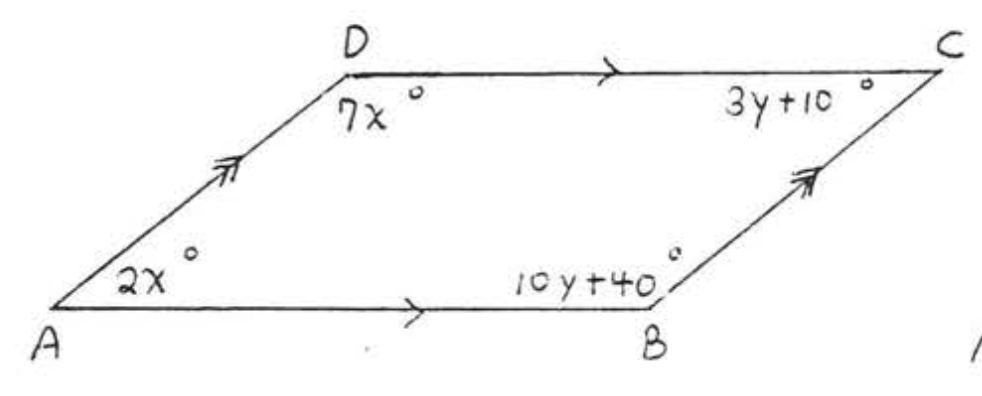
$Знімок екрана 2020-11-10 о 11.04.17 PM.png$

18. Знайти$x, y, \angle A, \angle B, \angle C$, і$\angle D$:

$Знімок екрана 2020-11-10 о 11.04.37 PM.png$

Заяви	причини
1. \(\angle 1 = \angle 2\).	1. Чергуються внутрішні кути паралельних ліній\(AB\) і\(CD\) рівні.
2. \(\angle 3 = \angle 4\).	2. Чергуються внутрішні кути паралельних ліній\(BC\) і\(AD\) рівні.
3. \(AC = AC\).	3. Ідентичність.
4. \(\triangle ABC \cong \triangle CDA\).	4. \(ASA = ASA\).
5. \(AB = CD\),\(BC = DA\).	5. Відповідні сторони конгруентних трикутників рівні.
6. \(\angle B = \angle D\).	6. Відповідні кути конгруентних трикутників рівні.
7. \(\angle A = \angle C\).	7. \(\angle A = \angle 1 +\angle 3 = \angle 2 + \angle 4 = \angle C\)(Додайте твердження 1 і 2).

Теорема\(\PageIndex{1}\)

Приклад\(\PageIndex{1}\)

Приклад\(\PageIndex{2}\)

Приклад\(\PageIndex{3}\)

Теорема\(\PageIndex{2}\)

Приклад\(\PageIndex{4}\)

Теорема\(\PageIndex{3}\)

Приклад\(\PageIndex{5}\)

Приклад\(\PageIndex{6}\)

Приклад\(\PageIndex{7}\)

Проблеми