6.3: Площа трикутника

Для кожного з трикутників на малюнку$\PageIndex{1}$ сторона$AB$ називається підставою і$CD$ називається висотою або висотою, намальованою до цієї основи. Підставою може бути будь-який стан трикутника, хоча зазвичай він вибирається як сторона, на якій трикутник, здається, спирається. Висота - лінія, проведена перпендикулярно підставі від протилежної вершини. Зверніть увагу, що висота може падати за межі трикутника, якщо трикутник тупий, і що висота може бути однією з ніжок, якщо трикутник є прямокутним трикутником.

Малюнок$\PageIndex{1}$: Трикутники з основою$b$ і висотою$h$.

Теорема$\PageIndex{1}$

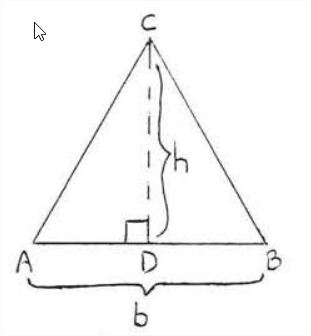
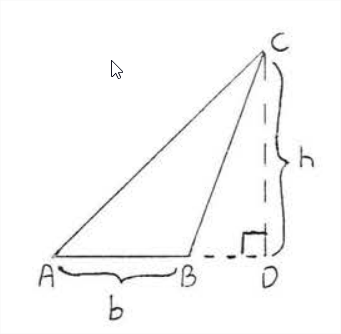
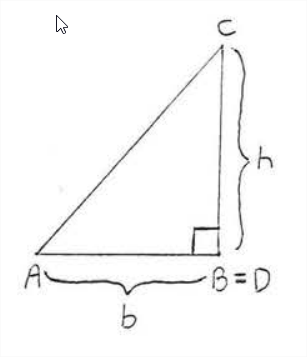
Площа трикутника дорівнює половині його підстави на висоту.

$$A = \dfrac{1}{2} bh$$

Доказ

Для кожного з трикутників, проілюстрованих на малюнку$\PageIndex{1}$, намалюйте$AE$ і$CE$$ABCE$ так, щоб був паралелограм (рис.$PageIndex{2}$). $\triangle ABC \cong \triangle CEA$так площа$\triangle ABC = \text{ area of } \triangle CEA$. Тому площа м$\triangle ABC = \dfrac{1}{2} \text{ area of parallelogram } ABCE = \dfrac{1}{2} bh$.

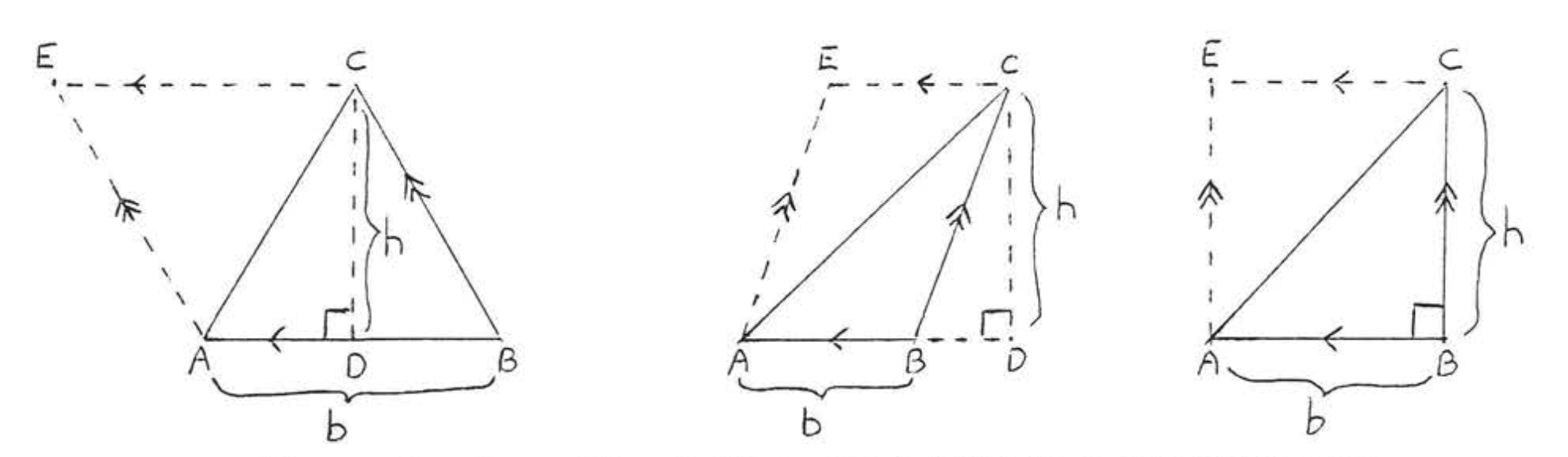
Малюнок$\PageIndex{2}$: Намалюйте$AE$ і$CE$$ABCE$ так, щоб був паралелограм.

Приклад$\PageIndex{1}$

Знайдіть місцевість:

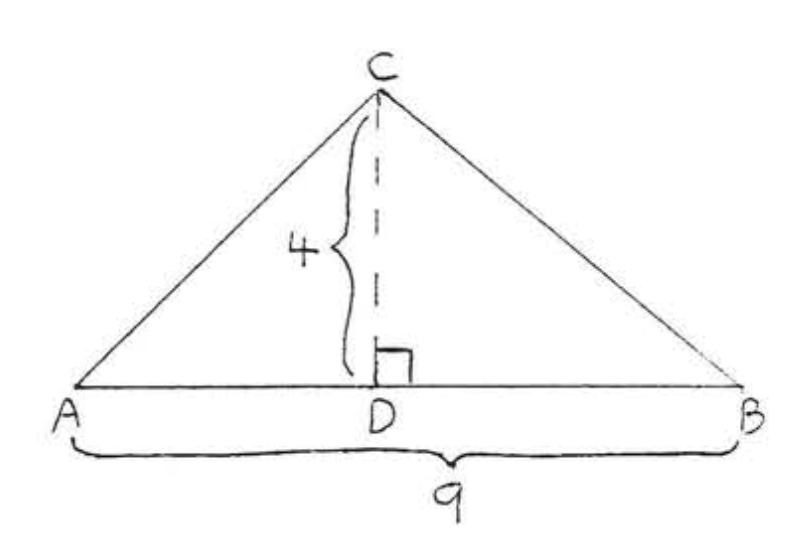
Рішення

$A = \dfrac{1}{2} bh = \dfrac{1}{2} (9) (4) = \dfrac{1}{2} (36) = 18.$

Відповідь: 18.

Приклад$\PageIndex{2}$

Знайдіть площу до найближчої десятої:

Рішення

Намалюйте висоту$h$, як показано на малюнку$\PageIndex{3}$

Малюнок$\PageIndex{3}$: Намалюйте висоту$h$.

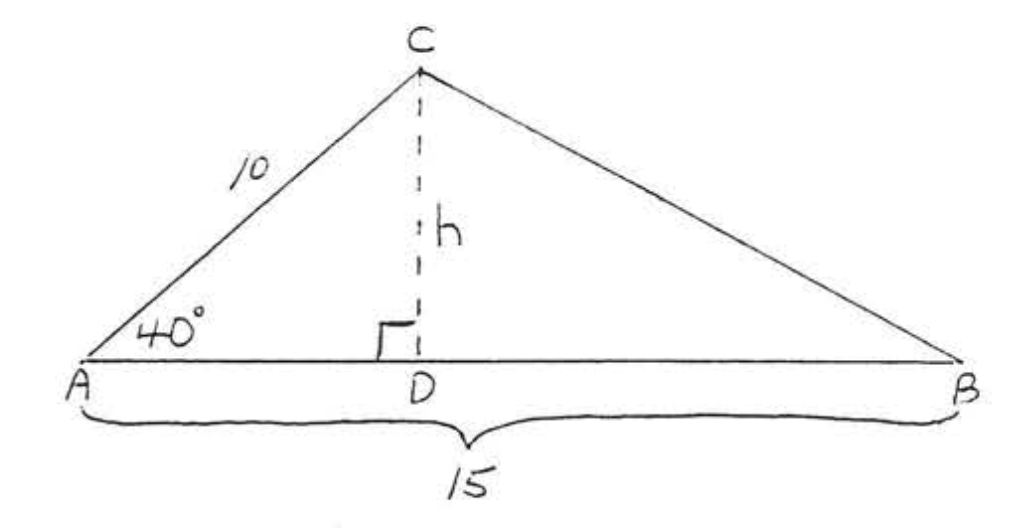
$$\begin{array} {rcl} {\sin 40^{\circ}} & = & {\dfrac{h}{10}} \\ {.6428} & = & {\dfrac{h}{10}} \\ {(10)(.6428)} & = & {\dfrac{h}{10}(10)} \\ {6.428} & = & {h} \end{array}$$

Площа =$\dfrac{1}{2} bh = \dfrac{1}{2} (15)(6.428) = \dfrac{1}{2} (96.420) = 48.21 = 48.2$

Відповідь:$A = 48.2$

Приклад$\PageIndex{3}$

Знайдіть площу і периметр:

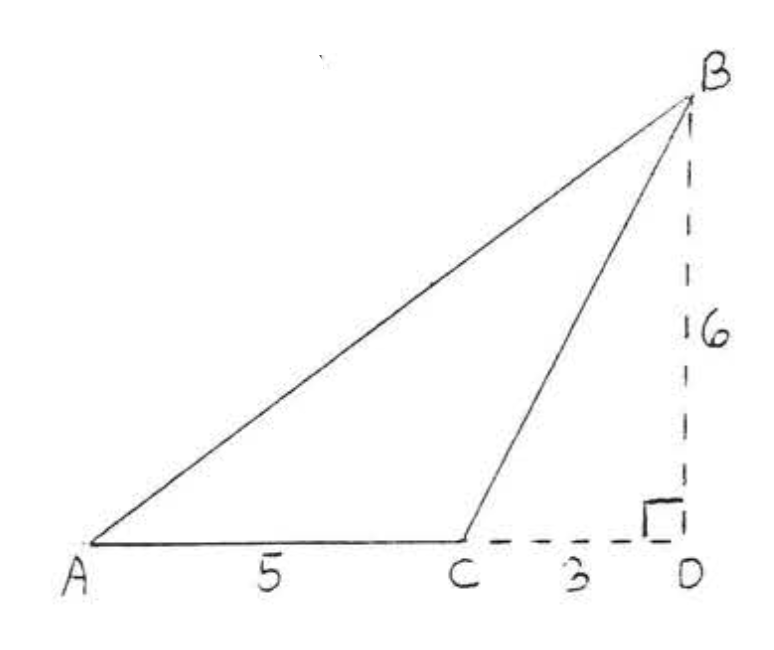
Рішення

$A = \dfrac{1}{2} bh = \dfrac{1}{2} (5)(6) = \dfrac{1}{2} (30) = 15.$

Щоб знайти$AB$ і$BC$ скористаємося теоремою Піфагора:

$\begin{array} {rcl} {\text{AD}^2 + \text{BD}^2} & = & {\text{AB}^2} \\ {8^2 + 6^2} & = & {\text{AB}^2} \\ {64 + 36} & = & {\text{AB}^2} \\ {100} & = & {\text{AB}^2} \\ {10} & = & {\text{AB}} \end{array}$$\begin{array} {rcl} {\text{CD}^2 + \text{BD}^2} & = & {\text{BC}^2} \\ {3^2 + 6^2} & = & {\text{BC}^2} \\ {9 + 36} & = & {\text{BC}^2} \\ {45} & = & {\text{BC}^2} \\ {\text{BC} = \sqrt{45}} & = & {\sqrt{9} \sqrt{5} = 3\sqrt{5}} \end{array}$

Периметр =$AB + AC + BC = 10 + 5 + 3\sqrt{5} = 15 + 3 \sqrt{5}$

Відповідь:$A = 15, P = 15 + 3\sqrt{5}$.

Приклад$\PageIndex{4}$

Знайдіть площу і периметр:

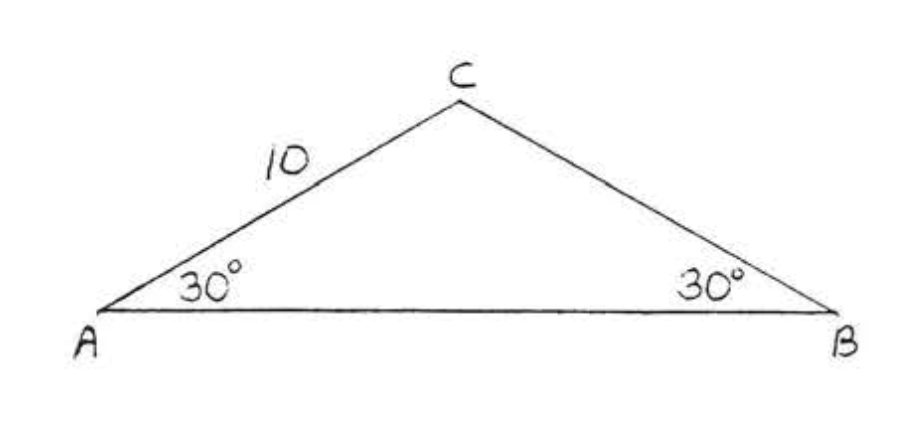
Рішення

$\angle A = \angle B = 30^{\circ}$так$\triangle ABC$ рівнобедрений с$BC = AC = 10$. Намалюйте висоту$h$, як на малюнку$\PageIndex{4}$.

Малюнок$\PageIndex{4}$: Намалюйте висоту$h$.

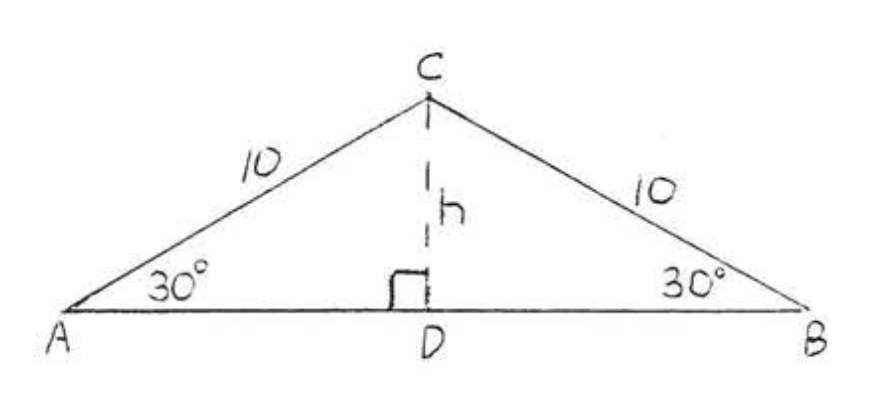
$\triangle ACD$це$30^{\circ} - 60^{\circ} -90^{\circ}$ трикутник, отже,

$$\begin{array} {rcl} {\text{hypotenuse}} & = & {2 (\text{short leg})} \\ {10} & = & {2h} \\ {5} & = & {h} \\ {\text{long leg}} & = & {(\text{short leg}) (\sqrt{3})} \\ {AD} & = & {h\sqrt{3} = 5\sqrt{3}.} \end{array}$$

Аналогічно$BD = 5\sqrt{3}$.

Площа =$\dfrac{1}{2} bh = \dfrac{1}{2} (5\sqrt{3} + 5\sqrt{3})(5) = \dfrac{1}{2} (10\sqrt{3})(5) = \dfrac{1}{2}(50\sqrt{3}) = 25\sqrt{3}$.

Периметр =$10 + 10 + 5\sqrt{3} + 5 \sqrt{3} = 20 + 10 \sqrt{3}$.

Відповідь:$A = 25\sqrt{3}, P = 20 + 10 \sqrt{3}$.

Проблеми

1 - 4. Знайдіть площу$\triangle ABC$:

1.

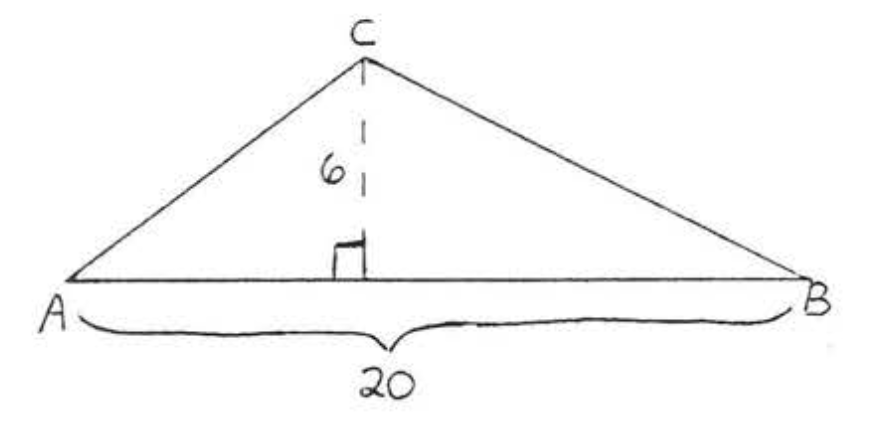
2.

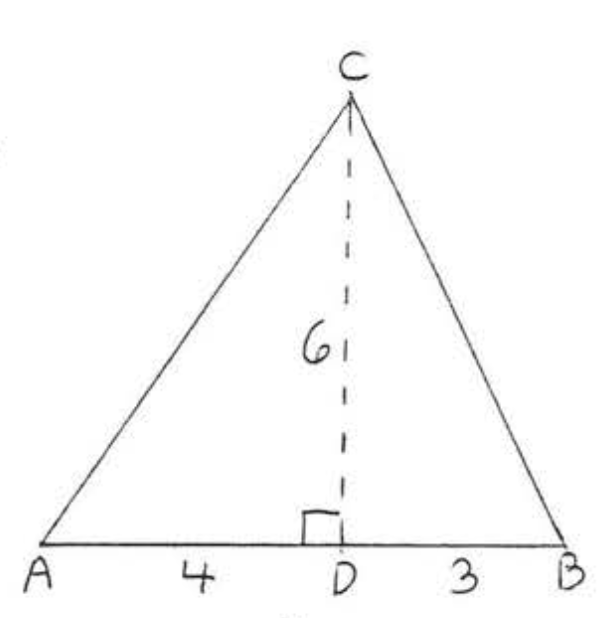
3.

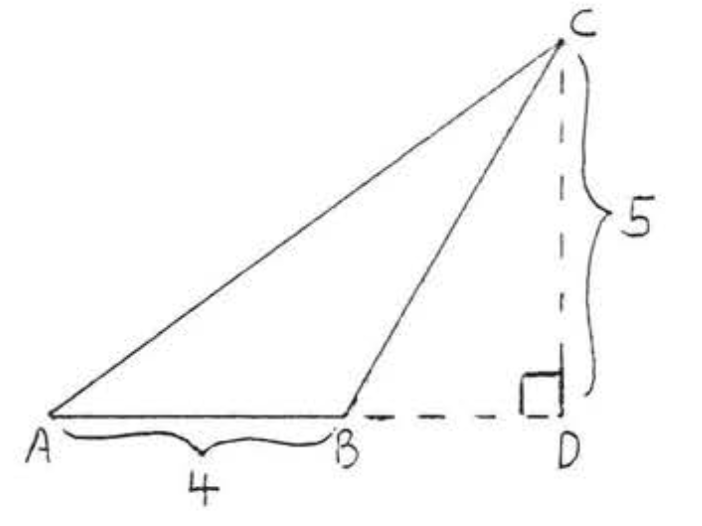
4.

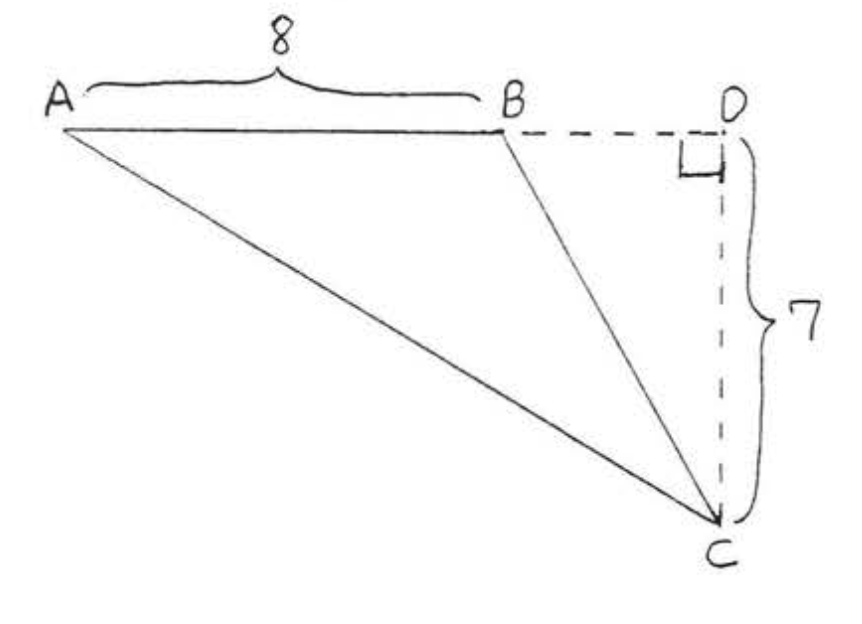
5 - 6. Знайдіть площу до найближчої десятої:

5.

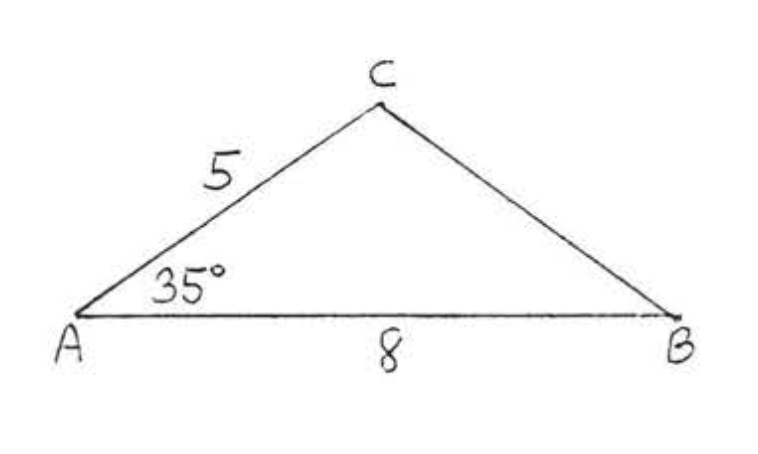
6.

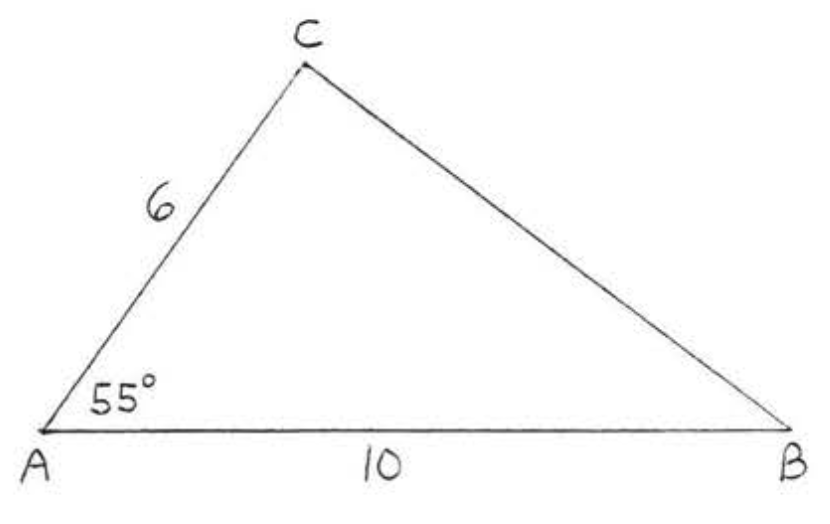
7 - 20. Знайдіть площу і периметр$\triangle ABC$:

7.

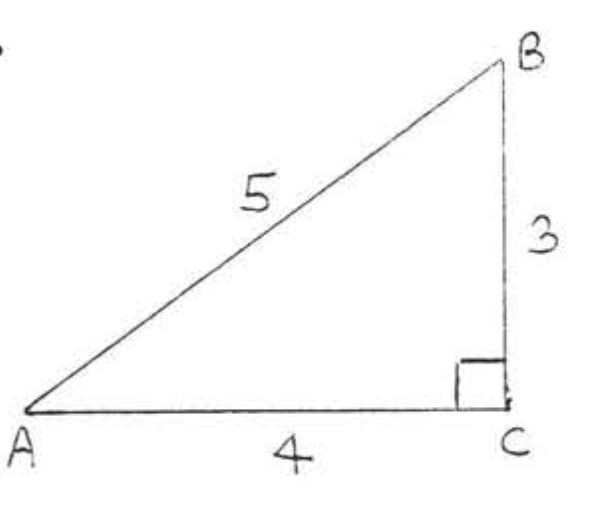
8.

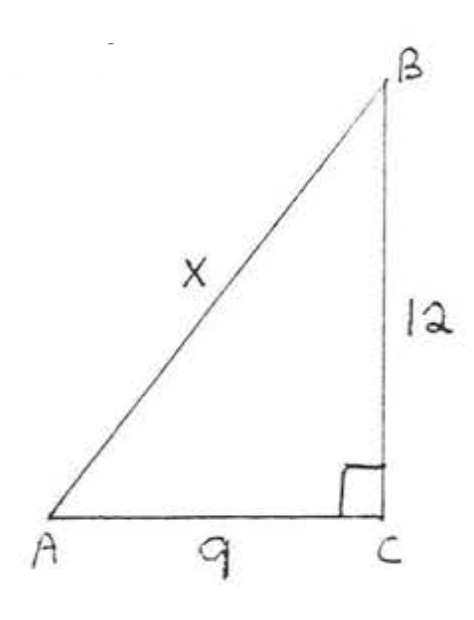
9.

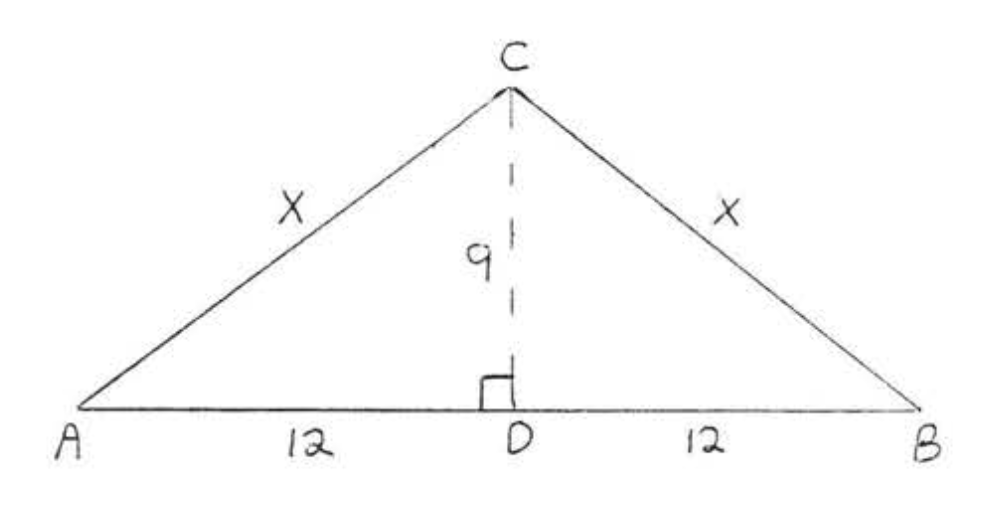
10.

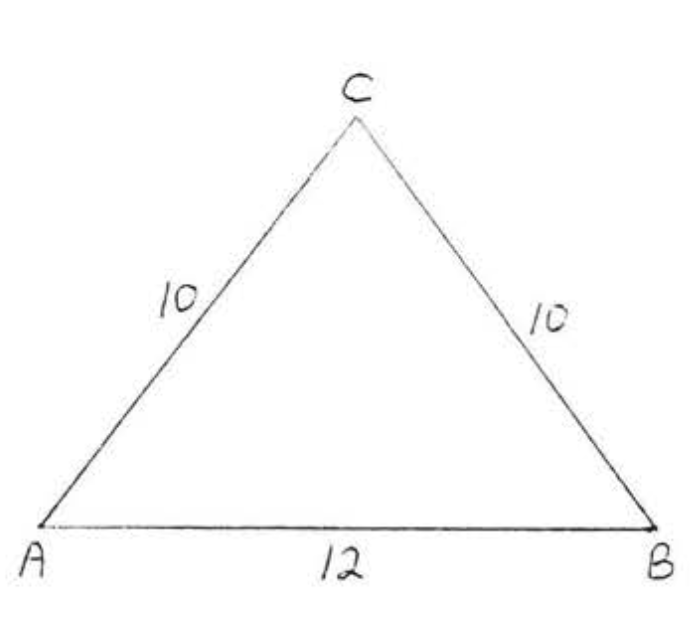
11.

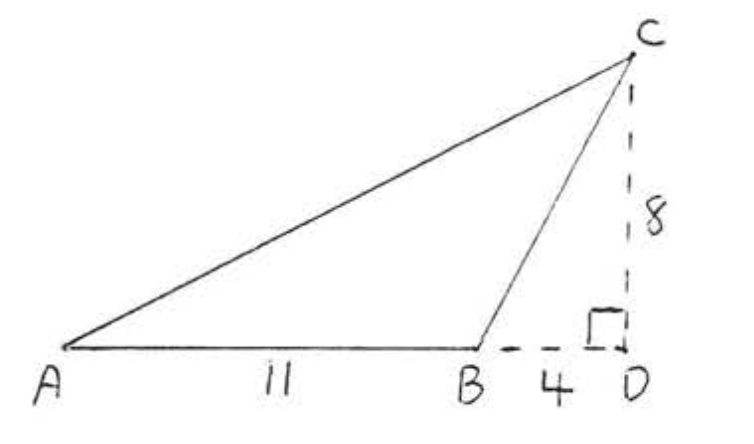
12.

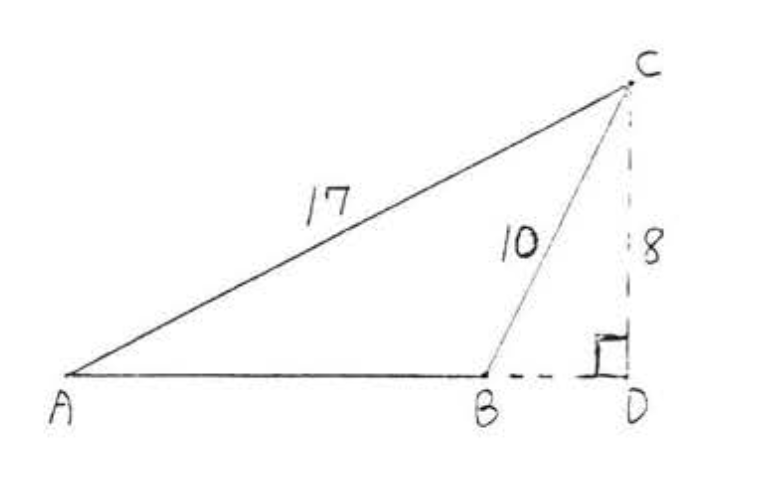
13.

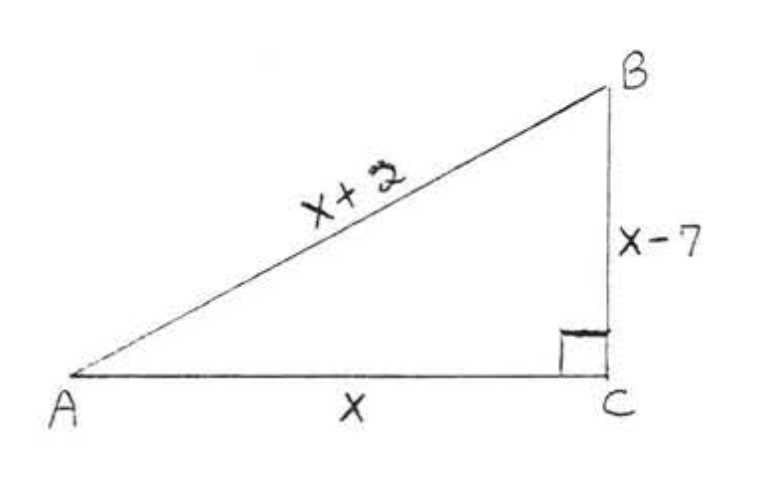
14.

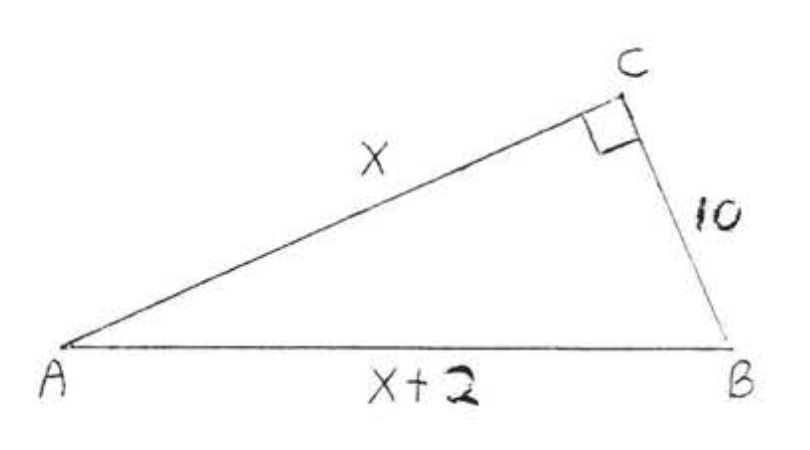
15.

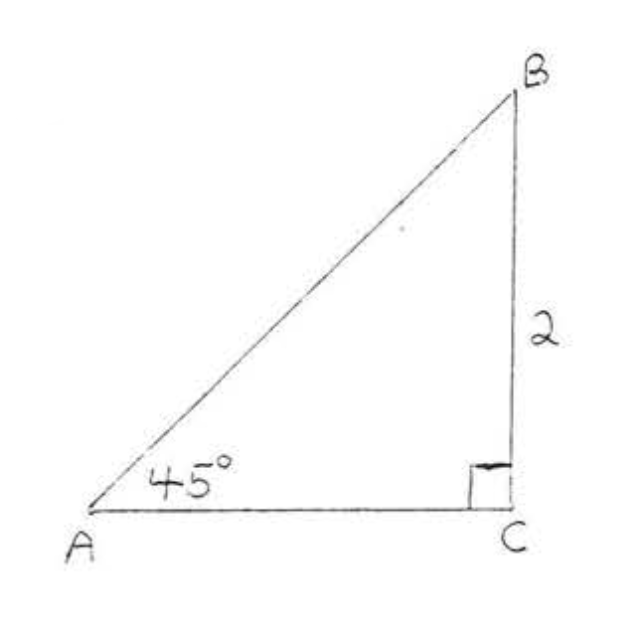
16.

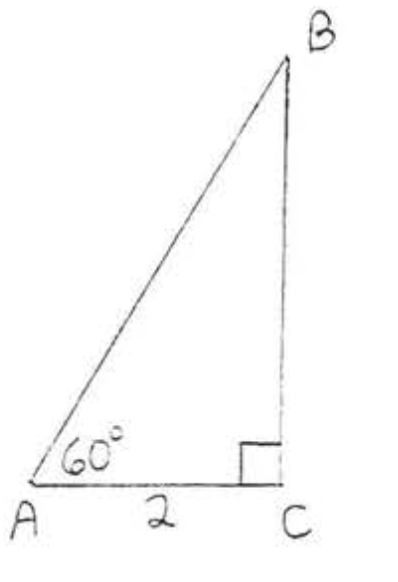
17.

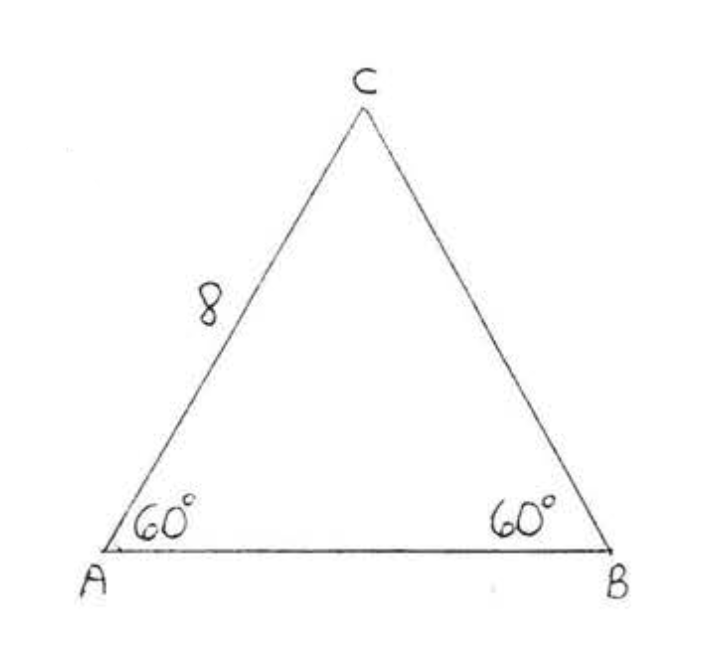
18.

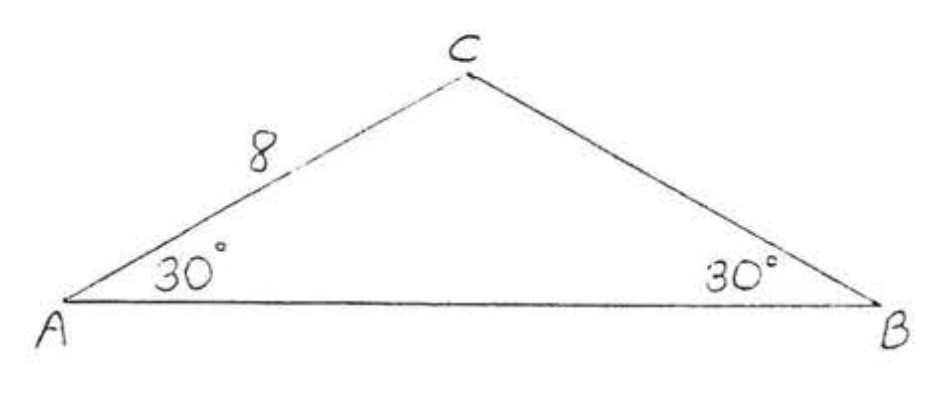
19 - 20. Знайдіть площу і периметр до найближчої десятої:

19.

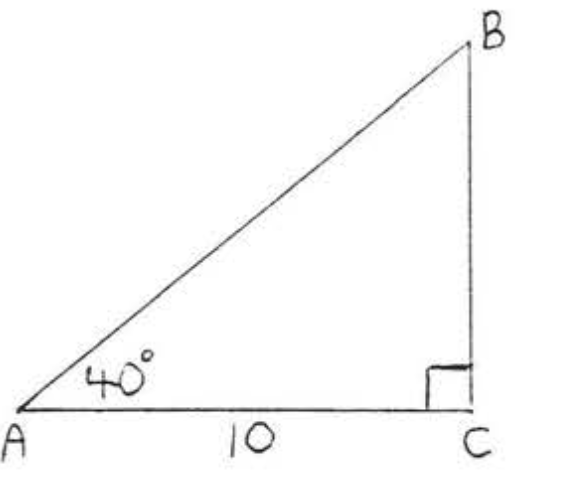
20.

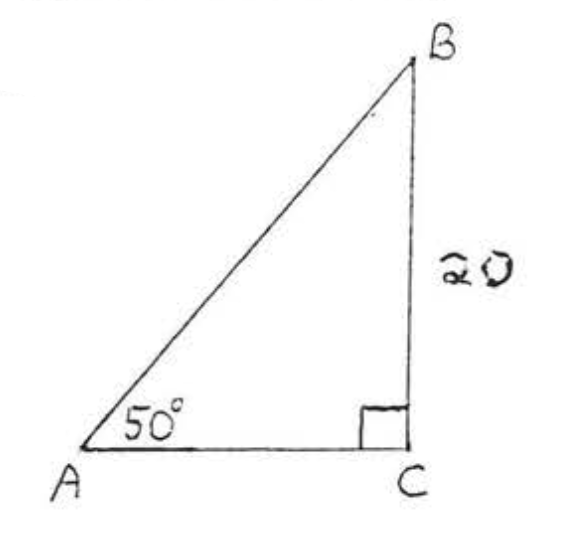
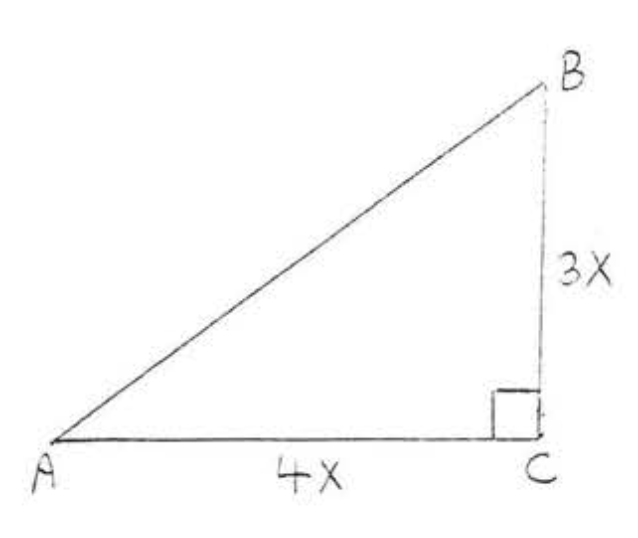
21. Знайти,$x$ якщо площа 35:$\triangle ABC$

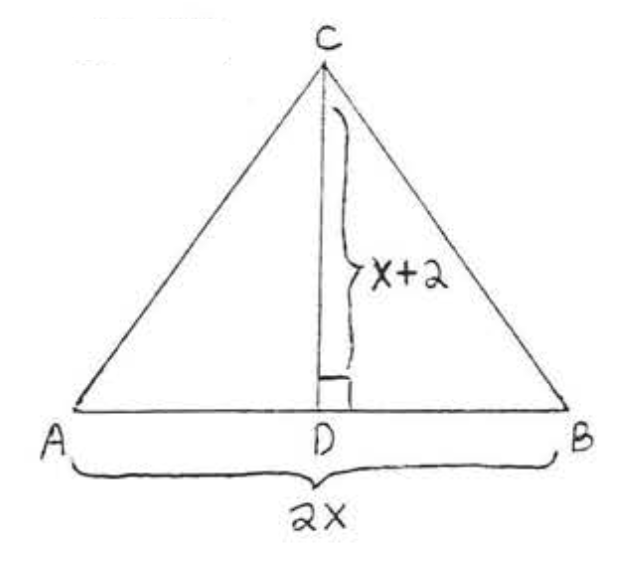
22. Знайти,$x$ якщо площа$\triangle ABC$ дорівнює 24.

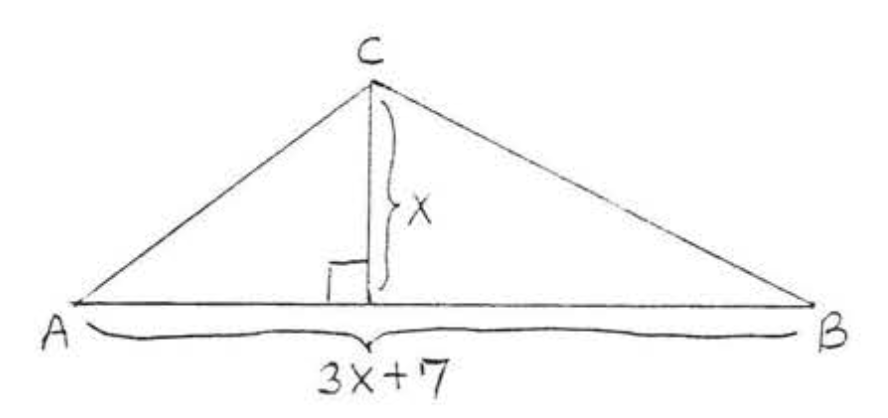
23. Знайти,$x$ якщо площа$\triangle ABC$ дорівнює 12:

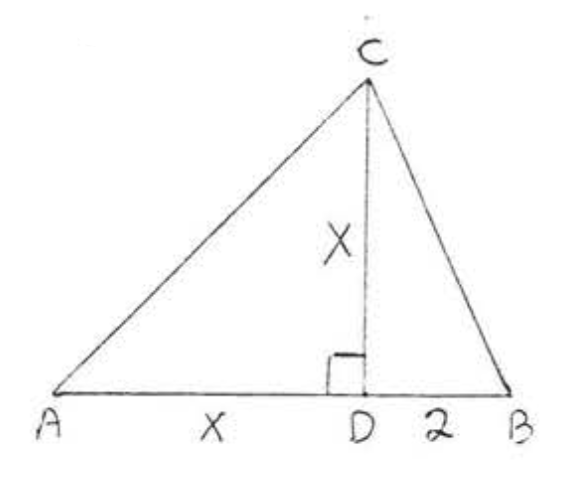
24. Знайти,$x$ якщо площа$\triangle ABC$ становить 108: