Skip to main content
LibreTexts - Ukrayinska

Глава 8 Огляд вправ

  1. Last updated
  2. Save as PDF
  • Page ID
    59661

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Розділ Огляд Вправи

    Спрощення виразів за допомогою коренів

    Вправа\(\PageIndex{1}\) Simplify Expressions with Roots

    У наступних вправах спростити.

      1. \(\sqrt{225}\)
      2. \(-\sqrt{16}\)
      1. \(-\sqrt{169}\)
      2. \(\sqrt{-8}\)
      1. \(\sqrt[3]{8}\)
      2. \(\sqrt[4]{81}\)
      3. \(\sqrt[5]{243}\)
      1. \(\sqrt[3]{-512}\)
      2. \(\sqrt[4]{-81}\)
      3. \(\sqrt[5]{-1}\)
    Відповідь

    1.

    1. \(15\)
    2. \(-4\)

    3.

    1. \(2\)
    2. \(3\)
    3. \(3\)
    Вправа\(\PageIndex{2}\) Estimate and Approximate Roots

    У наступних вправах оцініть кожен корінь між двома послідовними цілими числами.

      1. \(\sqrt{68}\)
      2. \(\sqrt[3]{84}\)
    Відповідь

    1.

    1. \(8<\sqrt{68}<9\)
    2. \(4<\sqrt[3]{84}<5\)
    Вправа\(\PageIndex{3}\) Estimate and Approximate Roots

    У наступних вправах наблизити кожен корінь і округлити до двох знаків після коми.

      1. \(\sqrt{37}\)
      2. \(\sqrt[3]{84}\)
      3. \(\sqrt[4]{125}\)
    Відповідь

    1. Вирішуйте для себе

    Вправа\(\PageIndex{4}\) Simplify Variable Expressions with Roots

    У наступних вправах спрощуйте використання абсолютних значень в міру необхідності.

      1. \(\sqrt[3]{a^{3}}\)
      2. \(\sqrt[7]{b^{7}}\)
      1. \(\sqrt{a^{14}}\)
      2. \(\sqrt{w^{24}}\)
      1. \(\sqrt[4]{m^{8}}\)
      2. \(\sqrt[5]{n^{20}}\)
      1. \(\sqrt{121 m^{20}}\)
      2. \(-\sqrt{64 a^{2}}\)
      1. \(\sqrt[3]{216 a^{6}}\)
      2. \(\sqrt[5]{32 b^{20}}\)
      1. \(\sqrt{144 x^{2} y^{2}}\)
      2. \(\sqrt{169 w^{8} y^{10}}\)
      3. \(\sqrt[3]{8 a^{51} b^{6}}\)
    Відповідь

    1.

    1. \(a\)
    2. \(|b|\)

    3.

    1. \(m^{2}\)
    2. \(n^{4}\)

    5.

    1. \(6a^{2}\)
    2. \(2b^{4}\)

    Спрощення радикальних виразів

    Вправа\(\PageIndex{5}\) Use the Product Property to Simplify Radical Expressions

    У наступних вправах використовуйте Product Property для спрощення радикальних виразів.

    1. \(\sqrt{125}\)
    2. \(\sqrt{675}\)
      1. \(\sqrt[3]{625}\)
      2. \(\sqrt[6]{128}\)
    Відповідь

    1. \(5\sqrt{5}\)

    3.

    1. \(5 \sqrt[3]{5}\)
    2. \(2 \sqrt[6]{2}\)
    Вправа\(\PageIndex{6}\) Use the Product Property to Simplify Radical Expressions

    У наступних вправах спростіть використання знаків абсолютного значення в міру необхідності.

      1. \(\sqrt{a^{23}}\)
      2. \(\sqrt[3]{b^{8}}\)
      3. \(\sqrt[8]{c^{13}}\)
      1. \(\sqrt{80 s^{15}}\)
      2. \(\sqrt[5]{96 a^{7}}\)
      3. \(\sqrt[6]{128 b^{7}}\)
      1. \(\sqrt{96 r^{3} s^{3}}\)
      2. \(\sqrt[3]{80 x^{7} y^{6}}\)
      3. \(\sqrt[4]{80 x^{8} y^{9}}\)
      1. \(\sqrt[5]{-32}\)
      2. \(\sqrt[8]{-1}\)
      1. \(8+\sqrt{96}\)
      2. \(\frac{2+\sqrt{40}}{2}\)
    Відповідь

    2.

    1. \(4\left|s^{7}\right| \sqrt{5 s}\)
    2. \(2 a \sqrt[5]{3 a^{2}}\)
    3. \(2|b| \sqrt[6]{2 b}\)

    4.

    1. \(-2\)
    2. не реальний
    Вправа\(\PageIndex{7}\) Use the Quotient Property to Simplify Radical Expressions

    У наступних вправах використовуйте властивість частки для спрощення квадратних коренів.

      1. \(\sqrt{\frac{72}{98}}\)
      2. \(\sqrt[3]{\frac{24}{81}}\)
      3. \(\sqrt[4]{\frac{6}{96}}\)
      1. \(\sqrt{\frac{y^{4}}{y^{8}}}\)
      2. \(\sqrt[5]{\frac{u^{21}}{u^{11}}}\)
      3. \(\sqrt[6]{\frac{v^{30}}{v^{12}}}\)
    3. \(\sqrt{\frac{300 m^{5}}{64}}\)
      1. \(\sqrt{\frac{28 p^{7}}{q^{2}}}\)
      2. \(\sqrt[3]{\frac{81 s^{8}}{t^{3}}}\)
      3. \(\sqrt[4]{\frac{64 p^{15}}{q^{12}}}\)
      1. \(\sqrt{\frac{27 p^{2} q}{108 p^{4} q^{3}}}\)
      2. \(\sqrt[3]{\frac{16 c^{5} d^{7}}{250 c^{2} d^{2}}}\)
      3. \(\sqrt[6]{\frac{2 m^{9} n^{7}}{128 m^{3} n}}\)
      1. \(\frac{\sqrt{80 q^{5}}}{\sqrt{5 q}}\)
      2. \(\frac{\sqrt[3]{-625}}{\sqrt[3]{5}}\)
      3. \(\frac{\sqrt[4]{80 m^{7}}}{\sqrt[4]{5 m}}\)
    Відповідь

    1.

    1. \(\frac{6}{7}\)
    2. \(\frac{2}{3}\)
    3. \(\frac{1}{2}\)

    3. \(\frac{10 m^{2} \sqrt{3 m}}{8}\)

    5.

    1. \(\frac{1}{2|p q|}\)
    2. \(\frac{2 c d \sqrt[5]{2 d^{2}}}{5}\)
    3. \(\frac{|m n| \sqrt[6]{2}}{2}\)

    Спрощення раціональних експонентів

    Вправа\(\PageIndex{8}\) Simplify Expressions with \(a^{\frac{1}{n}}\)

    У наступних вправах пишіть як радикальний вираз.

      1. \(r^{\frac{1}{2}}\)
      2. \(s^{\frac{1}{3}}\)
      3. \(t^{\frac{1}{4}}\)
    Відповідь

    1.

    1. \(\sqrt{r}\)
    2. \(\sqrt[3]{s}\)
    3. \(\sqrt[4]{t}\)
    Вправа\(\PageIndex{9}\) Simplify Expressions with \(a^{\frac{1}{n}}\)

    У наступних вправах пишіть з раціональним показником.

      1. \(\sqrt{21p}\)
      2. \(\sqrt[4]{8q}\)
      3. \(4\sqrt[6]{36r}\)
    Відповідь

    1. Вирішуйте для себе

    Вправа\(\PageIndex{10}\) Simplify Expressions with \(a^{\frac{1}{n}}\)

    У наступних вправах спростити.

      1. \(625^{\frac{1}{4}}\)
      2. \(243^{\frac{1}{5}}\)
      3. \(32^{\frac{1}{5}}\)
      1. \((-1,000)^{\frac{1}{3}}\)
      2. \(-1,000^{\frac{1}{3}}\)
      3. \((1,000)^{-\frac{1}{3}}\)
      1. \((-32)^{\frac{1}{5}}\)
      2. \((243)^{-\frac{1}{5}}\)
      3. \(-125^{\frac{1}{3}}\)
    Відповідь

    1.

    1. \(5\)
    2. \(3\)
    3. \(2\)

    3.

    1. \(-2\)
    2. \(\frac{1}{3}\)
    3. \(-5\)
    Вправа\(\PageIndex{11}\) Simplify Expressions with \(a^{\frac{m}{n}}\)

    У наступних вправах пишіть з раціональним показником.

      1. \(\sqrt[4]{r^{7}}\)
      2. \((\sqrt[5]{2 p q})^{3}\)
      3. \(\sqrt[4]{\left(\frac{12 m}{7 n}\right)^{3}}\)
    Відповідь

    1. Вирішуйте для себе

    Вправа\(\PageIndex{12}\) Simplify Expressions with \(a^{\frac{m}{n}}\)

    У наступних вправах спростити.

      1. \(25^{\frac{3}{2}}\)
      2. \(9^{-\frac{3}{2}}\)
      3. \((-64)^{\frac{2}{3}}\)
      1. \(-64^{\frac{3}{2}}\)
      2. \(-64^{-\frac{3}{2}}\)
      3. \((-64)^{\frac{3}{2}}\)
    Відповідь

    1.

    1. \(125\)
    2. \(\frac{1}{27}\)
    3. \(16\)
    Вправа\(\PageIndex{13}\) Use the Laws of Exponents to Simplify Expressions with Rational Exponents

    У наступних вправах спростити.

      1. \(6^{\frac{5}{2}} \cdot 6^{\frac{1}{2}}\)
      2. \(\left(b^{15}\right)^{\frac{3}{5}}\)
      3. \(\frac{w^{\frac{2}{7}}}{w^{\frac{9}{7}}}\)
      1. \(\frac{a^{\frac{3}{4}} \cdot a^{-\frac{1}{4}}}{a^{-\frac{10}{4}}}\)
      2. \(\left(\frac{27 b^{\frac{2}{3}} c^{-\frac{5}{2}}}{b^{-\frac{7}{3}} c^{\frac{1}{2}}}\right)^{\frac{1}{3}}\)
    Відповідь

    1.

    1. \(6^{3}\)
    2. \(b^{9}\)
    3. \(\frac{1}{w}\)

    Додавання, віднімання та множення радикальних виразів

    Вправа\(\PageIndex{14}\) add and Subtract Radical Expressions

    У наступних вправах спростити.

      1. \(7 \sqrt{2}-3 \sqrt{2}\)
      2. \(7 \sqrt[3]{p}+2 \sqrt[3]{p}\)
      3. \(5 \sqrt[3]{x}-3 \sqrt[3]{x}\)
      1. \(\sqrt{11 b}-5 \sqrt{11 b}+3 \sqrt{11 b}\)
      2. \(8 \sqrt[4]{11 c d}+5 \sqrt[4]{11 c d}-9 \sqrt[4]{11 c d}\)
      1. \(\sqrt{48}+\sqrt{27}\)
      2. \(\sqrt[3]{54}+\sqrt[3]{128}\)
      3. \(6 \sqrt[4]{5}-\frac{3}{2} \sqrt[4]{320}\)
      1. \(\sqrt{80 c^{7}}-\sqrt{20 c^{7}}\)
      2. \(2 \sqrt[4]{162 r^{10}}+4 \sqrt[4]{32 r^{10}}\)
    5. \(3 \sqrt{75 y^{2}}+8 y \sqrt{48}-\sqrt{300 y^{2}}\)
    Відповідь

    1.

    1. \(4\sqrt{2}\)
    2. \(9\sqrt[3]{p}\)
    3. \(2\sqrt[3]{x}\)

    3.

    1. \(7\sqrt{3}\)
    2. \(7\sqrt[3]{2}\)
    3. \(3\sqrt[4]{5}\)

    5. \(37 y \sqrt{3}\)

    Вправа\(\PageIndex{15}\) Multiply Radical Expressions

    У наступних вправах спростити.

      1. \((5 \sqrt{6})(-\sqrt{12})\)
      2. \((-2 \sqrt[4]{18})(-\sqrt[4]{9})\)
      1. \(\left(3 \sqrt{2 x^{3}}\right)\left(7 \sqrt{18 x^{2}}\right)\)
      2. \(\left(-6 \sqrt[3]{20 a^{2}}\right)\left(-2 \sqrt[3]{16 a^{3}}\right)\)
    Відповідь

    2.

    1. \(126 x^{2} \sqrt{2}\)
    2. \(48 a \sqrt[3]{a^{2}}\)
    Вправа\(\PageIndex{16}\) Use Polynomial Multiplication to Multiply Radical Expressions

    У наступних вправах помножте.

      1. \(\sqrt{11}(8+4 \sqrt{11})\)
      2. \(\sqrt[3]{3}(\sqrt[3]{9}+\sqrt[3]{18})\)
      1. \((3-2 \sqrt{7})(5-4 \sqrt{7})\)
      2. \((\sqrt[3]{x}-5)(\sqrt[3]{x}-3)\)
    3. \((2 \sqrt{7}-5 \sqrt{11})(4 \sqrt{7}+9 \sqrt{11})\)
      1. \((4+\sqrt{11})^{2}\)
      2. \((3-2 \sqrt{5})^{2}\)
    5. \((7+\sqrt{10})(7-\sqrt{10})\)
    6. \((\sqrt[3]{3 x}+2)(\sqrt[3]{3 x}-2)\)
    Відповідь

    2.

    1. \(71-22 \sqrt{7}\)
    2. \(\sqrt[3]{x^{2}}-8 \sqrt[3]{x}+15\)

    4.

    1. \(27+8 \sqrt{11}\)
    2. \(29-12 \sqrt{5}\)

    6. \(\sqrt[3]{9 x^{2}}-4\)

    Розділити радикальні вирази

    Вправа\(\PageIndex{17}\) Divide Square Roots

    У наступних вправах спростити.

      1. \(\frac{\sqrt{48}}{\sqrt{75}}\)
      2. \(\frac{\sqrt[3]{81}}{\sqrt[3]{24}}\)
      1. \(\frac{\sqrt{320 m n^{-5}}}{\sqrt{45 m^{-7} n^{3}}}\)
      2. \(\frac{\sqrt[3]{16 x^{4} y^{-2}}}{\sqrt[3]{-54 x^{-2} y^{4}}}\)
    Відповідь

    2.

    1. \(\frac{8 m^{4}}{3 n^{4}}\)
    2. \(-\frac{x^{2}}{2 y^{2}}\)
    Вправа\(\PageIndex{18}\) rationalize a One Term Denominator

    У наступних вправах раціоналізуйте знаменник.

      1. \(\frac{8}{\sqrt{3}}\)
      2. \(\sqrt{\frac{7}{40}}\)
      3. \(\frac{8}{\sqrt{2 y}}\)
      1. \(\frac{1}{\sqrt[3]{11}}\)
      2. \(\sqrt[3]{\frac{7}{54}}\)
      3. \(\frac{3}{\sqrt[3]{3 x^{2}}}\)
      1. \(\frac{1}{\sqrt[4]{4}}\)
      2. \(\sqrt[4]{\frac{9}{32}}\)
      3. \(\frac{6}{\sqrt[4]{9 x^{3}}}\)
    Відповідь

    2.

    1. \(\frac{\sqrt[3]{121}}{11}\)
    2. \(\frac{\sqrt[3]{28}}{6}\)
    3. \(\frac{\sqrt[3]{9 x}}{x}\)
    Вправа\(\PageIndex{19}\) Rationalize a Two Term Denominator

    У наступних вправах спростити.

    1. \(\frac{7}{2-\sqrt{6}}\)
    2. \(\frac{\sqrt{5}}{\sqrt{n}-\sqrt{7}}\)
    3. \(\frac{\sqrt{x}+\sqrt{8}}{\sqrt{x}-\sqrt{8}}\)
    Відповідь

    1. \(-\frac{7(2+\sqrt{6})}{2}\)

    3. \(\frac{(\sqrt{x}+2 \sqrt{2})^{2}}{x-8}\)

    Розв'язувати радикальні рівнян

    Вправа\(\PageIndex{20}\) Solve Radical Equations

    У наступних вправах вирішуйте.

    1. \(\sqrt{4 x-3}=7\)
    2. \(\sqrt{5 x+1}=-3\)
    3. \(\sqrt[3]{4 x-1}=3\)
    4. \(\sqrt{u-3}+3=u\)
    5. \(\sqrt[3]{4 x+5}-2=-5\)
    6. \((8 x+5)^{\frac{1}{3}}+2=-1\)
    7. \(\sqrt{y+4}-y+2=0\)
    8. \(2 \sqrt{8 r+1}-8=2\)
    Відповідь

    2. немає розчину

    4. \(u=3, u=4\)

    6. \(x=-4\)

    8. \(r=3\)

    Вправа\(\PageIndex{21}\) Solve Radical Equations with Two Radicals

    У наступних вправах вирішуйте.

    1. \(\sqrt{10+2 c}=\sqrt{4 c+16}\)
    2. \(\sqrt[3]{2 x^{2}+9 x-18}=\sqrt[3]{x^{2}+3 x-2}\)
    3. \(\sqrt{r}+6=\sqrt{r+8}\)
    4. \(\sqrt{x+1}-\sqrt{x-2}=1\)
    Відповідь

    2. \(x=-8, x=2\)

    4. \(x=3\)

    Вправа\(\PageIndex{22}\) Use Radicals in Applications

    У наступних вправах вирішуйте. Округлені наближення до одного знака після коми.

    1. Ландшафтний очеретяний хоче мати квадратний садовий ділянку на своєму задньому дворі. Йому вистачає компосту, щоб покрити площу\(75\) квадратних футів. Скористайтеся формулою,\(s=\sqrt{A}\) щоб знайти довжину кожної сторони свого саду. Округліть свої відповіді до найближчої десятої частки фута.
    2. Розслідування аварії Слідчий ДТП заміряв сліди занесення одного з транспортних засобів, що беруть участь у ДТП. Довжина слідів ковзання становила\(175\) ноги. Використовуйте формулу,\(s=\sqrt{24d}\) щоб знайти швидкість транспортного засобу до того, як були застосовані гальма. Округлите відповідь до найближчої десятої.
    Відповідь

    2. \(64.8\)ноги

    Використання радикалів у функціях

    Вправа\(\PageIndex{23}\) Evaluate a Radical Function

    У наступних вправах оцініть кожну функцію.

    1. \(g(x)=\sqrt{6 x+1}\), знайти
      1. \(g(4)\)
      2. \(g(8)\)
    2. \(G(x)=\sqrt{5 x-1}\), знайти
      1. \(G(5)\)
      2. \(G(2)\)
    3. \(h(x)=\sqrt[3]{x^{2}-4}\), знайти
      1. \(h(-2)\)
      2. \(h(6)\)
    4. Для функції\(g(x)=\sqrt[4]{4-4 x}\) знайдіть
      1. \(g(1)\)
      2. \(g(-3)\)
    Відповідь

    2.

    1. \(G(5)=2 \sqrt{6}\)
    2. \(G(2)=3\)

    4.

    1. \(g(1)=0\)
    2. \(g(-3)=2\)
    Вправа\(\PageIndex{24}\) Find the Domain of a Radical Function

    У наступних вправах знайдіть область функції і запишіть домен в інтервальне позначення.

    1. \(g(x)=\sqrt{2-3 x}\)
    2. \(F(x)=\sqrt{\frac{x+3}{x-2}}\)
    3. \(f(x)=\sqrt[3]{4 x^{2}-16}\)
    4. \(F(x)=\sqrt[4]{10-7 x}\)
    Відповідь

    2. \((2, \infty)\)

    4. \(\left[\frac{7}{10}, \infty\right)\)

    Вправа\(\PageIndex{25}\) graph Radical Functions

    У наступних вправах

    1. знайти домен функції
    2. графік функції
    3. використовувати графік для визначення діапазону
    1. \(g(x)=\sqrt{x+4}\)
    2. \(g(x)=2 \sqrt{x}\)
    3. \(f(x)=\sqrt[3]{x-1}\)
    4. \(f(x)=\sqrt[3]{x}+3\)
    Відповідь

    2.

    1. домен:\([0, \infty)\)

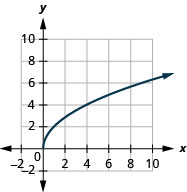
    2. На малюнку показано графік функції квадратного кореня на координатній площині x y. Вісь X площини проходить від 0 до 8. Вісь Y працює від 0 до 8. Функція має початкову точку в (0, 0) і проходить через точки (1, 2) і (4, 4).
      Малюнок 8.E.1
    3. діапазон:\([0, \infty)\)

    4.

    1. домен:\((-\infty, \infty)\)

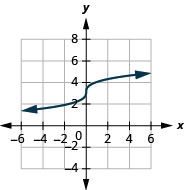
    2. На малюнку показано графік функції кореня куба на координатній площині x y. Вісь X площини проходить від негативних 4 до 4. Вісь Y проходить від негативних 2 до 6. Функція має центральну точку в (0, 3) і проходить через точки (негативні 1, 2) і (1, 4).
      Малюнок 8.E.2
    3. діапазон:\((-\infty, \infty)\)

    Використання комплексної системи числення

    Вправа\(\PageIndex{26}\) evaluate the Square Root of a Negative Number

    У наступних вправах запишіть кожен вираз з точки зору\(i\) і спростіть, якщо це можливо.

      1. \(\sqrt{-100}\)
      2. \(\sqrt{-13}\)
      3. \(\sqrt{-45}\)
    Відповідь

    Вирішуйте для себе

    Вправа\(\PageIndex{27}\) Add or Subtract Complex Numbers

    У наступних вправах додайте або відніміть.

    1. \(\sqrt{-50}+\sqrt{-18}\)
    2. \((8-i)+(6+3 i)\)
    3. \((6+i)-(-2-4 i)\)
    4. \((-7-\sqrt{-50})-(-32-\sqrt{-18})\)
    Відповідь

    1. \(8 \sqrt{2} i\)

    3. \(8+5 i\)

    Вправа\(\PageIndex{28}\) Multiply Complex Numbers

    У наступних вправах помножте.

    1. \((-2-5 i)(-4+3 i)\)
    2. \(-6 i(-3-2 i)\)
    3. \(\sqrt{-4} \cdot \sqrt{-16}\)
    4. \((5-\sqrt{-12})(-3+\sqrt{-75})\)
    Відповідь

    1. \(23+14 i\)

    3. \(-6\)

    Вправа\(\PageIndex{29}\) Multiply Complex Numbers

    У наступних вправах помножте, використовуючи візерунок добутку біноміальних квадратів.

    1. \((-2-3 i)^{2}\)
    Відповідь

    1. \(-5-12 i\)

    Вправа\(\PageIndex{30}\) Multiply Complex Numbers

    У наступних вправах помножте, використовуючи візерунок добутку складних кон'югатів.

    1. \((9-2 i)(9+2 i)\)
    Відповідь

    Вирішуйте для себе

    Вправа\(\PageIndex{31}\) divide Complex Numbers

    У наступних вправах розділіть.

    1. \(\frac{2+i}{3-4 i}\)
    2. \(\frac{-4}{3-2 i}\)
    Відповідь

    1. \(\frac{2}{25}+\frac{11}{25} i\)

    Вправа\(\PageIndex{32}\) Simplify Powers of \(i\)

    У наступних вправах спростити.

    1. \(i^{48}\)
    2. \(i^{255}\)
    Відповідь

    1. \(1\)

    Практика Тест

    Вправа\(\PageIndex{33}\)

    У наступних вправах спрощуйте використання абсолютних значень в міру необхідності.

    1. \(\sqrt[3]{125 x^{9}}\)
    2. \(\sqrt{169 x^{8} y^{6}}\)
    3. \(\sqrt[3]{72 x^{8} y^{4}}\)
    4. \(\sqrt{\frac{45 x^{3} y^{4}}{180 x^{5} y^{2}}}\)
    Відповідь

    1. \(5x^{3}\)

    3. \(2 x^{2} y \sqrt[3]{9 x^{2} y}\)

    Вправа\(\PageIndex{34}\)

    У наступних вправах спростити. Припустимо, що всі змінні є позитивними.

      1. \(216^{-\frac{1}{4}}\)
      2. \(-49^{\frac{3}{2}}\)
    2. \(\sqrt{-45}\)
    3. \(\frac{x^{-\frac{1}{4}} \cdot x^{\frac{5}{4}}}{x^{-\frac{3}{4}}}\)
    4. \(\left(\frac{8 x^{\frac{2}{3}} y^{-\frac{5}{2}}}{x^{-\frac{7}{3}} y^{\frac{1}{2}}}\right)^{\frac{1}{3}}\)
    5. \(\sqrt{48 x^{5}}-\sqrt{75 x^{5}}\)
    6. \(\sqrt{27 x^{2}}-4 x \sqrt{12}+\sqrt{108 x^{2}}\)
    7. \(2 \sqrt{12 x^{5}} \cdot 3 \sqrt{6 x^{3}}\)
    8. \(\sqrt[3]{4}(\sqrt[3]{16}-\sqrt[3]{6})\)
    9. \((4-3 \sqrt{3})(5+2 \sqrt{3})\)
    10. \(\frac{\sqrt[3]{128}}{\sqrt[3]{54}}\)
    11. \(\frac{\sqrt{245 x y^{-4}}}{\sqrt{45 x^{4} y^{3}}}\)
    12. \(\frac{1}{\sqrt[3]{5}}\)
    13. \(\frac{3}{2+\sqrt{3}}\)
    14. \(\sqrt{-4} \cdot \sqrt{-9}\)
    15. \(-4 i(-2-3 i)\)
    16. \(\frac{4+i}{3-2 i}\)
    17. \(i^{172}\)
    Відповідь

    1.

    1. \(\frac{1}{4}\)
    2. \(-343\)

    3. \(x^{\frac{7}{4}}\)

    5. \(-x^{2} \sqrt{3 x}\)

    7. \(36 x^{4} \sqrt{2}\)

    9. \(2-7 \sqrt{3}\)

    11. \(\frac{7 x^{5}}{3 y^{7}}\)

    13. \(3(2-\sqrt{3})\)

    15. \(-12+8i\)

    17. \(-i\)

    Вправа\(\PageIndex{35}\)

    У наступних вправах вирішуйте.

    1. \(\sqrt{2 x+5}+8=6\)
    2. \(\sqrt{x+5}+1=x\)
    3. \(\sqrt[3]{2 x^{2}-6 x-23}=\sqrt[3]{x^{2}-3 x+5}\)
    Відповідь

    2. \(x=4\)

    Вправа\(\PageIndex{36}\)

    У наступній вправі

    1. знайти домен функції
    2. графік функції
    3. використовувати графік для визначення діапазону
    1. \(g(x)=\sqrt{x+2}\)
    Відповідь

    1.

    1. домен:\([-2, \infty)\)

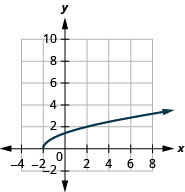
    2. На малюнку показано графік функції квадратного кореня на координатній площині x y. Вісь X площини проходить від негативних 2 до 6. Вісь Y працює від 0 до 8. Функція має початкову точку в (негативний 2, 0) і проходить через точки (негативні 1, 1) і (2, 2).
      Малюнок 8.E.3
    3. діапазон:\([0, \infty)\)