8.8: Використовуйте радикали у функціях

Цілі навчання

До кінця цього розділу ви зможете:

• Оцініть радикальну функцію
• Знайти область радикальної функції
• Радикальні функції графа

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

1. Вирішити:$1−2x≥0$.
   Якщо ви пропустили цю проблему, перегляньте приклад 2.50.
2. Для$f(x)=3x−4$, оцініть$f(2),f(−1),f(0)$.
   Якщо ви пропустили цю проблему, перегляньте приклад 3.48.
3. Графік$f(x)=\sqrt{x}$. Вкажіть область та діапазон функції в інтервальній нотації.
   Якщо ви пропустили цю проблему, перегляньте приклад 3.56.

Оцініть радикальну функцію

У цьому розділі ми продовжимо нашу попередню роботу функціями, щоб включити радикали. Якщо функція визначається радикальним виразом, ми називаємо її радикальною функцією.

• Функція квадратного кореня є$f(x)=\sqrt{x}$.
• Функція кореня куба є$f(x)=\sqrt[3]{x}$.

Визначення$\PageIndex{1}$: radical function

Радикальна функція - це функція, яка визначається радикальним виразом.

Щоб оцінити радикальну функцію, ми знаходимо значення$f(x)$ для заданого значення так$x$ само, як ми робили в нашій попередній роботі з функціями.

Приклад$\PageIndex{1}$

Для функції$f(x)=\sqrt{2 x-1}$ знайдіть

1. $f(5)$
2. $f(-2)$

Рішення:

а.

$f(x)=\sqrt{2 x-1}$

Для оцінки$f(5)$,$5$ замінюємо$x$.

$f(5)=\sqrt{2 \cdot 5-1}$

Спростити.

$f(5)=\sqrt{9}$

Візьміть квадратний корінь.

$f(5)=3$

б.

$f(x)=\sqrt{2 x-1}$

Для оцінки$f(-2)$,$-2$ замінюємо$x$.

$f(-2)=\sqrt{2(-2)-1}$

Спростити.

$f(-2)=\sqrt{-5}$

Оскільки квадратний корінь від'ємного числа не є дійсним числом, функція не має значення at$x=-2$.

Вправа$\PageIndex{1}$

Для функції$f(x)=\sqrt{3 x-2}$ знайдіть

1. $f(6)$
2. $f(0)$

Відповідь

1. $f(6)=4$
2. немає значення при$x=0$

Вправа$\PageIndex{2}$

Для функції$g(x)=\sqrt{5x+5}$ знайдіть

1. $g(4)$
2. $g(-3)$

Відповідь

1. $g(4)=5$
2. немає значення при$f(-3)$

Дотримуємося тієї ж процедури, щоб оцінити кубові корені.

Приклад$\PageIndex{2}$

Для функції$g(x)=\sqrt[3]{x-6}$ знайдіть

1. $g(14)$
2. $g(-2)$

Рішення:

а.

$g(x)=\sqrt[3]{x-6}$

Для оцінки$g(14)$,$14$ замінюємо$x$.

$g(14)=\sqrt[3]{14-6}$

Спростити.

$g(14)=\sqrt[3]{8}$

Беремо кубик кореня.

$g(14)=2$

б.

$g(x)=\sqrt[3]{x-6}$

Для оцінки$g(-2)$,$-2$ замінюємо$x$.

$g(-2)=\sqrt[3]{-2-6}$

Спростити.

$g(-2)=\sqrt[3]{-8}$

Беремо кубик кореня.

$g(-2)=-2$

Вправа$\PageIndex{3}$

Для функції$g(x)=\sqrt[3]{3 x-4}$ знайдіть

1. $g(4)$
2. $g(1)$

Відповідь

1. $g(4)=2$
2. $g(1)=-1$

Вправа$\PageIndex{4}$

Для функції$h(x)=\sqrt[3]{5 x-2}$ знайдіть

1. $h(2)$
2. $h(-5)$

Відповідь

1. $h(2)=2$
2. $h(-5)=-3$

Наступний приклад має четверте коріння.

Приклад$\PageIndex{3}$

Для функції$f(x)=\sqrt[4]{5 x-4}$ знайдіть

1. $f(4)$
2. $f(-12)$

Рішення:

а.

$f(x)=\sqrt[4]{5 x-4}$

Для оцінки$f(4)$,$4$ замінюємо$x$.

$f(4)=\sqrt[4]{5 \cdot 4-4}$

Спростити.

$f(4)=\sqrt[4]{16}$

Візьміть четвертий корінь.

$f(4)=2$

б.

$f(x)=\sqrt[4]{5 x-4}$

Для оцінки$f(-12)$,$-12$ замінюємо$x$.

$f(-12)=\sqrt[4]{5(-12)-4}$

Спростити.

$f(-12)=\sqrt[4]{-64}$

Оскільки четвертий корінь від'ємного числа не є дійсним числом, функція не має значення at$x=-12$.

Вправа$\PageIndex{5}$

Для функції$f(x)=\sqrt[4]{3 x+4}$ знайдіть

1. $f(4)$
2. $f(-1)$

Відповідь

1. $f(4)=2$
2. $f(-1)=1$

Вправа$\PageIndex{6}$

Для функції$g(x)=\sqrt[4]{5 x+1}$ знайдіть

1. $g(16)$
2. $g(3)$

Відповідь

1. $g(16)=3$
2. $g(3)=2$

Знайти область радикальної функції

Щоб знайти область і діапазон радикальних функцій, ми використовуємо наші властивості радикалів. Для радикала з парним індексом, ми сказали, що радиканд повинен бути більше або дорівнює нулю, оскільки парні корені від'ємних чисел не є дійсними числами. Для непарного індексу радиканд може бути будь-яким дійсним числом. Ми повторюємо властивості тут для довідки.

Властивості$\sqrt[n]{a}$

Коли$n$ парне число і:

• $a \geq 0$, то$\sqrt[n]{a}$ є дійсним числом.
• $a<0$, то не$\sqrt[n]{a}$ є дійсним числом.

Коли$n$ є непарним числом,$\sqrt[n]{a}$ є дійсним числом для всіх значень$a$.

Отже, щоб знайти область радикальної функції з парним індексом, встановимо радиканд більше або дорівнює нулю. Для непарного радикала індексу радикад може бути будь-яким дійсним числом.

Домен радикальної функції

Коли показник радикала парний, радикаі повинен бути більше або дорівнює нулю.

Коли індекс радикала непарний, радикаі може бути будь-яким дійсним числом.

Приклад$\PageIndex{4}$

Знайдіть домен функції,$f(x)=\sqrt{3 x-4}$. Запишіть домен в інтервальне позначення.

Рішення:

Так як функція,$f(x)=\sqrt{3 x-4}$ має радикал з індексом$2$, який парний, ми знаємо, радиканд повинен бути більше або дорівнює$0$. Ми встановлюємо радиканд більше або дорівнює,$0$ а потім вирішуємо, щоб знайти домен.

Вирішити.

$\begin{aligned} 3 x-4 & \geq 0 \\ 3 x & \geq 4 \\ x & \geq \frac{4}{3} \end{aligned}$

Домен всіх значень$f(x)=\sqrt{3 x-4}$,$x \geq \frac{4}{3}$ і ми запишемо його в інтервальне позначення як$\left[\frac{4}{3}, \infty\right)$.

Вправа$\PageIndex{7}$

Знайдіть домен функції,$f(x)=\sqrt{6 x-5}$. Запишіть домен в інтервальне позначення.

Відповідь

$\left[\frac{5}{6}, \infty\right)$

Вправа$\PageIndex{8}$

Знайдіть домен функції,$f(x)=\sqrt{4-5 x}$. Запишіть домен в інтервальне позначення.

Відповідь

$\left(-\infty, \frac{4}{5}\right]$

Приклад$\PageIndex{5}$

Знайдіть домен функції,$g(x)=\sqrt{\frac{6}{x-1}}$. Запишіть домен в інтервальне позначення.

Рішення:

Вирішити функцію,$g(x)=\sqrt{\frac{6}{x-1}}$ має радикал з індексом$2$, який парний, ми знаємо радиканд повинен бути більше або дорівнює$0$.

Радиканд не може бути нулем, оскільки чисельник не дорівнює нулю.

$\frac{6}{x-1}$Щоб бути більшим за нуль, знаменник повинен бути додатним, оскільки чисельник є додатним. Ми знаємо, що позитив, розділений на позитив, є позитивним.

Ставимо$x-1>0$ і вирішуємо.

$x-1>0$

Вирішити.

$x>1$

Крім того, оскільки радиканд - це дріб, ми повинні розуміти, що знаменник не може бути нулем.

Вирішуємо$x-1=0$ знайти значення, яке необхідно виключити з домену.

$x-1=0$

Вирішити.

$x=1$так$x/neq 1$ в домені.

Збираючи це разом, ми отримуємо домен,$x>1$ і ми пишемо його як$(1, \infty)$.

Вправа$\PageIndex{9}$

Знайдіть домен функції,$f(x)=\sqrt{\frac{4}{x+3}}$. Запишіть домен в інтервальне позначення.

Відповідь

$(-3, \infty)$

Вправа$\PageIndex{10}$

Знайдіть домен функції,$h(x)=\sqrt{\frac{9}{x-5}}$. Запишіть домен в інтервальне позначення.

Відповідь

$(5, \infty)$

Наступний приклад передбачає кубічний корінь і тому зажадає різного мислення.

Приклад$\PageIndex{6}$

Знайдіть домен функції,$f(x)=\sqrt[3]{2 x^{2}+3}$. Запишіть домен в інтервальне позначення.

Рішення:

Оскільки функція,$f(x)=\sqrt[3]{2 x^{2}+3}$ має радикал з індексом$3$, який непарний, ми знаємо радиканд може бути будь-яким дійсним числом. Це говорить нам, що домен - це будь-яке реальне число. У інтервальних позначеннях пишемо$(-\infty, \infty)$.

Домен всіх дійсних$f(x)=\sqrt[3]{2 x^{2}+3}$ чисел, і ми записуємо його в інтервальне позначення як$(-\infty, \infty)$.

Вправа$\PageIndex{11}$

Знайдіть домен функції,$f(x)=\sqrt[3]{3 x^{2}-1}$. Запишіть домен в інтервальне позначення.

Відповідь

$(-\infty, \infty)$

Вправа$\PageIndex{12}$

Знайдіть домен функції,$g(x)=\sqrt[3]{5 x-4}$. Запишіть домен в інтервальне позначення.

Відповідь

$(-\infty, \infty)$

Радикальні функції графа

Перш ніж ми графуємо будь-яку радикальну функцію, спочатку знайдемо область функції. Для функції індекс парний, і тому радиканд повинен бути більше або дорівнює$0$.$f(x)=\sqrt{x}$

Це говорить нам про домен,$x≥0$ і ми пишемо це в інтервалі позначення як$[0,∞)$.

Раніше ми використовували точкове побудова графіків для графіка функції,$f(x)=\sqrt{x}$. Ми вибрали$x$ -values, підставили їх в а потім створили діаграму. Зверніть увагу, що ми вибрали точки, які є ідеальними квадратами, щоб полегшити прийняття квадратного кореня.

Малюнок 8.7.1

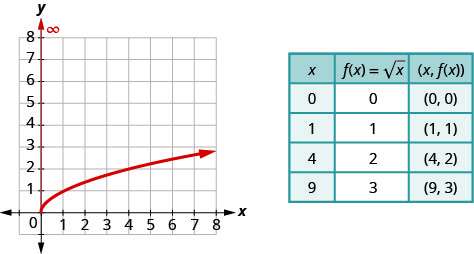
Як тільки ми побачимо графік, ми можемо знайти діапазон функції. $y$Значення функції більше або рівні нулю. Діапазон тоді є$[0,∞)$.

Приклад$\PageIndex{7}$

Для функції$f(x)=\sqrt{x+3}$,

1. знайти домен
2. графік функції
3. використовувати графік для визначення діапазону

Рішення:

1. Так як радикал має індекс$2$, ми знаємо радикаі повинен бути більше або дорівнює нулю. Якщо$x+3 \geq 0$, то$x \geq-3$. Це говорить нам, що домен - це всі значення$x \geq-3$ і записуються в інтервальних позначеннях як$[-3, \infty)$.
2. Для графіка функції ми вибираємо точки в інтервалі$[-3, \infty)$, який також дасть нам радикаі який буде легко взяти квадратний корінь.

Малюнок 8.7.2

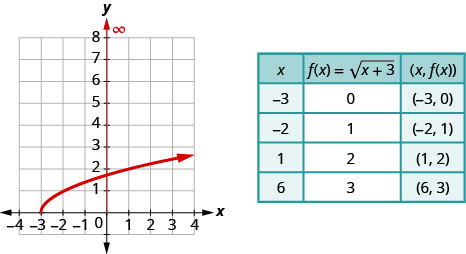
c Дивлячись на графік, ми бачимо$y$ -значення функції більше або рівні нулю. Діапазон тоді є$[0, \infty)$.

Вправа$\PageIndex{13}$

Для функції$f(x)=\sqrt{x+2}$,

1. знайти домен
2. графік функції
3. використовувати графік для визначення діапазону

Відповідь

1. домен:$[-2, \infty)$
2. 
   
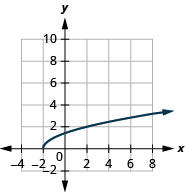
   Малюнок 8.7.3
3. діапазон:$[0, \infty)$

Вправа$\PageIndex{14}$

Для функції$f(x)=\sqrt{x-2}$,

1. знайти домен
2. графік функції
3. використовувати графік для визначення діапазону

Відповідь

1. домен:$[2, \infty)$
2. 
   
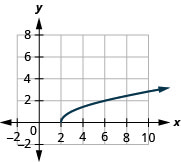
   Малюнок 8.7.4
3. діапазон:$[0, \infty)$

У нашій попередній роботі графічні функції, ми графували,$f(x)=x^{3}$ але ми не графували функцію$f(x)=\sqrt[3]{x}$. Ми зробимо це зараз в наступному прикладі.

Приклад$\PageIndex{8}$

Для функції$f(x)=\sqrt[3]{x}$,

1. знайти домен
2. графік функції
3. використовувати графік для визначення діапазону

Рішення:

а Оскільки радикал має індекс$3$, ми знаємо радиканд може бути будь-яким дійсним числом. Це говорить нам, що домен - це всі дійсні числа і записуються в інтервальних позначеннях як$(-\infty, \infty)$

б Для графіка функції ми вибираємо точки в інтервалі$(-\infty, \infty)$, який також дасть нам радикаі який буде легко взяти кубічний корінь.

Малюнок 8.7.5

c Дивлячись на графік, ми бачимо$y$ -значення функції - це всі дійсні числа. Діапазон тоді є$(-\infty, \infty)$.

Вправа$\PageIndex{15}$

Для функції$f(x)=-\sqrt[3]{x}$,

1. знайти домен
2. графік функції
3. використовувати графік для визначення діапазону

Відповідь

1. домен:$(-\infty, \infty)$
2. 
   
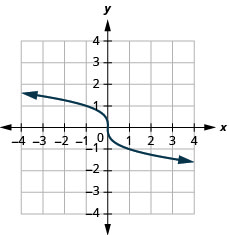
   Малюнок 8.7.6
3. діапазон:$(-\infty, \infty)$

Вправа$\PageIndex{16}$

Для функції$f(x)=\sqrt[3]{x-2}$,

1. знайти домен
2. графік функції
3. використовувати графік для визначення діапазону

Відповідь

1. домен:$(-\infty, \infty)$
2. 
   
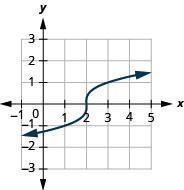
   Малюнок 8.7.7
3. діапазон:$(-\infty, \infty)$

Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з радикальними функціями.

• Домен радикальної функції
• Домен радикальної функції 2
• Пошук області радикальної функції

Ключові поняття

• Властивості$\sqrt[n]{a}$
  • Коли$n$ - парне число і:
    $a≥0$,$\sqrt[n]{a}$ то дійсне число.
    $a<0$, то не$\sqrt[n]{a}$ є дійсним числом.
  • Коли$n$ є непарним числом,$\sqrt[n]{a}$ є дійсним числом для всіх значень$a$.
• Домен радикальної функції
  • Коли показник радикала парний, радикаі повинен бути більше або дорівнює нулю.
  • Коли індекс радикала непарний, радикаі може бути будь-яким дійсним числом.

Глосарій

радикальна функція

Радикальна функція - це функція, яка визначається радикальним виразом.