8.7: Вирішити радикальні рівнян

Last updated
Save as PDF

Page ID: 59617

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

До кінця цього розділу ви зможете:

Розв'язувати радикальні рівнян
Розв'яжіть радикальні рівняння з двома
Використовуйте радикали в додатках

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

Спростити:$(y−3)^{2}$.
Якщо ви пропустили цю проблему, перегляньте приклад 5.31.
Вирішити:$2x−5=0$.
Якщо ви пропустили цю проблему, перегляньте приклад 2.2.
Вирішити$n^{2}−6n+8=0$.
Якщо ви пропустили цю проблему, перегляньте приклад 6.45.

Розв'язувати радикальні рівнян

У цьому розділі ми вирішимо рівняння, які мають змінну в радиканді радикального виразу. Рівняння такого типу називається радикальним рівнянням.

Визначення$\PageIndex{1}$

Рівняння, в якому змінна знаходиться в радикалі радикального виразу, називається радикальним рівнянням.

Як завжди, вирішуючи ці рівняння, те, що ми робимо з однією стороною рівняння, ми також повинні зробити з іншою стороною. Як тільки ми виділимо радикал, наша стратегія буде полягати в тому, щоб підняти обидві сторони рівняння до потужності індексу. Це дозволить усунути радикал.

Розв'язування радикальних рівнянь, що містять парний індекс, шляхом підняття обох сторін до ступеня індексу може ввести алгебраїчне рішення, яке не було б розв'язком вихідного радикального рівняння. Знову ж таки, ми називаємо це стороннім рішенням, як ми робили, коли ми вирішували раціональні рівняння.

У наступному прикладі ми побачимо, як вирішити радикальне рівняння. Наша стратегія заснована на піднятті радикала з індексом$n$ до$n^{th}$ влади. Це дозволить усунути радикал.

Для$a \geq 0,(\sqrt[n]{a})^{n}=a$.

Приклад$\PageIndex{1}$ how to solve a radical equation

Вирішити:$\sqrt{5 n-4}-9=0$.

Рішення:

Таблиця 8.6.1
Крок 1: Виділіть радикал з одного боку рівняння.	Щоб виділити корінь, додайте$9$ в обидві сторони. Спростити.	$\begin{array}{c}{\sqrt{5 n-4}-9=0} \\ {\sqrt{5 n-4}-9\color{red}{+9}\color{black}{=}0\color{red}{+9}} \\ {\sqrt{5 n-4}=9}\end{array}$
Крок 2: Підніміть обидві сторони рівняння до ступеня індексу.	Так як індекс квадратного кореня є$2$, ми квадратируем обидві сторони.	$(\sqrt{5 n-4})^{2}=(9)^{2}$
Крок 3: Вирішіть нове рівняння.	Пам'ятайте,$(\sqrt{a})^{2}=a$.	$\begin{aligned} 5 n-4 &=81 \\ 5 n &=85 \\ n &=17 \end{aligned}$
Крок 4: Перевірте відповідь у вихідному рівнянні.		Перевірте відповідь. $\begin{array}{r}{\sqrt{5 n-4}-9=0} \\ {\sqrt{5(\color{red}{17}\color{black}{)}-4}-9 \stackrel{?}{=} 0} \\ {\sqrt{85-4}-9 \stackrel{?}{=} 0} \\ {\sqrt{81}-9 \stackrel{?}{=} 0} \\ {9-9=0} \\ {0=0}\end{array}$ Рішення є$n=17$.

Вправа$\PageIndex{1}$

Вирішити:$\sqrt{3 m+2}-5=0$.

Відповідь: $m=\frac{23}{3}$

Вправа$\PageIndex{2}$

Вирішити:$\sqrt{10 z+1}-2=0$.

Відповідь: $z=\frac{3}{10}$

Розв'яжіть радикальне рівняння одним радикалом

Виділіть радикал з одного боку рівняння.
Підніміть обидві сторони рівняння до ступеня індексу.
Вирішити нове рівняння.
Перевірте відповідь у вихідному рівнянні.

Коли ми використовуємо радикальний знак, він вказує на основний або позитивний корінь. Якщо рівняння має радикал з парним індексом, рівним від'ємному числу, це рівняння не матиме розв'язку.

Приклад$\PageIndex{2}$

Вирішити:$\sqrt{9 k-2}+1=0$.

Рішення:

Таблиця 8.6.2
	$.$
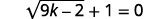Щоб виділити радикал, відніміть$1$ в обидві сторони.	$.$
Спростити.	$.$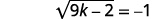

Оскільки квадратний корінь дорівнює від'ємному числу, рівняння не має розв'язку.

Вправа$\PageIndex{3}$

Вирішити:$\sqrt{2 r-3}+5=0$.

Відповідь: немає рішення

Вправа$\PageIndex{4}$

Вирішити:$\sqrt{7 s-3}+2=0$.

Відповідь: немає рішення

Якщо одна сторона рівняння з квадратним коренем є біноміальною, ми використовуємо візерунок добутку біноміальних квадратів, коли ми квадратизуємо його.

Визначення$\PageIndex{2}$

Біноміальні квадрати

$\begin{array}{l}{(a+b)^{2}=a^{2}+2 a b+b^{2}} \\ {(a-b)^{2}=a^{2}-2 a b+b^{2}}\end{array}$

Не забувайте про середній термін!

Приклад$\PageIndex{3}$

Вирішити:$\sqrt{p-1}+1=p$.

Рішення:

Таблиця 8.6.3
	$.$
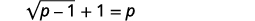Щоб виділити радикал, відніміть$1$ з обох сторін.	$.$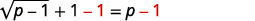
Спростити.	$.$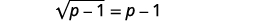
Квадратні обидві сторони рівняння.	$.$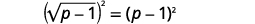
Спростити, використовуючи Добуток біноміальних квадратів візерунок праворуч, Потім вирішіть нове рівняння.	$.$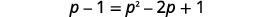
Це квадратне рівняння, тому отримайте нуль з одного боку.	$.$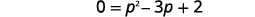
Фактор правого боку.	$.$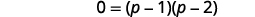
Використовуйте властивість нульового продукту.	$.$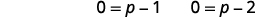
Вирішіть кожне рівняння.	$.$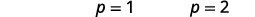
Перевірте відповіді.
$.$

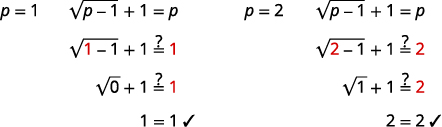Рішення є$p=1, p=2$.

Вправа$\PageIndex{5}$

Вирішити:$\sqrt{x-2}+2=x$.

Відповідь: $x=2, x=3$

Вправа$\PageIndex{6}$

Вирішити:$\sqrt{y-5}+5=y$.

Відповідь: $y=5, y=6$

Коли індекс радикала є$3$, ми куб обидві сторони, щоб видалити радикал.

$(\sqrt[3]{a})^{3}=a$

Приклад$\PageIndex{4}$

Вирішити:$\sqrt[3]{5 x+1}+8=4$.

Рішення:

Таблиця 8.6.4
	$\sqrt[3]{5 x+1}+8=4$
Щоб виділити радикал, відніміть$8$ з обох сторін.	$\sqrt[3]{5 x+1}=-4$
Куб обидві сторони рівняння.	$(\sqrt[3]{5 x+1})^{3}=(-4)^{3}$
Спростити.	$5 x+1=-64$
Розв'яжіть рівняння.	$5 x=-65$
	$x=-13$
Перевірте відповідь.
$.$
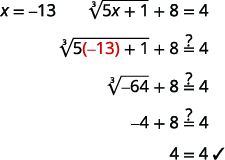	Рішення є$x=-13$.

Вправа$\PageIndex{7}$

Вирішити:$ \sqrt[3]{4 x-3}+8=5$

Відповідь: $x=-6$

Вправа$\PageIndex{8}$

Вирішити:$\sqrt[3]{6 x-10}+1=-3$

Відповідь: $x=-9$

Іноді рівняння буде містити раціональні показники замість радикала. Ми використовуємо ті ж методи для вирішення рівняння, що і коли ми маємо радикал. Піднімаємо кожну сторону рівняння до ступеня знаменника раціонального показника. Так як$\left(a^{m}\right)^{^{n}}=a^{m \cdot n}$, ми маємо, наприклад,

$\left(x^{\frac{1}{2}}\right)^{2}=x,\left(x^{\frac{1}{3}}\right)^{3}=x$

Пам'ятайте,$x^{\frac{1}{2}}=\sqrt{x}$ і$x^{\frac{1}{3}}=\sqrt[3]{x}$.

Приклад$\PageIndex{5}$

Вирішити:$(3 x-2)^{\frac{1}{4}}+3=5$.

Рішення:

Таблиця 8.6.5
	$(3 x-2)^{\frac{1}{4}}+3=5$
Щоб виділити термін з раціональним показником, відніміть$3$ з обох сторін.	$(3 x-2)^{\frac{1}{4}}=2$
Підніміть кожну сторону рівняння до четвертого ступеня.	$\left((3 x-2)^{\frac{1}{4}}\right)^{4}=(2)^{4}$
Спростити.	$3 x-2=16$
Розв'яжіть рівняння.	$3x=18$
	$x=6$
Перевірте відповідь.
$.$
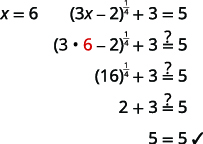	Рішення є$x=6$.

Вправа$\PageIndex{9}$

Вирішити:$(9 x+9)^{\frac{1}{4}}-2=1$

Відповідь: $x=8$

Вправа$\PageIndex{10}$

Вирішити:$(4 x-8)^{\frac{1}{4}}+5=7$

Відповідь: $x=6$

Іноді рішення радикального рівняння призводить до двох алгебраїчних розв'язків, але один з них може бути стороннім рішенням!

Приклад$\PageIndex{6}$

Вирішити:$\sqrt{r+4}-r+2=0$.

Рішення:

Таблиця 8.6.6
	$\sqrt{r+4}-r+2=0$
Виділяють радикал.	$\sqrt{r+4}=r-2$
Квадратні обидві сторони рівняння.	$(\sqrt{r+4})^{2}=(r-2)^{2}$
Спростити, а потім вирішити рівняння.	$r+4=r^{2}-4 r+4$
Якщо це квадратне рівняння, то отримайте нуль з одного боку.	$0=r^{2}-5 r$
Фактор правого боку.	$0=r(r-5)$
Використовуйте властивість нульового продукту.	$0=r \quad 0=r-5$
Розв'яжіть рівняння.	$r=0 \quad r=5$
Перевірте свою відповідь.
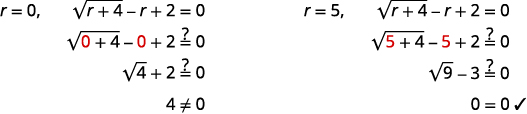$.$	Рішення є$r=5$.
	$r=0$є екстремальним рішенням.

Вправа$\PageIndex{11}$

Вирішити:$\sqrt{m+9}-m+3=0$

Відповідь: $m=7$

Вправа$\PageIndex{12}$

Вирішити:$\sqrt{n+1}-n+1=0$.

Відповідь: $n=3$

Коли перед радикалом стоїть коефіцієнт, ми повинні підняти його до потужності індексу теж.

Приклад$\PageIndex{7}$

Вирішити:$3 \sqrt{3 x-5}-8=4$.

Рішення:

Таблиця 8.6.7
	$3 \sqrt{3 x-5}-8=4$
Виділяють радикальний термін.	$3 \sqrt{3 x-5}=12$
Виділяють радикал, розділивши обидві сторони на$3$.	$\sqrt{3 x-5}=4$
Квадратні обидві сторони рівняння.	$(\sqrt{3 x-5})^{2}=(4)^{2}$
Спростити, а потім вирішити нове рівняння.	$3 x-5=16$
	$3x=21$
Розв'яжіть рівняння.	$x=7$
Перевірте відповідь.
$.$
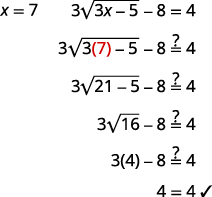	Рішення є$x=7$.

Вправа$\PageIndex{13}$

Вирішити:$2 \sqrt{4 a+4}-16=16$.

Відповідь: $a=63$

Вправа$\PageIndex{14}$

Вирішити:$3 \sqrt{2 b+3}-25=50$

Відповідь: $b=311$

Розв'яжіть радикальні рівняння з двома

Якщо радикальне рівняння має два радикали, ми починаємо з виділення одного з них. Часто виходить найпростіше спочатку виділити складніший радикал.

У наступному прикладі при виділенні одного радикала виділяють і другий радикал.

Приклад$\PageIndex{8}$

Вирішити:$\sqrt[3]{4 x-3}=\sqrt[3]{3 x+2}$.

Рішення:

Радикальні терміни виділяють.

$\sqrt[3]{4 x-3}=\sqrt[3]{3 x+2}$

Оскільки індекс є$3$, куб обидві сторони рівняння.

$(\sqrt[3]{4 x-3})^{3}=(\sqrt[3]{3 x+2})^{3}$

Спростити, а потім вирішити нове рівняння.

$\begin{aligned} 4 x-3 &=3 x+2 \\ x-3 &=2 \\ x &=5 \end{aligned}$

Рішення є$x=5$.

Перевірте відповідь.

Ми залишаємо це вам, щоб показати, що$5$ перевіряє!

Вправа$\PageIndex{15}$

Вирішити:$\sqrt[3]{5 x-4}=\sqrt[3]{2 x+5}$.

Відповідь: $x=3$

Вправа$\PageIndex{16}$

Вирішити:$\sqrt[3]{7 x+1}=\sqrt[3]{2 x-5}$.

Відповідь: $x=-\frac{6}{5}$

Іноді після підняття обох сторін рівняння до степеня, ми все ще маємо змінну всередині радикала. Коли це станеться, ми повторюємо кроки 1 та 2 нашої процедури. Виділяємо радикал і знову піднімаємо обидві сторони рівняння до ступеня індексу.

Приклад$\PageIndex{9}$ how to solve a radical equation

Вирішити:$\sqrt{m}+1=\sqrt{m+9}$.

Рішення:

Таблиця 8.6.8
Крок 1: Виділіть один з радикальних членів на одній стороні рівняння.	Радикал справа ізольований.	$\sqrt{m}+1=\sqrt{m+9}$
Крок 2: Підніміть обидві сторони рівняння до ступеня індексу.	Квадратуємо обидві сторони. Спрощуйте - будьте дуже обережні, коли ви розмножуєте!	$(\sqrt{m}+1)^{2}=(\sqrt{m+9})^{2}$
Крок 3: Чи є ще радикали? Якщо так, повторіть кроки 1 і 2 ще раз. Якщо ні, розв'яжіть нове рівняння.	У рівнянні все ще є радикал. Тому ми повинні повторити попередні кроки. Виділяють радикальний термін. Тут ми можемо легко виділити радикал, розділивши обидві сторони на$2$. Квадрат з обох сторін.	$\begin{aligned} m+2 \sqrt{m}+1 &=m+9 \\ 2 \sqrt{m} &=8 \\ \sqrt{m} &=4 \\(\sqrt{m})^{2} &=(4)^{2} \\ m &=16 \end{aligned}$
Крок 4: Перевірте відповідь у вихідному рівнянні.		$\begin{aligned}\sqrt{m}+1&=\sqrt{m+9} \\ \sqrt{\color{red}{16}}\color{black}{+}1& \stackrel{?}{=} \sqrt{\color{red}{16}\color{black}{+}9} \\ 4+1& \stackrel{?}{=} 5 \\ 5&=5\end{aligned}$ Рішення є$m=16$.

Вправа$\PageIndex{17}$

Вирішити:$3-\sqrt{x}=\sqrt{x-3}$.

Відповідь: $x=4$

Вправа$\PageIndex{18}$

Вирішити:$\sqrt{x}+2=\sqrt{x+16}$.

Відповідь: $x=9$

Ми підсумовуємо кроки тут. Ми скоригували наші попередні кроки, щоб включити більше одного радикала в рівняння Ця процедура тепер буде працювати для будь-яких радикальних рівнянь.

Вирішити радикальне рівняння

Виділіть один з радикальних членів з одного боку рівняння.
Підніміть обидві сторони рівняння до ступеня індексу.
Чи є ще радикали?
Якщо так, повторіть кроки 1 і 2 ще раз.
Якщо ні, розв'яжіть нове рівняння.
Перевірте відповідь у вихідному рівнянні.

Будьте обережні, коли ви квадратні біноми в наступному прикладі. Запам'ятайте візерунок в$(a+b)^{2}=a^{2}+2 a b+b^{2}$ або$(a-b)^{2}=a^{2}-2 a b+b^{2}$.

Приклад$\PageIndex{10}$

Вирішити:$\sqrt{q-2}+3=\sqrt{4 q+1}$.

Рішення:

Таблиця 8.6.9
	$.$
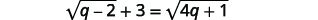Радикал справа ізольований. Квадрат з обох сторін.	$.$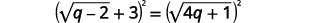
Спростити.	$.$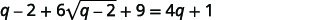
У рівнянні все ще є радикал, тому ми повинні повторити попередні кроки. Виділяють радикал.	$.$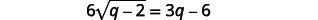
Квадрат з обох сторін. Не допомогло б розділити обидві сторони на$6$. Пам'ятайте, щоб квадрат як$6$ і на$\sqrt{q-2}$.	$.$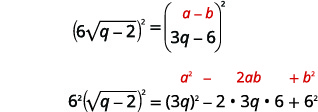
Спростити, а потім вирішити нове рівняння.	$.$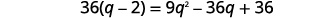
Розподілити.	$.$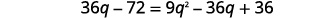
Це квадратне рівняння, тому отримайте нуль з одного боку.	$.$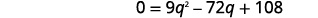
Фактор правого боку.	$.$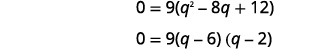
Використовуйте властивість нульового продукту.	$.$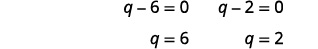
Чеки залишені вам.	Рішення є$q=6$ і$q=2$.

Вправа$\PageIndex{19}$

Вирішити:$\sqrt{x-1}+2=\sqrt{2 x+6}$

Відповідь: $x=5$

Вправа$\PageIndex{20}$

Вирішити:$\sqrt{x}+2=\sqrt{3 x+4}$

Відповідь: $x=0 x=4$

Використовуйте радикали в додатках

Коли ви просуваєтеся через курси коледжу, ви зіткнетеся з формулами, які включають радикали в багатьох дисциплін. Ми трохи змінимо нашу стратегію вирішення проблем для додатків геометрії, щоб дати нам план вирішення додатків з формулами з будь-якої дисципліни.

Використовуйте стратегію вирішення проблем для додатків з формулами

Прочитайте проблему і переконайтеся, що всі слова та ідеї зрозумілі. Коли це доречно, намалюйте фігуру і позначте її заданою інформацією.
Визначте, що ми шукаємо.
Назвіть те, що ми шукаємо, вибравши змінну для її представлення.
Перевести в рівняння, написавши відповідну формулу або модель для ситуації. Підставляємо в задану інформацію.
Вирішіть рівняння, використовуючи хороші методи алгебри.
Перевірте відповідь в проблемі і переконайтеся, що це має сенс.
Відповісти на питання повним реченням.

Одне застосування радикалів має відношення до впливу сили тяжіння на падаючі предмети. Формула дозволяє визначити, скільки часу знадобиться впав предмет, щоб потрапити в землю.

Визначення$\PageIndex{2}$

Падаючі об'єкти

На Землі, якщо об'єкт скидається з висоти$h$ футів, час у секундах, який знадобиться для досягнення землі, знаходиться за допомогою формули

$t=\frac{\sqrt{h}}{4}$

Наприклад, якщо об'єкт скидається з висоти$64$ ніг, ми можемо знайти час, необхідний для досягнення землі, підставивши$h=64$ формулу.

Таблиця 8.6.10
	$.$
	$.$
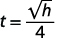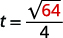Візьміть квадратний корінь$64$.	$.$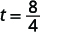
Спростити дріб.	$.$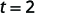

Це займе$2$ секунди, щоб об'єкт, впав з висоти$64$ ноги, досяг землі.

Приклад$\PageIndex{11}$

Марісса впустила свої сонцезахисні окуляри з моста$400$ ноги над річкою. Використовуйте формулу,$t=\frac{\sqrt{h}}{4}$ щоб знайти, скільки секунд знадобилося сонцезахисні окуляри, щоб дістатися до річки.

Рішення:

Таблиця 8.6.11
Крок 1: Прочитайте проблему.
Крок 2: Визначте, що ми шукаємо.	Час, необхідний для того, щоб сонцезахисні окуляри досягли річки.
Крок 3: Назвіть те, що ми шукаємо.	Нехай (t =\) час.
Крок 4: Переведіть в рівняння, написавши відповідну формулу. Підставляємо в задану інформацію.	$.$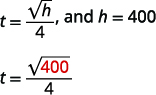
Крок 5: Вирішіть рівняння.	$.$
	$.$
Крок 6: Перевірте відповідь у проблемі і переконайтеся, що це має сенс.	$.$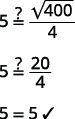
Чи здаються$5$ секунди розумною тривалістю часу?	Так.
Крок 7: Дайте відповідь на рівняння.	Це займе$5$ секунди, щоб сонцезахисні окуляри дісталися до річки.

Вправа$\PageIndex{21}$

Вертоліт скинув рятувальний пакет з висоти$1,296$ ніг. Скористайтеся формулою,$t=\frac{\sqrt{h}}{4}$ щоб знайти, скільки секунд знадобилося, щоб пакет досяг землі.

Відповідь: $9$секунд

Вправа$\PageIndex{22}$

Омивач вікон скинув ракель з$196$ ніг платформи над тротуаром. Використовуйте формулу,$t=\frac{\sqrt{h}}{4}$ щоб знайти, скільки секунд знадобилося, щоб ракель досяг тротуару.

Відповідь: $3.5$секунд

Співробітники поліції, що розслідують автомобільні аварії, вимірюють довжину слідів заносу на тротуарі. Потім вони використовують квадратні корені, щоб визначити швидкість, в милі на годину, автомобіль їхав перед застосуванням гальм.

Визначення$\PageIndex{3}$

Відмітки занесення та швидкість автомобіля

Якщо довжина слідів заносу -$d$ ноги, то швидкість,, автомобіля до того$s$, як були застосовані гальма, можна дізнатися, скориставшись формулою

$s=\sqrt{24 d}$

Приклад$\PageIndex{12}$

Після автомобільної аварії мітки заносу для одного автомобіля відміряли$190$ ноги. Використовуйте формулу,$s=\sqrt{24d}$ щоб знайти швидкість автомобіля до того, як були застосовані гальма. Округлите відповідь до найближчої десятої.

Рішення:

Таблиця 8.6.12
Крок 1: Прочитайте проблему.
Крок 2: Визначте, що ми шукаємо.	Швидкість автомобіля.
Крок 3: Назвіть те, що ми шукаємо.	Нехай$s=$ швидкість.
Крок 4: Переведіть в рівняння, написавши відповідну формулу. Підставляємо в задану інформацію.	$.$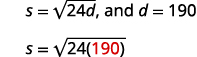
Крок 5: Вирішіть рівняння.	$.$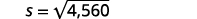
	$.$
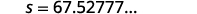$1$Округлення до десяткового знака.	$.$
	$.$
	Швидкість автомобіля до того, як були застосовані гальма, становила$67.5$ милі на годину.

Вправа$\PageIndex{23}$

Слідчий ДТП заміряв сліди занесення автомобіля. Довжина слідів ковзання становила$76$ ноги. Використовуйте формулу,$s=\sqrt{24d}$ щоб знайти швидкість автомобіля до того, як були застосовані гальма. Округлите відповідь до найближчої десятої.

Відповідь: $42.7$ноги

Вправа$\PageIndex{24}$

Відмітки ковзання транспортного засобу, що беруть участь у ДТП, були довжиною$122$ ноги. Використовуйте формулу,$s=\sqrt{24d}$ щоб знайти швидкість транспортного засобу до того, як були застосовані гальма. Округлите відповідь до найближчої десятої.

Відповідь: $54.1$ноги

Отримайте доступ до цих онлайн-ресурсів для додаткової інструкції та практики з розв'язуванням радикальних рівнянь.

Розв'язування рівняння за участю єдиного радикала
Розв'язування рівнянь з радикалами та раціональними показниками
Рішення радикальних рівнянь
Розв'язувати радикальні рівнян
Застосування радикального рівняння

Ключові концепції

Біноміальні квадрати
$\begin{array}{l}{(a+b)^{2}=a^{2}+2 a b+b^{2}} \\ {(a-b)^{2}=a^{2}-2 a b+b^{2}}\end{array}$
Вирішити радикальне рівняння
1. Виділіть один з радикальних членів з одного боку рівняння.
2. Підніміть обидві сторони рівняння до ступеня індексу.
3. Чи є ще радикали?
  Якщо так, повторіть кроки 1 і 2 ще раз.
  Якщо ні, розв'яжіть нове рівняння.
4. Перевірте відповідь у вихідному рівнянні.
Стратегія вирішення проблем для додатків з формулами
1. Прочитайте проблему і переконайтеся, що всі слова та ідеї зрозумілі. Коли це доречно, намалюйте фігуру і позначте її заданою інформацією.
2. Визначте, що ми шукаємо.
3. Назвіть те, що ми шукаємо, вибравши змінну для її представлення.
4. Перевести в рівняння, написавши відповідну формулу або модель для ситуації. Підставляємо в задану інформацію.
5. Вирішіть рівняння, використовуючи хороші методи алгебри.
6. Перевірте відповідь в проблемі і переконайтеся, що це має сенс.
7. Відповісти на питання повним реченням.
Падаючі об'єкти
- На Землі, якщо об'єкт скидається з висоти$h$ футів, час у секундах, який знадобиться для досягнення землі, знаходиться за допомогою формули$t=\frac{\sqrt{h}}{4}$.
Відмітки занесення та швидкість автомобіля
- Якщо довжина слідів заносу -$d$ ноги, то швидкість, автомобіля до того$s$, як були застосовані гальма, можна дізнатися, скориставшись формулою$s=\sqrt{24d}$.

Глосарій

радикальне рівняння: Рівняння, в якому змінна знаходиться в радикалі радикального виразу, називається радикальним рівнянням.

Крок 1: Виділіть радикал з одного боку рівняння.	Щоб виділити корінь, додайте\(9\) в обидві сторони. Спростити.	\(\begin{array}{c}{\sqrt{5 n-4}-9=0} \\ {\sqrt{5 n-4}-9\color{red}{+9}\color{black}{=}0\color{red}{+9}} \\ {\sqrt{5 n-4}=9}\end{array}\)
Крок 2: Підніміть обидві сторони рівняння до ступеня індексу.	Так як індекс квадратного кореня є\(2\), ми квадратируем обидві сторони.	\((\sqrt{5 n-4})^{2}=(9)^{2}\)
Крок 3: Вирішіть нове рівняння.	Пам'ятайте,\((\sqrt{a})^{2}=a\).	\(\begin{aligned} 5 n-4 &=81 \\ 5 n &=85 \\ n &=17 \end{aligned}\)
Крок 4: Перевірте відповідь у вихідному рівнянні.		Перевірте відповідь. \(\begin{array}{r}{\sqrt{5 n-4}-9=0} \\ {\sqrt{5(\color{red}{17}\color{black}{)}-4}-9 \stackrel{?}{=} 0} \\ {\sqrt{85-4}-9 \stackrel{?}{=} 0} \\ {\sqrt{81}-9 \stackrel{?}{=} 0} \\ {9-9=0} \\ {0=0}\end{array}\) Рішення є\(n=17\).

	\(\sqrt[3]{5 x+1}+8=4\)
Щоб виділити радикал, відніміть\(8\) з обох сторін.	\(\sqrt[3]{5 x+1}=-4\)
Куб обидві сторони рівняння.	\((\sqrt[3]{5 x+1})^{3}=(-4)^{3}\)
Спростити.	\(5 x+1=-64\)
Розв'яжіть рівняння.	\(5 x=-65\)
	\(x=-13\)
Перевірте відповідь.
$.$
	Рішення є\(x=-13\).

	\((3 x-2)^{\frac{1}{4}}+3=5\)
Щоб виділити термін з раціональним показником, відніміть\(3\) з обох сторін.	\((3 x-2)^{\frac{1}{4}}=2\)
Підніміть кожну сторону рівняння до четвертого ступеня.	\(\left((3 x-2)^{\frac{1}{4}}\right)^{4}=(2)^{4}\)
Спростити.	\(3 x-2=16\)
Розв'яжіть рівняння.	\(3x=18\)
	\(x=6\)
Перевірте відповідь.
$.$
	Рішення є\(x=6\).

	\(\sqrt{r+4}-r+2=0\)
Виділяють радикал.	\(\sqrt{r+4}=r-2\)
Квадратні обидві сторони рівняння.	\((\sqrt{r+4})^{2}=(r-2)^{2}\)
Спростити, а потім вирішити рівняння.	\(r+4=r^{2}-4 r+4\)
Якщо це квадратне рівняння, то отримайте нуль з одного боку.	\(0=r^{2}-5 r\)
Фактор правого боку.	\(0=r(r-5)\)
Використовуйте властивість нульового продукту.	\(0=r \quad 0=r-5\)
Розв'яжіть рівняння.	\(r=0 \quad r=5\)
Перевірте свою відповідь.
$.$	Рішення є\(r=5\).
	\(r=0\)є екстремальним рішенням.

	\(3 \sqrt{3 x-5}-8=4\)
Виділяють радикальний термін.	\(3 \sqrt{3 x-5}=12\)
Виділяють радикал, розділивши обидві сторони на\(3\).	\(\sqrt{3 x-5}=4\)
Квадратні обидві сторони рівняння.	\((\sqrt{3 x-5})^{2}=(4)^{2}\)
Спростити, а потім вирішити нове рівняння.	\(3 x-5=16\)
	\(3x=21\)
Розв'яжіть рівняння.	\(x=7\)
Перевірте відповідь.
$.$
	Рішення є\(x=7\).

Приклад\(\PageIndex{1}\) how to solve a radical equation

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)

Приклад\(\PageIndex{2}\)

Вправа\(\PageIndex{3}\)

Вправа\(\PageIndex{4}\)

Приклад\(\PageIndex{3}\)

Вправа\(\PageIndex{5}\)

Вправа\(\PageIndex{6}\)

Приклад\(\PageIndex{4}\)

Вправа\(\PageIndex{7}\)

Вправа\(\PageIndex{8}\)

Приклад\(\PageIndex{5}\)

Вправа\(\PageIndex{9}\)

Вправа\(\PageIndex{10}\)

Приклад\(\PageIndex{6}\)

Вправа\(\PageIndex{11}\)

Вправа\(\PageIndex{12}\)

Приклад\(\PageIndex{7}\)

Вправа\(\PageIndex{13}\)

Вправа\(\PageIndex{14}\)

Приклад\(\PageIndex{8}\)

Вправа\(\PageIndex{15}\)

Вправа\(\PageIndex{16}\)

Приклад\(\PageIndex{9}\) how to solve a radical equation

Вправа\(\PageIndex{17}\)

Вправа\(\PageIndex{18}\)

Приклад\(\PageIndex{10}\)

Вправа\(\PageIndex{19}\)

Вправа\(\PageIndex{20}\)

Приклад\(\PageIndex{11}\)

Вправа\(\PageIndex{21}\)

Вправа\(\PageIndex{22}\)

Приклад\(\PageIndex{12}\)

Вправа\(\PageIndex{23}\)

Вправа\(\PageIndex{24}\)

	$.$
Щоб виділити радикал, відніміть\(1\) в обидві сторони.	$.$
Спростити.	$.$

	$.$
Щоб виділити радикал, відніміть\(1\) з обох сторін.	$.$
Спростити.	$.$
Квадратні обидві сторони рівняння.	$.$
Спростити, використовуючи Добуток біноміальних квадратів візерунок праворуч, Потім вирішіть нове рівняння.	$.$
Це квадратне рівняння, тому отримайте нуль з одного боку.	$.$
Фактор правого боку.	$.$
Використовуйте властивість нульового продукту.	$.$
Вирішіть кожне рівняння.	$.$
Перевірте відповіді.
$.$

Крок 1: Виділіть один з радикальних членів на одній стороні рівняння.	Радикал справа ізольований.	\(\sqrt{m}+1=\sqrt{m+9}\)
Крок 2: Підніміть обидві сторони рівняння до ступеня індексу.	Квадратуємо обидві сторони. Спрощуйте - будьте дуже обережні, коли ви розмножуєте!	\((\sqrt{m}+1)^{2}=(\sqrt{m+9})^{2}\)
Крок 3: Чи є ще радикали? Якщо так, повторіть кроки 1 і 2 ще раз. Якщо ні, розв'яжіть нове рівняння.	У рівнянні все ще є радикал. Тому ми повинні повторити попередні кроки. Виділяють радикальний термін. Тут ми можемо легко виділити радикал, розділивши обидві сторони на\(2\). Квадрат з обох сторін.	\(\begin{aligned} m+2 \sqrt{m}+1 &=m+9 \\ 2 \sqrt{m} &=8 \\ \sqrt{m} &=4 \\(\sqrt{m})^{2} &=(4)^{2} \\ m &=16 \end{aligned}\)
Крок 4: Перевірте відповідь у вихідному рівнянні.		\(\begin{aligned}\sqrt{m}+1&=\sqrt{m+9} \\ \sqrt{\color{red}{16}}\color{black}{+}1& \stackrel{?}{=} \sqrt{\color{red}{16}\color{black}{+}9} \\ 4+1& \stackrel{?}{=} 5 \\ 5&=5\end{aligned}\) Рішення є\(m=16\).

	$.$
	$.$
Візьміть квадратний корінь\(64\).	$.$
Спростити дріб.	$.$