9.4: Радикальні вирази

У попередніх двох розділах ми дізналися, як розмножувати і ділити квадратні коріння. Зокрема, ми зараз озброєні наступними двома властивостями.

Нерухомість$\PageIndex{1}$

Нехай a і b будуть будь-якими двома дійсними невід'ємними числами. Потім,

$$\sqrt{a}\sqrt{b} = \sqrt{ab},$$

і, забезпечити$b \ne 0$,

$$\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}$$

У цьому розділі ми спростимо ряд більш широких виразів, що містять квадратні корені, особливо ті, які є основоположними для вашої роботи на майбутніх курсах математики. Почнемо з побудови деяких фундаментальних навичок.

Асоціативна властивість

Згадуємо асоціативну властивість множення.

Асоціативна властивість множення

Нехай a, b і c будуть будь-якими дійсними числами. Асоціативне властивість множення стверджує, що

$$(ab)c = a(bc) \label{associativeprop}$$

Зауважте, що порядок чисел з кожного боку Equation\ ref {associativeprop} не змінився. Числа з кожного боку рівняння знаходяться в порядку$a$$b$, а потім$c$.

Однак угруповання змінилося. Ліворуч, дужки навколо добутку$a$ і$b$ доручити нам спочатку виконати цей твір, а потім помножити результат на$c$. Праворуч угруповання відрізняється; дужки навколо b і c доручають нам спочатку виконати цей твір, а потім помножити на$a$. Ключовим моментом, який слід зрозуміти, є той факт, що різні групи не мають ніякої різниці. Ми отримуємо однакову відповідь в будь-якому випадку.

Наприклад, розглянемо продукт$2 \cdot 3 \cdot 4$. Якщо спочатку помножити 2 і 3, то отриманий результат множимо на 4, отримаємо

$(2 \cdot 3) \cdot 4 = 6 \cdot 4 =24$

З іншого боку, якщо спочатку помножити 3 і 4, то множимо результат на 2, отримаємо

$2 \cdot (3 \cdot 4) = 2 \cdot 12 =24$

Зверніть увагу, що ми отримуємо однаковий результат в будь-якому випадку. Тобто,

$(2 \cdot 3) \cdot 4 = 2 \cdot (3 \cdot 4)$

Асоціативна властивість, здавалося б, тривіальна, набуває додаткового рівня витонченості, якщо застосувати його до виразів, що містять радикали. Давайте розглянемо приклад.

Приклад$\PageIndex{3}$

Спростити вираз$3(2\sqrt{5})$. Помістіть свою відповідь в простій радикальній формі.

В даний час дужки навколо 2 і$\sqrt{5}$ require that we multiply those two numbers first. However, the associative property of multiplication allows us to regroup, розміщуючи дужки навколо 3 та 2, спочатку множивши ці два числа, а потім множимо результат на$\sqrt{5}$. Влаштовуємо роботу наступним чином.

$3(2\sqrt{5})=(3 \cdot 2)\sqrt{5}=6\sqrt{5}$.

Читачам варто відзначити схожість з дуже звичною маніпуляцією.

$3(2x) = (3 \cdot 2)x = 6x$

На практиці, коли ми стали впевнені в цій перегрупуванні, ми почали пропускати проміжний крок і просто стверджувати, що 3 (2х) = 6х. Подібним чином, як тільки ви станете впевненими в перегрупуванні, ви повинні просто заявити, що$3(2\sqrt{5}) = 6\sqrt{5}$. Якщо ви покликані пояснити свою відповідь, ви повинні бути готові пояснити, як ви перегрупували відповідно до асоціативної властивості множення. Аналогічно,

$−4(5\sqrt{7})=−20\sqrt{7}$,$12(5\sqrt{11})=60\sqrt{11}$, і$−5(−3\sqrt{3})=15\sqrt{3}$.

Комутативна властивість множення

Згадуємо комутативну властивість множення.

Комутативна властивість множення

Нехай a і b будуть будь-якими дійсними числами. Комутативна властивість множення стверджує, що

аб = ба

Комутативна властивість стверджує, що порядок множення не має значення. Наприклад,$2 \cdot 3$ це те ж саме, що$3 \cdot 2$; they both equal 6. This seemingly trivial property, coupled with the associative property of multiplication, allows us to change the order of multiplication and regroup as we please.

Приклад$\PageIndex{5}$

Спростити вираз$\sqrt{5}(2\sqrt{3})$. Помістіть свою відповідь в простій радикальній формі.

Те, що ми дійсно хотіли б зробити, це спочатку помножити$\sqrt{5}$ and $\sqrt{3}$. In order to do this, we must first regroup, then switch the order of multiplication as follows.

$\sqrt{5}(2\sqrt{3}) = (\sqrt{5} \cdot 2)\sqrt{3} = (2\sqrt{5})\sqrt{3}$

Це допускається асоціативними і комутативними властивостями множення. Тепер ми знову перегрупуємо і множимо.

$(2\sqrt{5})\sqrt{3} = 2(\sqrt{5}\sqrt{3}) = 2\sqrt{15}$

На практиці це занадто велика робота для такого простого розрахунку. Як тільки ми зрозуміємо асоціативні та комутативні властивості множення, вираз$a \cdot b \cdot c$ однозначний. Дужки не потрібні. Ми знаємо, що можемо змінювати порядок множення і перегрупувати як завгодно. Тому при поданні добутку трьох чисел просто помножте два за вашим вибором разом, потім помножте отриманий результат на третє число, що залишилося.

У разі$\sqrt{5}(2\sqrt{3})$, ми вибираємо спочатку помножити$\sqrt{5}$ і$\sqrt{3}$, тобто$\sqrt{15}$, потім помножити цей результат на 2, щоб отримати$2\sqrt{15}$. Аналогічно,

$\sqrt{5}(2\sqrt{7})=2\sqrt{35}$і$\sqrt{x}(3\sqrt{5})=3\sqrt{5x}$.

Приклад$\PageIndex{6}$

Спростити вираз$\sqrt{6}(4\sqrt{8})$. Помістіть свою відповідь в простій радикальній формі.

Починаємо з множення$\sqrt{6}$ and $\sqrt{8}$, then the result by 4.

$\sqrt{6}(4\sqrt{8})=4\sqrt{48}$

Тепер\(48 = 16 \cdot 3\), щоб ми могли витягти ідеальний квадрат.

$4\sqrt{48}=4(\sqrt{16}\sqrt{3})=4(4\sqrt{3})$

Знову вибираємо множити четвірки, потім результат на квадратний корінь з трьох. Тобто,

$4(4\sqrt{3})=16\sqrt{3}$.

За індукції можна стверджувати, що асоціативні і комутативні властивості дозволять нам групувати і розташувати добуток більше трьох чисел в будь-якому порядку, який нам подобається.

Приклад$\PageIndex{7}$

Спростити вираз$2\sqrt{12}(3\sqrt{3})$. Помістіть свою відповідь в простій радикальній формі.

Ми спочатку візьмемо твір 2 і 3, потім твір$\sqrt{12}$ and $\sqrt{3}$, then multiply these results together.

$2\sqrt{12}(3\sqrt{3}) = (2 \cdot 3)(\sqrt{12}\sqrt{3}) = 6\sqrt{36}$

Звичайно$\sqrt{36} = 6$, так ми можемо спростити далі.

$6\sqrt{36} = 6 \cdot 6 = 36$

Розподільна власність

Згадаймо розподільне властивість для дійсних чисел.

Розподільна власність

Нехай a, b і c будуть будь-якими дійсними числами. Потім,

а (б+с) = аб + змінний струм

Ви можете згадати наступну операцію, де ви «розподіляєте 2», множивши кожен член у дужках на 2.

2 (3 + х) = 6 + 2х

Точно те ж саме можна зробити і з радикальними виразами.

$2(3+\sqrt{5})=6+2\sqrt{5}$

Як і в звичному прикладі вище, ми «розподілили 2», помноживши кожен член в дужках на 2.

Давайте розглянемо докладніше приклади.

Приклад$\PageIndex{9}$

Використовуйте властивість distributive, щоб розширити вираз$\sqrt{12}(3+\sqrt{3})$, помістивши свою остаточну відповідь в простій радикальній формі.

Спочатку розподіліть$\sqrt{12}$, multiplying each term in the parentheses by $\sqrt{12}$. Note те$\sqrt{12}\sqrt{3} = \sqrt{36}$.

$\sqrt{12}(3+\sqrt{3})=3\sqrt{12}+\sqrt{36}=3\sqrt{12}+6$

Однак цей останній вислів не в простій радикальній формі, оскільки ми можемо виділити ідеальний квадрат$(12 = 4 \cdot 3)$.

$3\sqrt{12}+6=3(\sqrt{4}\sqrt{3})+6 = 3(2\sqrt{3})+6 = 6\sqrt{3}+6$

Неважливо, чи є мономіальний коефіцієнт спереду чи ззаду суми, ви все одно розподіляєте мономіальні часи кожного члена в дужках.

Приклад$\PageIndex{10}$

Використовуйте властивість distributive для розширення$(\sqrt{3}+2\sqrt{2})\sqrt{6}$. Помістіть свою відповідь в простій радикальній формі.

Спочатку помножте кожен член в дужках на$\sqrt{6}$.

$(\sqrt{3}+2\sqrt{2})\sqrt{6} = \sqrt{18}+2\sqrt{12}$

Щоб отримати другий член цього результату, ми вирішили спочатку помножити$\sqrt{2}$ і$\sqrt{6}$, тобто$\sqrt{12}$, потім ми помножили цей результат на 2. Тепер ми можемо враховувати ідеальні квадрати як з 18, так і з 12.

$\sqrt{18}+2\sqrt{12}= \sqrt{9}\sqrt{2}+2(\sqrt{4}\sqrt{3}) = 3\sqrt{2}+2(2\sqrt{3}) = 3\sqrt{2}+4\sqrt{3}$

Пам'ятайте, що ви можете перевірити свої результати за допомогою калькулятора. На малюнку 1 (a) ми знайшли десяткове наближення для вихідного виразу$(\sqrt{3}+2\sqrt{2})\sqrt{6}$, а на малюнку 1 (b) ми маємо десяткове наближення для нашого розв'язку$3\sqrt{2}+4\sqrt{3}$. Зверніть увагу, що вони однакові, надаючи докази того, що наше рішення правильне.

Малюнок 1. Порівняння вихідного виразу з його простою радикальною формою.

Дистрибутивна властивість також відповідає за те, щоб допомогти нам поєднувати «подібні терміни». Наприклад, ви можете пам'ятати, що 3x + 5x = 8x, здавалося б, простий розрахунок, але саме розподільна властивість насправді забезпечує це рішення. Зверніть увагу, як ми використовуємо розподільну властивість для множника x з кожного члена.

3х+5х = (3+5) х

Значить, 3х+ 5х = 8х. Те ж саме можна зробити і з радикальними виразами.

$3\sqrt{2}+5\sqrt{2} = (3+5)\sqrt{2}$

Звідси$3\sqrt{2}+5\sqrt{2} = 8\sqrt{2}$ і структура цього результату ідентична тій, яка показана в 3х + 5х = 8х. Немає різниці в тому, як ми поєднуємо ці «подібні терміни». Повторюємо загальний коефіцієнт і додаємо коефіцієнти. Наприклад,

$2\sqrt{3}+9\sqrt{3} = 11\sqrt{3}$,$−4\sqrt{2}+2\sqrt{2} = −2\sqrt{2}$, і$−3x\sqrt{x}+5x\sqrt{x}=2x\sqrt{x}$.

У кожному випадку вище, ми додаємо «як терміни», повторюючи загальний коефіцієнт і додаючи коефіцієнти.

У випадку, якщо у нас немає подібних термінів, як у 3x+5y, нічого не поробиш. Подібним чином, кожне з наступних виразів не має подібних термінів, які ви можете комбінувати. Вони настільки ж спрощені, як і збираються отримати.

$3\sqrt{2}+5\sqrt{3}$,$2\sqrt{11}−8\sqrt{10}$, і$2\sqrt{x} + 5\sqrt{y}$

Однак бувають випадки, коли це може виглядати так, ніби у вас немає подібних термінів, але коли ви розміщуєте все в простій радикальній формі, ви виявляєте, що у вас є подібні терміни, які можна поєднувати, додаючи коефіцієнти.

Приклад$\PageIndex{11}$

Спростити вираз$5\sqrt{27}+8\sqrt{3}$, помістивши кінцевий вираз в просту радикальну форму.

Ми можемо витягти ідеальний квадрат ($27 = 9 \cdot 3$).

$5\sqrt{27}+8\sqrt{3} = 5(\sqrt{9}\sqrt{3})+8\sqrt{3} = 5(3\sqrt{3})+8\sqrt{3} = 15\sqrt{3}+8\sqrt{3}$

Зверніть увагу, що тепер у нас є «подібні терміни», які можна комбінувати, додаючи коефіцієнти.

$15\sqrt{3}+8\sqrt{3} =23\sqrt{3}$

Порівняння вихідного виразу і його спрощеної форми показано на малюнках 2 (а) і (б).

Малюнок 2. Порівняння вихідного виразу з його спрощеною формою.

Приклад$\PageIndex{12}$

Спростіть вираз$2\sqrt{20}+\sqrt{8}+3\sqrt{5}+4\sqrt{2}$, помістивши результат в просту радикальну форму.

Ми можемо витягти ідеальні квадрати ($20 = 4 \cdot 5$ and $8 = 4 \cdot 2$).

$2\sqrt{20}+\sqrt{8}+3\sqrt{5}+4\sqrt{2} = 2(\sqrt{4}\sqrt{5})+\sqrt{4}\sqrt{2}+3\sqrt{5}+4\sqrt{2} = 2(2\sqrt{5})+2\sqrt{2}+3\sqrt{5}+4\sqrt{2} = 4\sqrt{5}+2\sqrt{2}+3\sqrt{5}+4\sqrt{2}$

Тепер ми можемо комбінувати подібні терміни, додаючи коефіцієнти.

$4\sqrt{5}+2\sqrt{2}+3\sqrt{5}+4\sqrt{2} = 7\sqrt{5}+6\sqrt{2}$

Дроби можуть бути трохи хитрими.

Приклад$\PageIndex{13}$

Спростити$\sqrt{27}+\frac{1}{\sqrt{12}}$, помістивши результат в просту радикальну форму.

Ми можемо витягти ідеальний квадратний корінь$(27 = 9 \cdot 3)$ Знаменник у другому члені є$\sqrt{12} = 2\sqrt{2} \cdot \sqrt{3}$, тому в знаменнику потрібно ще 3, щоб зробити ідеальний квадрат.

$\sqrt{27}+\frac{1}{\sqrt{12}} = \sqrt{9}\sqrt{3}+\frac{1}{\sqrt{12}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = 3\sqrt{3}+\frac{\sqrt{3}}{\sqrt{36}} = 3\sqrt{3} + \frac{\sqrt{3}}{6}$

Щоб скласти ці дроби, нам знадобиться спільний знаменник 6.

$3\sqrt{3} + \frac{\sqrt{3}}{6} = \frac{18\sqrt{3}}{6} + \frac{\sqrt{3}}{6} = \frac{19\sqrt{3}}{6}$

Тепер ми можемо комбінувати чисельники, додаючи коефіцієнти.

$\frac{18\sqrt{3}}{6} + \frac{\sqrt{3}}{6} = \frac{19\sqrt{3}}{6}$

Десяткові наближення вихідного виразу і його спрощена форма показані на малюнках 3 (а) і (б).

Малюнок 3. Порівняння вихідного виразу з його спрощеною формою.

На перший погляд, відсутність мономіалу в продукті (х + 1) (х + 3) змушує думати, що розподільна властивість не допоможе нам знайти товар. Однак, якщо ми думаємо про другий фактор як про єдину одиницю, ми можемо розподілити його раз на кожен термін у першому факторі.

(х+1) (х+3) = х (х+3) +1 (х+3)

Застосовуйте розподільну властивість вдруге, а потім об'єднайте подібні терміни.

$x(x+3)+1(x+3)=x^2+3x+x+3 = x^2+4x+3$

Ми можемо обробляти продукти з радикальними виразами таким же чином.

Приклад$\PageIndex{14}$

Спростити$(2+\sqrt{2})(3+5\sqrt{2})$. Помістіть свій результат в простій радикальній формі.

Подумайте про другий фактор як про єдину одиницю і розподіліть його раз на кожен термін у першому факторі.

$(2+\sqrt{2})(3+5\sqrt{2}) = 2(3+5\sqrt{2})+\sqrt{2}(3+5\sqrt{2})$

Тепер знову використовуйте розподільну властивість.

$2(3+5\sqrt{2})+\sqrt{2}(3+5\sqrt{2}) = 6+10\sqrt{2}+3\sqrt{2}+5\sqrt{4}$

Зверніть увагу, що при знаходженні останнього терміну,$\sqrt{2}\sqrt{2} = \sqrt{4}$. Тепер\ sqrt {4} = 2, тоді ми можемо об'єднати як терміни.

$6+10\sqrt{2}+3\sqrt{2}+5\sqrt{4} = 6+10\sqrt{2}+3\sqrt{2}+5(2) = 6+10\sqrt{2}+3\sqrt{2}+10 = 16+13\sqrt{2}$

Десяткові наближення вихідного виразу і його проста радикальна форма показані на малюнках 4 (а) і (б).

Малюнок 4. Порівняння вихідного виразу з його спрощеною формою.

Спеціальні продукти

Є два спеціальні продукти, які мають важливі програми, що включають радикальні вирази, можливо, одне більше, ніж інше. Перший - добре відома відмінність малюнка двох квадратів.

різниця квадратів

Нехай a і b будуть будь-якими числами. Потім,

$(a+b)(a−b)=a^2−b^2$.

Ця закономірність включає в себе два біноміальних множника, що мають однакові перший і другий члени, члени в одному множнику розділені знаком плюс, члени в іншому множнику розділені знаком мінус. Коли ми бачимо цю закономірність множення, ми повинні квадрат першого члена будь-якого фактора, квадрат другого члена, а потім відняти результати. Наприклад,

$(2x+3)(2x−3) = 4x^2−9$.

Цей спеціальний продукт однаково добре застосовується, коли перші та/або другі члени включають радикальні вирази.

Приклад$\PageIndex{15}$

Використовуйте різницю квадратів візерунків для множення$(2+\sqrt{11})(2−\sqrt{11})$

Зауважте, що це множення має вигляд (a + b) (a − b), тому ми застосовуємо шаблон різниці квадратів, щоб отримати

$(2+\sqrt{11})(2−\sqrt{11}) = (2)^2−(\sqrt{11})^2$

Звичайно,$2^2 = 4$ і$(\sqrt{11})^2 = 11$, так ми можемо закінчити наступним чином.

$(2)^2−(\sqrt{11})^2 = 4−11 = −7$

Приклад$\PageIndex{16}$

Використовуйте візерунок різниці квадратів для множення$(2\sqrt{5}+3\sqrt{7})(2\sqrt{5}−3\sqrt{7})$.

Знову ж таки, цей виріб має спеціальну форму (a + b) (a − b), тому ми застосовуємо різницю квадратів візерунка, щоб отримати

$(2\sqrt{5}+3\sqrt{7})(2\sqrt{5}−3\sqrt{7}) = (2\sqrt{5})^2−(3\sqrt{7})^2$

Далі квадратизируем добуток двох факторів за правилом$(ab)^2 = a^{2}b^2$. Таким чином,

$(2\sqrt{5})^2 = (2)^{2}(\sqrt{5})^2 = 4 \cdot 5 = 20$

і

$(3\sqrt{7})^2 =(3)^{2}(\sqrt{7})^2 = 9 \cdot 7 = 63$.

Таким чином, ми можемо завершити множення за$(2\sqrt{5}+3\sqrt{7})(2\sqrt{5}−3\sqrt{7})$ допомогою

$(2\sqrt{5})^2−(3\sqrt{7})^2 =20−63=−43$.

Цей результат легко перевірити за допомогою калькулятора, як показано на малюнку 5.

Малюнок 5. Наближення$(2\sqrt{5}+3\sqrt{7})(2\sqrt{5}−3\sqrt{7})$.

Другий шаблон, що представляє інтерес, - це ярлик для квадратизації біноміала.

Квадратування біноміального

Нехай a і b - числа. Потім,

$(a + b)^2 = a^2 + 2ab + b^2$.

Тут ми квадратизируем перший і другий члени біноміалу, потім виробляємо середній член результату, множивши перший і другий члени і подвоюючи цей результат. Наприклад,

$(2x+9)^2 = (2x)^2 +2(2x)(9)+(9)^2 = 4x^2 +36x+81$.

Цей візерунок також може бути застосований до біноміалів, що містять радикальні вирази.

Приклад$\PageIndex{17}$

Використовуйте квадрат біноміального візерунка, щоб розширити$(2\sqrt{x} + \sqrt{5})^2$. Помістіть свій результат в простій радикальній формі. Припустімо, що x є додатним дійсним числом (x > 0).

Застосовуючи квадрат двочленний візерунок, отримуємо

$(2\sqrt{x} + \sqrt{5})^2 = (2\sqrt{x})^2 + 2(2\sqrt{x})(\sqrt{5}) + (\sqrt{5})^2$.

Як і раніше,$(2\sqrt{x})^2 = (2)^{2}(\sqrt{x})^2 = 4x$ і$(\sqrt{5})^2 = 5$. У випадку з$2(2\sqrt{x})(\sqrt{5})$, зверніть увагу, що ми множимо чотири числа разом. Асоціативні та комутативні властивості стверджують, що ми можемо помножити ці чотири числа в будь-якому порядку, який нам подобається. Отже, добуток 2 і 2 дорівнює 4, добуток$\sqrt{x}$ і$\sqrt{5}$ є$\sqrt{5x}$, потім ми множимо ці результати, щоб отримати результат$4\sqrt{5x}$. Таким чином,

$(2\sqrt{x})^2 + 2(2\sqrt{x})(\sqrt{5}) + (\sqrt{5})^2 = 4x + 4\sqrt{5x} + 5$.

Раціоналізація знаменників

Як ми бачили в попередньому розділі, інструкція «раціоналізувати знаменник» - це прохання прибрати всі радикальні вирази зі знаменника. Звичайно, це «третій орієнтир простої радикальної форми», але бувають випадки, особливо в обчисленні, коли інструкція змінюється на «раціоналізувати чисельник». Звичайно, це прохання прибрати з чисельника всі радикали.

Ви не можете мати обидва світи. Ви можете видалити радикальні вирази з знаменника або з чисельника, але не обидва. Якщо вказівки не дано, припустимо, що в грі діє «третя орієнтир простої радикальної форми» і видаліть всі радикальні вирази зі знаменника. Ми вже зробили трохи цього в попередніх розділах, але тут ми звертаємося до трохи більш складного типу вираження.

Приклад$\PageIndex{18}$

У виразі$\frac{3}{2+\sqrt{2}}$ раціоналізуйте знаменник.

Секрет полягає в різниці квадратів візерунком,$(a+b)(a−b) = a^2−b^2$. For example,

$(2+\sqrt{2})(2−\sqrt{2}) = (2)^2−(\sqrt{2})^2 = 4−2 = 2$.

Це дає приголомшливий натяк на те, як діяти з раціоналізацією знаменника виразу$\frac{3}{(2+\sqrt{2})}$. Помножте чисельник і знаменник на$2−\sqrt{2}$.

$\frac{3}{2+\sqrt{2}} = \frac{3}{2+2\sqrt{2}} \cdot \frac{2−\sqrt{2}}{2−\sqrt{2}}$

Множимо чисельники і знаменники.

$\frac{3}{2+2\sqrt{2}} \cdot \frac{2−\sqrt{2}}{2−\sqrt{2}} = \frac{3(2−\sqrt{2})}{(2+\sqrt{2})(2−\sqrt{2})} = \frac{6−3\sqrt{2}}{(2)^2−(\sqrt{2})^2} = \frac{6−3\sqrt{2}}{4−2} = \frac{6−3\sqrt{2}}{2}$

Зверніть увагу, що заманливо скасувати 2 в знаменнику на 6 в чисельнику, але вам не дозволяється скасовувати терміни, розділені знаком мінус. Це поширена помилка, тому не ставайте жертвою цієї помилки.

На рисунках 6 (a) і (b) ми порівняємо десяткові наближення вихідного виразу і його простої радикальної форми.

Малюнок 6. Порівняння вихідного виразу з його простою радикальною формою.

Приклад$\PageIndex{19}$

У виразі$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}−\sqrt{2}}$ раціоналізуйте знаменник.

Помножити чисельник і знаменник на$\sqrt{3} + \sqrt{2}$.

$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}−\sqrt{2}} = \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}−\sqrt{2}} \cdot \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}}$.

Множимо чисельники і знаменники.

$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}−\sqrt{2}} \cdot \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}} = \frac{(\sqrt{3}+\sqrt{2})^2}{(\sqrt{3}−\sqrt{2})(\sqrt{3}+\sqrt{2})}$

У знаменнику ми маємо різницю в два квадрати. Таким чином,

$(\sqrt{3}−\sqrt{2})(\sqrt{3}+\sqrt{2}) = (\sqrt{3})^2−(\sqrt{2})^2 =3−2=1$.

Зверніть увагу, що це очищає знаменник від радикалів. Саме тому ми множимо чисельник і знаменник на$\sqrt{3} + \sqrt{2}$. У чисельнику ми можемо використовувати квадрат біноміального ярлика для множення.

$(\sqrt{3} + \sqrt{2})^2 = (\sqrt{3})^2 + 2(\sqrt{3})(\sqrt{2}) + (\sqrt{2})^2 = 3+2\sqrt{6} +2 = 5+2\sqrt{6}$

Таким чином, ми можемо завершити спрощення, розпочате вище.

$\frac{(\sqrt{3}+\sqrt{2})^2}{(\sqrt{3}−\sqrt{2})(\sqrt{3}+\sqrt{2})} = \frac{5+2\sqrt{6}}{1} = 5+2\sqrt{6}$

На малюнках 7 (а) і (b) ми порівняємо десяткові наближення вихідного виразу з його простою радикальною формою.

Малюнок 7. Порівняння вихідного виразу з його простою радикальною формою.

Переглянути квадратичну формулу

Ми можемо використовувати те, що ми навчилися розміщувати рішення, надані квадратичною формулою, у простій формі. Давайте розглянемо приклад.

Приклад$\PageIndex{20}$

Розв'яжіть рівняння$x^2 = 2x + 2$ для x. Помістіть своє рішення в простій радикальній формі.

Рівняння нелінійне, тому зробіть одну сторону нулем.

$x^2−2x−2=0$

Порівняйте цей результат із загальним виглядом$ax^2 +bx+c = 0$ і зверніть увагу, що a = 1, b = −2 і c = −2. Запишіть квадратичну формулу, зробіть підстановки, потім спростіть.

$x = \frac{−b \pm \sqrt{b^2−4ac}}{2a} = \frac{−(−2) \pm \sqrt{(−2)^2−4(1)(−2)}}{2(1)} = \frac{2 \pm \sqrt{12}}{2}$

Зауважте, що ми можемо перерахувати ідеальний квадрат від радикала в чисельнику.

$x= \frac{2 \pm \sqrt{12}}{2} = \frac{2 \pm \sqrt{4}\sqrt{3}}{2} = \frac{2 \pm 2\sqrt{3}}{2}$

У цьому пункті зверніть увагу, що і чисельник, і знаменник діляться на 2. Є кілька способів, за якими ми можемо приступити до скорочення.

• Деякі люди вважають за краще фактор, потім скасовувати.

$\frac{2 \pm 2\sqrt{3}}{2} = \frac{2(1 \pm \sqrt{3})}{2} = 1 \pm \sqrt{3}$

• Деякі вважають за краще використовувати розподільне властивість.

$\frac{2 \pm 2\sqrt{3}}{2} = \frac{2}{2} \pm \frac{2\sqrt{3}}{2} = 1 \pm \sqrt{3}$

У кожному конкретному випадку остаточна форма відповіді знаходиться в простій радикальній формі і вона зводиться до найнижчих.

Попередження$\PageIndex{21}$

При роботі з квадратичною формулою однією з найпоширеніших помилок алгебри є скасування доповнення замість множників, як в

$\frac{2 \pm 2\sqrt{3}}{2} = \pm 2\sqrt{3}$

Будь ласка, намагайтеся уникати цієї помилки.

Давайте розглянемо інший приклад.

Приклад$\PageIndex{22}$

Розв'яжіть рівняння$3x^2 − 2x = 6$ для x. Помістіть своє рішення в простій радикальній формі.

Це рівняння нелінійне. Перемістіть кожен член в одну сторону рівняння, зробивши іншу сторону рівняння рівняння рівнянням рівняння рівнянням.

$3x^2−2x−6=0$

Порівняйте із загальною формою$ax^2 +bx+c = 0$ і зверніть увагу, що a = 3, b = −2, а c = −6. Запишіть квадратичну формулу і підставляйте.

$x = \frac{−b \pm \sqrt{b^2−4ac}}{2a} = \frac{−(−2) \pm \sqrt{(−2)^2−4(3)(−6)}}{2(3)} = \frac{2 \pm \sqrt{76}}{6}$

Фактор досконалий квадрат від радикала в чисельнику.

$x = \frac{2 \pm \sqrt{76}}{6} = \frac{2 \pm \sqrt{4}\sqrt{19}}{6} = \frac{2 \pm 2\sqrt{19}}{6}$

Ми вибираємо фактор і скасовуємо.

$x = \frac{2 \pm 2\sqrt{19}}{6} = \frac{2(1 \pm \sqrt{19})}{2 \cdot 3} = \frac{1 \pm \sqrt{19}}{3}$

У вправах 1 - 14 помістіть кожне з радикальних виразів в простій радикальній формі. Перевірте свою відповідь за допомогою калькулятора.

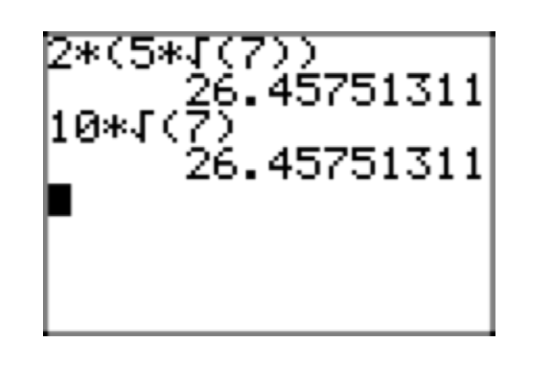
Вправа$\PageIndex{1}$

$2(5\sqrt{7})$

Відповідь

Перегрупувати за допомогою асоціативного властивості і спростити.

$2(5\sqrt{7})=(2 \cdot 5)\sqrt{7}=10\sqrt{7}$

Перевірка.

Вправа$\PageIndex{2}$

$−3(2\sqrt{3})$

Вправа$\PageIndex{3}$

$−\sqrt{3}(2\sqrt{5})$

Відповідь

Комутативні та асоціативні властивості дозволяють нам змінювати порядок та перегрупувати.

$−\sqrt{3}(2\sqrt{5})=2(−\sqrt{3}\sqrt{5})=2(−\sqrt{15})=−2\sqrt{15}$

Перевірка.

Вправа$\PageIndex{4}$

$\sqrt{2}(3\sqrt{7})$

Вправа$\PageIndex{5}$

$\sqrt{3}(5\sqrt{6})$

Відповідь

Комутативні та асоціативні властивості дозволяють нам змінювати порядок та перегрупувати.

$\sqrt{3}(5\sqrt{6})=5(\sqrt{3}\sqrt{6})=5(\sqrt{18})$

Це не в простій формі, оскільки можна виділити ідеальний квадрат.

$5\sqrt{18}=5\sqrt{9}\sqrt{2}=5 \cdot 3\sqrt{2}=15\sqrt{2}$

Перевірка.

Вправа$\PageIndex{6}$

$\sqrt{2}(−3\sqrt{10})$

Вправа$\PageIndex{7}$

$(2\sqrt{5})(−3\sqrt{3})$

Відповідь

Комутативні та асоціативні властивості дозволяють нам змінювати порядок та перегрупувати.

$(2\sqrt{5})(−3\sqrt{3})=(2 \cdot −3)(\sqrt{5}\sqrt{3})=−6\sqrt{15}$

Перевірка.

Вправа$\PageIndex{8}$

$(−5\sqrt{2})(−2\sqrt{7})$

Вправа$\PageIndex{9}$

$(−4\sqrt{3})(2\sqrt{6})$

Відповідь

Комутативні та асоціативні властивості дозволяють нам змінювати порядок та перегрупувати.

$(−4\sqrt{3})(2\sqrt{6}) = (−4 \cdot 2)(\sqrt{3}\sqrt{6})=−8\sqrt{18}$

Ця відповідь не проста, оскільки ми можемо врахувати ідеальний квадрат.

$−8\sqrt{18} = −8\sqrt{9}\sqrt{2} = −8 \cdot 3\sqrt{2} = −24\sqrt{2}$

Перевірка.

Вправа$\PageIndex{10}$

$(2\sqrt{5})(−3\sqrt{10})$

Вправа$\PageIndex{11}$

$(2\sqrt{3})^2$

Відповідь

Нагадаємо, що$(ab)^2 = a^{2}b^2$.

$(2\sqrt{3})^2 = (2)^{2}(\sqrt{3})^2 = 4 \cdot 3 = 12$

Перевірка.

Вправа$\PageIndex{12}$

$(−3\sqrt{5})^2$

Вправа$\PageIndex{13}$

$(−5\sqrt{2})^2$

Відповідь

Нагадаємо, що$(ab)^2 = a^{2}b^2$.

$(−5\sqrt{2})^2 = (−5)^{2}(\sqrt{2})^2 = 25 \cdot 2 = 50$

Перевірка.

Вправа$\PageIndex{14}$

$(7\sqrt{11})^2$

У вправах 15 - 22 використовуйте розподільну властивість для множення. Помістіть остаточну відповідь у простій радикальній формі. Перевірте результат за допомогою калькулятора.

Вправа$\PageIndex{15}$

$2(3 +\sqrt{5})$

Відповідь

Нагадаємо розподільне властивість: a (b + c) = ab + ac.

$2(3+\sqrt{5}) = 2(3)+2(\sqrt{5}) = 6+2\sqrt{5}$

Перевірка.

Вправа$\PageIndex{16}$

$−3(4−\sqrt{7})$

Вправа$\PageIndex{17}$

$2(−5+4\sqrt{2})$

Відповідь

Нагадаємо розподільне властивість: a (b + c) = ab + ac.

$2(−5+4\sqrt{2})=2(−5)+2(4\sqrt{2})=−10+8\sqrt{2}$

Перевірка.

Вправа$\PageIndex{18}$

$−3(4−3\sqrt{2})$

Вправа$\PageIndex{19}$

$\sqrt{2}(2+\sqrt{2})$

Відповідь

Нагадаємо розподільне властивість: a (b + c) = ab + ac.

$\sqrt{2}(2+\sqrt{2}) = \sqrt{2}(2)+\sqrt{2}(\sqrt{2}) = 2\sqrt{2}+\sqrt{4}=2\sqrt{2}+2$

Перевірка.

Вправа$\PageIndex{20}$

$\sqrt{3}(4−\sqrt{6})$

Вправа$\PageIndex{21}$

$\sqrt{2}(\sqrt{10}+\sqrt{14})$

Відповідь

Нагадаємо розподільне властивість: a (b + c) = ab + ac.

$\sqrt{2}(\sqrt{10}+\sqrt{14}) = \sqrt{2}(\sqrt{10})+ \sqrt{2}(\sqrt{14}) = \sqrt{20}+\sqrt{28}$

Однак ця відповідь не в простій формі, тому що ми можемо враховувати ідеальні квадрати.

$\sqrt{20}+\sqrt{28} = \sqrt{4}\sqrt{5}+\sqrt{4}\sqrt{7} = 2\sqrt{5}+2\sqrt{7}$

Перевірка.

Вправа$\PageIndex{22}$

$\sqrt{3}(\sqrt{15}−\sqrt{33})$

У вправах 23 - 30 комбінуйте подібні терміни. Помістіть остаточну відповідь у простій радикальній формі. Перевірте своє рішення за допомогою калькулятора.

Вправа$\PageIndex{23}$

$−5\sqrt{2}+7\sqrt{2}$

Відповідь

Використовуйте розподільну властивість для розрахунку$\sqrt{2}$.

$−5\sqrt{2}+7\sqrt{2} = (−5+7)\sqrt{2} = 2\sqrt{2}$

На практиці ми зазвичай просто об'єднаємо$−5\sqrt{2}+7\sqrt{2}$ багато, як ми робимо −5x+7x = 2x і просто пишемо$−5\sqrt{2}+7\sqrt{2}=2\sqrt{2}$.

Перевірка.

Вправа$\PageIndex{24}$

$2\sqrt{3}+3\sqrt{3}$

Вправа$\PageIndex{25}$

$2\sqrt{6}−8\sqrt{6}$

Відповідь

Використовуйте розподільну властивість для розрахунку$\sqrt{6}$.

$2\sqrt{6}−8\sqrt{6} = (2−8)\sqrt{6} = −6\sqrt{6}$

На практиці ми зазвичай просто об'єднаємо$2\sqrt{6}−8\sqrt{6}$ так само, як і 2x−8x = −6x і просто пишемо$2\sqrt{6}−8\sqrt{6}=−6\sqrt{6}$.

Перевірка.

Вправа$\PageIndex{26}$

$\sqrt{7}−3\sqrt{7}$

Вправа$\PageIndex{27}$

$2\sqrt{3}−4\sqrt{2}+3\sqrt{3}$

Відповідь

Комутативні та асоціативні властивості додавання дозволяють нам змінювати порядок та перегрупувати, тоді ми поєднуємо подібні терміни.

$2\sqrt{3}−4\sqrt{2}+3\sqrt{3} = (2\sqrt{3}+3\sqrt{3})−4\sqrt{2} = 5\sqrt{3}−4\sqrt{2}$

Перевірка.

Вправа$\PageIndex{28}$

$7\sqrt{5}+2\sqrt{7}−3\sqrt{5}$

Вправа$\PageIndex{29}$

$2\sqrt{3}+5\sqrt{2}−7\sqrt{3}+2\sqrt{2}$

Відповідь

Комутативні та асоціативні властивості додавання дозволяють нам змінювати порядок та перегрупувати, тоді ми можемо додавати подібні терміни.

$2\sqrt{3}+5\sqrt{2}−7\sqrt{3}+2\sqrt{2} = (2\sqrt{3}−7\sqrt{3})+(5\sqrt{2}+2\sqrt{2})=−5\sqrt{3}+7\sqrt{2}$

Перевірка.

Вправа$\PageIndex{30}$

$3\sqrt{11}−2\sqrt{7}−2\sqrt{11}+4\sqrt{7}$

У вправах 31 - 40 поєднуйте подібні терміни, де це можливо. Помістіть остаточну відповідь у простій радикальній формі. Скористайтеся калькулятором, щоб перевірити результат.

Вправа$\PageIndex{31}$

$\sqrt{45}+\sqrt{20}$

Відповідь

$\sqrt{45}+\sqrt{20} = \sqrt{3^{2} \cdot 5}+ \sqrt{2^2 \cdot 5} = 3\sqrt{5}+2\sqrt{5} = (3+2)\sqrt{5} =5\sqrt{5}$

Перевірка.

Вправа$\PageIndex{32}$

$−4\sqrt{45}−4\sqrt{20}$

Вправа$\PageIndex{33}$

$2\sqrt{18} − \sqrt{8}$

Відповідь

$2\sqrt{18}−\sqrt{8} = 2\sqrt{3^2 \cdot 2}−\sqrt{2^2 \cdot 2} = 6\sqrt{2}−2\sqrt{2} = (6−2)\sqrt{2} = 4\sqrt{2}$

Перевірка.

Вправа$\PageIndex{34}$

$−\sqrt{20}+4\sqrt{45}$

Вправа$\PageIndex{35}$

$−5\sqrt{27}+5\sqrt{12}$

Відповідь

$−5\sqrt{27}+5\sqrt{12} = −5\sqrt{3^2 \cdot 3}+5\sqrt{2^2 \cdot 3} = −15\sqrt{3}+10\sqrt{3} = (−15+10)\sqrt{3} = −5\sqrt{3}$

Перевірка.

Вправа$\PageIndex{36}$

$3\sqrt{12}−2\sqrt{27}$

Вправа$\PageIndex{37}$

$4\sqrt{20}+4\sqrt{45}$

Відповідь

$4\sqrt{20}+4\sqrt{45} = 4\sqrt{2^2 \cdot 5}+4\sqrt{3^2 \cdot 5} = 8\sqrt{5}+12\sqrt{5} = (8+12)\sqrt{5} =20\sqrt{5}$

Перевірка.

Вправа$\PageIndex{38}$

$−2\sqrt{18}−5\sqrt{8}$

Вправа$\PageIndex{39}$

$2\sqrt{45}+5\sqrt{20}$

Відповідь

$2\sqrt{45}+5\sqrt{20} = 2\sqrt{3^2 \cdot 5}+5\sqrt{2^2 \cdot 5} = 6\sqrt{5}+10\sqrt{5} = 16\sqrt{5}$

Перевірка.

Вправа$\PageIndex{40}$

$3\sqrt{27}−4\sqrt{12}$

У вправах 41 - 48 спростити кожне з заданих раціональних виразів. Помістіть остаточну відповідь у простій радикальній формі. Перевірте результат за допомогою калькулятора.

Вправа$\PageIndex{41}$

$\sqrt{2}−\frac{1}{\sqrt{2}}$

Відповідь

Помістіть другий термін в простій радикальній формі.

$\sqrt{2}−\frac{1}{\sqrt{2}} = \sqrt{2}−\frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \sqrt{2}−\frac{\sqrt{2}}{\sqrt{4}} = \sqrt{2}−\frac{\sqrt{2}}{2}$

Напишіть кожен член над спільним знаменником 2.

$\sqrt{2}−\frac{\sqrt{2}}{2} = \sqrt{2} \cdot \frac{2}{2}−\frac{\sqrt{2}}{2} = \frac{2\sqrt{2}}{2}−\frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{2}$

Перевірка.

Вправа$\PageIndex{42}$

$3\sqrt{3}−\frac{3}{\sqrt{3}}$

Вправа$\PageIndex{43}$

$2\sqrt{2}−\frac{2}{\sqrt{2}}$

Відповідь

Помістіть другий термін в простій радикальній формі.

$2\sqrt{2}−\frac{2}{\sqrt{2}} = 2\sqrt{2}−\frac{2}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = 2\sqrt{2}−\frac{2\sqrt{2}}{\sqrt{4}}$

Продовжуючи,

$2\sqrt{2}−\frac{2\sqrt{2}}{\sqrt{4}} = 2\sqrt{2}−\frac{2\sqrt{2}}{2} = 2\sqrt{2}−\sqrt{2} = \sqrt{2}$

Перевірка.

Вправа$\PageIndex{44}$

$4\sqrt{5}−\frac{5}{\sqrt{5}}$

Вправа$\PageIndex{45}$

$5\sqrt{2}+\frac{3}{\sqrt{2}}$

Відповідь

Помістіть другий термін в простій радикальній формі.

$5\sqrt{2}+\frac{3}{\sqrt{2}} = 5\sqrt{2}+\frac{3}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = 5\sqrt{2}+\frac{3\sqrt{2}}{\sqrt{4}} = 5\sqrt{2}+\frac{3\sqrt{2}}{2}$

Запишіть еквівалентні дроби із загальним знаменником і додайте.

$\sqrt{2}+\frac{3\sqrt{2}}{2} = 5\sqrt{2} \cdot \frac{2}{2}+\frac{3\sqrt{2}}{2} = \frac{10\sqrt{2}}{2}+\frac{3\sqrt{2}}{2} = \frac{13\sqrt{2}}{2}$

Перевірка.

Вправа$\PageIndex{46}$

$6\sqrt{3}+\frac{2}{\sqrt{3}}$

Вправа$\PageIndex{47}$

$\sqrt{8}−\frac{12}{\sqrt{2}}−3\sqrt{2}$

Відповідь

Помістіть перший і другий члени в простій радикальній формі.

$\sqrt{8}−\frac{12}{\sqrt{2}}−3\sqrt{2} = \sqrt{4}\sqrt{2}−\frac{12}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}}−3\sqrt{2} = 2\sqrt{2}−\frac{12\sqrt{2}}{2}−3\sqrt{2}$

Зменшіть дробовий другий член, потім об'єднайте подібні терміни.

$2\sqrt{2}−\frac{12\sqrt{2}}{2}−3\sqrt{2} = 2\sqrt{2}−6\sqrt{2}−3\sqrt{2} = −7\sqrt{2}$

Перевірка.

Вправа$\PageIndex{48}$

$\sqrt{27}−\frac{6}{\sqrt{3}}−5\sqrt{3}$

У вправах 49 - 60 множте, щоб розширити кожне з заданих радикальних виразів. Помістіть остаточну відповідь у простій радикальній формі. Скористайтеся калькулятором, щоб перевірити результат.

Вправа$\PageIndex{49}$

$(2+\sqrt{3})(3−\sqrt{3})$

Відповідь

Розподіліть другий множник раз на кожен термін першого фактора, потім застосуйте розподільну властивість вдруге.

$(2+\sqrt{3})(3−\sqrt{3})=2(3−\sqrt{3})+\sqrt{3}(3−\sqrt{3})=6−2\sqrt{3}+3\sqrt{3}−\sqrt{9}$

Спрощуйте і комбінуйте подібні терміни.

$6−2\sqrt{3}+3\sqrt{3}−\sqrt{9}=6−2\sqrt{3}+3\sqrt{3}−3=3+\sqrt{3}$

Перевірка.

Вправа$\PageIndex{50}$

$(5+\sqrt{2})(2−\sqrt{2})$

Вправа$\PageIndex{51}$

$(4+3\sqrt{2})(2−5\sqrt{2})$

Відповідь

Використовуйте розподільну властивість, щоб помножити другий множник на кожен член першого фактора, потім використовуйте розподільну властивість вдруге.

$(4+3\sqrt{2})(2−5\sqrt{2}) = 4(2−5\sqrt{2})+3\sqrt{2}(2−5\sqrt{2}) = 8−20\sqrt{2}+6\sqrt{2}−15\sqrt{4}$

Спрощуйте, а потім комбінуйте подібні терміни.

$8−20\sqrt{2}+6\sqrt{2}−15\sqrt{4}=8−20\sqrt{2}+6\sqrt{2}−30=−22−14\sqrt{2}$

Перевірка.

Вправа$\PageIndex{52}$

$(3+5\sqrt{3})(1−2\sqrt{3})$

Вправа$\PageIndex{53}$

$(2+3\sqrt{2})(2−3\sqrt{2})$

Відповідь

Тут ми використовуємо різницю квадратів візерунка:$(a+b)(a−b) = a^2−b^2$.

$(2+3\sqrt{2})(2−3\sqrt{2}) = (2)^2−(3\sqrt{2})^2$

Нагадаємо, що$(ab)^2 = a^{2}b^2$.

$(2)^2 −(3\sqrt{2})^2 =4−(3)^{2}(\sqrt{2})^2 = 4−9 \cdot 2 = 4−18 = −14$

Перевірка.

Вправа$\PageIndex{54}$

$(3 + 2\sqrt{5})(3 − 2\sqrt{5})$

Вправа$\PageIndex{55}$

$(2\sqrt{3}+3\sqrt{2})(2\sqrt{3}−3\sqrt{2})$

Відповідь

Тут ми використовуємо різницю квадратів візерунка:$(a+b)(a−b) = a^2−b^2$.

$(2\sqrt{3}+3\sqrt{2})(2\sqrt{3}−3\sqrt{2}) = (2\sqrt{3})^2−(3\sqrt{2})^2$

Нагадаємо, що$(ab)^2 = a^{2}b^2$.

$(2\sqrt{3})^2 −(3\sqrt{2})^2 =(2)^2(\sqrt{3})^2−(3)^{2}(\sqrt{2})^2 = 4 \cdot 3−9 \cdot 2 = 12−18 = −6$

Перевірка.

Вправа$\PageIndex{56}$

$(8\sqrt{2}+\sqrt{5})(8\sqrt{2}−\sqrt{5})$

Вправа$\PageIndex{57}$

$(2+\sqrt{5})^2$

Відповідь

Тут ми використовуємо квадрат біноміального візерунка:$(a+b)^2 = a^2+2ab+b^2$.

Нагадаємо, що$(ab)^2 = a^{2}b^2$.

$(2+\sqrt{5})^2 = (2)^2+2(2)(\sqrt{5})+(\sqrt{5})^2 = 4+4\sqrt{5}+5 = 9+4\sqrt{5}$

Перевірка.

Вправа$\PageIndex{58}$

$(3−\sqrt{2})^2$

Вправа$\PageIndex{59}$

$(\sqrt{3}−2\sqrt{5})^2$

Відповідь

Тут ми використовуємо квадрат біноміального візерунка:$(a−b)^2 = a^2−2ab+b^2$.

Нагадаємо, що$(ab)^2 = a^{2}b^2$.

$(\sqrt{3}−2\sqrt{5})^2 = (\sqrt{3})^2−2(\sqrt{3})(2\sqrt{5})+(2\sqrt{5})^2 = 3−4\sqrt{15}+ 4 \cdot 5 = 3−4\sqrt{15}+20 = 23−4\sqrt{15}$

Перевірка.

Вправа$\PageIndex{60}$

$(2\sqrt{3} + 3\sqrt{2})^2$

У вправах 61 - 68 помістіть кожне з заданих раціональних виразів в простій радикальній формі шляхом «раціоналізації знаменника». Перевірте результат за допомогою калькулятора.

Вправа$\PageIndex{61}$

$\frac{1}{\sqrt{5}+\sqrt{3}}$

Відповідь

Помножте чисельник і знаменник на$\sqrt{5}−\sqrt{3}$. Згадаймо різницю квадратів візерунка:$(a+b)(a−b)=a^2−b^2$.

$\frac{1}{\sqrt{5}+\sqrt{3}} = \frac{1}{\sqrt{5}+\sqrt{3}} \cdot \frac{\sqrt{5}−\sqrt{3}}{\sqrt{5}−\sqrt{3}} = \frac{\sqrt{5}−\sqrt{3}}{(\sqrt{5})^2−(\sqrt{3})^2}$

Продовжуючи.

$\frac{\sqrt{5}−\sqrt{3}}{(\sqrt{5})^2−(\sqrt{3})^2} = \frac{\sqrt{5}−\sqrt{3}}{5−3} = \frac{\sqrt{5}−\sqrt{3}}{2}$

Перевірка.

Вправа$\PageIndex{62}$

$\frac{1}{2\sqrt{3}−2}$

Вправа$\PageIndex{63}$

$\frac{6}{2\sqrt{5}−\sqrt{2}}$

Відповідь

Помножте чисельник і знаменник на$2\sqrt{5}+\sqrt{2}$. Згадаймо різницю квадратів візерунка:$(a+b)(a−b)=a^2−b^2$.

$\frac{6}{2\sqrt{5}−\sqrt{2}} = \frac{6}{2\sqrt{5}−\sqrt{2}} \cdot \frac{2\sqrt{5}+\sqrt{2}}{2\sqrt{5}+\sqrt{2}} = \frac{12\sqrt{5}+6\sqrt{2}}{(2\sqrt{5})^2−(\sqrt{2})^2}$

Продовжуючи.

$\frac{12\sqrt{5}+6\sqrt{2}}{(2\sqrt{5})^2−(\sqrt{2})^2} = \frac{12\sqrt{5}+6\sqrt{2}}{20−2} = \frac{12\sqrt{5}−6\sqrt{2}}{18}$.

Зменшити. Коефіцієнт чисельника і знаменника і скасувати.

$\frac{12\sqrt{5}−6\sqrt{2}}{18} = \frac{6(2\sqrt{5}−\sqrt{2})}{6 \cdot 3} = \frac{2\sqrt{5}−\sqrt{2}}{3}$.

Перевірка.

Вправа$\PageIndex{64}$

$\frac{9}{3\sqrt{3}−\sqrt{6}}$

Вправа$\PageIndex{65}$

$\frac{2+\sqrt{3}}{2−\sqrt{3}}$

Відповідь

Помножте чисельник і знаменник на$2+\sqrt{3}$.

$\frac{2+\sqrt{3}}{2−\sqrt{3}} = \frac{2+\sqrt{3}}{2−\sqrt{3}} \cdot \frac{2+\sqrt{3}}{2+\sqrt{3}} = \frac{(2+\sqrt{3})^2}{(2−\sqrt{3})(2−\sqrt{3})}$.

Використовуйте квадрат біноміального візерунка$(a+b)^2 = a^2+2ab+b^2$ на чисельнику і різниці квадратів візерунка$(a+b)(a−b) = a^2−b^2$ на знаменнику.

$\frac{(2+\sqrt{3})^2}{(2−\sqrt{3})(2−\sqrt{3})} = \frac{(2)^2+2(2)(\sqrt{3})+(\sqrt{3})^2}{2^2−(\sqrt{3})^2}$.

Продовжуючи.

$\frac{(2)^2+2(2)(\sqrt{3})+(\sqrt{3})^2}{2^2−(\sqrt{3})^2} = \frac{4+4\sqrt{3}+3}{4−3} = 7+4\sqrt{3}$

Перевірка.

Вправа$\PageIndex{66}$

$\frac{3−\sqrt{5}}{3+\sqrt{5}}$

Вправа$\PageIndex{67}$

$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}−\sqrt{2}}$

Відповідь

Помножте чисельник і знаменник на$\sqrt{3}+\sqrt{2}$.

$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}−\sqrt{2}} = \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}−\sqrt{2}} \cdot \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}} = \frac{(\sqrt{3}+\sqrt{2})^2}{(\sqrt{3}−\sqrt{2})(\sqrt{3}+\sqrt{2})}$.

Використовуйте квадрат біноміального візерунка$(a+b)^2 = a^2+2ab+b^2$ на чисельнику і різниці квадратів візерунка$(a+b)(a−b) = a^2−b^2$ на знаменнику.

$\frac{(\sqrt{3}+\sqrt{2})^2}{(\sqrt{3}−\sqrt{2})(\sqrt{3}+\sqrt{2})}= \frac{(\sqrt{3})^2+2(\sqrt{3})(\sqrt{2})+(\sqrt{2})^2}{(\sqrt{3})^2−(\sqrt{2})^2}$.

Продовжуючи.

$\frac{(\sqrt{3})^2+2(\sqrt{3})(\sqrt{2})+(\sqrt{2})^2}{(\sqrt{3})^2−(\sqrt{2})^2} = \frac{3+2\sqrt{6}+2}{3−2} = 5+2\sqrt{6}$

Перевірка.

Вправа$\PageIndex{68}$

$\frac{2\sqrt{3}+\sqrt{2}}{\sqrt{3}−\sqrt{2}}$

У вправах 69 - 76 використовуйте квадратичну формулу для пошуку розв'язків заданого рівняння. Розмістіть свої рішення в простій радикальній формі і зведіть свої рішення до найнижчих термінів.

Вправа$\PageIndex{69}$

$3x^2−8x=5$

Відповідь

Рівняння нелінійне, тому зробіть одну сторону нулем.

$3x^2−8x−5=0$

Порівняйте$3x^2−8x−5 = 0$ з$ax^2+bx+c = 0$ і зверніть увагу, що a = 3, b = −8, а c = −5. Запишіть квадратичну формулу і підставляйте.

$x = \frac{−b \pm \sqrt{b^2−4ac}}{2a} = \frac{−(−8) \pm \sqrt{��(−8)^2 −4(3)(−5)}}{2(3)} = \frac{8 \pm \sqrt{124}}{6}$

Фактор досконалий квадрат від радикала в чисельнику.

$x = \frac{8 \pm \sqrt{4}\sqrt{31}}{6} = \frac{8 \pm 2\sqrt{31}}{6}$

Фактор чисельника і скасування.

$x = \frac{8 \pm 2\sqrt{31}}{6} = \frac{2(4 \pm \sqrt{31})}{2 \cdot 3} = \frac{4 \pm \sqrt{31}}{3}$

Вправа$\PageIndex{70}$

$5x^2−2x=1$

Вправа$\PageIndex{71}$

$5x^2=2x+1$

Відповідь

Рівняння нелінійне, тому зробіть одну сторону нулем.

$5x^2−2x−1=0$

Порівняйте$5x^2−2x−1 = 0$ з$ax^2+bx+c = 0$ і зверніть увагу, що a = 5, b = −2, а c = −1. Запишіть квадратичну формулу і підставляйте.

$x = \frac{−b \pm \sqrt{b^2−4ac}}{2a} = \frac{−(−2) \pm \sqrt{��(−2)^2 −4(5)(−1)}}{2(5)} = \frac{2 \pm \sqrt{24}}{10}$

Фактор досконалий квадрат від радикала в чисельнику.

$x = \frac{2 \pm \sqrt{4}\sqrt{6}}{10} = \frac{2 \pm 2\sqrt{6}}{10}$

Фактор чисельника і скасування.

$x = \frac{2 \pm 2\sqrt{6}}{10} = \frac{2(1 \pm \sqrt{6})}{2 \cdot 5} = \frac{1 \pm \sqrt{6}}{5}$

Вправа$\PageIndex{72}$

$3x^2−2x=11$

Вправа$\PageIndex{73}$

$7x^2=6x+2$

Відповідь

Рівняння нелінійне, тому зробіть одну сторону нулем.

$7x^2−6x−2=0$

Порівняйте$7x^2−6x−2 = 0$ з$ax^2+bx+c = 0$ і зверніть увагу, що a = 7, b = −6, а c = −2. Запишіть квадратичну формулу і підставляйте.

$x = \frac{−b \pm \sqrt{b^2−4ac}}{2a} = \frac{−(−6) \pm \sqrt{��(−6)^2 −4(7)(−2)}}{2(7)} = \frac{6 \pm \sqrt{92}}{14}$

Фактор досконалий квадрат від радикала в чисельнику.

$x = \frac{6 \pm \sqrt{4}\sqrt{23}}{14} = \frac{6 \pm 2\sqrt{23}}{14}$

Фактор чисельника і скасування.

$x = \frac{6 \pm 2\sqrt{23}}{14} = \frac{2(3 \pm \sqrt{23})}{2 \cdot 7} = \frac{6 \pm \sqrt{23}}{7}$

Вправа$\PageIndex{74}$

$11x^2+6x=4$

Вправа$\PageIndex{75}$

$x^2=2x+19$

Відповідь

Рівняння нелінійне, тому зробіть одну сторону нулем.

$x^2−2x−19=0$

Порівняйте$x^2−2x−19 = 0$ з$ax^2+bx+c = 0$ і зверніть увагу, що a = 1, b = −2, а c = −19. Запишіть квадратичну формулу і підставляйте.

$x = \frac{−b \pm \sqrt{b^2−4ac}}{2a} = \frac{−(−2) \pm \sqrt{��(−2)^2 −4(1)(−19)}}{2(1)} = \frac{2 \pm \sqrt{80}}{2}$

Фактор досконалий квадрат від радикала в чисельнику.

$x = \frac{2 \pm \sqrt{16}\sqrt{5}}{2} = \frac{2 \pm 4\sqrt{5}}{2}$

Фактор чисельника і скасування.

$x = \frac{2 \pm 4\sqrt{5}}{2} = \frac{2(1 \pm 2\sqrt{5})}{2 \cdot 1} = 1 \pm 2\sqrt{5}$

Вправа$\PageIndex{76}$

$100x^2=40x−1$

У Вправах 77 - 80 ми призупинимо звичне правило, що слід раціоналізувати знаменник. Замість цього, тільки цей раз, раціоналізувати чисельник результуючого виразу.

Вправа$\PageIndex{77}$

Дано$f(x) = \sqrt{x}$, оцініть вираз$\frac{f(x)−f(2)}{x−2}$, а потім «раціоналізуйте чисельник».

Відповідь

Якщо$f(x) = \sqrt{x}$, то

$\frac{f(x)−f(2)}{x−2} = \frac{\sqrt{x}−\sqrt{2}}{x−2}$.

Щоб «раціоналізувати чисельник», помножте чисельник і знаменник на$\sqrt{x}+\sqrt{2}$, а потім використовуйте шаблон різниці квадратів для спрощення.

$\frac{\sqrt{x}−\sqrt{2}}{x−2} = \frac{\sqrt{x}−\sqrt{2}}{x−2} \cdot \frac{\sqrt{x}+\sqrt{2}}{\sqrt{x}+\sqrt{2}} = \frac{(\sqrt{x})^2−(\sqrt{2})^2}{(x−2)(\sqrt{x}+\sqrt{2})} = \frac{x−2}{(x−2)(\sqrt{x}+\sqrt{2})}$

Чисельник і знаменник враховуються, так що ми можемо скасувати,

$\frac{x−2}{(x−2)(\sqrt{x}+\sqrt{2})} = \frac{1}{\sqrt{x}+\sqrt{2}}$,

за умови, звичайно, що$x \ne 2$.

Вправа$\PageIndex{78}$

Дано$f(x) = \sqrt{x+2}$, оцініть вираз$\frac{f(x)−f(3)}{x−3}$, а потім «раціоналізуйте чисельник».

Вправа$\PageIndex{79}$

Дано$f(x) = \sqrt{x}$, оцініть вираз$\frac{f(x+h)−f(x)}{h}$, а потім «раціоналізуйте чисельник».

Відповідь

Якщо$f(x) = \sqrt{x}$, то

$\frac{f(x+h)−f(x)}{h} = \frac{\sqrt{x+h}−\sqrt{x}}{h}$

Щоб «раціоналізувати чисельник», помножте чисельник і знаменник на$\sqrt{x+h}+\sqrt{x}$, а потім використовуйте шаблон різниці квадратів для спрощення.

$\frac{\sqrt{x+h}−\sqrt{x}}{h} = \frac{\sqrt{x+h}−\sqrt{x}}{h} \cdot \frac{\sqrt{x+h}+\sqrt{x}}{\sqrt{x+h}+\sqrt{x}} = \frac{(\sqrt{x+h})^2−(\sqrt{x})^2}{h(\sqrt{x+h}+\sqrt{x})} = \frac{x+h−x}{h(\sqrt{x+h}+\sqrt{x})}$

Спростити, а потім скасувати.

$\frac{x+h−x}{h(\sqrt{x+h}+\sqrt{x})} = \frac{h}{h(\sqrt{x+h}+\sqrt{x})} = \frac{1}{\sqrt{x+h}+\sqrt{x}}$

Результат дійсний за умови$h \ne 0$.

Вправа$\PageIndex{80}$

Дано$f(x) = \sqrt{x−3}$, оцініть вираз$\frac{f(x+h)−f(x)}{h}$, а потім «раціоналізуйте чисельник».