9.3: Властивості поділу радикалів

Кожне з рівнянь\(x^2 = a\)\(x^2 = b\) має унікальне додатне рішення,\(x = \sqrt{a}\) і, відповідно\(x =\sqrt{b}\), передбачені\(a\) і\(b\) є додатними дійсними числами. Далі, оскільки вони є розв'язками, їх можна підставити в рівняння\(x^2 = a\) і\(x^2 = b\) отримати результати

\((\sqrt{a})^2 = a\)і\((\sqrt{b})^2 =b\),

відповідно. Ці результати залежать від того, що a і b є додатними дійсними числами.

Аналогічно рівняння

\[x^2 = \frac{a}{b} \nonumber\]

має унікальне позитивне рішення

\[x = \sqrt{\frac{a}{b}} \nonumber\]

передбачені\(a\) і\(b\) є додатними дійсними числами. Однак зауважте, що

\[\left(\frac{\sqrt{a}}{\sqrt{b}}\right)^2 = \frac{(\sqrt{a})^2}{(\sqrt{b})^2} = \frac{a}{b}, \nonumber \]

прийняття другого\(\frac{\sqrt{a}}{\sqrt{b}}\) позитивного рішення\(x^2 = \frac{a}{b}\). Однак, оскільки\(\sqrt{\frac{a}{b}}\) є унікальним позитивним рішенням\(x^2 = \frac{a}{b}\), це змушує

\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \nonumber\]

Ця дискусія призводить нас до наступного властивості радикалів.

Нерухомість 1

\(b\)Дозволяти\(a\) і бути позитивними дійсними числами. Потім,

\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\]

Цей результат можна використовувати двома чітко різними способами.

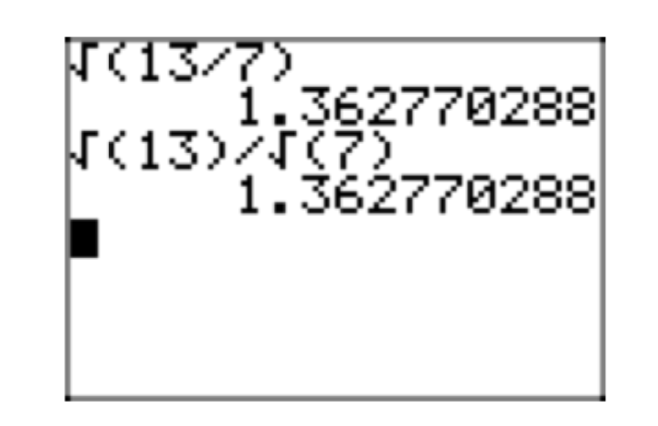
• Ви можете використовувати результат для поділу двох квадратних коренів, як в\[\frac{\sqrt{13}}{\sqrt{7}} = \sqrt{\frac{13}{7}} \nonumber\]
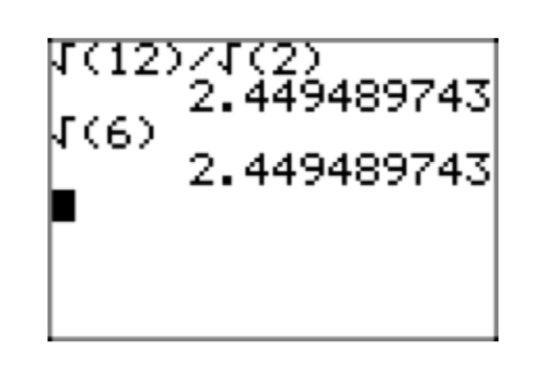
• Ви також можете використовувати результат, щоб взяти квадратний корінь дробу. Просто візьміть квадратний корінь як чисельника, так і знаменника, як в\[\sqrt{\frac{13}{7}} = \frac{\sqrt{13}}{\sqrt{7}} \nonumber\]

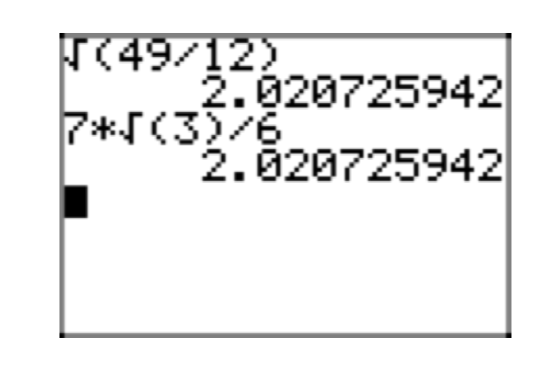
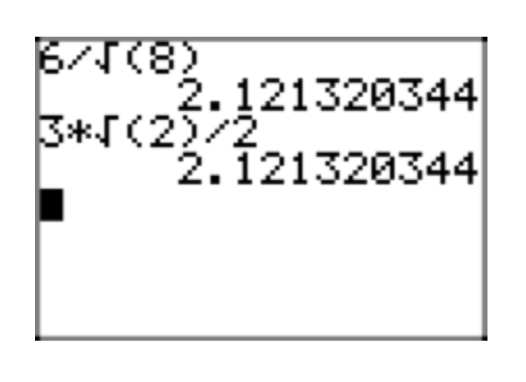
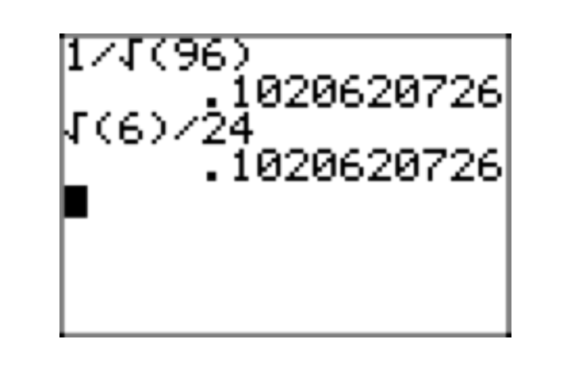
Цікаво перевірити ці результати на калькуляторі, як показано на малюнку 1.

Малюнок 1. Перевіряючи це\(\sqrt{\frac{13}{7}} = \frac{\sqrt{13}}{\sqrt{7}}\)

Проста радикальна форма Продовження

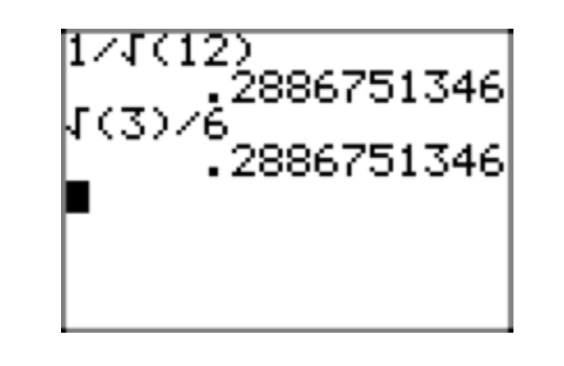
Девід і Марта знову працюють над домашньою проблемою. Марта отримує рішення\(\sqrt{\frac{1}{12}}\), але рішення Девіда, здавалося б, інше.\(\frac{1}{(2\sqrt{3})}\) Вивчивши свій урок в більш ранньому завданні, вони використовують свої калькулятори для пошуку десяткових наближень своїх розв'язків. Наближення Марти показано на малюнку 2 (а), а наближення Давида показано на малюнку 2 (b).

Малюнок 2. Порівняння Марти\(\sqrt{\frac{1}{12}}\) з Девідом\(\frac{1}{(2\sqrt{3})}\)

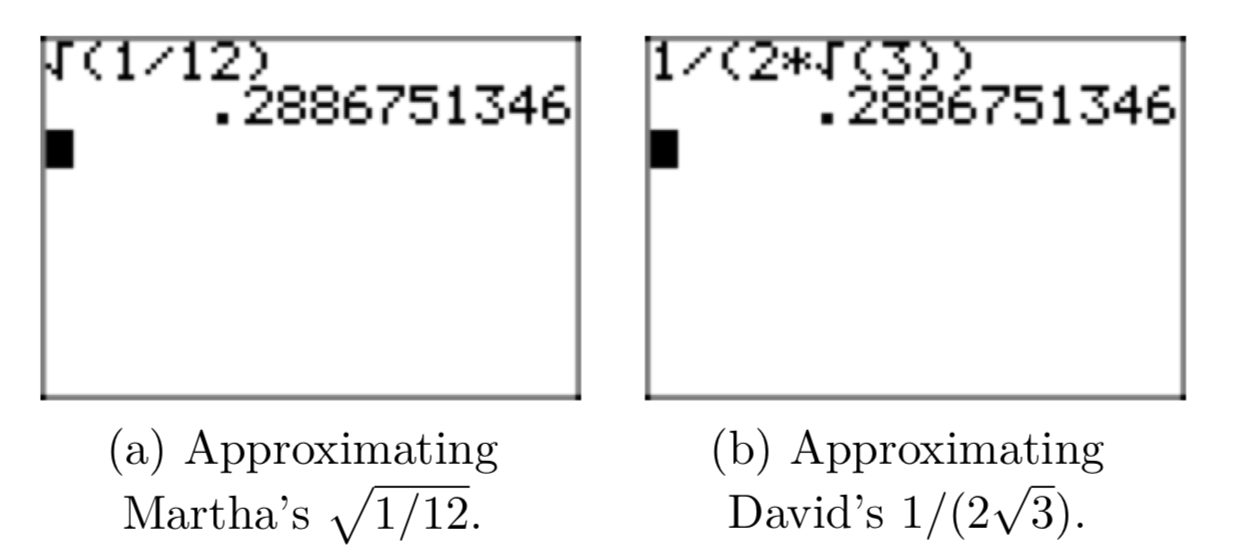
Марта знаходить це,\(\sqrt{\frac{1}{12}} \approx 0.2886751346\) і Девід знаходить це\(\frac{1}{(2\sqrt{3})} \approx 0.2886751346\). Вони роблять висновок, що їхні відповіді збігаються, але вони хочуть знати, чому такі різні відповіді однакові.

Наступний розрахунок показує, чому результат Марти ідентичний Давидові. По-перше, використовуйте властивість ділення радикалів (Property 1), щоб взяти квадратний корінь як чисельника, так і знаменника.

\[\sqrt{\frac{1}{12}} = \frac{\sqrt{1}}{\sqrt{12}} = \frac{1}{\sqrt{12}}\]

Далі використовуйте «перший орієнтир для простої радикальної форми» і введіть ідеальний квадрат від знаменника.

\[\frac{1}{\sqrt{12}} = \frac{1}{\sqrt{4}\sqrt{3}} = \frac{1}{2\sqrt{3}}\]

Це наочно демонструє, що рішення Девіда і Марти ідентичні.

Дійсно, існують інші можливі форми для вирішення домашньої роботи Девіда та Марти. Почніть з розв'язку Марти, потім помножте чисельник і деномінатор дробу під радикалом на 3.

\[\sqrt{\frac{1}{12}} = \sqrt{\frac{1}{12} \cdot \frac{3}{3}} = \sqrt{\frac{3}{36}}\]

Тепер використовуйте властивість ділення радикалів (Property 1), взявши квадратний корінь як чисельника, так і знаменника.

\[\sqrt{\frac{3}{36}} = \frac{\sqrt{3}}{\sqrt{36}} = \frac{\sqrt{3}}{6}\]

Зауважте, що наближення наближень на\(\frac{\sqrt{3}}{6}\) малюнку 3 ідентичне наближенням Марти та Давида на рисунках 2 (а) та (b).

Малюнок 3. Знаходження наближення\(\frac{\sqrt{3}}{6}\)

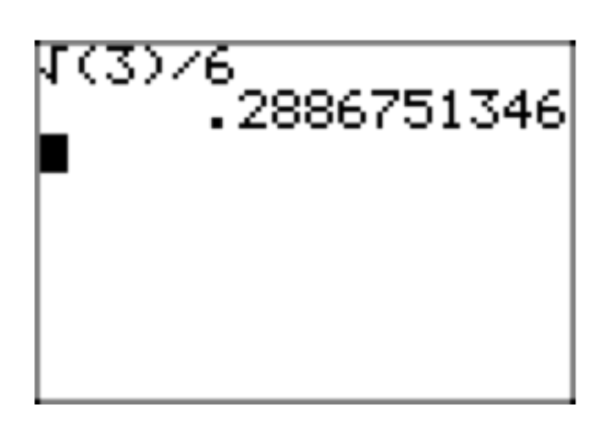
Хоча всі три форми рішення (\(\sqrt{\frac{1}{12}}\)\(\frac{1}{(2\sqrt{3})}\), і\(\frac{\sqrt{3}}{6}\)) ідентичні, дуже неприємно мати стільки форм, особливо коли ми хочемо порівняти рішення. Отже, ми змушені встановити ще два орієнтири для простої радикальної форми.

Другий орієнтир для простої радикальної форми

Не залишайте фракції під радикалом.

Таким чином, Марфа\(\sqrt{\frac{1}{12}}\) знаходиться не в простій радикальній формі, оскільки містить дріб під радикалом.

Третій орієнтир для простої радикальної форми

Не залишайте радикали в знаменнику дробу.

Таким чином, Давид\(\frac{1}{(2\sqrt{3})}\) знаходиться не в простій радикальній формі, тому що знаменник його дробу містить радикал.

Тільки еквівалентна форма\(\frac{\sqrt{3}}{6}\) підпорядковується всім трьом правилам простої радикальної форми.

1. Неможливо фактор ідеального квадрата з будь-якого радикалу у виразі\(\frac{\sqrt{3}}{6}\).
2. У виразі немає дробів під радикалом\(\frac{\sqrt{3}}{6}\).
3. Знаменник у виразі не\(\frac{\sqrt{3}}{6}\) містить радикалів.

У цьому тексті та в цьому курсі ми завжди будемо дотримуватися трьох рекомендацій щодо простої радикальної форми.

Проста радикальна форма

Коли ваша відповідь радикальний вираз:

1. Якщо є можливість, враховуйте ідеальний квадрат.
2. Не залишайте фракції під радикалом.
3. Не залишайте радикали в знаменнику дробу.

У наступних прикладах (і у вправах) корисно, якщо ви знаєте квадрати перших 25 натуральних чисел. Ми перерахували їх у полі для вас у таблиці 1 для подальшого використання.

Давайте розмістимо кілька радикальних виразів у простій радикальній формі. Ми почнемо з деяких радикальних виразів, які містять дроби під радикалом.

Приклад\(\PageIndex{2}\)

Помістіть вираз\(\sqrt{\frac{1}{8}}\) в простій радикальній формі.

Рішення

Вираз\(\sqrt{\frac{1}{8}}\) містить дріб під радикалом. Ми могли б взяти квадратний корінь як чисельник і знаменник, але це буде виробляти\(\frac{\sqrt{1}}{\sqrt{8}}\), який ставить радикал в знаменник.

Краща стратегія полягає в тому, щоб змінити форму\(\frac{1}{8}\) так, щоб у нас був ідеальний квадрат у знаменнику, перш ніж приймати квадратний корінь чисельника та знаменника. Відзначимо, що якщо помножити 8 на 2, в результаті вийде 16, ідеальний квадрат. Це сподівається, тому ми починаємо спрощення з множення чисельника і знаменника\(\frac{1}{8}\) на 2.

\(\sqrt{\frac{1}{8}} = \sqrt{\frac{1}{8} \cdot \frac{2}{2}} = \sqrt{\frac{2}{16}}\)

Тепер беремо квадратний корінь як чисельника, так і знаменника. Оскільки знаменник тепер ідеальний квадрат, результат не матиме радикала в знаменнику.

\(\sqrt{\frac{2}{16}} = \frac{\sqrt{2}}{\sqrt{16}} = \frac{\sqrt{2}}{4}\)

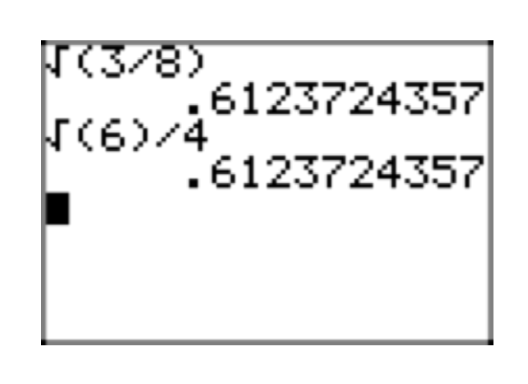
Цей останній результат,\(\frac{\sqrt{2}}{4}\) знаходиться в простій радикальній формі. Неможливо перерахувати ідеальний квадрат з будь-якого радикала, немає дробів під будь-яким радикалом, а знаменник вільний від радикалів.

Ви можете легко перевірити своє рішення за допомогою калькулятора, щоб порівняти оригінальний вираз з простою радикальною формою. На малюнку 4 (a) ми наблизили вихідний вираз,\(\sqrt{\frac{1}{8}}\). На малюнку 4 (b) ми наблизили нашу просту радикальну форму\(\frac{\sqrt{2}}{4}\). Зверніть увагу, що вони дають однакові десяткові наближення.

Малюнок 4. Порівняння\(\sqrt{\frac{1}{8}}\) і\(\frac{\sqrt{2}}{4}\)

Давайте розглянемо інший приклад.

Приклад\(\PageIndex{3}\)

Місце\(\sqrt{\frac{3}{20}}\) в простій радикальній формі.

Рішення

Слідуючи свинцю з прикладу 2, відзначимо\(5 \cdot 20 = 100\), що, ідеальний квадрат. Отже, множимо і чисельник і знаменник на 5, потім беремо квадратний корінь як чисельника, так і знаменника, як тільки у нас є ідеальний квадрат в знаменнику.

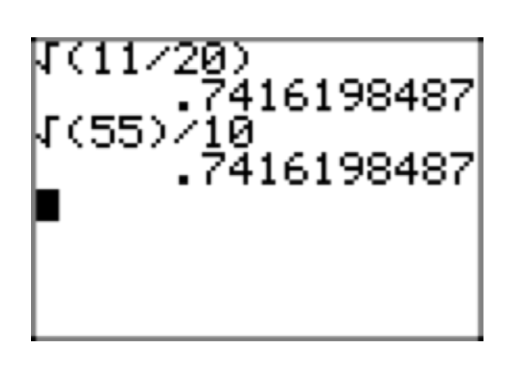
\(\sqrt{\frac{3}{20}} = \sqrt{\frac{3}{20} \cdot \frac{5}{5}} = \sqrt{\frac{15}{100}} = \frac{\sqrt{15}}{\sqrt{100}} = \frac{\sqrt{15}}{10}\)

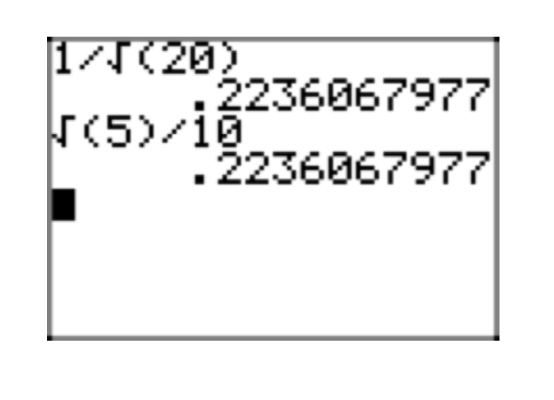
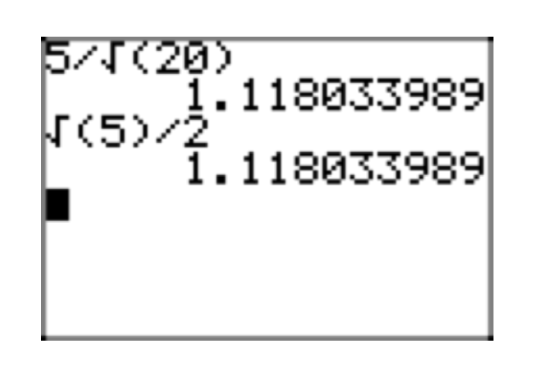
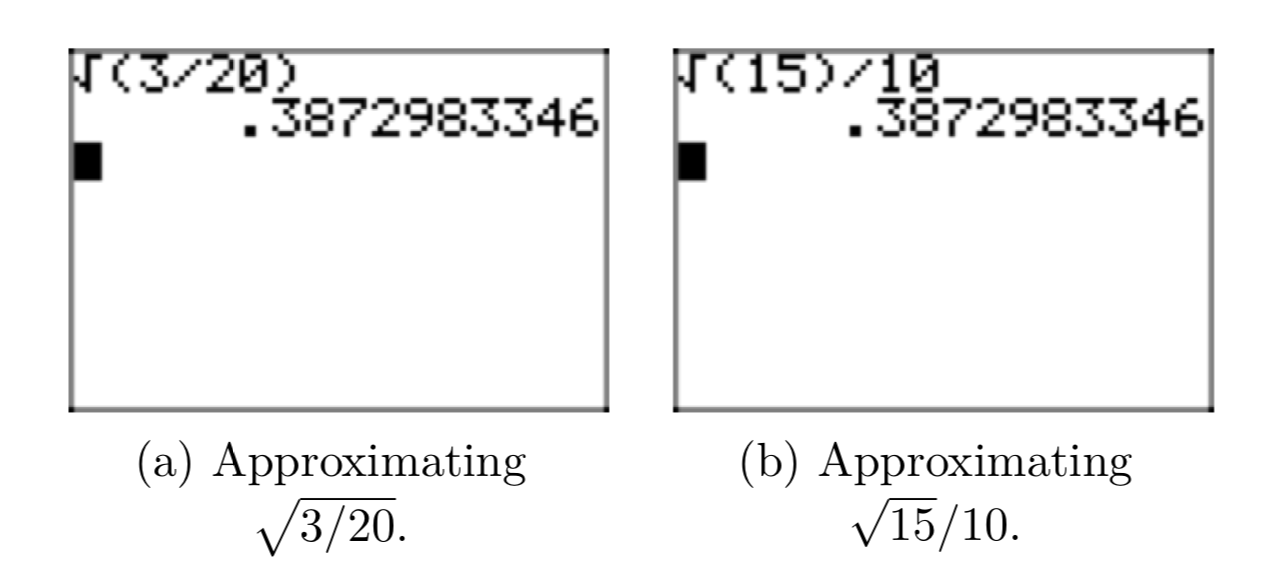
Зверніть увагу, що десяткове наближення простої радикальної форми на\(\frac{\sqrt{15}}{10}\) малюнку 5 (б) відповідає десятковому наближенню вихідного виразу на\(\frac{3}{20}\) малюнку 5 (а).

Малюнок 5. Порівняння оригіналу\(\sqrt{\frac{3}{20}}\) з простою радикальною формою\(\frac{\sqrt{15}}{10}\)

Зараз ми покажемо, як боротися з виразом, що має радикал у своєму знаменнику, але спочатку ми зробимо паузу, щоб пояснити нову термінологію.

Раціоналізація знаменника

Процес усунення радикалів із знаменника називається раціоналізацією знаменника, оскільки він призводить до дробу, де знаменник вільний від радикалів і є раціональним числом.

Вправа\(\PageIndex{4}\)

Помістіть вираз\(\frac{5}{\sqrt{18}}\) в простій радикальній формі.

Рішення

У попередніх прикладах зробити знаменник ідеальним квадратом здавалося хорошою тактикою. Ми застосовуємо ту ж тактику в цьому прикладі, зазначивши, що\(2 \cdot 18 = 36\) це ідеальний квадрат. Однак стратегія трохи інша, так як ми починаємо рішення з множення і чисельника, і знаменника на\(\sqrt{2}\).

\[\frac{5}{\sqrt{18}} = \frac{5}{\sqrt{18}} \cdot \frac{\sqrt{2}}{\sqrt{2}}\]

Тепер множимо чисельники і знаменники. У знаменнику використовується властивість множення радикалів,\(\sqrt{18}\sqrt{2} = \sqrt{36}\).

\[\frac{5}{\sqrt{18}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{5\sqrt{2}}{\sqrt{36}}\]

Стратегія тепер повинна бути зрозумілою. Тому що знаменник - це ідеальний квадрат\(\sqrt{36} = 6\), очищаючи всі радикали від знаменника нашого результату.

\[\frac{5\sqrt{2}}{\sqrt{36}} = \frac{5\sqrt{2}}{6}\]

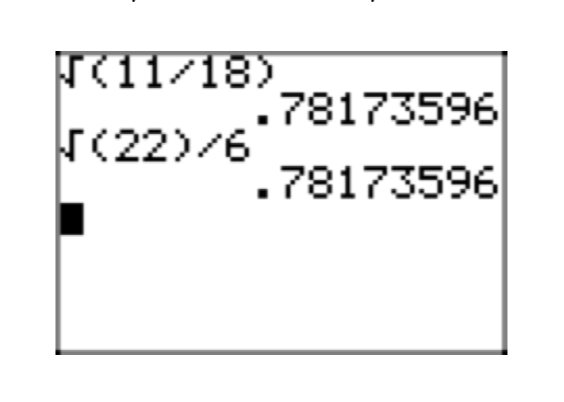
Останній результат - в простій радикальній формі. Витягти ідеальний квадратний корінь з будь-якого радикала неможливо, немає дробів під будь-яким радикалом, а знаменник вільний від радикалів.

На малюнку 6 ми порівняємо наближення для нашого вихідного виразу з\(\frac{5}{\sqrt{18}}\) нашою простою радикальною формою\(\frac{5\sqrt{2}}{6}\).

Малюнок 6. Порівняння\(\frac{5}{\sqrt{18}}\) з\(\frac{5\sqrt{2}}{6}\)

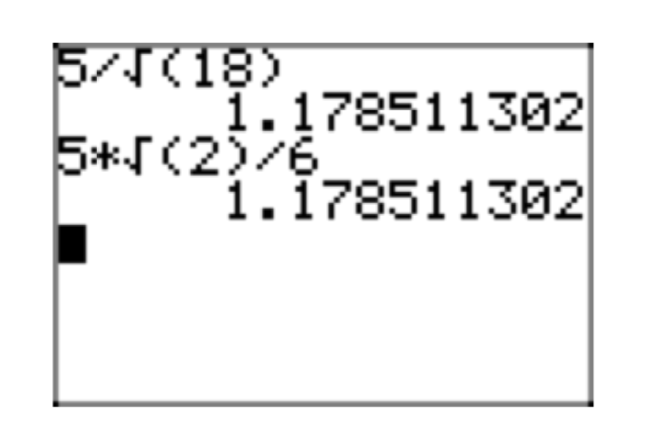
Давайте розглянемо інший приклад.

Приклад\(\PageIndex{5}\)

Помістіть вираз\(\frac{18}{\sqrt{27}}\) в простій радикальній формі.

Рішення

Зверніть увагу, що\(3 \cdot 27 = 81\) це ідеальний квадрат. Починаємо з множення і чисельника, і знаменника нашого виразу\(\sqrt{3}\).

\(\frac{18}{\sqrt{27}} = \frac{18}{\sqrt{27}} \cdot \frac{\sqrt{3}}{\sqrt{3}}\)

Множимо чисельники і знаменники. У знаменників,\(\sqrt{27}\sqrt{3} = \sqrt{81}\)

\(\frac{18}{\sqrt{27}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{18\sqrt{3}}{\sqrt{81}}\)

Звичайно\(\sqrt{81} = 9\), так

\(\frac{18\sqrt{3}}{\sqrt{81}} = \frac{18\sqrt{3}}{9}\)

Тепер ми можемо зменшити до найнижчих членів, розділивши чисельник і знаменник на 9.

\(\frac{18\sqrt{3}}{9} = 2\sqrt{3}\)

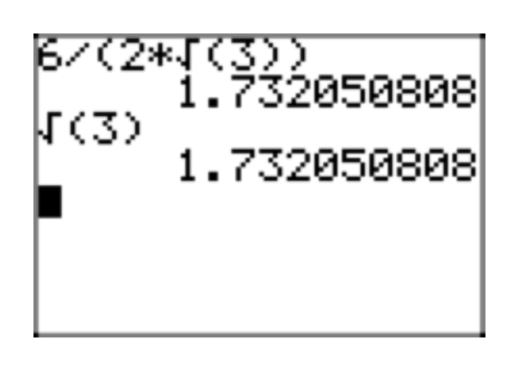
На малюнку 7 ми порівняємо наближення вихідного виразу\(\frac{18}{\sqrt{27}}\) і його простої радикальної форми\(2\sqrt{3}\).

Малюнок 7. Порівнюючи\(\frac{18}{\sqrt{27}}\) з його простою радикальною формою\(2\sqrt{3}\).

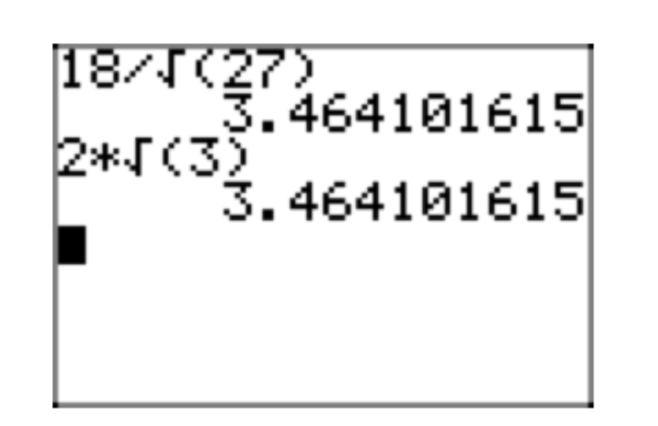
Корисні поради

У попередньому розділі ми дізналися, що якщо ви квадратично добуток експоненціальних виразів, ви помножите кожен з показників на 2.

\((2^{3}3^{4}5^{5})^2 = 2^{6}3^{8}5^{10}\)

Оскільки беручи квадратний корінь є «зворотним» квадратом, ми ділимо кожен з показників на 2.

\(\sqrt{2^{6}3^{8}5^{10}} = 2^{3}3^{4}5^{5}\)

Ми також дізналися, що просте факторизація є надзвичайно потужним інструментом, який досить корисний при розміщенні радикальних виразів у простій радикальній формі. Ми побачимо, що це ще більш вірно в цьому розділі.

Давайте розглянемо приклад.

Приклад\(\PageIndex{6}\)

Помістіть вираз\(\sqrt{\frac{1}{98}}\) в простій радикальній формі.

Рішення

Іноді буває непросто розібратися, як масштабувати знаменник, щоб отримати ідеальний квадрат, навіть якщо він забезпечений таблицею ідеальних квадратів. Це коли на допомогу може прийти просте коефіцієнт ізації і надати підказку. Отже, спочатку виражаємо знаменник як добуток простих чисел в експоненціальному вигляді:\(98 = 2 \cdot 49 = 2 \cdot 7^2\)

\(\sqrt{\frac{1}{98}} = \sqrt{\frac{1}{2 \cdot 7^2}}\)

Тепер ми можемо легко побачити, що заважає знаменнику бути ідеальним квадратом. Проблема полягає в тому, що не всі показники в знаменнику діляться на 2. Ми можемо виправити це, помноживши і чисельник, і знаменник на 2.

\(\sqrt{\frac{1}{2 \cdot 7^2}} = \sqrt{\frac{1}{2 \cdot 7^2} \cdot \frac{2}{2}} = \sqrt{\frac{2}{2^{2}7^{2}}}\)

Зверніть увагу, що кожен простий у знаменнику тепер має показник, який ділиться на 2. Тепер ми можемо взяти квадратний корінь як чисельника, так і знаменника.

\(\sqrt{\frac{2}{2^{2}7^{2}}} = \frac{\sqrt{2}}{\sqrt{2^{2}7^{2}}}\)

Візьміть квадратний корінь знаменника, розділивши кожну експоненту на 2.

\(\frac{\sqrt{2}}{\sqrt{2^{2}7^{2}}} = \frac{\sqrt{2}}{2^{1} \cdot 7^{1}}\)

Тоді, звичайно,\(2 \cdot 7 = 14\).

\(\frac{\sqrt{2}}{2 \cdot 7} = \frac{\sqrt{2}}{14}\)

На малюнку 8 зверніть увагу на те, як десяткові наближення вихідного виразу\(\sqrt{\frac{1}{98}}\) та його проста радикальна форма\(\frac{\sqrt{2}}{14}\) збігаються, що є вагомим доказом того, що ми знайшли правильну просту радикальну форму. Тобто ми не можемо взяти ідеальний квадрат з будь-якого радикала, немає дробів під будь-яким радикалом, а знаменники чисті від усіх радикалів.

Малюнок 8. Порівняння оригіналу\(\sqrt{\frac{1}{98}}\) з його простою радикальною формою\(\frac{\sqrt{2}}{14}\)

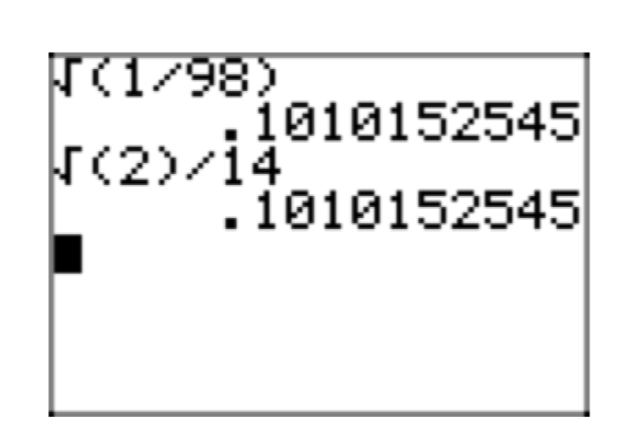
Давайте розглянемо інший приклад.

Приклад\(\PageIndex{7}\)

Помістіть вираз\(\frac{12}{\sqrt{54}}\) в простій радикальній формі.

Рішення

Простий коефіцієнт знаменника:\( 54 = 2 \cdot 27 = 2 \cdot 3^3\).

\(\frac{12}{\sqrt{54}} = \frac{12}{\sqrt{2 \cdot 3^3}}\)

Жоден простий у знаменнику не має показника, що ділиться на 2. Якби ми мали ще 2 і ще один 3, то експоненти були б ділилися б на 2. Це спонукає нас помножити і чисельник, і знаменник на\(\sqrt{2 \cdot 3}\).

\(\frac{12}{\sqrt{2 \cdot 3^3}} = \frac{12}{\sqrt{2 \cdot 3^3}} \cdot \frac{\sqrt{2 \cdot 3}}{\sqrt{2 \cdot 3}} = \frac{12\sqrt{2 \cdot 3}}{\sqrt{2^{2}3^4}}\)

Розділіть кожен з показників у знаменнику на 2.

\(\frac{12\sqrt{2 \cdot 3}}{\sqrt{2^{2}3^4}} = \frac{12\sqrt{2 \cdot 3}}{2^{1} \cdot 3^2}\)

Потім і в чисельнику\(2 \cdot 3 = 6\), і в знаменнику,\(2 \cdot 3^2 = 18\).

\(\frac{12\sqrt{2 \cdot 3}}{2 \cdot 3^{2}} = \frac{12\sqrt{6}}{18}\)

Нарешті, зведіть до найнижчих членів, розділивши як чисельник, так і знаменник на 6.

\(\frac{12\sqrt{6}}{18} = \frac{2\sqrt{6}}{3}\)

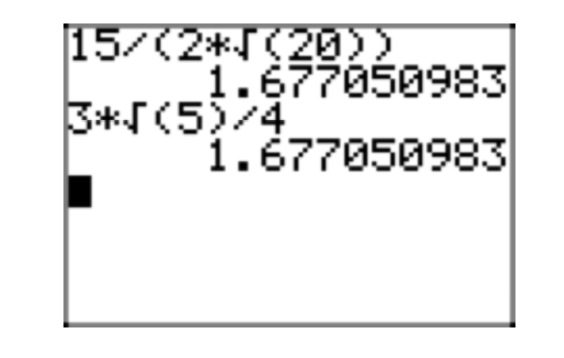
На малюнку 9 наближення вихідного виразу\(\frac{12}{\sqrt{54}}\) збігається з наближенням його простої радикальної форми\(\frac{2\sqrt{6}}{3}\)

Малюнок 9. Порівняння оригіналу\(\frac{12}{\sqrt{54}}\) з його простою радикальною формою\(\frac{2\sqrt{6}}{3}\)

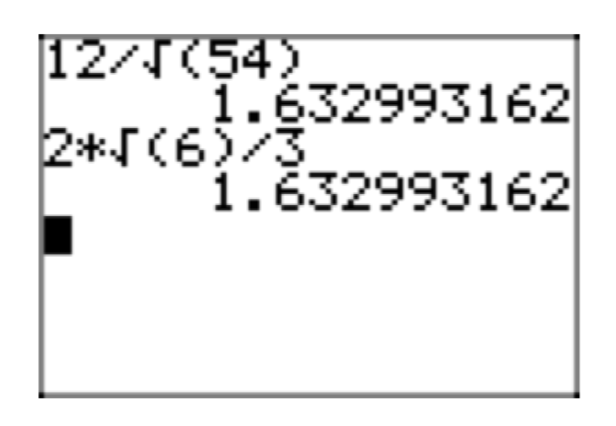
Змінні вирази

Якщо х є будь-яким дійсним числом, нагадайте ще раз, що

\[\sqrt{x^2} = |x| \nonumber \]

Якщо ми об'єднаємо закон експонентів для квадратування частки з нашою властивістю для прийняття квадратного кореня частки, ми можемо написати

\[\sqrt{(\frac{a}{b})^2} = \sqrt{\frac{a^2}{b^2}} = \frac{\sqrt{a^2}}{\sqrt{b^2}} \nonumber \]

Втім\(\sqrt{(\frac{a}{b})^2} = |\frac{a}{b}|\), поки\(\frac{\sqrt{a^2}}{\sqrt{b^2}} = \frac{|a|}{|b|}\). Ця дискусія призводить до наступного ключового результату.

Частне правило для абсолютного значення

Якщо a і b є будь-якими дійсними числами, то

\[\left|\dfrac{a}{b}\right| = \frac{|a|}{|b|} \nonumber\]

за умови\(b \ne 0\). У словах абсолютне значення частки є часткою від абсолютних значень.

Ми бачили цю властивість раніше в розділі про функцію абсолютного значення, де ми надали інший підхід до доказу властивості. Цікаво, що ми можемо довести цю властивість абсолютно по-новому, використовуючи властивості квадратного кореня. Ми побачимо, що у нас є потреба в частковому правилі для абсолютного значення в наступних прикладах.

Наприклад, якщо x є будь-яким дійсним числом, крім нуля, використовуючи часткове правило для абсолютного значення, ми могли б написати

\[\left|\dfrac{3}{x}\right| = \frac{|3|}{|x|} = \frac{3}{|x|}\nonumber\]

Однак немає ніякого способу видалити стовпчики абсолютних значень, які оточують x, якщо ми не знаємо знак x Якщо x > 0 (пам'ятайте, немає нулів у знаменнику), то |x| = x і вираз стає

\[\frac{3}{|x|} = \frac{3}{x} \nonumber \]

З іншого боку, якщо x < 0, то |x| = −x і вираз стане

\[\frac{3}{|x|} = \frac{3}{−x} = −\frac{3}{x} \nonumber\]

Давайте розглянемо інший приклад.

Приклад\(\PageIndex{8}\)

Помістіть вираз\(\sqrt{\frac{18}{x^6}}\) в простій радикальній формі. Обговоріть домен.

Рішення

Зверніть увагу, що x не може дорівнювати нулю, інакше знаменник\(\sqrt{\frac{18}{x^6}}\) буде нулем, що не допускається. Однак, чи є x позитивним чи негативним,\(x^6\) will be a positive number (raising a nonzero number to an even power always produces a positive real number), and \(\sqrt{\frac{18}{x^6}}\) is well-defined.

Маючи на увазі, що х ненульовий, але може бути позитивним або негативним, ми продовжуємо спочатку викликати властивість 1, взявши позитивний квадратний корінь як чисельника, так і знаменника нашого радикального виразу.

\[\sqrt{\frac{18}{x^6}} = \frac{\sqrt{18}}{\sqrt{x^6}} \nonumber \]

З чисельника множимо ідеальний квадрат. У знаменнику ми використовуємо бруски абсолютних значень, щоб застрахувати позитивний квадратний корінь.

\(\frac{\sqrt{18}}{\sqrt{x^6}} = \frac{\sqrt{9}\sqrt{2}}{|x^3|} = \frac{3\sqrt{2}}{|x^3|}\)

Ми можемо використовувати Правило продукту для абсолютного значення для запису\(|x^3| = |x^2||x| = x^{2}|x|\). Зауважте, що нам не потрібно обертати\(x^2\) в абсолютні бари, оскільки\(x^2\) це вже позитивне значення.

\[\frac{3\sqrt{2}}{|x^3|} = \frac{3\sqrt{2}}{x^{2}|x|} \nonumber \]

Оскільки x може бути позитивним або негативним, ми не можемо видалити стовпчики абсолютних значень навколо x.

Давайте розглянемо інший приклад.

Приклад\(\PageIndex{9}\)

Помістіть вираз\(\sqrt{\frac{12}{x^5}}\) в простій радикальній формі. Обговоріть домен.

Рішення

Зверніть увагу, що x не може дорівнювати нулю, інакше знаменник\(\sqrt{\frac{12}{x^5}}\) буде нулем, що не допускається. Далі, якщо x є від'ємним числом, то також\(x^5\) буде від'ємним числом (підвищення негативного числа до непарної потужності дає негативне число). Якби x були від'ємними, то також\(\frac{12}{x^5}\) було\(\sqrt{\frac{12}{x^5}}\) б від'ємним і було б невизначено (ви не можете взяти квадратний корінь від'ємного числа). Таким чином, x має бути додатним дійсним числом або\(\sqrt{\frac{12}{x^5}}\) вираз невизначений.

Продовжуємо, маючи на увазі, що\(x\) це позитивне дійсне число. Один з можливих підходів полягає в тому, щоб спочатку відзначити, що інший коефіцієнт x потрібен, щоб зробити знаменник ідеальним квадратом. Це мотивує нас множити як чисельник, так і знаменник всередині радикала на\(x\).

\[\sqrt{\frac{12}{x^5}} = \sqrt{\frac{12}{x^5} \cdot \frac{x}{x}} = \sqrt{\frac{12x}{x^6}} \nonumber\]

Тепер ми можемо використовувати властивість 1, щоб взяти квадратний корінь як чисельника, так і знаменника.

\[\sqrt{\frac{12x}{x^6}} = \frac{\sqrt{12x}}{\sqrt{x^6}} \nonumber\]

У чисельнику ми враховуємо ідеальний квадрат. У знаменнику бари абсолютних значень застрахували б позитивний квадратний корінь. Однак ми заявили, що х повинен бути додатним числом,\(x^3\) тому вже позитивні та абсолютні бари значення не потрібні.

\[\frac{\sqrt{12x}}{\sqrt{x^6}} = \frac{\sqrt{4}\sqrt{3x}}{x^3} = \frac{2\sqrt{3x}}{x^3} \nonumber\]

Давайте розглянемо інший приклад.

Приклад\(\PageIndex{10}\)

Враховуючи, що x < 0, місце\(\sqrt{\frac{27}{x^{10}}}\) в простій радикальній формі.

Рішення

Одним з можливих підходів було б врахувати ідеальний квадрат і написати

\[\sqrt{\frac{27}{x^{10}}} = \sqrt{\frac{9}{x^{10}} \cdot \sqrt{3}} = \sqrt{(\frac{3}{x^5})^2}\sqrt{3} = |\frac{3}{x^5}|\sqrt{3}.\]

Тепер\(|\frac{3}{x^5}| = \frac{|3|}{(|x^4||x|} = \frac{3}{x^{4}|x|}\), з тих пір\(x^4 > 0\). Таким чином,

\[|\frac{3}{x^5}|\sqrt{3} = \frac{3}{x^{4}|4|}\sqrt{3}. \nonumber \]

Однак ми маємо, що x < 0, тому |x| = −x і ми можемо записати

\[\frac{3}{x^{4}|x|}\sqrt{3} = \frac{3}{x^{4}|x|}\sqrt{3} = \frac{3}{x^{4}(−x)}\sqrt{3} = −\frac{3}{x^5}\sqrt{3}\]

Ми можемо перейти\(\sqrt{3}\) в чисельник і написати

\[−\frac{3}{x^5}\sqrt{3} = −\frac{3\sqrt{3}}{x^5}.\]

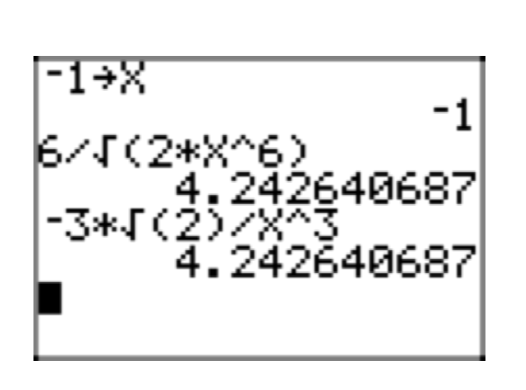
Знову ж таки, це повчально перевірити достовірність цього результату за допомогою графічного калькулятора. Імовірно, результат вірний для всіх значень x < 0. Отже, зберігайте −1 у x, потім введіть вихідний вираз та його просту радикальну форму, потім порівняйте наближення, як показано на малюнках 10 (a), (b) та (c).

Малюнок 10. Порівняння вихідного виразу та його простої радикальної форми при x = −1.

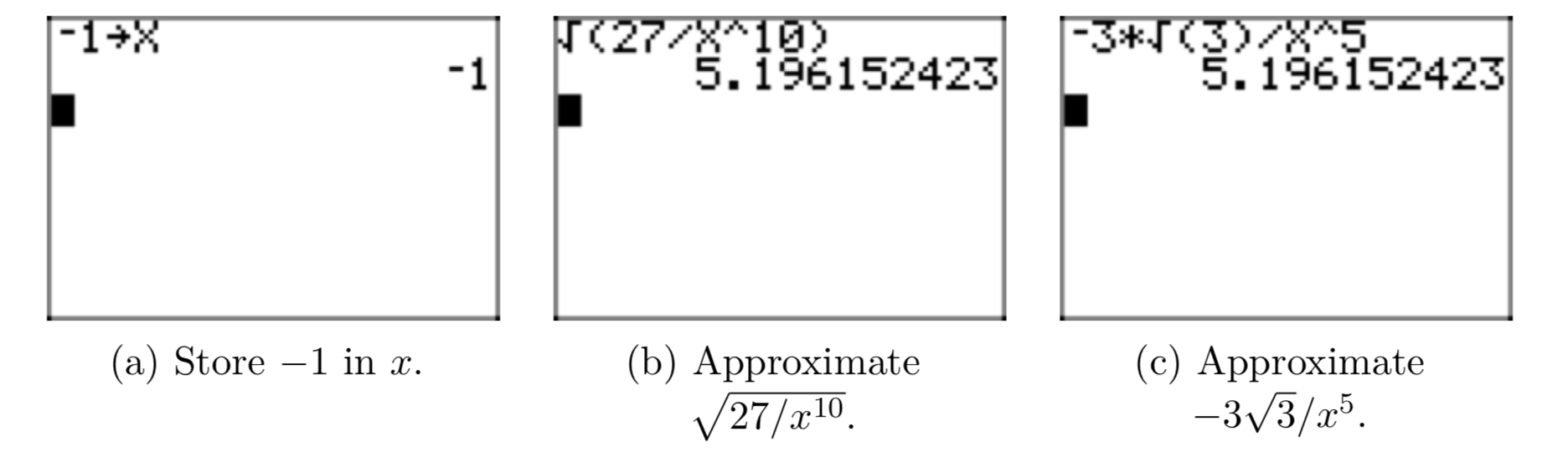
Альтернативний підхід. Трохи інший підхід знову почнеться з взяття квадратного кореня як чисельника, так і знаменника.

\(\sqrt{\frac{27}{x^{10}}} = \frac{\sqrt{27}}{\sqrt{x^{10}}}\)

Тепер,\(\sqrt{27} = \sqrt{9}\sqrt{3} = 3\sqrt{3}\) і ми застрахуємо, що\(\sqrt{x^{10}}\) виробляє додатне число за допомогою абсолютних значень барів. Тобто,\(\sqrt{x^{10}} = |x^5|\) і

\(\frac{\sqrt{27}}{\sqrt{x^{10}}} = \frac{3\sqrt{3}}{|x^5|}\)

Однак, використовуючи правило продукту для абсолютного значення і той факт\(x^4 > 0\), що,\(|x^5| =|x^4||x| = x^{4}|x|\) і

\(\frac{3\sqrt{3}}{|x^5|} = \frac{3\sqrt{3}}{x^{4}|x|}\)

Нарешті, ми маємо, що x < 0, тому |x| = −x і ми можемо записати

\(\frac{3\sqrt{3}}{x^{4}|x|} = \frac{3\sqrt{3}}{x^{4}(−x)} = −\frac{3\sqrt{3}}{x^5}\).

Вправа\(\PageIndex{11}\)

Використовуйте калькулятор, щоб спочатку наблизити\(\frac{\sqrt{5}}{\sqrt{2}}\). На цьому ж екрані приблизний\(\sqrt{\frac{5}{2}}\). Повідомте про результати на домашній папері.

Відповідь

Обидва\(\frac{\sqrt{5}}{\sqrt{2}} = \sqrt{\frac{5}{2}} \approx = 1.58113883\)

Вправа\(\PageIndex{2}\)

Використовуйте калькулятор, щоб спочатку наблизити\(\frac{\sqrt{7}}{\sqrt{5}}\). На цьому ж екрані приблизний\(\sqrt{\frac{7}{5}}\). Повідомте про результати на домашній папері.

Вправа\(\PageIndex{3}\)

Використовуйте калькулятор, щоб спочатку наблизити\(\frac{\sqrt{12}}{\sqrt{2}}\). На цьому ж екрані приблизний\(\sqrt{6}\). Повідомте про результати на домашній папері.

Відповідь

Обидва\(\frac{\sqrt{12}}{\sqrt{2}} = \sqrt{6} \approx 2.449489743\).

Вправа\(\PageIndex{4}\)

Використовуйте калькулятор, щоб спочатку наблизити\(\frac{\sqrt{15}}{\sqrt{5}}\). На цьому ж екрані приблизний\(\sqrt{3}\). Повідомте про результати на домашній папері.

У вправах 5 - 16 помістіть кожне радикальне вираз в просту радикальну форму. Як і в прикладі 2 в розповіді, перевірте свій результат за допомогою калькулятора.

Вправа\(\PageIndex{5}\)

\(\sqrt{\frac{3}{8}}\)

Відповідь

\(\sqrt{\frac{3}{8}} = \sqrt{\frac{3}{8} \cdot \frac{2}{2}} = \sqrt{\frac{6}{16}} = \frac{\sqrt{6}}{4}\)

Вправа\(\PageIndex{6}\)

\(\sqrt{\frac{5}{12}}\)

Вправа\(\PageIndex{7}\)

\(\sqrt{\frac{11}{20}}\)

Відповідь

\(\sqrt{\frac{11}{20}} = \sqrt{\frac{11}{20} \cdot \frac{5}{5}} = \sqrt{\frac{55}{100}} = \frac{\sqrt{55}}{10}\)

Вправа\(\PageIndex{8}\)

\(\sqrt{\frac{3}{2}}\)

Вправа\(\PageIndex{9}\)

\(\sqrt{\frac{11}{18}}\)

Відповідь

\(\sqrt{\frac{11}{18}} = \sqrt{\frac{11}{18} \cdot \frac{2}{2}} = \sqrt{\frac{22}{36}} = \frac{\sqrt{22}}{6}\)

Вправа\(\PageIndex{10}\)

\(\sqrt{\frac{7}{5}}\)

Вправа\(\PageIndex{11}\)

\(\sqrt{\frac{4}{3}}\)

Відповідь

\(\sqrt{\frac{4}{3}} = \sqrt{\frac{4}{3} \cdot \frac{3}{3}} = \sqrt{\frac{12}{9}} = \frac{\sqrt{3}\sqrt{4}}{3}\)

Вправа\(\PageIndex{12}\)

\(\sqrt{\frac{16}{5}}\)

Вправа\(\PageIndex{13}\)

\(\sqrt{\frac{49}{12}}\)

Відповідь

\(\sqrt{\frac{49}{12}} = \sqrt{\frac{49}{12} \cdot \frac{3}{3}} = \sqrt{\frac{49 \cdot 3}{36}} = \frac{\sqrt{49}\sqrt{3}}{6} = \frac{7\sqrt{3}}{6}\)

Вправа\(\PageIndex{14}\)

\(\sqrt{\frac{81}{20}}\)

Вправа\(\PageIndex{15}\)

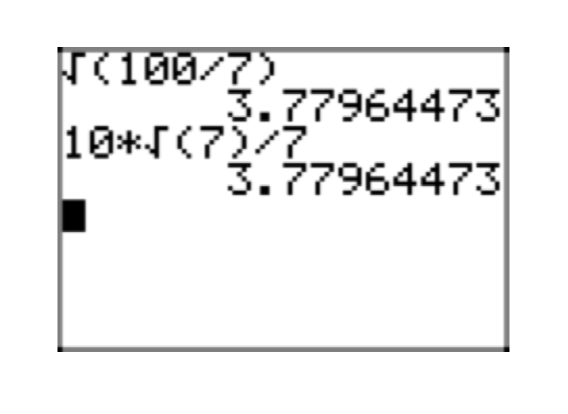
\(\sqrt{\frac{100}{7}}\)

Відповідь

\(\sqrt{\frac{100}{7}} = \sqrt{\frac{100}{7} \cdot \frac{7}{7}} = \sqrt{\frac{100 \cdot 7}{49}} = \frac{\sqrt{100}\sqrt{7}}{7} = \frac{10\sqrt{7}}{7}\)

Вправа\(\PageIndex{16}\)

\(\sqrt{\frac{36}{5}}\)

У вправах 17 - 28 помістіть кожне радикальне вираз в просту радикальну форму. Як і в прикладі 4 в оповіданні, перевірте свій результат за допомогою калькулятора.

Вправа\(\PageIndex{17}\)

\(\frac{1}{\sqrt{12}}\)

Відповідь

\(\frac{1}{\sqrt{12}} = \frac{1}{\sqrt{12}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{\sqrt{36}} = \frac{\sqrt{3}}{6}\)

Вправа\(\PageIndex{18}\)

\(\frac{1}{\sqrt{8}}\)

Вправа\(\PageIndex{19}\)

\(\frac{1}{\sqrt{20}}\)

Відповідь

\(\frac{1}{\sqrt{20}} = \frac{1}{\sqrt{20}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{\sqrt{5}}{\sqrt{100}} = \frac{\sqrt{5}}{10}\)

Вправа\(\PageIndex{20}\)

\(\frac{1}{\sqrt{27}}\)

Вправа\(\PageIndex{21}\)

\(\frac{6}{\sqrt{8}}\)

Відповідь

\(\frac{6}{\sqrt{8}} = \frac{6}{\sqrt{8}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{6\sqrt{2}}{\sqrt{16}} = \frac{6\sqrt{2}}{4} = \frac{3\sqrt{2}}{2}\)

Вправа\(\PageIndex{22}\)

\(\frac{4}{\sqrt{12}}\)

Вправа\(\PageIndex{23}\)

\(\frac{5}{\sqrt{20}}\)

Відповідь

\(\frac{5}{\sqrt{20}} = \frac{5}{\sqrt{20}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{5\sqrt{5}}{\sqrt{100}} = \frac{5\sqrt{5}}{10} = \frac{\sqrt{5}}{2}\)

Вправа\(\PageIndex{24}\)

\(\frac{9}{\sqrt{27}}\)

Вправа\(\PageIndex{25}\)

\(\frac{6}{2\sqrt{3}}\)

Відповідь

\(\frac{6}{2\sqrt{3}} = \frac{6}{2\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{6\sqrt{3}}{2\sqrt{9}} =\frac{6\sqrt{3}}{6} = \sqrt{3}\)

Вправа\(\PageIndex{26}\)

\(\frac{10}{3\sqrt{5}}\)

Вправа\(\PageIndex{27}\)

\(\frac{15}{2\sqrt{20}}\)

Відповідь

\(\frac{15}{2\sqrt{20}} = \frac{15}{2\sqrt{20}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{15\sqrt{5}}{2\sqrt{100}} = \frac{15\sqrt{5}}{20} = \frac{3\sqrt{5}}{4}\)

Вправа\(\PageIndex{28}\)

\(\frac{3}{2\sqrt{18}}\)

У вправах 29 - 36 помістіть дане радикальний вираз в простій формі. Використовуйте просту факторизацію, як у прикладі 8 в розповіді, щоб допомогти вам у розрахунках. Як і в прикладі 6, перевірте результат за допомогою калькулятора.

Вправа\(\PageIndex{29}\)

\(\frac{1}{\sqrt{96}}\)

Відповідь

\(\frac{1}{\sqrt{96}} = \frac{1}{\sqrt{2^5 \cdot 3}} = \frac{1}{\sqrt{2^5 \cdot 3}} \cdot \frac{\sqrt{2 \cdot 3}}{\sqrt{2 \cdot 3}} = \frac{\sqrt{2 \cdot 3}}{2^6 \cdot 3^2} = \frac{\sqrt{2 \cdot 3}}{2^3 \cdot 3} = \frac{\sqrt{6}}{24}\)

Вправа\(\PageIndex{30}\)

\(\frac{1}{\sqrt{432}}\)

Вправа\(\PageIndex{31}\)

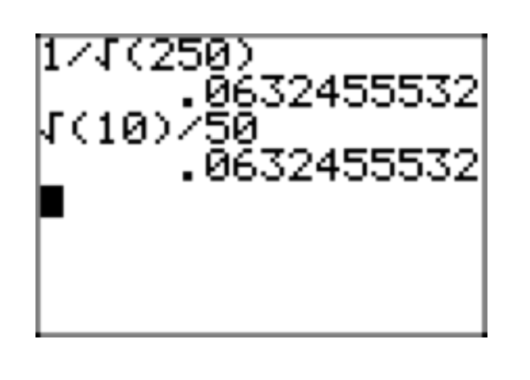
\(\frac{1}{\sqrt{250}}\)

Відповідь

\(\frac{1}{\sqrt{250}} = \frac{1}{\sqrt{2 \cdot 5^3}} = \frac{1}{\sqrt{2 \cdot 5^3}} \cdot \frac{\sqrt{2 \cdot 5}}{\sqrt{2 \cdot 5}} = \frac{\sqrt{2 \cdot 5}}{2^2 \cdot 5^4} = \frac{\sqrt{2 \cdot 5}}{2 \cdot 5^2} = \frac{\sqrt{10}}{50}\)

Вправа\(\PageIndex{32}\)

\(\frac{1}{\sqrt{108}}\)

Вправа\(\PageIndex{33}\)

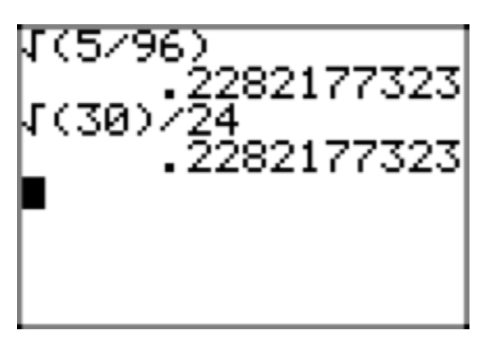
\(\sqrt{\frac{5}{96}}\)

Відповідь

\(\sqrt{\frac{5}{96}} = \sqrt{\frac{5}{2^5 \cdot 3}} = \sqrt{\frac{5}{2^5 \cdot 3} \cdot \frac{2 \cdot 3}{2 \cdot 3}} = \sqrt{\frac{2 \cdot 3 \cdot 5}{2^6 \cdot 3^2}} = \frac{\sqrt{2 \cdot 3 \cdot 5}}{2^3 \cdot 3} = \frac{\sqrt{30}}{24}\)

Вправа\(\PageIndex{34}\)

\(\sqrt{\frac{2}{135}}\)

Вправа\(\PageIndex{35}\)

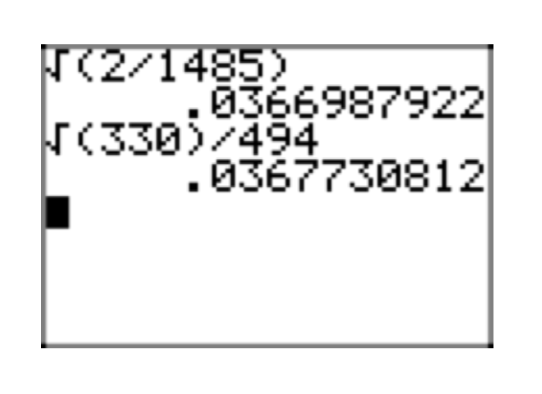
\(\sqrt{\frac{2}{1485}}\)

Відповідь

\(\sqrt{\frac{2}{1485}} = \sqrt{\frac{2}{3^3 \cdot 5 \cdot 11}} = \sqrt{\frac{2}{3^3 \cdot 5 \cdot 11} \cdot \frac{3 \cdot 5 \cdot 11}{3 \cdot 5 \cdot 11}} = \sqrt{\frac{2 \cdot 3 \cdot 5 \cdot 11}{3^4 \cdot 5^2 \cdot 11^2}} = \frac{\sqrt{2 \cdot 3 \cdot 5 \cdot 11}}{3^2 \cdot 5 \cdot 11} = \frac{\sqrt{330}}{494}\)

Вправа\(\PageIndex{36}\)

\(\sqrt{\frac{3}{280}}\)

У Вправах 37 - 44 помістіть кожне з заданих радикальних виразів в простій радикальній формі. Не робіть припущень про знак будь-якої змінної. Змінні можуть представляти як позитивні, так і від'ємні числа.

Вправа\(\PageIndex{37}\)

\(\sqrt{\frac{8}{x^4}}\)

Відповідь

\(\sqrt{\frac{8}{x^4}} = \frac{\sqrt{8}}{\sqrt{x^4}} = \frac{\sqrt{4}\sqrt{2}}{|x^2|} = \frac{2\sqrt{2}}{x^2}\)

Вправа\(\PageIndex{38}\)

\(\sqrt{\frac{12}{x^6}}\)

Вправа\(\PageIndex{39}\)

\(\sqrt{\frac{20}{x^2}}\)

Відповідь

\(\sqrt{\frac{20}{x^2}} = \frac{\sqrt{20}}{\sqrt{x^2}} = \frac{\sqrt{4}\sqrt{5}}{|x|} = \frac{2\sqrt{5}}{|x|}\)

Вправа\(\PageIndex{40}\)

\(\sqrt{\frac{32}{x^{12}}}\)

Вправа\(\PageIndex{41}\)

\(\frac{2}{\sqrt{8x^8}}\)

Відповідь

\(\frac{2}{\sqrt{8x^8}} = \frac{2}{\sqrt{8x^8}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{2\sqrt{2}}{\sqrt{16x^8}} = \frac{2\sqrt{2}}{|4x^4|} = \frac{2\sqrt{2}}{4x^4}\)

Вправа\(\PageIndex{42}\)

\(\frac{3}{\sqrt{12x^6}}\)

Вправа\(\PageIndex{43}\)

\(\frac{10}{\sqrt{20x^{10}}}\)

Відповідь

\(\frac{10}{\sqrt{20x^{10}}} = \frac{10}{\sqrt{20x^{10}}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{10\sqrt{5}}{\sqrt{100x^{10}}} = \frac{10\sqrt{5}}{|10x^5|}\)

Однак\(|10x^5| = |10||x^4||x| = 10x^{4}|x|\), так

\(\frac{10}{\sqrt{20x^{10}}} = \frac{10\sqrt{5}}{10x^{4}|x|} = \frac{\sqrt{5}}{x^{4}|x|}\).

Вправа\(\PageIndex{44}\)

\(\frac{12}{\sqrt{6x^4}}\)

У вправах 45-48 дотримуйтесь наведення Прикладу 8 в розповіді, щоб створити рішення.

Вправа\(\PageIndex{45}\)

Враховуючи, що x < 0, помістіть радикальний вираз\(\frac{6}{\sqrt{2x^6}}\) у простій радикальній формі. Перевірте рішення у вашому калькуляторі для x = −1.

Відповідь

\(\frac{6}{\sqrt{2x^6}} = \frac{6}{\sqrt{2x^6}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{6\sqrt{2}}{\sqrt{4x^6}} = \frac{6\sqrt{2}}{|2x^3|}\)

Однак\(|2x^3| = |2||x^2||x| = 2x^{2}|x|\), так

\(\frac{6\sqrt{2}}{|2x^3|} = \frac{6\sqrt{2}}{2x^{2}|x|} = \frac{3\sqrt{2}}{x^{2}|x|}\).

Якщо x < 0, то |x| = −x і

\(\frac{3\sqrt{2}}{x^{2}|x|} = \frac{3\sqrt{2}}{x^{2}(−x)} = −\frac{3\sqrt{2}}{x^3}\).

Перевірка x = −1.

Вправа\(\PageIndex{46}\)

Враховуючи, що x > 0, помістіть радикальний вираз\(\frac{4}{\sqrt{12x^3}}\) у простій радикальній формі. Перевірте своє рішення на калькуляторі для x = 1.

Вправа\(\PageIndex{47}\)

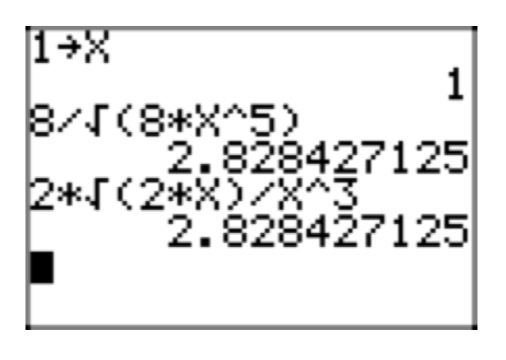
Враховуючи, що x > 0, помістіть радикальний вираз\(\frac{8}{\sqrt{8x^5}}\) у простій радикальній формі. Перевірте своє рішення на калькуляторі для x = 1.

Відповідь

\(\frac{8}{\sqrt{8x^5}} = \frac{8}{\sqrt{8x^5}} \cdot \frac{\sqrt{2x}}{\sqrt{2x}} = \frac{8\sqrt{2x}}{\sqrt{16x^6}} = \frac{8\sqrt{2x}}{|4x^3|}\)

Однак\(|4x^3| = |4||x^2||x| = 4x^{2}|x|\), так

\(\frac{8\sqrt{2x}}{|4x^3|} = \frac{8\sqrt{2x}}{4x^{2}|x|} = \frac{2\sqrt{2x}}{x^{2}|x|}\).

Але х > 0, тому |x| = х і

\(\frac{2\sqrt{2x}}{x^{2}|x|} = \frac{2\sqrt{2x}}{x^{2}(x)} = \frac{2\sqrt{2x}}{x^3}\).

Перевірка х = 1.

Вправа\(\PageIndex{48}\)

Враховуючи, що x < 0, помістіть радикальний вираз\(\frac{15}{\sqrt{20x^6}}\) у простій радикальній формі. Перевірте рішення у вашому калькуляторі для x = −1.

У вправах 49 - 56 помістіть кожне з радикальних виразів в простій формі. Припустимо, що всі змінні представляють собою позитивні числа.

Вправа\(\PageIndex{49}\)

\(\sqrt{\frac{12}{x}}\)

Відповідь

\(\sqrt{\frac{12}{x}} = \sqrt{\frac{12}{x} \cdot \frac{x}{x}} = \sqrt{\frac{12x}{x^2}} = \frac{\sqrt{4}\sqrt{3x}}{\sqrt{x^2}} = \frac{2\sqrt{3x}}{x}\)

Вправа\(\PageIndex{50}\)

\(\sqrt{\frac{18}{x}}\)

Вправа\(\PageIndex{51}\)

\(\sqrt{\frac{50}{x^3}}\)

Відповідь

\(\sqrt{\frac{50}{x^3}} = \sqrt{\frac{50}{x^3} \cdot \frac{x}{x}} = \sqrt{\frac{50x}{x^4}} = \frac{\sqrt{25}\sqrt{2x}}{\sqrt{x^4}} = \frac{5\sqrt{2x}}{x^2}\)

Вправа\(\PageIndex{52}\)

\(\sqrt{\frac{72}{x^5}}\)

Вправа\(\PageIndex{53}\)

\(\frac{1}{\sqrt{50x}}\)

Відповідь

\(\frac{1}{\sqrt{50x}} = \frac{1}{\sqrt{50x}} \cdot \frac{\sqrt{2x}}{\sqrt{2x}} = \frac{\sqrt{2x}}{\sqrt{100x^2}} = \frac{\sqrt{2x}}{10x}\)

Вправа\(\PageIndex{54}\)

\(\frac{2}{\sqrt{18x}}\)

Вправа\(\PageIndex{55}\)

\(\frac{3}{\sqrt{27x^3}}\)

Відповідь

\(\frac{3}{\sqrt{27x^3}} = \frac{3}{\sqrt{27x^3}} \cdot \frac{\sqrt{3x}}{\sqrt{3x}} = \frac{3\sqrt{3x}}{\sqrt{81x^4}} = \frac{3\sqrt{3x}}{9x^2} = \frac{\sqrt{3x}}{3x^2}\)

Вправа\(\PageIndex{56}\)

\(\frac{5}{\sqrt{10x^5}}\)