9.5: радикальні рівняння

Last updated
Save as PDF

Page ID: 58027

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

радикальні рівняння

У цьому розділі ми вирішимо рівняння, які містять одне або кілька радикальних виразів. У випадку, коли ми можемо виділити радикальний вираз на одній стороні рівняння, ми можемо просто підняти обидві сторони рівняння до сили, яка усуне радикальний вираз. Наприклад, якщо

$\sqrt{x−1} = 2$(1)

то ми можемо квадратувати обидві сторони рівняння, усуваючи радикал.

$\sqrt{x−1}^2 = (2)^2$

х−1=4

Тепер, коли радикал усунений, ми можемо звернутися до добре зрозумілих методів для вирішення рівняння, яке залишається. У цьому випадку нам потрібно лише додати 1 до обох сторін рівняння, щоб отримати

х = 5.

Це рішення легко перевіряється. Підставити x = 5 у вихідне рівняння (1).

$\sqrt{x−1} = 2$

$\sqrt{5−1} = 2$

$\sqrt{4} = 2$

Останній рядок є дійсним, оскільки «позитивний квадратний корінь 4» дійсно дорівнює 2.

Це здається досить прямо вперед, але є деякі тонкощі. Давайте розглянемо інший приклад, один з рівнянням, дуже схожим на рівняння.

Приклад$\PageIndex{2}$

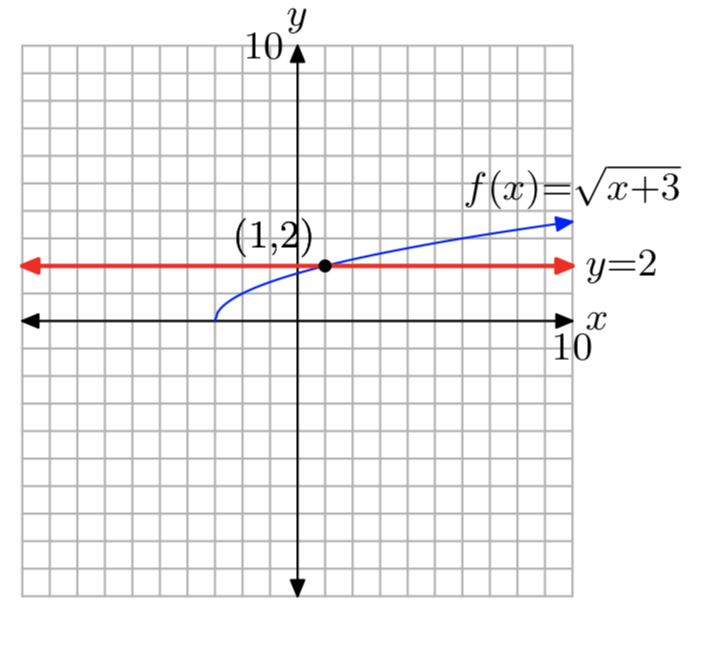
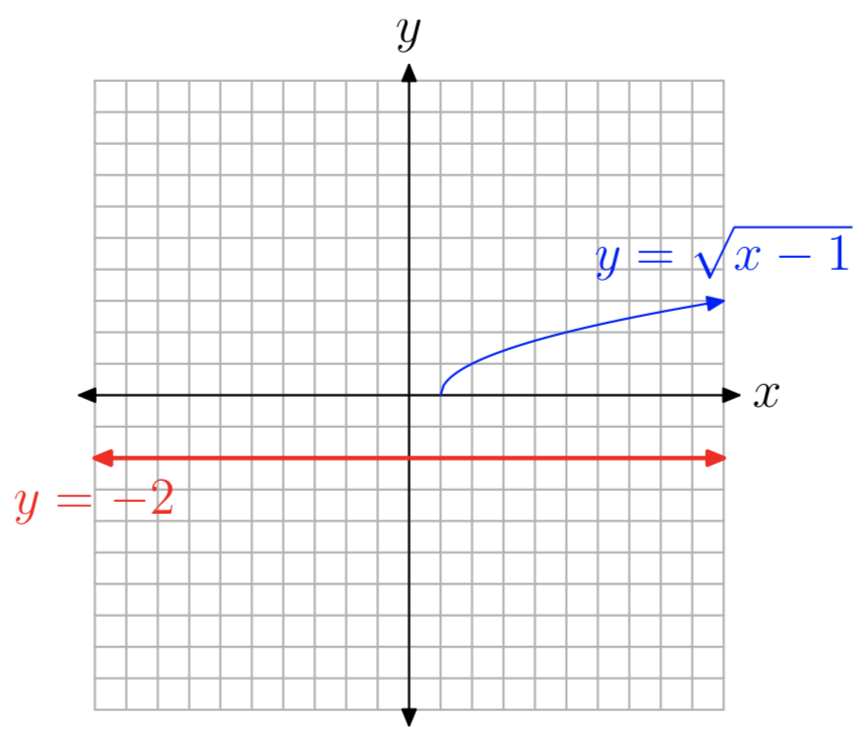
Розв'яжіть рівняння$\sqrt{x−1} = −2$ для x.

Якщо уважно вивчити рівняння

$\sqrt{x−1} = −2$(3)

Ви можете негайно виявити труднощі. Ліва частина рівняння вимагає «позитивного квадратного кореня», але права частина рівняння від'ємна. Інтуїтивно рішень бути не може.

Погляд на графіки кожної сторони рівняння також виявляє проблему. Графіки$y = \sqrt{x−1}$ і y = −2 наведені на малюнку 1. Зверніть увагу, що графіки не перетинаються, тому рівняння не$\sqrt{x−1} = −2$ має рішення.

Однак зверніть увагу, що відбувається, коли ми квадратизуємо обидві сторони рівняння (3).

$(\sqrt{x − 1})^2 = (−2)^2$

$x−1=4$(4)

Знімок екрана 2019-07-05 в 1.13.02 PM.png — Малюнок 1. графік$y = \sqrt{x−1}$ і y = −2 не перетинаються

Цей результат ідентичний результату, який ми отримали, коли ми звели в квадрат обидві сторони рівняння$\sqrt{x−1} = 2$ вище. Якщо продовжити, додавши 1 до обох сторін рівняння, отримаємо

х = 5.

Але це не може бути правильним, оскільки і інтуїція, і графіки на малюнку 1 показали, що рівняння не$\sqrt{x−1} = −2$ має рішення.

Давайте перевіримо рішення x = 5 у вихідному рівнянні.

$\sqrt{x−1} = −2$

$\sqrt{5−1} = −2$

$\sqrt{4} = −2$

Оскільки «позитивний квадратний корінь 4» не дорівнює − 2, цей останній рядок є неправильним, і розв'язок x = 5 не перевіряє рівняння$\sqrt{x−1} = −2$. Оскільки єдине рішення, яке ми знайшли, не перевіряє, рівняння не має розв'язків.

Обговорення в прикладі 2 диктує обережність.

ПОПЕРЕДЖЕННЯ$\PageIndex{5}$

Всякий раз, коли ви квадратуєте обидві сторони рівняння, існує ймовірність того, що ви можете ввести сторонні рішення, «зайві» рішення, які не перевірятимуть вихідну задачу.

Існує тільки один спосіб уникнути цієї дилеми сторонніх рівнянь.

ПЕРЕВІРКА РІШЕНЬ

Кожного разу, коли ви квадратуєте обидві сторони рівняння, ви повинні перевірити кожне з ваших рішень у вихідному рівнянні. Тільки так ви можете бути впевнені, що у вас є дійсне рішення.

Квадратне біноміальне

Як ми бачили знову і знову, квадрат біноміальної моделі має надзвичайно важливе значення.

КВАДРАТ БІНОМІАЛЬНОГО

Якщо a і b є будь-якими дійсними числами, то

$(a+b)^2 = a^2+2ab+b^2$.

Квадратування біноміального візерунка буде грати головну роль в інших прикладах у цьому розділі.

Давайте розглянемо кілька прикладів його використання.

Приклад$\PageIndex{6}$

Розширити і спростити можна$(1+\sqrt{x})^2$ за допомогою квадратного біноміального візерунка. Припустимо, що$x \ge 0$.

Припущення,$x \ge 0$ що потрібно, інакше вираз$\sqrt{x}$ передбачає квадратний корінь від'ємного числа, яке не є дійсним числом.

Квадрат біноміального візерунка говорить нам про квадрат першого та другого членів. Однак існує і середній термін, який знаходять, взявши добуток першого і другого членів, потім множивши результат на 2.

$(1 + \sqrt{x})^2 = (1)^2 + 2(1)(\sqrt{x}) + (\sqrt{x})^2$

=$1+2\sqrt{x}+x$

Давайте розглянемо інший приклад.

Приклад$\PageIndex{7}$

Розширити і спростити можна$(\sqrt{x+1}−\sqrt{x})^2$ за допомогою квадратного біноміального візерунка. Прокоментуйте домен цього виразу.

Для того, щоб цей вираз мав сенс, ми повинні уникати взяття квадратного кореня негативного числа. Отже, обидва вирази під квадратними коренями повинні бути невід'ємними (додатними або нульовими). Тобто,

\[\begin{array}{ccc} {x+1 \ge 0}&{\text{and}}&{x \ge 0}\\ \nonumber \end{array}\]

Вирішуючи кожне з цих нерівностей самостійно, отримуємо той факт, що

\[\begin{array}{ccc} {x \ge −1}&{\text{and}}&{x \ge 0}\\ \nonumber \end{array}\]

Через слова «і» запитуваний домен - це сукупність всіх чисел, які задовольняють обом нерівностям, а саме безліч всіх дійсних чисел, які більше або рівні нулю. Тобто область виразу є${x : x ≥ 0}$.

Тепер ми будемо розширювати вираз,$(\sqrt{x+1}−\sqrt{x})^2$ використовуючи квадрат біноміальний візерунок.

$(\sqrt{x+1}−\sqrt{x})^2 = (\sqrt{x+1})^2−2(\sqrt{x+1})(\sqrt{x})+(\sqrt{x})^2$

=$x+1+2\sqrt{(x+1)x}+x$

=$2x+1+2\sqrt{x^2 +x}$

Ізолювати радикалу

Нашою мантрою буде стратегічна фраза «Ізолювати радикала».

ІЗОЛЮЄМО РАДИКАЛ

Коли ви вирішуєте рівняння, що містять один радикал, ізолюйте радикал сам по собі на одній стороні рівняння.

Хоча це не завжди можливо (деякі рівняння можуть містити більше одного радикального виразу), це можливо в нашому наступному прикладі.

Приклад$\PageIndex{8}$

Розв'яжіть рівняння
$1+\sqrt{4x+13} = 2x$ для x (9)

Давайте розглянемо рішення графічного калькулятора. Ми завантажили ліву та праву сторони$1+\sqrt{4x+13} = 2x$ в Y1 та Y2 відповідно, як показано на малюнку 2 (а). Потім ми використовуємо 6: ZStandard і утиліту intersect в меню CALC для визначення координат точки перетину$y = 1+\sqrt{4x+13}$ і y = 2x, як показано на малюнку 2 (b).

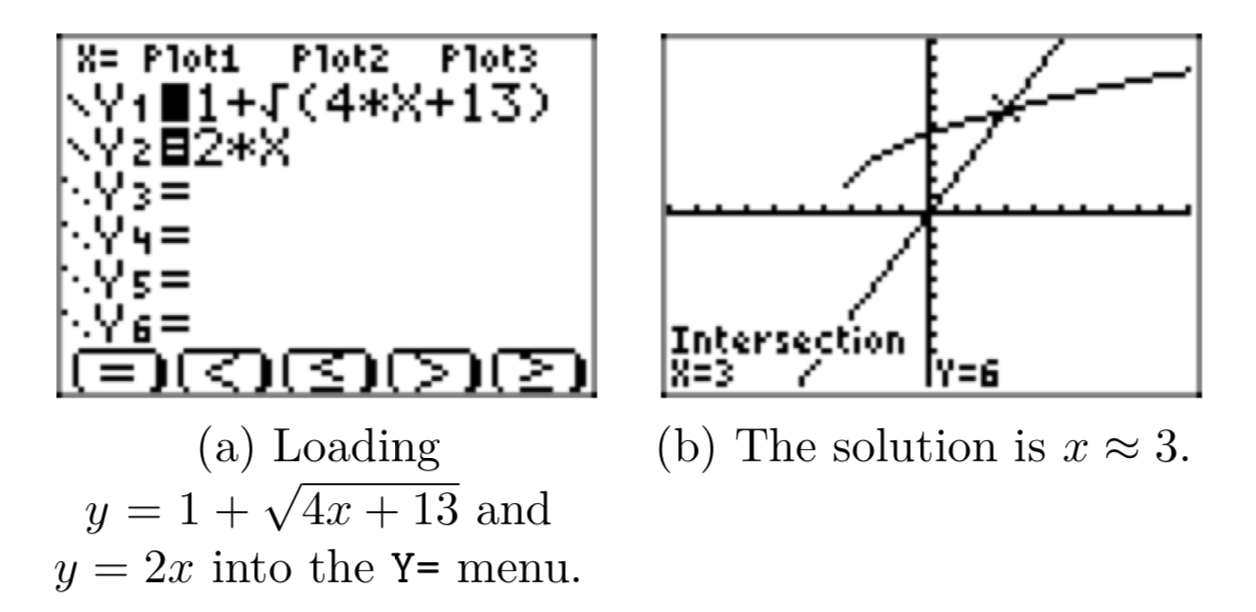
Знімок екрана 2019-07-05 в 1.39.48 PM.png — Малюнок 2. Рішення$1+\sqrt{4x+13} = 2x$ на графічному калькуляторі. Зверніть увагу, що є тільки одна точка перетину.

Зараз ми представимо алгебраїчне рішення, але зауважте, що нас попереджають, що існує лише одне рішення, і ми вважаємо, що рішення є$x \approx 3$. Звичайно, це лише наближення, як це завжди буває, коли ми підбираємо наш калькулятор (нашу апроксимаційну машину).

Скандуйте стратегічну фразу «ізолюйте радикал», а потім виділіть радикал з одного боку рівняння. Ми виконаємо цю директиву, віднімаючи 1 з обох сторін рівняння.

$1+\sqrt{4x+13} = 2x$

$\sqrt{4x+13} = 2x−1$

Далі квадрат обидві сторони рівняння.

$(\sqrt{4x + 13})^2 = (2x−1)^2$
Квадратування усуває радикал ліворуч, але ми повинні використовувати квадрат біноміального візерунка, щоб квадратувати біном у правій частині рівняння.

$4x+13 = (2x)^2−2(2x)(1)+(1)^2$

$4x+13 = 4x^2−4x+1$

Ми досягли успіху в очищенні всіх квадратних коренів від рівняння за допомогою нашої стратегії «ізолювати радикал». Рівняння, яке залишається нелінійним (є сила х вище 1), тому ми хочемо зробити одну сторону рівняння рівняння рівною нулю. Ми зробимо це, віднімаючи 4x і 13 з обох сторін рівняння.

$0 = 4x^2−4x+1−4x−13$

$0 = 4x^2−8x−12$

На цьому етапі зверніть увагу, що кожен член в правій частині рівняння ділиться на 4. Розділіть обидві сторони рівняння на 4, потім використовуйте ac-тест для множення результату.

$0 = x^2−2x−3$
0 = (х−3) (х+1)

Встановіть кожен коефіцієнт праворуч від цього останнього рівняння, щоб отримати розв'язки x = 3 та x = −1.

Зауважте, що x = 3 відповідає розв'язку, знайденому графіком на малюнку 2 (b). Однак з'явилося «додаткове» рішення x = −1. Пам'ятайте, що ми звели в квадрат обидві сторони вихідного рівняння, тому не виключено, що були введені сторонні розв'язки. Нам потрібно перевірити кожне наше рішення, підставивши їх у вихідне рівняння (9).

Наш графік на малюнку 2 (b) додає довіру до аналітичного рішення x = 3, тому давайте перевіримо це спочатку. Заставте x = 3 у вихідне рівняння.

$1+\sqrt{4x+13} = 2x$

$1+\sqrt{4(3)+13} = 2(3)$

$1+ \sqrt{25} = 6$

$1+5 = 6$

Зрозуміло, що х = 3 перевіряє і є дійсним рішенням.

Далі перевіримо «підозрюваний» розв'язок x = − 1, підставивши його до вихідного рівняння.

$1+\sqrt{4x+13} = 2x$

$1 + \sqrt{4(−1) + 13} = 2(−1)$

$1+\sqrt{9} = −2$

$1+3 = −2$

Зрозуміло, що x = −1 не перевіряє і не є рішенням.

Таким чином, єдиним рішенням$1+\sqrt{4x+13} = 2x$ є х = 3. Читачі повинні взяти до уваги, як це графічне рішення та аналітичне рішення доповнюють один одного.

Перш ніж розглядати інший приклад, давайте розглянемо одну з найпоширеніших помилок, допущених при алгебраїчному розв'язанні рівняння.

Поширена алгебраїчна помилка

У цьому розділі ми обговоримо одну з найпоширеніших алгебраїчних помилок, що виникають при розв'язанні рівнянь, що містять радикальні вирази.

ПОПЕРЕДЖЕННЯ$\PageIndex{10}$

Багато обчислень в цьому розділі невірні. Вони є прикладами поширених помилок алгебри, допущених при розв'язанні рівнянь, що містять радикали. Майте це на увазі і читайте матеріал в цьому розділі дуже уважно.

Коли представлено рівняння

$1+\sqrt{4x+13} = 2x$, (11)

деякі будуть квадратні обидві сторони рівняння наступним чином.

$(1)^2 + (\sqrt{4x+13})^2 = (2x)^2$. (12)

прибуття в

$1+4x+13 = 4x^2$.

Зробіть одну сторону нулем, потім розділіть обидві сторони отриманого рівняння на 2.

$0=4x^2 −4x−14$

$0=2x^2 −2x−7$

Уважний читач вже зрозуміє, що ми пройшли неправильний шлях, оскільки цей результат зовсім відрізняється від такого в аналогічній точці рішення Прикладу 8. Однак ми можемо продовжити розв'язання, використовуючи квадратичну формулу для розв'язання останнього рівняння для x. Якщо порівнювати$2x^2−2x−7$ з$ax^2+bx+c$, зверніть увагу, що a = 2, b=−2 та c=−7. Таким чином,

$x = \frac{−b \pm \sqrt{b^2−4ac}}{2a}$

=$\frac{−(−2) \pm \sqrt{(−2)^2−4(2)(−7)}}{2(2)}$

=$\frac{2 \pm \sqrt{60}}{4}$

Однак жодне з цих «рішень» не є правильним рішенням, знайденим у прикладі 8, а саме x = 3. Отже, що ми зробили не так?

Помилка сталася на самому першому кроці, коли ми звели в квадрат обидві сторони рівняння (11). Дійсно, щоб отримати рівняння (12), ми насправді не квадрат обидві сторони рівняння (11). Швидше, ми склали в квадрат кожен з окремих членів на кожній стороні рівняння.

Це серйозна помилка. По суті, ми почали з рівняння, що має вигляд

а + б = с, (13)

потім в квадрат «обидві сторони» наступним чином.

$a^2 + b^2 = c^2$. (14)

Це не є дійсним. Наприклад, почніть з

2 + 3 = 5,

цілком дійсне рівняння, оскільки сума 2 і 3 дорівнює 5. Тепер «квадрат», як ми зробили в рівнянні (14), щоб отримати

$2^2 + 3^2 = 5^2$.

Однак зауважте, що це спрощує як

4+9 = 25,

тому ми більше не маємо дійсного рівняння.

Помилка, зроблена тут, полягає в тому, що ми звели в квадрат кожен з окремих членів на кожній стороні рівняння замість квадрата «кожної сторони» рівняння. Якби ми це зробили, у нас було б все гаразд, як видно з цього розрахунку.

2+3=5

$(2+3)^2 =5^2$

$2^2 +2(2)(3)+3^2 =5^2$

4+12+9 = 25

Тільки пам'ятайте, a+b = c не має на увазі$a^2+b^2 = c^2$.

ПОПЕРЕДЖЕННЯ$\PageIndex{15}$

Тепер ми повернемося до правильних обчислень.

Більше одного радикалу

Давайте розглянемо рівняння, яке містить більше одного радикала.

Приклад$\PageIndex{16}$

Розв'яжіть рівняння

$\sqrt{2x}+\sqrt{2x+3} = 3$(17)

для х.

Почнемо з графічного рішення рівняння. Спочатку завантажте рівняння$y = \sqrt{2x}+\sqrt{2x+3}$ і y = 3 в меню Y =, як показано на малюнку 3 (а).

Ми не можемо взяти квадратний корінь від'ємного числа, тому, коли ми розглядаємо функцію, визначену рівнянням$y = \sqrt{2x}+\sqrt{2x+3}$, обидва вирази під радикалами повинні бути невід'ємними. Тобто,

\[\begin{array}{ccc} {2x \ge 0}&{\text{and}}&{2x+3 \ge 0}\\ \nonumber \end{array}\]

Вирішуючи кожне з них самостійно,

\[\begin{array}{ccc} {x \ge 0}&{\text{and}}&{x \ge −\frac{3}{2}}\\ \nonumber \end{array}\]

Числа, які більше або рівні нулю і більше або рівні,$−\frac{3}{2}$ є числами більше або дорівнює нулю. Отже, область функції, визначеної рівнянням$y = \sqrt{2x}+\sqrt{2x+3}$, є {x:$x \ge 0$}. Таким чином, він не повинен наступати як шок, коли графік$y = \sqrt{2x}+\sqrt{2x+3}$ лежить цілком праворуч від нуля, як показано на малюнку 3 (б).

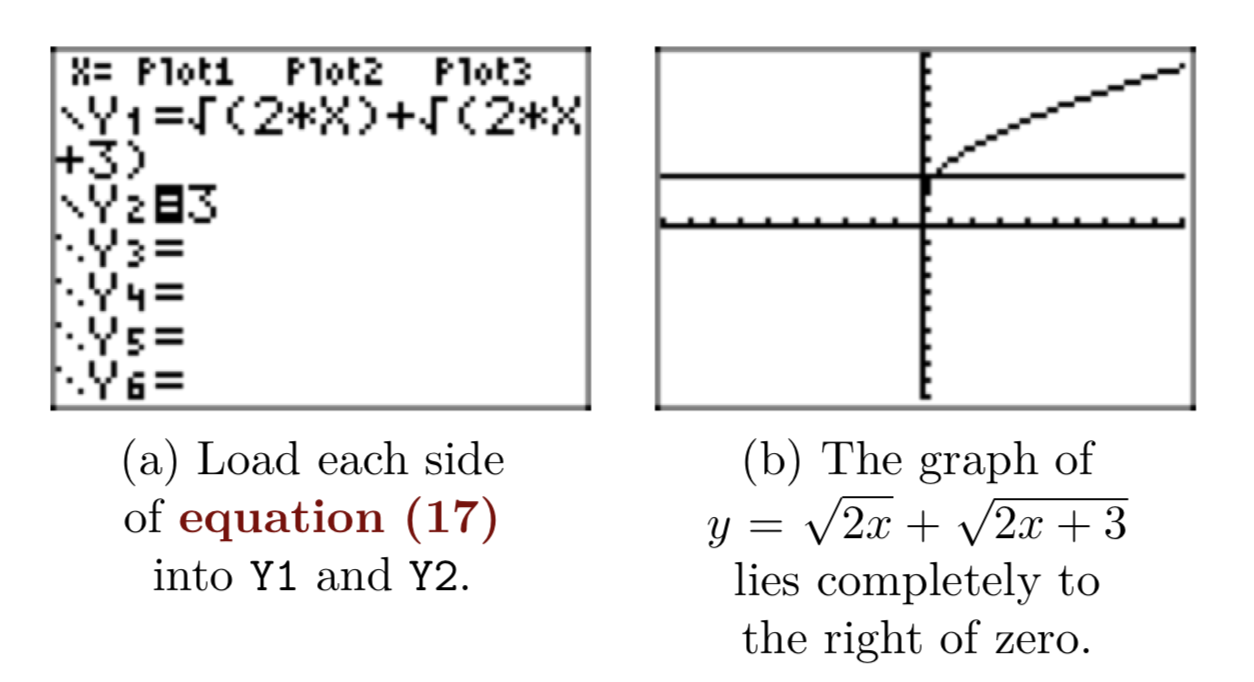
Знімок екрана 2019-07-08 в 1.43.25 PM.png — Малюнок 3. Креслення графіків$y = \sqrt{2x}+\sqrt{2x+3}$ і y = 3.

Трохи важко побачити точку перетину на малюнку 3 (b), тому давайте налаштуємо параметри WINDOW, як показано на малюнку 4 (а). Як бачите на малюнку 4 (b), це трохи чіткіше підкреслює точку перетину, а утиліта 5:intersect в меню CALC знаходить точку перетину, показану на малюнку 4 (b).

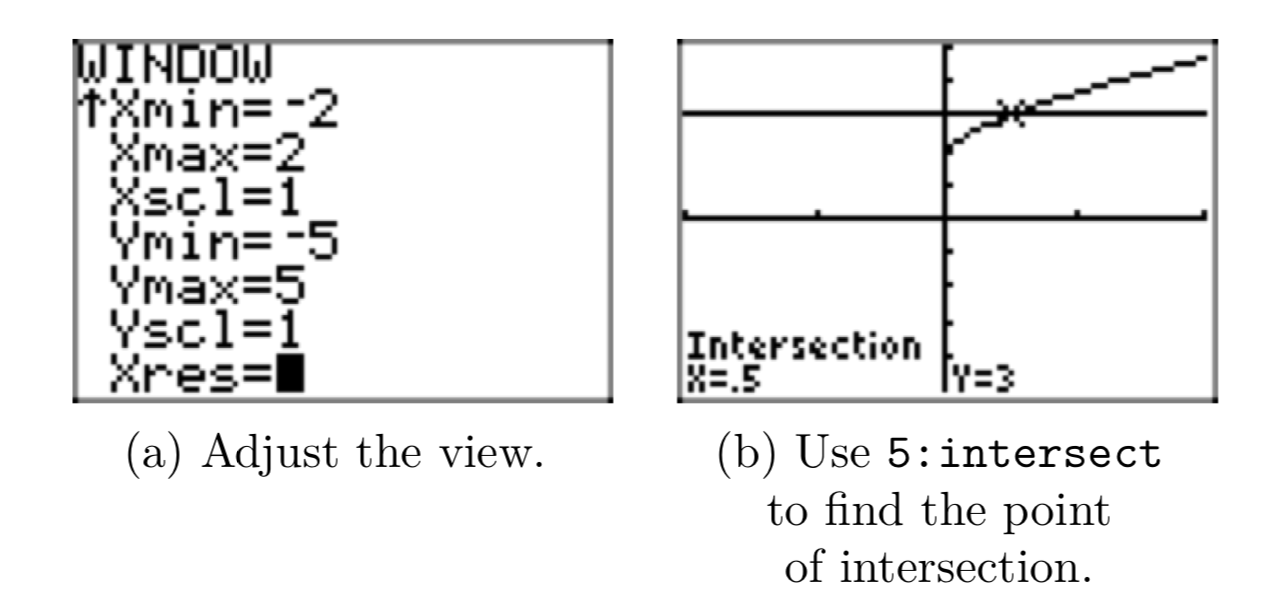
Знімок екрана 2019-07-08 в 5.48.42 PM.png — Малюнок 4. Рішення$\sqrt{2x}+\sqrt{2x+3} = 3$ графічно.

Графічний калькулятор повідомляє одне рішення (є лише одна точка перетину), а значення x точки перетину приблизно$x \approx 0.5$.

Тепер давайте розглянемо алгебраїчне рішення. Оскільки в цьому рівнянні два радикальних вирази, ми виділимо одне з них на одній стороні рівняння. Ми вибираємо, щоб виділити більш складні з двох радикальних виразів на лівій стороні рівняння, а потім квадратні обидві сторони результуючого рівняння.

$\sqrt{2x}+\sqrt{2x+3} = 3$

$\sqrt{2x+3} = 3−\sqrt{2x}$

$(\sqrt{2x+3})^2 = (3−\sqrt{2x})^2$

Зліва квадрат усуває корінний. Для квадратного біноміального праворуч використовуємо квадрат біноміального візерунка для отримання

$2x+3 = (3)^2−2(3)(\sqrt{2x})+(\sqrt{2x})^2$

$2x+3 = 9−6\sqrt{2x}+2x$.

У нас залишилося одне радикальне вираз зліва праворуч від цього рівняння, тому ми будемо слідувати мантрі «ізолювати радикал». Спочатку відніміть 2x з обох сторін рівняння, щоб отримати

$3=9−6\sqrt{2x}$,

потім відніміть 9 з обох сторін рівняння.

$−6=−6\sqrt{2x}$,

Нам вдалося виділити радикальний член на одній стороні рівняння. Тепер розділіть обидві сторони рівняння на −6, а потім квадрат обидві сторони отриманого рівняння.

$1 = \sqrt{2x}$

$(1)^2 = (\sqrt{2x})^2$

$1 = 2x$

Розділіть обидві сторони останнього результату на 2.

$x = \frac{1}{2}$

Зауважте, що це добре узгоджується з нашим графічним рішенням ($x \approx 0.5$), але давайте перевіримо наше рішення шляхом підстановки$x = \frac{1}{2}$ у вихідне рівняння.

$\sqrt{2x}+\sqrt{2x+3} = 3$

$\sqrt{2(\frac{1}{2})}+\sqrt{2(\frac{1}{2})+3} = 3$

$\sqrt{1}+\sqrt{4} = 3$

1+2 = 3

Це останнє твердження вірно, тому рішення$x = \frac{1}{2}$ перевіряє.

Вправа

Для раціональних функцій у вправах 1 - 6 виконайте кожне з наступних завдань.

Завантажте функцію f та рядок y = k у ваш графічний калькулятор. Налаштуйте вікно перегляду таким чином, щоб усі точки перетину двох графіків були видимими у вікні перегляду.
Скопіюйте зображення у вікні перегляду на домашній папір. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax. Позначте графіки їх рівняннями. Не забудьте намалювати всі лінії лінійкою.
Використовуйте утиліту intersect для визначення координат точки (ів) перетину. Помістіть точку перетину на домашньому папері і позначте її координатами.
Вирішити рівняння f (x) = k алгебраїчно. Розмістіть свою роботу та рішення поруч із графіком. Чи погоджуються рішення?

Вправа$\PageIndex{1}$

$f(x) = \sqrt{x+3}$, к = 2

Відповідь

х = 1

$Знімок екрана 2019-07-14 в 4.11.16 PM.png$

Вправа$\PageIndex{2}$

$f(x) = \sqrt{4−x}$, к = 3

Вправа$\PageIndex{3}$

$f(x) = \sqrt{7−2x}$, к = 4

Відповідь

$x = −\frac{9}{2}$

$Знімок екрана 2019-07-14 в 4.12.07 PM.png$

Вправа$\PageIndex{4}$

$f(x) = \sqrt{3x+5}$, к = 5

Вправа$\PageIndex{5}$

$f(x) = \sqrt{5+x}$, к = 4

Відповідь

х = 11

$Знімок екрана 2019-07-14 в 4.12.42 PM.png$

Вправа$\PageIndex{6}$

$f(x) = \sqrt{4−x}$, к = 5

У вправах 7 - 12 використовуйте алгебраїчну техніку для вирішення заданого рівняння. Перевірте свої рішення.

Вправа$\PageIndex{7}$

$\sqrt{−5x+5} = 2$

Відповідь: $\frac{1}{5}$

Вправа$\PageIndex{8}$

$\sqrt{4x+6} = 7$

Вправа$\PageIndex{9}$

$\sqrt{6x−8} = 8$

Відповідь: 12

Вправа$\PageIndex{10}$

$\sqrt{2x+4} = 2$

Вправа$\PageIndex{11}$

$\sqrt{−3x+1} = 3$

Відповідь: $x = −\frac{8}{3}$

Вправа$\PageIndex{12}$

$\sqrt{4x+7} = 3$

За раціональні функції у вправах 13-16 виконують кожне з наступних завдань.

Завантажте функцію f та рядок y = k у ваш графічний калькулятор. Налаштуйте вікно перегляду таким чином, щоб усі точки перетину двох графіків були видимими у вікні перегляду.
Скопіюйте зображення у вікні перегляду на домашній папір. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax. Позначте графіки їх рівняннями. Не забудьте намалювати всі лінії лінійкою.
Використовуйте утиліту intersect для визначення координат точки (ів) перетину. Помістіть точку перетину на домашньому папері і позначте її координатами.
Вирішити рівняння f (x) = k алгебраїчно. Розмістіть свою роботу та рішення поруч із графіком. Чи погоджуються рішення?

Вправа$\PageIndex{13}$

$f(x) = \sqrt{x+3}+x$, к = 9

Відповідь

х = 6

$Знімок екрана 2019-07-14 в 4.13.59 PM.png$

Вправа$\PageIndex{14}$

$f(x) = \sqrt{x+6}−x$, к = 4

Вправа$\PageIndex{15}$

$f(x) = \sqrt{x−5}−x$, k = −7

Відповідь

х = 9

$Знімок екрана 2019-07-14 в 4.14.38 PM.png$

Вправа$\PageIndex{16}$

$f(x) = \sqrt{x+5}+x$, к = 7

У Exercise17 - 24 використовуйте алгебраїчну техніку для вирішення даного рівняння. Перевірте свої рішення.

Вправа$\PageIndex{17}$

$\sqrt{x+1}+x = 5$

Відповідь: 3

Вправа$\PageIndex{18}$

$\sqrt{x+8}−x = 8$

Вправа$\PageIndex{19}$

$\sqrt{x+4}+x = 8$

Відповідь: 5

Вправа$\PageIndex{20}$

$\sqrt{x+8}−x = 2$

Вправа$\PageIndex{21}$

$\sqrt{x+5}−x = 3$

Відповідь: −1

Вправа$\PageIndex{22}$

$\sqrt{x+5}+x = 7$

Вправа$\PageIndex{23}$

$\sqrt{x+9}−x = 9$

Відповідь: −8, −9

Вправа$\PageIndex{24}$

$\sqrt{x+7}+x = 5$

Для раціональних функцій у вправах 25 - 28 виконайте кожне з наступних завдань.

Завантажте функцію f та рядок y = k у свій графічний калькулятор. Налаштуйте вікно перегляду таким чином, щоб усі точки перетину двох графіків були видимими у вікні перегляду.
Скопіюйте зображення у вікні перегляду на домашній папір. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax. Позначте графіки їх рівняннями. Не забудьте намалювати всі лінії лінійкою.
Використовуйте утиліту intersect для визначення координат точки (ів) перетину. Помістіть точку перетину на домашньому папері і позначте її координатами.
Вирішити рівняння f (x) = k алгебраїчно. Розмістіть свою роботу та рішення поруч із графіком. Чи погоджуються рішення?

Вправа$\PageIndex{25}$

$f(x) = \sqrt{x−1}+\sqrt{x+6}, k = 7$

Відповідь

х = 10

$Знімок екрана 2019-07-14 в 4.16.02 PM.png$

Вправа$\PageIndex{26}$

$f(x) = \sqrt{x+2}+\sqrt{x+9}, k = 7$

Вправа$\PageIndex{27}$

$f(x)= \sqrt{x+2}+\sqrt{3x+4}, k = 2$

Відповідь

x = −1

$Знімок екрана 2019-07-14 в 4.16.42 PM.png$

Вправа$\PageIndex{28}$

$f(x)= \sqrt{6x+7}+\sqrt{3x+3}, k = 1$

У вправах 29 - 40 використовуйте алгебраїчну техніку для вирішення даного рівняння. Перевірте свої рішення.

Вправа$\PageIndex{29}$

$\sqrt{x+46}−\sqrt{x−35} = 1$

Відповідь: 1635

Вправа$\PageIndex{30}$

$\sqrt{x−16}+\sqrt{x+16} = 8$

Вправа$\PageIndex{31}$

$\sqrt{x−19}+\sqrt{x−6} = 13$

Відповідь: 55

Вправа$\PageIndex{32}$

$\sqrt{x+31}−\sqrt{x+12} = 1$

Вправа$\PageIndex{33}$

$\sqrt{x−2}−\sqrt{x−49} = 1$

Відповідь: 578

Вправа$\PageIndex{34}$

$\sqrt{x+13}+\sqrt{x+8} = 5$

Вправа$\PageIndex{35}$

$\sqrt{x+27}−\sqrt{x−22} = 1$

Відповідь: 598

Вправа$\PageIndex{36}$

$\sqrt{x+10}+\sqrt{x+13} = 3$

Вправа$\PageIndex{37}$

$\sqrt{x+30}−\sqrt{x−38} = 2$

Відповідь: 294

Вправа$\PageIndex{38}$

$\sqrt{x+36}−\sqrt{x+11} = 1$

Вправа$\PageIndex{39}$

$\sqrt{x−17}+\sqrt{x+3} = 10$

Відповідь: 33

Вправа$\PageIndex{40}$

$\sqrt{x+18}+\sqrt{x+13} = 5$