8.1: Показники та коріння

Перш ніж визначити наступне сімейство функцій, експоненціальні функції, нам потрібно буде детально обговорити позначення показника. Як ми побачимо, показники можуть бути використані для опису не тільки повноважень (таких як\(5^2\) і\(2^3\)), але і коренів (наприклад, квадратних коренів -\(\sqrt{2}\) і кубових коренів -\(\sqrt[3]{2}\)). По дорозі ми визначимо вищі коріння і розвинемо кілька їх властивостей. Більш детальна робота з корінням буде потім взята в наступному розділі.

Цілочисельні показники

Нагадаємо, що використання натуральної цілої експоненти є просто скороченням для повторного множення. Наприклад,

\[5^2 = 5 \cdot 5 \label{1}\]

і

\[2^3 = 2 \cdot 2 \cdot 2. \label{2}\]

Загалом,\(b^n\) позначає кількість,\(b\) помножене на себе\(n\) раз. З цим визначенням дотримуються наступні Закони експонентів.

Закони експонентів

1. \(b^{r}b^s = b^{r+s}\)
2. \(\frac{b^r}{b^s} = b^{r−s}\)
3. \((b^r)^s=b^{rs}\)

Закони експонентів ілюструються наступними прикладами.

Приклад\(\PageIndex{3}\)

1. \(2^{3}2^2 = (2 \cdot 2 \cdot 2)(2 \cdot 2) = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 = 2^5 = 2^{3+2}\)
2. \(\frac{2^4}{2^2} = \frac{2 \cdot 2 \cdot 2 \cdot 2}{2 \cdot 2} = 2 \cdot 2 =2^2 = 2^{4−2}\)
3. \((2^3)^2 = (2^3)(2^3) = (2 \cdot 2 \cdot 2)(2 \cdot 2 \cdot 2) = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 = 2^6 = 2^{3 \cdot 2}\)

Зауважте, що другий закон має сенс лише для\(r > s\), оскільки в іншому випадку показник\(r − s\) буде негативним або 0. Але насправді, виявляється, що ми можемо створити визначення для негативних показників і 0 експоненти, і, отже, видалити це обмеження.

Негативні показники, а також показник 0 просто визначаються таким чином, що Закони експонентів працюватимуть для всіх цілих показників.

• Для показника 0 перший закон має на увазі це\(b^{0}b^1 = b^{0+1}\), і тому\(b^{0}b = b\). Якщо\(b \ne 0\), ми можемо розділити обидві сторони\(b\) на отримання\(b^{0} = 1\) (є один виняток:\(0^0\) не визначено).
• Для негативних показників другий закон передбачає, що\[b^{−n} = b^{0−n} = \frac{b^0}{b^n} = \frac{1}{b^n}\]

за умови, що\(b \ne 0\). Наприклад\(2^{−3} = \frac{1}{2^3} = \frac{1}{8}\), і\(2^{−4} = \frac{1}{2^4} = \frac{1}{16}\). Отже, негативні показники та показник 0 визначаються наступним чином:

Визначення\(\PageIndex{4}\)

\(b^{−n} = \frac{1}{b^n}\)і\(b^0 = 1\)

за умови, що\(b \ne 0\).

Приклад\(\PageIndex{5}\)

а)\(4^{−3} = \frac{1}{4^3} = \frac{1}{64}\)

б)\(6^0 = 1\)

в)\((\frac{1}{5})^{−2} = \frac{1}{(\frac{1}{5})^2} = \frac{1}{\frac{1}{25}} = 25\)

Тепер ми\(b^n\) визначили для всіх цілих чисел п, таким чином, що Закони експонентів тримати. Можливо, дивно дізнатися, що ми можемо також визначати вирази, використовуючи раціональні показники\(2^{\frac{1}{3}}\), наприклад, послідовно. Однак, перш ніж це зробити, нам потрібно буде зробити об'їзд і визначити коріння.

Коріння

Квадратні корені: Давайте почнемо з визначення квадратного кореня дійсного числа. Ми використовували квадратний корінь у багатьох розділах цього тексту, тому це має бути знайоме поняття. Проте в цьому розділі ми розглянемо квадратні коріння більш докладно.

Визначення\(\PageIndex{6}\)

Задано дійсне число a, «квадратний корінь a» - це число x таке, що\(x^2 = a\).

Наприклад, 3 - квадратний корінь з 9, оскільки\(3^2 = 9\). Likewise, − 4 - квадратний корінь з 16 з\((−4)^2 = 16\). У певному сенсі взяття квадратного кореня є «протилежністю» квадратного, тому визначення квадратного кореня має бути тісно пов'язане з графом\(y = x^2\), the squaring function. We investigate square roots in more detail by looking for solutions of the equation

\(x^2 = a\). (7)

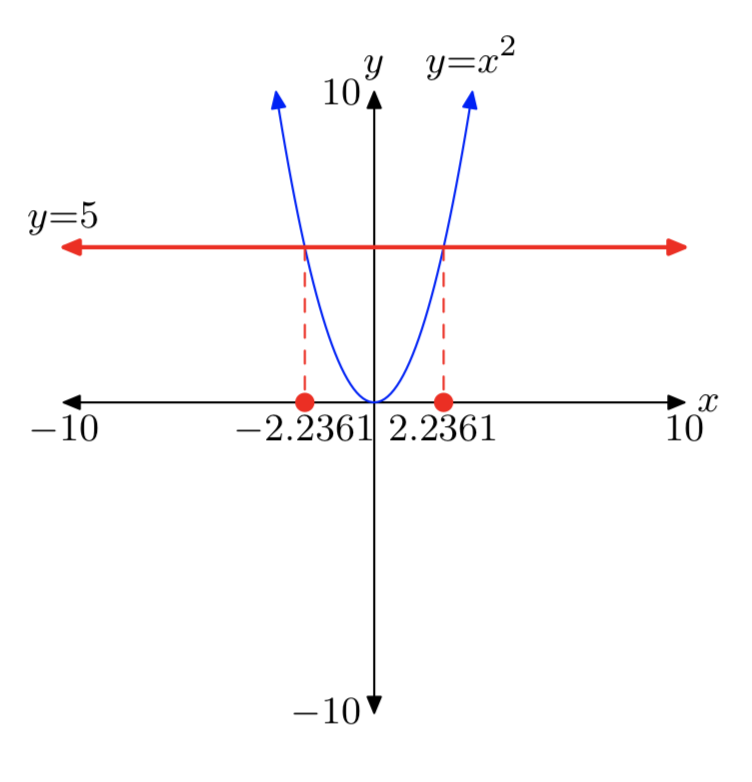
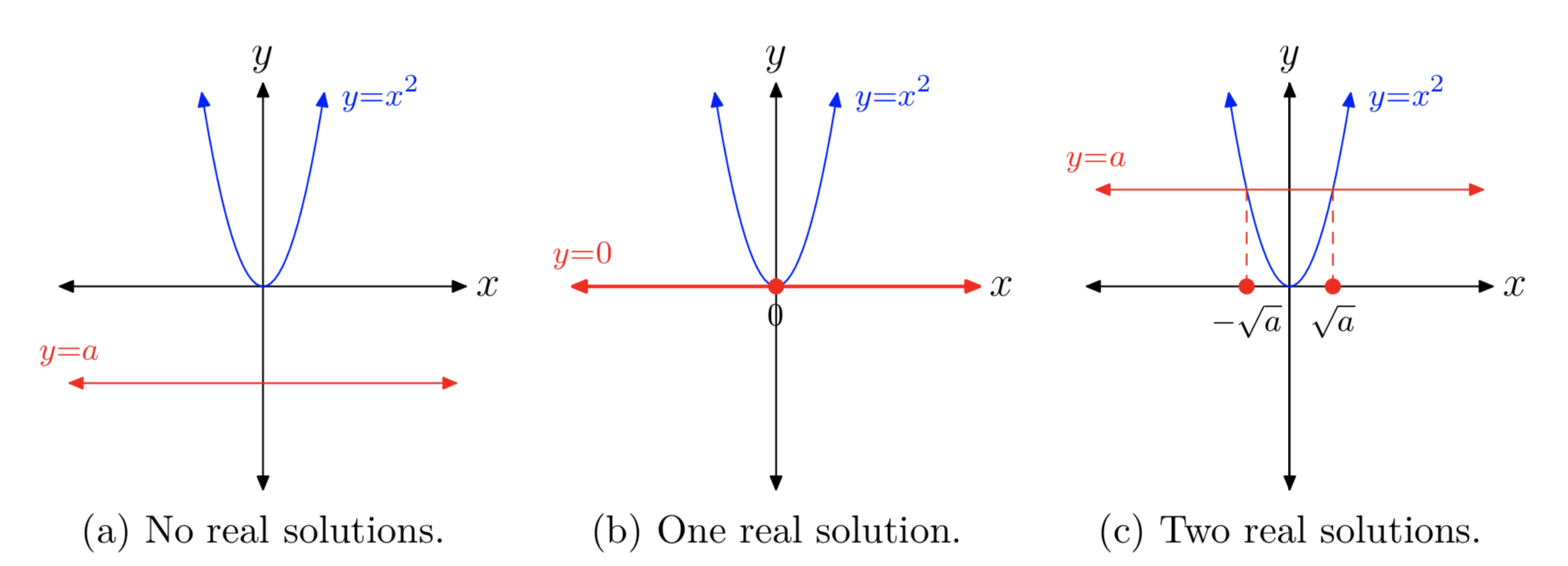
Існує три випадки, кожен залежно від значення та знака a У кожному випадку графіком лівої сторони\(x^2 = a\) є параболою, показаною на малюнках 1 (a), (b) та (c).

• Випадок I: a < 0

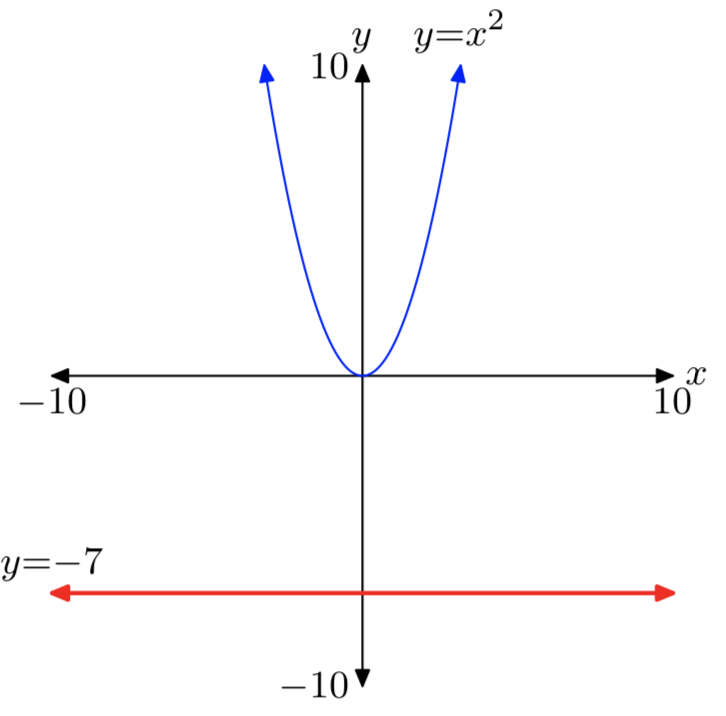
  Графік правої частини - це\(x^2 = a\) горизонтальна лінія, розташована на одиниці нижче осі х. Значить, графіки\(y = x^2\) і y = a не перетинаються і рівняння не\(x^2 = a\) має реальних розв'язків. Цей випадок показаний на малюнку 1 (а). Звідси випливає, що негативне число не має квадратного кореня.

• Випадок II: а = 0

  Графік правої частини\(x^2 = 0\) - це горизонтальна лінія, яка збігається з віссю х. Графік\(y = x^2\) перетинає графік y = 0 в одній точці, в

  вершина параболи. Таким чином, єдиним рішенням\(x^2 = 0\) є х = 0, як видно на малюнку 2 (b). Розчин - квадратний корінь 0, і позначається\(\sqrt{0}\), так випливає\(\sqrt{0} = 0\).

• Випадок III: а > 0

  Графік правої частини\(x^2 = a\) являє собою горизонтальну лінію, розташовану на одиниці вище осі х. Графіки\(y = x^2\) і y = a мають дві точки перетину, і тому рівняння\(x^2 = a\) має два реальних рішення, як показано на малюнку 1 (в). Рішення\(x^2 = a\) є\(x = \pm \sqrt{a}\). Зверніть увагу, що у нас є два позначення, одне, яке вимагає позитивного рішення, а друге, яке вимагає негативного рішення.

Малюнок 1: Рішення\(x^2 = a\) залежать від знака і значення\(a\).

Давайте розглянемо кілька прикладів.

Приклад\(\PageIndex{8}\)

Які рішення\(x^2 = −5\)?

Графік лівої частини\(x^2 = −5\) - парабола, зображена на малюнку 1 (а). Графік правого боку\(x^2 = −5\) являє собою горизонтальну лінію, розташовану на 5 одиниць нижче осі х. Таким чином, графіки не перетинаються і рівняння не\(x^2 = −5\) має реальних розв'язків.

Ви також можете міркувати наступним чином. Нас попросять знайти розв'язок\(x^2 = −5\), тому вам слід знайти число, квадрат якого дорівнює −5. Однак, коли ви квадратуєте дійсне число, результат завжди невід'ємний (нуль або позитивний). Неможливо зробити квадрат дійсного числа і отримати −5.

Зверніть увагу, що це також означає, що не можна взяти квадратний корінь від'ємного числа. Тобто не\(\sqrt{−5}\) є дійсним числом.

Приклад\(\PageIndex{9}\)

Які рішення\(x^2 = 0\)?

Існує тільки одне рішення, а саме х = 0. Зверніть увагу, що це означає, що\(\sqrt{0} = 0\).

Приклад\(\PageIndex{10}\)

Які рішення\(x^2 = 25\)?

Графік лівої частини\(x^2 = 25\) - парабола, зображена на малюнку 1 (в). Графік правої частини\(x^2 = 25\) являє собою горизонтальну лінію, розташовану на 25 одиниць вище осі х. Графіки будуть перетинатися в двох точках, тому рівняння\(x^2 = 25\) має два реальних рішення.

Розчини\(x^2 = 25\) називаються квадратними коренями 25 і пишуться\(x = \pm \sqrt{25}\). В цьому випадку ми можемо спростити далі і написати\(x = \pm 5\).

Вкрай важливо відзначити симетрію на малюнку 1 (в) і відзначити, що у нас є два реальних рішення, одне негативне і одне позитивне. Таким чином, нам потрібні два позначення: одне для позитивного квадратного кореня 25 і одне для негативного квадратного кореня 25.

Зверніть увагу\((5)^2 = 25\), що, так x = 5 є позитивним рішенням\(x^2 = 25\). Для позитивного рішення використовуємо позначення

\(\sqrt{25} = 5\).

Це вимовляється «позитивний квадратний корінь 25 дорівнює 5».

З іншого боку, зауважте\((−5)^2 = 25\), що x = −5 є негативним розв'язком\(x^2 = 25\). Для негативного рішення використовуємо позначення

\(−\sqrt{25} = −5\).

Це вимовляється «негативний квадратний корінь 25 дорівнює −5».

Ця дискусія призводить до наступного детального резюме.

РЕЗЮМЕ: КВАДРАТНИЙ КОРІНЬ

Розчини\(x^2 = a\) називаються «квадратними коренями а».

• Випадок I: a < 0. Рівняння не\(x^2 = a\) має реальних розв'язків.
• Випадок II: а = 0. Рівняння\(x^2 = a\) має одне дійсне рішення, а саме x = 0. Таким чином,\(\sqrt{0} = 0\).
• Випадок III: а > 0. Рівняння\(x^2 = a\) має два реальних рішення,\(x = \pm \sqrt{a}\). Позначення\(\sqrt{a}\) вимагає позитивного квадратного кореня a, тобто позитивного рішення\(x^2 = a\). Позначення\(−\sqrt{a}\) вимагає негативного квадратного кореня a, тобто негативного рішення\(x^2 = a\).

Коріння куба: Давайте перейдемо до визначення кубових коренів.

Визначення\(\PageIndex{11}\)

Задано дійсне число a, «кубічний корінь a» - це число x таке, що\(x^3 = a\).

Наприклад, 2 є кубовим коренем з 8, оскільки\(2^3 = 8\). Likewise, −4 є кубовим коренем −64 з тих пір\((−4)^3 = −64\). Таким чином, взяття кубового кореня є «протилежністю» кубінгу, тому визначення кореня куба повинно бути тісно пов'язане з графом\(y = x^3\), the cubing function. Therefore, we look for solutions of

\(x^3 = a\). (12)

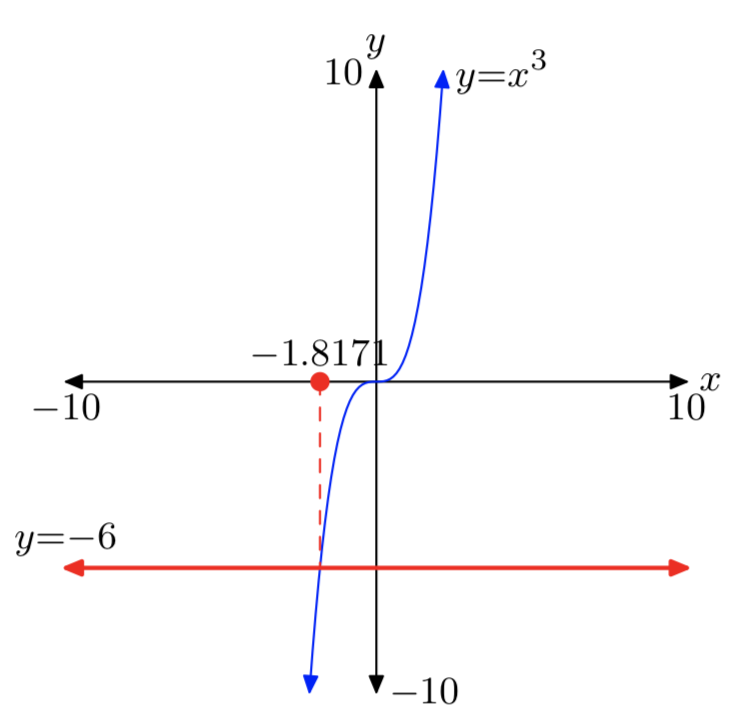
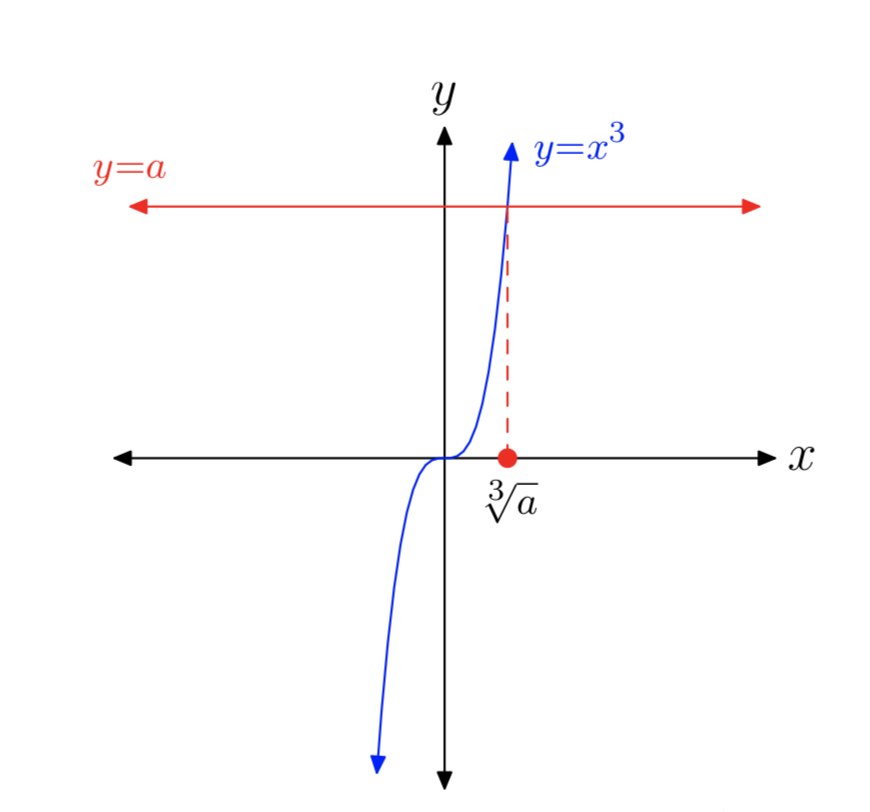
Через форму графіка\(y = x^3\), є тільки один випадок, щоб розглянути. Графік лівого боку\(x^3 = a\) показаний на малюнку 2. Графік правого боку\(x^3 = a\) - це горизонтальна лінія, розташована одиницями вище, на або нижче осі х, в залежності від знака і значення a Незалежно від розташування горизонтальної лінії y = a, буде тільки одна точка перетину, як показано на малюнку 2.

Далі докладний підсумок кубових коренів.

РЕЗЮМЕ: КОРІНЬ КУБА

Розчини\(x^3 = a\) називаються «кубовими коренями а». Незалежно від того, чи є a негативним, нульовим чи позитивним, не має різниці. Є рівно одне реальне рішення, а саме\(x = \sqrt[3]{a}\).

Малюнок 2. Графік\(y = x^3\) міжсекції граф y = a рівно в одному місці.

Давайте розглянемо кілька прикладів.

Приклад\(\PageIndex{13}\)

Які рішення\(x^3 = 8\)?

Графік лівої частини\(x^3 = 8\) - це кубічний многочлен, показаний на малюнку 2. Графік правого боку\(x^3 = 8\) являє собою горизонтальну лінію, розташовану на 8 одиниць вище осі х. Графіки мають одну точку перетину, тому рівняння\(x^3 = 8\) має рівно одне дійсне рішення.

Розчини\(x^3 = 8\) називаються «кубовими коренями 8». Як показано з графіка, існує рівно одне реальне рішення\(x^3 = 8\), а саме\(x = \sqrt[3]{8}\). З тих пір\((2)^3 = 8\), як випливає, що х = 2 є реальним рішенням\(x^3 = 8\). Отже, кубічний корінь з 8 дорівнює 2, і пишемо

\(\sqrt[3]{8} = 2\).

Зауважте, що у випадку кубічного кореня немає необхідності в двох позначеннях, які ми бачили у випадку квадратного кореня (один для позитивного квадратного кореня, один для негативного квадратного кореня). Це тому, що існує лише один справжній кубічний корінь. Таким чином,\(\sqrt[3]{8}\) вимовляється позначення «кубічний корінь 8».

Приклад\(\PageIndex{14}\)

Які рішення\(x^3 = 0\)?

Існує тільки одне рішення\(x^3 = 0\), namely x = 0. Це означає, що\(\sqrt[3]{0} = 0\).

Приклад\(\PageIndex{15}\)

Які рішення\(x^3 = −8\)?

Графік лівої частини\(x^3 = −8\) - це кубічний многочлен, показаний на малюнку 2. Графік правого боку\(x^3 = −8\) являє собою горизонтальну лінію, розташовану на 8 одиниць нижче осі х. Графіки мають тільки одну точку перетину, тому рівняння\(x^3 = −8\) має рівно одне дійсне рішення, позначене\(x = \sqrt[3]{−8}\). З тих пір\((−2)^3 = −8\), як випливає, що x = −2 є реальним розв'язком\(x^3 = −8\). Отже, корінь куба −8 дорівнює −2, і ми пишемо

\(\sqrt[3]{−8} = −2\).

Знову ж таки, оскільки існує лише одне реальне рішення\(x^3 = −8\), позначення\(\sqrt[3]{−8}\) вимовляється «кубічний корінь −8». Зауважте, що, на відміну від квадратного кореня від'ємного числа, допускається кубічний корінь від'ємного числа.

Вищі коріння: Попередні обговорення легко узагальнюються до вищих коренів, таких як четверте коріння, п'яте коріння, шосте коріння тощо.

Визначення\(\PageIndex{16}\)

Задано дійсне число a та натуральне число n, «\(n^{th}\)корінь a» - це число x таке, що\(x^n = a\).

Наприклад, 2 є\(6^{th}\) коренем 64, оскільки\(2^6 = 64\) і −3 є п'ятим коренем −243 з тих пір\((−3)^5 = −243\).

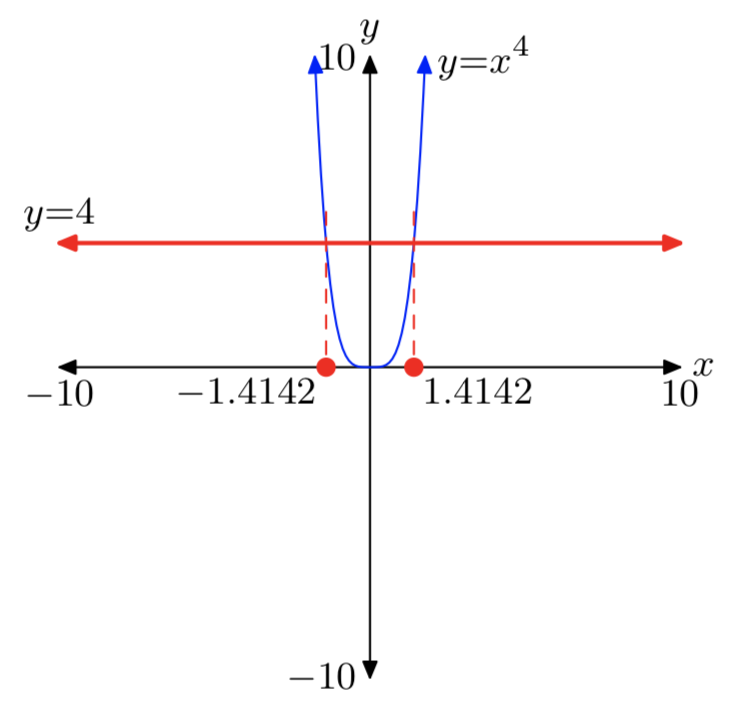
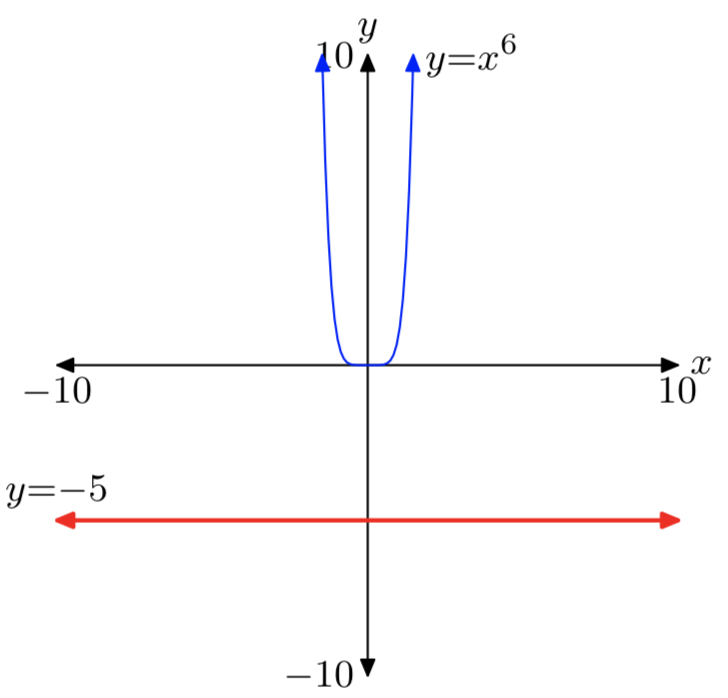
Випадок парних коренів (тобто, коли n парне) тісно паралельно випадку квадратних коренів. Це тому, що коли показник n парний, графік дуже\(y = x^n\) нагадує, що з\(y = x^2\). Наприклад, спостерігайте за випадком четвертих коренів, показаних на малюнках 3 (a), (b) та (c).

Малюнок 3. Рішення\(x^4 = a\) залежать від знака і значення a.

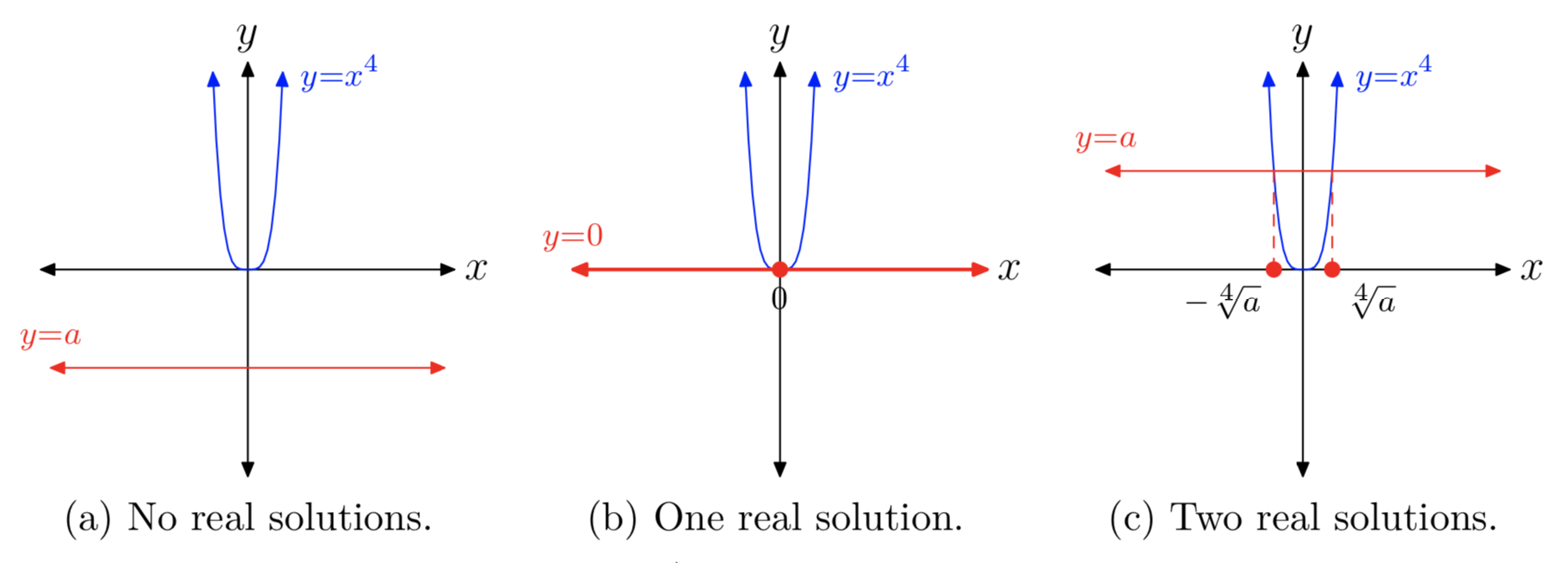
Обговорення рівних\(n^{th}\) коренів тісно паралелі, які представлені при введенні квадратних коренів, тому без зайвих прихильностей переходимо прямо до резюме.

РЕЗЮМЕ: НАВІТЬ\(N^{th}\) ROOT

Якщо n - натуральне парне число, то розв'язки\(x^n = a\) називаються «\(n^{th}\)коренями a».

• Випадок I: a < 0. Рівняння не\(x^n = a\) має реальних розв'язків.
• Випадок II: а = 0. Рівняння\(x^n = a\) має рівно одне дійсне рішення, а саме x = 0. Таким чином,\(\sqrt[n]{0} = 0\).
• Випадок III: а > 0. Рівняння\(x^n =a\) має два реальних рішення,\(x = \pm \sqrt[n]{a}\). Позначення\(\sqrt[n]{a}\) вимагає позитивного\(n^{th}\) кореня a, тобто позитивного рішення\(x^n = a\). Позначення\(−\sqrt[n]{a}\) вимагає негативного\(n^{th}\) кореня a, тобто негативного рішення\(x^n = a\).

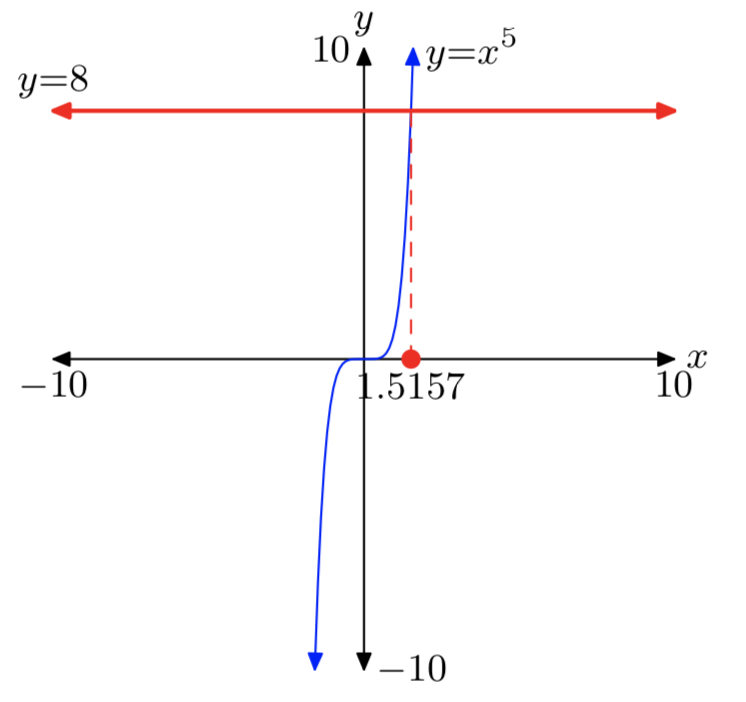
Так само випадок непарних коренів (тобто, коли n непарне) тісно паралельно випадку кубових коренів. Це тому, що коли показник n непарний, графік дуже\(y = x^n\) нагадує, що з\(y = x^3\). Наприклад, спостерігайте за випадком для п'ятих коренів, показаних на малюнку 4.

Малюнок 4. Графік\(y = x^5\) перетинає граф y = a рівно в одному місці.

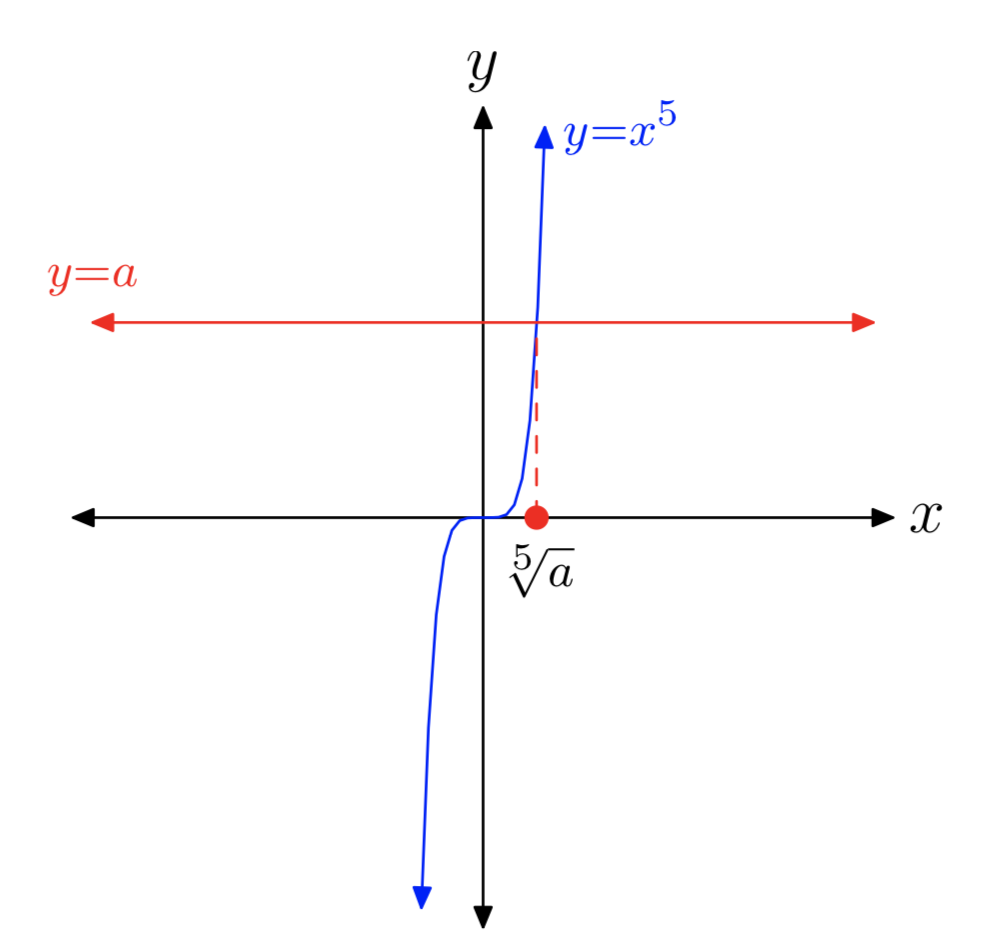
Обговорення непарних\(n^{th}\) коренів тісно паралельно з введенням кубових коренів, про які ми говорили раніше. Отже, не мудруючи лукаво, приступаємо прямо до резюме.

РЕЗЮМЕ: НЕПАРНІ\(N^{th}\) ROOT

Якщо n - натуральне непарне число, то\(x^n = a\) розв'язки називаються «\(n^{th}\)коренями a». Незалежно від того, чи є a негативним, нульовим чи позитивним, не має різниці. Існує рівно одне реальне рішення\(x^n = a\), позначається\(x = \sqrt[n]{a}\).

Зауваження 17. Символи\(\sqrt{}\) і\(\sqrt[n]{}\) для квадратного кореня і\(n^{th}\) root, respectively, are also called radicals.

Ми закриємо цей розділ ще кількома прикладами.

Приклад\(\PageIndex{18}\)

Які рішення\(x^4 = 16\)?

Графік лівої частини -\(x^4 = 16\) це квартичний многочлен, показаний на малюнку 3 (в). Графік правого боку\(x^4 = 16\) являє собою горизонтальну лінію, розташовану на 16 одиниць вище осі х. Графіки будуть перетинатися в двох точках, тому рівняння\(x^4 = 16\) має два реальних рішення.

Розчини\(x^4 = 16\) називаються четвертими коренями з 16 і пишуться\(x = \pm \sqrt[4]{16}\). Вкрай важливо відзначити симетрію на малюнку 3 (в) і відзначити, що у нас є два реальних рішення\(x^4 = 16\), один з яких негативний, а інший позитивний. Отже, нам потрібні два позначення, одне для позитивного четвертого кореня 16 і одне для негативного четвертого кореня 16.

Зауважте\(2^4 = 16\), що, так x = 2 є позитивним реальним рішенням\(x^4 = 16\). Для цього позитивного рішення використовуємо позначення

\(\sqrt[4]{16} = 2\).

Це вимовляється «позитивний четвертий корінь з 16 дорівнює 2».

З іншого боку, зауважте\((−2)^4 = 16\), що x = −2 є негативним дійсним розв'язком\(x^4 = 16\). Для цього негативного рішення використовуємо позначення

\(−\sqrt[4]{16} = −2\). (19)

Це вимовляється «негативний четвертий корінь 16 дорівнює −2».

Приклад\(\PageIndex{19}\)

Які рішення\(x^5 = −32\)?

Графік лівої сторони\(x^5 = −32\) - квінтичний многочлен, зображений на малюнку 4. Графік правого боку\(x^5 = −32\) являє собою горизонтальну лінію, розташовану на 32 одиниці нижче осі х. Графіки мають одну точку перетину, тому рівняння\(x^5 = −32\) має рівно одне дійсне рішення.

Розчини\(x^5 = −32\) називаються «п'ятим корінням −32». Як показано з графіка, існує рівно одне реальне рішення\(x^5 = −32\), а саме\(x = \sqrt[5]{−32}\). З тих пір\((−2)^5 = −32\), як випливає, що x = −2 є розв'язком\(x^5 = −32\). Отже, п'ятий корінь −32 дорівнює −2, і ми пишемо

\(\sqrt[5]{−32} = −2\).

Оскільки існує лише одне реальне рішення, позначення\(\sqrt[5]{−32}\) вимовляється «п'ятий корінь −32». Знову ж таки, на відміну від квадратного кореня або четвертого кореня від'ємного числа, допускається п'ятий корінь негативного числа.

Далеко не всі корені спрощують до раціональних чисел. Якби це було так, навіть не потрібно було б реалізовувати радикальні позначення. Розглянемо наступний приклад.

ПРИКЛАД\(\PageIndex{20}\)

Знайдіть всі реальні розв'язки рівняння\(x^2 = 7\), як графічно, так і алгебраїчно, і порівняйте свої результати.

Ми могли б легко намалювати грубі графіки\(y = x^2\) і y = 7 вручну, але давайте шукати більш високий рівень точності, попросивши графічний калькулятор впоратися з цим завданням.

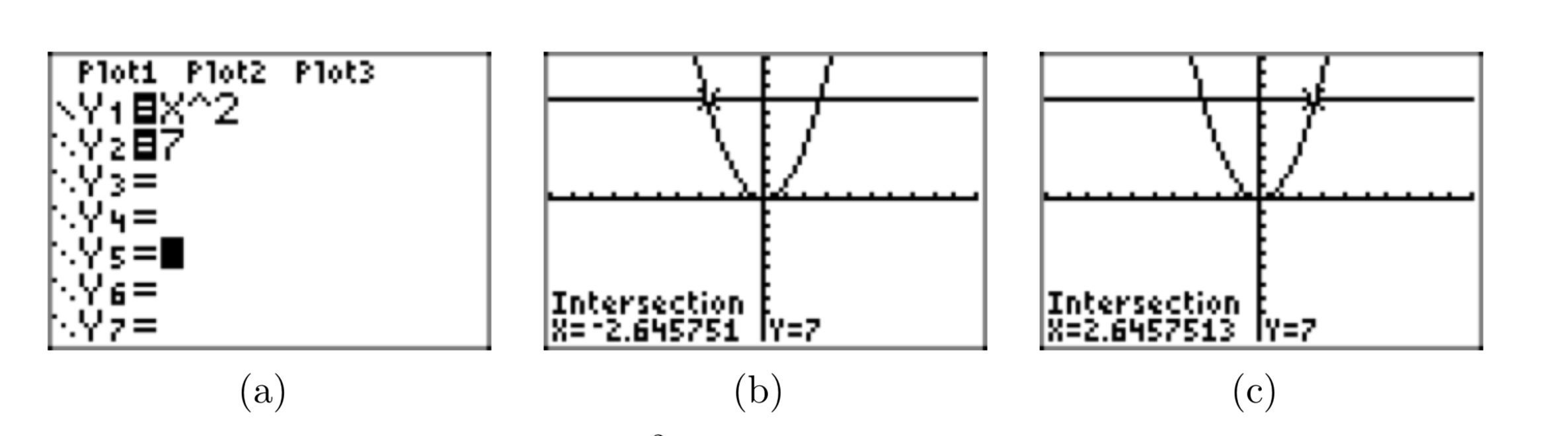
• Завантажте рівняння\(y = x^2\) і y = 7 в Y1 та Y2 у меню Y= калькулятора відповідно. Це показано на малюнку 5 (а).
• Використовуйте утиліту Intersect на графічному калькуляторі, щоб знайти координати точок перетину. X-координати цих точок, показані на малюнку 5 (b) і (c), є розв'язками рівняння\(x^2 = 7\).

Малюнок 5. Рішення\(x^2 = 7\) є\(x \approx −2.645751\) або\(x \approx 2.6457513\).

Керівні принципи для звітності графічного калькулятора рішень. Згадаймо стандартний метод звітування графічного калькулятора результатів по домашньому завданню:

• Скопіюйте зображення з вікна перегляду на домашній папір. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax, а потім позначте кожен графік своїм рівнянням, як показано на малюнку 6.
• Відкиньте пунктирні вертикальні лінії від кожної точки перетину до осі x. Затіньте та позначте свої рішення на осі x.

Малюнок 6. Рішення\(x^2 = 7\) є\(x \approx −2.645751\) або\(x \approx 2.6457513\).

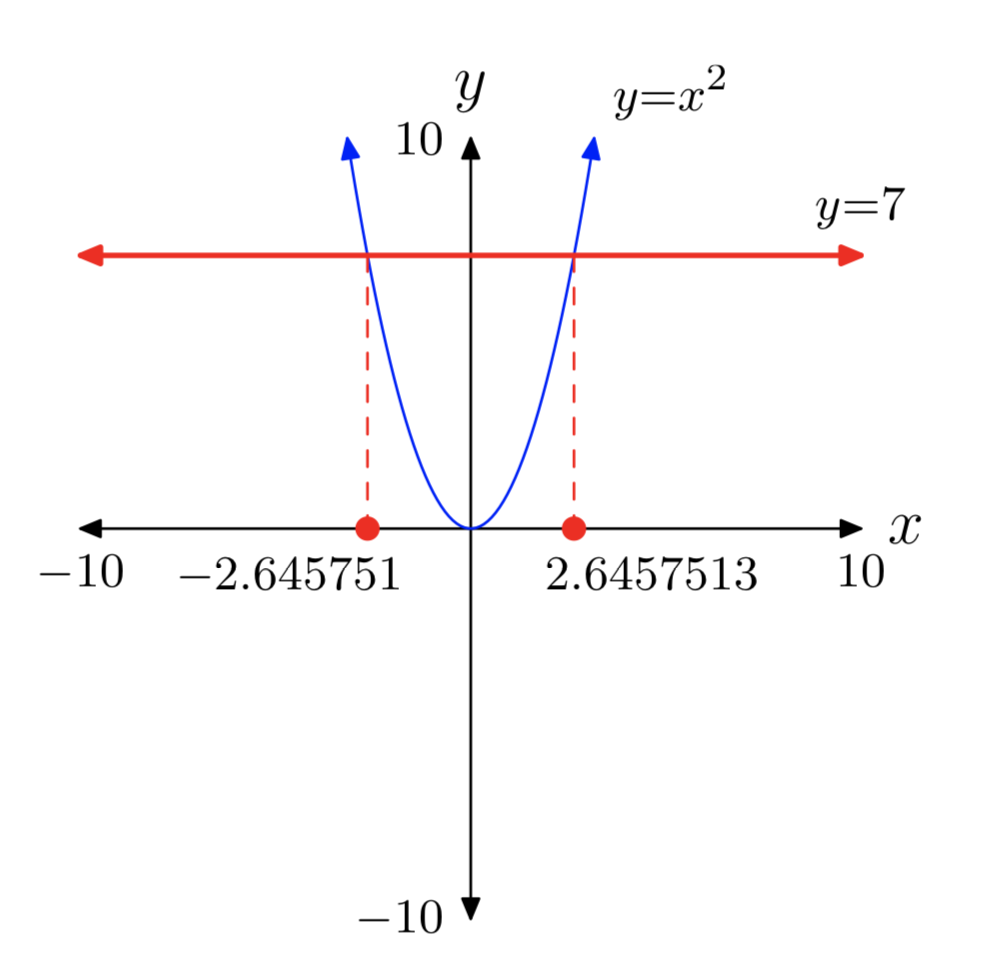
Значить, приблизними рішеннями є\(x \approx −2.645751\) або\(x \approx 2.6457513\).

З іншого боку, щоб знайти аналітичні рішення\(x^2 = 7\), ми просто беремо плюс-мінус квадратний корінь 7.

\(x^2 = 7\)

\(\sqrt{x} = \pm 7\)

Щоб порівняти ці точні рішення з приблизними розв'язками, знайденими за допомогою графічного калькулятора, скористайтеся калькулятором для обчислення\(\pm \sqrt{7}\), як показано на малюнку 7.

Малюнок 7. Наближення\(\pm \sqrt{7}\).

Зауважте, що ці наближення\(−\sqrt{7}\) та\(\sqrt{7}\) узгоджуються з рішеннями, знайденими за допомогою корисності перетину графічного калькулятора та повідомлених на малюнку 6.

Обидва\(−\sqrt{7}\) і\(\sqrt{7}\) є прикладами ірраціональних чисел, тобто чисел, які не можуть бути виражені у вигляді\(\frac{p}{q}\), де p і q - цілі числа.

Раціональні показники

Як і у випадку з визначенням негативних і нульових показників, розглянутих раніше в цьому розділі, виявляється, що раціональні показники можуть бути визначені таким чином, що Закони експонентів все ще будуть застосовуватися (і насправді, є тільки один спосіб зробити це).

Третій закон дає нам підказку, як визначити раціональні показники. Наприклад, припустимо, що ми хочемо визначити\(2^{\frac{1}{3}}\). Тоді за третім законом,

\((2^{\frac{1}{3}})^3 = 2^{\frac{1}{3} \cdot 3} = 2^1 = 2\),

Отже, взявши кубові коріння обох сторін, ми повинні визначити\(2^{\frac{1}{3}}\). за формулою

\(2^{\frac{1}{3}} = \sqrt[3]{2}\).

Цей же аргумент показує, що якщо n - будь-яке непарне натуральне число, то\(2^{\frac{1}{n}}\) має бути визначено за формулою

\(2^{\frac{1}{n}} = \sqrt[n]{2}\).

Однак для парного цілого числа n, здається, є вибір. Припустимо, що ми хочемо визначити\(2^{\frac{1}{2}}\). Тоді

\((2^{\frac{1}{2}})^2 = 2^{\frac{1}{2} \cdot 2} = 2^1 = 2\),

Отже,

\(2^{\frac{1}{2}} = \sqrt{2}\).

Однак негативний вибір для показника\(\frac{1}{2}\) призводить до проблем, оскільки тоді певні вирази не визначаються. Наприклад, з третього закону випливає, що

\((2^{\frac{1}{2}})^\frac{1}{2} = −\sqrt{−\sqrt{2}}\).

Але\(−\sqrt{2}\) є негативним,\(\sqrt{−\sqrt{2}}\) тому не визначено. Тому є сенс використовувати тільки позитивний вибір. Таким чином, для всіх n, парних і непарних,\(2^{\frac{1}{n}}\) визначається за формулою

\(2^{\frac{1}{n}} = \sqrt[n]{2}\).

Аналогічним чином для загального позитивного раціонального\(\frac{m}{n}\) третього закону мається на увазі, що

\(2^{\frac{m}{n}} = (2^m)^{\frac{1}{n}} = \sqrt[n]{2^m}\)

Але також,

\(2^{\frac{m}{n}} = (2^{\frac{1}{n}})^m = (\sqrt[n]{2})^m\)

Таким чином,

\(2^{\frac{m}{n}} = \sqrt[n]{2^m} = (\sqrt[n]{2})^m\)

Нарешті, негативні раціональні показники визначаються звичайним чином для негативних показників:

\(2^{−\frac{m}{n}} = \frac{1}{2^{\frac{m}{n}}}\)

Якщо говорити більш загально, то ось остаточне загальне визначення. З цим визначенням, Закони експонентів дотримуються для всіх раціональних показників.

Визначення\(\PageIndex{22}\)

Для позитивного раціонального показника\(\frac{m}{n}\), а b > 0

\(b^{\frac{m}{n}} = \sqrt[n]{b^m} = (\sqrt[n]{b})^m\)(23)

Для негативного раціонального показника\(−\frac{m}{n}\),

\(b^{−\frac{m}{n}} = \frac{1}{b^{\frac{m}{n}}}\)(24)

Зауваження 25. Для b < 0 ті ж визначення мають сенс лише тоді, коли n непарне. Наприклад,\((−2)^{\frac{1}{4}}\) не визначено.

Приклад\(\PageIndex{26}\)

Обчислити точні значення

(а)\(4^{\frac{5}{2}}\)

(б)\(64^{\frac{2}{3}}\)

(c)\(81^{−\frac{3}{4}}\)

Відповідь

(а)\(4^{\frac{5}{2}} = (4^{\frac{1}{2}})^5 = (\sqrt{4})^5 = 2^5 = 32\)

(б)\(64^{\frac{2}{3}} = (64^\frac{1}{3})^2 = (\sqrt[3]{64})^2 = 4^2 = 16\)

(c)\(81^{−\frac{3}{4}} = \frac{1}{81^{\frac{3}{4}}} = \frac{1}{(81^{\frac{1}{4}})^3} = \frac{1}{3^3} = \frac{1}{27}\)

Приклад\(\PageIndex{27}\)

Спростіть такі вирази, і запишіть їх у вигляді\(x^r\):

(а)\(x^{\frac{2}{3}}x^{\frac{1}{4}}\)

(б)\(\frac{x^{\frac{2}{3}}}{x^{\frac{1}{4}}}\)

(c)\((x^{−\frac{2}{3}})^{\frac{1}{4}}\)

Відповідь

(а)\(x^{\frac{2}{3}}x^{\frac{1}{4}} = x^{\frac{2}{3}+\frac{1}{4}} = x^{\frac{11}{12}}\)

(б)\(\frac{x^{\frac{2}{3}}}{x^{\frac{1}{4}}} = x^{\frac{2}{3}−\frac{1}{4}} = x^{\frac{5}{12}}\)

(c)\((x^{−\frac{2}{3}})^{\frac{1}{4}} = x^{−\frac{2}{3} \cdot \frac{1}{4}} = x^{−\frac{1}{6}}\)

Приклад\(\PageIndex{28}\)

Використовуйте раціональні показники для спрощення\(\sqrt[5]{\sqrt{x}}\), і запишіть його як єдиний радикал.

Відповідь

\(\sqrt[5]{\sqrt{x}} = (\sqrt{x})^{\frac{1}{5}} = (x^{\frac{1}{2}})^{\frac{1}{5}} = (x^{\frac{1}{2} \cdot \frac{1}{5}} = x^{\frac{1}{10}} = \sqrt[10]{x}\)

Приклад\(\PageIndex{29}\)

Використовуйте калькулятор для наближення\(2^{\frac{5}{8}}\).

Відповідь

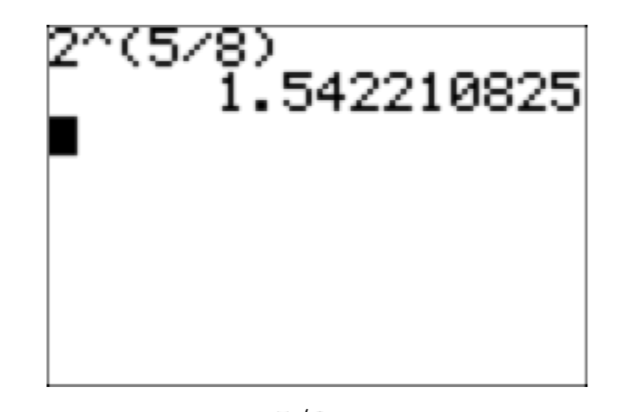
Малюнок 8. \(2^{\frac{5}{8}} \approx 1.542210825\)

Ірраціональні експоненти

А як щодо ірраціональних показників? Чи є спосіб визначити числа на кшталт\(2^{\sqrt{2}}\) і\(3^{\pi}\)? Виявляється, відповідь - так. Хоча суворе визначення того,\(b^s\) коли s є ірраціональним, виходить за рамки цієї книги, це не важко зрозуміти, як можна продовжити, щоб знайти значення для такого числа. Наприклад, якщо ми хочемо обчислити значення\(2^{\sqrt{2}}\), ми можемо почати з раціональних наближень для\(\sqrt{2}\). Оскільки\(\sqrt{2}\) = 1.41421356237310., послідовні повноваження

\(2^1\),\(2^{1.4}\),\(2^{1.41}\)\(2^{1.414}\),\(2^{1.4142}\),\(2^{1.41421}\),\(2^{1.414213}\),\(2^{1.4142135}\),\(2^{1.41421356}\),\(2^{1.414213562}\)\(2^{1.4142135623}\),,,.

повинні бути ближче і ближче наближені до потрібного значення\(2^{\sqrt{2}}\).

Насправді, використовуючи більш просунуту математичну теорію (в кінцевому підсумку засновану на фактичній побудові дійсної системи числення), можна показати, що ці сили наближаються\(2^{\sqrt{2}}\) до єдиного дійсного числа, і ми визначаємо, що це число. Використовуючи свій калькулятор, ви можете спостерігати цю конвергенцію і отримати наближення, обчисливши наведені вище потужності.

Малюнок 9.

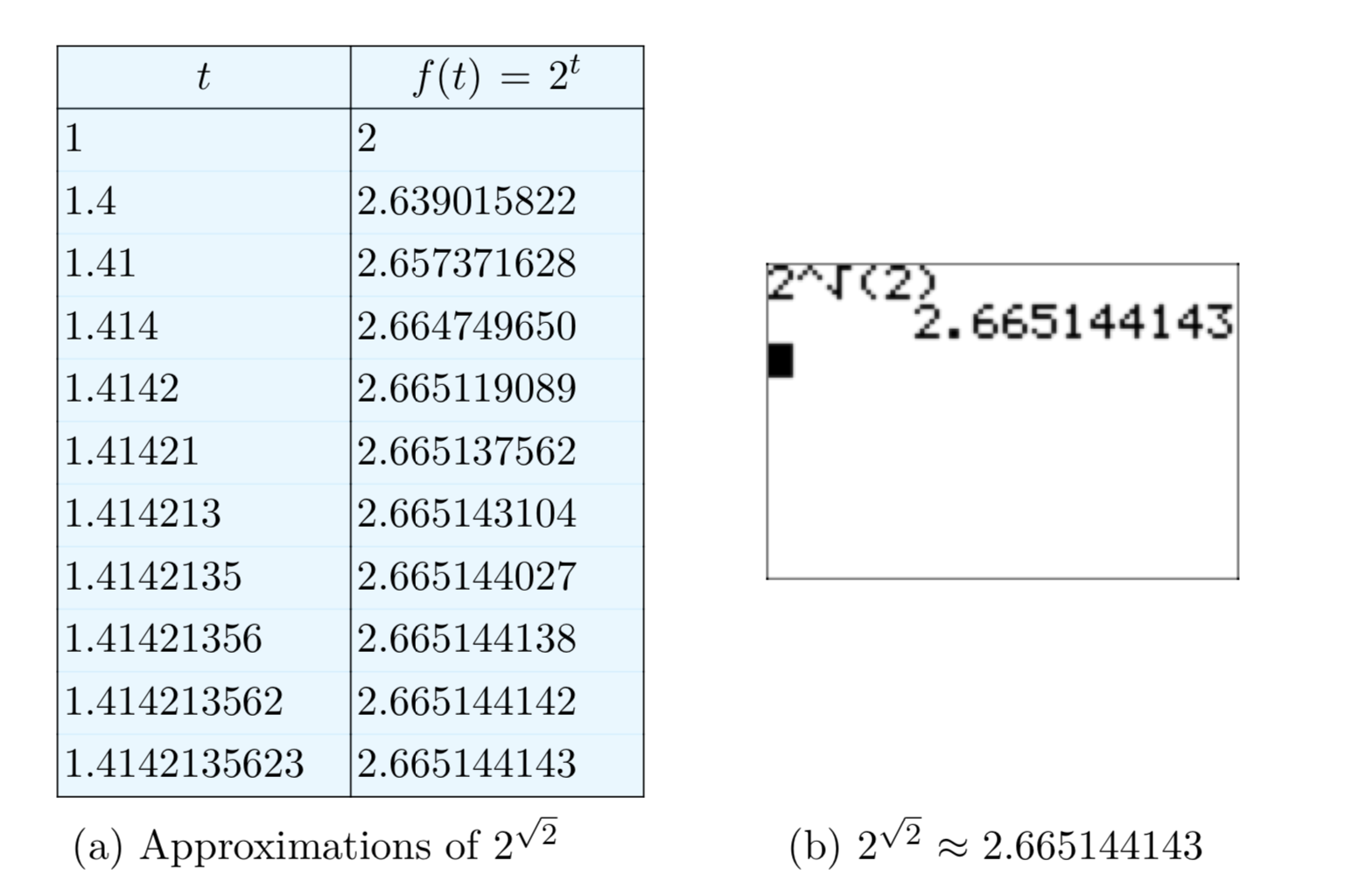
Останнє значення в таблиці на малюнку 9 (а) - правильне наближення\(2^{\sqrt{2}}\) до 10 цифр точності. Ваш калькулятор отримає таке ж наближення, коли ви попросите його обчислити\(2^{\sqrt{2}}\) безпосередньо (див. Рисунок 9 (b)).

Аналогічним чином,\(b^s\) може бути визначено для будь-якого ірраціонального показника s та будь-якого b > 0. У поєднанні з попередньою роботою в цьому розділі випливає, що\(b^s\) визначається для кожного реального показника s.

Вправа

У вправах 1 - 12 обчислити точне значення.

Вправа\(\PageIndex{1}\)

\(3^{−5}\)

Відповідь

\(\frac{1}{243}\)

Вправа\(\PageIndex{2}\)

\(4^2\)

Вправа\(\PageIndex{3}\)

\((\frac{3}{2})^3\)

Відповідь

\(\frac{27}{8}\)

Вправа\(\PageIndex{4}\)

\((\frac{2}{3})^1\)

Вправа\(\PageIndex{5}\)

\(6^{−2}\)

Відповідь

\(\frac{1}{36}\)

Вправа\(\PageIndex{6}\)

\(4^{−3}\)

Вправа\(\PageIndex{7}\)

\((\frac{2}{3})^{−3}\)

Відповідь

\(\frac{27}{8}\)

Вправа\(\PageIndex{8}\)

\((\frac{1}{3})^{−3}\)

Вправа\(\PageIndex{9}\)

\(7^1\)

Відповідь

7

Вправа\(\PageIndex{10}\)

\((\frac{3}{2})^{−4}\)

Вправа\(\PageIndex{11}\)

\((\frac{5}{6})^3\)

Відповідь

\(\frac{125}{216}\)

Вправа\(\PageIndex{12}\)

\(3^2\)

У вправах 13 - 24 виконайте кожне з наступних завдань для даного рівняння.

1. Завантажте ліву та праву сторони заданого рівняння в Y1 і Y2 відповідно. Налаштуйте параметри WINDOW, доки всі точки перетину (якщо такі є) не будуть видимі у вікні перегляду. Використовуйте утиліту intersect в меню CALC для визначення координат будь-яких точок перетину.
2. Зробіть копію зображення у вікні перегляду на домашньому папері. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax. Позначте кожен граф своїм рівнянням. Відкиньте пунктирні вертикальні лінії від кожної точки перетину до осі x, потім затіньте та позначте кожний розв'язок заданого рівняння на осі x. Не забудьте намалювати всі лінії лінійкою.
3. Вирішіть кожну задачу алгебраїчно. Скористайтеся калькулятором для наближення будь-яких радикалів і порівняйте ці рішення з тими, що знаходяться в частинок (1) і (2).

Вправа\(\PageIndex{13}\)

\(x^2 = 5\)

Відповідь

\(x = \pm \sqrt{5}\)

Вправа\(\PageIndex{14}\)

\(x^2 = 7\)

Вправа\(\PageIndex{15}\)

\(x^2 = −7\)

Відповідь

Ніяких реальних рішень.

Вправа\(\PageIndex{16}\)

\(x^2 = −3\)

Вправа\(\PageIndex{17}\)

\(x^3 = −6\)

Відповідь

\(x = \sqrt[3]{−6}\)

Вправа\(\PageIndex{18}\)

\(x^3 = −4\)

Вправа\(\PageIndex{19}\)

\(x^4 = 4\)

Відповідь

\(x = \pm \sqrt[4]{4}\)

Вправа\(\PageIndex{20}\)

\(x^4 = −7\)

Вправа\(\PageIndex{21}\)

\(x^5 = 8\)

Відповідь

\(x = \sqrt[5]{8}\)

Вправа\(\PageIndex{22}\)

\(x^5 = 4\)

Вправа\(\PageIndex{23}\)

\(x^6 = −5\)

Відповідь

Ніяких реальних рішень.

Вправа\(\PageIndex{24}\)

\(x^6 = 9\)

У вправах 25 - 40 спростіть даний радикальний вираз.

Вправа\(\PageIndex{25}\)

\(\sqrt{49}\)

Відповідь

7

Вправа\(\PageIndex{26}\)

\(\sqrt{121}\)

Вправа\(\PageIndex{27}\)

\(\sqrt{−36}\)

Відповідь

Чи не дійсне число.

Вправа\(\PageIndex{28}\)

\(\sqrt{−100}\)

Вправа\(\PageIndex{29}\)

\(\sqrt[3]{−1}\)

Відповідь

3

Вправа\(\PageIndex{30}\)

\(\sqrt[3]{−1}\)

Вправа\(\PageIndex{31}\)

\(\sqrt[3]{−125}\)

Відповідь

−5

Вправа\(\PageIndex{32}\)

\(\sqrt[3]{64}\)

Вправа\(\PageIndex{33}\)

\(\sqrt[4]{−16}\)

Відповідь

Чи не дійсне число.

Вправа\(\PageIndex{34}\)

\(\sqrt[4]{81}\)

Вправа\(\PageIndex{35}\)

\(\sqrt[4]{16}\)

Відповідь

2

Вправа\(\PageIndex{36}\)

\(\sqrt[3]{−625}\)

Вправа\(\PageIndex{37}\)

\(\sqrt[5]{−32}\)

Відповідь

−2

Вправа\(\PageIndex{38}\)

\(\sqrt[5]{243}\)

Вправа\(\PageIndex{39}\)

\(\sqrt[5]{1024}\)

Відповідь

4

Вправа\(\PageIndex{40}\)

\(\sqrt[5]{−3125}\)

Вправа\(\PageIndex{41}\)

Порівняйте і\(\sqrt{(−2)^2}\) контрастуйте і\((\sqrt{−2})^2\).

Відповідь

\(\sqrt{(−2)^2} = 2\), Хоча не\((\sqrt{−2})^2\) є дійсним числом.

Вправа\(\PageIndex{42}\)

Порівняйте і\(\sqrt[4]{(−3)^4}\) контрастуйте і\((\sqrt[4]{−3})^4\).

Вправа\(\PageIndex{43}\)

Порівняйте і\(\sqrt[3]{(−5)^3}\) контрастуйте і\((\sqrt[3]{−5})^3\).

Відповідь

Обидва рівні −5.

Вправа\(\PageIndex{44}\)

Порівняйте і\(\sqrt[5]{(−2)^5}\) контрастуйте і\((\sqrt[5]{−2})^5\).

У вправах 45 - 56 обчислити точне значення.

Вправа\(\PageIndex{45}\)

\(25^{−\frac{3}{2}}\)

Відповідь

\(\frac{1}{125}\)

Вправа\(\PageIndex{46}\)

\(16^{−\frac{5}{4}}\)

Вправа\(\PageIndex{47}\)

\(8^{\frac{4}{3}}\)

Відповідь

16

Вправа\(\PageIndex{48}\)

\(625^{−\frac{3}{4}}\)

Вправа\(\PageIndex{49}\)

\(16^{\frac{3}{2}}\)

Відповідь

64

Вправа\(\PageIndex{50}\)

\(64^{\frac{2}{3}}\)

Вправа\(\PageIndex{51}\)

\(27^{\frac{2}{3}}\)

Відповідь

9

Вправа\(\PageIndex{52}\)

\(625^{\frac{3}{4}}\)

Вправа\(\PageIndex{53}\)

\(256^{\frac{5}{4}}\)

Відповідь

1024

Вправа\(\PageIndex{54}\)

\(4^{−\frac{3}{2}}\)

Вправа\(\PageIndex{55}\)

\(256^{−\frac{3}{4}}\)

Відповідь

\(\frac{1}{64}\)

Вправа\(\PageIndex{56}\)

\(81^{−\frac{5}{4}}\)

У Вправи 57 - 64 спростіть твір, і напишіть свою відповідь у формі\(x^r\).

Вправа\(\PageIndex{57}\)

\(x^{\frac{5}{4}}x^{\frac{5}{4}}\)

Відповідь

\(x^{\frac{5}{2}}\)

Вправа\(\PageIndex{58}\)

\(x^{\frac{5}{3}}x^{−\frac{5}{4}}\)

Вправа\(\PageIndex{59}\)

\(x^{−\frac{1}{3}}x^{\frac{5}{2}}\)

Відповідь

\(x^{\frac{13}{6}}\)

Вправа\(\PageIndex{60}\)

\(x^{−\frac{3}{5}}x^{\frac{3}{2}}\)

Вправа\(\PageIndex{61}\)

\(x^{\frac{4}{5}}x^{−\frac{4}{3}}\)

Відповідь

\(x^{−\frac{8}{15}}\)

Вправа\(\PageIndex{62}\)

\(x^{−\frac{5}{4}}x^{\frac{1}{2}}\)

Вправа\(\PageIndex{63}\)

\(x^{−\frac{2}{5}}x^{−\frac{3}{2}}\)

Відповідь

\(x^{−\frac{19}{10}}\)

Вправа\(\PageIndex{64}\)

\(x^{−\frac{5}{4}}x^{\frac{5}{2}}\)

У вправах 65 - 72 спростіть частку, і напишіть свою відповідь у формі\(x^r\).

Вправа\(\PageIndex{65}\)

\(\frac{x^{−\frac{5}{4}}}{x^{\frac{1}{5}}}\)

Відповідь

\(x^{−\frac{29}{20}}\)

Вправа\(\PageIndex{66}\)

\(\frac{x^{−\frac{2}{3}}}{x^{\frac{1}{4}}}\)

Вправа\(\PageIndex{67}\)

\(\frac{x^{−\frac{1}{2}}}{x^{−\frac{3}{5}}}\)

Відповідь

\(x^{\frac{1}{10}}\)

Вправа\(\PageIndex{68}\)

\(\frac{x^{−\frac{5}{2}}}{x^{\frac{5}{2}}}\)

Вправа\(\PageIndex{69}\)

\(\frac{x^{\frac{3}{5}}}{x^{−\frac{1}{4}}}\)

Відповідь

\(x^{\frac{17}{20}}\)

Вправа\(\PageIndex{70}\)

\(\frac{x^{\frac{1}{3}}}{x^{−\frac{1}{2}}}\)

Вправа\(\PageIndex{71}\)

\(\frac{x^{−\frac{5}{4}}}{x^{\frac{2}{3}}}\)

Відповідь

\(x^{−\frac{23}{12}}\)

Вправа\(\PageIndex{72}\)

\(\frac{x^{\frac{1}{3}}}{x^{\frac{1}{2}}}\)

У вправах 73 - 80 спростіть вираз, і напишіть свою відповідь у формі\(x^r\).

Вправа\(\PageIndex{73}\)

\((x^{\frac{1}{2}})^{\frac{4}{3}}\)

Відповідь

\(x^{\frac{2}{3}}\)

Вправа\(\PageIndex{74}\)

\((x^{−\frac{1}{2}})^{−\frac{1}{2}}\)

Вправа\(\PageIndex{75}\)

\((x^{−\frac{5}{4}})^{\frac{1}{2}}\)

Відповідь

\(x^{−\frac{5}{8}}\)

Вправа\(\PageIndex{76}\)

\((x^{−\frac{1}{5}})^{−\frac{3}{2}}\)

Вправа\(\PageIndex{77}\)

\((x^{−\frac{1}{2}})^{\frac{3}{2}}\)

Відповідь

\(x^{−\frac{3}{4}}\)

Вправа\(\PageIndex{78}\)

\((x^{−\frac{1}{3}})^{−\frac{1}{2}}\)

Вправа\(\PageIndex{79}\)

\((x^{\frac{1}{5}})^{−\frac{1}{2}}\)

Відповідь

\(x^{−\frac{1}{10}}\)

Вправа\(\PageIndex{80}\)

\((x^{\frac{2}{5}})^{−\frac{1}{5}}\)

​​​​​​​