5.1: Коріння і радикали

Last updated
Save as PDF

Page ID: 58161

Anonymous
LibreTexts

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Визначте та оцініть квадратні та кубові корені.
Визначте область функцій за участю квадратних і кубових коренів.
Оцініть\(n\) коріння.
Спрощення радикалів, використовуючи продукт і часткові правила для радикалів.

Квадратні та кубові корені

Нагадаємо, що квадратний корінь ¹ числа - це число, яке при множенні на себе дає вихідне число. Наприклад,\(5\) це квадратний корінь\(25\), тому що\(5^{2} = 25\). Так як\((−5)^{2} = 25\), можна сказати, що\(−5\) це квадратний корінь\(25\), а також. Кожне додатне дійсне число має два квадратних кореня, один позитивний і один негативний. З цієї причини ми використовуємо знак радикала для\(√\) позначення головного (невід'ємного) квадратного кореня ² і негативний знак перед радикалом\(−√\) для позначення негативного квадратного кореня.

\(\begin{aligned} \sqrt { 25 } & = 5 \quad\quad\color{Cerulean} { Positive\: square \:root \:of \: 25} \\ - \sqrt { 25 } & = - 5 \quad\:\color{Cerulean} { Negative \:square\: root \:of\: 25} \end{aligned}\)

Нуль - єдине дійсне число з одним квадратним коренем.

\(\sqrt { 0 } = 0 \text { because } 0 ^ { 2 } = 0\)

Приклад\(\PageIndex{1}\):

Оцінити.

\(\sqrt { 121 }\)
\(- \sqrt { 81 }\)

Рішення

\(\sqrt { 121 } = \sqrt { 11 ^ { 2 } } = 11\)
\(- \sqrt { 81 } = - \sqrt { 9 ^ { 2 } } = - 9\)

Якщо радиканд ³, число всередині знака радикала, може враховуватися як квадрат іншого числа, то очевидний квадратний корінь числа. В даному випадку ми маємо наступну властивість:

\(\sqrt { a ^ { 2 } } = a \quad \text { if } \quad a \geq 0\)

Або загалом,

\(\sqrt { a ^ { 2 } } = | a | \quad \text { if } \quad a \in R\)

Абсолютне значення має важливе значення, оскільки\(a\) може бути від'ємним числом, а знак радикала позначає основний квадратний корінь. Наприклад,

\(\sqrt { ( - 8 ) ^ { 2 } } = | -8| = 8\)

Використовуйте абсолютне значення, щоб забезпечити позитивний результат.

Приклад\(\PageIndex{2}\):

Спростити:\(\sqrt { ( x - 2 ) ^ { 2 } }\).

Рішення

Тут змінний вираз\(x − 2\) може бути від'ємним, нульовим або позитивним. Оскільки знак залежить від невідомої кількості\(x\), ми повинні переконатися, що ми отримуємо основний квадратний корінь, використовуючи абсолютне значення.

\(\sqrt { ( x - 2 ) ^ { 2 } } = | x - 2 |\)

Відповідь:

\(| x - 2 |\)

Важливість використання абсолютного значення в попередньому прикладі очевидна, коли ми оцінюємо за допомогою значень, які роблять радикаі негативним. Наприклад, коли\(x = 1\),

\(\begin{aligned} \sqrt { ( x - 2 ) ^ { 2 } } & = | x - 2 | \\ & = | 1 - 2 | \\ & = | - 1 | \\ & = 1 \end{aligned}\)

Далі розглянемо квадратний корінь від'ємного числа. Щоб визначити квадратний корінь\(−25\), ви повинні знайти число, яке при квадраті призводить до\(−25\):

\(\sqrt { - 25 } = \color{Cerulean}{?} \color{black}\quad{ \text { or }} \quad( \color{Cerulean}{?}\color{black}{ )} ^ { 2 } = - 25\)

Однак будь-яке дійсне число в квадраті завжди призводить до позитивного числа. Квадратний корінь від'ємного числа в даний час залишається невизначеною. Наразі ми будемо констатувати, що\(\sqrt { - 25 }\) це не реальне число. Отже, функція квадратного кореня ⁴, задана не\(f ( x ) = \sqrt { x }\) є дійсним числом, якщо\(x\) -значення від'ємні. Найменше значення в домені дорівнює нулю. Наприклад,\(f ( 0 ) = \sqrt { 0 } = 0\) і\(f ( 4 ) = \sqrt { 4 } = 2\). Нагадаємо графік функції квадратного кореня.

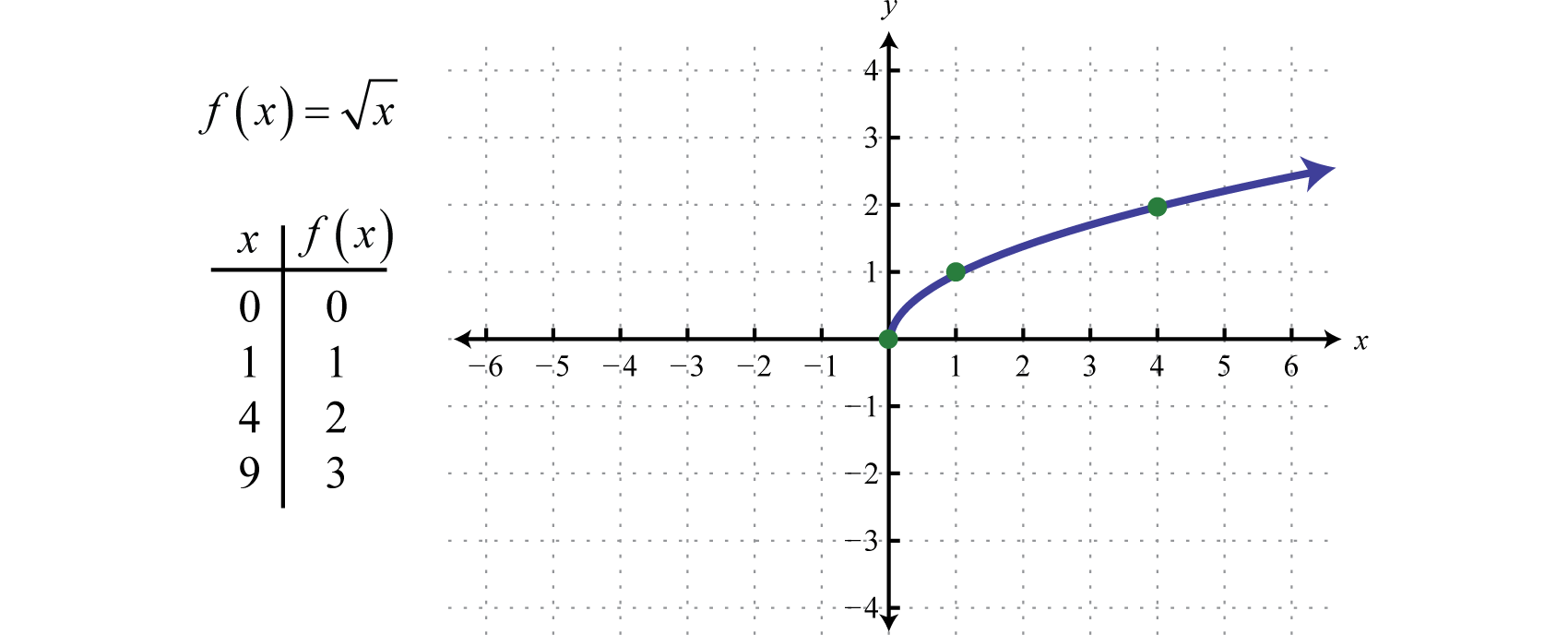
Домен і діапазон складаються з дійсних чисел, більших або рівних нулю:\([0, ∞)\). Щоб визначити область функції з квадратним коренем, ми розглянемо радиканд і знаходимо значення, які дають невід'ємні результати.

Приклад\(\PageIndex{3}\):

Визначте область функції, визначеної за допомогою\(f ( x ) = \sqrt { 2 x + 3 }\).

Рішення

Ось радиканд\(2x + 3\). Цей вираз має бути нульовим або позитивним. Іншими словами,

\(2 x + 3 \geq 0\)

Вирішити для\(x\).

\(\begin{aligned} 2 x + 3 & \geq 0 \\ 2 x & \geq - 3 \\ x & \geq - \frac { 3 } { 2 } \end{aligned}\)

Відповідь:

Домен:\(\left[ - \frac { 3 } { 2 } , \infty \right)\)

Кубичний корінь ⁵ числа - це число, яке при помноженні на себе три рази дає початкове число. Крім того, ми позначаємо кубічний корінь за допомогою символу\(\sqrt [ 3 ] { }\), де\(3\) називається індекс ⁶. Наприклад,

\(\sqrt [ 3 ] { 64 } = 4 , \text { because } 4 ^ { 3 } = 64\)

Твір трьох рівних факторів буде позитивним, якщо фактор позитивний і негативний, якщо фактор негативний. З цієї причини будь-яке дійсне число матиме лише один реальний кубічний корінь. Звідси технічні характеристики, пов'язані з основним коренем, не застосовуються. Наприклад,

\(\sqrt [ 3 ] { - 64 } = - 4 , \text { because } ( - 4 ) ^ { 3 } = - 64\)

Загалом, з огляду на будь-яке дійсне число\(a\), ми маємо наступну властивість:

\(\sqrt [ 3 ] { a ^ { 3 } } = a \quad \text { if } \quad a \in R\)

Спрощуючи кубічні корені, шукайте фактори, які є ідеальними кубами.

Приклад\(\PageIndex{4}\):

Оцінити.

\(\sqrt [ 3 ] { 8 }\)
\(\sqrt [ 3 ] { 0 }\)
\(\sqrt [ 3 ] { \frac { 1 } { 27 } }\)
\(\sqrt [ 3 ] { - 1 }\)
\(\sqrt [ 3 ] { - 125 }\)

Рішення

\(\sqrt [ 3 ] { 8 } = \sqrt [ 3 ] { 2 ^ { 3 } } = 2\)
\(\sqrt [ 3 ] { 0 } = \sqrt [ 3 ] { 0 ^ { 3 } } = 0\)
\(\sqrt [ 3 ] { \frac { 1 } { 27 } } = \sqrt [ 3 ] { \left( \frac { 1 } { 3 } \right) ^ { 3 } } = \frac { 1 } { 3 }\)
\(\sqrt [ 3 ] { - 1 } = \sqrt [ 3 ] { ( - 1 ) ^ { 3 } } = - 1\)
\(\sqrt [ 3 ] { - 125 } = \sqrt [ 3 ] { ( - 5 ) ^ { 3 } } = - 5\)

Може трапитися так, що радиканд не є ідеальним квадратом або кубом. Якщо ціле число не є ідеальною силою індексу, то його корінь буде нераціональним. Наприклад,\(\sqrt [ 3 ] { 2 }\) це ірраціональне число, яке можна наблизити на більшості калькуляторів за допомогою\(\sqrt [ x ] { }\) кореневої кнопки. Залежно від калькулятора, ми зазвичай набираємо індекс перед натисканням кнопки, а потім радиканд наступним чином:

\(3 \quad\sqrt [ x ] {y }\quad2\quad=\)

Тому у нас є

\(\sqrt [ 3 ] { 2 } \approx 1.260 , \quad \text { because } \quad 1.260 ^{\wedge} 3 \approx 2\)

Оскільки кубові корені можуть бути від'ємними, нульовими або додатними, ми не використовуємо жодних абсолютних значень.

Приклад\(\PageIndex{5}\):

Спростити:\(\sqrt [ 3 ] { ( y - 7 ) ^ { 3 } }\).

Рішення

Кубичний корінь кількості в кубі - це така кількість.

\(\sqrt [ 3 ] { ( y - 7 ) ^ { 3 } } = y - 7\)

Відповідь:

\(y-7\)

Вправа\(\PageIndex{1}\)

Оцініть:\(\sqrt [ 3 ] { - 1000 }\).

Відповідь

\(=10\)

www.youtube.com/В/Б06Ніс-3Гіг

Далі розглянемо функцію кореня куба ⁷:

\(f ( x ) = \sqrt [ 3 ] { x } \quad\color{Cerulean}{Cube\:root\:function.}\)

Оскільки кубічний корінь може бути як негативним, так і позитивним, робимо висновок, що домен складається з усіх дійсних чисел. Намалюйте графік, намалювавши точки. Виберіть деякі позитивні і від'ємні значення для\(x\), а також нуль, а потім обчислити відповідні\(y\) -значення.

Таблиця\(\PageIndex{1}\)
\(x\)	\(f(x)\)	\(f ( x ) = \sqrt [ 3 ] { x }\)	\(\color{Cerulean}{Ordered\:Pairs}\)
\ (x\) ">\(-8\)	\ (f (x)\) ">\(\color{Cerulean}{-2}\)	\ (f (x) =\ sqrt [3] {x}\) ">\(f ( - 8 ) = \sqrt [ 3 ] { - 8 } = - 2\)	\ (\ color {Cerulean} {Упорядковано\ :Пари}\) ">\((-8,-2)\)
\ (x\) ">\(-1\)	\ (f (x)\) ">\(\color{Cerulean}{-1}\)	\ (f (x) =\ sqrt [3] {x}\) ">\(f ( - 1 ) = \sqrt [ 3 ] { - 1 } = - 1\)	\ (\ color {Cerulean} {Упорядковано\ :Пари}\) ">\((-1,-1)\)
\ (x\) ">\(0\)	\ (f (x)\) ">\(\color{Cerulean}{0}\)	\ (f (x) =\ sqrt [3] {x}\) ">\(f ( 0 ) = \sqrt [ 3 ] { 0 } = 0\)	\ (\ color {Cerulean} {Упорядковано\ :Пари}\) ">\((0,0)\)
\ (x\) ">\(1\)	\ (f (x)\) ">\(\color{Cerulean}{1}\)	\ (f (x) =\ sqrt [3] {x}\) ">\(f ( 1 ) = \sqrt [ 3 ] { 1 } = 1\)	\ (\ color {Cerulean} {Упорядковано\ :Пари}\) ">\((1,1)\)
\ (x\) ">\(8\)	\ (f (x)\) ">\(\color{Cerulean}{2}\)	\ (f (x) =\ sqrt [3] {x}\) ">\(f ( 8 ) = \sqrt [ 3 ] { 8 } = 2\)	\ (\ color {Cerulean} {Упорядковано\ :Пари}\) ">\((8,2)\)

Побудуйте точки та намалюйте графік функції кореня куба.

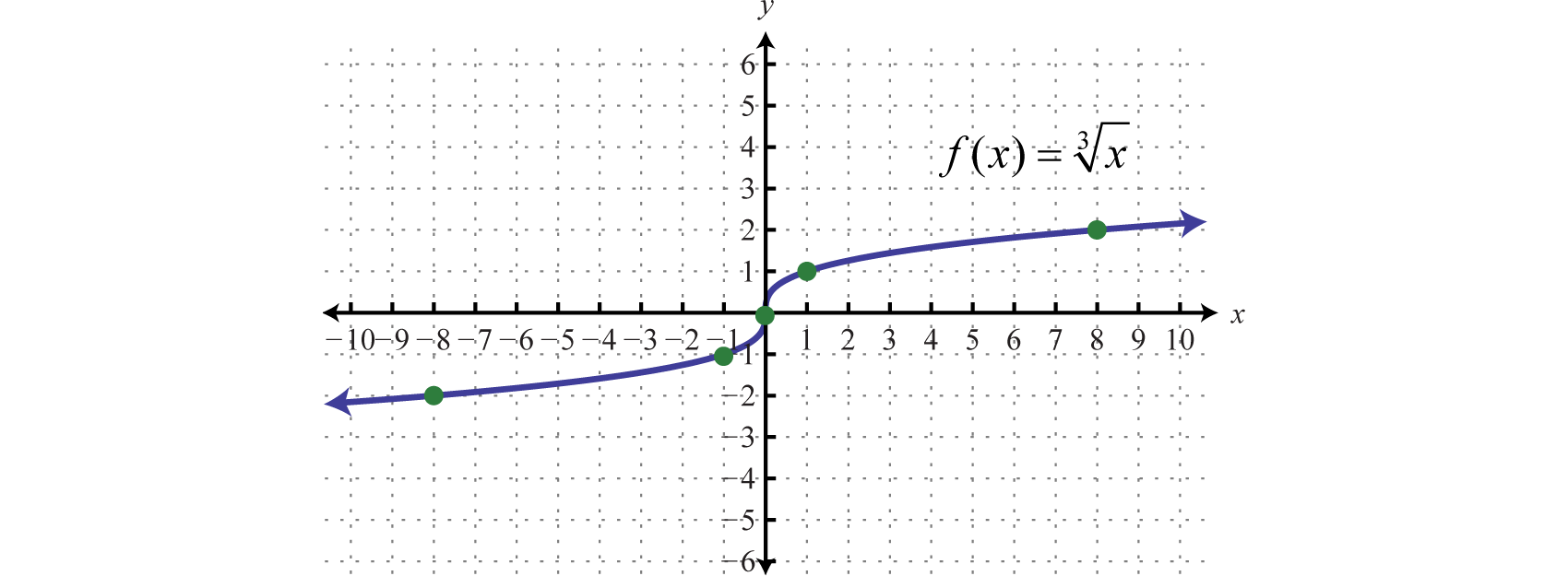
Графік проходить тест вертикальної лінії і дійсно є функцією. Крім того, діапазон складається з усіх дійсних чисел.

Приклад\(\PageIndex{6}\):

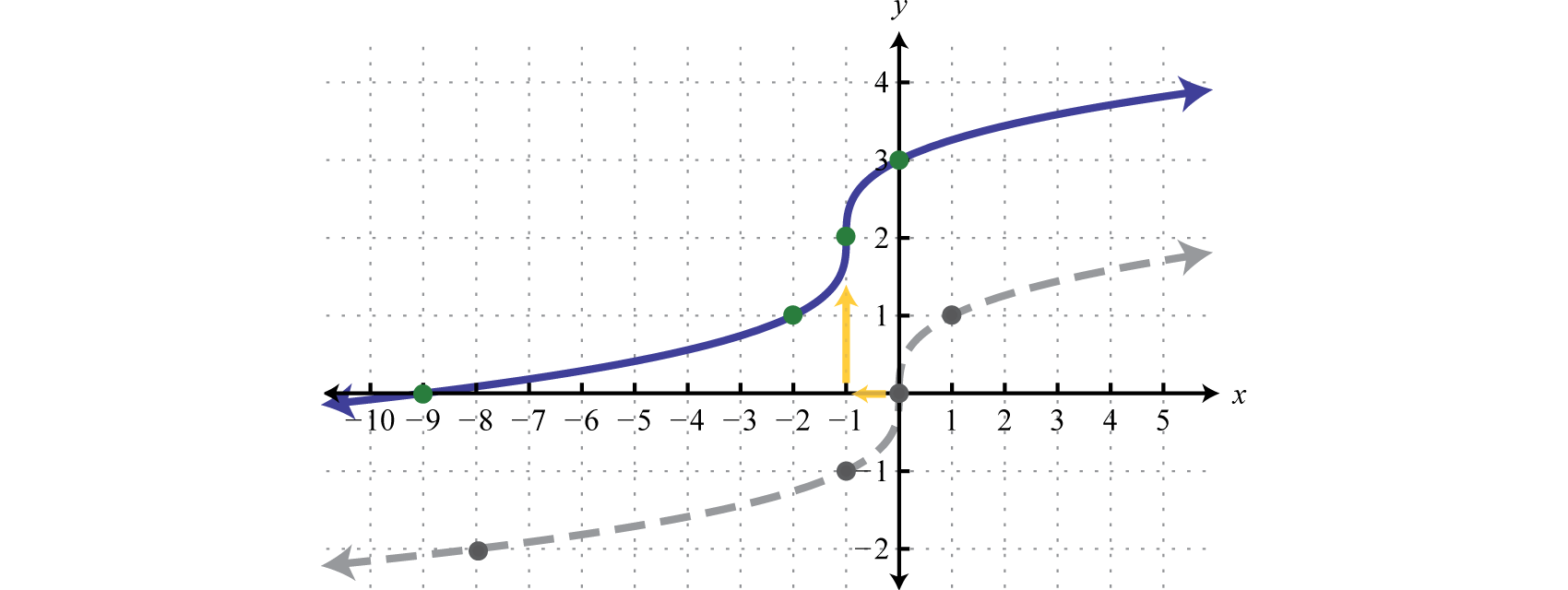
Дано\(g ( x ) = \sqrt [ 3 ] { x + 1 } + 2\), знайдіть\(g ( - 9 ) , g ( - 2 ) , g ( - 1 )\), і\(g(0)\). Намалюйте графік\(g\).

Рішення

\(x\)Замініть на задані значення.

Таблиця\(\PageIndex{2}\)
\(x\)	\(g(x)\)	\(g ( x ) = \sqrt [ 3 ] { x + 1 } + 2\)	\(\color{Cerulean}{Ordered\:Pairs}\)
\ (x\) ">\(-9\)	\ (g (x)\) ">\(\color{Cerulean}{0}\)	\ (g (x) =\ sqrt [3] {x + 1} + 2\) ">\(g ( \color{OliveGreen}{- 9}\color{black}{ )} = \sqrt [ 3 ] { \color{OliveGreen}{- 9}\color{black}{ +} 1 } + 2 = \sqrt [ 3 ] { - 8 } + 2 = - 2 + 2 = 0\)	\ (\ color {Cerulean} {Упорядковано\ :Пари}\) ">\((-9,0)\)
\ (x\) ">\(-2\)	\ (g (x)\) ">\(\color{Cerulean}{1}\)	\ (g (x) =\ sqrt [3] {x + 1} + 2\) ">\(g ( \color{OliveGreen}{- 2}\color{black}{ )} = \sqrt [ 3 ] {\color{OliveGreen}{ - 2}\color{black}{ +} 1 } + 2 = \sqrt [ 3 ] { - 1 } + 2 = - 1 + 2 = 1\)	\ (\ color {Cerulean} {Упорядковано\ :Пари}\) ">\((-2,1)\)
\ (x\) ">\(-1\)	\ (g (x)\) ">\(\color{Cerulean}{2}\)	\ (g (x) =\ sqrt [3] {x + 1} + 2\) ">\(g ( \color{OliveGreen}{- 1}\color{black}{ )} = \sqrt [ 3 ] { \color{OliveGreen}{- 1}\color{black}{ +} 1 } + 2 = \sqrt [ 3 ] { 0 } + 2 = 0 + 2 = 2\)	\ (\ color {Cerulean} {Упорядковано\ :Пари}\) ">\((-1,2)\)
\ (x\) ">\(0\)	\ (g (x)\) ">\(\color{Cerulean}{3}\)	\ (g (x) =\ sqrt [3] {x + 1} + 2\) ">\(g ( \color{OliveGreen}{0}\color{black}{ )} = \sqrt [ 3 ] { \color{OliveGreen}{0}\color{black}{ +} 1 } + 2 = \sqrt [ 3 ] { 1 } + 2 = 1 + 2 = 3\)	\ (\ color {Cerulean} {Упорядковано\ :Пари}\) ">\((0,3)\)

Ми також можемо намалювати графік, використовуючи такі переклади:

\(\begin{array} { l } { y = \sqrt [ 3 ] { x } \quad\quad\quad\quad \color{Cerulean} { Basic\: cube \:root\: function } } \\ { y = \sqrt [ 3 ] { x + 1 } \quad \quad\:\color{Cerulean} { Horizontal\: shift\: left\: 1\: unit } } \\ { y = \sqrt [ 3 ] { x + 1 } + 2 \:\:\:\color{Cerulean} { Vertical\: shift\: up\: 2\: units } } \end{array}\)

Відповідь:

\(n\)Коріння

Для будь-якого цілого числа\(n ≥ 2\) ми визначаємо корінь ⁸ додатного дійсного числа як число, яке при підвищенні до\(n\) ї степені дає початкове число.\(n\) З огляду на будь-яке невід'ємне дійсне число\(a\), ми маємо таку властивість:

\(\sqrt [ n ] { a ^ { n } } = a , \quad \text { if } \quad a \geq 0\)

Тут n називається індексом і\(a^{n}\) називається радикандом. Крім того, ми можемо називати весь\(\sqrt [ n ] { A }\) вираз радикалом ⁹. Коли індекс є цілим числом більше або дорівнює\(4\), ми говоримо «четвертий корінь», «п'ятий корінь» і так далі. Корінь будь-якого числа очевидний, якщо ми можемо записати радиканд з показником, рівним індексу.\(n\)

Приклад\(\PageIndex{7}\):

Спростити:

\(\sqrt [ 4 ] { 81 }\)
\(\sqrt [ 5 ] { 32 }\)
\(\sqrt [ 7 ] { 1 }\)
\(\sqrt [ 4 ] { \frac { 1 } { 16 } }\)

Рішення

\(\sqrt [ 4 ] { 81 } = \sqrt [ 4 ] { 3 ^ { 4 } } = 3\)
\(\sqrt [ 5 ] { 32 } = \sqrt [ 5 ] { 2 ^ { 5 } } = 2\)
\(\sqrt [ 7 ] { 1 } = \sqrt [ 7 ] { 1 ^ { 7 } } = 1\)
\(\sqrt [ 4 ] { \frac { 1 } { 16 } } = \sqrt [ 4 ] { \left( \frac { 1 } { 2 } \right) ^ { 4 } } = \frac { 1 } { 2 }\)

Примітка

Якщо індекс є\(n = 2\), то радикал вказує на квадратний корінь і прийнято писати радикал без індексу;\(\sqrt [ 2 ] { a } = \sqrt { a }\).

Ми вже подбали про визначення основного квадратного кореня дійсного числа. У цей момент ми поширюємо цю ідею до n-го коренів, коли n парне. Наприклад,\(3\) це четвертий корінь\(81\), тому що\(3^{4} = 81\). А оскільки\((−3)^{4} = 81\), можна сказати, що\(−3\) це четвертий корінь\(81\), а також. Отже, ми використовуємо радикальний знак\(\sqrt [ n ] { }\) для позначення основного (ненегативного)\(n\) го кореня ¹⁰, коли\(n\) парний. У цьому випадку для будь-якого реального числа\(a\) ми використовуємо таку властивість:

\(\sqrt [ n ] { a ^ { n } } = | a | \quad \color{Cerulean} { When\:n\:is\:even } \)

Наприклад,

\(\begin{aligned} \sqrt [ 4 ] { 81 } & = \sqrt [ 4 ] { 3 ^ { 4 } } \quad\quad= |3| \:\:\:\:\:= 3 \\ \sqrt [ 4 ] { 81 } & = \sqrt [ 4 ] { ( - 3 ) ^ { 4 } } \:\:= | - 3 | = 3 \end{aligned}\)

Негативний\(n\) й корінь, коли\(n\) парний, буде позначатися за допомогою негативного знака перед радикалом\(- \sqrt [ n ] { }\).

\(- \sqrt [ 4 ] { 81 } = - \sqrt [ 4 ] { 3 ^ { 4 } } = - 3\)

Ми бачили, що квадратний корінь негативного числа не є реальним, тому що будь-яке дійсне число, яке знаходиться в квадраті, призведе до позитивного числа. Насправді подібна проблема виникає при будь-якому парному показнику:

\(\sqrt [ 4 ] { - 81 } =\color{Cerulean}{ ?} \quad \color{black}{\text { or }} \quad (\color{Cerulean}{ ?}\color{black}{ )} ^ { 4 } = - 81\)

Ми бачимо, що четвертий корінь не\(−81\) є дійсним числом, тому що четверта ступінь будь-якого дійсного числа завжди позитивна.

\(\left. \begin{array} { l } { \sqrt { - 4 } } \\ { \sqrt [ 4 ] { - 81 } } \\ { \sqrt [ 6 ] { - 64 } } \end{array} \right\} \quad \color{Cerulean}{These\:radicals\:are\:not\:real\:numbers.}\)

Вам рекомендується спробувати все це на калькуляторі. Що це говорить?

Приклад\(\PageIndex{8}\):

Спростити.

\(\sqrt [ 4 ] { ( - 10 ) ^ { 4 } }\)
\(\sqrt [ 4 ] { - 10 ^ { 4 } }\)
\(\sqrt [ 6 ] { ( 2 y + 1 ) ^ { 6 } }\)

Рішення

Оскільки індекси рівні, використовуйте абсолютні значення для забезпечення ненегативних результатів.

\(\sqrt [ 4 ] { ( - 10 ) ^ { 4 } } = | - 10 | = 10\)
\(\sqrt [ 4 ] { - 10 ^ { 4 } } = \sqrt [ 4 ] { - 10,000 }\)не є дійсним числом.
\(\sqrt [ 6 ] { ( 2 y + 1 ) ^ { 6 } } = | 2 y + 1 |\)

Коли показник\(n\) непарний, таких же проблем не виникає. Твір непарного числа позитивних чинників позитивне, а добуток непарного числа негативних чинників - негативним. Отже, коли індекс\(n\) непарний, існує лише один\(n\) дійсний корінь для будь-якого дійсного числа\(a\). І ми маємо наступну властивість:

\(\sqrt [ n ] { a ^ { n } } = a \quad \color{Cerulean} { When \: n\:is\:odd}\)

Приклад\(\PageIndex{9}\):

Спростити.

\(\sqrt [ 5 ] { ( - 10 ) ^ { 5 } }\)
\(\sqrt [ 5 ] { - 32 }\)
\(\sqrt [ 7 ] { ( 2 y + 1 ) ^ { 7 } }\)

Рішення

Так як індекси непарні, то абсолютне значення не використовується.

\(\sqrt [ 5 ] { ( - 10 ) ^ { 5 } } = - 10\)
\(\sqrt [ 5 ] { - 32 } = \sqrt [ 5 ] { ( - 2 ) ^ { 5 } } = - 2\)
\(\sqrt [ 7 ] { ( 2 y + 1 ) ^ { 7 } } = 2 y + 1\)

Підсумовуючи, для будь-якого реального числа\(a\) ми маємо,

\(\begin{aligned} \sqrt [ n ] { a^ { n } } & = | a | \color{Cerulean}\:\:\: { When \: n\: is\: even } \\ \sqrt [ n ] {a^ { n } } & = a \quad\: \color{Cerulean} { When \: n\: is\: odd } \end{aligned}\)

Коли\(n\) непарний\(n\), то корінь позитивний або негативний в залежності від знака радиканда.

\(\begin{aligned} \sqrt [ 3 ] { 27 } & = \sqrt [ 3 ] { 3 ^ { 3 } } = 3 \\ \sqrt [ 3 ] { - 27 } & = \sqrt [ 3 ] { ( - 3 ) ^ { 3 } } = - 3 \end{aligned}\)

Коли\(n\) парний, корінь позитивний або не реальний в залежності від знака радиканда.\(n\)

\(\begin{aligned} \sqrt [ 4 ] { 16 } & = \sqrt [ 4 ] { 2 ^ { 4 } } \quad\:\:= 2 \\ \sqrt [ 4 ] { 16 } & = \sqrt [ 4 ] { ( - 2 ) ^ { 4 } } = | - 2| = 2 \\ \sqrt [ 4 ] { - 16 } & \quad\color{Cerulean} { Not \:a \:real\: number } \end{aligned}\)

Вправа\(\PageIndex{2}\)

Спростити:\(- 8 \sqrt [ 5 ] { - 32 }\).

Відповідь

\(16\)

www.youtube.com/В/ІК1ХХГК18Ф0

Спрощення радикалів

Не завжди буде так, що радиканд - це досконала сила даного індексу. Якщо це не так, то ми використовуємо правило продукту для радикалів ¹¹ і часткове правило для радикалів ¹², щоб спростити їх. Дано дійсні числа\(\sqrt [ n ] { A }\) і\(\sqrt [ n ] { B }\),

Таблиця\(\PageIndex{3}\)
Правило продукту для радикалів:	\(\sqrt [ n ] { A \cdot B } = \sqrt [ n ] { A } \cdot \sqrt [ n ] { B }\)
Частота правило для радикалів:	\(\sqrt [ n ] { \frac { A } { B } } = \frac { \sqrt [ n ] { A } } { \sqrt [ n ] { B } }\)

Радикал спрощується ¹³, якщо він не містить жодних факторів, які можна записати як досконалі сили індексу.

Приклад\(\PageIndex{10}\):

Спростити:\(\sqrt { 150 }\).

Рішення

Тут\(150\) можна записати як\(2 \cdot 3 \cdot 5 ^ { 2 }\).

\(\begin{aligned} \sqrt { 150 } & = \sqrt { 2 \cdot 3 \cdot 5 ^ { 2 } }\quad\quad \color{Cerulean} { Apply\: the\: product \:rule\: for\: radicals.} \\ & = \sqrt { 2 \cdot 3 } \cdot \sqrt { 5 ^ { 2 } }\quad\: \color{Cerulean} { Simplify. } \\ & = \sqrt { 6 } \cdot 5 \\ & = 5 \sqrt { 6 } \end{aligned}\)

Ми можемо перевірити нашу відповідь на калькуляторі:

\(\sqrt { 150 } \approx 12.25 \quad\text { and }\quad 5 \sqrt { 6 } \approx 12.25\)

Також варто відзначити, що

\(12.25 ^ { 2 } \approx 150\)

Відповідь:

\(5 \sqrt { 6 }\)

Примітка

\(5 \sqrt { 6 }\)є точною відповіддю і\(12.25\) є приблизною відповіддю. Ми представляємо точні відповіді, якщо не сказано інше.

Приклад\(\PageIndex{11}\):

Спростити:\(\sqrt [ 3 ] { 160 }\).

Рішення

Скористайтеся простою факторизацією,\(160\) щоб знайти найбільший коефіцієнт ідеального куба:

\(\begin{aligned} 160 & = 2 ^ { 5 } \cdot 5 \\ & = \color{Cerulean}{2 ^ { 3} }\color{black}{ \cdot} 2 ^ { 2 } \cdot 5 \end{aligned}\)

Замініть радиканд цією факторизацією, а потім застосуйте правило продукту для радикалів.

\(\begin{aligned} \sqrt [ 3 ] { 160 } & = \sqrt [ 3 ] { 2 ^ { 3 } \cdot 2 ^ { 2 } \cdot 5 } \quad\quad\color{Cerulean} { Apply\:the\: product\: rule\: for\: radicals.} \\ & = \sqrt [ 3 ] { 2 ^ { 3 } } \cdot \sqrt [ 3 ] { 2 ^ { 2 } \cdot 5 }\quad \color{Cerulean} { Simplify. } \\ & = 2 \cdot \sqrt [ 3 ] { 20 } \end{aligned}\)

Ми можемо перевірити нашу відповідь на калькуляторі.

\(\sqrt [ 3 ] { 160 } \approx 5.43 \text { and } 2 \sqrt [ 3 ] { 20 } \approx 5.43\)

Відповідь:

\(2 \sqrt [ 3 ] { 20 }\)

Приклад\(\PageIndex{12}\):

Спростити:\(\sqrt [ 5 ] { - 320 }\).

Рішення

Тут відзначимо, що індекс непарний, а радиканд негативний; отже, результат буде негативним. Ми можемо зарахувати радиканд наступним чином:

\(- 320 = - 1 \cdot 32 \cdot 10 = ( - 1 ) ^ { 5 } \cdot ( 2 ) ^ { 5 } \cdot 10\)

Тоді спростіть:

\(\begin{aligned} \sqrt [ 5 ] { - 320 } & = \sqrt [ 5 ] { ( - 1 ) ^ { 5 } \cdot ( 2 ) ^ { 5 } \cdot 10 } \quad\quad\quad\color{Cerulean} { Apply\: the\: product\: rule\: for\: radicals.} \\ & = \sqrt [ 5 ] { ( - 1 ) ^ { 5 } } \cdot \sqrt [ 5 ] { ( 2 ) ^ { 5 } } \cdot \sqrt [ 5 ] { 10 }\quad \color{Cerulean} { Simplify. } \\ &= -1\cdot2\cdot \sqrt[5]{10} \\ &=-2\cdot \sqrt[5]{10}\end{aligned}\)

Відповідь:

\(- 2 \sqrt [ 5 ] { 10 }\)

Приклад\(\PageIndex{13}\):

Спростити:\(\sqrt [ 3 ] { - \frac { 8 } { 64 } }\).

Рішення

У цьому випадку розглянемо еквівалентний дріб з\(−8 = (−2)^{3}\) в чисельнику і\(64 = 4^{3}\) в знаменнику і потім спростити.

\(\begin{aligned} \sqrt [ 3 ] { - \frac { 8 } { 64 } } & = \sqrt [ 3 ] { \frac { - 8 } { 64 } } \quad\quad\quad\color{Cerulean} { Apply\: the\: quotient \:rule\: for\: radicals.} \\ & = \frac { \sqrt [ 3 ] { ( - 2 ) ^ { 3 } } } { \sqrt [ 3 ] { 4 ^ { 3 } } }\quad\:\:\: \color{Cerulean} { Simplify. } \\ & = \frac { - 2 } { 4 } \\ & = - \frac { 1 } { 2 } \end{aligned}\)

Відповідь:

\(-\frac{1}{2}\)

Вправа\(\PageIndex{3}\)

Спростити:\(\sqrt [ 4 ] { \frac { 80 } { 81 } }\)

Відповідь

\(\frac { 2 \sqrt [ 4 ] { 5 } } { 3 }\)

www.youtube.com/В/8cwbdbfo2FQ

Ключові виноси

Щоб спростити квадратний корінь, шукайте найбільший ідеальний квадратний коефіцієнт радиканда, а потім застосуйте правило продукту або частки для радикалів.
Щоб спростити кубічний корінь, шукайте найбільший ідеальний кубовий коефіцієнт радиканда, а потім застосуйте правило продукту або частки для радикалів.
При роботі з n-м корінням\(n\) визначає визначення, яке застосовується. Ми використовуємо\(\sqrt [ n ] { a ^ { n } } = a _ { 1 }\) коли\(n\) непарне, а\(\sqrt [ n ] { a ^ { n } } = | a | \)\(n\) коли парне.
Щоб спростити\(n\) коріння, шукайте фактори, які мають силу, рівну індексу,\(n\) а потім застосуйте правило продукту або частки для радикалів. Як правило, процес впорядковується, якщо працювати з простою факторизацією радиканда.

Вправа\(\PageIndex{4}\)

Спростити.

\(\sqrt { 36 }\)
\(\sqrt { 100 }\)
\(\sqrt { \frac { 4 } { 9 } }\)
\(\sqrt { \frac { 1 } { 64 } }\)
\(- \sqrt { 16 }\)
\(- \sqrt { 1 }\)
\(\sqrt { ( - 5 ) ^ { 2 } }\)
\(\sqrt { ( - 1 ) ^ { 2 } }\)
\(\sqrt { - 4 }\)
\(\sqrt { - 5 ^ { 2 } }\)
\(- \sqrt { ( - 3 ) ^ { 2 } }\)
\(- \sqrt { ( - 4 ) ^ { 2 } }\)
\(\sqrt { x ^ { 2 } }\)
\(\sqrt { ( - x ) ^ { 2 } }\)
\(\sqrt { ( x - 5 ) ^ { 2 } }\)
\(\sqrt { ( 2 x - 1 ) ^ { 2 } }\)
\(\sqrt [ 3 ] { 64 }\)
\(\sqrt [ 3 ] { 216 }\)
\(\sqrt [ 3 ] { - 216 }\)
\(\sqrt [ 3 ] { - 64 }\)
\(\sqrt [ 3 ] { - 8 }\)
\(\sqrt [ 3 ] { 1 }\)
\(- \sqrt [ 3 ] { ( - 2 ) ^ { 3 } }\)
\(- \sqrt [ 3 ] { ( - 7 ) ^ { 3 } }\)
\(\sqrt [ 3 ] { \frac { 1 } { 8 } }\)
\(\sqrt [ 3 ] { \frac { 8 } { 27 } }\)
\(\sqrt [ 3 ] { ( - y ) ^ { 3 } }\)
\(- \sqrt [ 3 ] { y ^ { 3 } }\)
\(\sqrt [ 3 ] { ( y - 8 ) ^ { 3 } }\)
\(\sqrt [ 3 ] { ( 2 x - 3 ) ^ { 3 } }\)

Відповідь

1. \(6\)

3. \(\frac{2}{3}\)

5. \(−4\)

7. \(5\)

9. Чи не дійсне число

11. \(−3\)

13. \(|x|\)

15. \(|x − 5|\)

17. \(4\)

19. \(−6\)

21. \(−2\)

23. \(2\)

25. \(\frac{1}{2}\)

27. \(−y\)

29. \(y − 8\)

Вправа\(\PageIndex{5}\)

Визначте область заданої функції.

\(g ( x ) = \sqrt { x + 5 }\)
\(g ( x ) = \sqrt { x - 2 }\)
\(f ( x ) = \sqrt { 5 x + 1 }\)
\(f ( x ) = \sqrt { 3 x + 4 }\)
\(g ( x ) = \sqrt { - x + 1 }\)
\(g ( x ) = \sqrt { - x - 3 }\)
\(h ( x ) = \sqrt { 5 - x }\)
\(h ( x ) = \sqrt { 2 - 3 x }\)
\(g ( x ) = \sqrt [ 3 ] { x + 4 }\)
\(g ( x ) = \sqrt [ 3 ] { x - 3 }\)

Відповідь

1. \([ - 5 , \infty )\)

3. \(\left[ - \frac { 1 } { 5 } , \infty \right)\)

5. \(( - \infty , 1 ]\)

7. \(( - \infty , 5 ]\)

9. \(( - \infty , \infty )\)

Вправа\(\PageIndex{6}\)

Оцінити задане визначення функції.

Дано\(f ( x ) = \sqrt { x - 1 }\), знайдіть\(f ( 1 ) , f ( 2 )\), і\(f ( 5 )\)
Дано\(f ( x ) = \sqrt { x + 5 }\), знайдіть\(f ( - 5 ) , f ( - 1 )\), і\(f ( 20 )\)
Дано\(f ( x ) = \sqrt { x } + 3\), знайдіть\(f ( 0 ) , f ( 1 )\), і\(f(16)\)
Дано\(f ( x ) = \sqrt { x } - 5\), знайдіть\(f ( 0 ) , f ( 1 )\), і\(f(25)\)
Дано\(g ( x ) = \sqrt [ 3 ] { x }\), знайдіть\(g ( - 1 ) , g ( 0 )\), і\(g(1)\)
Дано\(g ( x ) = \sqrt [ 3 ] { x } - 2\) знахідку\(g ( - 1 ) , g ( 0 )\), і\(g(8)\)
Дано\(g ( x ) = \sqrt [ 3 ] { x + 7 }\), знайдіть\(g ( - 15 ) , g ( - 7 )\), і\(g(20)\)
Дано\(g ( x ) = \sqrt [ 3 ] { x - 1 } + 2\), знайдіть\(g ( 0 ) , g ( 2 ) \), і\(g(9)\)

Відповідь

1. \(f ( 1 ) = 0 ; f ( 2 ) = 1 ; f ( 5 ) = 2\)

3. \(f ( 0 ) = 3 ; f ( 1 ) = 4 ; f ( 16 ) = 7\)

5. \(g ( - 1 ) = - 1 ; g ( 0 ) = 0 ; g ( 1 ) = 1\)

7. \(g ( - 15 ) = - 2 ; g ( - 7 ) = 0 ; g ( 20 ) = 3\)

Вправа\(\PageIndex{7}\)

Намалюйте графік заданої функції і задайте її область і діапазон.

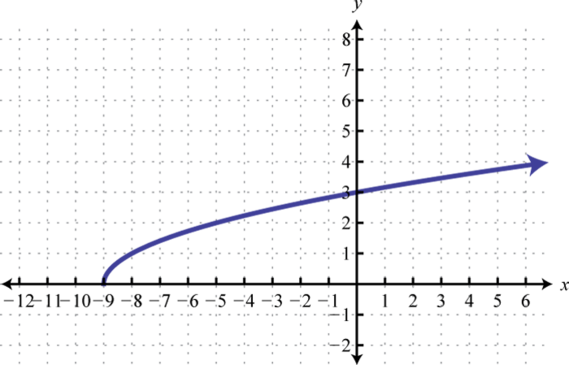
\(f ( x ) = \sqrt { x + 9 }\)
\(f ( x ) = \sqrt { x - 3 }\)
\(f ( x ) = \sqrt { x - 1 } + 2\)
\(f ( x ) = \sqrt { x + 1 } + 3\)
\(g ( x ) = \sqrt [ 3 ] { x - 1 }\)
\(g ( x ) = \sqrt [ 3 ] { x + 1 }\)
\(g ( x ) = \sqrt [ 3 ] { x } - 4\)
\(g ( x ) = \sqrt [ 3 ] { x } + 5\)
\(g ( x ) = \sqrt [ 3 ] { x + 2 } - 1\)
\(g ( x ) = \sqrt [ 3 ] { x - 2 } + 3\)
\(f ( x ) = - \sqrt [ 3 ] { x }\)
\(f ( x ) = - \sqrt [ 3 ] { x - 1 }\)

Відповідь

1. Домен:\([ - 9 , \infty )\); діапазон:\([ 0 , \infty )\)

3. Домен:\([ 1 , \infty )\); діапазон:\([ 2 , \infty )\)

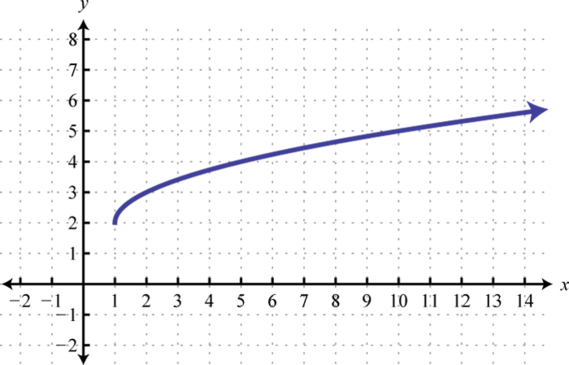
5. Домен:\(\mathbb { R }\); діапазон;\(\mathbb { R }\)

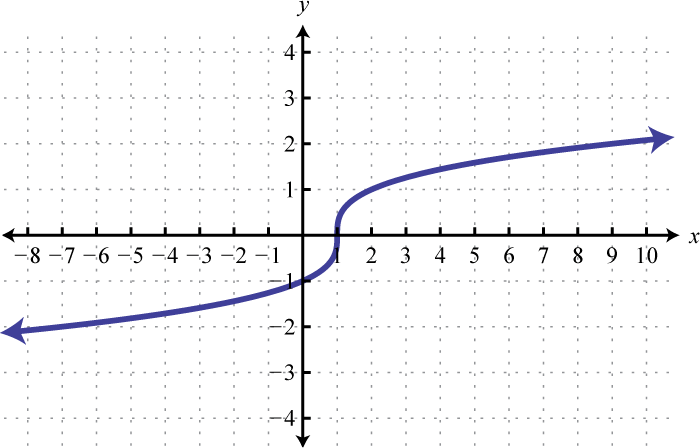
7. Домен:\(\mathbb { R }\); діапазон;\(\mathbb { R }\)

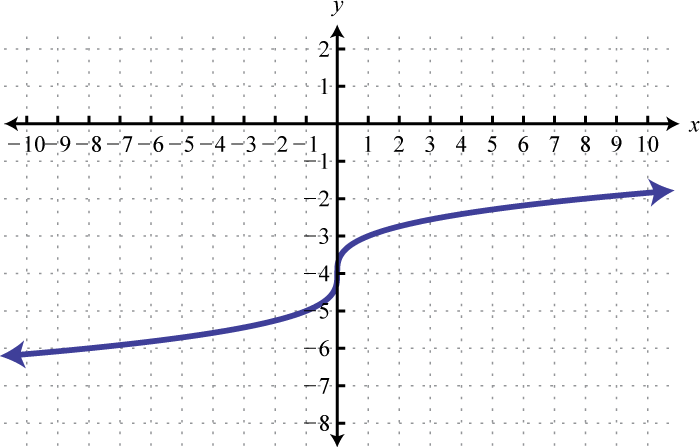
9. Домен:\(\mathbb { R }\); діапазон;\(\mathbb { R }\)

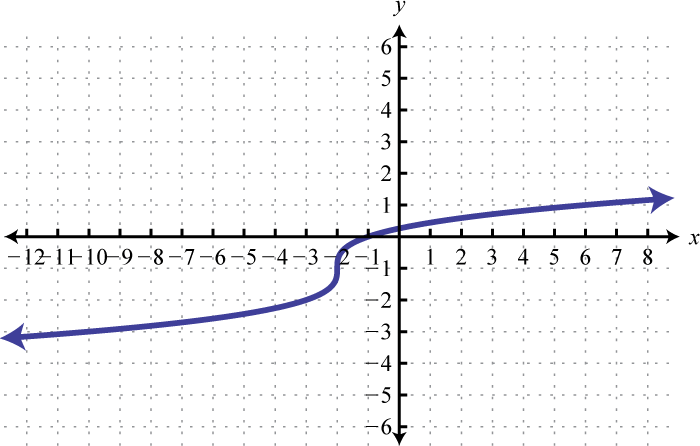
11. Домен:\(\mathbb { R }\); діапазон;\(\mathbb { R }\)

Вправа\(\PageIndex{8}\)

Спростити.

\(\sqrt [ 4 ] { 64 }\)
\(\sqrt [ 4 ] { 16 }\)
\(\sqrt [ 4 ] { 625 }\)
\(\sqrt [ 4 ] { 1 }\)
\(\sqrt [ 4 ] { 256 }\)
\(\sqrt [ 4 ] { 10,000 }\)
\(\sqrt [ 5 ] { 243 }\)
\(\sqrt [ 5 ] { 100,000 }\)
\(\sqrt [ 5 ] { \frac { 1 } { 32 } }\)
\(\sqrt [ 5 ] { \frac { 1 } { 243 } }\)
\(- \sqrt [ 4 ] { 16 }\)
\(- \sqrt [ 6 ] { 1 }\)
\(\sqrt [ 5 ] { - 32 }\)
\(\sqrt [ 5 ] { - 1 }\)
\(\sqrt { - 1 }\)
\(\sqrt [ 4 ] { - 16 }\)
\(- 6 \sqrt [ 3 ] { - 27 }\)
\(- 5 \sqrt [ 3 ] { - 8 }\)
\(2 \sqrt [ 3 ] { - 1,000 }\)
\(7 \sqrt [ 5 ] { - 243 }\)
\(6 \sqrt [ 4 ] { - 16 }\)
\(12 \sqrt [ 6 ] { - 64 }\)
\(\sqrt [ 3 ] { \frac { 25 } { 16 } }\)
\(6 \sqrt { \frac { 16 } { 9 } }\)
\(5 \sqrt [ 3 ] { \frac { 27 } { 125 } }\)
\(7 \sqrt [ 5 ] { \frac { 32 } { 7 ^ { 5 } } }\)
\(- 5 \sqrt [ 3 ] { \frac { 8 } { 27 } }\)
\(- 8 \sqrt [ 4 ] { \frac { 625 } { 16 } }\)
\(2 \sqrt [ 5 ] { 100,000 }\)
\(2 \sqrt [ 7 ] { 128 }\)

Відповідь

1. \(4\)

3. \(5\)

5. \(4\)

7. \(3\)

9. \(\frac{1}{2}\)

11. \(−2\)

13. \(−2\)

15. Чи не дійсне число

17. \(18\)

19. \(−20\)

21. Чи не дійсне число

23. \(\frac{15}{4}\)

25. \(3\)

27. \(−\frac{10}{3}\)

29. \(20\)

Вправа\(\PageIndex{9}\)

Спростити.

\(\sqrt { 96 }\)
\(\sqrt { 500 }\)
\(\sqrt { 480 }\)
\(\sqrt { 450 }\)
\(\sqrt { 320 }\)
\(\sqrt { 216 }\)
\(5 \sqrt { 112 }\)
\(10 \sqrt { 135 }\)
\(- 2 \sqrt { 240 }\)
\(- 3 \sqrt { 162 }\)
\(\sqrt { \frac { 150 } { 49 } }\)
\(\sqrt { \frac { 200 } { 9 } }\)
\(\sqrt { \frac { 675 } { 121 } }\)
\(\sqrt { \frac { 192 } { 81 } }\)
\(\sqrt [ 3 ] { 54 }\)
\(\sqrt [ 3 ] { 24 }\)
\(\sqrt [ 3 ] { 48 }\)
\(\sqrt [ 3 ] { 81 }\)
\(\sqrt [ 3 ] { 40 }\)
\(\sqrt [ 3 ] { 120 }\)
\(\sqrt [ 3 ] { 162 }\)
\(\sqrt [ 3 ] { 500 }\)
\(\sqrt [ 3 ] { \frac { 54 } { 125 } }\)
\(\sqrt [ 3 ] { \frac { 40 } { 343 } }\)
\(5 \sqrt [ 3 ] { - 48 }\)
\(2 \sqrt [ 3 ] { - 108 }\)
\(8 \sqrt [ 4 ] { 96 }\)
\(7 \sqrt [ 4 ] { 162 }\)
\(\sqrt [ 5 ] { 160 }\)
\(\sqrt [ 5 ] { 486 }\)
\(\sqrt [ 5 ] { \frac { 224 } { 243 } }\)
\(\sqrt [ 5 ] { \frac { 5 } { 32 } }\)
\(\sqrt [ 5 ] { - \frac { 1 } { 32 } }\)
\(\sqrt [ 6 ] { - \frac { 1 } { 64 } }\)

Відповідь

1. \(4 \sqrt { 6 }\)

3. \(4 \sqrt { 30 }\)

5. \(8 \sqrt { 5 }\)

7. \(20 \sqrt { 7 }\)

9. \(- 8 \sqrt { 15 }\)

11. \(\frac { 5 \sqrt { 6 } } { 7 }\)

13. \(\frac { 15 \sqrt { 3 } } { 11 }\)

15. \(3 \sqrt [ 3 ] { 2 }\)

17. \(2 \sqrt [ 3 ] { 6 }\)

19. \(2 \sqrt [ 3 ] { 5 }\)

21. \(3 \sqrt [ 3 ] { 6 }\)

23. \(\frac { 3 \sqrt [ 3 ] { 2 } } { 5 }\)

25. \(- 10 \sqrt [ 3 ] { 6 }\)

27. \(16 \sqrt [ 4 ] { 6 }\)

29. \(2 \sqrt [ 5 ] { 5 }\)

31. \(\frac { 2 \sqrt [ 5 ] { 7 } } { 3 }\)

33. \(- \frac { 1 } { 2 }\)

Вправа\(\PageIndex{10}\)

Спростити. Дайте точну відповідь і приблизну відповідь округляйте до найближчих сотих.

\(\sqrt { 60 }\)
\(\sqrt { 600 }\)
\(\sqrt { \frac { 96 } { 49 } }\)
\(\sqrt { \frac { 192 } { 25 } }\)
\(\sqrt [ 3 ] { 240 }\)
\(\sqrt [ 3 ] { 320 }\)
\(\sqrt [ 3 ] { \frac { 288 } { 125 } }\)
\(\sqrt [ 3 ] { \frac { 625 } { 8 } }\)
\(\sqrt [ 4 ] { 486 }\)
\(\sqrt [ 5 ] { 288 }\)

Відповідь

1. \(2 \sqrt { 15 } ; 7.75\)

3. \(\frac { 4 \sqrt { 6 } } { 7 } ; 1.40\)

5. \(2 \sqrt [ 3 ] { 30 } ; 6.21\)

7. \(\frac { 2 \sqrt [ 3 ] { 36 } } { 5 } ; 1.32\)

9. \(3 \sqrt [ 4 ] { 6 } ; 4.70\)

Вправа\(\PageIndex{11}\)

Перепишіть наступне як радикальний вираз з коефектом\(1\).

\(2 \sqrt { 15 }\)
\(3 \sqrt { 7 }\)
\(5 \sqrt { 10 }\)
\(10 \sqrt { 3 }\)
\(2 \sqrt [ 3 ] { 7 }\)
\(3 \sqrt [ 3 ] { 6 }\)
\(2 \sqrt [ 4 ] { 5 }\)
\(3\sqrt [ 4 ] { 2 }\)
Кожна сторона квадрата має довжину, яка дорівнює квадратному кореню площі квадрата. Якщо площа квадрата дорівнює\(72\) квадратним одиницям, знайдіть довжину кожної з його сторін.
Кожне ребро куба має довжину, яка дорівнює кореню куба об'єму куба. Якщо обсяг куба дорівнює\(375\) кубічним одиницям, знайдіть довжину кожного з його ребер.
Струм,\(I\) виміряний в амперах, задається за формулою,\(I = \sqrt { \frac { P } { R } }\) де\(P\) використовується потужність, виміряна у ватах і опір,\(R\) виміряний в Омах. Якщо\(100\) ватна лампочка має\(160\) Ом опору, знайдіть необхідний струм. (Округлити до найближчої сотої частки ампера.)
Час у секундах, коли об'єкт знаходиться у вільному падінні, задається формулою,\(t = \frac { \sqrt { s } } { 4 }\) де\(s\) відображається відстань у футах, на яку впав об'єкт. Скільки часу знадобиться об'єкту, щоб впасти на землю з вершини драбини на\(8\) ногу? (Округлення до найближчої десятої частки секунди.)

Відповідь

1. \(\sqrt { 60 }\)

3. \(\sqrt { 250 }\)

5. \(\sqrt [ 3 ] { 56 }\)

7. \(\sqrt [ 4 ] { 80 }\)

9. \(6 \sqrt { 2 }\)одиниць

11. \(0.79\)ампер

Вправа\(\PageIndex{12}\)

Поясніть, чому існує два дійсних квадратних кореня для будь-якого позитивного дійсного числа і один реальний кубічний корінь для будь-якого дійсного числа.
Що таке квадратний корінь\(1\) і що таке кубічний корінь\(1\)? Поясніть чому.
Поясніть\(\sqrt { - 1 }\), чому не реальне число і\(\sqrt [ 3 ] { - 1 }\) чому реальне число.
Дослідити та обговорити методи розрахунку квадратних коренів перед загальним використанням електронних калькуляторів.

Відповідь

1. Відповідь може відрізнятися

3. Відповідь може відрізнятися

Виноски

¹ Число, яке при множенні на себе дає вихідне число.

² Позитивний квадратний корінь позитивного дійсного числа, що позначається символом\(√\).

³ Вираз\(A\) всередині радикального знака,\(\sqrt [ n ] { A }\).

⁴ Функція, визначена\(f ( x ) = \sqrt { x }\).

⁵ Число, яке при використанні як множника з собою тричі дає початкове число, позначається символом\(\sqrt [ 3 ] { }\).

⁶ Натуральне число\(n\) в позначенні\(\sqrt [ n ] { }\), яке використовується для позначення n-го кореня.

⁷ Функція, визначена\(f ( x ) = \sqrt [ 3 ] { x }\).

⁸ Число, яке при підвищенні до\(n\) ї потужності\((n ≥ 2)\) дає початкове число.

⁹ Використовується при зверненні до виразу форми\(\sqrt [ n ] { A }\).

¹⁰ Позитивний\(n\) той корінь\(n\), коли парний.

¹¹ Дано дійсні числа\(\sqrt [ n ] { A }\) і\(\sqrt [ n ] { B }\),\(\sqrt [ n ] { A \cdot B } = \sqrt [ n ] { A } \cdot \sqrt [ n ] { B }\).

¹² Дано дійсні числа\(\sqrt [ n ] { A }\) і\(\sqrt [ n ] { B }\),\(\sqrt [ n ] { \frac { A } { B } } = \frac { \sqrt [ n ] { A } } { \sqrt [ n ] { B } }\) де\(B ≠ 0\).

¹³ Радикал, де радиканд не складається з будь-яких факторів, які можна записати як досконалі сили індексу.