8.2: Експоненціальні функції

Припустимо, що нинішнє населення міста Плезантвілля становить 10000 і що населення зростає зі швидкістю 2% на рік. Для того, щоб проаналізувати приріст населення за період років, ми спробуємо розробити формулу для населення як функції часу, а потім графік результату.

По-перше, відзначимо, що за підсумками одного року приріст населення становить 2% від 10000, або 200 чоловік. Зараз у нас було б 10 200 людей у Плезантвіллі. Наприкінці другого року візьміть ще 2% від 10200, що є збільшенням на 204 людини, загалом 10404. Оскільки збільшення щороку не є постійним, графік чисельності населення проти часу не може бути лінією. Отже, наша можлива функція населення не буде лінійною.

Щоб розробити нашу формулу популяції, ми починаємо з того, що функція P (t) представляє популяцію Плезантвіля в час t, де ми вимірюємо t в роках. Ми почнемо час при t = 0, коли початкова чисельність населення Плезантвілля становить 10000. Іншими словами, Р (0) = 10000. Ключем до розуміння цього прикладу є той факт, що населення щороку збільшується на 2%. Тут ми робимо припущення, що це загальне зростання припадає на народження, смерть та люди, які приїжджають і залишають Плезантвілл. Тобто в кінці першого року населення Плезантвілля становитиме 102% від початкового населення. Таким чином,

$$P(1) = 1.02P(0) = 1.02(10000). \label{1}$$

Ми могли б помножити праву частину цього рівняння, але насправді буде корисніше залишити його в поточному вигляді.

Зараз з кожним роком чисельність населення збільшується на 2%. Тому в кінці другого року чисельність населення в кінці першого року становитиме 102% населення. Іншими словами,

$$P(2) = 1.02P(1). \label{2}$$

Якщо замінити$P(1)$ в Equation\ ref {2} на результат, знайдений в Equation\ ref {1}, то

$$P(2) = (1.02)(1.02)(10000) = (1.02)^{2}(10000). \label{3}$$

Давайте повторюємо ще один рік. На кінець третього року чисельність населення становитиме 102% населення в кінці другого року, тому

$$P(3) = 1.02P(2). \label{4}$$

Однак, якщо замінити$P(2)$ в Equation\ ref {4} на результат, знайдений в Equation\ ref {3}, то отримаємо

$$P(3) = (1.02)(1.02)^{2}(10000) = (1.02)^{3}(10000). \label{5}$$

Візерунок тепер повинен бути чітким. Чисельність населення в кінці$t$ років дається функцією.

$$P(t) = (1.02)^{t}(10000)$$

У математиці та науці традиційно розміщувати початкову популяцію попереду в цій формулі, замість цього пишучи

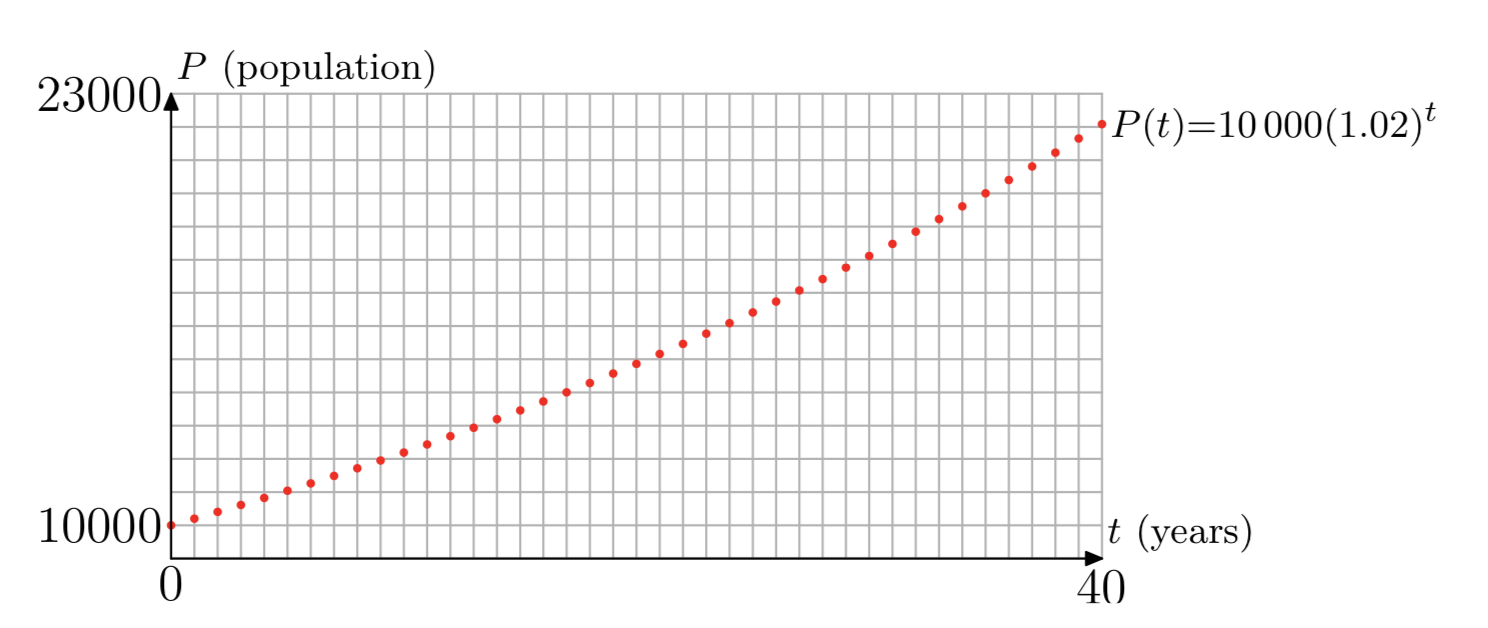
$$P(t) = 10000(1.02)^{t}. \label{6}$$

Наша функція$P(t)$ визначається Equation\ ref {6} для всіх натуральних чисел {1, 2, 3,.}, і$P(0) = 10000$, початкової сукупності. На малюнку 1 показаний сюжет нашої функції. Хоча точки будуються тільки при цілих значеннях t від 0 до 40, цього достатньо, щоб показати тенденцію чисельності населення з плином часу. Населення починається з 10000, збільшується з часом, і щорічне збільшення (різниця в чисельності населення від року до наступного) також стає більшим з часом.

Малюнок 1. Графік населення P (t) Плезантвілля для t = 0, 1, 2, 3,...

Вправа$\PageIndex{7}$

Тепер ми можемо використовувати функцію P (t) для прогнозування чисельності населення в наступні роки. Якщо припустити, що темпи зростання 2% тривають, яким буде населення Плезантвілля після 40 років? Що це буде через 100 років?

Рішення

$t = 40$ and $t = 100$ intoРівняння заміни\ ref {6}. Поп-гуляція через 40 років буде

$$P(40) = 10000(1.02)^{40} \approx 22080 \nonumber$$

і населення через 100 років буде

$$P(100) = 10000(1.02)^{100} \approx 72446. \nonumber$$

Що було б інакше, якби ми почали з населення 12000? Простежуючи наші попередні кроки, повинно бути легко побачити, що нова формула буде

$$P(t) = 12000(1.02)^{t}. \nonumber$$

Аналогічно, якби темпи зростання становили 3% на рік замість 2%, то ми б закінчили з формулою

$$P(t) = 10000(1.03)^t. \nonumber$$

Таким чином, дозволивши$P_{0}$ представляти початкову сукупність, і$r$ представляти швидкість зростання (в десятковій формі), ми можемо узагальнити формулу до

$$P(t) = P_{0}(1+r)^{t}. \label{8)}$$

Зауважте, що наша формула для функції$P(t)$ відрізняється від попередніх функцій, які ми вивчали досі, тим, що вхідна змінна$t$ є частиною показника у формулі. Таким чином, це новий тип функції.

Тепер давайте порівняємо ситуацію в Плезантвіллі з динамікою населення Ghosttown. Ghosttown також починається з населення 10000, але кілька заводів закрилися, тому деякі люди їдуть за кращими можливостями. У цьому випадку населення Ghosttown зменшується зі швидкістю 2% на рік. Ми знову розробимо формулу для населення в залежності від часу, а потім графік результату.

По-перше, відзначимо, що за підсумками одного року чисельність населення зменшується на 2% від 10000, або 200 чоловік. Тепер у нас було б 9800 людей, що залишилися в Ghosttown. Наприкінці другого року візьміть ще 2% з 9800, що є зменшенням на 196 осіб, загалом 9604. Як і раніше, оскільки зменшення щороку не є постійним, графік населення проти часу не може бути лінією, тому наша можлива функція населення не буде лінійною.

Тепер нехай функція$P(t)$ представляє населення Ghosttown в той час$t$, де ми вимірюємо$t$ в роках. Початкове населення Ghosttown на$t = 0$ 10000, так що$P(0) = 10,000$. Оскільки населення зменшується на 2% щороку, наприкінці першого року населення Ghosttown становитиме 98% від початкового населення. Таким чином,

$$P(1) = 0.98P(0) = 0.98(10000). \label{9}$$

Щороку населення зменшується на 2%. Тому в кінці другого року чисельність населення становитиме 98% населення в кінці першого року. Іншими словами,

$$P(2) = 0.98P(1). \label{10}$$

Якщо замінити$P (1)$ в Equation\ ref {10} на результат, знайдений в Equation\ ref {9}, то

$$P(2) = (0.98)(0.98)(10 000) = (0.98)^{2}(10000). \label{11}$$

Давайте повторюємо ще один рік. В кінці третього року чисельність населення становитиме 98% населення в кінці другого року, тому

$$P(3) = 0.98P(2). \label{12}$$

Однак, якщо замінити$P (2)$ в Equation\ ref {12} на результат, знайдений в Equation\ label {11}, то отримаємо

$$P(3) = (0.98)(0.98)^{2}(10000) = (0.98)^{3}(10000). \label{13}$$

Візерунок тепер повинен бути чітким. Чисельність населення в кінці$t$ років дається функцією

$$P(t) = (0.98)^{t}(10000), \nonumber$$

Або еквівалентно,

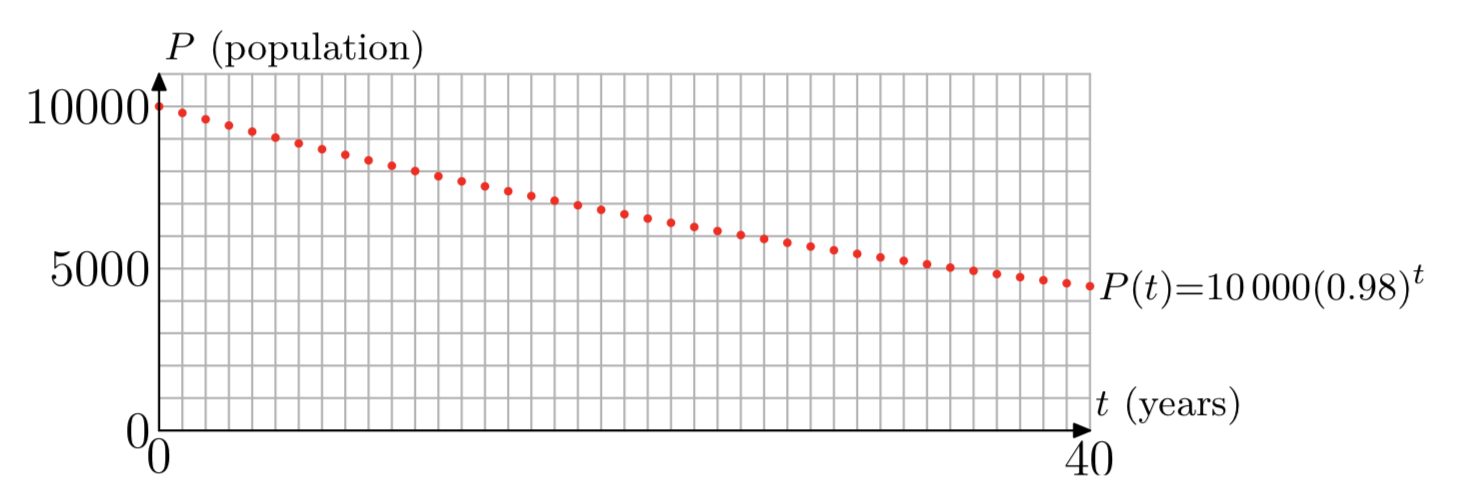
$$P(t) = 10000(0.98)^t\). \label{14}$$

Наша функція$P(t)$ визначається рівнянням\ ref {14} для всіх натуральних чисел {1, 2, 3,.}, і P (0) = 10000, початкової сукупності. На малюнку 2 показаний сюжет нашої функції. Хоча точки будуються тільки при цілих значеннях t від 0 до 40, цього достатньо, щоб показати тенденцію чисельності населення з плином часу. Населення починається з 10 000, з часом зменшується, а щорічне зменшення (різниця в чисельності населення від року до наступного) також стає меншим з часом.

Малюнок 2. Графік чисельності населення P (t) міста-привидів для t = 0, 1, 2, 3,...

Вправа$\PageIndex{15}$

Припускаючи, що темпи зниження продовжуються на рівні 2%, прогнозують населення Ghosttown через 40 років і після 100 років.

Рішення

$t = 40$ and $t = 100$ inЗамініть рівняння\ ref {14}. Населення в 40 років становитиме

$P(40) = 10000(0.98)^{40} \approx 4457$,

і населення через 100 років буде

$P(100) = 10000(0.98)^{100} \approx 1326$.

Зауважте, що якби ми замість цього почали з населенням 9000, наприклад, то нова формула була б

$P(t) = 9000(0.98)^t$.

Аналогічно, якби темп зниження становив 5% на рік замість 2%, то ми б закінчили з формулою

$P(t) = 10000(0.95)^t$.

Таким чином, дозволивши$P_{0}$ представляти початкову сукупність, і$r$ представляти швидкість зростання (в десятковій формі), ми можемо узагальнити формулу до

$$P(t) = P_{0}(1−r)^t. \label{16}$$

Визначення

Як зазначалося раніше, наші функції$P(t)$ в наших прикладах Pleasantville і Ghosttown є новим типом функції, оскільки вхідна змінна$t$ є частиною показника у формулі.

Визначення$\PageIndex{17}$: Exponential Function

Експоненціальна функція - це функція виду

$f(t) = b^t$

де b > 0 і$b \ne 1$. $b$називається основою експоненціальної функції. Більш загально, функція форми

$f(t) = Ab^t$,

де b > 0$b \ne 1$, і$A \ne 0$, також називається експоненціальною функцією. У цьому випадку значення функції при t = 0 дорівнює f (0) = A, тому A - початкова сума.

У додатках ви майже завжди будете стикатися з експоненціальними функціями в більш загальному вигляді$Ab^t$. Насправді зауважте, що в попередніх прикладах популяції функція P (t) має таку форму$P(t) = Ab^t$, з$A = P_{0}$,$b = 1+r$ в Плезантвіллі, і$b = 1−r$ в Ghosttown. Зокрема,$A = P_{0}$ це початкова популяція.

Оскільки експоненціальні функції часто використовуються для моделювання процесів, які змінюються з часом, ми зазвичай використовуємо вхідну змінну$t$ (хоча, звичайно, може бути використана будь-яка змінна). Крім того, вам може бути цікаво, чому визначення говорить$b \ne 1$, оскільки$1^t$ просто дорівнює 1. Ми пояснимо цю цікавість в кінці цього розділу.

Графіки експоненціальних функцій

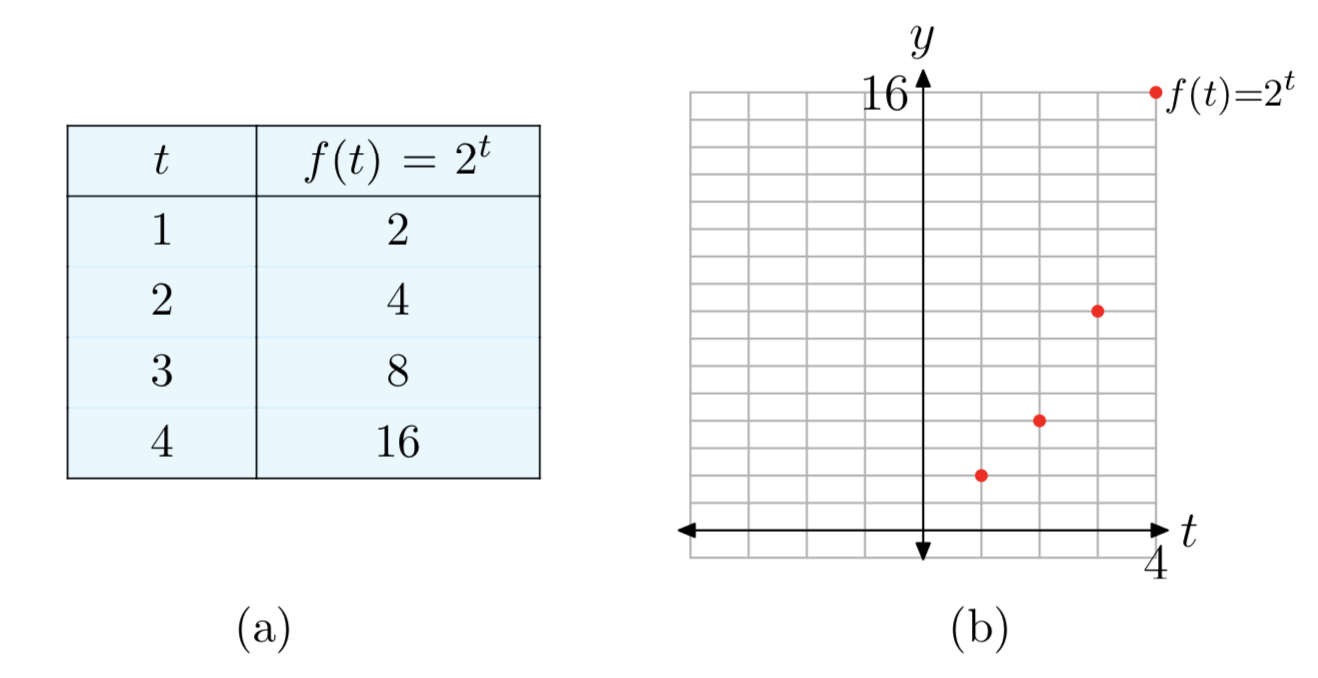
$b^t$Спочатку ми розробимо властивості базової експоненціальної функції, а потім відзначимо незначні зміни для більш загальної форми$Ab^t$. Для робочого прикладу давайте використаємо base b = 2, а потім обчислимо деякі значення$f(t) = 2^t$ і побудуємо результат (рис. 3).

Малюнок 3. Побудова точок (t, f (t)), визначених функцією$f(t) = 2^t$, з t = 1, 2, 3, 4,...

Нагадаємо з попереднього розділу, що 2t також визначено для негативних показників t та показника 0. Таким чином, експоненціальна функція$f(t) = 2^t$ визначається для всіх цілих чисел. На малюнку 4 показано нову таблицю та графік з точками, доданими у 0 та від'ємних цілих значеннях.

Рисунок 4. побудова точок (t, f (t)), визначених функцією$f(t) = 2^t$, з t =..., −3, −2, −1, 0, 1, 2, 3...

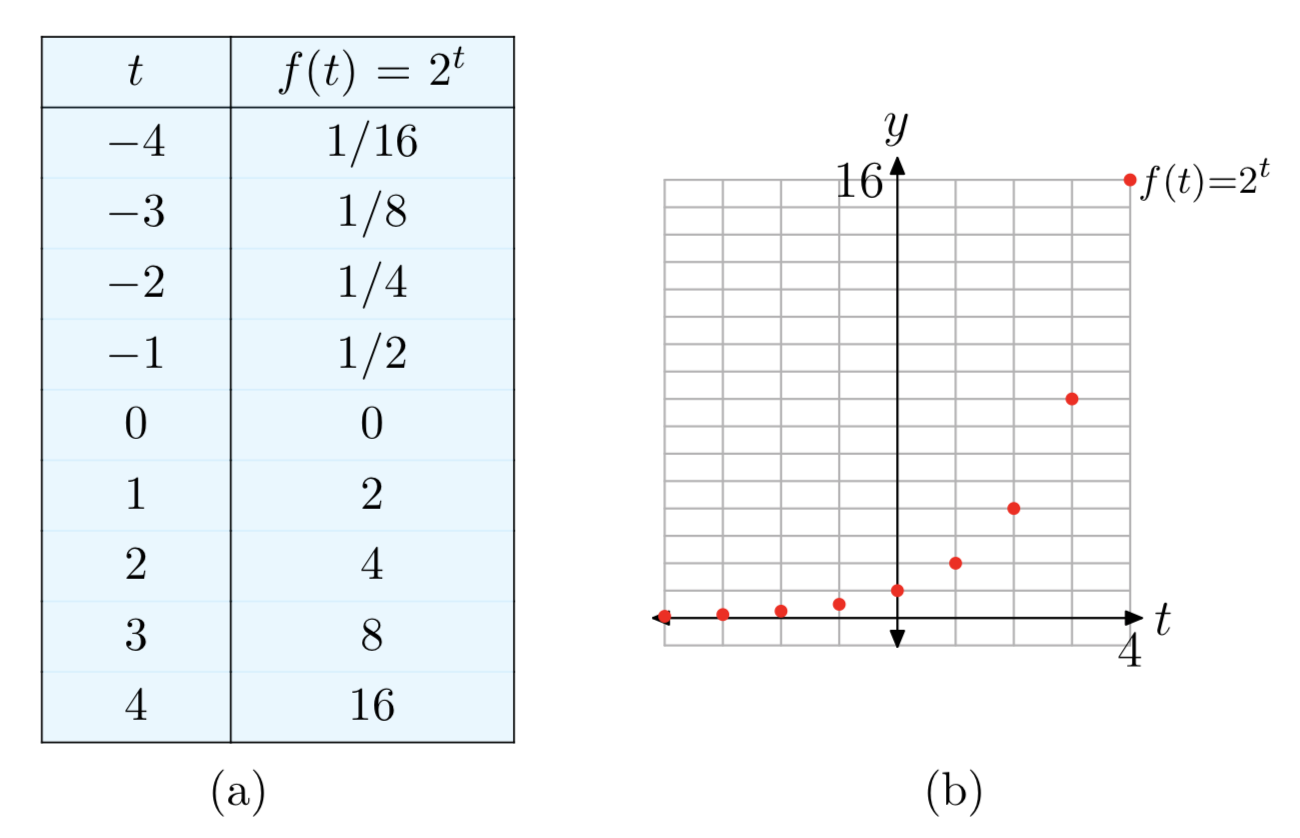
Однак попередній розділ показав,$2^t$ що також визначено для раціональних та ірраціональних показників. Тому область експоненціальної функції$f(t) = 2^t$ - це множина всіх дійсних чисел. Коли ми додаємо значення функції при всіх раціональних і ірраціональних значеннях$t$, отримуємо остаточну безперервну криву, як показано на малюнку 5.

Малюнок 5.

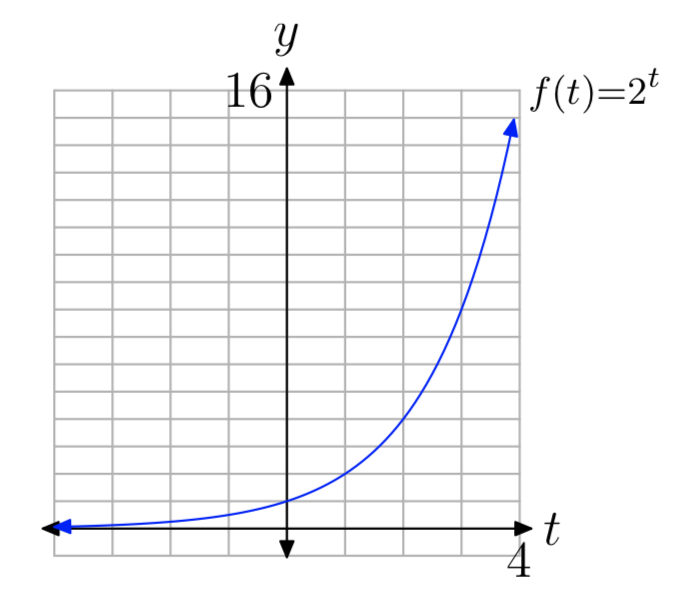
Зверніть увагу на кілька властивостей графіка на малюнку 5:

1. Рухаючись зліва направо, крива піднімається, а це означає, що функція збільшується в міру її збільшення. Насправді функція швидко зростає для позитивного t.
2. Графік лежить над віссю t, тому значення функції завжди позитивні. Тому діапазон функції є$(0, \infty)$.
3. Графік має горизонтальну асимптоту y = 0 (вісь t) з лівого боку. Це означає, що функція майже «згасає» (значення стають все ближче і ближче до 0) у міру наближення t$−\infty$.

А як щодо графіків інших експоненціальних функцій з різними базами? Ми скористаємося калькулятором, щоб вивчити кілька з них.

По-перше, скористайтеся калькулятором для порівняння$y_{1}(x) = 2^x$ і$y_{2}(x) = 3^x$. Як видно на малюнку 6 (а), графік$3^x$ піднімається швидше, ніж$2^x$ для x > 0, і вимирає швидше для x < 0.

Малюнок 6. Порівняння функцій$y_{1}(x) = 2^x$$y_{2}(x) = 3^x$, і$y_{3}(x) = 4^x$

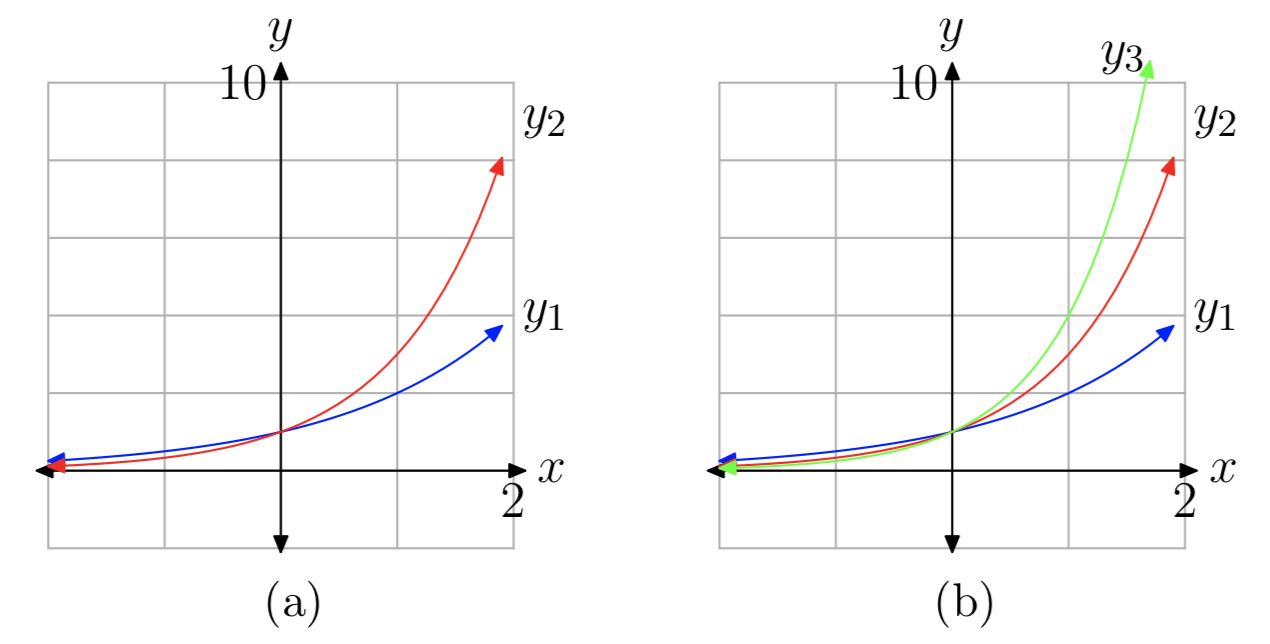
Далі додаємо в$y_{3}(x) = 4^x$. Результат показаний на малюнку 6 (б). Знову ж таки, збільшення розміру бази до b = 4 призводить до функції, яка піднімається ще швидше праворуч і так само швидше вимирає зліва. Якщо ви продовжите збільшувати розмір бази b, ви побачите, що ця тенденція продовжується. Це не страшно дивно, тому що, якщо ми обчислимо значення цих функцій при фіксованому додатному x, наприклад при x = 2, то значення збільшуються:$2^2 < 3^2 < 4^2 < ....$ Аналогічно, при x = −2 значення зменшуються:$2^{−2} > 3^{−2} > 4^{−2} >....$

Всі функції в наших експериментах досі поділяють властивості, перераховані в (a) — (c) вище: функція збільшується, діапазон є$(0, \infty)$, а графік має горизонтальну асимптоту y = 0 з лівого боку. Тепер спробуємо менші значення бази b Спочатку скористайтеся калькулятором для побудови графіка$y_{1}(x) = (\frac{1}{2})^x$ (див. Рис. 7 (а)).

Малюнок 7.

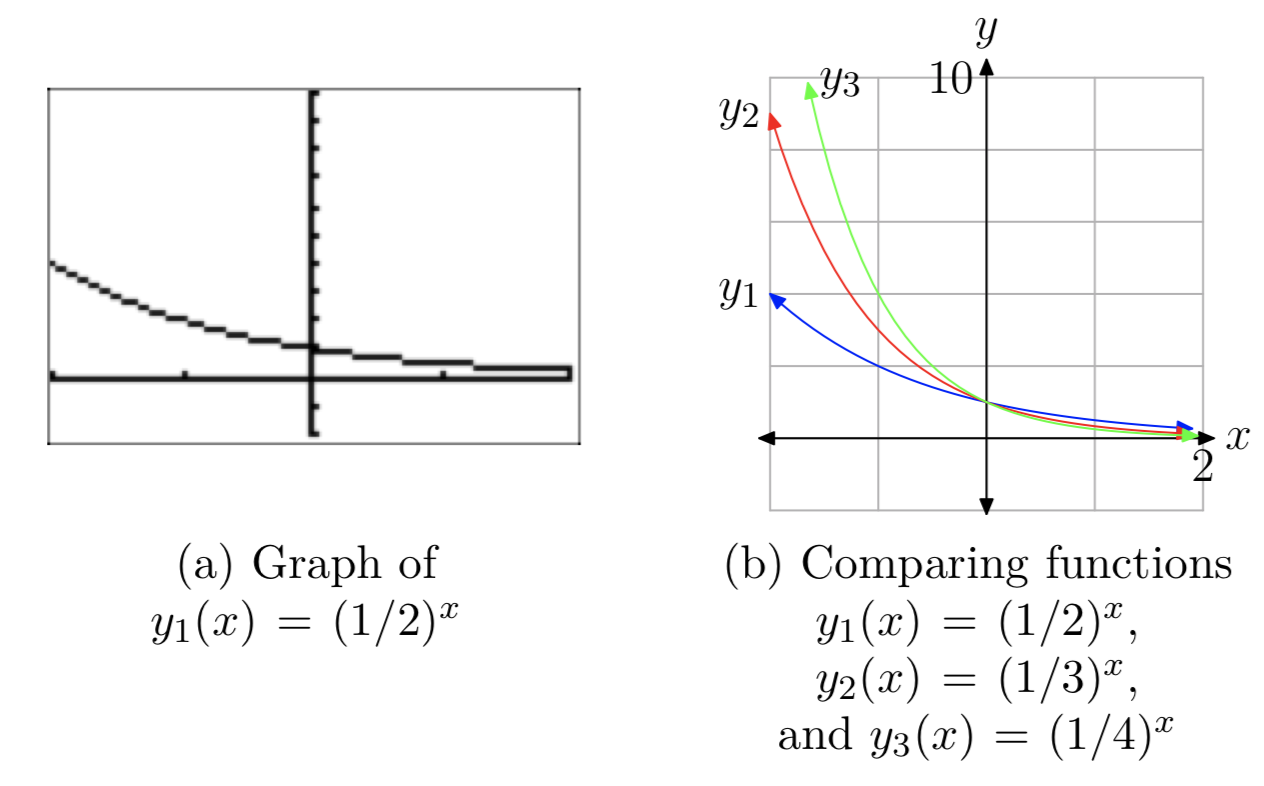
Цей графік сильно відрізняється. Вона стрімко піднімається вліво, а праворуч майже вимирає. Порівняйте це з$y_{2}(x) = (\frac{1}{3})^x$ і$y_{3}(x) = (\frac{1}{4})^x$ (див. Рис. 7 (б)). Оскільки база стає меншою, графік піднімається швидше зліва, а праворуч вимирає швидше.

Використовуючи властивості відображення, легко зрозуміти зовнішній вигляд цих трьох останніх графіків. Зверніть увагу, що

$(\frac{1}{2})^x = (2^{−1})^x = 2^{−x}$

Отже, випливає, що графік$(\frac{1}{2})^x$ - це всього лише відображення у -осі графіка$2^x$ (див. Рис.

Малюнок 8. Порівняння функцій$f(x) = 2^x$ і$g(x) = (\frac{1}{2})^x = 2^{−x}$

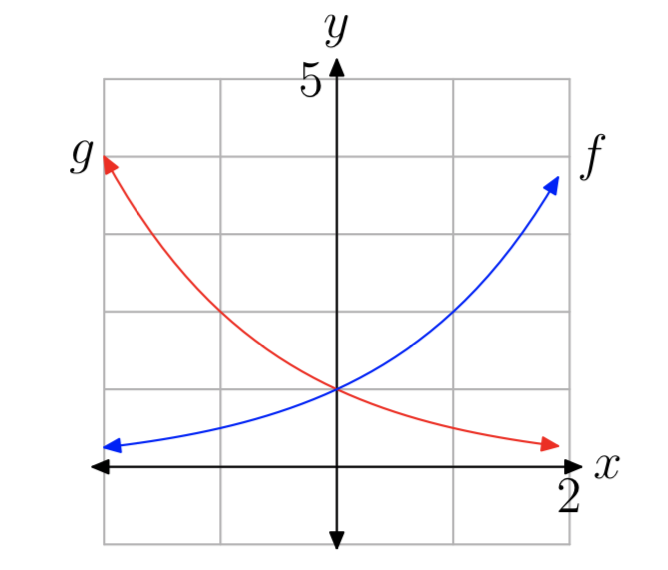
Таким чином, ми, здається, маємо два різних типи графіків, а отже, два типи експоненціальних функцій: один тип збільшується, а інший зменшується. Наші експерименти вище, разом з трохи більше експериментів, повинні переконати вас,$b^x$ що збільшується для b > 1, і зменшується на 0 < b < 1. Перший тип функцій називається експоненціальними функціями зростання, а другий тип - експоненціальні функції розпаду.

ВЛАСТИВОСТІ ЕКСПОНЕНЦІАЛЬНИХ ФУНКЦІЙ РОСТУ:$F(X) = B^X$ WITH B > 1

• Домен - це набір всіх дійсних чисел.
• Рухаючись зліва направо, графік піднімається, а це означає, що функція збільшується зі збільшенням x. Функція швидко зростає для позитивного x.
• Графік лежить вище осі x, тому значення функції завжди позитивні. Тому асортимент є$(0, \infty)$.
• Графік має горизонтальну асимптоту y = 0 (вісь x) з лівого боку. Це означає, що функція майже «вимирає» (значення стають все ближче і ближче до 0) у міру наближення x$−\infty$.

Друге властивість вище заслуговує деякого додаткового пояснення. Дивлячись на малюнок 6 (b), здається, що$y_{2}$ і швидко$y_{3}$ збільшуються, коли x збільшується, але,$y_{1}$ здається, повільно збільшується. Однак це пов'язано з тим, що графік$y_{1}(x) = 2^x$ показаний лише на інтервалі [− 2, 2]. На малюнку 5 та сама функція зображена на інтервалі [− 4, 4], і вона, безумовно, швидко зростає на цьому графіку. Справа тут в тому, що експоненціальні функції зростання в кінцевому підсумку швидко зростають у міру збільшення x. Якщо ви графуєте функцію на досить великому інтервалі, функція в кінцевому підсумку стане дуже крутою в правій частині графіка. Це важлива властивість функцій експоненціального зростання, і вона буде вивчена далі у вправах.

ВЛАСТИВОСТІ ЕКСПОНЕНЦІАЛЬНИХ ФУНКЦІЙ РОЗПАДУ:$F(X) = B^X$ WITH 0 < B < 1

• Домен - це набір всіх дійсних чисел.
• Рухаючись зліва направо, графік падає, а це означає, що функція де- згинається при збільшенні x. Функція швидко зменшується для від'ємного x.
• Графік лежить вище осі x, тому значення функції завжди позитивні. Тому асортимент є$(0, \infty)$.
• Графік має горизонтальну асимптоту y = 0 (вісь x) з правого боку. Це означає, що функція майже «вимирає» (значення стають все ближче і ближче до 0) у міру наближення x$\infty$.

Чому ми утримуємося від використання бази b = 1? Адже,$1^x$ безумовно, визначено: воно має значення 1 для всіх х. Але це означає, що$f(x) = 1^x$ це просто постійна лінійна функція — її графік є горизонтальною лінією. Тому ця функція не має тих самих властивостей, що й інші експоненціальні функції, і ми вже класифікували її як лінійну функцію. Таким чином, не$1^x$ вважається експоненціальною функцією.

Приклад$\PageIndex{19}$

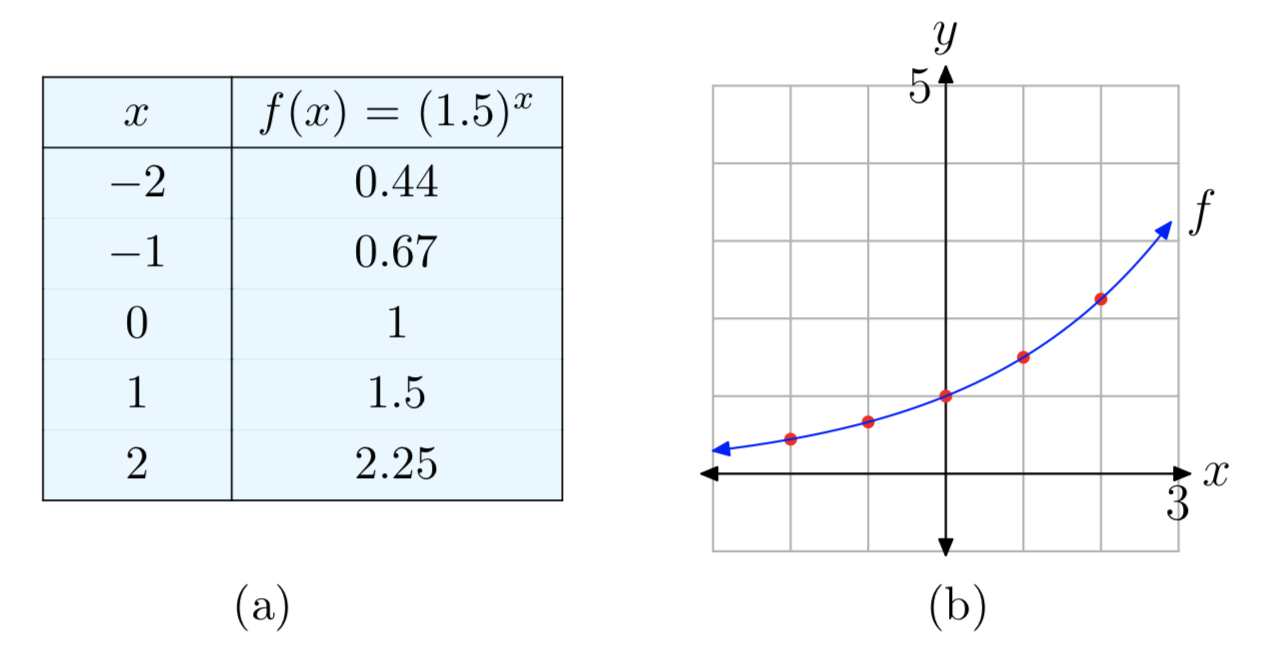
Побудуйте графік функції$f(x) = (1.5)^x$. Визначте діапазон функції і горизонтальну асимптоту.

Рішення

Оскільки база 1.5 більше 1, це експоненціальна функція зростання. Тому його графік матиме форму, подібну до графіків на малюнку 6. Графік піднімається, на лівій стороні буде горизонтальна асимптота y = 0, а діапазон функції -$(0, \infty)$. Граф потім можна побудувати вручну, використовуючи ці знання разом з приблизними значеннями при x = - 2, − 1, 0, 1, 2. Див. Рисунок 9.

Малюнок 9. Графік$f(x) = (1.5)^x$

Приклад$\PageIndex{20}$

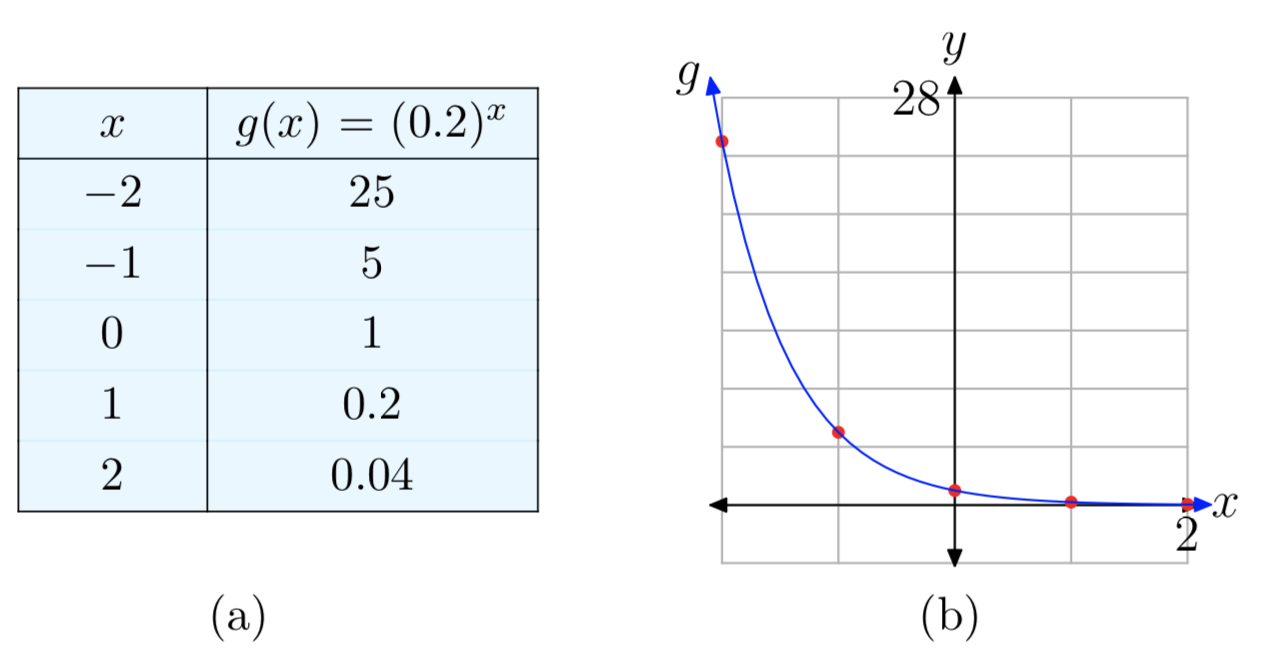
Побудуйте графік функції$g(x) = (0.2)^x$. Визначте діапазон функції і горизонтальну асимптоту.

Рішення

Оскільки база 0,2 менше 1, це експоненціальна функція розпаду. Тому його графік матиме форму, подібну до графіків на малюнку 7. Графік падає, з правого боку буде горизонтальна асимптота y = 0, а діапазон функції\((0, \infty)\). The graph can then be plotted by hand by using this knowledge along with approximate values at x = − 2, − 1, 0, 1, 2. Див. Малюнок 10.

Малюнок 10. Графік$f(x) = (0.2)^x$

 

Приклад$\PageIndex{21}$

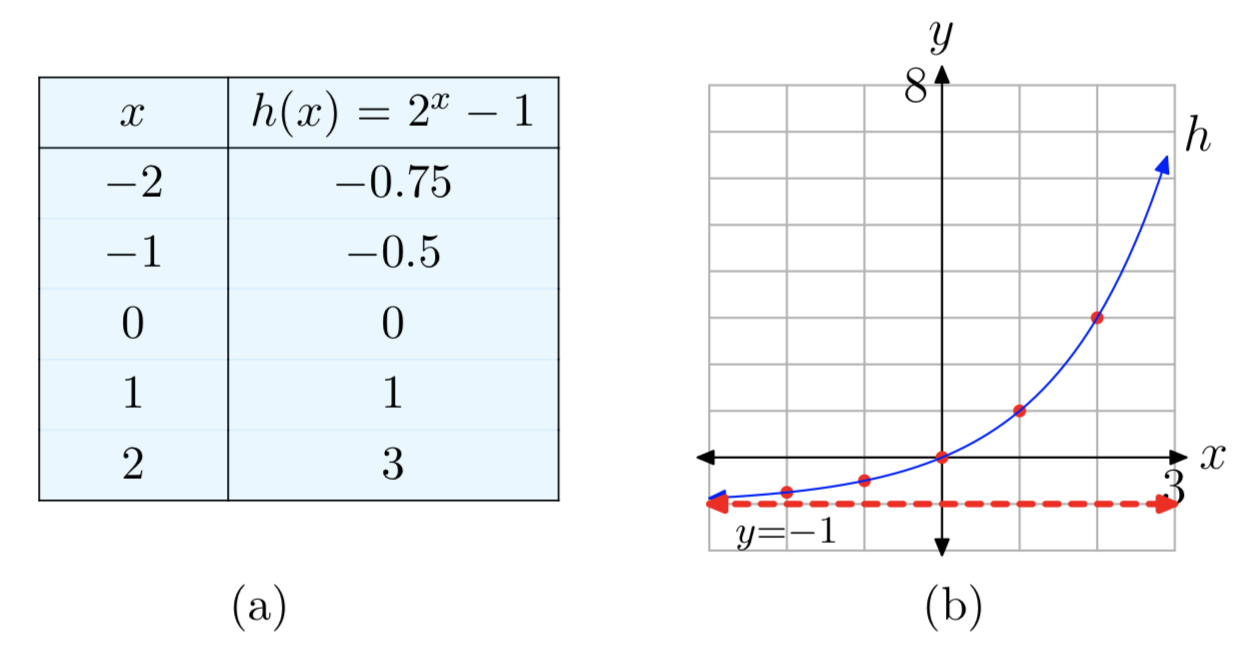
Побудуйте графік функції$f(x) = 2^x−1$. Визначте діапазон функції і горизонтальну асимптоту.

Рішення

Графік h можна отримати з графіка$f(x) = 2^x$ (див. Рис. 5) вертикальним зсувом вниз на 1 одиницю. Отже, горизонтальна асимптота y = 0 графа f також буде зрушена вниз на 1 одиницю, тому графік h має горизонтальну асимптоту y = − 1. Аналогічно діапазон f буде зміщений вниз до\((−1, \infty)\) = Range (h). Потім графік можна побудувати вручну, використовуючи ці знання разом з приблизними значеннями при x = − 2, − 1, 0, 1, 2. Див. Рисунок 11.

Малюнок 11. Графік$f(x) = 2^x−1$

У наступних розділах цієї глави ми також побачимо більш загальні експоненціальні функції форми$f(x) = Ab^x$ (насправді функції Pleasantville і Ghosttown на початку цього розділу мають таку форму). Якщо A позитивний, то графіки цих функцій можна отримати з основних експоненціальних графіків шляхом вертикального масштабування, тому графіки матимуть таку ж загальну форму, як або експоненціальні криві зростання (якщо b > 1), або експоненціальні криві розпаду (якщо$0 < b < 1$), які ми будували раніше.

Вправа

Вправа$\PageIndex{1}$

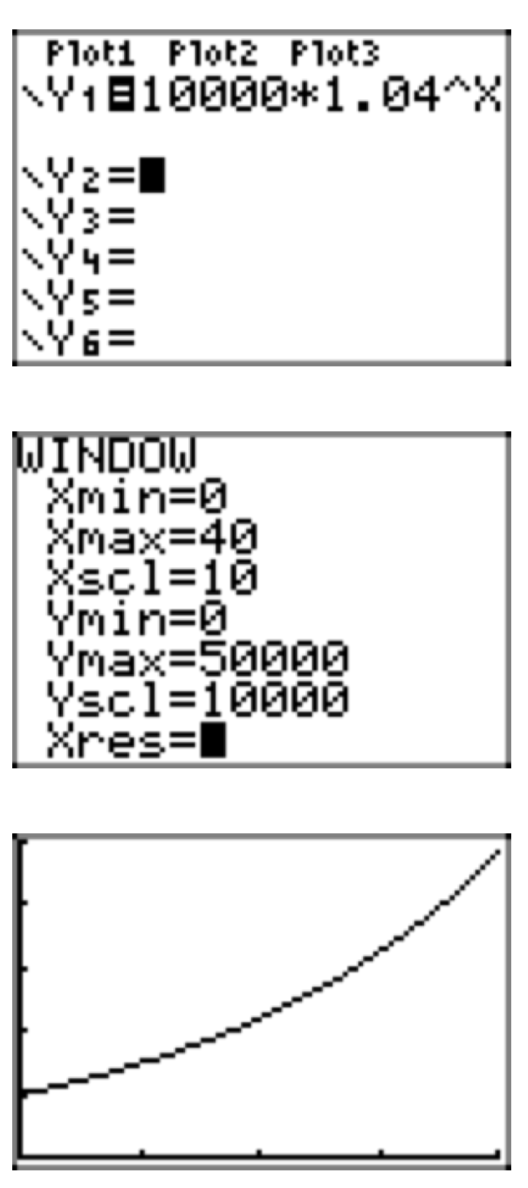
Нинішнє населення Фортуни становить 10 000 сердечних душ. Відомо, що чисельність населення зростає зі швидкістю 4% в рік. Припускаючи, що ця норма залишається постійною, виконайте кожне з наступних завдань.

1. Налаштуйте рівняння, яке моделює сукупність P (t) як функцію часу t.
2. Використовуйте модель в попередній частині для прогнозування населення через 40 років.
3. Скористайтеся калькулятором, щоб намалювати графік населення протягом наступних 40 років.

Відповідь

1. $P(t) = 10000(1.04)^t$
2. $P(40) \approx 48101$
3.  

Вправа$\PageIndex{2}$

Населення містечка Уява в даний час налічує 12 000 чоловік. Відомо, що чисельність населення зростає зі швидкістю 6% в рік. Припускаючи, що ця норма залишається постійною, виконайте кожне з наступних завдань.

1. Налаштуйте рівняння, яке моделює сукупність P (t) як функцію часу t.
2. Використовуйте модель в попередній частині для прогнозування чисельності населення через 30 років.
3. Використовуйте калькулятор, щоб намалювати графік населення протягом наступних 30 років.

Вправа$\PageIndex{3}$

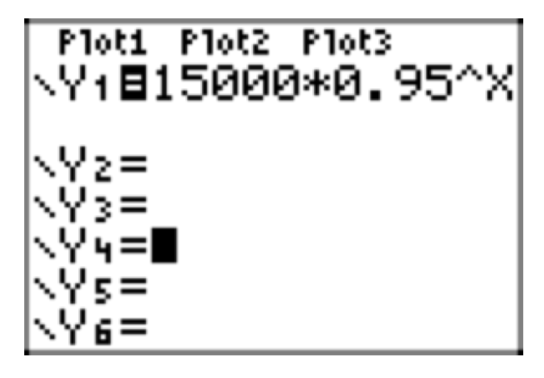
Населення міста Деспайрія в даний час налічує 15 000 особин. Відомо, що населення розпадається зі швидкістю 5% в рік. Припускаючи, що ця норма залишається постійною, виконайте кожне з наступних завдань.

1. Налаштуйте рівняння, яке моделює сукупність P (t) як функцію часу t.
2. Використовуйте модель в попередній частині для прогнозування населення через 50 років.
3. Використовуйте калькулятор, щоб намалювати графік населення протягом наступних 50 років.

Відповідь

1. $p(t) = 15 000(0.95)^t$
2. $P(50) \approx 1154$
3.  

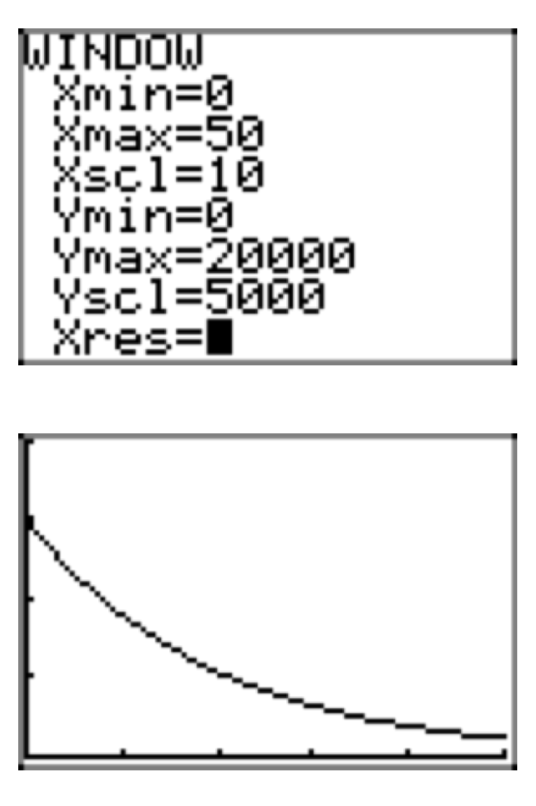
Вправа$\PageIndex{4}$

Населення містечка Безнадійний в даний час налічує 25 000 особин. Відомо, що населення розпадається зі швидкістю 6% на рік. Припускаючи, що ця норма залишається постійною, виконайте кожне з наступних завдань.

1. Налаштуйте рівняння, яке моделює сукупність P (t) як функцію часу t.
2. Використовуйте модель в попередній частині для прогнозування населення через 40 років.
3. Скористайтеся калькулятором, щоб намалювати графік населення протягом наступних 40 років.

У вправах 5 - 12 виконайте кожне з наступних завдань для даної функції.

1. Знайти y-перехоплення графіка функції. Крім того, скористайтеся калькулятором, щоб знайти дві точки на графіку праворуч від осі Y та дві точки ліворуч.
2. Використовуючи п'ять точок з (a) як орієнтир, налаштуйте систему координат на графічному папері. Виберіть і позначте відповідні шкали для кожної осі. Побудуйте п'ять точок, і будь-які додаткові точки, які ви відчуваєте, необхідні для розрізнення форми графіка.
3. Намалюйте горизонтальну асимптоту пунктирною лінією і позначте її рівнянням.
4. Намалюйте графік функції.
5. Використовуйте інтервальне позначення для опису як домену, так і діапазону функції.

Вправа$\PageIndex{5}$

$f(x) = (2.5)^x$

Відповідь

1. Y-перехоплення є (0, 1). Оцінювання функції при x = 1, 2, −1, −2 для отримання балів (1, 2,5), (2, 6,25), (−1, 0,4), (−2, 0,16) (можливі інші відповіді).
2. Див. Графік в частині (4).
3. Горизонтальна асимптота дорівнює y = 0. Див. Графік в частині (4).
4. 
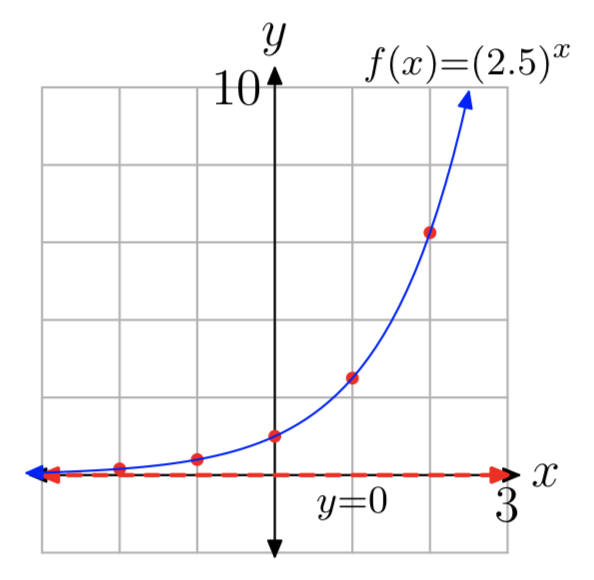
5. Домен =$(−\infty, \infty)$, Діапазон =$(0, \infty)$

Вправа$\PageIndex{6}$

$f(x) = (0.1)^x$

Вправа$\PageIndex{7}$

$f(x) = (0.75)^x$

Відповідь

1. Y-перехоплення є (0, 1). Оцінити функцію при x = 1, 2, −1, −2, щоб отримати точки (1, 0,75), (2, 0,56), (−1, 1,34), (−2, 1,78) (можливі інші відповіді).
2. Див. Графік в частині (4).
3. Горизонтальна асимптота дорівнює y = 0. Див. Графік в частині (4).
4. 
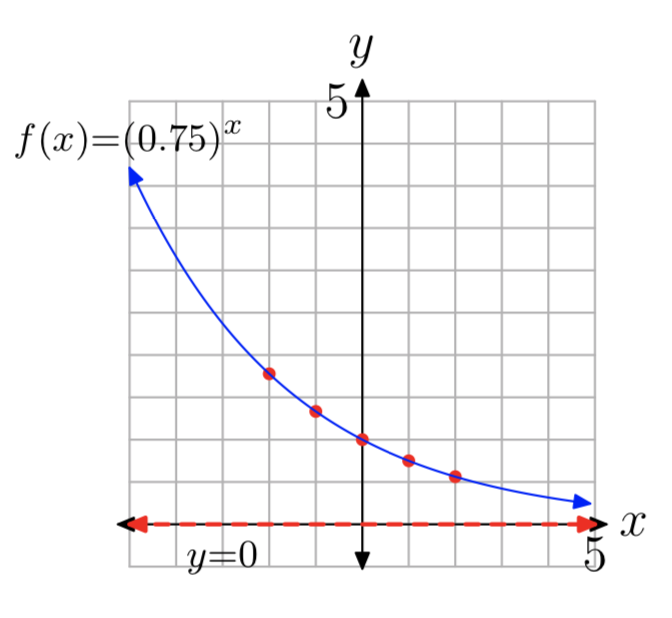
5. Домен =$(−\infty, \infty)$, Діапазон =$(0, \infty)$

Вправа$\PageIndex{8}$

$f(x) = (1.1)^x$

Вправа$\PageIndex{9}$

$f(x) = 3^x+1$

Відповідь

1. Y-перехоплення є (0, 2). Оцінити функцію при x = 1, 2, −1, −2, щоб отримати точки (1, 4), (2, 10), (−1, 1.34), (−2, 1.11) (можливі інші відповіді).
2. Див. Графік в частині (4).
3. Горизонтальна асимптота y = 1. Див. Графік в частині (4).
4. 
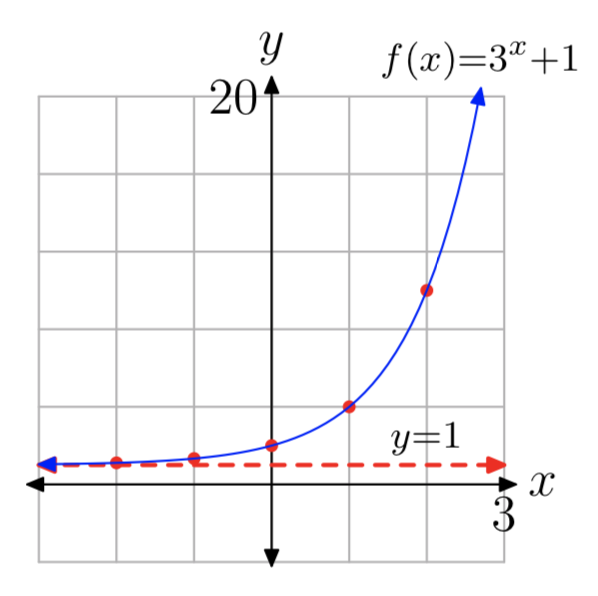
5. Домен =$(−\infty, \infty)$, Діапазон =$(1, \infty)$

Вправа$\PageIndex{10}$

$f(x) = 4^x−5$

Вправа$\PageIndex{11}$

$f(x) = 2^x−3$

Відповідь

1. Перехоплення y дорівнює (0, −2). Оцінити функцію за x = 1, 2, −1, −2, щоб отримати точки (1, −1), (2, 1), (−1, −2.5), (−2, −2,75) (можливі інші відповіді).
2. Див. Графік в частині (4).
3. Горизонтальна асимптота дорівнює y = −3. Див. Графік в частині (4).
4. 
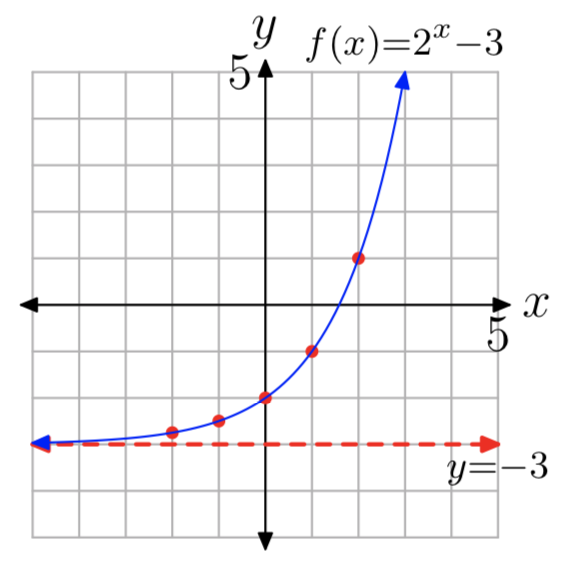
5. Домен =$(−\infty, \infty)$, Діапазон =$(−3, \infty)$

Вправа$\PageIndex{12}$

$f(x) = 5^x+2$

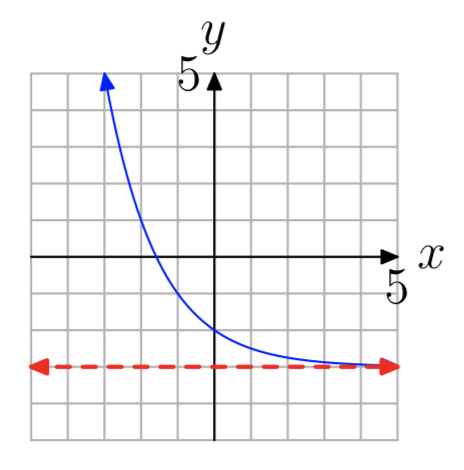
У вправах 13 - 20 показаний графік ex ponential функції форми$f(x) = b^x+c$. Пунктирна червона лінія - горизонтальна асимптота. Визначте діапазон функції. Висловіть свою відповідь в інтервальних позначеннях.

Вправа$\PageIndex{13}$

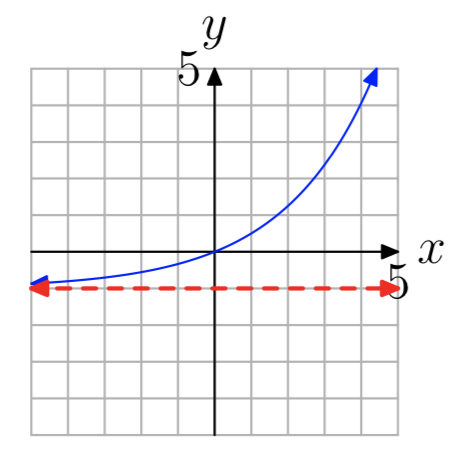
Відповідь

$(−1, \infty)$

Вправа$\PageIndex{14}$

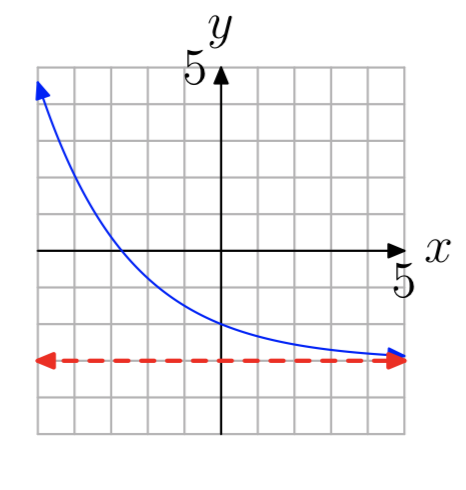
Вправа$\PageIndex{15}$

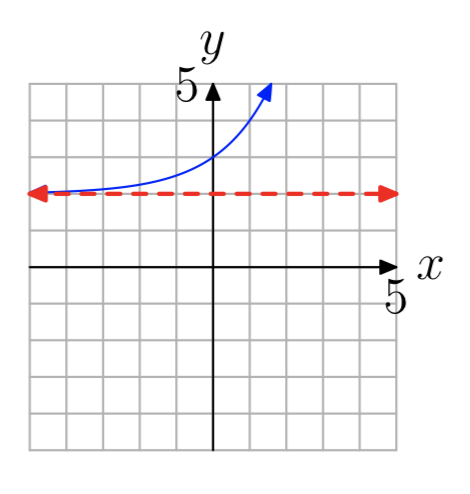
Відповідь

$(2, \infty)$

Вправа$\PageIndex{16}$

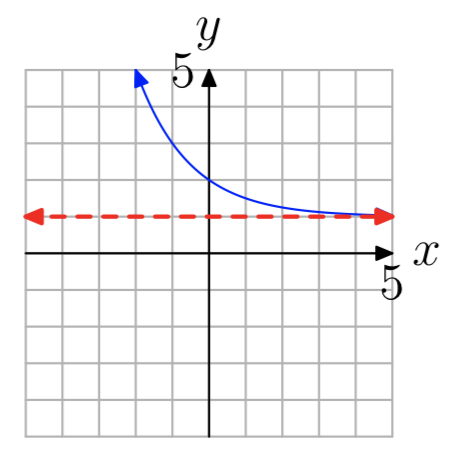
Вправа$\PageIndex{17}$

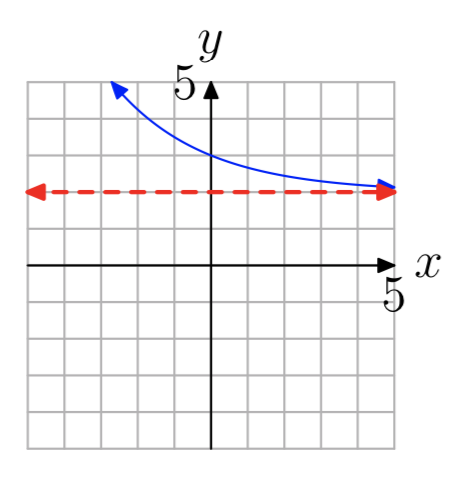
Відповідь

$(2, \infty)$

Вправа$\PageIndex{18}$

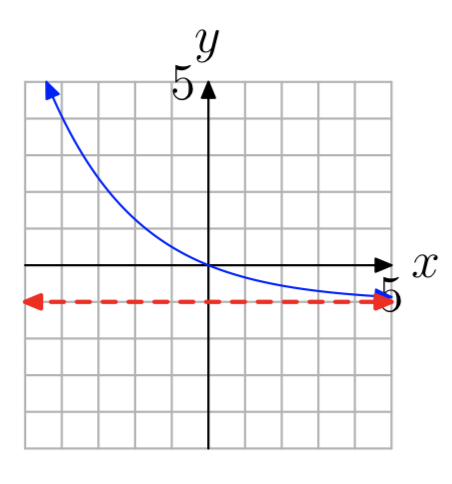
Вправа$\PageIndex{19}$

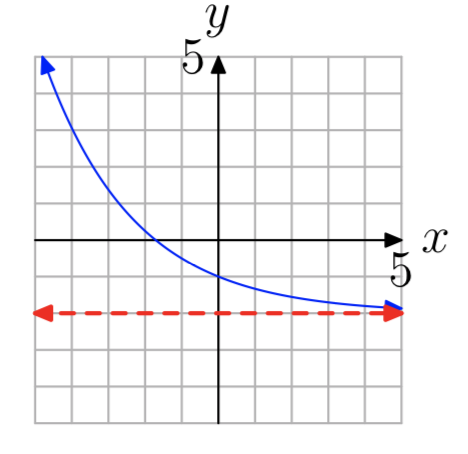
Відповідь

$(−2, \infty)$

Вправа$\PageIndex{20}$

У вправах 21 - 32 обчислити f (p) при заданому значенні p.

Вправа$\PageIndex{21}$

$f(x) = (\frac{1}{3})^x$; р = −4

Відповідь

81

Вправа$\PageIndex{22}$

$f(x) = (\frac{3}{4})^x$; р = 1

Вправа$\PageIndex{23}$

$f(x) = 5^x$; р = 5

Відповідь

3125

Вправа$\PageIndex{24}$

$f(x) = (\frac{1}{3})^x$; р = 4

Вправа$\PageIndex{25}$

$f(x) = 4^x$; р = −4

Відповідь

$\frac{1}{256}$

Вправа$\PageIndex{26}$

$f(x) = 5^x$; р = −3

Вправа$\PageIndex{27}$

$f(x) = (\frac{5}{2})^x$; р = −3

Відповідь

$\frac{8}{125}$

Вправа$\PageIndex{28}$

$f(x) = 9^x$; р = 3

Вправа$\PageIndex{29}$

$f(x) = 5^x$; р = −4

Відповідь

$\frac{1}{625}$

Вправа$\PageIndex{30}$

$f(x) = 9^x$; р = 0

Вправа$\PageIndex{31}$

$f(x) = (\frac{6}{5})^x$; р = −4

Відповідь

$\frac{625}{1296}$

Вправа$\PageIndex{32}$

$f(x) = (\frac{3}{5})^x$; р = 0

У Вправи 33 - 40 скористайтеся калькулятором для оцінки функції за заданим значенням p Округліть відповідь до найближчої сотої.

Вправа$\PageIndex{33}$

$f(x) = 10^x$; р = −0,7.

Відповідь

0,20

Вправа$\PageIndex{34}$

$f(x) = 10^x$; р = −1,6.

Вправа$\PageIndex{35}$

$f(x) = (\frac{2}{5})^x$; р = 3,67.

Відповідь

0,03

Вправа$\PageIndex{36}$

$f(x) = 2^x$;$p = −\frac{3}{4}$.

Вправа$\PageIndex{37}$

$f(x) = 10^x$; р = 2,07.

Відповідь

117.49

Вправа$\PageIndex{38}$

$f(x) = 7^x$;$p = \frac{4}{3}$.

Вправа$\PageIndex{39}$

$f(x) = 10^x$;$p = −\frac{1}{5}$.

Відповідь

0,63

Вправа$\PageIndex{40}$

$f(x) = (\frac{4}{3})^x$; р = 1,15

Вправа$\PageIndex{41}$

Ця вправа досліджує властивість, що функції експоненціального зростання в кінцевому підсумку швидко зростають у міру збільшення x. Нехай$f(x) = 1.05^x$. Використовуйте графічний калькулятор для графіка f на інтервалах

(а) [0, 10] і (б) [0, 100].

Для (а) використовуйте Ymin = 0 і Ymax = 10.

Для (b) використовуйте Ymin = 0 і Ymax = 100.

Зробіть точні копії зображень у вікні перегляду на домашньому папері. Що ви спостерігаєте, порівнюючи два графіки?

Відповідь

(а) Графік на інтервалі [0, 10] збільшується дуже повільно. Насправді графік виглядає майже лінійним.

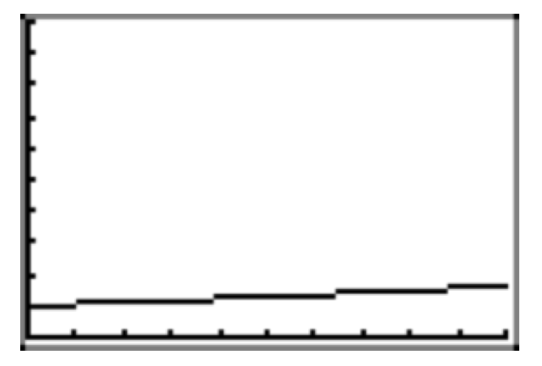
(б) Графік на інтервалі [0, 100] спочатку повільно збільшується, але потім дуже швидко зростає на другій половині інтервалу.