1.4: Дроби

Цілі навчання

До кінця цього розділу ви зможете:

• Спрощення дробів
• Множення і ділення дробів
• Додавання та віднімання дробів
• Використовуйте порядок операцій для спрощення дробів
• Оцінити змінні вирази з дробами

Більш ретельне ознайомлення з темами, висвітленими в цьому розділі, можна знайти в розділі Елементарна алгебра, Основи.

Спрощення дробів

Дріб - це спосіб представлення частин цілого. Дріб\(\frac{2}{3}\) являє собою дві з трьох рівних частин (рис.\(\PageIndex{1}\)). У\(\frac{2}{3}\) дробі 2 називається чисельником, а 3 - знаменником. Лінія називається брусом дробу.

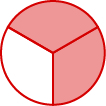
Малюнок\(\PageIndex{1}\): У\(\frac{2}{3}\) колі коло заштриховано - 2 з 3 рівних частин.

ФРАКЦІЯ

Пишуть дріб\(\dfrac{a}{b}\), де\(b\neq 0\) і

\(a\)є чисельником і\(b\) є знаменником.

Дріб являє собою частини цілого. Знаменник\(b\) - це кількість рівних частин, на які було поділено ціле, а чисельник\(a\) вказує, скільки частин включено.

Дроби, які мають однакове значення, є еквівалентними дробами. Еквівалентні дроби

Властивість дозволяє нам знаходити еквівалентні дроби, а також спростити дроби.

Якщо\(a\),\(b\), і\(c\) є числами де\(b\neq 0,c\neq 0\),

потім\(\dfrac{a}{b}=\dfrac{a·c}{b·c}\) і\(\dfrac{a·c}{b·c}=\dfrac{a}{b}.\)

Дріб вважається спрощеним, якщо в його чисельнику і знаменнику відсутні загальні множники, крім 1.

Наприклад,

\(\dfrac{2}{3}\)спрощується, оскільки відсутні загальні фактори\(2\) і\(3\).

\(\dfrac{10}{15}\)не спрощується, тому що\(5\) є загальним фактором\(10\) і\(15\).

Спрощуємо, або зменшуємо дріб, видаливши загальні множники чисельника і знаменника. Дріб не спрощується, поки не будуть видалені всі загальні фактори. Якщо вираз має дроби, воно не спрощується повністю, поки дроби не будуть спрощені.

Іноді буває непросто знайти загальні чинники чисельника і знаменника. Коли це станеться, гарна ідея полягає в тому, щоб перерахувати чисельник і знаменник на прості числа. Потім розділіть загальні фактори, використовуючи властивість еквівалентних дробів.

Спростити\(\dfrac{−315}{770}\).

Відповідь

Спростити\(−\dfrac{69}{120}\).

Відповідь

\(−\dfrac{23}{40}\)

ПРИКЛАД\(\PageIndex{3}\)

Спростити\(−\dfrac{120}{192}\).

Відповідь

\(−\dfrac{5}{8}\)

Тепер ми підсумовуємо кроки, які слід виконати для спрощення дробів.

СПРОСТІТЬ ДРІБ.

1. Перепишіть чисельник і знаменник, щоб показати загальні фактори.
   Якщо потрібно, спочатку перерахуйте чисельник і знаменник на прості числа.
2. Спростіть використання властивості еквівалентних дробів шляхом поділу загальних факторів.
3. Помножте всі інші фактори.

Множення та ділення дробів

Багато людей вважають, що множення та ділення дробів простіше, ніж додавання та віднімання дробів.

Для множення дробів множимо чисельники і множимо знаменники.

МНОЖЕННЯ ДРОБУ

Якщо\(a\),\(b\),\(c\), і\(d\) є числами де\(b≠0\), і\(d≠0\), то

\[\frac{a}{b}·\frac{c}{d}=\frac{ac}{bd}\]

Для множення дробів помножте чисельники і помножте знаменники.

При множенні дробів властивості позитивних і негативних чисел все ж застосовуються, звичайно. Непогано визначити ознаку продукту в якості першого кроку. У прикладі ми помножимо негатив і позитив, тому твір буде негативним.

При множенні дробу на ціле число може бути корисним записати ціле число як дріб. Будь-яке ціле число, a, може бути записано як\(\dfrac{a}{1}\). Так, наприклад,\(3=\dfrac{3}{1}\).

Вправа\(\PageIndex{4}\)

Помножити:\(−\dfrac{12}{5}(−20x).\)

Відповідь

Насамперед необхідно знайти ознаку вироби. Так як ознаки однакові, продукт позитивний.

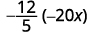
Визначте ознаку вироби. Ознаки однакові, тому продукт позитивний.
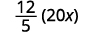
Запишіть 20 х як дріб.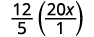
Помножити.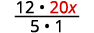
Перепишіть 20, щоб показати загальний коефіцієнт 5 і розділити його.
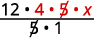
Спростити.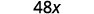

Вправа\(\PageIndex{5}\)

Помножити:\(\dfrac{1}{13}(−9a)\).

Відповідь

\(−33a\)

Вправа\(\PageIndex{6}\)

Помножити:\(\dfrac{13}{7}(−14b)\).

Відповідь

\(−26b\)

Тепер, коли ми знаємо, як множити дроби, ми майже готові ділити. Перш ніж ми зможемо це зробити, нам потрібен певний словниковий запас. Зворотний дріб знаходять шляхом інвертування дробу, розміщення чисельника в знаменнику і знаменника в чисельнику. Відповідне\(\frac{2}{3}\) є\(\frac{3}{2}\). Оскільки 4 пишеться в дробовій формі як\(\frac{4}{1}\), то зворотне 4 є\(\frac{1}{4}\).

Для поділу дробів множимо перший дріб на зворотний другий.

ДІЛЕННЯ ФРАКЦІЇ

Якщо\(a\),\(b\),\(c\), і\(d\) є числами де\(b≠0\)\(c≠0\), і\(d≠0\), то

\[\frac{a}{b}÷\frac{c}{d}=\frac{a}{b}⋅\frac{d}{c}\]

Для поділу дробів множимо перший дріб на зворотний другий.

Ми повинні сказати\(b≠0\), і\(c≠0\), щоб бути впевненим\(d≠0\), що ми не ділимо на нуль!

Вправа\(\PageIndex{7}\)

Знайдіть частку:\(−\dfrac{7}{18}÷(−\dfrac{14}{27}).\)

Відповідь

	\(−\dfrac{7}{18}÷(−\dfrac{14}{27})\)
Для поділу помножте перший дріб на зворотний другий.
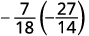
Визначте ознаку виробу, а потім множте.
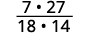
Перепишіть, показуючи загальні фактори.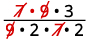
Видаліть загальні фактори.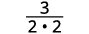
Спростити.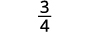

Розділити:\(−\dfrac{7}{27}÷(−\dfrac{35}{36})\).

Відповідь

\(\dfrac{4}{15}\)

Вправа\(\PageIndex{9}\)

Розділити:\(−\dfrac{5}{14}÷(−\dfrac{15}{28}).\)

Відповідь

\(\dfrac{2}{3}\)

Чисельники або знаменники деяких дробів містять самі дроби. Дріб, в якому чисельником або знаменником є дріб, називається складним дробом.

Визначення: СКЛАДНА ДРІБ

Складний дріб - це дріб, в якому чисельник або знаменник містить дріб.

Деякі приклади складних дробів:

\[\dfrac{\frac{6}{7}}{3} \quad \dfrac{\frac{3}{4}}{\frac{5}{8}} \quad \dfrac{\frac{x}{2}}{ \frac{5}{6}}\]

Щоб спростити складний дріб, пам'ятайте, що брусок фракції означає поділ. Наприклад, складний дріб\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) означає\(\dfrac{3}{4}÷\frac{5}{8}.\)

Вправа\(\PageIndex{10}\)

Спростити:\(\dfrac{\dfrac{x}{2}}{ \dfrac{xy}{6}}\).

Відповідь

\(\begin{array}{lc} \text{} & \dfrac{\dfrac{x}{2}}{ \dfrac{xy}{6}} \\[6pt] \text{Rewrite as division.} & \dfrac{x}{2}÷\dfrac{xy}{6} \\[6pt] \text{Multiply the first fraction by the reciprocal of the second.} & \dfrac{x}{2}·\dfrac{6}{xy} \\[6pt] \text{Multiply.} & \dfrac{x·6}{2·xy} \\[6pt] \text{Look for common factors.} & \dfrac{ \cancel{x}·3·\cancel{2}}{\cancel{2}·\cancel{x}·y} \\[6pt] \text{Divide common factors and simplify.} & \dfrac{3}{y} \end{array}\)

Спростити:\(\dfrac{\dfrac{a}{8}}{ \dfrac{ab}{6}}\).

Відповідь

\(\dfrac{3}{4b}\)

Спростити:\(\dfrac{\dfrac{p}{2}}{ \dfrac{pq}{8}}\).

Відповідь

\(\dfrac{4}{q}\)

Додавання та віднімання дробів

Коли ми множили дроби, ми просто помножили чисельники і множили знаменники прямо поперек. Для додавання або віднімання дробів вони повинні мати спільний знаменник.

ДОДАВАННЯ ТА ВІДНІМАННЯ ДРОБУ

Якщо\(a\),\(b\), і\(c\) є числами де\(c≠0\), то

\[\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \text{ and } \dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\]

Щоб додати або відняти дроби, додайте або відніміть чисельники і помістіть результат над спільним знаменником.

Найменший спільний знаменник (РК) двох дробів - це найменше число, яке можна використовувати як спільний знаменник дробів. РК-дисплей двох дробів є найменш загальним кратним (LCM) їх знаменників.

НАЙМЕНШ СПІЛЬНИЙ ЗНАМЕННИК

Найменш спільний знаменник (РК) двох дробів - найменш спільний кратний (НКМ) їх знаменників.

Після того, як ми знайдемо найменш спільний знаменник двох дробів, перетворюємо дроби в еквівалентні дроби з РК. Складання цих кроків дозволяє нам додавати та віднімати дроби, оскільки їх знаменники будуть однаковими!

ПРИКЛАД\(\PageIndex{13}\): How to Add or Subtract Fractions

Додати:\(\dfrac{7}{12}+\dfrac{5}{18}\).

Відповідь

ПРИКЛАД\(\PageIndex{14}\)

Додати:\(\dfrac{7}{12}+\dfrac{11}{15}\).

Відповідь

\(\dfrac{79}{60}\)

ПРИКЛАД\(\PageIndex{15}\)

Додати:\(\dfrac{13}{15}+\dfrac{17}{20}\).

Відповідь

\(\dfrac{103}{60}\)

ДОДАВАННЯ АБО ВІДНІМАННЯ ДРОБІВ.

1. Чи мають вони спільний знаменник?
   • Так—перейдіть до кроку 2.
   • Ні - перепишіть кожен дріб з РК-дисплеєм (найменш спільний знаменник).
     • Знайдіть РК-дисплей.
     • Змініть кожен дріб на еквівалентний дріб з LCD як його знаменником.
2. Додавання або віднімання дробів.
3. Спрощуйте, якщо це можливо.

Тепер у нас є всі чотири операції для дробів. Таблиця підсумовує операції дробу.

Множення дробу	Розділ дробу
\(\dfrac{a}{b}⋅\dfrac{c}{d}=\dfrac{ac}{bd}\)	\(\dfrac{a}{b}÷\dfrac{c}{d}=\dfrac{a}{b}⋅\dfrac{d}{c}\)
Множимо чисельники і множимо знаменники	Помножте перший дріб на зворотний другий.
Додавання дробу	Віднімання дробу
\(\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c}\)	\(\dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\)
Додайте чисельники і помістіть суму над спільним знаменником.	Відніміть чисельники і помістіть різницю над спільним знаменником.
Для множення або поділу дробів РК-дисплей НЕ потрібен. Для додавання або віднімання дробів потрібен РК-дисплей.

Починаючи вправу, завжди визначте операцію, а потім згадуйте методи, необхідні для цієї операції.

Спрощення: ⓐ\(\dfrac{5x}{6}−\dfrac{3}{10}\) ⓑ\(\dfrac{5x}{6}·\dfrac{3}{10}\).

Відповідь

Спочатку запитайте: «Що таке операція?» Ідентифікація операції визначить, чи потрібен нам спільний знаменник. Пам'ятайте, нам потрібен спільний знаменник, щоб скласти або відняти, але не множити або ділити.

ⓐ

\ (\ begin {масив} {lc}\ text {Що таке операція? Операція віднімання.}\\ [6pt]\ text {Чи мають дроби спільний знаменник? Ні.} &\ dfrac {5x} {6} −\ dfrac {3} {10}\\ [6pt]\ text {Знайти РК-дисплей} 6\ текст {і} 10 &\ текст {РК-дисплей 30.}\\ [6pt] {\ begin {align*} 6 & =2·3\\ [6pt]\;\;\;\ підкреслення {
\;\;\;\;\;\;\;\;\;\;\;\;; 10\;\;\;\;} &\ підкреслення {=2·5\;\;\;\;}\\ [6pt]\;\ [6pt]
\ текст {РК-дисплей} & =2·3·5\\ [6] pt]
\ text {LCD} & =30\ end {align*}}\\ [6pt]\\
\ text {Перепишіть кожен дріб як еквівалентний дріб з РК-дисплеєм.} &\ dfrac {5x·5} {6·5} −\ dfrac {3·3} {10·3}\\ [6pt]
\ text {} &\ dfrac {25x} {30} {30}\\ [6pt]
\ text {Відніміть чисельники і помістіть}\\ [6pt]
\ текст {різниця над загальною знаменники.} &\ dfrac {25x−9} {30}\\ [6pt]\\
\ text {Спростіть, якщо можливо.}\\ [6pt]
\ text {Дріб спрощено.} \ end {масив}\)

ⓑ

\(\begin{array}{lc} \text{What is the operation? Multiplication.} & \dfrac{25x}{6}·\dfrac{3}{10} \\ \text{To multiply fractions,multiply the numerators} \\ \text{and multiply the denominators.} & \dfrac{25x·3}{6·10} \\ \text{Rewrite, showing common factors.} \\ \text{Remove common factors.} & \dfrac{\cancel{5} x · \cancel{3}}{2·\cancel{3}·2·\cancel{5}} \\ \text{Simplify.} & \dfrac{x}{4} \end{array}\)

Зверніть увагу, нам потрібен був РК-дисплей, щоб додати\(\dfrac{25x}{6}−\dfrac{3}{10}\), але не множити\(\dfrac{25x}{6}⋅\dfrac{3}{10}\).

ПРИКЛАД\(\PageIndex{17}\)

Спрощення: ⓐ\(\dfrac{3a}{4}−\dfrac{8}{9}\) ⓑ\(\dfrac{3a}{4}·\dfrac{8}{9}\).

Відповідь

ⓐ\(\dfrac{27a−32}{36}\) ⓑ\(\dfrac{2a}{3}\)

ПРИКЛАД\(\PageIndex{18}\)

Спрощення: ⓐ\(\dfrac{4k}{5}−\dfrac{1}{6}\) ⓑ\(\dfrac{4k}{5}⋅\dfrac{1}{6}\).

Відповідь

ⓐ\(\dfrac{24k−5}{30}\) ⓑ\(\dfrac{2k}{15}\)

Використовуйте порядок операцій для спрощення дробів

Рядок дробу у дробі виступає символом групування. Потім порядок операцій говорить нам, щоб спростити чисельник, а потім знаменник. Потім ділимо.

СПРОСТІТЬ ВИРАЗ ЗА ДОПОМОГОЮ РЯДКА ДРОБУ.

1. Спростити вираз в чисельнику. Спростити вираз в знаменнику.
2. Спростити дріб.

Куди йде негативний знак в дробі? Зазвичай негативний знак знаходиться перед дробом, але іноді ви побачите дріб з негативним чисельником, а іноді і з негативним знаменником. Пам'ятайте, що дроби являють собою поділ. Коли чисельник і знаменник мають різні знаки, частка негативна.

\[\dfrac{−1}{3}=−\dfrac{1}{3} \; \; \; \; \; \; \dfrac{\text{negative}}{\text{positive}}=\text{negative}\]

\[\dfrac{1}{−3}=−\dfrac{1}{3} \; \; \; \; \; \; \dfrac{\text{positive}}{\text{negative}}=\text{negative}\]

РОЗМІЩЕННЯ НЕГАТИВНОГО ЗНАКА В ДРОБІ

Для будь-яких позитивних чисел\(a\) і\(b\),

\[\dfrac{−a}{b}=\dfrac{a}{−b}=−\dfrac{a}{b}\]

ПРИКЛАД\(\PageIndex{19}\)

Спростити:\(\dfrac{4(−3)+6(−2)}{−3(2)−2}\).

Відповідь

Рядок дробу діє як символ групування. Так повністю спростите чисельник і знаменник окремо.

\(\begin{array}{lc} \text{} & \dfrac{4(−3)+6(−2)}{−3(2)−2} \\[5pt] \text{Multiply.} & \dfrac{−12+(−12)}{−6−2} \\[5pt] \text{Simplify.} & \dfrac{−24}{−8} \\[5pt] \text{Divide.} & 3 \end{array}\)

ПРИКЛАД\(\PageIndex{20}\)

Спростити:\(\dfrac{8(−2)+4(−3)}{−5(2)+3}\).

Відповідь

4

ПРИКЛАД\(\PageIndex{21}\)

Спростити:\(\dfrac{7(−1)+9(−3)}{−5(3)−2}\).

Відповідь

2

Тепер ми розглянемо складні дроби, де чисельник або знаменник містить вираз, який можна спростити. Тому ми спочатку повинні повністю спростити чисельник і знаменник окремо, використовуючи порядок операцій. Потім ділимо чисельник на знаменник, оскільки брусок дробу означає ділення.

ПРИКЛАД\(\PageIndex{22}\): How to Simplify Complex Fractions

Спростити:\(\dfrac{\left(\frac{1}{2}\right)^2}{4+3^2}\).

Відповідь

ПРИКЛАД\(\PageIndex{23}\)

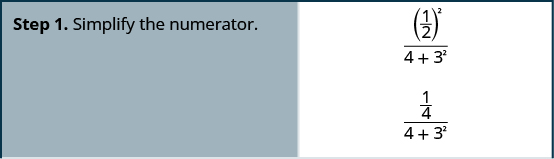
Спростити:\(\dfrac{\left(\frac{1}{3}\right)^2}{2^3+2}\).

Відповідь

\(\frac{1}{90}\)

ПРИКЛАД\(\PageIndex{24}\)

Спростити:\(\dfrac{1+4^2}{\left(\frac{1}{4}\right)^2}\).

Відповідь

272

СПРОСТІТЬ СКЛАДНІ ДРОБИ.

1. Спростити чисельник.
2. Спростити знаменник.
3. Розділіть чисельник на знаменник. Спрощуйте, якщо це можливо.

ПРИКЛАД\(\PageIndex{25}\)

Спростити:\(\dfrac{\dfrac{1}{2}+\dfrac{2}{3}}{\dfrac{3}{4}−\dfrac{1}{6}}\).

Відповідь

Це може допомогти поставити круглі дужки навколо чисельника та знаменника.

\(\begin{array}{lc}\text{} & \dfrac{\dfrac{1}{2}+\dfrac{2}{3}}{\dfrac{3}{4}−\dfrac{1}{6}} \\[6pt] \text{Simplify the numerator }(LCD=6)\text{ and } \\[6pt] \text{simplify the denominator }(LCD=12). & \dfrac{\left(\dfrac{3}{6}+\dfrac{4}{6}\right)}{\left(\dfrac{9}{12}−\dfrac{2}{12}\right)} \\[6pt] \text{Simplify.} & \left(\dfrac{7}{6}\right)\left(\dfrac{7}{12}\right) \\[6pt] \text{Divide the numerator by the denominator.} & \dfrac{7}{6}÷\dfrac{7}{12} \\[6pt] \text{Simplify.} & \dfrac{7}{6}⋅\dfrac{12}{7} \\[6pt] \text{Divide out common factors.} & \dfrac{\cancel{7}⋅\cancel{6}⋅2}{ \cancel{6}⋅\cancel{7}⋅1} \\[6pt] \text{Simplify.} & 2 \end{array}\)

ПРИКЛАД\(\PageIndex{26}\)

Спростити:\( \dfrac{\dfrac{1}{3}+\dfrac{1}{2}}{ \dfrac{3}{4}−\dfrac{1}{3}}\).

Відповідь

2

ПРИКЛАД\(\PageIndex{27}\)

Спростити:\(\dfrac{\dfrac{2}{3}−\dfrac{1}{2}}{ \dfrac{1}{4}+\dfrac{1}{3}}\).

Відповідь

\(\frac{2}{7}\)

Обчислення змінних виразів за допомогою дробів

Ми обчислювали вирази раніше, але тепер ми можемо оцінювати вирази з дробами. Пам'ятайте, щоб оцінити вираз, ми підставляємо значення змінної в вираз, а потім спрощуємо.

ПРИКЛАД\(\PageIndex{28}\)

Оцініть\(2x^2y\), коли\(x=\frac{1}{4}\) і\(y=−\frac{2}{3}\).

Відповідь

Підставляємо значення у вираз.

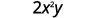
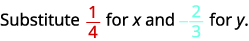
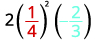
Спростіть експоненти спочатку.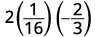
Помножити; розділити загальні фактори. Зверніть увагу, що ми пишемо 16 як 2⋅2⋅42·2·4, щоб було легко видалити загальні фактори.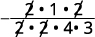
Спростити.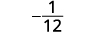

ПРИКЛАД\(\PageIndex{29}\)

Оцініть\(3ab^2\), коли\(a=−\frac{2}{3}\) і\(b=−\frac{1}{2}\).

Відповідь

\(−\dfrac{1}{2}\)

ПРИКЛАД\(\PageIndex{30}\)

Оцініть\(4c^3d\), коли\(c=−\frac{1}{2}\) і\(d=−\frac{4}{3}\).

Відповідь

\(\dfrac{2}{3}\)

Отримайте доступ до цього інтернет-ресурсу для додаткової інструкції та практики з дробами.

• Додавання дробів з відмінними знаменниками

Ключові концепції

• Якщо\(a\),\(b\), і\(c\) є числами де\(b≠0,c≠0\), то

\(\dfrac{a}{b}=\dfrac{a·c}{b·c}\)і\(\dfrac{a·c}{b·c}=\dfrac{a}{b}.\)

• Як спростити дріб.
  1. Перепишіть чисельник і знаменник, щоб показати загальні фактори.
     Якщо потрібно, спочатку перерахуйте чисельник і знаменник на прості числа.
  2. Спростіть використання властивості еквівалентних дробів шляхом поділу загальних факторів.
  3. Помножте всі інші фактори.
• Якщо\(a\),\(b\),\(c\), і\(d\) є числами де\(b≠0\), і\(d≠0\), то

  \(\dfrac{a}{b}·\dfrac{c}{d}=\dfrac{ac}{bd}\)

  Для множення дробів помножте чисельники і помножте знаменники.

• Якщо\(a\),\(b\),\(c\), і\(d\) є числами де\(b≠0\)\(c≠0\), і\(d≠0\), то

  \(\dfrac{a}{b}÷\dfrac{c}{d}=\dfrac{a}{b}⋅\dfrac{d}{c}\)

  Для поділу дробів множимо перший дріб на зворотний другий.

• Якщо\(a\),\(b\), і\(c\) є числами де\(c≠0\), то

  \(\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \text{ and } \dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\)

  Щоб додати або відняти дроби, додайте або відніміть чисельники і помістіть результат над спільним знаменником.

• Як додати або відняти дроби.
  1. Чи мають вони спільний знаменник?
     • Так—перейдіть до кроку 2.
     • Ні - перепишіть кожен дріб з РК-дисплеєм (найменш спільний знаменник).
       • Знайдіть РК-дисплей.
       • Змініть кожен дріб на еквівалентний дріб з LCD як його знаменником.
  2. Додавання або віднімання дробів.
  3. Спрощуйте, якщо це можливо.
• Як спростити вираз за допомогою дробової смуги.
  1. Спростити вираз в чисельнику. Спростити вираз в знаменнику.
  2. Спростити дріб.
• Для будь-яких позитивних чисел\(a\) і\(b\),

  \(\dfrac{−a}{b}=\dfrac{a}{−b}=−\dfrac{a}{b}\)

• Як спростити складні дроби.
  1. Спростити чисельник.
  2. Спростити знаменник.
  3. Розділіть чисельник на знаменник. Спрощуйте, якщо це можливо.

Глосарій

складний дріб

Дріб, в якому чисельником або знаменником є дріб, називається складним дробом.

знаменник

У дробі,\(\dfrac{a}{b}\) написаному\(b≠0\), де, знаменник\(b\) - це кількість рівних частин, на які було поділено ціле.

еквівалентні дроби

Еквівалентні дроби - це дроби, які мають однакове значення.

фракція

Записується дріб\(\dfrac{a}{b}\)\(b≠0\), де, а - чисельник і\(b\) є знаменником. Дріб являє собою частини цілого.

найменш спільний знаменник

Найменш спільний знаменник (РК) двох дробів - найменш спільний кратний (НКМ) їх знаменників.

чисельник

У дробі\(\dfrac{a}{b}\), записаному\(b≠0\), де, чисельник а вказує, скільки частин включено.

зворотний

Зворотний дріб знаходять шляхом інвертування дробу, розміщення чисельника в знаменнику і знаменника в чисельнику.