7.7: Рішення раціональних рівнянь

При спрощенні складних дробів в попередньому розділі ми побачили, що множення і чисельника, і знаменника на відповідний вираз може «очистити» всі дроби від чисельника і знаменника, значно спростивши раціональний вираз.

У цьому розділі використовується подібна техніка.

Очистити дроби з раціонального рівняння

Якщо ваше рівняння має раціональні вирази, помножте обидві сторони рівняння на найменш спільний знаменник, щоб очистити рівняння раціональних виразів.

Давайте розглянемо приклад.

Приклад$\PageIndex{1}$

Вирішіть наступне рівняння для x.

$$\frac{x}{2}-\frac{2}{3}=\frac{3}{4}$$

Рішення

Щоб очистити це рівняння дробів, ми помножимо обидві сторони на загальний знаменник для 2, 3 і 4, що дорівнює 12. Розподіліть 12 на другому кроці.

$$\begin{aligned} \color{blue}{12}\left(\frac{x}{2}-\frac{2}{3}\right) &=\left(\frac{3}{4}\right) \color{blue}{12} \\ \color{blue}{12}\left(\frac{x}{2}\right)-\color{blue}{12}\left(\frac{2}{3}\right) &=\left(\frac{3}{4}\right) \color{blue}{12} \end{aligned}$$

Помножити.

$$6 x-8=9$$

Нам вдалося очистити раціональні вирази з рівняння шляхом множення на спільний знаменник. Тепер у нас є просте лінійне рівняння, яке можна вирішити, спочатку додаючи 8 до обох сторін рівняння, а потім розділивши обидві сторони рівняння на 6.

$$\begin{aligned} 6 x &=17 \\ x &=\frac{17}{6} \end{aligned}$$

Ми залишимо це нашим читачам, щоб перевірити це рішення.

Спробуємо інший приклад.

Приклад$\PageIndex{2}$

Розв'яжіть наступне рівняння для x. $$6=\frac{5}{x}+\frac{6}{x^{2}}$$

Рішення

У цьому рівнянні знаменниками є 1, х, і$x^2$, а спільний знаменник для обох сторін рівняння -$x^2$. Отже, розв'язок починаємо з того, що спочатку множимо обидві сторони рівняння на$x^2$.

$$\begin{array}{l}{\color{blue}{x^{2}}(6)=\left(\frac{5}{x}+\frac{6}{x^{2}}\right) \color{blue}{x^{2}}} \\ {\color{blue}{x^{2}}(6)=\left(\frac{5}{x}\right) \color{blue}{x^{2}}+\left(\frac{6}{x^{2}}\right) \color{blue}{x^{2}}}\end{array}$$

Спростити.

$$6 x^{2}=5 x+6$$

Зауважте, що множення обох сторін вихідного рівняння на найменш спільний знаменник очищає рівняння всіх раціональних виразів. Це останнє рівняння нелінійне, тому зробіть одну сторону рівняння рівною нулю, віднімаючи 5x і 6 з обох сторін рівняння.

$$6 x^{2}-5 x-6=0$$

Щоб перерахувати ліву частину цього рівняння, зауважте, що воно є квадратичним триноміалом з ac = (6) (−6) = −36. Пари цілих чисел 4 та −9 мають добуток −36 та суму −5. Розділіть середній термін за допомогою цієї пари та коефіцієнта шляхом групування.

$$\begin{aligned} 6 x^{2}+4 x-9 x-6 &=0 \\ 2 x(3 x+2)-3(3 x+2) &=0 \\(2 x-3)(3 x+2) &=0 \end{aligned}$$

Нульова властивість продукту змушує або

$$2 x-3=0 \quad \text { or } \quad 3 x+2=0$$

Кожне з цих лінійних рівнянь легко вирішується.

$$x=\frac{3}{2} \quad \text { or } \quad x=-\frac{2}{3}$$

Звичайно, ми завжди повинні перевіряти наші рішення. Підставивши x = 3/2 в праву частину вихідного рівняння (4),

$$\frac{5}{x}+\frac{6}{x^{2}}=\frac{5}{3 / 2}+\frac{6}{(3 / 2)^{2}}=\frac{5}{3 / 2}+\frac{6}{9 / 4}$$

У кінцевому виразі помножте верхню і нижню частину першого дробу на 2, верхню і нижню частину другого дробу на 4.

$$\frac{5}{3 / 2} \cdot \color{blue}{\frac{2}{2}}+\frac{6}{9 / 4} \cdot \color{blue}{\frac{4}{4}}=\frac{10}{3}+\frac{24}{9}$$

Зробіть еквівалентні дроби із загальним знаменником 9 і додайте.

$$\frac{10}{3} \cdot \color{blue}{\frac{3}{3}}+\frac{24}{9}=\frac{30}{9}+\frac{24}{9}=\frac{54}{9}=6$$

Зауважте, що цей результат ідентичний лівій частині вихідного рівняння (4). Таким чином, х = 3/2 чеки.

Цей приклад наочно демонструє, що перевірка може бути такою ж складною і такою ж трудомісткою, як обчислення, яке використовувалося для початкового вирішення рівняння. З цієї причини ми, як правило, лінуємося і не перевіряємо свої відповіді, як слід. Однак є допомога, оскільки графічний калькулятор може допомогти нам перевірити рішення рівнянь.

Спочатку введіть рішення 3/2 на екрані калькулятора, натисніть кнопку STOI, потім натисніть кнопку X, і виконайте отриману команду на екрані, натиснувши клавішу ENTER. Результат показаний на малюнку$\PageIndex{1}$ (а).

Далі вводимо вираз 5/X+6/X2 і виконуємо отриману команду на екрані натисканням клавіші ENTER. Результат показаний на малюнку$\PageIndex{1}$ (б). Зверніть увагу, що результат 6, такий же, як обчислюється вручну вище, і він відповідає лівій стороні вихідного рівняння (4). Ми також використовували калькулятор для перевірки другого розв'язку x = −2/3. Це показано на малюнку$\PageIndex{4}$ (в).

Малюнок$\PageIndex{1}$. Використання графічного калькулятора для перевірки розв'язків рівняння (4).

Давайте розглянемо інший приклад.

Приклад$\PageIndex{3}$

Вирішіть наступне рівняння для x.

$$\frac{2}{x^{2}}=1-\frac{2}{x}$$

Рішення

Спочатку помножте обидві сторони рівняння (6) на загальний знаменник$x^2$.

$$\begin{aligned} \color{blue}{x^{2}}\left(\frac{2}{x^{2}}\right) &=\left(1-\frac{2}{x}\right) \color{blue}{x^{2}} \\ 2 &=x^{2}-2 x \end{aligned}$$

Зробіть одну сторону нулем.

$$0=x^{2}-2 x-2$$

Права сторона є квадратичним тріноміалом з ac = (1) (−2) = −2. Немає цілих пар з добутком −2, які сумуються −2, тому цей квадратичний тріноміал не множник. На щастя, рівняння квадратичне (другий ступінь), тому ми можемо використовувати квадратичну формулу з a = 1, b = −2, а c = −2.

$$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}=\frac{-(-2) \pm \sqrt{(-2)^{2}-4(1)(-2)}}{2(1)}=\frac{2 \pm \sqrt{12}}{2}$$

Це дає нам два рішення,$x=(2-\sqrt{12}) / 2$ і$x=(2+\sqrt{12}) / 2$. Давайте перевіримо рішення$x=(2-\sqrt{12}) / 2$. Спочатку введіть цей результат у свій калькулятор, натисніть кнопку STOI, натисніть X, потім натисніть клавішу ENTER для виконання команди і збережіть рішення у змінній X. Ця команда показана на малюнку$\PageIndex{2}$ (а).

Введіть ліву частину вихідного рівняння (6) як 2/x2 і натисніть клавішу ENTER, щоб виконати цю команду. Це показано на малюнку$\PageIndex{2}$ (б).

Введіть праву частину вихідного рівняння (6) як 1-2/X і натисніть клавішу ENTER, щоб виконати цю команду. Це показано на малюнку$\PageIndex{2}$ (в). Зверніть увагу, що ліва і права сторони рівняння (6) обидва показані рівнозначними 3.732050808 at$x=(2-\sqrt{12}) / 2$ (при X = -0.7320508076), як показано на малюнку$\PageIndex{2}$ (c). Це показує, що$x=(2-\sqrt{12}) / 2$ є розв'язком рівняння (6).

Ми залишаємо це нашим читачам, щоб перевірити друге рішення,$x=(2+\sqrt{12}) / 2$.

Малюнок$\PageIndex{2}$. За допомогою графічного калькулятора для перевірки розв'язків рівняння (6).

Давайте подивимося на інший приклад, це один з участю позначення функції.

Приклад$\PageIndex{4}$

Розглянемо функцію, визначену $$f(x)=\frac{1}{x}+\frac{1}{x-4}$$ Розв'яжіть рівняння f (x) = 2 для x, використовуючи як графічні, так і аналітичні методи, а потім порівняйте розв'язки. Виконайте кожне з наступних завдань.

а. намалюйте графік f на графічному папері. Позначте нулі f з їх координатами, а асимптоти f - їх рівняннями.

b. додайте графік y = 2 на свій графік і оцініть координати того, де граф f перетинає граф y = 2.

c Використовуйте утиліту intersect на вашому калькуляторі, щоб знайти кращі наближення точок, де графи f і y = 2 перетинаються.

d Розв'яжіть рівняння f (x) = 2 алгебраїчно і порівняйте свої рішення з тими, що знайдені в частині (c).

Рішення

Для графіка в частині (a) нам потрібно знайти нулі f і рівняння будь-яких вертикальних або горизонтальних асимптотів.

Щоб знайти нуль функції f, знайдемо спільний знаменник і складаємо два раціональних вирази в рівнянні (8).

$$f(x)=\frac{1}{x}+\frac{1}{x-4}=\frac{x-4}{x(x-4)}+\frac{x}{x(x-4)}=\frac{2 x-4}{x(x-4)}$$

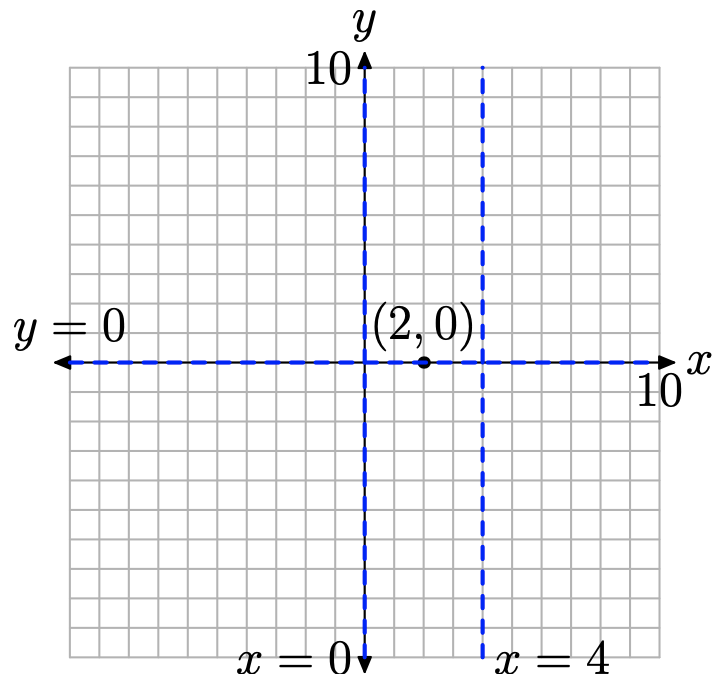
Зверніть увагу, що чисельник цього результату дорівнює нулю (але не знаменнику), коли х = 2. Це нуль f Таким чином, графік f має х перехоплення в (2, 0), як показано на рис$\PageIndex{4}$.

Зауважте, що раціональна функція в рівнянні (9) зводиться до найнижчих. Знаменники х і х + 4 в рівнянні (9) дорівнюють нулю, коли х = 0 і х = 4. Це наші вертикальні асимптоти, як показано на малюнку$\PageIndex{4}$.

Щоб знайти горизонтальні асимптоти, нам потрібно вивчити, що відбувається зі значеннями функції, коли x збільшується (або зменшується) без обмежень. Введіть функцію в меню Y= за допомогою 1/X+1/ (X-4), як показано на малюнку$\PageIndex{3}$ (а). Натисніть 2nd TBLSET, потім виділіть ASK для незалежної змінної і натисніть ENTER, щоб зробити цей вибір постійним, як показано на малюнку$\PageIndex{3}$ (b).

Натисніть 2nd TABLE, потім введіть 10, 100, 1000 і 10 000, як показано на малюнку$\PageIndex{3}$ (c). Зверніть увагу, як значення Y1 наближаються до нуля. На малюнку$\PageIndex{3}$ (d), оскільки x зменшується без обмежень, кінцева поведінка однакова. Це вказівка на горизонтальну асимптоту при y = 0, як показано на малюнку$\PageIndex{4}$.

Малюнок$\PageIndex{3}$. Вивчення кінцевої поведінки f за допомогою графічного калькулятора.

Малюнок$\PageIndex{4}$. Розміщення горизонтальних і вертикальних асимптотів і x-перехоплення графа функції f.

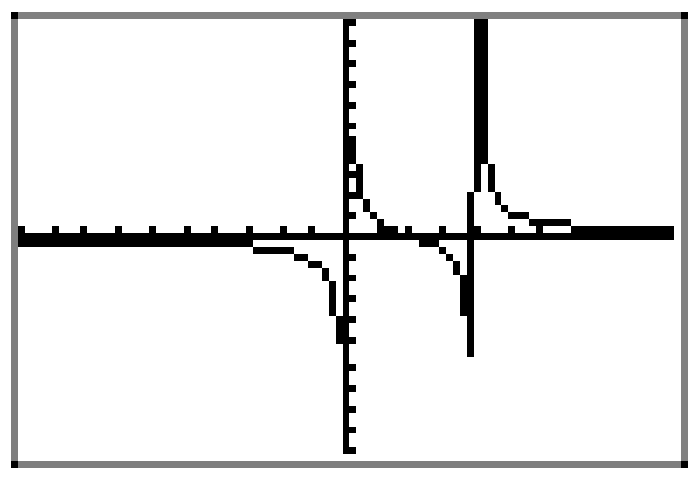
На даний момент у нас вже є наша функція f завантажена в Y1, тому ми можемо натиснути кнопку ZOOM і вибрати 6:zStandard, щоб створити графік, показаний на малюнку$\PageIndex{5}$. Як і очікувалося, графічний калькулятор не дуже добре справляється з раціональною функцією f, особливо поблизу розривів на вертикальних асимптотах. Однак є достатньо інформації на малюнку$\PageIndex{5}$, в парі з нашою просунутою роботою, підсумованою на малюнку$\PageIndex{4}$, щоб намалювати дуже хороший графік раціональної функції на нашому графічному папері, як показано на малюнку$\PageIndex{6}$ (а). Примітка: Ми не позначили асимптоти рівняннями, ні нулями з координатами, на малюнку$\PageIndex{6}$ (а), оскільки ми думали, що картинка може бути трохи переповнена. Однак ви повинні позначити кожну з цих частин на своєму графічному папері, як ми це робили на малюнку$\PageIndex{4}$.

Малюнок$\PageIndex{5}$. Графік f намальований на калькуляторі.

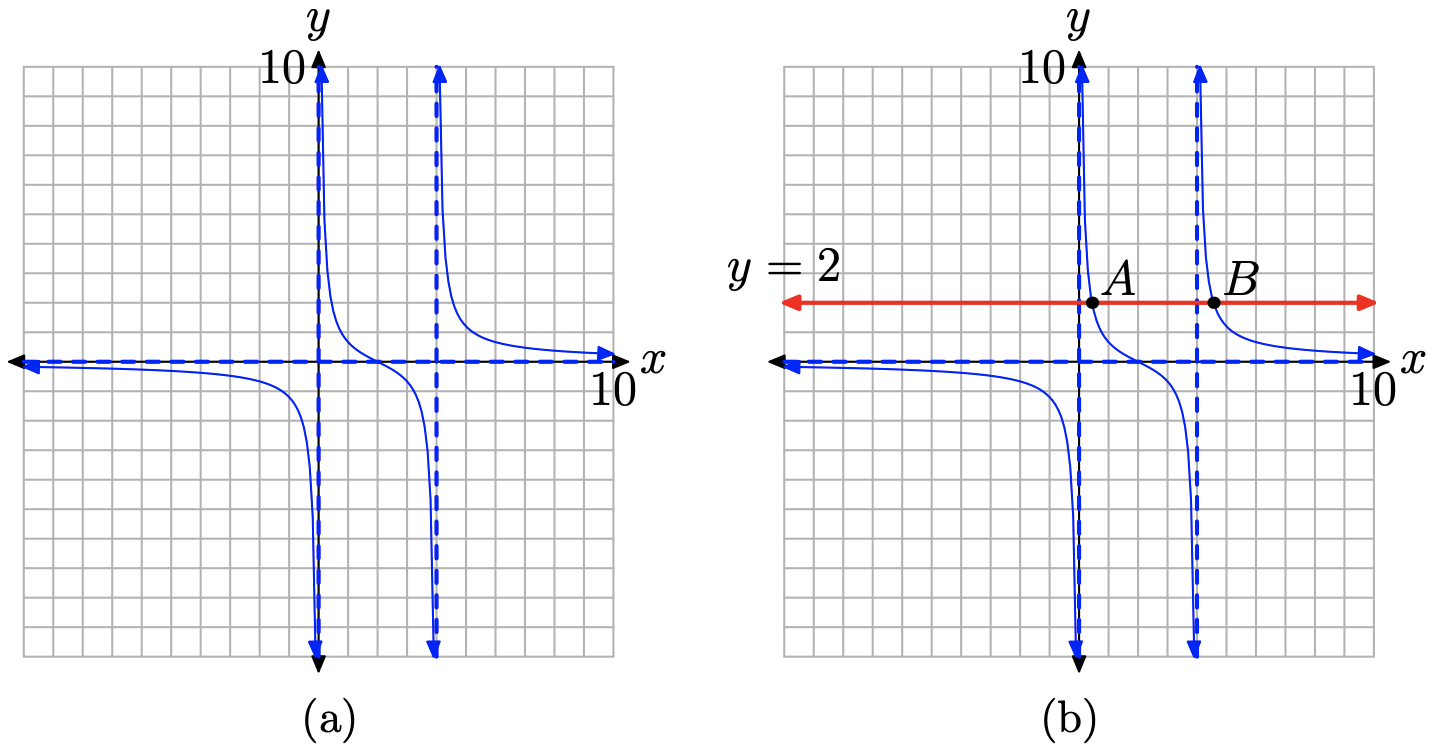
Давайте тепер звернемося до частини (b), додавши горизонтальну лінію y = 2 до графіка, як показано на малюнку$\PageIndex{6}$ (b). Зауважимо, що графік y = 2 перетинає графік раціональної функції f в двох точках A і B. X-значення точок A і B є розв'язками нашого рівняння f (x) = 2.

Ми можемо отримати грубу оцінку x-координат точок A і B відразу з нашого графічного паперу. Значення x точки А приблизно$x \approx 0.3$, тоді як значення x точки B здається приблизно$x \approx 4.6$.

Малюнок$\PageIndex{6}$. Розв'язування f (x) = 2 графічно.

Далі звернемося до завдання, необхідного в частині (c). Ми маємо дуже обґрунтовані оцінки розв'язків f (x) = 2 на основі даних, представлених на малюнку$\PageIndex{6}$ (б). Давайте скористаємося графічним калькулятором для покращення цих оцінок.

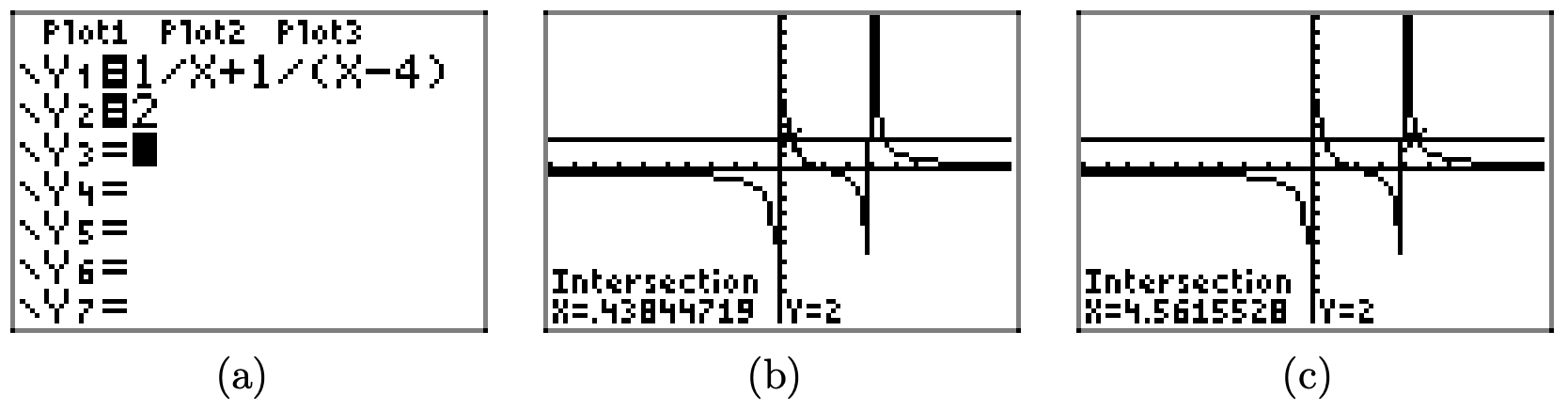
Спочатку завантажте рівняння Y2 = 2 в меню Y=, як показано на малюнку$\PageIndex{7}$ (а). Нам потрібно знайти, де граф Y1 перетинає граф Y2, тому натискаємо 2nd CALC і вибираємо 5: перетин з меню. У звичайному порядку виберіть «Перша крива», «Друга крива» і наведіть курсор близько до точки, яку ви хочете оцінити. Це твій «Вгадай». Виконайте аналогічні завдання для другої точки перетину.

Наші результати показані на малюнках$\PageIndex{7}$ (b) та малюнках$\PageIndex{7}$ (c). Оцінка на малюнку$\PageIndex{7}$ (b) має$x \approx 0.43844719$, тоді як на малюнку$\PageIndex{7}$ (c) має$x \approx 4.5615528$. Зауважте, що вони більш точні, ніж наближення$x \approx 0.3$ та$x \approx 4.6$ зняті з нашого мальованого зображення на малюнку$\PageIndex{6}$ (b).

Малюнок$\PageIndex{7}$. Розв'язування f (x) = 2 графічно.

Нарешті, звернемося до запиту алгебраїчного розв'язку f (x) = 2 в частині (d). Спочатку замініть f (x) на 1/x + 1/ (x − 4), щоб отримати

$$\begin{aligned} f(x) &=2 \\ \frac{1}{x}+\frac{1}{x-4} &=2 \end{aligned}$$

Помножте обидві сторони цього рівняння на спільний знаменник x (x − 4).

$$\begin{aligned} \color{blue}{x(x-4)}\left[\frac{1}{x}+\frac{1}{x-4}\right] &=[2] \color{blue}{x(x-4)} \\ \color{blue}{x(x-4)}\left[\frac{1}{x}\right]+\color{blue}{x(x-4)}\left[\frac{1}{x-4}\right] &=[2] \color{blue}{x(x-4)}\end{aligned}$$

Скасувати.

$$\begin{aligned} \color{blue}{\not{x}(x-4)}\left[\frac{1}{\not{x}}\right]+\color{blue}{x(x-4)}\left[\frac{1}{x-4}\right] &=[2] \color{blue}{x(x-4)} \\(x-4)+x &=2 x(x-4) \end{aligned}$$

Спростити кожну сторону.

$$2 x-4=2 x^{2}-8 x$$

Це останнє рівняння нелінійне, тому ми робимо одну сторону нуля, віднімаючи 2x і додаючи 4 до обох сторін рівняння.

$$\begin{array}{l}{0=2 x^{2}-8 x-2 x+4} \\ {0=2 x^{2}-10 x+4}\end{array}$$

Зверніть увагу, що кожен коефіцієнт з правого боку цього останнього рівняння ділиться на 2. Давайте розділимо обидві сторони рівняння на 2, розподіляючи ділення через кожен член по правій частині рівняння.

$$0=x^{2}-5 x+2$$

Триноміал праворуч - квадратик з ac = (1) (2) = 2. Немає цілих пар, що мають добуток 2 та суму −5, тому цей триноміал не множник. Натомість ми будемо використовувати квадратичну формулу з a = 1, b = −5 та c = 2.

$$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}=\frac{-(-5) \pm \sqrt{(-5)^{2}-4(1)(2)}}{2(1)}=\frac{5 \pm \sqrt{17}}{2}$$

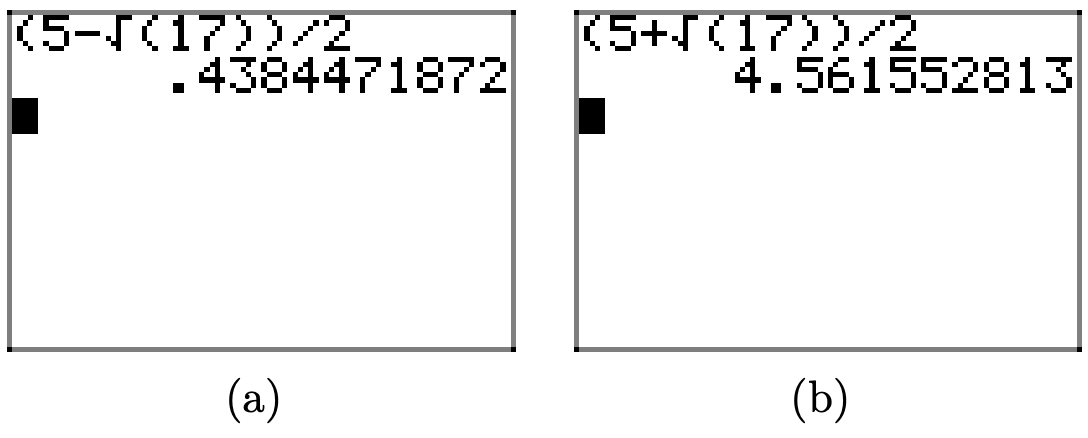
Залишається порівняти їх з графічними рішеннями, знайденими в частині (c). Отже, введіть рішення$(5-\sqrt{( } 17) ) /(2)$ на екрані калькулятора, як показано на малюнку$\PageIndex{8}$ (а). Введіть$(5+\sqrt{( } 17) ) /(2)$, як показано на малюнку$\PageIndex{8}$ (b). Таким чином,

\[$\frac{5-\sqrt{17}}{2} \approx 0.4384471872 \quad$ and $\quad \frac{5+\sqrt{17}}{2} \approx 4.561552813$\]

Зверніть увагу на тісну згоду з наближеннями, знайденими в частині (c).

Малюнок$\PageIndex{8}$. Наближення точних розв'язків.

Давайте розглянемо інший приклад.

Приклад$\PageIndex{5}$

Розв'яжіть наступне рівняння для x, як графічно, так і аналітично $$\frac{1}{x+2}-\frac{x}{2-x}=\frac{x+6}{x^{2}-4}$$

Рішення

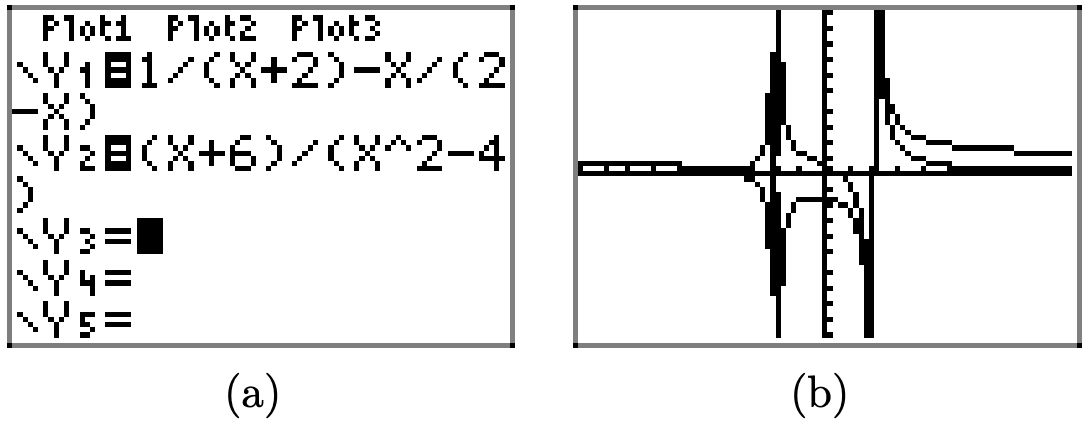
Ми починаємо графічне рішення звичайним способом, завантажуючи ліву і праву частини рівняння (11) в Y1 і Y2, як показано на малюнку$\PageIndex{9}$ (а). Зверніть увагу, що в отриманому графіку, показаному на малюнку$\PageIndex{9}$ (б), дуже важко інтерпретувати, де графік лівої сторони перетинає графік правої частини рівняння (11).

Малюнок$\PageIndex{9}$. Намалюйте ліву та праву сторони рівняння (11).

У цій ситуації кращою стратегією є зробити одну сторону рівняння (11) рівною нулю.

$$\frac{1}{x+2}-\frac{x}{2-x}-\frac{x+6}{x^{2}-4}=0$$

Наш підхід тепер зміниться. Ми побудуємо ліву частину рівняння (12), а потім знайдемо, де ліва сторона дорівнює нулю; тобто знайдемо, де графік лівої сторони рівняння (12) перехоплює вісь x.

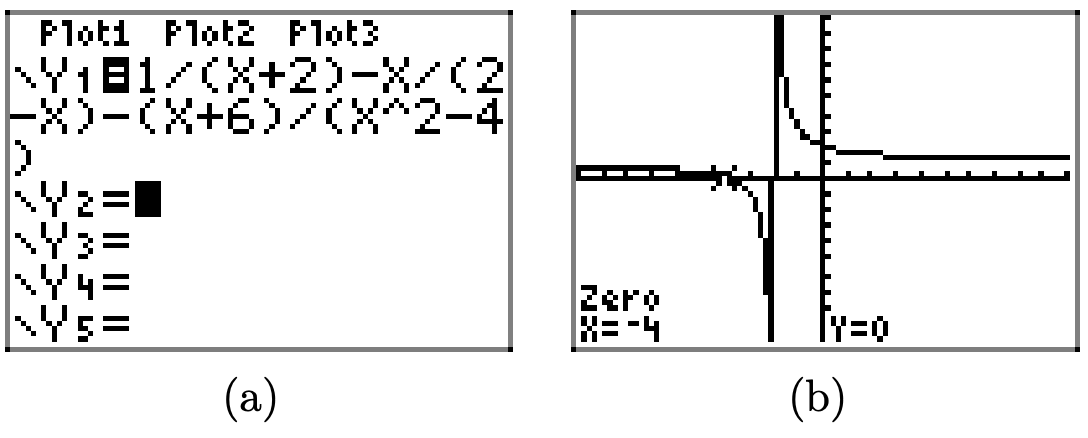
Маючи на увазі цю думку, завантажте ліву частину рівняння (12) в Y1, як показано на малюнку$\PageIndex{10}$ (а). Зауважте, що графік на малюнку$\PageIndex{10}$ (b) має лише одну вертикальну асимптоту при x = −2 (деяке скасування має вилучити коефіцієнт x − 2 із знаменника, коли ви об'єднаєте члени лівої частини рівняння (12) 3). Далі, коли ви використовуєте нульову утиліту в меню CALC графічного калькулятора, з'являється нуль при x = −4, як показано на малюнку$\PageIndex{10}$ (b).

Малюнок$\PageIndex{10}$. Знаходження нуля лівої частини рівняння (12).

Тому рівняння (12), здається, має лише одне рішення, а саме х = 4.

Далі шукаємо аналітичне рішення рівняння (11). Нам потрібно буде перерахувати знаменники, щоб виявити спільний знаменник.

$$\frac{1}{x+2}-\frac{x}{2-x}=\frac{x+6}{(x+2)(x-2)}$$

Спокусливо використовувати знаменник$(x + 2)(2 − x)(x − 2)$. Однак знаменник другого члена ліворуч цього останнього рівняння, 2 − х, знаходиться в іншому порядку, ніж множники в інших знаменниках, x−2 та x+2, тому давайте виконаємо зміну знака на цьому терміні і зворотний порядок. Ми зведемо нанівець рядок дробу і зведемо нанівець знаменник. Це дві зміни знаків, тому термін залишається незмінним, коли ми пишемо

$$\frac{1}{x+2}+\frac{x}{x-2}=\frac{x+6}{(x+2)(x-2)}$$

Тепер ми бачимо, що достатньо спільного знаменника (x + 2) (x − 2). Давайте помножимо обидві сторони останнього рівняння на$(x + 2)(x − 2)$.

$$\begin{aligned}\color{blue}{(x+2)(x-2)}\left[\frac{1}{x+2}+\frac{x}{x-2}\right] &=\left[\frac{x+6}{(x+2)(x-2)}\right]\color{blue}{(x+2)(x-2)} \\\color{blue}{(x+2)(x-2)}\left[\frac{1}{x+2}\right]+\color{blue}{(x+2)(x-2)}\left[\frac{x}{x-2}\right] &=\left[\frac{x+6}{(x+2)(x-2)}\right]\color{blue}{(x+2)(x-2)} \end{aligned}$$

Скасувати.

$$\begin{aligned}\color{blue}{(x+2)(x-2)}\left[\frac{1}{x+2}\right]+\color{blue}{(x+2)(x-2)}\left[\frac{x}{x-2}\right] &=\left[\frac{x+6}{(x+2)(x-2)}\right]\color{blue}{(x+2)(x-2)} \\(x-2)+x(x+2) &=x+6 \end{aligned}$$

Спростити.

$$\begin{array}{r}{x-2+x^{2}+2 x=x+6} \\ {x^{2}+3 x-2=x+6}\end{array}$$

Це останнє рівняння є нелінійним через наявність степеня x більше 1 (зверніть увагу на$x^2$ термін). Тому стратегія полягає в тому, щоб одна сторона рівняння дорівнювала нулю. Віднімемо х і віднімемо 6 з обох сторін рівняння.

$$\begin{aligned} x^{2}+3 x-2-x-6 &=0 \\ x^{2}+2 x-8 &=0 \end{aligned}$$

Ліва сторона є квадратичним тріноміалом з ac = (1) (−8) = −8. Пари цілих чисел 4 та −2 мають добуток −8 та суму 2. Таким чином,

$$(x+4)(x-2)=0$$

Використовуючи властивість нульового добутку, або

$$x+4=0 \quad \text { or } \quad x-2=0$$

так $$x=-4 \quad \text { or } \quad x=2$$

Те, що ми знайшли дві відповіді за допомогою аналітичного методу, викликає занепокоєння. Адже графік на малюнку$\PageIndex{10}$ (b) вказує лише на одне рішення, а саме x = −4. Втішає те, що одним з наших аналітичних рішень також є x = −4, але все ще бентежить, що наш аналітичний підхід виявляє другу «відповідь», а саме x = 2.

Однак зверніть увагу, що ми не звертали жодної уваги на обмеження, спричинені знаменниками до цього моменту. Дійсно, ретельний розгляд рівняння (11) виявляє множники x+2 та x−2 у знаменниках. Отже, x = −2 і x = 2 є обмеженнями.

Зверніть увагу, що одна з наших відповідей, а саме x = 2, є обмеженою величиною. Це зробить деякі знаменники рівняння (11) рівнянням нулю, тому це не може бути рішенням. Таким чином, єдиним життєздатним рішенням є x = −4. Можна, звичайно, перевірити це рішення вручну, але давайте скористаємося графічним калькулятором, щоб допомогти нам у перевірці.

Спочатку вводимо -4, натискаємо$\blacktriangleright$ кнопку STO, натискаємо X, потім натискаємо ENTER для виконання отриманої команди і зберігаємо -4 в змінній X. Результат показаний на малюнку$\PageIndex{11}$ (а).

Далі обчислюємо значення лівої частини рівняння (11) при цьому значенні X. Введіть ліву частину рівняння (11) як 1/ (X+2) -X/ (2-X), потім натисніть клавішу ENTER, щоб виконати оператор і отримати результат, показаний на малюнку$\PageIndex{11}$ (b).

Нарешті, введіть праву частину рівняння (11) як (X+6)/(x2-4) і натисніть клавішу ENTER, щоб виконати операцію. Результат показаний на малюнку$\PageIndex{11}$ (в). Зверніть увагу, що обидві сторони рівняння дорівнюють .1666666667 при X = -4. Таким чином, розв'язок x = −4 перевіряє.

Малюнок$\PageIndex{11}$. Використання графічного калькулятора для перевірки розв'язку x = −4 рівняння (11).

Вправа

Для кожної з раціональних функцій, наведених у Вправах 1 - 6, виконайте кожну з наступних завдань.

1. Налаштуйте систему координат на графічному папері. Позначте та масштабуйте кожну вісь. Не забудьте намалювати всі лінії лінійкою.
2. Покладіть нуль раціональної функції на вашій системі координат і позначте його координатами. Покладіть вертикальні та горизонтальні асимптоти на вашій системі координат та позначте їх рівняннями. Використовуйте цю інформацію (і ваш графічний калькулятор), щоб намалювати графік f.
3. Покладіть горизонтальну лінію y = k на вашій системі координат і позначте цю лінію її рівнянням.
4. Скористайтеся програмою intersect вашого калькулятора, щоб визначити розв'язку f (x) = k. Позначте цю точку на графіку її координатами.
5. Вирішіть рівняння f (x) = k алгебраїчно, розмістивши роботу для цього рішення на графічному папері поруч із вашою системою координат, що містить графічне рішення. Чи згодні відповіді?

Вправа$\PageIndex{1}$

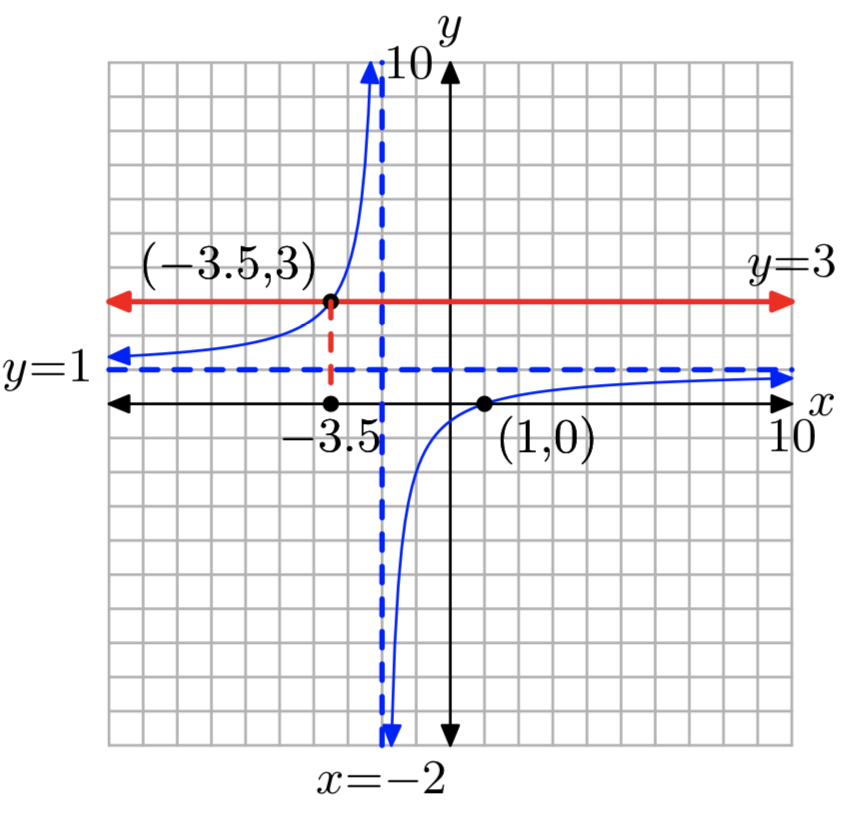
$f(x) = \frac{x−1}{x+2}$; к = 3

Відповідь

$x = −\frac{7}{2}$

Вправа$\PageIndex{2}$

$f(x) = \frac{x+1}{x−2}$; k = −3

Вправа$\PageIndex{3}$

$f(x) = \frac{x+1}{3−x}$; к = 2

Відповідь

$x = \frac{5}{3}$

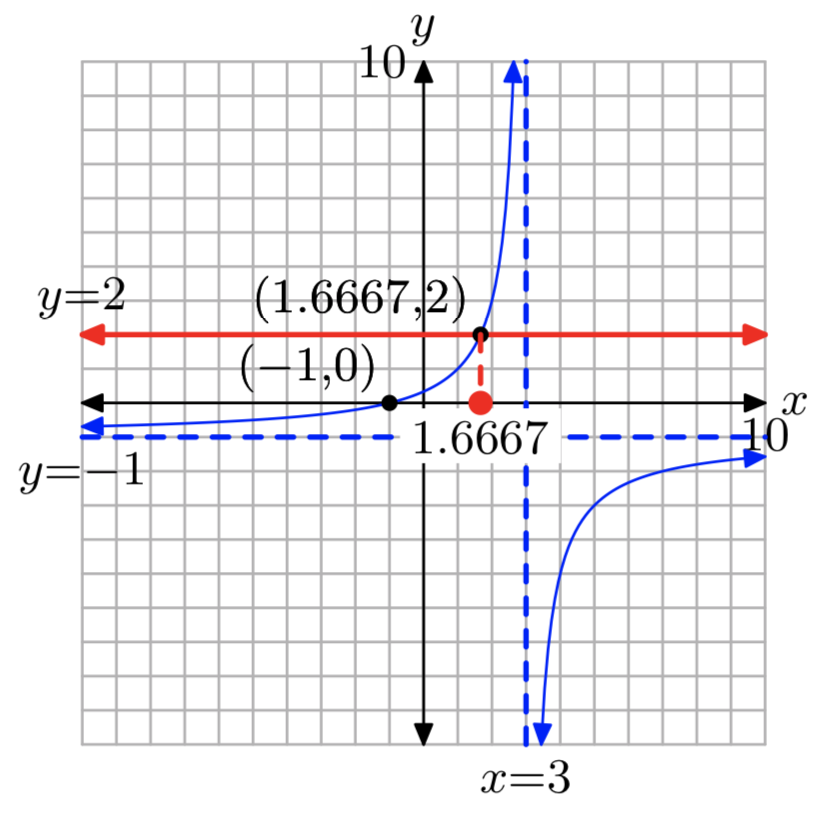
Вправа$\PageIndex{4}$

$f(x) = \frac{x+3}{2−x}$; к = 2

Вправа$\PageIndex{5}$

$f(x) = \frac{2x+3}{x−1}$; k = −3

Відповідь

х = 0

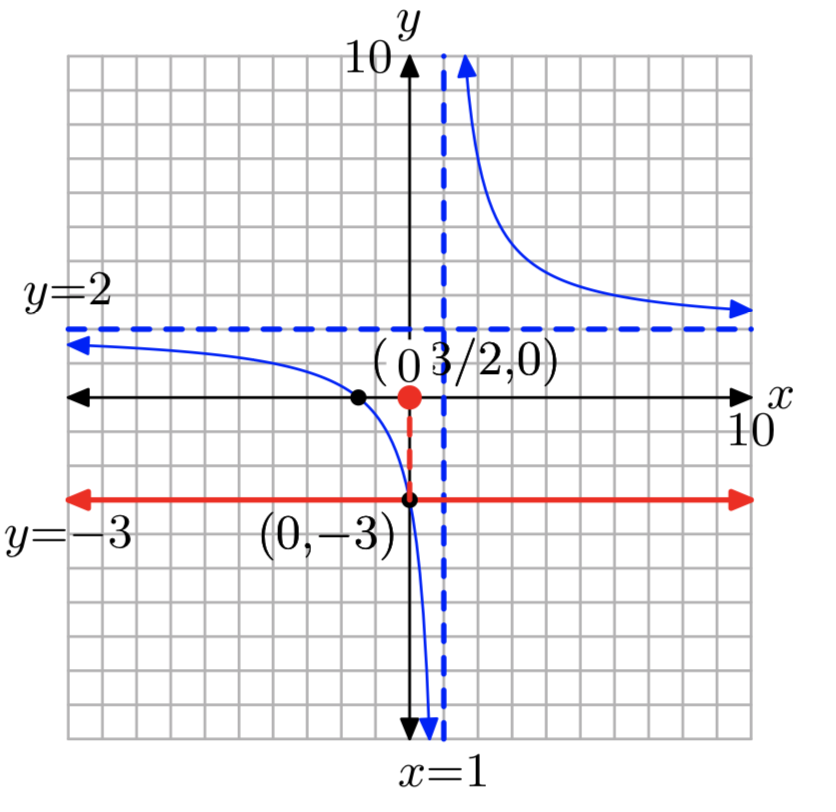
Вправа$\PageIndex{6}$

$f(x)= \frac{5−2x}{x−1}$; к = 3

У Вправах 7 - 14 використовуйте суворо алгебраїчну техніку для вирішення рівняння f (x) = k для заданої функції та значення k.

Вправа$\PageIndex{7}$

$f(x) = \frac{16x−9}{2x−1}$; к = 8

Відповідь

жоден

Вправа$\PageIndex{8}$

$f(x) = \frac{10x−3}{7x+7}$; к = 1

Вправа$\PageIndex{9}$

$f(x) = \frac{5x+8}{4x+1}$; k = −11

Відповідь

$−\frac{19}{49}$

Вправа$\PageIndex{10}$

$f(x) = −\frac{6x−11}{7x−2}$; k = −6

Вправа$\PageIndex{11}$

$f(x) = −\frac{35x}{7x+1​​2}$; k = −5

Відповідь

жоден

Вправа$\PageIndex{12}$

$f(x) = −\frac{66x−5}{6x−10}$; k = −11

Вправа$\PageIndex{13}$

$f(x) = \frac{8x+2}{x−11}$; к = 11

Відповідь

41

Вправа$\PageIndex{14}$

$f(x) = \frac{36x−7}{3x−4}$; к = 12

У вправах 15 - 20 використовуйте строго алгебраїчну техніку для вирішення даного рівняння. Вам рекомендується перевірити свій результат за допомогою калькулятора.

Вправа$\PageIndex{15}$

$\frac{x}{7}+\frac{8}{9} = −\frac{8}{7}$

Відповідь

$−\frac{128}{9}$

Вправа$\PageIndex{16}$

$\frac{x}{3}+\frac{9}{2} = −\frac{3}{8}$

Вправа$\PageIndex{17}$

$−\frac{57}{x}=27−\frac{40}{x^2}$

Відповідь

$−\frac{8}{5}, \frac{3}{9}$

Вправа$\PageIndex{18}$

$−\frac{117}{x} = 54+\frac{54}{x^2}$

Вправа$\PageIndex{19}$

$\frac{7}{x} = 4−\frac{3}{x^2}$

Відповідь

$\frac{7+\sqrt{97}}{8}, \frac{7−\sqrt{97}}{8}$

Вправа$\PageIndex{20}$

$\frac{3}{x^2} = 5−\frac{3}{x}$

Для кожної з раціональних функцій, наведених у Вправах 21 - 26, виконують кожну з наступних завдань.

1. Налаштуйте систему координат на графічному папері. Позначте та масштабуйте кожну вісь. Re- член, щоб намалювати всі лінії за допомогою лінійки.
2. Покладіть нуль раціональної функції на вашій системі координат і позначте його координатами. Ви можете використовувати нульову утиліту вашого калькулятора, щоб знайти це, якщо хочете.
3. Покладіть вертикальні та горизонтальні асимптоти на вашій системі координат та позначте їх рівняннями. Використовуйте асимптоту та нульову інформацію (і ваш графічний калькулятор), щоб намалювати графік f.
4. Покладіть горизонтальну лінію y = k на вашій системі координат і позначте цю лінію її рівнянням.
5. Скористайтеся програмою intersect вашого калькулятора, щоб визначити розв'язку f (x) = k. Позначте цю точку на графіку її координатами.
6. Вирішіть рівняння f (x) = k алгебраїчно, розмістивши роботу для цього рішення на графічному папері поруч із вашою системою координат, що містить графічне рішення. Чи згодні відповіді?

Вправа$\PageIndex{21}$

$f(x) = \frac{1}{x}+\frac{1}{x+5}$,$k = \frac{9}{14}$

Відповідь

$x = −\frac{35}{9}$або х = 2

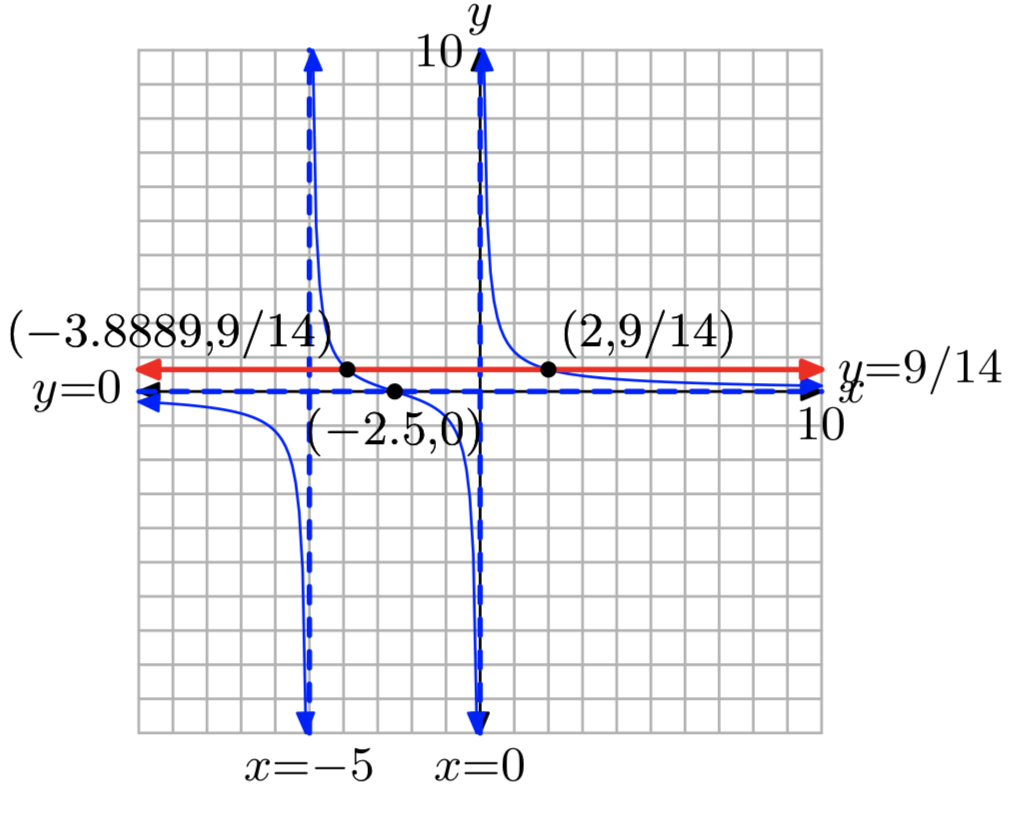
Вправа$\PageIndex{22}$

$f(x) = \frac{1}{x}+\frac{1}{x−2}$,$k = \frac{8}{15}$

Вправа$\PageIndex{23}$

$f(x) = \frac{1}{x−1}−\frac{1}{x+1}$,$k = \frac{1}{4}$

Відповідь

х = −3 або х = 3

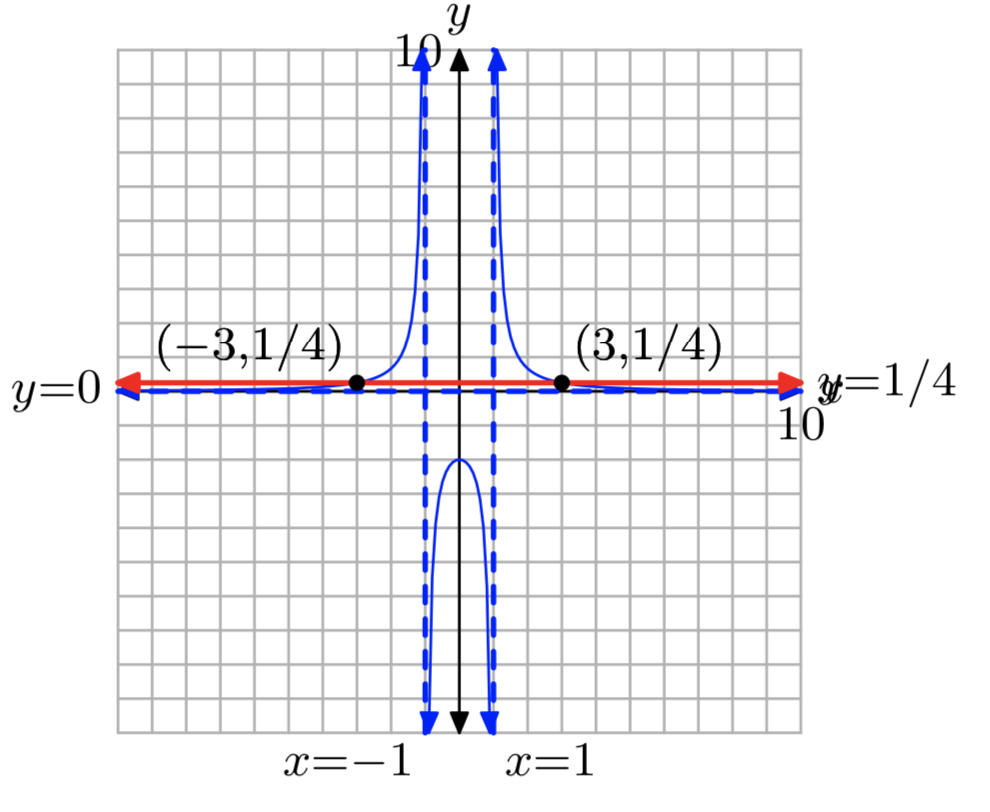
Вправа$\PageIndex{24}$

$f(x) = \frac{1}{x−1}−\frac{1}{x+2}$,$k = \frac{1}{6}$

Вправа$\PageIndex{25}$

$f(x) = \frac{1}{x−2}+\frac{1}{x+2}$, к = 4

Відповідь

$x = \frac{1+\sqrt{65}}{4}, \frac{1−\sqrt{65}}{4}$

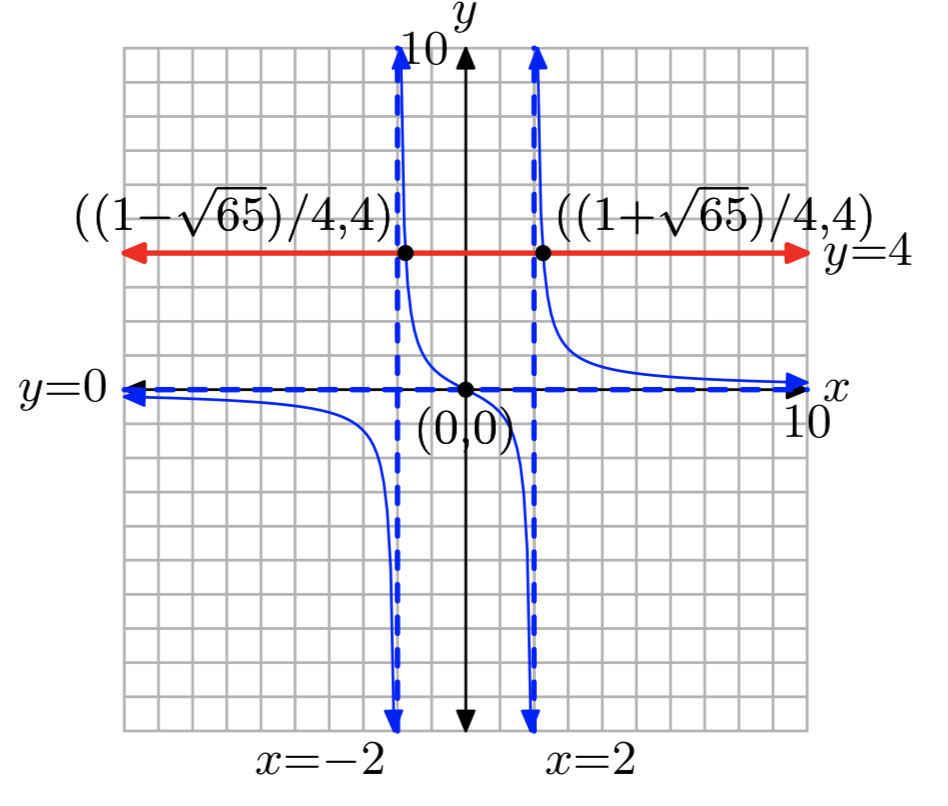
Вправа$\PageIndex{26}$

$f(x) = \frac{1}{x−3}+\frac{1}{x+2}$, к = 5

У вправах 27 - 34 використовуйте строго алгебраїчну техніку для вирішення даного рівняння. Вам рекомендується перевірити свій результат за допомогою калькулятора.

Вправа$\PageIndex{27}$

$\frac{2}{x+1}+\frac{4}{x+2} = −3$

Відповідь

$\frac{−15+\sqrt{57}}{6}, \frac{−15−\sqrt{57}}{6}$

Вправа$\PageIndex{28}$

$\frac{2}{x−5}−\frac{7}{x−7} = 9$

Вправа$\PageIndex{29}$

$\frac{3}{x+9}−\frac{2}{x+7} = −3$

Відповідь

$\frac{−49+\sqrt{97}}{6}, \frac{−49−\sqrt{97}}{6}$

Вправа$\PageIndex{30}$

$\frac{3}{x+9}−\frac{6}{x+7} = 9$

Вправа$\PageIndex{31}$

$\frac{2}{x+9}+\frac{2}{x+6} = −1$

Відповідь

−7, −12

Вправа$\PageIndex{32}$

$\frac{5}{x−6}−\frac{8}{x−7} = −1$

Вправа$\PageIndex{33}$

$\frac{3}{x+3}+\frac{6}{x+2} = −2$

Відповідь

$\frac{−19+\sqrt{73}}{4}, \frac{−19−\sqrt{73}}{4}$

Вправа$\PageIndex{34}$

$\frac{2}{x−4}−\frac{2}{x−1} = 1$

Для кожного з рівнянь у Вправи 35 - 40 виконайте кожне з наступних завдань.

1. Дотримуйтесь наведення Прикладу 10 в тексті. Зробіть одну сторону рівняння рівною нулю. Завантажте ненульову сторону в калькулятор і намалюйте її графік.
2. Визначте вертикальні асимптоти, проаналізувавши рівняння і отриманий графік на вашому калькуляторі. Використовуйте функцію TABLE вашого калькулятора, щоб визначити будь-яку горизонтальну асимптотну поведінку.
3. Використовуйте утиліту пошуку нуля в меню CALC, щоб визначити нуль ненульової сторони отриманого рівняння.
4. Налаштуйте систему координат на графічному папері. Позначте та масштабуйте кожну вісь. Не забудьте намалювати всі лінії лінійкою.Намалюйте графік ненульової сторони рівняння. Намалюйте вертикальні та горизонтальні асимптоти та позначте їх рівняннями. Побудуйте перехоплення x і позначте його координатами.
5. Використовуйте алгебраїчну техніку, щоб стримувати рішення рівняння та порівняти його з розв'язком, знайденим графічним аналізом вище.

Вправа$\PageIndex{35}$

$\frac{x}{x+1}+\frac{8}{x^2−2x−3} = \frac{2}{x−3}$

Відповідь

х = 2

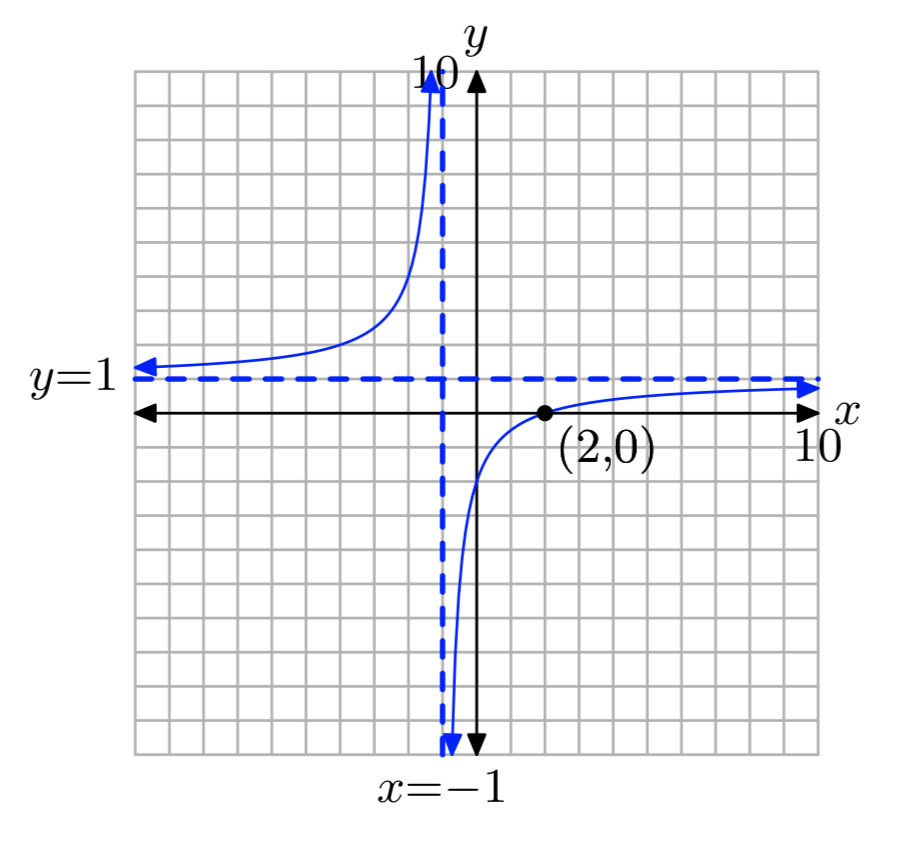
Вправа$\PageIndex{36}$

$\frac{x}{x+4}−\frac{2}{x+1} = \frac{12}{x^2+5x+4}$

Вправа$\PageIndex{37}$

$\frac{x}{x+1}−\frac{4}{2x+1} = \frac{2x−1}{2x^2+3x+2}$

Відповідь

х = 3

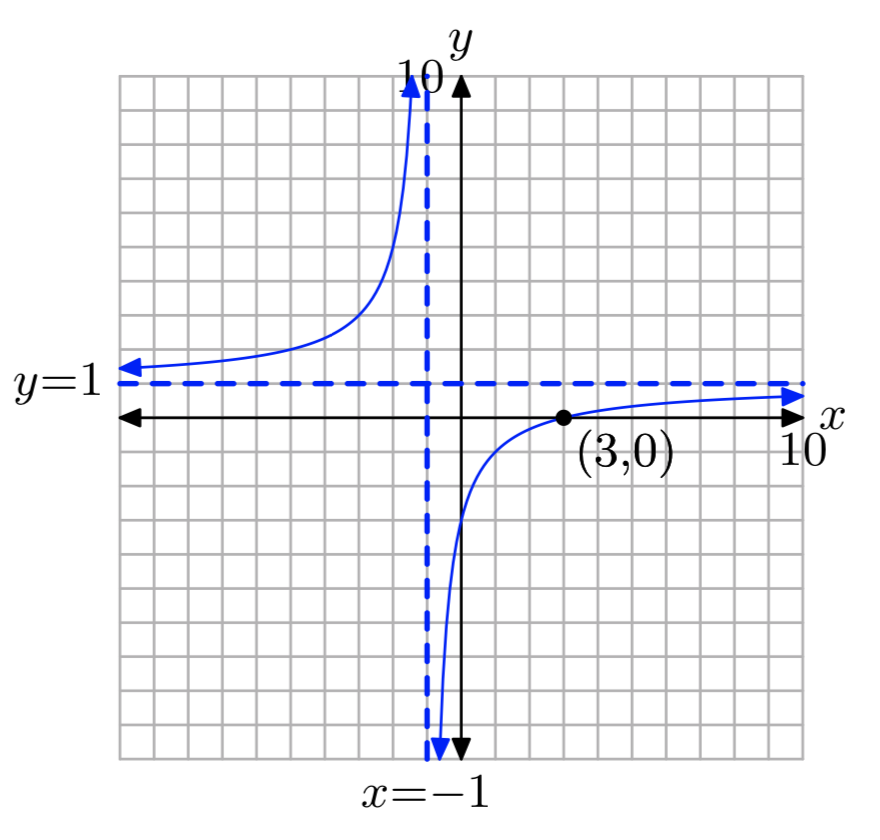
Вправа$\PageIndex{38}$

$\frac{2x}{x−4}−\frac{1}{x+1} = \frac{4x+24}{x^2−3x−4}$

Вправа$\PageIndex{39}$

$\frac{x}{x−2}+\frac{3}{x+2} = \frac{8}{4−x^2}$

Відповідь

$x = \frac{5−\sqrt{17}}{2}, \frac{−5−\sqrt{17}}{2}$

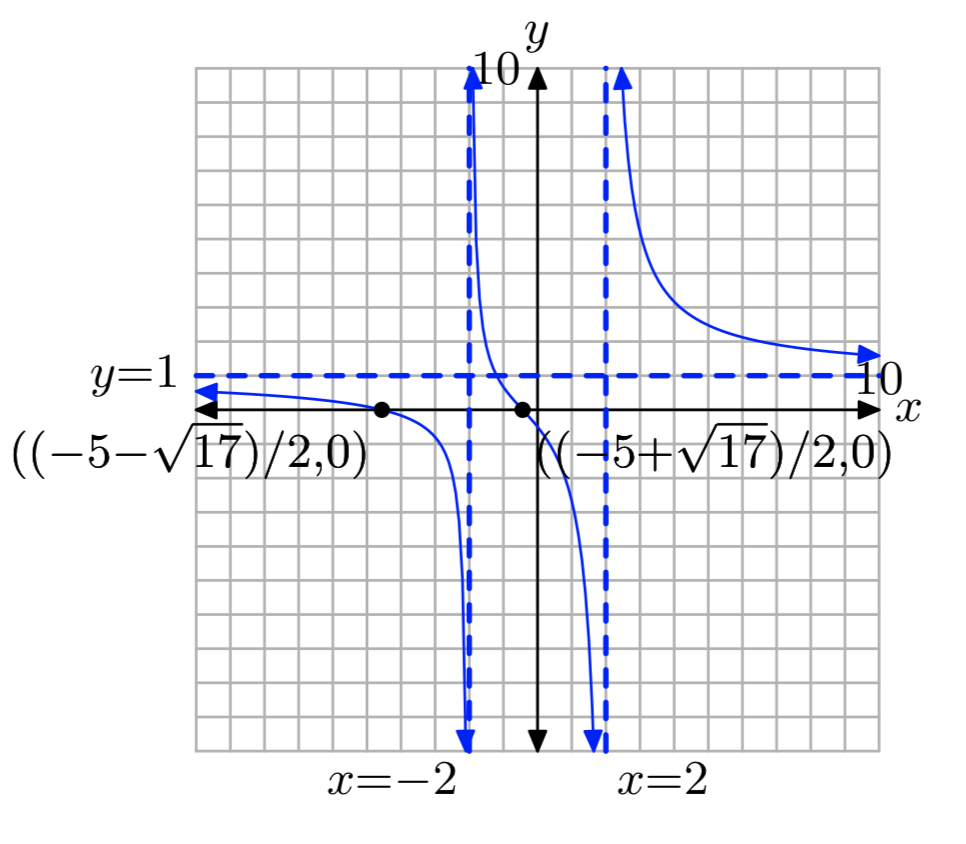
Вправа$\PageIndex{40}$

$\frac{x}{x−6​​​​​1​}−\frac{4}{x+1} = \frac{x−6}{1−x^2}$

У вправах 41 - 68 використовуйте строго алгебраїчну техніку для вирішення даного рівняння. Вам рекомендується перевірити свій результат за допомогою калькулятора.

Вправа$\PageIndex{41}$

$\frac{x}{3x−9}−\frac{9}{x} = \frac{1}{x−3}$

Відповідь

27

Вправа$\PageIndex{42}$

$\frac{5x}{x+2}+\frac{5}{x−5} = \frac{x+6}{x^2−3x−10}$

Вправа$\PageIndex{43}$

$\frac{3x}{x+2}−\frac{7}{x} = −\frac{1}{2x+4}$

Відповідь

$\frac{7}{2}, −\frac{4}{3}$

Вправа$\PageIndex{44}$

$\frac{4x}{x+6}−\frac{4}{x+4} = \frac{x−4}{x^2+10x+24}$

Вправа$\PageIndex{45}$

$\frac{x}{x−5}+\frac{9}{4−x} = \frac{x+5}{x^2−9x+20}$

Відповідь

10

Вправа$\PageIndex{46}$

$\frac{6x}{x−5}−\frac{2}{x−3} = \frac{x−8}{x^2−8x+15}$

Вправа$\PageIndex{47}$

$\frac{2x}{x−4}+\frac{5}{2−x} = \frac{x+8}{x^2−6x+8}$

Відповідь

3

Вправа$\PageIndex{48}$

$\frac{x}{x−7}−\frac{8}{5−x} = \frac{x+7}{x^2−12x+35}$

Вправа$\PageIndex{49}$

$−\frac{x}{2x+2}−\frac{6}{x} = −\frac{2}{x+1}$

Відповідь

−6, −2

Вправа$\PageIndex{50}$

$\frac{7x}{x+3}−\frac{4}{2−x} = \frac{x+8}{x^2+x−6}$

Вправа$\PageIndex{51}$

$\frac{2x}{x+5}−\frac{2}{6−x} = \frac{x−2}{x^2−x−30}$

Відповідь

4,$\frac{3}{2}$

Вправа$\PageIndex{52}$

$\frac{4x}{x+1}+\frac{6}{x+3} = \frac{x−9}{x^2+4x+3}$

Вправа$\PageIndex{53}$

$\frac{x}{x+7}−\frac{2}{x+5}​​​​​​​ = \frac{x+1}{x^2+12x+35}$

Відповідь

3

Вправа$\PageIndex{54}$

$\frac{5x}{6x+4}+\frac{6}{x} = \frac{1}{3x+2}$

Вправа$\PageIndex{55}$

$\frac{2x}{3x+9​​​​​​​}−\frac{4}{x} = −\frac{2}{x+3}$

Відповідь

6

Вправа$\PageIndex{56}$

$\frac{7x}{x+1}−\frac{4}{x+2} = \frac{x+6}{x^2+3x+2}$

Вправа$\PageIndex{57}$

$\frac{x}{2x−8​​​​​​​} + \frac{8}{x} = \frac{2}{x−4}$

Відповідь

−16

Вправа$\PageIndex{58}$

$\frac{3x}{x−6}+\frac{6}{x−6} = \frac{x+2}{x^2−12x+36}$

Вправа$\PageIndex{59}$

$\frac{x}{x+2}+\frac{2}{x} = −\frac{5}{2x+4}$

Відповідь

$\frac{−9+\sqrt{17}}{4}, \frac{−9−\sqrt{17}}{4}$

Вправа$\PageIndex{60}$

$\frac{4x}{x−2}+\frac{2}{2−x} = \frac{x+4}{x^2−4x+4}$

Вправа$\PageIndex{61}$

$−\frac{2x}{3x−9​​​​​​​}−\frac{3}{x} = −\frac{2}{x−3}$

Відповідь

$−\frac{9}{2}$

Вправа$\PageIndex{62}$

$\frac{2x}{x+1}−\frac{2}{x} = \frac{1}{2x+2}$

Вправа$\PageIndex{63}$

$\frac{x}{x+1}+\frac{5}{x} = \frac{1}{4x+4}$

Відповідь

$\frac{−19+\sqrt{41}}{8}, \frac{−19−\sqrt{41}}{8}$

Вправа$\PageIndex{64}$

$\frac{2x}{x−4}−\frac{8}{x−7} = \frac{x+2}{x^2−11x+28}$

Вправа$\PageIndex{65}$

$−\frac{9x}{x−2}+\frac{2}{x} = −\frac{2}{4x−1}$

Відповідь

$\frac{9}{2}$, 5

Вправа$\PageIndex{66}$

$\frac{2x}{x−3​​​​​​​}−\frac{4}{4−x} = \frac{x−9}{x^2−7x+12}$

Вправа$\PageIndex{67}$

$\frac{4x}{x+6}−\frac{5}{7−x} = \frac{x−5}{x^2−x−42}$

Відповідь

$\frac{7}{2}, \frac{5}{2}$

Вправа$\PageIndex{68}$

$\frac{x}{x−1​​​​​​​}−\frac{4}{x} = \frac{1}{5x−5}$

​​​​​​​