7.1: Впровадження раціональних функцій
- Page ID
- 58096
У попередньому розділі ми вивчали многочлени, функції, що мають форму рівняння
\[p(x)=a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n}\]
Незважаючи на те, що цей многочлен представлений у висхідних\(x\) ступенях, провідним терміном многочлена все ще є\(a_{n} x^{n}\), термін з найвищою силою\(x\). Ступінь многочлена - це найвища сила (х\) присутніх, тому в даному випадку ступінь многочлена дорівнює\(n\).
У цьому розділі наше дослідження приведе нас до раціональних функцій. Зверніть увагу на кореневе слово «співвідношення» в терміні «раціональний». Чи нагадує воно вам слово «дріб»? Вона повинна, оскільки раціональні функції є функціями в дуже специфічній дробовій формі.
Визначення: Раціональні функції
Раціональна функція - це функція, яку можна записати як частку двох поліноміальних функцій. У символах функція
\[f(x)=\frac{a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n}}{b_{0}+b_{1} x+b_{2} x^{2}+\cdots+b_{m} x^{m}}\]
називається раціональною функцією.
Наприклад,
\[f(x)=\frac{1+x}{x+2}, \quad g(x)=\frac{x^{2}-2 x-3}{x+4}, \quad \text { and } \quad h(x)=\frac{3-2 x-x^{2}}{x^{3}+2 x^{2}-3 x-5} \label{4}\]
є раціональними функціями, в той час як
\[f(x)=\frac{1+\sqrt{x}}{x^{2}+1}, \quad g(x)=\frac{x^{2}+2 x-3}{1+x^{1 / 2}-3 x^{2}}, \quad \text { and } \quad h(x)=\sqrt{\frac{x^{2}-2 x-3}{x^{2}+4 x-12}} \label{5}\]
не є раціональними функціями.
Кожна з функцій в Equation\ ref {4} є раціональними функціями, оскільки в кожному випадку чисельник і знаменник даного виразу є дійсним поліномом.
Однак у Equation\ ref {5} чисельник не\(f(x)\) є поліномом (поліноми не дозволяють квадратний корінь незалежної змінної). Тому не\(f\) є раціональною функцією. Аналогічно, знаменник\(g(x)\) in Equation\ ref {5} не є поліномом. Дроби не допускаються як експоненти в многочленах. Таким чином, не\(g\) є раціональною функцією. Нарешті, у випадку функції\(h\) в Equation\ ref {5}, хоча радиканд (вираз всередині радикала) є раціональною функцією, квадратний корінь заважає h бути раціональною функцією.
Важливим навиком для розвитку є вміння малювати графік раціональної функції. Почнемо з малювання графіка однієї з найпростіших (але найбільш фундаментальних) раціональних функцій.
Графік y = 1/х
У всіх нових ситуаціях, коли нам представлено рівняння, графік якого ми не розглядали або не розпізнаємо, ми починаємо процес малювання графіка, створюючи таблицю точок, які задовольняють рівнянню. Важливо пам'ятати, що графік рівняння - це сукупність усіх точок, які задовольняють рівнянню. Відзначимо, що нуль знаходиться не в області\(y = 1/x\) (ділення на нуль не має сенсу і не визначено), а створимо таблицю точок, що задовольняють рівнянню, показаному на рис\(\PageIndex{1}\).
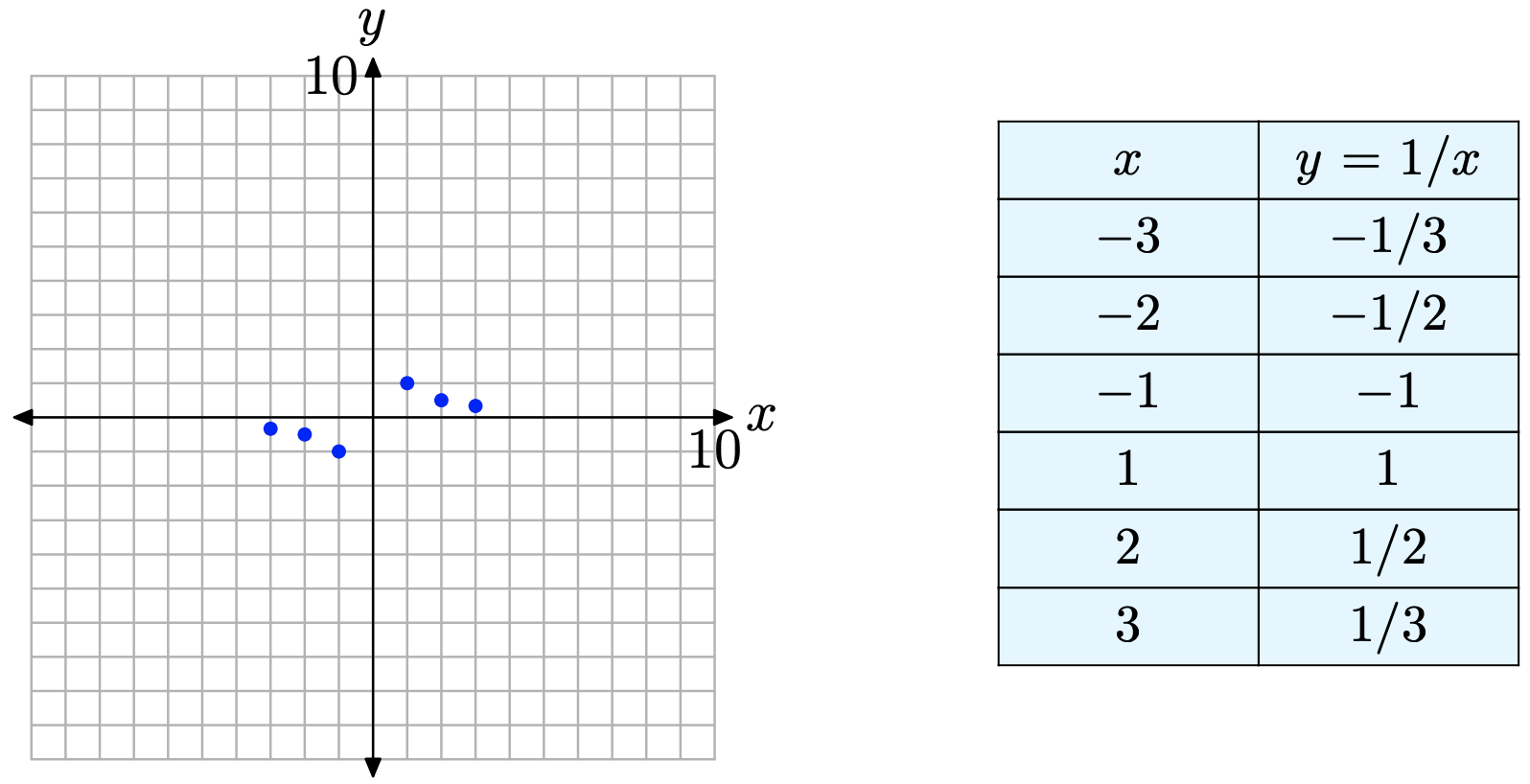
На цьому етапі (рис.\(\PageIndex{1}\)), Це досить ясно, що графік робить між\(x = −3\) і\(x = −1\). Так само зрозуміло, що відбувається між x = 1 і x = 3. Однак є деякі відкриті сфери, що викликають занепокоєння.
- Що відбувається з графіком, коли x збільшується без обмежень? Тобто, що відбувається з графіком, коли х рухається назустріч\(\infty\)?
- Що відбувається з графіком, коли x зменшується без обмежень? Тобто, що відбувається з графіком, коли х рухається назустріч\(-\infty\)?
- Що відбувається з графіком, коли х наближається до нуля справа?
- Що відбувається з графіком, коли х наближається до нуля зліва?
Давайте відповімо на кожне з цих питань по черзі. Ми почнемо з обговорення «endbehavior» раціональної функції, визначеної y = 1/x. Що відбувається, коли x збільшується без прив'язки? Тобто, що відбувається, коли x збільшується до ∞? У таблиці\(\PageIndex{1a}\) ми обчислили y = 1/x для х, що дорівнює 100, 1000 і 10000. Зверніть увагу, як значення y в таблиці\(\PageIndex{1a}\) є позитивними і наближаються до нуля.
Студенти в обчисленні використовують такі позначення для цієї ідеї.
\[\lim _{x \rightarrow \infty} y=\lim _{x \rightarrow \infty} \frac{1}{x}=0\]
Кажуть, «межа y, коли х наближається до нескінченності, дорівнює нулю». Тобто, коли х наближається до нескінченності, y наближається до нуля.
| х | у = 1/х |
|---|---|
| 100 | 0,01 |
| 1000 | 0,001 |
| 10000 | 0,0001 |
Абсолютно подібна подія відбувається на лівому кінці. Оскільки x зменшується без обмежень, тобто, коли x зменшується в бік\(-\infty\), зверніть увагу, що значення y в таблиці\(\PageIndex{1}\) (b) є негативними і наближаються до нуля. Студенти обчислення мають аналогічні позначення для цієї ідеї.
\[\lim _{x \rightarrow-\infty} y=\lim _{x \rightarrow-\infty} \frac{1}{x}=0\]
Вони кажуть, що «межа y, коли x наближається до негативної нескінченності, дорівнює нулю». Тобто, коли х наближається до негативної нескінченності, y наближається до нуля.
| х | y=1/х |
|---|---|
| -100 | -0.01 |
| -1000 | -0,001 |
| -10000 | -0,0001 |
Ці цифри в таблицях\(\PageIndex{1a}\) і\(\PageIndex{1b}\), а також ідеї, описані вище, передбачають правильну кінцеву поведінку графіка\(y = 1/x\). На кожному кінці осі x значення y повинні наближатися до нуля. Це означає, що графік\(y = 1/x\) повинен наближатися до осі x для значень x на крайньому правому та лівому кінцях графіка. У цьому випадку ми говоримо, що вісь x діє як горизонтальна асимптота для графа\(y = 1/x\). У міру\(x\) наближення або позитивної, або негативної нескінченності графік\(y = 1/x\) наближається до осі х. Така поведінка показано на малюнку\(\PageIndex{2}\).

Наше останнє розслідування буде на проміжку від\(x = −1\) до\(x = 1\). Читачам знову нагадують, що функція y = 1/x не визначена при x = 0. Отже, ми розбиваємо цю область навпіл, спочатку досліджуючи, що відбувається на області між x = 0 і x = 1. Оцінюємо y = 1/x при х = 1/2, х = 1/4, а х = 1/8, як показано в таблиці на малюнку\(\PageIndex{3}\), потім намічаємо отримані точки.
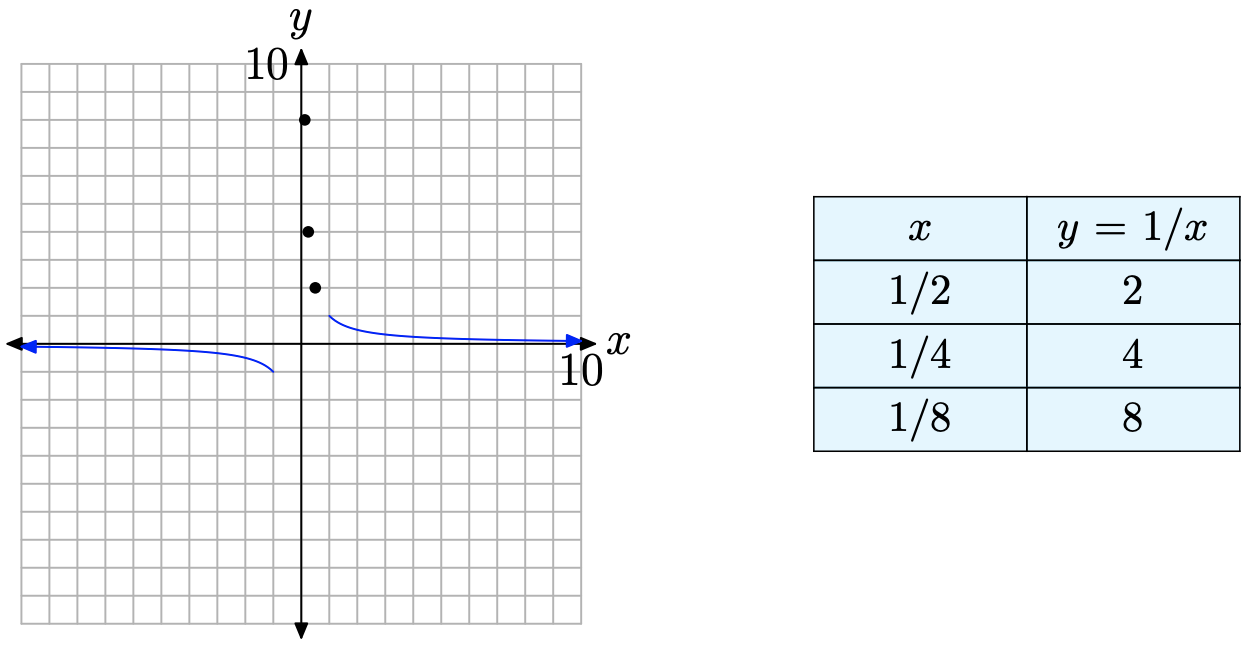
Зверніть увагу, що значення x в таблиці на малюнку\(\PageIndex{3}\) наближаються до нуля справа, тоді зверніть увагу, що відповідні значення y стають все більшими і більшими. Ми могли б продовжити в цьому ключі, додаючи бали. Наприклад, якщо\(x = 1/16\), то\(y = 16\). Якщо\(x = 1/32\), то\(y = 32\). Якщо\(x = 1/64\), то\(y = 64\). Кожен раз, коли ми зменшуємо вдвічі наше значення x, отримане значення x ближче до нуля, а відповідне значення y подвоюється в розмірі. Обчислення студентів описують таку поведінку за допомогою позначення
\[\lim _{x \rightarrow 0^{+}} y=\lim _{x \rightarrow 0^{+}} \frac{1}{x}=\infty\]
Тобто, коли «х наближається до нуля справа, значення y зростає до нескінченності». Це видно на графіку на малюнку\(\PageIndex{3}\), де ми бачимо, що побудовані точки рухаються ближче до вертикальної осі, одночасно рухаючись вгору без обмежень. Аналогічне відбувається і з іншого боку вертикальної осі, як показано на малюнку\(\PageIndex{4}\).
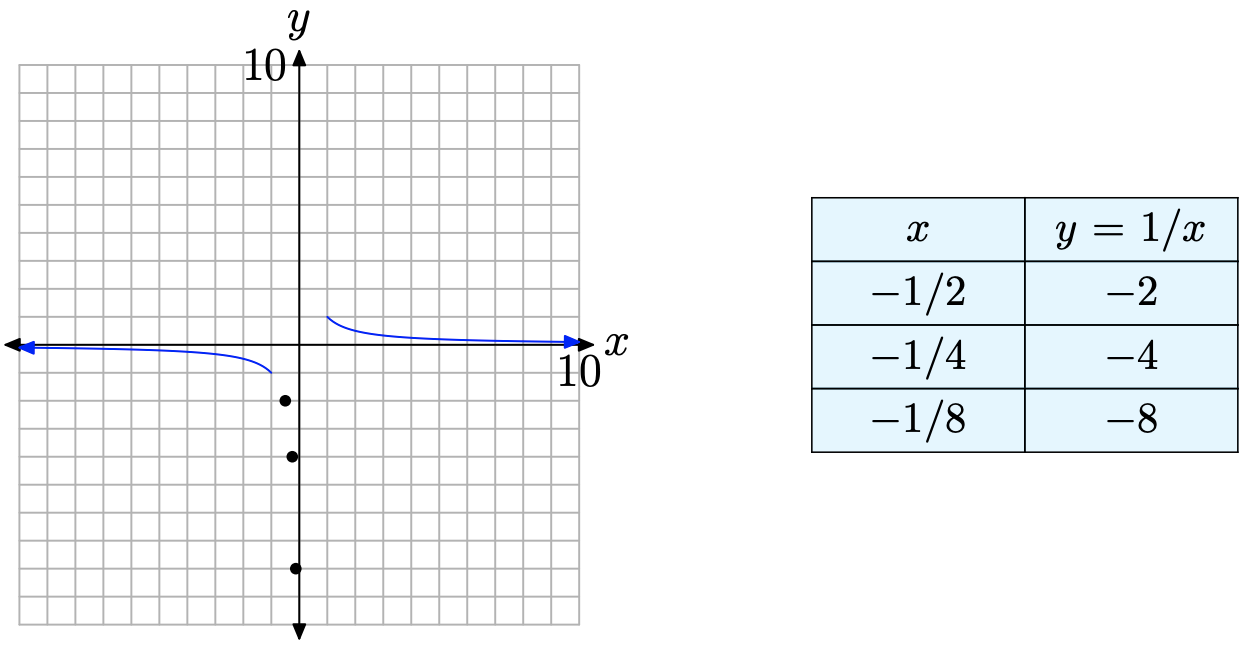
Знову ж таки, студенти обчислення пишуть\[\lim _{x \rightarrow 0^{-}} y=\lim _{x \rightarrow 0^{-}} \frac{1}{x}=-\infty\]
Тобто, «коли х наближається до нуля зліва, значення y зменшуються до негативної нескінченності». На малюнку видно\(\PageIndex{4}\), що коли точки рухаються ближче до вертикальної осі (коли х наближається до нуля) зліва, графік зменшується без обмежень. Зібрані до цього моменту докази свідчать про те, що
Зібрані до цього моменту докази вказують на те, що вертикальна вісь діє як вертикальна асимптота. Коли х наближається до нуля з обох сторін, графік наближається до вертикальної осі, або піднімаючись до нескінченності, або падаючи до негативної нескінченності. Графік не може перетнути вертикальну вісь, оскільки функція там не визначена. Заповнений графік показаний на малюнку\(\PageIndex{5}\).
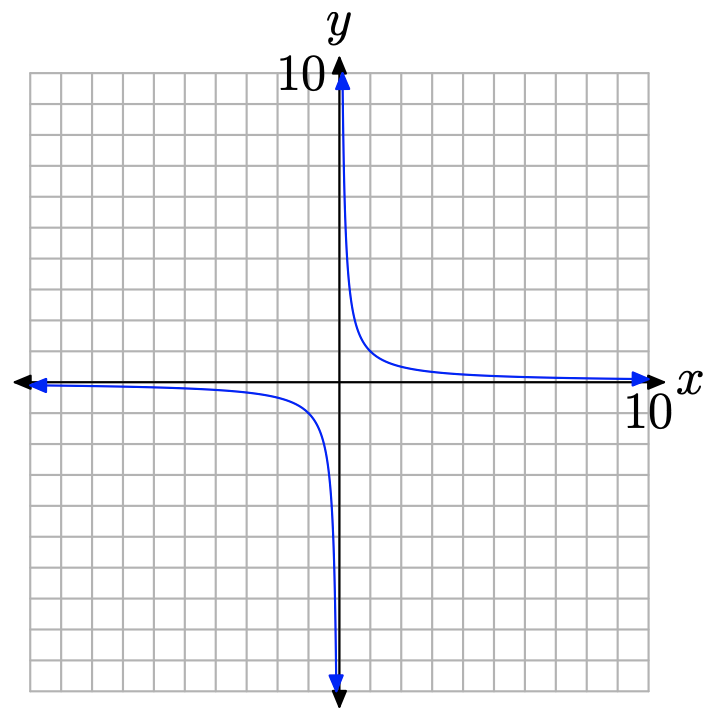
Повний графік y = 1/x на малюнку\(\PageIndex{5}\) називається гіперболою і служить основоположною відправною точкою для всього подальшого обговорення в цьому розділі.
Раніше ми відзначали, що область функції, визначеної рівнянням y = 1/x, є множиною\(D=\{x : x \neq 0\}\). Нуль виключається з домену, оскільки ділення на нуль не визначено. Це не випадково, що графік має вертикальну асимптоту при x = 0. Ми побачимо, що ці відносини посилені в подальших прикладах.
Переклади
У цьому розділі ми переведемо графік y = 1/x як в горизонтальному, так і в вертикальному напрямках.
Приклад\(\PageIndex{1}\)
Намалюйте графік
\[y=\frac{1}{x+3}-4 \nonumber\]
Рішення
Технічно функція, визначена y = 1/ (x + 3) − 4, не має загального вигляду (3) раціональної функції. Однак у наступних розділах ми покажемо, як y = 1/ (x + 3) − 4 можна маніпулювати у загальну форму раціональної функції.
Ми знаємо, як виглядає графік y = 1/x. Якщо ми замінимо x на x + 3, це змістить графік y = 1/x три одиниці вліво, як показано на малюнку\(\PageIndex{6}\) (а). Зауважте, що вертикальна асимптота також змістилася на 3 одиниці ліворуч від початкового положення (вісь y) і тепер має рівняння x = −3. За традицією малюємо вертикальну асимптоту у вигляді пунктирної лінії.
Якщо відняти 4 від результату на малюнку\(\PageIndex{6}\) (а), це змістить графік на малюнку\(\PageIndex{6}\) (а) на чотири одиниці вниз, щоб отримати графік, показаний на малюнку\(\PageIndex{6}\) (b). Зауважте, що горизонтальна асимптота також змістилася на 4 одиниці вниз від початкового положення (вісь x) і тепер має рівняння y = −4.
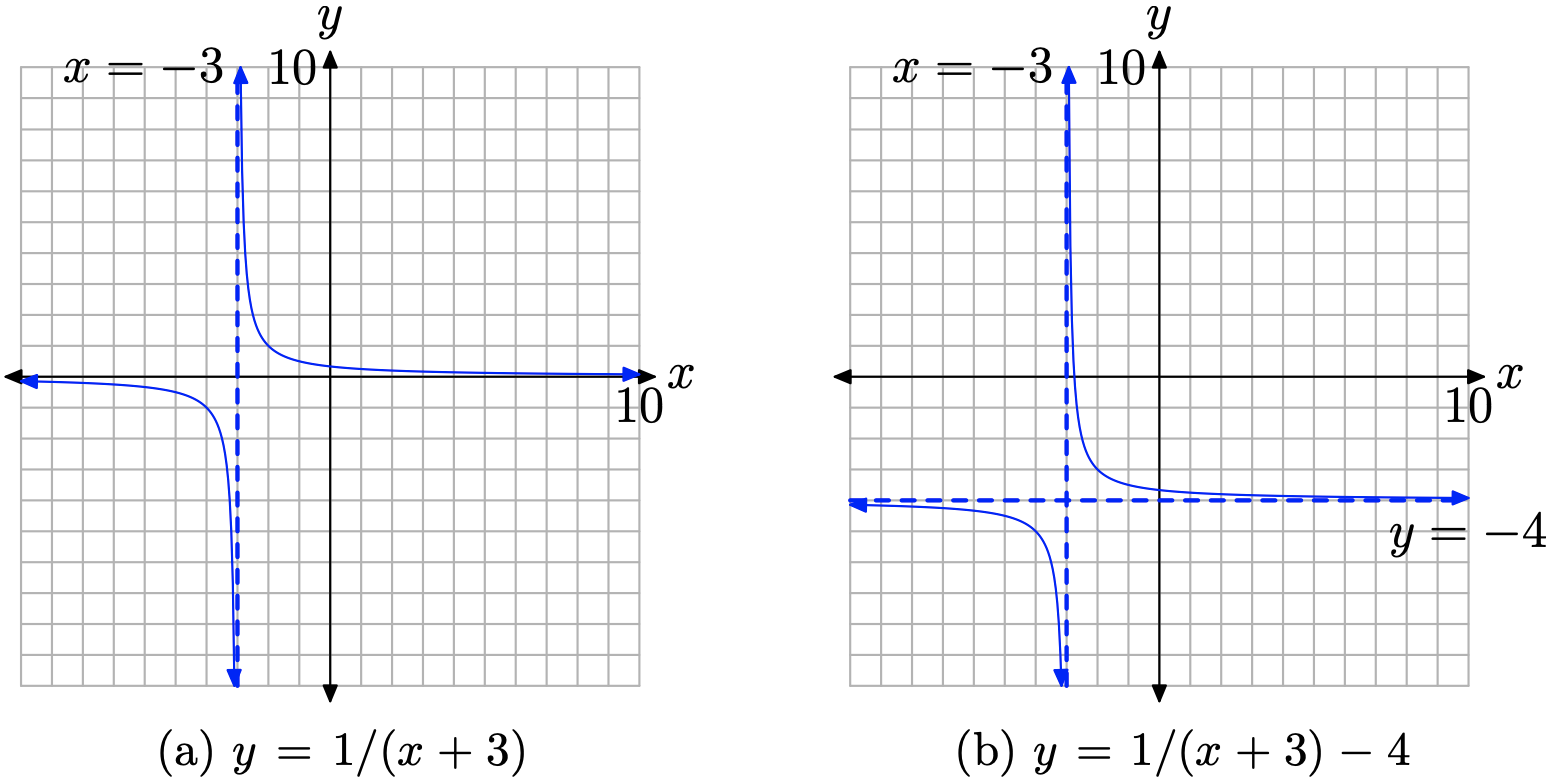
Якщо ви вивчите рівняння (11), ви зауважте, що ви не можете використовувати x = −3, оскільки це зробить знаменник рівняння (11) рівним нулю. На малюнку\(\PageIndex{6}\) (b) зауважте, що на графіку рівняння (11) існує вертикальна асимптота при x = −3. Це звичайне явище, яке буде центральною темою цієї глави.
Давайте задамо ще одне ключове питання.
Приклад\(\PageIndex{2}\)
Які області та діапазон раціональної функції представлені в прикладі\(\PageIndex{1}\)?
Рішення
Ви можете поглянути на рівняння
\[y=\frac{1}{x+3}-4\nonumber\]
Приклад\(\PageIndex{1}\) і зауважте, що x = −3 робить знаменник нулем і має бути виключено з домену. Значить, область цієї функції є\(D=\{x : x \neq-3\}\).
Однак визначити область також можна, вивчивши графік функції на малюнку\(\PageIndex{6}\) (b). Зверніть увагу, що графік триває нескінченно вліво і вправо. Спочатку можна здогадатися, що область є дійсними числами, якби не вертикальна асимптота при x = −3 переривала неперервність графа. Оскільки графік функції довільно наближається до цієї вертикальної асимптоти (з обох боків), фактично не торкаючись асимптоти, графік не містить точки, що має значення x, рівне −3. Отже, домен такий, як зазначено вище,\(D=\{x : x \neq-3\}\). Це втішає те, що графічний аналіз узгоджується з нашим попереднім аналітичним визначенням домену.
Графік особливо корисний при визначенні діапазону функції. Зверніть увагу, що графік піднімається до позитивної нескінченності і падає до негативної нескінченності. Спочатку можна було б здогадатися, що діапазон - це всі дійсні числа, якби не горизонтальна асимптота при y = −4 перериває неперервність графа. Оскільки графік довільно наближається до горизонтальної асимптоти (з обох боків), фактично не торкаючись асимптоти, графік не містить точки, що має значення y, рівне −4. Отже, −4 виключається з діапазону. Тобто,\(R=\{y : y \neq-4\}\).
Масштабування та відображення
У цьому розділі ми будемо як масштабувати, так і відображати графік y = 1/x, Для додаткової міри ми також кидаємо переклади в горизонтальному і вертикальному напрямках.
Приклад\(\PageIndex{3}\)
Намалюйте графік\[y=-\frac{2}{x-4}+3\nonumber\]
Рішення
Спочатку множимо рівняння y = 1/x на −2, щоб отримати
\[y=-\frac{2}{x}\nonumber\]
Множення на 2 має розтягнути графік у вертикальних напрямках (як позитивних, так і негативних) на коефіцієнт 2. Зауважте, що точки, які знаходяться дуже близько осі x, при подвоюванні не збираються занадто далеко відхилятися від осі x, тому горизонтальна асимптота залишиться колишньою. Нарешті, множення на −2 не лише розтягне графік, але й відображатиме графік по осі x, як показано на малюнку\(\PageIndex{7}\) (b).
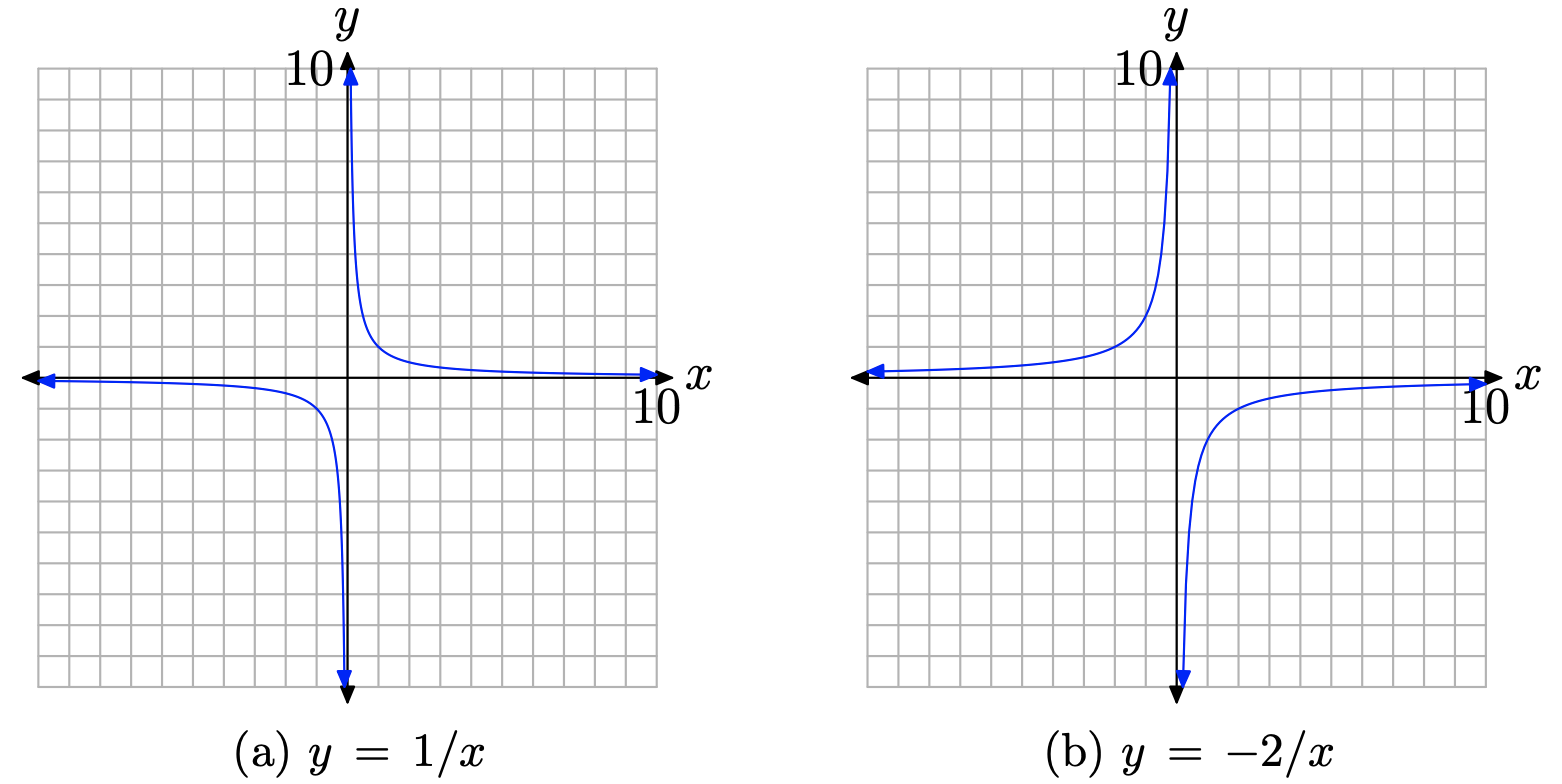
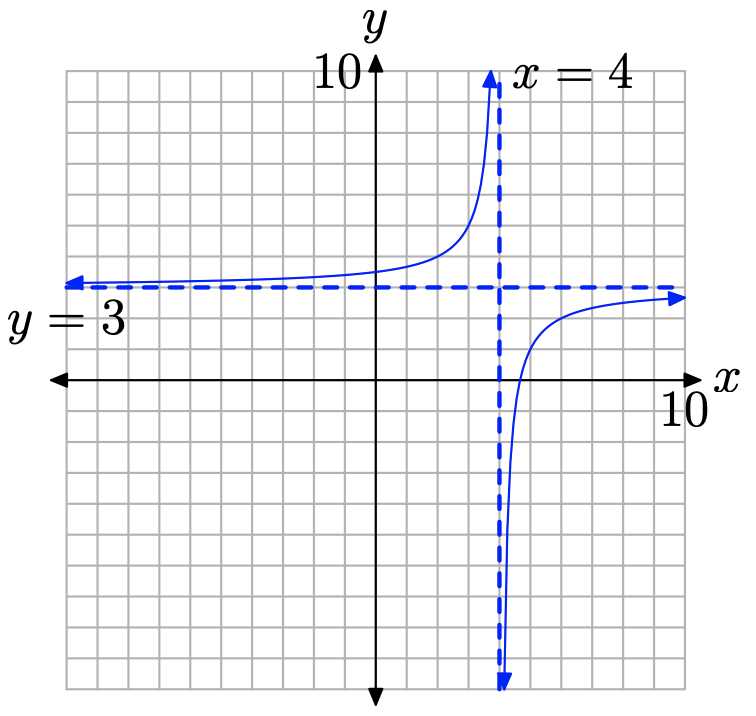
Заміна x на x − 4 змістить графік на 4 одиниці вправо, тоді додавання 3 змістить графік на 3 одиниці вгору, як показано на малюнку\(\PageIndex{8}\). Знову зауважте, що x = 4 робить знаменник y = −2/ (x − 4) + 3 рівним нулю і існує вертикальна асимптота при x = 4. Доменом цієї функції є\(D=\{x : x \neq 4\}\).
Коли x наближається до позитивної або від'ємної нескінченності, точки на графіку y = −2/ (x−4) + 3 довільно наближаються до горизонтальної асимптоти y = 3, але ніколи не торкаються її. Тому на графіку немає точки, яка має значення y 3. Таким чином, діапазон функції - це безліч\(R=\{y : y \neq 3\}\).
Труднощі з графічним калькулятором
Графічний калькулятор дуже добре справляється з малюванням графіків «безперервних функцій».
Безперервна функція - це та, яку можна намалювати одним безперервним штрихом, ніколи не піднімаючи ручку або олівець з паперу під час малювання.
Поліноми, такі як той, що на малюнку\(\PageIndex{9}\), є неперервними функціями.
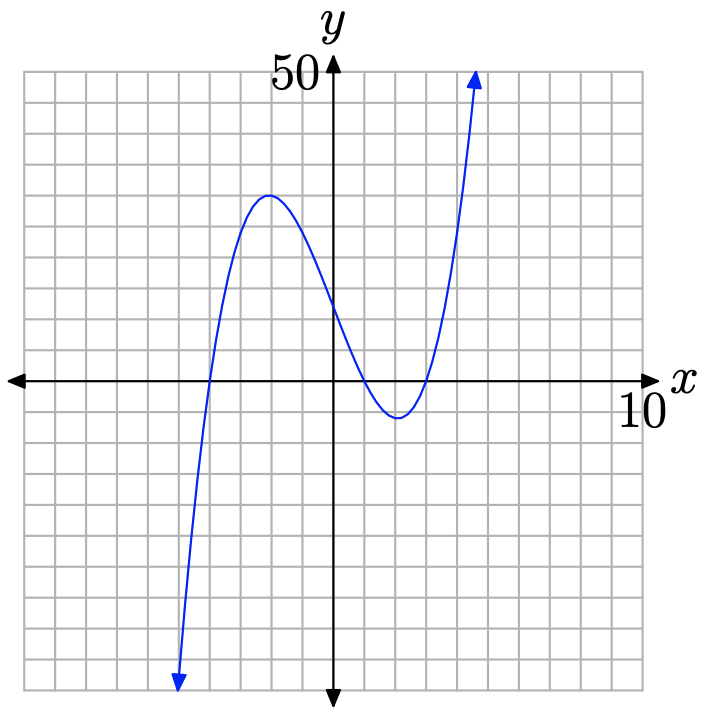
На жаль, раціональна функція з вертикальною асимптотою (s) не є неперервною функцією. По-перше, ви повинні підняти перо в точках, де знаменник дорівнює нулю, тому що функція невизначена в цих точках. По-друге, не рідкість доводиться стрибати з позитивної нескінченності на негативну нескінченність (або навпаки) при перетині вертикальної асимптоти. Коли це станеться, ми повинні підняти ручку і зрушити її, перш ніж продовжувати малювати.
Однак графічний калькулятор не знає, як зробити цей «підйом» пера поблизу вертикальних асимптотів. Калькулятор графіків знає лише одну техніку, намалюйте точку, потім з'єднайте її з відрізком до останньої побудованої точки, перемістіть додаткову відстань і повторіть. Отже, коли графічний калькулятор перетинає вертикальну асимптоту, де відбувається зсув від одного типу нескінченності до іншого (наприклад, від позитивного до негативного), калькулятор малює «помилкову лінію» з'єднання, таку, яку він не повинен малювати. Продемонструємо цю аберацію на прикладі.
Приклад\(\PageIndex{4}\)
Використовуйте графічний калькулятор, щоб намалювати графік раціональної функції у прикладі\(\PageIndex{3}\).
Рішення
Завантажте рівняння у свій калькулятор, як показано на малюнку\(\PageIndex{10}\) (а). Встановіть вікно, як показано на малюнку\(\PageIndex{10}\) (b), потім натисніть кнопку GRAPH, щоб намалювати графік, показаний на малюнку\(\PageIndex{10}\) (c). Результати можуть відрізнятися на деяких калькуляторах, але в нашому випадку зверніть увагу на «помилкову лінію», проведену зверху екрану вниз, намагаючись «з'єднати» дві гілки гіперболи.
Деякі можуть радіти і стверджувати: «Гей, мій графічний калькулятор малює вертикальні асимптоти». Однак, перш ніж ви занадто збуджуєтеся, зверніть увагу, що\(\PageIndex{8}\) на малюнку вертикальна асимптота повинна відбуватися рівно при x = 4. Якщо ви дуже уважно подивитеся на «вертикальну лінію» на малюнку\(\PageIndex{10}\) (c), то зауважте, що вона просто пропускає галочку при x = 4. Ця «вертикальна лінія» - це лінія, яку калькулятор не повинен малювати. Калькулятор намагається намалювати безперервну функцію, де її не існує.

Одним з можливих способів вирішення є натискання кнопки MODE на клавіатурі, яка відкриває меню, показане на малюнку\(\PageIndex{11}\) (а). За допомогою клавіш зі стрілками виділіть DOT замість CONNECTED і натисніть клавішу ENTER, щоб зробити вибір постійним. Натисніть кнопку GRAPH, щоб намалювати графік на малюнку\(\PageIndex{11}\) (b).
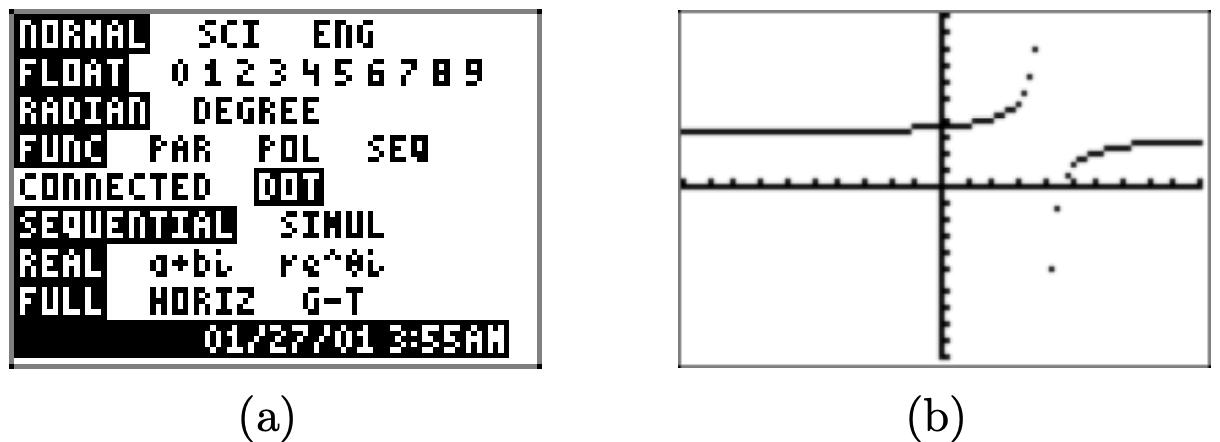
Цей «точковий режим» на вашому калькуляторі обчислює наступну точку на графіку та відображає точку, але він не з'єднує її відрізком лінії з раніше нанесеною точкою. Цей режим корисний для демонстрації того, що вертикальна лінія на малюнку\(\PageIndex{10}\) (c) насправді не є частиною графіка, але ми втрачаємо деякі частини графіка, який ми дійсно хотіли б бачити. Компроміс в порядку.
Цей приклад наочно показує, що інтелектуальне використання калькулятора є обов'язковою складовою цього курсу. Калькулятор - це не просто «чорний ящик», який автоматично робить те, що ви хочете зробити. Зокрема, коли ви малюєте раціональні функції, це допомагає заздалегідь дізнатися розміщення вертикальних асимптотів. Знання асимптотів у поєднанні з тим, що ви бачите на екрані калькулятора, повинно дозволити вам намалювати графік настільки точно, як показано на малюнку\(\PageIndex{8}\).
Ніжне нагадування. Ви хочете, щоб ваш калькулятор повернувся в «підключений режим». Для цього натисніть кнопку MODE на клавіатурі, щоб знову відкрити меню на малюнку\(\PageIndex{10}\) (а). Використовуйте клавіші зі стрілками, щоб виділити CONNECTED, а потім натисніть клавішу ENTER, щоб зробити вибір постійним.
Вправа
У вправах 1 - 14 виконайте кожне з наступних завдань для заданої раціональної функції.
- Налаштуйте систему координат на аркуші графічного паперу. Позначте та масштабуйте кожну вісь.
- Використовуйте геометричні перетворення, як у прикладах 10, 12 та 13, щоб намалювати графіки кожної з наступних раціональних функцій. Намалюйте вертикальні та горизонтальні асимптоти у вигляді пунктирних ліній та позначте кожну своїм рівнянням. Ви можете скористатися калькулятором для перевірки рішення, але ви повинні мати можливість малювати раціональну функцію без використання калькулятора.
- Використовуйте нотацію set-builder для опису області та діапазону заданої раціональної функції.
Вправа\(\PageIndex{1}\)
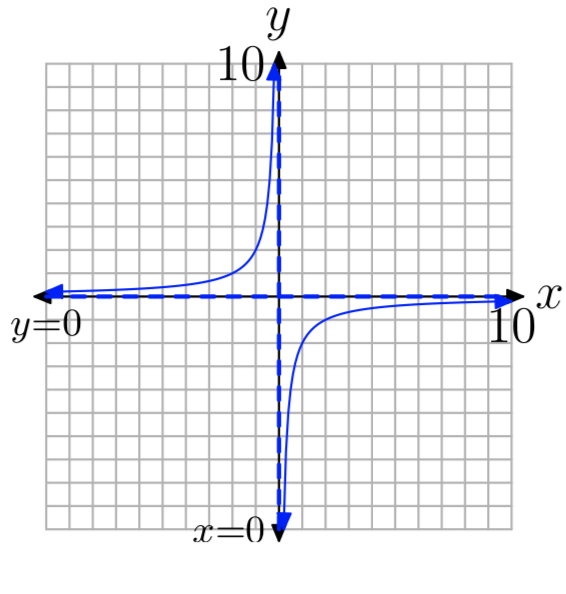
\(f(x) = −\frac{2}{x}\)
- Відповідь
-
D = {x:\(x \ne 0\)}, R = {у:\(y \ne 0\)}
Вправа\(\PageIndex{2}\)
\(f(x) = \frac{3}{x}\)
Вправа\(\PageIndex{3}\)
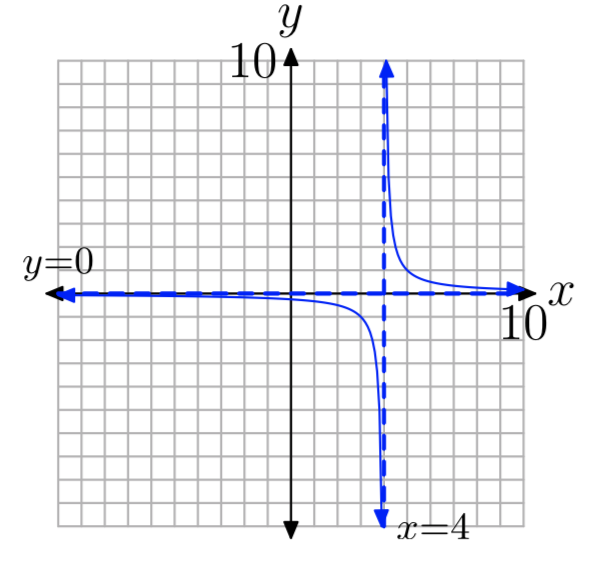
\(f(x) = \frac{1}{x−4}\)
- Відповідь
-
D = {x:\(x \ne 4\)}, R = {у:\(y \ne 0\)}
Вправа\(\PageIndex{4}\)
\(f(x) = \frac{1}{x+3}\)
Вправа\(\PageIndex{5}\)
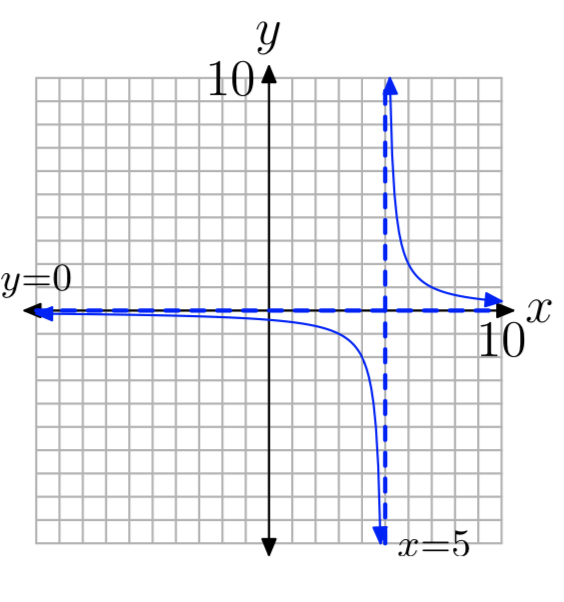
\(f(x) = \frac{2}{x−5}\)
- Відповідь
-
D = {x:\(x \ne 5\)}, R = {у:\(y \ne 0\)}
Вправа\(\PageIndex{6}\)
\(f(x) = −\frac{3}{x+6}\)
Вправа\(\PageIndex{7}\)
\(f(x) = \frac{1}{x}−2\)
- Відповідь
-
D = {x:\(x \ne 0\)}, R = {у:\(y \ne −2\)}
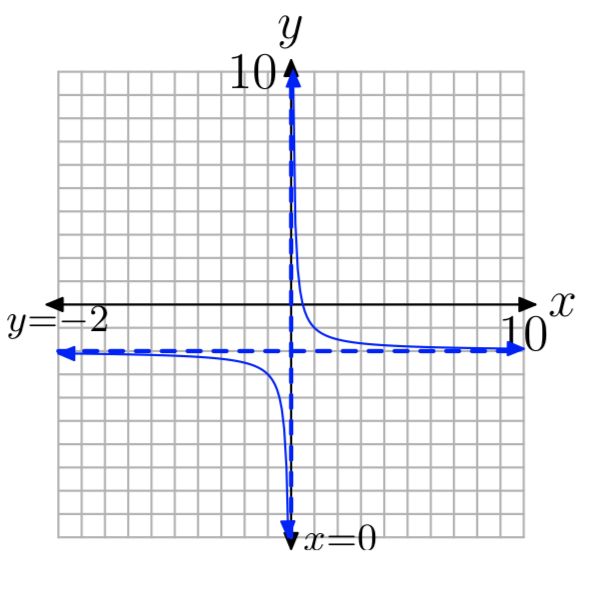
Вправа\(\PageIndex{8}\)
\(f(x) = −\frac{1}{x}+4\)
Вправа\(\PageIndex{9}\)
\(f(x) = −\frac{2}{x}−5\)
- Відповідь
-
D = {x:\(x \ne 0\)}, R = {у:\(y \ne −5\)}
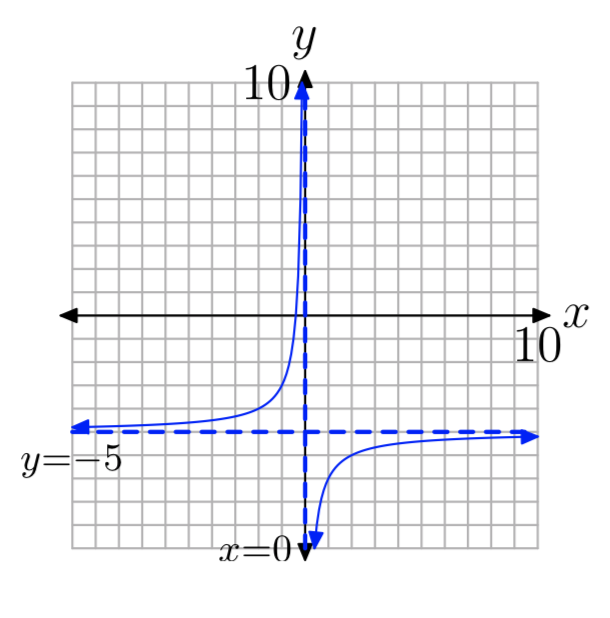
Вправа\(\PageIndex{10}\)
\(f(x) = \frac{3}{x}−5\)
Вправа\(\PageIndex{11}\)
\(f(x) = \frac{1}{x−2}−3\)
- Відповідь
-
D = {x:\(x \ne 2\)}, R = {у:\(y \ne −3\)}
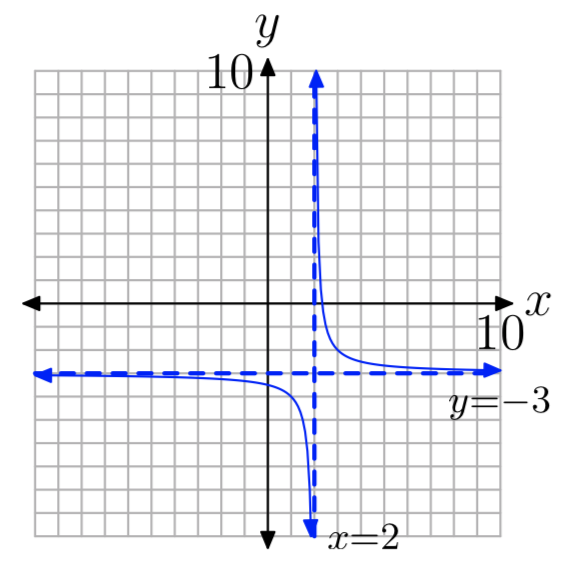
Вправа\(\PageIndex{12}\)
\(f(x) = −\frac{1}{x+1}+5\)
Вправа\(\PageIndex{13}\)
\(f(x) = −\frac{2}{x−3}−4\)
- Відповідь
-
D = {x:\(x \ne 3\)}, R = {у:\(y \ne −4\)}
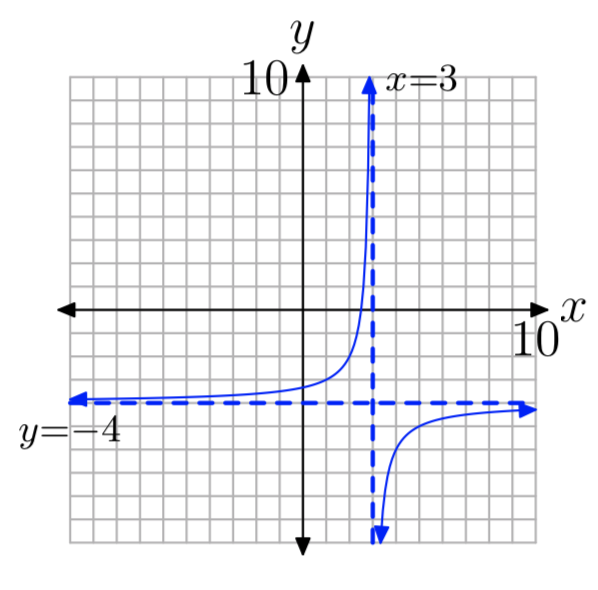
Вправа\(\PageIndex{14}\)
\(f(x) = \frac{3}{x+5}−2\)
У Вправах 15 - 22 знайдіть всю вертикаль у вигляді симптотів, якщо такі є, графіка заданої функції.
Вправа\(\PageIndex{15}\)
\(f(x) = −\frac{5}{x+1}−3\)
- Відповідь
-
Вертикальна асимптота: x = −1
Вправа\(\PageIndex{16}\)
\(f(x) = \frac{6}{x+8}+2\)
Вправа\(\PageIndex{17}\)
\(f(x) = −\frac{9}{x+2}−6\)
- Відповідь
-
Вертикальна асимптота: x = −2
Вправа\(\PageIndex{18}\)
\(f(x) = −\frac{8}{x−4}−5\)
Вправа\(\PageIndex{19}\)
\(f(x) = \frac{2}{x+5}+1\)
- Відповідь
-
Вертикальна асимптота: x = −5
Вправа\(\PageIndex{20}\)
\(f(x) = −\frac{3}{x+9}+2\)
Вправа\(\PageIndex{21}\)
\(f(x) = \frac{7}{x+8}−9\)
- Відповідь
-
Вертикальна асимптота: x = −8
Вправа\(\PageIndex{22}\)
\(f(x) = \frac{6}{x−5}−8\)
У Вправах 23 - 30 знайти всі горизонтальні асимптоти, якщо такі є, графіка заданої функції.
Вправа\(\PageIndex{23}\)
\(f(x) = \frac{5}{x+7}+9\)
- Відповідь
-
Горизонтальна асимптота: y = 9
Вправа\(\PageIndex{24}\)
\(f(x) = −\frac{8}{x+7}−4\)
Вправа\(\PageIndex{25}\)
\(f(x) = \frac{8}{x+5}−1\)
- Відповідь
- Горизонтальна асимптота: y = −1
Вправа\(\PageIndex{26}\)
\(f(x) = −\frac{2}{x+3}+8\)
Вправа\(\PageIndex{27}\)
\(f(x) = \frac{7}{x+1}−9\)
- Відповідь
-
Горизонтальна асимптота: y = −9
Вправа\(\PageIndex{28}\)
\(f(x) = −\frac{2}{x−1}+5\)
Вправа\(\PageIndex{29}\)
\(f(x) = \frac{5}{x+2}−4\)
- Відповідь
-
Горизонтальна асимптота: y = −4
Вправа\(\PageIndex{30}\)
\(f(x) = −\frac{6}{x−1}−2\)
У вправах 31 - 38 викладіть область заданої раціональної функції за допомогою множинних позначень.
Вправа\(\PageIndex{31}\)
\(f(x) = −\frac{4}{x+5}+5\)
- Відповідь
-
Домен = {x:\(x \ne −5\)}
Вправа\(\PageIndex{32}\)
\(f(x) = −\frac{7}{x−6}+1\)
Вправа\(\PageIndex{33}\)
\(f(x) = \frac{6}{x−5}+1\)
- Відповідь
-
Домен = {x:\(x \ne 5\)}
Вправа\(\PageIndex{34}\)
\(f(x) = −\frac{5}{x−3}−9\)
Вправа\(\PageIndex{35}\)
\(f(x) = \frac{1}{x+7}+2\)
- Відповідь
-
Домен = {x:\(x \ne −7\)}
Вправа\(\PageIndex{36}\)
\(f(x) = −\frac{2}{x−5}+4\)
Вправа\(\PageIndex{37}\)
\(f(x) = −\frac{4}{x+2}+2\)
- Відповідь
-
Домен = {x:\(x \ne −2\)}
Вправа\(\PageIndex{38}\)
\(f(x) = \frac{2}{x+6}+9\)
У Вправи 39 - 46 знайдіть діапазон заданої функції, і висловіть свою відповідь у встановлених позначеннях.
Вправа\(\PageIndex{39}\)
\(f(x) = \frac{2}{x−3}+8\)
- Відповідь
-
Діапазон = {y:\(y \ne 8\)}
Вправа\(\PageIndex{40}\)
\(f(x) = \frac{4}{x−3}+5\)
Вправа\(\PageIndex{41}\)
\(f(x) = −\frac{5}{x−8}−5\)
- Відповідь
-
Діапазон = {y:\(y \ne −5\)}
Вправа\(\PageIndex{42}\)
\(f(x) = −\frac{2}{x+1}+6\)
Вправа\(\PageIndex{43}\)
\(f(x) = \frac{7}{x+7}+5\)
- Відповідь
-
Діапазон = {y:\(y \ne 5\)}
Вправа\(\PageIndex{44}\)
\(f(x) = −\frac{8}{x+3}+9\)
Вправа\(\PageIndex{45}\)
\(f(x) = \frac{4}{x+3}−2\)
- Відповідь
-
Діапазон = {y:\(y \ne −2\)}
Вправа\(\PageIndex{46}\)
\(f(x) = −\frac{5}{x−4}+9\)
