6.2: Нулі многочленів
- Page ID
- 58133
У попередньому розділі ми вивчали кінцеву поведінку многочленів. Ми знаємо, що кінцева поведінка полінома ідентична кінцевій поведінці його провідного терміна. Наша увага була зосереджена на крайньому правому та лівому кінцях графіка, а не на тому, що відбувається між ними. У цьому розділі наш фокус зміщується на інтер'єр. Є дві важливі області концентрації: локальні максимуми і мінімуми многочлена, і розташування х-перехоплень або нулів многочлена. У цьому розділі ми зосередимося на пошуку нулів многочлена.
Нулі
Почнемо з формального визначення нулів многочлена.
Визначення: Нуль многочлена
\(p(x)=a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n}\)Дозволяти поліном з дійсними коефіцієнтами. Ми говоримо, що\(a\) це нуль многочлена якщо і тільки якщо\(p(a) = 0\).
Визначення також має місце, якщо коефіцієнти складні, але це тема для більш просунутого курсу.
Наприклад, −5 є нулем многочлена,\(p(x)=x^{2}+3 x-10\) оскільки
\[\begin{aligned} p(-5) &=(-5)^{2}+3(-5)-10 \\ &=25-15-10 \\ &=0 \end{aligned}\]
Аналогічно, −1 є нулем многочлена,\(p(x)=x^{3}+3 x^{2}-x-3\) оскільки
\[\begin{aligned} p(-1) &=(-1)^{3}+3(-1)^{2}-(-1)-3 \\ &=-1+3+1-3 \\ &=0 \end{aligned}\]
Давайте розглянемо більш великий приклад.
Приклад\(\PageIndex{1}\)
Знайти нулі многочлена, визначеного
\[p(x)=(x+3)(x-2)(x-5). \nonumber\]
Рішення
На перший погляд функція, здається, не має вигляду многочлена. Однак два застосування розподільного майна забезпечують добуток останніх двох факторів.
\[\begin{aligned} p(x) &=(x+3)(x(x-5)-2(x-5)) \\ &=(x+3)\left(x^{2}-5 x-2 x+10\right) \\ &=(x+3)\left(x^{2}-7 x+10\right) \end{aligned}\]
Третє і четверте застосування розподільної властивості розкриває природу нашої функції.
\[\begin{aligned} p(x) &=x\left(x^{2}-7 x+10\right)+3\left(x^{2}-7 x+10\right) \\ &=x^{3}-7 x^{2}+10 x+3 x^{2}-21 x+30 \\ &=x^{3}-4 x^{2}-11 x+30 \end{aligned}\]
Значить, p - це явно многочлен. Однак початкова факторна форма забезпечує більш швидкий доступ до нулів цього многочлена. Використовуючи визначення 1, нам потрібно знайти значення x, які роблять p (x) = 0. Тобто нам потрібно вирішити рівняння\[p(x)=0\]
Звичайно, p (x) = (x + 3) (x − 2) (x − 5), отже, рівняння нам потрібно розв'язати рівняння
\[(x+3)(x-2)(x-5)=0\]
За властивістю нульового продукту, або
\[x+3=0 \quad \text { or } \quad x-2=0 \quad \text { or } \quad x-5=0\]
Це лінійні (першого ступеня) рівняння, кожне з яких можна вирішити самостійно. Таким чином, або
\[x=-3 \quad \text { or } \quad x=2 \quad \text { or } \quad x=5\]
Отже, нулями многочлена p є −3, 2 і 5.
Давайте скористаємося рівнянням (4), щоб перевірити, що −3 є нулем многочлена p. Замініть −3 для x in\(p(x)=x^{3}-4 x^{2}-11 x+30\).
\[\begin{aligned} p(-3) &=(-3)^{3}-4(-3)^{2}-11(-3)+30 \\ &=-27-36+33+30 \\ &=0 \end{aligned}\]
Цей розрахунок підтверджує, що −3 є нулем многочлена p. Однак набагато простіше перевірити, що −3 є нулем многочлена за допомогою рівняння (3). Замініть −3 для x у p (x) = (x + 3) (x − 2) (x − 5).
\[\begin{aligned} p(-3) &=(-3+3)(-3-2)(-3-5) \\ &=(0)(-5)(-8) \\ &=0 \end{aligned}\]
Ми залишимо це нашим читачам, щоб перевірити, що 2 і 5 також є нулями многочлена p.
Дуже важливо зазначити, що як тільки ви знаєте лінійні (першого ступеня) фактори многочлена, нулі слідують з легкістю. В останньому прикладі p (x) = (x+3) (x−2) (x−5), тому лінійними факторами є x + 3, x − 2 та x − 5. Отже, нулі складають −3, 2 і 5.
Перш ніж продовжувати, ми беремо хвилинку, щоб переглянути важливу схему множення.
Різниця двох квадратів
Особливий візерунок множення, який часто з'являється в цьому тексті, називається різницею двох квадратів. Використовуйте розподільну властивість для розширення (a + b) (a − b).
\[\begin{aligned}(a+b)(a-b) &=a(a-b)+b(a-b) \\ &=a^{2}-a b+b a-b^{2} \end{aligned}\]
Так як\(ab = ba\), ми маємо наступний результат.
Властивість 5: Різниця двох квадратів візерунок
\[(a+b)(a-b)=a^{2}-b^{2}\]
Таким чином, якщо у вас два двочлени з однаковими першим і другим долями, але члени одного розділені знаком плюс, тоді як члени другого розділені знаком мінус, то ви множите, зводячи в квадрат перше і друге члени і розділивши ці квадрати знаком мінус. Звідси і назва, «різниця двох квадратів».
Наприклад,
\[(2 x+3)(2 x-3)=(2 x)^{2}-(3)^{2}=4 x^{2}-9 \nonumber\]
Зверніть увагу, як ми просто квадрат збігаються перший і другий члени, а потім розділили наші квадрати зі знаком мінус. У подібній моді,
\[\begin{aligned}(x+5)(x-5) &=x^{2}-25 \\(5 x+4)(5 x-4) &=25 x^{2}-16 \\(3 x-7)(3 x+7) &=9 x^{2}-49 \end{aligned}\]
У кожному випадку зверніть увагу на те, як ми зрівняли збігаються перший і другий члени, а потім розділили квадрати зі знаком мінус.
Після того, як ви освоїли множення за допомогою шаблону «Різниця квадратів», легко фактор, використовуючи той самий шаблон. Ви просто скасовуєте процедуру. Наприклад
\[4 x^{2}-9=(2 x+3)(2 x-3) \nonumber\]
Починаємо з того, що беремо квадратний корінь з двох квадратів. Таким чином, квадратний корінь з 4\(x^{2}\) дорівнює 2x, а квадратний корінь з 9 дорівнює 3. Потім ми формуємо два біноміали з результатами 2x і 3 як збігаються перший і другий члени, розділяючи одну пару зі знаком плюс, іншу пару зі знаком мінус.
У подібній моді,\[9 x^{2}-49=(3 x+7)(3 x-7) \nonumber\]
Знову відзначимо, як ми беремо квадратний корінь кожного члена, формуємо два бічлена з результатами, потім відокремлюємо одну пару плюсом, іншу з мінусом.
Ми знайдемо шаблон «Різниця квадратів» зручним у наступному.
Пошук нулів шляхом факторингу
Зараз ми вивчимо, як можна знайти нулі полінома шляхом факторингу з подальшим застосуванням властивості нульового добутку. Важливо розуміти, що поліноми цього розділу були ретельно відібрані, щоб ви могли їх враховувати, використовуючи різні методи, які слідують.
Давайте вивчимо факторинг шляхом групування.
Приклад\(\PageIndex{2}\)
Знайти нулі многочлена\[p(x)=x^{3}+2 x^{2}-25 x-50\]
Рішення
У прикладі\(\PageIndex{1}\) ми дізналися, що легко визначити нулі многочлена, якщо многочлен виражається як добуток лінійних (першого ступеня) множників. У цьому прикладі многочлен не враховується, тому здавалося б, що перше, що нам доведеться зробити, це множник нашого многочлена.
Всякий раз, коли вам представлено чотири термінові вирази, одна річ, яку ви можете спробувати - це факторинг шляхом групування. Отже, маючи на увазі цю думку, давайте перерахуємо x з перших двох членів, а потім −25 з двох других членів.
\[\begin{aligned} p(x) &=x^{3}+2 x^{2}-25 x-50 \\ &=x^{2}(x+2)-25(x+2) \end{aligned}\]
Зверніть увагу, що цей останній результат є різницею двох членів. Поліном ще не повністю врахований, оскільки він ще не є добутком двох або більше факторів. Однак зауважте, що кожен з двох термінів має загальний коефіцієнт х + 2. Давайте розглянемо цей загальний фактор.
\[p(x)=\left(x^{2}-25\right)(x+2)\]
Ми все ще не повністю врахували наш многочлен. Перший фактор є різницею двох квадратів і може бути врахований далі.
\[p(x)=(x+5)(x-5)(x+2)\]
Поліном p тепер повністю враховується. Щоб знайти нулі многочлена p, нам потрібно вирішити рівняння\[p(x)=0\]
Однак p (x) = (x + 5) (x − 5) (x + 2), тому еквівалентно нам потрібно розв'язати рівняння\[(x+5)(x-5)(x+2)=0\]
Ми можемо використовувати властивість нульового продукту. Або\[x+5=0 \quad \text { or } \quad x-5=0 \quad \text { or } \quad x+2=0\]
Знову ж таки, кожне з цих лінійних (першого ступеня) рівнянь може бути вирішено самостійно. Або\[x=-5 \quad \text { or } \quad x=5 \quad \text { or } \quad x=-2\]
Таким чином, нулями многочлена p є −5, 5 та −2. Ми залишимо це нашим читачам, щоб перевірити ці результати.
Знову ж таки, дуже важливо усвідомити, що після визначення лінійних (першого ступеня) факторів слідують нулі многочлена. У цьому прикладі лінійними факторами є x + 5, x − 5 та x + 2. Відразу випливає, що нулями многочлена є −5, 5 та −2.
У наступному прикладі ми побачимо, що іноді першим кроком є врахування найбільшого спільного фактора.
Приклад\(\PageIndex{3}\)
Знайти нулі многочлена\[p(x)=x^{4}+2 x^{3}-16 x^{2}-32 x\]
Рішення
Щоб знайти нулі многочлена, нам потрібно вирішити рівняння\[p(x)=0\]
Аналогічно тому\(p(x)=x^{4}+2 x^{3}-16 x^{2}-32 x\), що нам потрібно вирішити рівняння
\[x^{4}+2 x^{3}-16 x^{2}-32 x=0\]
Зауважте, що кожен термін на лівій стороні має загальний коефіцієнт х, таким чином, наш перший крок полягає в тому, щоб врахувати цей загальний коефіцієнт х.
\[x\left[x^{3}+2 x^{2}-16 x-32\right]=0\]
Чотирьохчленний вираз всередині дужок виглядає звично. Спробуємо факторинг шляхом групування. Фактор a\(x^2\) з перших двох членів, потім −16 з третього та четвертого членів.
\[x\left[x^{2}(x+2)-16(x+2)\right]=0\]
Тепер у нас є загальний коефіцієнт х + 2, тому ми враховуємо його.
\[x\left[\left(x^{2}-16\right)(x+2)\right]=0\]
Дужки більше не потрібні (множення асоціативне), тому ми залишаємо їх вимкненими, а потім використовуємо різницю квадратів шаблону для фактора\(x^2 − 16\).
\[x(x+4)(x-4)(x+2)=0\]
Властивість нульового продукту говорить нам, що або
\[x=0 \quad \text { or } \quad \text { or } \quad x+4=0 \quad \text { or } \quad x-4=0 \quad \text { or } \quad \text { or } \quad x+2=0\]
Кожен з цих лінійних (першого ступеня) факторів можна вирішити самостійно. Або
\[x=0 \quad \text { or } \quad x=-4 \quad \text { or } \quad x=4 \quad \text { or } \quad x=-2\]
Таким чином, нулями многочлена p є 0, −4, 4 та −2. Ми залишимо це нашим читачам, щоб перевірити ці результати.
Знову ж таки, дуже важливо зазначити, що як тільки ви визначили лінійні (першого ступеня) множники полінома, то ви знаєте нулі. У цьому випадку лінійними факторами є x, x + 4, x − 4 та x + 2. Отже, нулі дорівнюють 0, −4, 4 та −2 відповідно. Це обговорення призводить до результату, який називається теоремою фактора.
Теорема про коефіцієнт
\(p(x)=a_{0}+a_{1} x+a_{2} x^{2}+\ldots+a_{n} x^{n}\)Дозволяти поліном з дійсними коефіцієнтами. Якщо x − a є множником многочлена p (x), то a — нуль многочлена. Тобто, якщо x − a є множником многочлена p (x), то p (a) = 0.
Підсумок всіх цих зауважень полягає в тому, що, якщо ви знаєте лінійні множники многочлена, то ви знаєте нулі. Зворотне також вірно, але нам це не знадобиться в цьому курсі.
Розглянемо зв'язок між нулями многочлена і x-перехопленнями графа многочлена.
X-перехоплення та нулі полінома
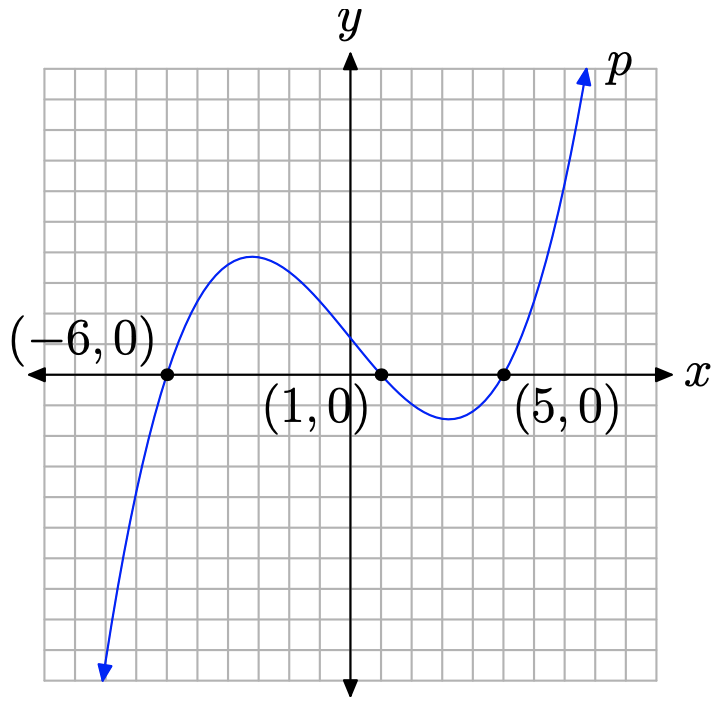
Для обговорення, яке слід, припустимо, що незалежна змінна є x, а залежна змінна - y, Відповідно до цих призначень, ми також припустимо, що ми позначили горизонтальну вісь x і вертикальну вісь з y, як показано на малюнку\(\PageIndex{1}\).
Ключовим фактом для залишку цього розділу є те, що функція дорівнює нулю в точках, де її графік перетинає вісь x. Фрази «значення функції» та «y-значення» еквівалентні (за умови, що ваша залежна змінна y), тому, коли вас запитують, де значення вашої функції дорівнює нулю, вас насправді запитують «де ваше значення y дорівнює нулю?» Звичайно, y = 0, де графік функції перетинає горизонтальну вісь (знову ж таки, якщо ви використовуєте букву y для вашої залежної змінної - маркування вертикальної осі y).
Многочлен - це функція, тому, як і будь-яка функція, многочлен дорівнює нулю там, де його графік перетинає горизонтальну вісь. Як видно на малюнку\(\PageIndex{1}\), графік многочлена перетинає горизонтальну вісь при x = −6, x = 1, а x = 5. Зверніть увагу, що при кожному з цих перехоплень значення y (значення функції) дорівнює нулю. Нулями многочлена є −6, 1 і 5. Тому x-перехоплення графа многочлена розташовані за адресою (−6, 0), (1, 0) та (5, 0).
Давайте використаємо ці ідеї для побудови графіків декількох поліномів.
Приклад\(\PageIndex{4}\)
Намалюйте графік многочлена у прикладі\(\PageIndex{2}\).
Рішення
У прикладі многочлен\(\PageIndex{2}\),\(p(x)=x^{3}+2 x^{2}-25 x-50\) врахований на лінійні множники\[p(x)=(x+5)(x-5)(x+2)\]
Отже, нулі многочлена становили −5, 5 та −2. Таким чином, x-перехоплення графа многочлена розташовані за адресою (−5, 0), (5, 0) та (−2, 0).
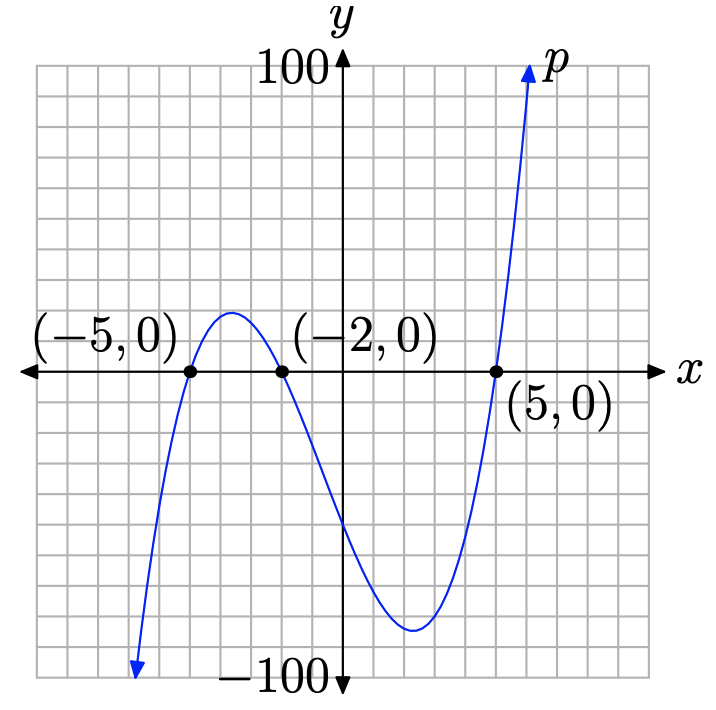
Многочлен\(p(x)=x^{3}+2 x^{2}-25 x-50\) має провідний термін\(x^3\). Отже, коли ми розгойдуємо очима зліва направо, графік многочлена p повинен піднятися з негативної нескінченності, погойдуватися через його х-перехоплення, потім продовжувати підніматися до позитивної нескінченності. У нас немає іншого вибору, як намалювати графік, подібний до того, що на малюнку\(\PageIndex{2}\).
Зверніть увагу, що на малюнку є дві «поворотні точки» многочлена\(\PageIndex{2}\). Ви можете запитати, як ми знали, де поставити ці «поворотні точки» многочлена. Відповідь: «ми не знали, куди їх покласти». Ми знаємо, що вони повинні бути там, але ми не знаємо їх точного місцезнаходження. Ось чому ми не масштабували вертикальну вісь, тому що без допомоги калькулятора важко визначити точне розташування поворотних точок, показаних на малюнку\(\PageIndex{2}\).
Однак зауважте, що знання кінцевої поведінки і нулів полінома дозволяє побудувати розумне факсиміле фактичного графа. Якщо ми хочемо більше точності, ніж забезпечує грубе наближення, наприклад, точність, відображена на малюнку\(\PageIndex{2}\), нам доведеться використовувати наш графічний калькулятор, як показано на малюнку\(\PageIndex{3}\).
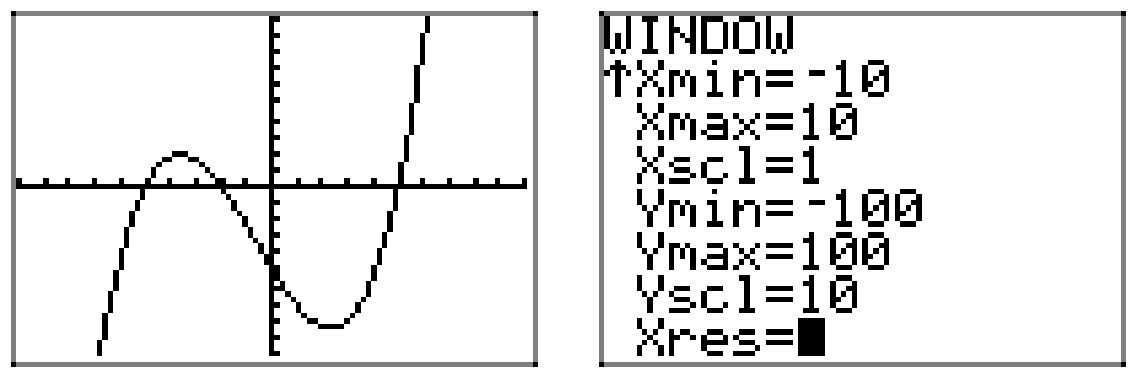
Ми будемо більше сказати про «поворотні точки» (відносні екстреми) в наступному розділі. Наразі давайте продовжимо зосереджуватися на кінцевій поведінці та нулі.
Давайте розглянемо інший приклад.
Приклад\(\PageIndex{5}\)
Намалюйте графік многочлена у прикладі\(\PageIndex{3}\).
Рішення
У прикладі многочлен\(\PageIndex{3}\),\(p(x)=x^{4}+2 x^{3}-16 x^{2}-32 x\) врахований у добуток лінійних факторів
\[p(x)=x(x+4)(x-4)(x+2)\]
Отже, нулями многочлена є 0, −4, 4 та −2. Таким чином, x-перехоплення графа многочлена розташовані за адресою (0, 0), (−4, 0), (4, 0) та (−2, 0).
Многочлен\(p(x)=x^{4}+2 x^{3}-16 x^{2}-32 x\) має провідний термін\(x^4\). Отже, коли ми розгойдуємо очима зліва направо, графік многочлена p повинен впасти з позитивної нескінченності, погойдуватися через його х-перехоплення, потім піднятися назад до позитивної нескінченності. У нас немає іншого вибору, як намалювати графік, подібний до того, що на малюнку\(\PageIndex{4}\).
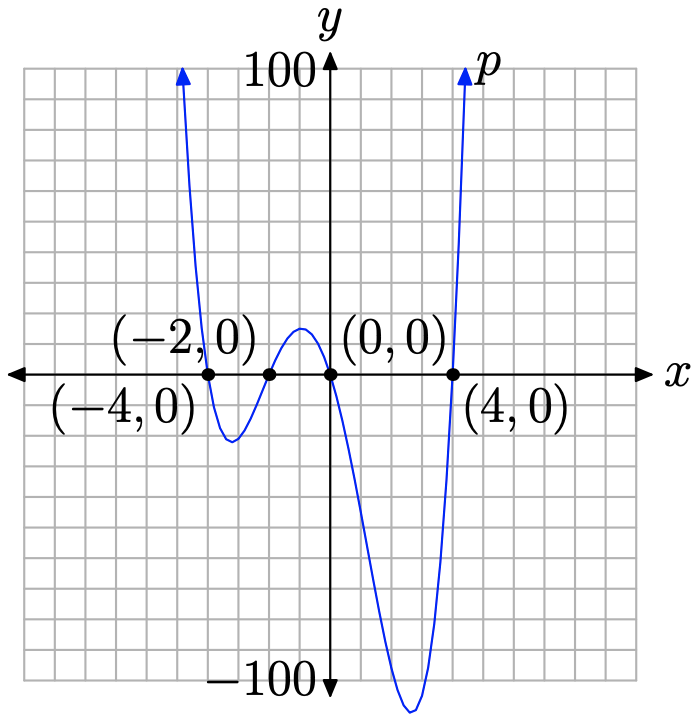
Знову ж таки, ми можемо намалювати ескіз графіка без використання калькулятора, використовуючи тільки кінцеву поведінку і нулі многочлена. Однак, якщо ми хочемо точності, зображеної на малюнку\(\PageIndex{4}\), особливо знайти правильні місця розташування «поворотних точок», нам доведеться вдатися до використання графічного калькулятора. Це показано на малюнку\(\PageIndex{5}\).
Давайте розглянемо остаточний приклад, який вимагає факторингу найбільшого загального фактора, за яким слідує ак-тест.
Приклад\(\PageIndex{6}\)
Знайти нулі многочлена\[p(x)=4 x^{3}-2 x^{2}-30 x\]
Рішення
По-перше, зверніть увагу, що кожен член цього триноміала ділиться на 2x. Це найбільший спільний дільник, або еквівалентно, найбільший спільний фактор. Ви завжди повинні враховувати найбільший загальний фактор на першому кроці.
\[\begin{aligned} p(x) &=4 x^{3}-2 x^{2}-30 x \\ &=2 x\left[2 x^{2}-x-15\right] \end{aligned}\]
Далі порівняйте триноміал\(2 x^{2}-x-15\) з\(a x^{2}+b x+c\) і зверніть увагу, що ac = −30. Пара цілих чисел {5, −6} має добуток −30 та суму −1. Перепишіть середній термін з\(2 x^{2}-x-15\) точки зору цієї пари і фактора шляхом групування.
\[\begin{aligned} p(x) &=2 x\left[2 x^{2}+5 x-6 x-15\right] \\ &=2 x[x(2 x+5)-3(2 x+5)] \\ &=2 x(x-3)(2 x+5) \end{aligned}\]
Щоб знайти нулі, нам потрібно вирішити рівняння полінома p (x) = 0, або еквівалентно,
\[2 x(x-3)(2 x+5)=0\]
Використовуючи властивість нульового добутку, або
\[2 x=0, \quad \text { or } \quad x-3=0, \quad \text { or } \quad 2 x+5=0\]
Кожен з цих лінійних факторів можна вирішити самостійно. Таким чином, або
\[x=0, \quad \text { or } \quad x=3, \quad \text { or } \quad x=-\frac{5}{2}\]
Таким чином, нулями многочлена є 0, 3 та −5/2.
Крім того, можна перерахувати 2 з третього фактора в рівнянні (12).
\[\begin{aligned} p(x) &=2 x(x-3)(2)\left(x+\frac{5}{2}\right) \\ &=4 x(x-3)\left(x+\frac{5}{2}\right) \end{aligned}\]
У такому вигляді
- x - множник, тому х = 0 дорівнює нулю,
- x − 3 є множником, тому x = 3 дорівнює нулю, а
- x + 5/2 є коефіцієнтом, тому x = −5/2 дорівнює нулю.
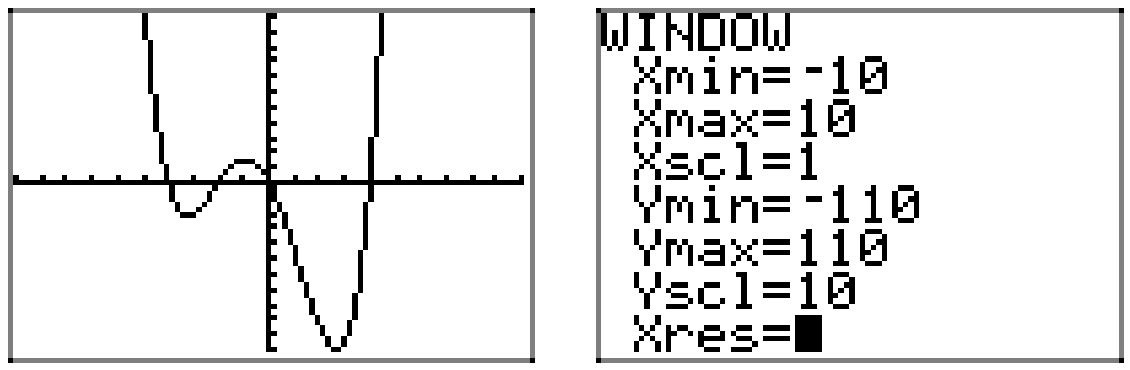
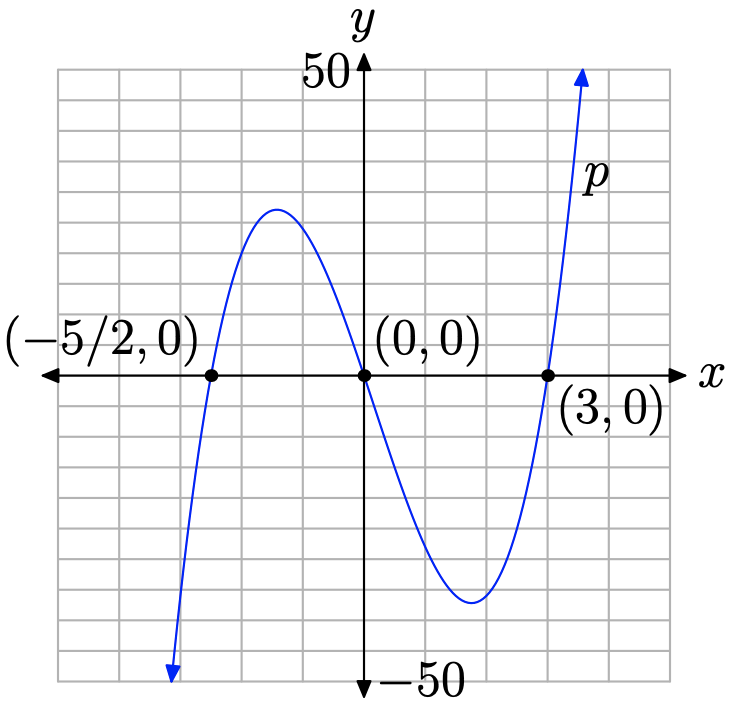
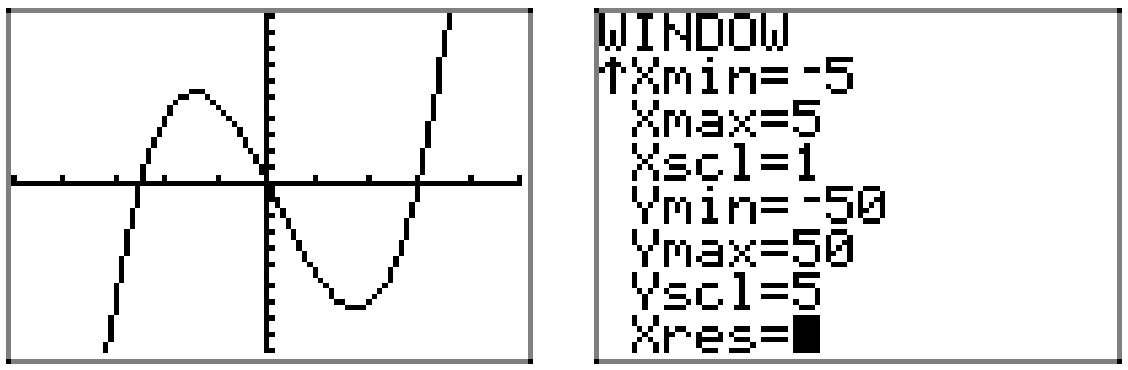
Провідний член 4\(x^{2}\), так як наші очі гойдаються зліва направо, графік многочлена повинен піднятися з негативної нескінченності, погойдуватися через його нулі, а потім піднятися до позитивної нескінченності.\(p(x)=4 x^{3}-2 x^{2}-30 x\) Тому графік повинен бути схожим на графік, показаний на малюнку\(\PageIndex{6}\).
Знову ж таки, перехоплення та кінцева поведінка забезпечують достатню кількість підказок до форми графіка, але, якщо ми хочемо точність, зображену на малюнку 6, то ми повинні покладатися на графічний калькулятор. Використовувані параметри графіка і вікна наведені на рисунку\(\PageIndex{7}\).
Вправа
У вправах 1 - 6 використовуйте пряму підстановку, щоб показати, що задане значення є нулем заданого многочлена.
Вправа\(\PageIndex{1}\)
\(p(x) = x^3−3x^2−13x+15\), x = −3
- Відповідь
-
p (−3) = (−3) 3−3 (−3) 2−13 (−3) +15 = 0
Вправа\(\PageIndex{2}\)
\(p(x) = x^3−2x^2−13x−10\), x = −2
Вправа\(\PageIndex{3}\)
\(p(x) = x^4−x^3−12x^2\), х = 4
- Відповідь
-
\(p(4) = 4^4−4^3−12(4)^2 = 0\)
Вправа\(\PageIndex{4}\)
\(p(x) = x^4−2x^3−3x^2\), x = −1
Вправа\(\PageIndex{5}\)
\(p(x) = x^4+x^2−20\), x = −2
- Відповідь
-
\(p(−2) = (−2)^4+(−2)^2−20 = 0\)
Вправа\(\PageIndex{6}\)
\(p(x) = x^4+x^3−19x^2+11x+30\), x = −1
У вправах 7 - 28 визначити всі нулі заданого полінома без допомоги калькулятора. Використовуйте алгебраїчну техніку і покажіть всю роботу (коефіцієнт, коли це необхідно), необхідну для отримання нулів.
Вправа\(\PageIndex{7}\)
р (х) = (х−2) (х+4) (х−5)
- Відповідь
-
− 4, 2 та 5
Вправа\(\PageIndex{8}\)
р (х) = (х−1) (х−3) (х+8)
Вправа\(\PageIndex{9}\)
р (х) = −2 (х−3) (х+4) (х−2)
- Відповідь
-
− 4, 2 та 3
Вправа\(\PageIndex{10}\)
p (x) = −3 (х+1) (х−1) (х−8)
Вправа\(\PageIndex{11}\)
р (х) = х (х−3) (2х+1)
- Відповідь
-
\(−\frac{1}{2}\), 0 і 3
Вправа\(\PageIndex{12}\)
р (х) = −3х (х+5) (3х−2)
Вправа\(\PageIndex{13}\)
р (х) = −2 (х+3) (3х−5) (2х+1)
- Відповідь
-
−3\(−\frac{1}{2}\), і\(\frac{5}{3}\)
Вправа\(\PageIndex{14}\)
р (х) = 3 (х−2) (2х+5) (3х−4)
Вправа\(\PageIndex{15}\)
\(p(x) = 3x^3+5x^2−12x−20\)
- Відповідь
-
−2\(−\frac{5}{3}\), і 2
Вправа\(\PageIndex{16}\)
\(p(x) = 3x^3+x^2−12x−4\)
Вправа\(\PageIndex{17}\)
\(p(x) = 2x^3+5x^2−2x−5\)
- Відповідь
-
\(−\frac{5}{2}\), −1, і 1
Вправа\(\PageIndex{18}\)
\(p(x) = 2x^3−5x^2−18x+45\)
Вправа\(\PageIndex{19}\)
\(p(x) = x^4+4x^3−9x^2−36x\)
- Відповідь
-
0, −3, 3 та −4
Вправа\(\PageIndex{20}\)
\(p(x) = −x^4+4x^3+x^2−4x\)
Вправа\(\PageIndex{21}\)
\(p(x) = −2x^4−10x^3+8x^2+40x\)
- Відповідь
-
0, −2, 2 та −5
Вправа\(\PageIndex{22}\)
\(p(x) = 3x^4+6x^3−75x^2−150x\)
Вправа\(\PageIndex{23}\)
\(p(x) = 2x^3−7x^2−15x\)
- Відповідь
-
\(−\frac{3}{2}\), 0 і 5
Вправа\(\PageIndex{24}\)
\(p(x) = 2x^3−x^2−10x\)
Вправа\(\PageIndex{25}\)
\(p(x) = −6x^3+4x^2+16x\)
- Відповідь
-
\(−\frac{4}{3}\), 0 і 2
Вправа\(\PageIndex{26}\)
\(p(x) = 9x^3+3x^2−30x\)
Вправа\(\PageIndex{27}\)
\(p(x) = −2x^7−10x^6+8x^5+40x^4\)
- Відповідь
-
0, −2, 2 та −5
Вправа\(\PageIndex{28}\)
\(p(x) = 6x^5−21x^4−45x^3\)
У вправах 29 - 34 наведено графік многочлена. Виконуйте кожне з наступних завдань
- Скопіюйте зображення на домашній папір. Позначте та масштабуйте свої осі, а потім позначте кожен x-перехоплення своїми координатами.
- Визначте нулі многочлена.
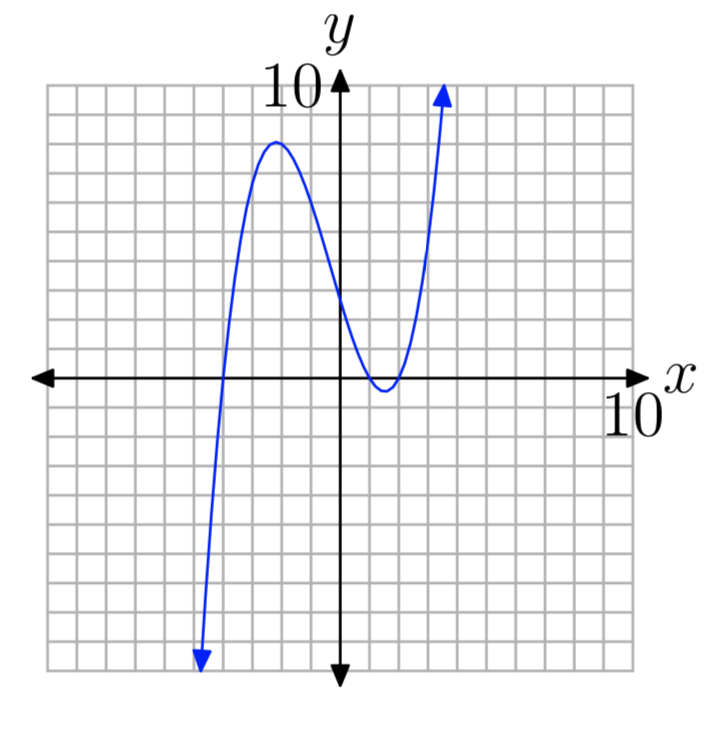
Вправа\(\PageIndex{29}\)
- Відповідь
-
Нулі: −4, 1 і 2
Вправа\(\PageIndex{30}\)
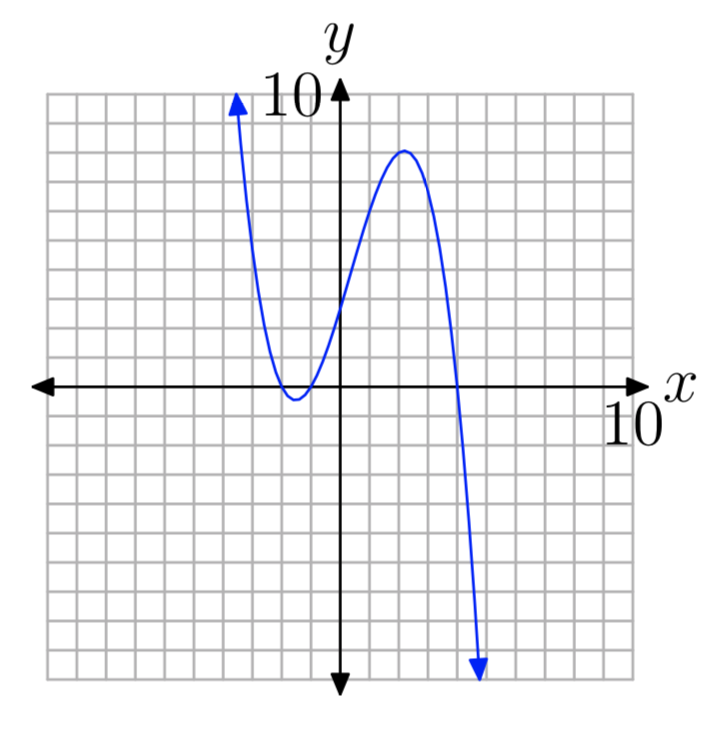
Вправа\(\PageIndex{31}\)
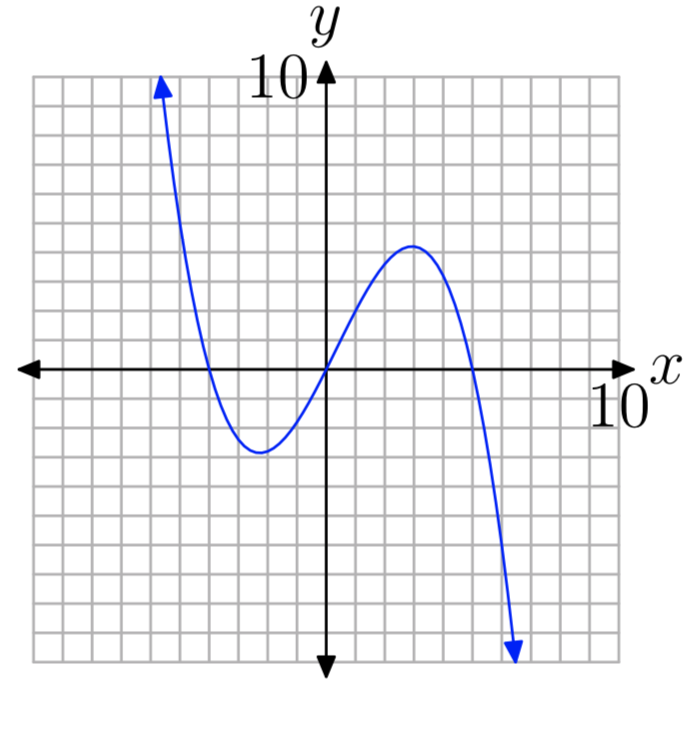
- Відповідь
-
Нулі: − 4, 0 та 5
Вправа\(\PageIndex{32}\)
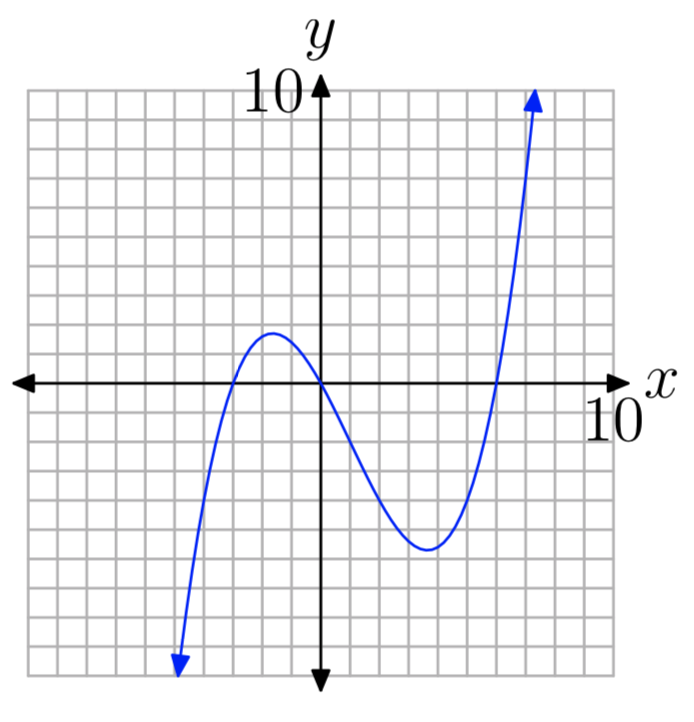
Вправа\(\PageIndex{33}\)
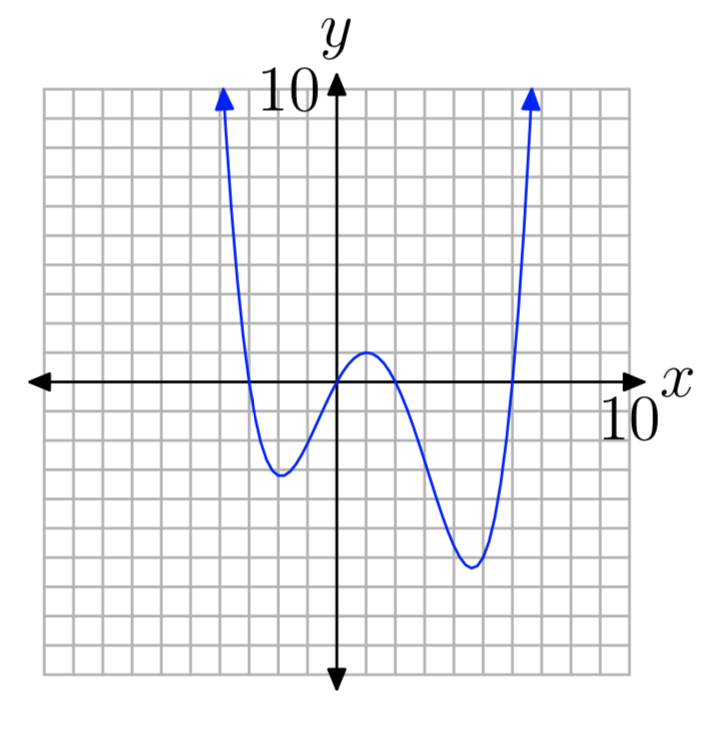
- Відповідь
-
Нулів: 0, 6, − 3, 2
Вправа\(\PageIndex{34}\)
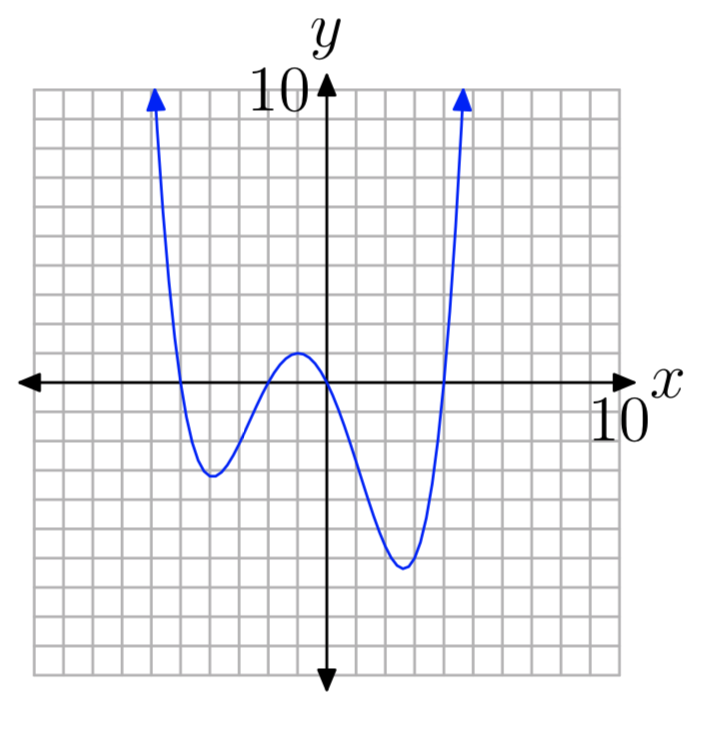
Для кожного з поліномів у Вправах 35 - 46 виконайте кожне з наступних завдань.
- Множник многочлена для отримання нулів. Покажіть свою роботу.
- Налаштуйте систему координат на графічному папері. Позначте та масштабуйте горизонтальну вісь. Використовуйте нулі та поведінку кінця, щоб допомогти намалювати графік многочлена без використання калькулятора.
- Перевірте результат за допомогою графічного калькулятора.
Вправа\(\PageIndex{35}\)
\(p(x) = 5x^3+x^2−45x−9\)
- Відповідь
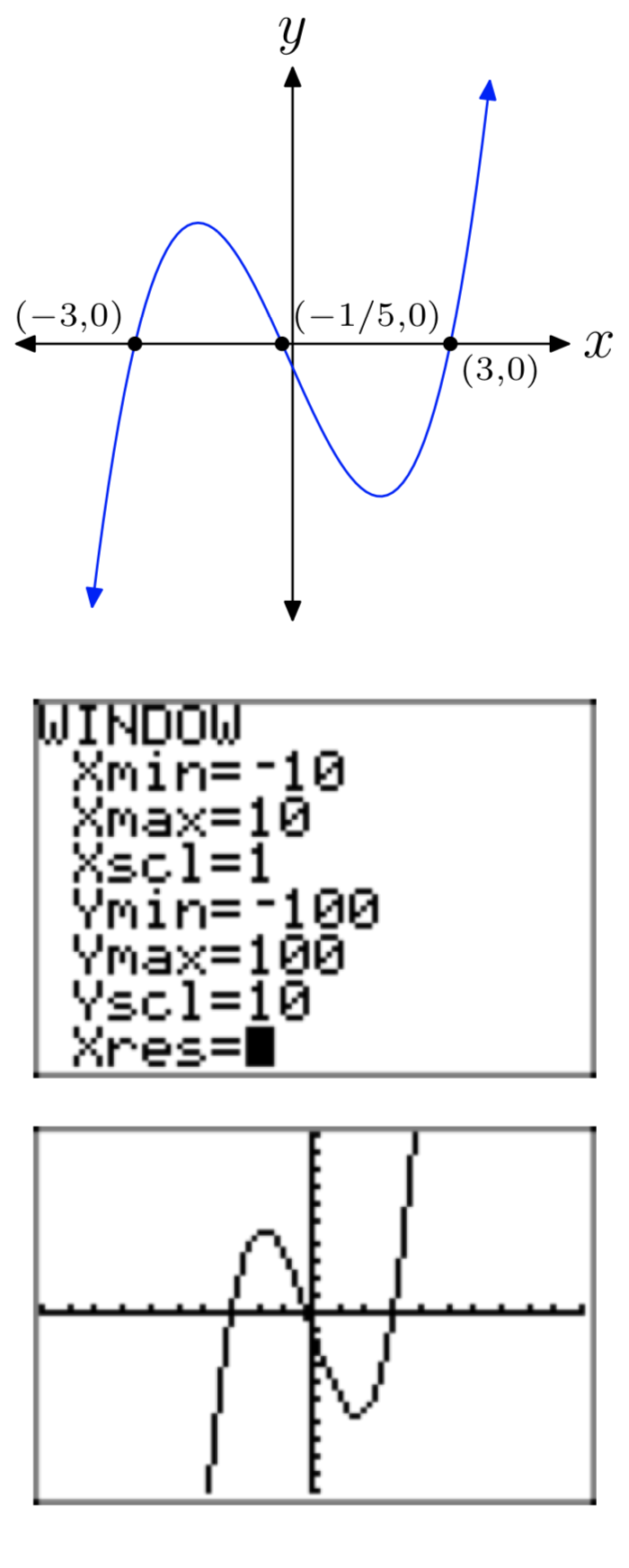
Вправа\(\PageIndex{36}\)
\(p(x) = 4x^3+3x^2−64x−48\)
Вправа\(\PageIndex{37}\)
\(p(x) = 4x^3−12x^2−9x+27\)
- Відповідь
-
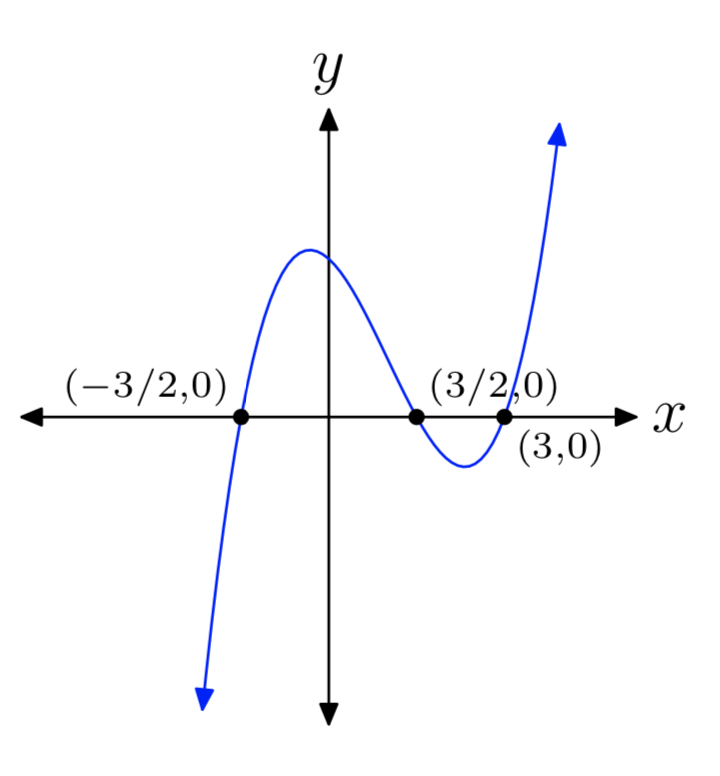
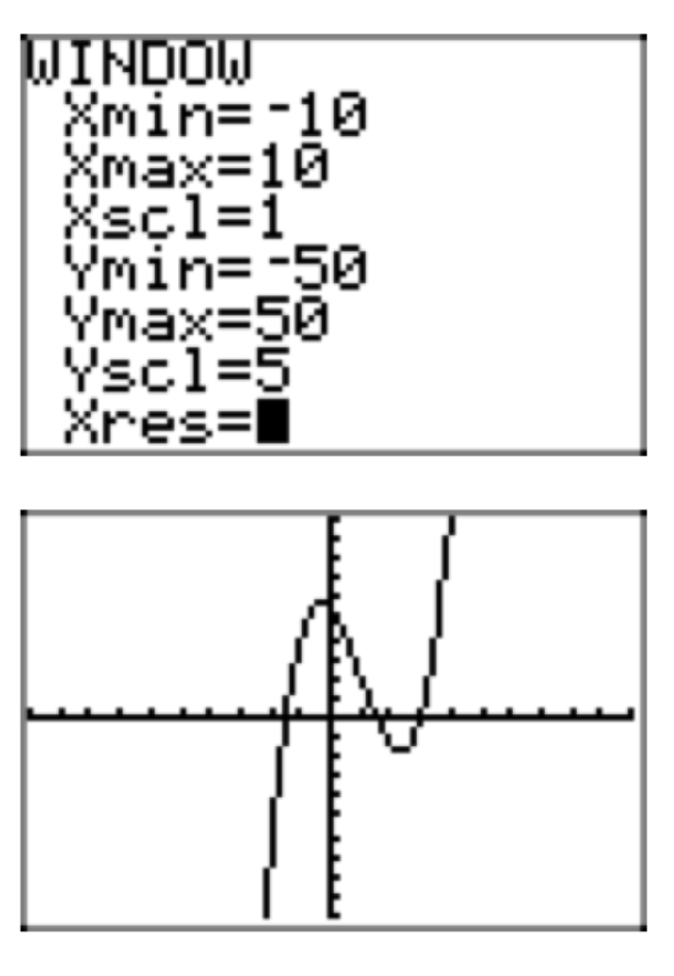
Вправа\(\PageIndex{38}\)
\(p(x) = x^3+x^2−16x−16\)
Вправа\(\PageIndex{39}\)
\(p(x) = x^4+2x^3−25x^2−50x\)
- Відповідь
-
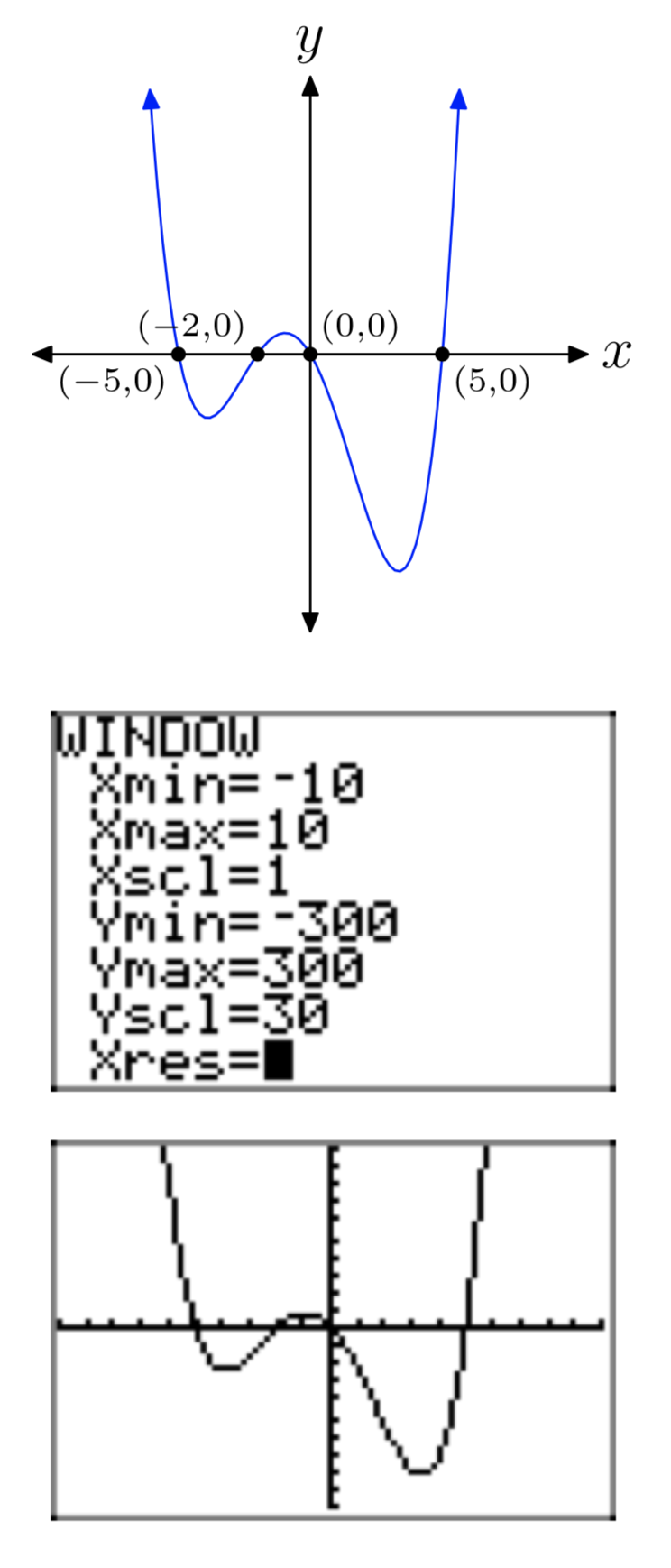
Вправа\(\PageIndex{40}\)
\(p(x) = −x^4−5x^3+4x^2+20x\)
Вправа\(\PageIndex{41}\)
\(p(x) = −3x^4−9x^3+3x^2+9x\)
- Відповідь
-
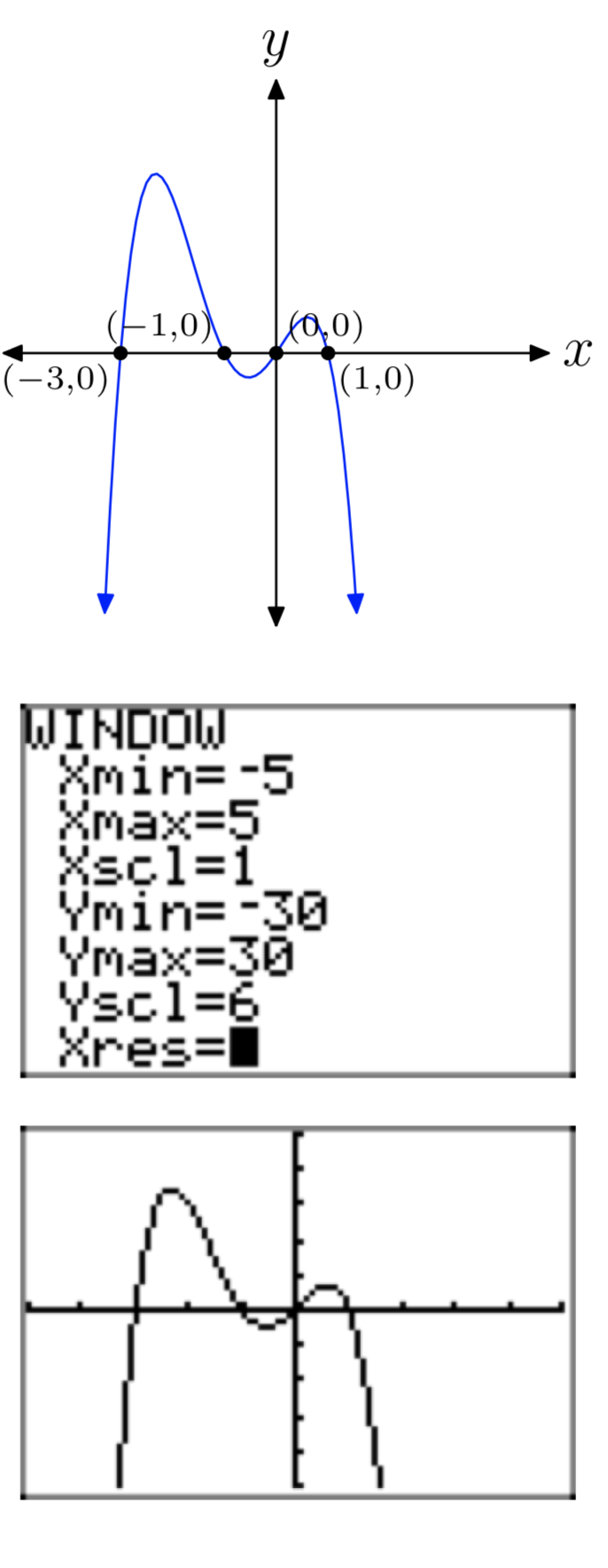
Вправа\(\PageIndex{42}\)
\(p(x) = 4x^4−29x^2+25\)
Вправа\(\PageIndex{43}\)
\(p(x) = −x^3−x^2+20x\)
- Відповідь
-
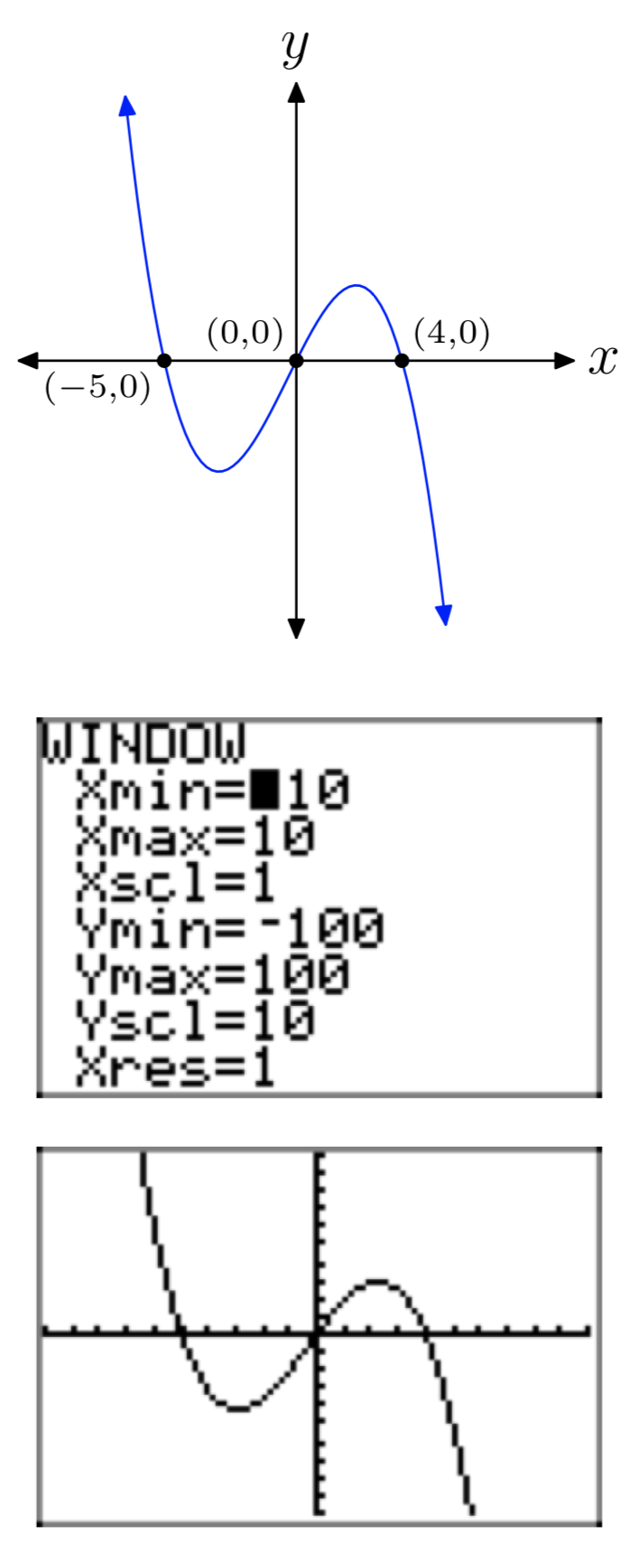
Вправа\(\PageIndex{44}\)
\(p(x) = 2x^3−7x^2−30x\)
Вправа\(\PageIndex{45}\)
\(p(x) = 2x^3+3x^2−35x\)
- Відповідь
-
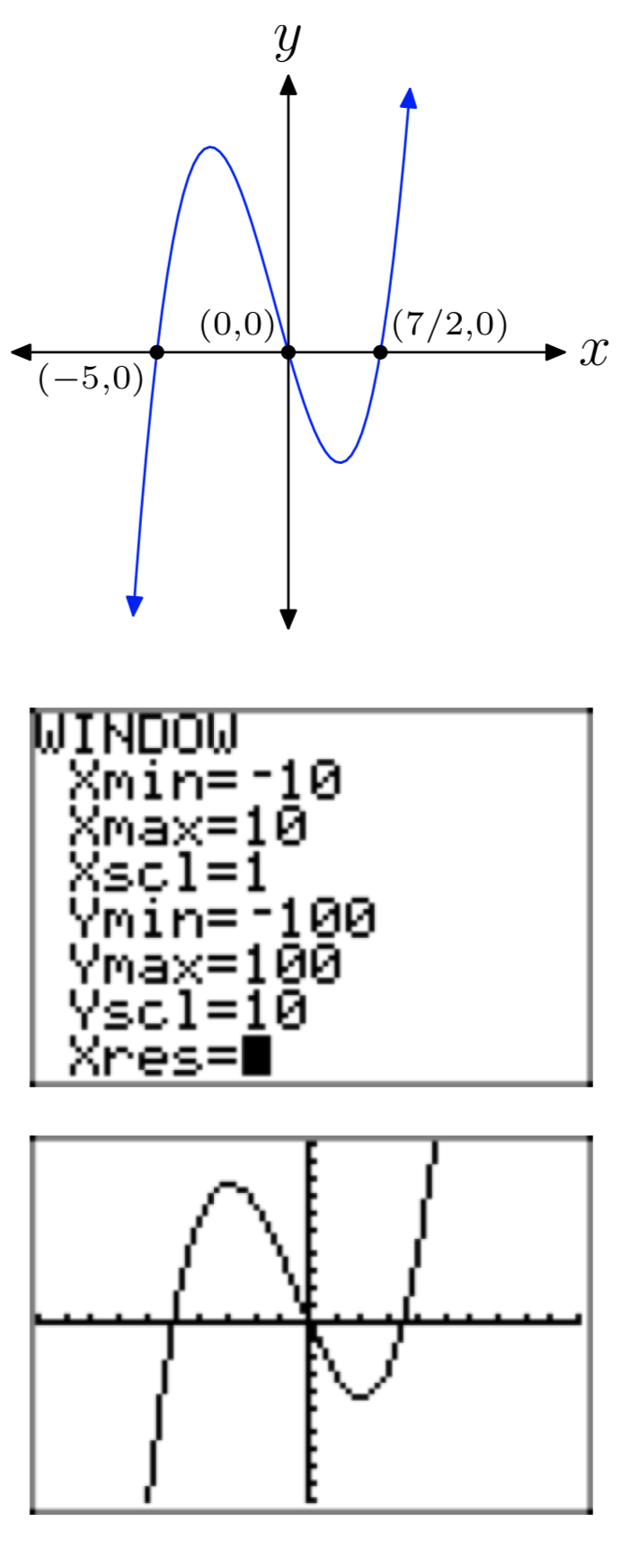
Вправа\(\PageIndex{46}\)
\(p(x) = −2x^3−11x^2+21x\)
