Skip to main content
LibreTexts - Ukrayinska

4.3: Графік з перехопленнями

  1. Last updated
  2. Save as PDF
  • Page ID
    58853

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    До кінця цього розділу ви зможете:

    • Визначте x- і y- перехоплення на графіку
    • Знайти x- і y- перехоплення з рівняння прямої
    • Графік лінії за допомогою перехоплень
    Примітка

    Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

    1. Вирішити:\(3\cdot 0+4y=−2\).
      Якщо ви пропустили цю проблему, перегляньте Вправа 2.2.13.

    Визначте x - і y - перехоплення на графіку

    Кожне лінійне рівняння може бути представлено унікальною лінією, яка показує всі розв'язки рівняння. Ми бачили, що при графіку лінії шляхом побудови точок, ви можете використовувати будь-які три рішення для графіка. Це означає, що двоє людей, які графують лінію, можуть використовувати різні набори з трьох точок.

    На перший погляд, їх дві лінії можуть здатися не однаковими, оскільки вони мали б різні точки позначені. Але якщо всі роботи були виконані правильно, лінії повинні бути абсолютно однаковими. Один із способів розпізнати, що вони справді є однією лінією, - це подивитися, де лінія перетинає вісь x та вісь y. Ці точки називаються перехопленнями лінії.

    ПЕРЕХОПЛЕННЯ ЛІНІЇ

    Точки, де пряма перетинає вісь x та вісь y -, називаються перехопленнями прямої.

    Давайте розглянемо графіки ліній на малюнку\(\PageIndex{1}\).

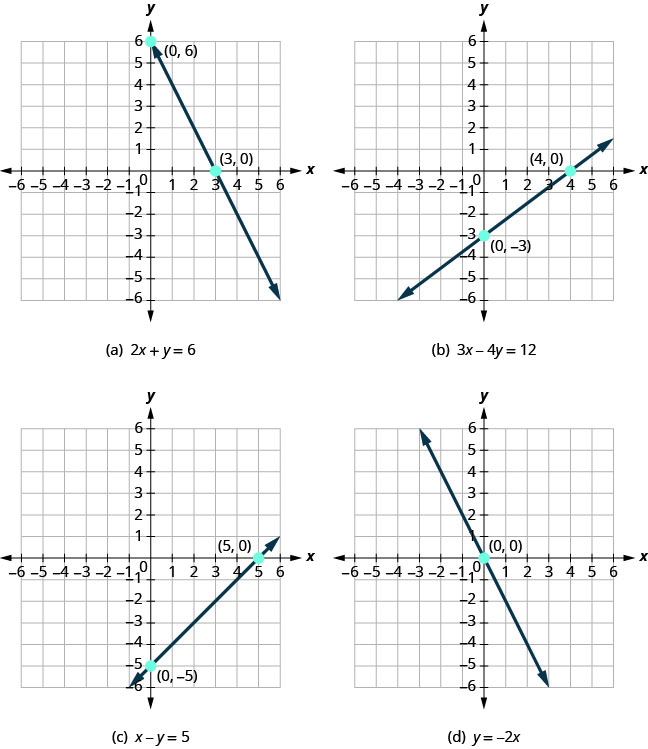
    Чотири фігури, кожна з яких показує іншу пряму лінію на координатній площині x y. Вісь х площин проходить від негативних 7 до 7. Вісь y- площин проходить від негативних 7 до 7. На малюнку a показана пряма лінія, що перетинає вісь x в точці (3, 0) і перетинає вісь y в точці (0, 6). Графік позначений рівнянням 2x плюс y дорівнює 6. На малюнку b показана пряма лінія, що перетинає вісь x в точці (4, 0) і перетинає вісь y в точці (0, негативний 3). Графік позначений рівнянням 3x мінус 4y дорівнює 12. На малюнку c показана пряма лінія, що перетинає вісь x в точці (5, 0) і перетинає вісь y в точці (0, негативний 5). Графік позначений рівнянням x мінус y дорівнює 5. На малюнку d показана пряма лінія, що перетинає вісь x і y- вісь у точці (0, 0). Графік позначений рівнянням y дорівнює від'ємним 2x.
    Малюнок\(\PageIndex{1}\): Приклади графіків, що перетинають вісь x.

    Спочатку зверніть увагу, де кожна з цих рядків перетинає негативну вісь x. Див\(\PageIndex{1}\). Малюнок.

    Таблиця\(\PageIndex{1}\)
    Малюнок Лінія перетинає вісь x за адресою: Замовлена пара цієї точки
    Малюнок (а) 3 (3,0)
    Малюнок (б) 4 (4,0)
    Малюнок (c) 5 (5,0)
    Малюнок (d) 0 (0,0)

    Ви бачите візерунок?

    Для кожного ряду y - координата точки, де пряма перетинає вісь x, дорівнює нулю. Точка, де пряма перетинає вісь x - має вигляд (a,0) і називається x - перехопленням прямої. X - перехоплення відбувається, коли y дорівнює нулю. Тепер давайте подивимося на точки, де ці лінії перетинають вісь y. Див\(\PageIndex{2}\). Таблицю.

    Таблиця\(\PageIndex{2}\)
    Малюнок Лінія перетинає вісь x за адресою: Замовлена пара цієї точки
    Малюнок (а) 6 (0,6)
    Малюнок (б) −3 (0, −3)
    Малюнок (c) −5 (0,5)
    Малюнок (d) 0 (0,0)

    Який тут візерунок?

    У кожному ряду x - координата точки, де пряма перетинає вісь y - дорівнює нулю. Точка, де пряма перетинає вісь y - має вигляд (0, b) і називається y- перехопленням прямої. Y - перехоплення відбувається, коли x дорівнює нулю.

    X- ПЕРЕХОПЛЕННЯ І Y- ПЕРЕХОПЛЕННЯ ЛІНІЇ

    Перехоплення x - це точка (a,0), де пряма перетинає вісь x.

    Перехоплення y - це точка (0, b), де пряма перетинає вісь y.

    Без тексту Alt
    Малюнок\(\PageIndex{2}\)
    Вправа\(\PageIndex{1}\)

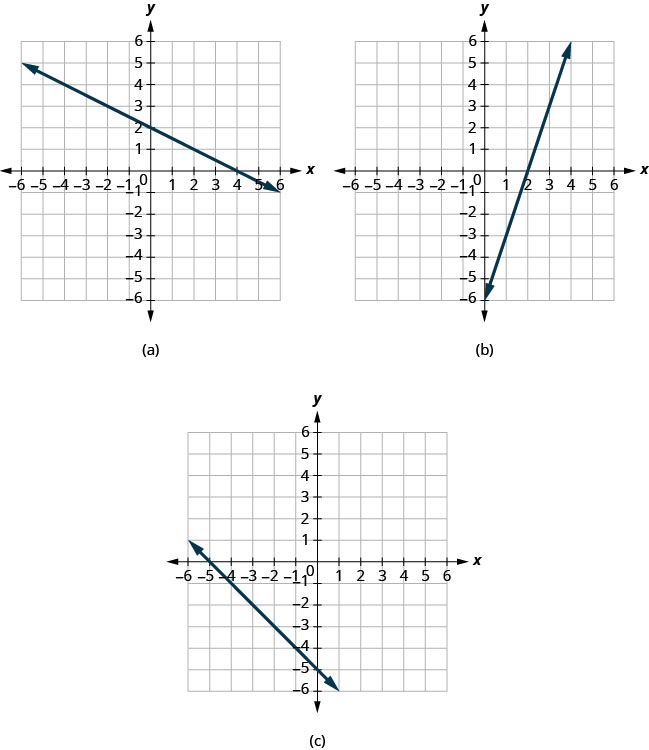
    Знайдіть x - і y - перехоплення на кожному графіку.

    Три фігури, кожна з яких показує іншу пряму лінію на координатній площині x y. Вісь х площин проходить від негативних 7 до 7. Вісь y- площин проходить від негативних 7 до 7. На малюнку а показана пряма лінія, що проходить через точки (негативні 6, 5), (негативні 4, 4), (негативні 2, 3), (0, 2), (2, 1), (4, 0) і (6, негативні 1). На малюнку b показана пряма лінія, що проходить через точки (0, негативний 6), (1, негативний 3), (2, 0), (3, 3) і (4, 6). На малюнку c показана пряма лінія, що проходить через точки (негативний 6, 1), (негативний 5, 0), (негативний 4, негативний 1), (негативний 3, негативний 2), (негативний 2, негативний 3), (негативний 1, негативний 4), (0, негативний 5) і (1, негативний 6).
    Малюнок\(\PageIndex{3}\)
    Відповідь

    (а) Графік перетинає вісь x у точці (4,0). X - перехоплення дорівнює (4,0).
    Графік перетинає вісь y - в точці (0,2). У - перехоплення дорівнює (0,2).

    (b) Графік перетинає вісь x - в точці (2,0). X - перехоплення дорівнює (2,0)
    Графік перетинає вісь y у точці (0, −6). Y - перехоплення дорівнює (0, −6).

    (c) Графік перетинає вісь x у точці (−5,0). Перехоплення x - дорівнює (−5,0).
    Графік перетинає вісь y - у точці (0, −5). Y - перехоплення дорівнює (0, −5).

    Вправа\(\PageIndex{2}\)

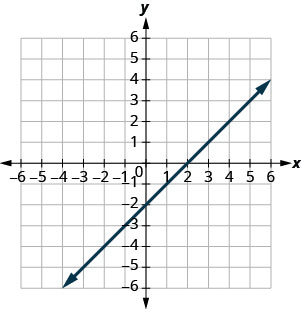
    Знайдіть x - і y - перехоплення на графіку.

    Фігура, що показує пряму лінію на координатній площині x y. Вісь х площини проходить від негативних 10 до 10. Вісь y- площин проходить від негативних 10 до 10. Пряма проходить через точки (негативний 8, негативний 10), (негативний 6, негативний 8), (негативний 4, негативний 6), (негативний 2, негативний 4), (0, негативний 2), (2, 0), (4, 2), (6, 4), (8, 6) і (10, 8).

    Відповідь

    x - перехоплення: (2,0); y - перехоплення: (0, −2)

    Вправа\(\PageIndex{3}\)

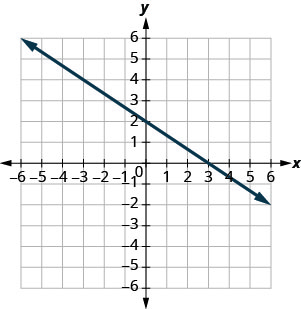
    Знайдіть x - і y - перехоплення на графіку.

    На малюнку показана пряма лінія на координатній площині x y. Вісь х площини проходить від негативних 10 до 10. Вісь y- площин проходить від негативних 10 до 10. Пряма проходить через точки (негативні 9, 8), (негативні 6, 6), (негативні 3, 4), (0, 2), (3, 0), (6, негативні 2), і (9, негативні 4).

    Відповідь

    x - перехоплення: (3,0), y - перехоплення: (0,2)

    Знайти x - і y - перехоплення з рівняння прямої

    Визнаючи, що x - перехоплення відбувається, коли y дорівнює нулю і що y - перехоплення відбувається, коли x дорівнює нулю, дає нам метод знайти перехоплення рядка з його рівняння. Щоб знайти x - перехопити, нехай y=0 і вирішити для x. Щоб знайти y - перехопити, нехай x=0 і вирішити для y.

    X- І Y - ПЕРЕХОПЛЕННЯ З РІВНЯННЯ ПРЯМОЇ

    Використовуйте рівняння прямої. Щоб знайти:

    • x - перехоплення рядка, нехай y=0 і вирішувати для x.
    • y - перехоплення рядка, нехай x=0 і вирішувати для y.
    Вправа\(\PageIndex{4}\)

    Знайдіть перехоплення 2x+y=6.

    Відповідь

    Ми дозволимо y=0 знайти x - перехоплення, і нехай x = 0, щоб знайти y - перехоплення. Ми заповнимо таблицю, яка нагадує нам про те, що нам потрібно знайти.

    На малюнку представлена таблиця з чотирма рядками і двома стовпцями. Перший рядок є рядком заголовка і він позначає таблицю рівнянням 2 х плюс y дорівнює 6. Другий рядок є рядком заголовка, і він позначає кожен стовпець. Перший заголовок стовпця - «x», а другий - «y». Третій рядок має позначення «x- intercept» і має перший стовпець порожній і 0 у другому стовпці. Четвертий рядок має позначення «y- перехоплення» і має 0 в першому стовпці з порожнім другим стовпцем.

    Щоб знайти x - перехопити, нехай y=0.

    Таблиця\(\PageIndex{3}\)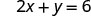
      .
    Нехай y = 0. .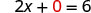
    Спростити. .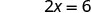
      .
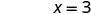
    X -перехоплення є (3, 0)
    Щоб знайти y -перехоплення, нехай x = 0.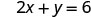  
      .
    Нехай х = 0. .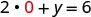
    Спростити. .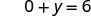
      .
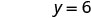
    Y -перехоплення є (0, 6)
    Перехоплення - це точки (3,0) і (0,6), як показано в табл\(\PageIndex{4}\).
    Таблиця\(\PageIndex{4}\)
    2х+р=6
    х у
    3 0
    0 6
    Вправа\(\PageIndex{5}\)

    Знайдіть перехоплення 3x+y=12.

    Відповідь

    x - перехоплення: (4,0), y - перехоплення: (0,12)

    Вправа\(\PageIndex{6}\)

    Знайдіть перехоплення x+4y=8.

    Відповідь

    x - перехоплення: (8,0), y - перехоплення: (0,2)

    Вправа\(\PageIndex{7}\)

    Знайдіть перехоплення 4x—3y=12.

    Відповідь
    Щоб знайти x -перехоплення, нехай y = 0.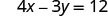  
      .
    Нехай y = 0. .
    Спростити. .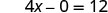
      .
      .
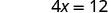
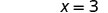
    X -перехоплення є (3, 0)
    Щоб знайти y -перехоплення, нехай x = 0.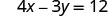  
      .
    Нехай х = 0. .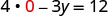
    Спростити. .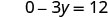
      .
      .
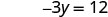
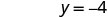
    Y -перехоплення є (0, −4)
    Таблиця\(\PageIndex{5}\)

    Перехоплення — це точки (3, 0) та (0, −4), як показано у наступній таблиці.

    Таблиця\(\PageIndex{6}\)
    4х−3р=12
    х у
    3 0
    0 −4
    Вправа\(\PageIndex{8}\)

    Знайдіть перехоплення 3x—4y=12.

    Відповідь

    x - перехоплення: (4,0), y - перехоплення: (0, −3)

    Вправа\(\PageIndex{9}\)

    Знайдіть перехоплення 2x—4y=8.

    Відповідь

    x - перехоплення: (4,0), y - перехоплення: (0, −2)

    Графік лінії за допомогою перехоплення

    Щоб скласти графік лінійного рівняння шляхом побудови точок, потрібно знайти три точки, координати яких є розв'язками рівняння. Ви можете використовувати x - і y - перехоплення як дві з трьох ваших точок. Знайдіть перехоплення, а потім знайдіть третю точку, щоб забезпечити точність. Переконайтеся, що точки вирівнюються вгору, а потім намалюйте лінію. Цей метод часто є найшвидшим способом графіка лінії.

    Вправа\(\PageIndex{10}\): How to Graph a Line Using Intercepts

    Графік —x+2y=6 за допомогою перехоплень.

    Відповідь

    На малюнку показана таблиця із загальною процедурою побудови графіка лінії за допомогою перехоплення разом із конкретним прикладом, використовуючи рівняння негативне x плюс 2y дорівнює 6. Крок 1 загальної процедури - «Знайти x і y- перехоплення рядка. Нехай у дорівнює 0 і вирішувати для х Нехай х дорівнює 0 і вирішити для y». Крок 1 для прикладу являє собою ряд тверджень і рівнянь: «Знайти х- перехоплення. Нехай у дорівнює 0», негативний х плюс 2y дорівнює 6, негативний х плюс 2 (0) дорівнює 6 (де 0 червоний), негативний х дорівнює 6, х дорівнює негативному 6, «х- перехоплення є (негативний 6, 0)», «Знайти y- перехоплення. Нехай х дорівнює 0», негативний х плюс 2y дорівнює 6, негативний 0 плюс 2y дорівнює 6 (де 0 червоний), 2y дорівнює 6, у дорівнює 3, і «Y- перехоплення є (0, 3)».Крок 2 загальної процедури - «Знайдіть інше рішення рівняння». Крок 2 для прикладу являє собою ряд тверджень і рівнянь: «Ми будемо використовувати х дорівнює 2», «Нехай х дорівнює 2», негативний х плюс 2y дорівнює 6, негативний 2 плюс 2y дорівнює 6 (де перший 2 червоний), 2y дорівнює 8, y дорівнює 4, і «Третя точка (2, 4)». Крок 3 загальної процедури - «Складіть три пункти. 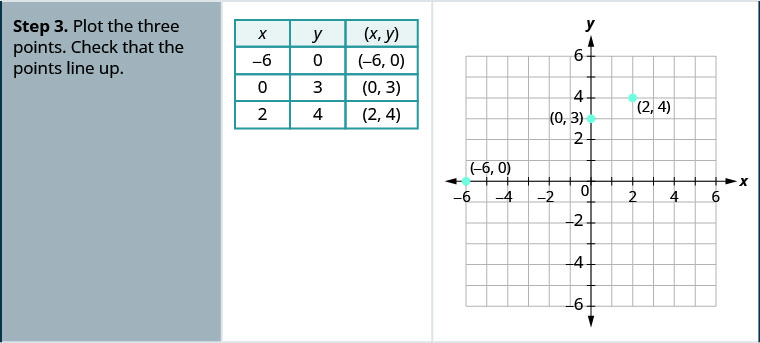Переконайтеся, що точки вирівнюються».Крок 3 для прикладу - таблиця і графік. Таблиця складається з чотирьох рядків і трьох стовпців. Перший рядок є рядком заголовка, і він позначає кожен стовпець. Перший заголовок стовпця - «x», другий - «y», а третій - «(x, y)». Під першим стовпцем знаходяться числа від'ємні 6, 0 і 2. Під другим стовпцем знаходяться цифри 0, 3 і 4. Під третім стовпцем знаходяться впорядковані пари (від'ємні 6, 0), (0, 3) та (2, 4). Графік має три точки на координатній площині x- y. Вісь х площини проходить від від'ємного 7 до 7. Вісь y- площин проходить від негативних 7 до 7. 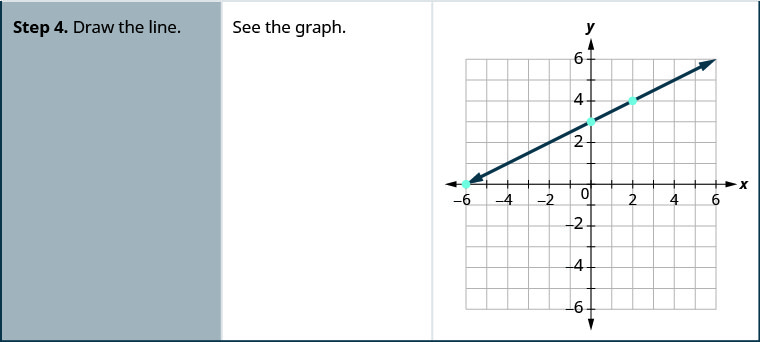Три точки відзначені в (негативні 6, 0), (0, 3), і (2, 4).Крок 4 загальної процедури - «Намалюйте лінію». Для конкретного прикладу є твердження «Див графік» і графік прямої, що проходить через три точки на координатній площині x y. Вісь х площини проходить від від'ємного 7 до 7. Вісь y- площин проходить від негативних 7 до 7. Три точки відзначені в (негативні 6, 0), (0, 3), і (2, 4). Пряма лінія проводиться через точки (негативні 6, 0), (негативні 4, 1), (негативні 2, 2), (0, 3), (2, 4), (4, 5), і (6, 6).

    Вправа\(\PageIndex{11}\)

    Графік x—2y=4 за допомогою перехоплень.

    Відповідь

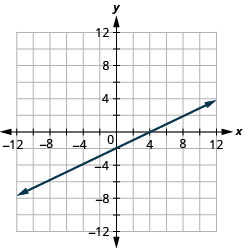
    На малюнку показана пряма лінія на координатній площині x y. Вісь х площини проходить від негативних 12 до 12. Вісь y- площин проходить від негативних 12 до 12. Пряма проходить через точки (негативний 10, негативний 7), (негативний 8, негативний 6), (негативний 6, негативний 5), (негативний 4, негативний 4), (негативний 2, негативний 3), (0, негативний 2), (2, негативний 1), (4, 0), (6, 1), (8, 2) і (10, 3).

    Вправа\(\PageIndex{12}\)

    Графік —x+3y=6 за допомогою перехоплень.

    Відповідь

    На малюнку показана пряма лінія на координатній площині x y. Вісь х площини проходить від негативних 12 до 12. Вісь y- площин проходить від негативних 12 до 12. Пряма проходить через точки (негативний 12, негативний 2), (негативний 9, негативний 1), (негативний 6, 0), (негативний 3, 1), (0, 2), (3, 3), (6, 4), (9, 5), і (12, 6).

    Кроки для побудови графіка лінійного рівняння за допомогою перехоплень підсумовуються нижче.

    ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ВИКОРИСТАННЯМ ПЕРЕХОПЛЕНЬ.
    1. Знайдіть x - і y - перехоплення рядка.
      • Нехай y=0 і вирішити для x
      • Нехай x = 0 і вирішити для y.
    2. Знайдіть третій розв'язок рівняння.
    3. Побудуйте три точки і перевірте, щоб вони вишикувалися.
    4. Намалюйте лінію.
    Вправа\(\PageIndex{13}\)

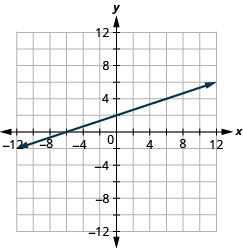
    Графік 4x—3y=12 з використанням перехоплень.

    Відповідь

    Знайдіть перехоплення і третю точку.

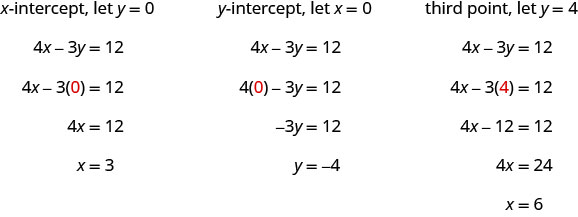
    На малюнку показаний ряд тверджень і рівнянь: «Знайдіть х- перехоплення. Нехай у дорівнює 0», 4x мінус 3y дорівнює 12, 4x мінус 3 (0) дорівнює 12 (де 0 червоний), 4x дорівнює 12, х дорівнює 3, «Знайти у- перехоплення. Нехай х дорівнює 0», 4x мінус 3y дорівнює 12, 4 (0) мінус 3y дорівнює 12 (де 0 червоний), негативний 3y дорівнює 12, у дорівнює негативний 4, «третя точка, нехай у дорівнює 4», 4x мінус 3y дорівнює 12, 4x мінус 3 (4) дорівнює 12 (де другий 4 червоний), 4x 12 мінус дорівнює 12, 4х дорівнює 24, а х дорівнює 6.

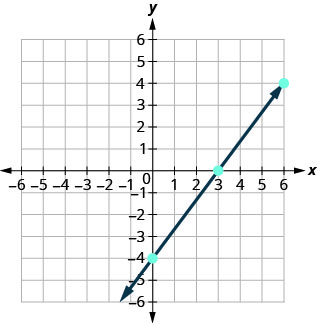
    Перерахуємо пункти в таблиці\(\PageIndex{7}\) і покажемо графік нижче.

    4х−3р=12
    х у (х, у)
    3 0 (3,0)
    0 −4 (0, −4)
    6 4 (6,4)
    Таблиця\(\PageIndex{7}\)

    На малюнку показаний графік прямої лінії, що проходить через три точки на координатній площині x y. Вісь х площини проходить від від'ємного 7 до 7. Вісь y- площин проходить від негативних 7 до 7. Три точки відзначені в (0, негативні 4), (3, 0), і (6, 4). Пряма лінія проводиться через точки (0, від'ємний 4), (3, 0), і (6, 4).

    Вправа\(\PageIndex{14}\)

    Графік 5x—2y=10 з використанням перехоплень.

    Відповідь

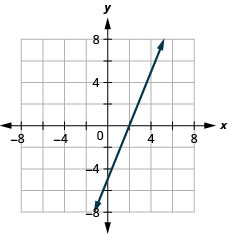
    На малюнку показаний графік прямої на координатній площині x y. Вісь х площини проходить від від'ємного 7 до 7. Вісь y- площин проходить від негативних 7 до 7. Пряма проходить через точки (0, від'ємний 5), (2, 0), і (4, 5).

    Вправа\(\PageIndex{15}\)

    Графік 3x—4y=12 з використанням перехоплень.

    Відповідь

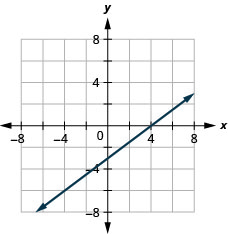
    На малюнку показаний графік прямої на координатній площині x y. Вісь х площини проходить від від'ємного 7 до 7. Вісь y- площин проходить від негативних 7 до 7. Пряма проходить через точки (від'ємний 4, негативний 6), (0, негативний 3), і (4, 0).

    Вправа\(\PageIndex{16}\)

    Графік y=5x за допомогою перехоплення.

    Відповідь

    На малюнку показано два набори тверджень та рівнянь, щоб знайти перехоплення з рівняння. Перший набір тверджень і рівнянь «x- перехоплення», «нехай y дорівнює 0», y дорівнює 5x, 0 дорівнює 5x (де 0 червоний), 0 дорівнює x, (0, 0). Другий набір тверджень і рівнянь - «y- перехоплення», «нехай x дорівнює 0», y дорівнює 5x, y дорівнює 5 (0) (де 0 червоний), y дорівнює 0, (0, 0).

    Ця лінія має тільки один перехоплення. Це точка (0,0).

    Для забезпечення точності нам потрібно побудувати три точки. Оскільки перехоплення x - і y - це одна і та ж точка, нам потрібно ще дві точки для графіка лінії.

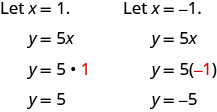
    На малюнку показано два набори тверджень та рівнянь, щоб знайти дві точки з рівняння. Перший набір тверджень і рівнянь «Нехай х дорівнює 1», у дорівнює 5x, y дорівнює 5 (1) (де 1 червоний), у дорівнює 5. Другий набір тверджень і рівнянь - «Нехай х дорівнює негативному 1», у дорівнює 5x, y дорівнює 5 (негативний 1) (де негативний 1 червоний), y дорівнює негативному 5.

    Див\(\PageIndex{8}\). Таблицю.

    y=5x
    х у (х, у)
        (0,0)
        (1,5)
    −1 −5 (−1, −5)
    Таблиця\(\PageIndex{8}\)

    Намалюйте три точки, перевірте, щоб вони вишикувалися, і проведіть лінію.

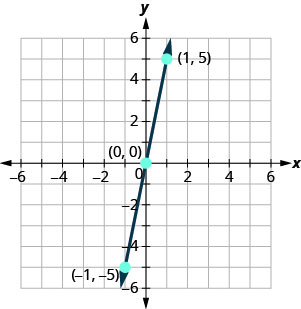
    На малюнку показаний графік прямої лінії, що проходить через три точки на координатній площині x y. Вісь х площини проходить від негативних 10 до 10. Вісь y- площин проходить від негативних 10 до 10. Три точки позначені та позначені їх координатами в (від'ємний 1, від'ємний 5), (0, 0) і (1, 5). Пряма лінія проводиться через точки (від'ємний 1, негативний 5), (0, 0), і (1, 5).

    Вправа\(\PageIndex{17}\)

    Графік y=4x за допомогою перехоплення.

    Відповідь

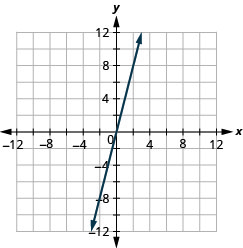
    На малюнку показана пряма лінія на координатній площині x y. Вісь х площини проходить від негативних 12 до 12. Вісь y- площин проходить від негативних 12 до 12. Пряма проходить через точки (негативний 4, негативний 12), (негативний 3, негативний 9), (негативний 2, негативний 6), (негативний 1, негативний 3), (0, 0), (1, 3), (2, 6), (3, 9) і (4, 12).

    Вправа\(\PageIndex{18}\)

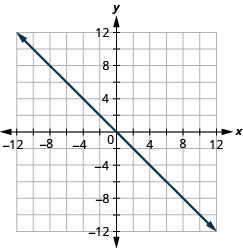
    Графік y=−x перехоплення.

    Відповідь

    На малюнку показана пряма лінія на координатній площині x y. Вісь х площини проходить від негативних 12 до 12. Вісь y- площин проходить від негативних 12 до 12. Пряма лінія проходить через точки (негативні 10, 10), (негативні 9, 9), (негативні 8, 8), (негативні 7, 7), (негативні 6, 6), (негативні 5, 5), (негативні 4, 4), (негативні 3, 3), (негативні 2, 2), (негативні 1, 1), (0, 0), (1, негативні 1), (2, негативні 1) 2), (3, негативний 3), (4, негативний 4), (5, негативний 5), (6, негативні (6), (7, негативні 7), (8, негативні 8), (9, негативні 9), і (10, негативні 10).

    Ключові концепції

    • Знайти x - і y - перехоплення з рівняння прямої
      • Використовуйте рівняння прямої, щоб знайти x - перехоплення прямої, нехай y=0 і вирішити для x.
      • Використовуйте рівняння прямої, щоб знайти y - перехоплення прямої, нехай x = 0 і вирішити для y.
    • Графік лінійного рівняння з використанням перехоплювачів
      1. Знайдіть x - і y - перехоплення рядка.
        Нехай y=0 і вирішити для x.
        Нехай x = 0 і вирішити для y.
      2. Знайдіть третій розв'язок рівняння.
      3. Побудуйте три точки, а потім перевірте, щоб вони вишикувалися.
      4. Намалюйте лінію.
    • Стратегія вибору найбільш зручного методу для побудови графіка лінії:
      • Розглянемо форму рівняння.
      • Якщо він має лише одну змінну, це вертикальна або горизонтальна лінія.
        x=a - вертикальна лінія, що проходить через вісь x - на a
        y=b - горизонтальна лінія, що проходить через вісь y в b.
      • Якщо y ізольовано на одній стороні рівняння, графуйте шляхом побудови точок.
      • Виберіть будь-які три значення для x, а потім вирішіть для відповідних y - значень.
      • Якщо рівняння має вигляд ax+by=c, знайдіть перехоплення. Знайдіть x - і y - перехоплює, а потім третю точку.

    Глосарій

    перехоплення лінії
    Точки, де пряма перетинає вісь x - і вісь y - називаються перехопленнями прямої.
    x - перехоплення
    Точка (a,0), де пряма перетинає вісь x -; x - перехоплення відбувається, коли y дорівнює нулю.
    y -перехоплення
    Точка (0, b), де пряма перетинає вісь y - осі; y - перехоплення відбувається, коли x дорівнює нулю.