Skip to main content
LibreTexts - Ukrayinska

11.5: Графік з перехопленнями (частина 1)

  1. Last updated
  2. Save as PDF
  • Page ID
    57767

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання
    • Визначте перехоплення на графіку
    • Знайти перехоплення з рівняння прямої
    • Графік лінії за допомогою перехоплень
    • Виберіть найбільш зручний метод для побудови графіка лінії
    будьте готові!

    Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

    1. Вирішити: 3x + 4y = −12 для x, коли y = 0. Якщо ви пропустили цю проблему, перегляньте приклад 9.11.6.
    2. Чи є точка (0, −5) на осі x або осі y? Якщо ви пропустили цю проблему, перегляньте приклад 11.1.5.
    3. Які впорядковані пари є розв'язками рівняння 2x − y = 6? (а) (6, 0) (б) (0, −6) (c) (4, −2). Якщо ви пропустили цю проблему, перегляньте приклад 11.2.8.

    Визначте перехоплення на графіку

    Кожне лінійне рівняння має унікальну лінію, яка представляє всі розв'язки рівняння. Під час побудови графіків лінії шляхом побудови точок, кожна людина, яка графіки лінії може вибрати будь-які три точки, тому двоє людей, що графують лінію, можуть використовувати різні набори точок.

    На перший погляд, їх дві лінії можуть виглядати різними, оскільки вони будуть мати різні точки, позначені. Але якщо всі роботи були виконані правильно, лінії будуть точно такими ж рядками. Один із способів розпізнати, що вони справді є однією лінією, - зосередитись на тому, де лінія перетинає осі. Кожна з цих точок називається перехопленням лінії.

    Визначення: Перехоплення лінії

    Кожна з точок, в якій пряма перетинає вісь x і вісь y, називається перехопленням прямої.

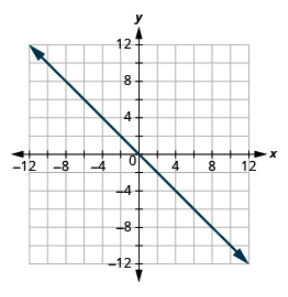
    Давайте розглянемо графік ліній, показаний на малюнку\(\PageIndex{1}\).

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Лінія проходить через дві мічені точки, «впорядкована пара 0, 6» і впорядкована пара 3, 0».

    Малюнок\(\PageIndex{1}\)

    Спочатку зверніть увагу, де кожна з цих ліній перетинає вісь x:

    Таблиця\(\PageIndex{1}\)
    Малюнок: Лінія перетинає вісь x за адресою: Впорядкована пара цієї точки
    Малюнок\(\PageIndex{1a}\) 3 (3,0)
    Малюнок\(\PageIndex{1b}\) 4 (4,0)
    Малюнок\(\PageIndex{1c}\) 5 (5,0)
    Малюнок\(\PageIndex{1d}\) 0 (0,0)

    Ви бачите візерунок?

    Для кожного рядка y-координата точки, де пряма перетинає вісь x, дорівнює нулю. Точка, де пряма перетинає вісь x, має вигляд (a, 0); і називається x-перехопленням прямої. Перехоплення x відбувається, коли y дорівнює нулю.

    Тепер давайте подивимося на точки, де ці лінії перетинають вісь y.

    Таблиця\(\PageIndex{2}\)
    Малюнок: Лінія перетинає вісь x за адресою: Впорядкована пара цієї точки
    Малюнок\(\PageIndex{1a}\) 6 (0, 6)
    Малюнок\(\PageIndex{1b}\) -3 (0, -3)
    Малюнок\(\PageIndex{1c}\) -5 (0, -5)
    Малюнок\(\PageIndex{1d}\) 0 (0, 0)
    Визначення: x-перехоплення та y-перехоплення прямої

    X-перехоплення - це точка, (a, 0), де графік перетинає вісь x.

    Перехоплення x відбувається, коли y дорівнює нулю.

    Y-перехоплення - це точка, (0, b), де графік перетинає вісь y.

    Перехоплення y відбувається, коли x дорівнює нулю.

    Приклад\(\PageIndex{1}\)

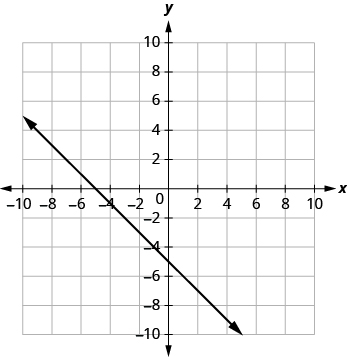
    Знайдіть x- і y-перехоплення кожного рядка:

    (а) х + 2у = 4

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Через точки «впорядкована пара 0, 2» і «впорядкована пара 4, 0» проходить лінія.

    (б) 3х - у = 6

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Лінія проходить через точки «впорядкована пара 0, -6» і «впорядкована пара 2, 0».

    (в) х + у = -5

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Лінія проходить через точки «впорядкована пара 0, -5» і «впорядкована пара -5, 0».

    Рішення

    (а)

    Графік перетинає вісь x у точці (4, 0). X-перехоплення є (4, 0).
    Графік перетинає вісь y в точці (0, 2). X-перехоплення є (0, 2).

    (б)

    Графік перетинає вісь x у точці (2, 0). X-перехоплення є (2, 0).
    Графік перетинає вісь y в точці (0, -6). X-перехоплення є (0, -6).

    (c)

    Графік перетинає вісь x у точці (-5, 0). X-перехоплення дорівнює (-5, 0).
    Графік перетинає вісь y в точці (0, -5). X-перехоплення дорівнює (0, -5).
    Вправа\(\PageIndex{1A}\)

    Знайти x- і y-перехоплення графа: x − y = 2.

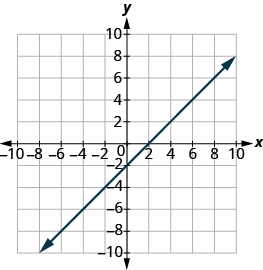
    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Через точки «впорядкована пара 0, 2» і «впорядкована пара 2, 0» проходить лінія.

    Відповідь

    x-перехоплення (2,0); y-перехоплення (0, -2)

    Вправа\(\PageIndex{1B}\)

    Знайдіть x- і y-перехоплення графіка: 2x + 3y = 6.

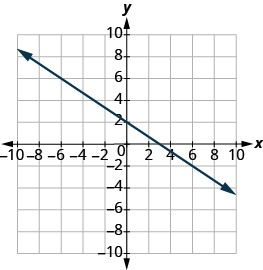
    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Через точки «впорядкована пара 0, 2» і «впорядкована пара 3, 0» проходить лінія.

    Відповідь

    x-перехоплення (3,0); y-перехоплення (0,2)

    Знайти перехоплення з рівняння прямої

    Визнаючи, що перехоплення x відбувається, коли y дорівнює нулю, і що y-перехоплення відбувається, коли х дорівнює нулю, дає нам метод знайти перехоплення лінії з її рівняння. Щоб знайти перехоплення x, дайте y = 0 і вирішіть для x, щоб знайти y-перехоплення, нехай x = 0 і вирішіть для y.

    Означення: Знайти x та y з рівняння прямої

    Використовуйте рівняння, щоб знайти:

    • x-перехоплення лінії, нехай y = 0 і вирішувати для x.
    • y-перехоплення рядка, нехай x = 0 і вирішувати для y
    Таблиця\(\PageIndex{3}\)
    х у
      0
    0  
    Приклад\(\PageIndex{2}\)

    Знайти перехоплення 2x + y = 6

    Рішення

    Ми заповнимо малюнок\(\PageIndex{2}\).

    ...

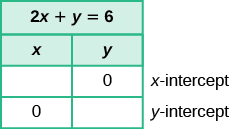
    Малюнок\(\PageIndex{2}\)

    Щоб знайти x- перехоплення, нехай y = 0:

    Замініть 0 на y. \(2x + \textcolor{red}{0} = 6\)
    Додати. 2х = 6
    Ділимо на 2. х = 3

    X-перехоплення є (3, 0).

    Щоб знайти y- перехоплення, нехай x = 0:

    Замініть 0 на x. \(2 \cdot \textcolor{red}{0} + y = 6\)
    Помножити. 0 + у = 6
    Додати. у = 6

    Y-перехоплення є (0, 6).

    2х+ у = 6
    х у
    3 0
    0 6

    Малюнок\(\PageIndex{3}\)

    Перехоплення - це точки (3, 0) і (0, 6).

    Вправа\(\PageIndex{2A}\)

    Знайдіть перехоплення: 3x + y = 12.

    Відповідь

    перехоплення x (4,0); y-перехоплення (0,12)

    Вправа\(\PageIndex{2B}\)

    Знайдіть перехоплення: x + 4y = 8.

    Відповідь

    x-перехоплення (8,0); y-перехоплення (0,2)

    Приклад\(\PageIndex{3}\)

    Знайти перехоплення 4x−3y = 12.

    Рішення

    Щоб знайти перехоплення x, нехай y = 0.

    Замініть 0 на y. 4х − 3 • 0 = 12
    Помножити. 4x − 0 = 12
    Відніміть. 4х = 12
    Розділити на 4. х = 3

    Перехоплення y дорівнює (0, −4). Перехоплення — це точки (−3, 0) та (0, −4).

    4х - 3й = 12
    х у
    3 0
    0 -4
    Вправа\(\PageIndex{3A}\)

    Знайти перехоплення рядка: 3x−4y = 12.

    Відповідь

    x-перехоплення (4,0); y-перехоплення (0, -3)

    Вправа\(\PageIndex{3B}\)

    Знайдіть перехоплення рядка: 2x−4y = 8.

    Відповідь

    x-перехоплення (4,0); y-перехоплення (0, -2)

    Графік лінії за допомогою перехоплення

    Для побудови графіка лінійного рівняння шляхом побудови точок, ви можете використовувати перехоплення як дві з трьох точок. Знайдіть два перехоплення, а потім третю точку, щоб забезпечити точність, і проведіть лінію. Цей метод часто є найшвидшим способом графіка лінії.

    Приклад\(\PageIndex{4}\)

    Графік −x + 2y = 6 за допомогою перехоплень.

    Рішення

    Спочатку знайдіть X-перехоплення. Нехай у = 0,

    \[\begin{split} -x + 2y &= 6 \\ -x + 2(0) &= 6 \\ -x &= 6 \\ x &= -6 \end{split}\]

    Перехоплення x дорівнює (—6, 0).

    Тепер знайдіть y-перехоплення. Нехай х = 0.

    \[\begin{split} -x + 2y &= 6 \\ -0 + 2y &= 6 \\ 2y &= 6 \\ y &= 3 \end{split}\]

    Y-перехоплення є (0, 3).

    Знайдіть третю точку. Ми будемо використовувати x = 2,

    \[\begin{split} -x + 2y &= 6 \\ -2 + 2y &= 6 \\ 2y &= 8 \\ y &= 4 \end{split}\]

    Третім рішенням рівняння є (2, 4).

    Підсумуйте три пункти в таблиці, а потім побудуйте їх на графіку.

    -х + 2у = 6
    х у (х, у)
    -6 0 (−6, 0)
    0 3 (0, 3)
    2 4 (2, 4)

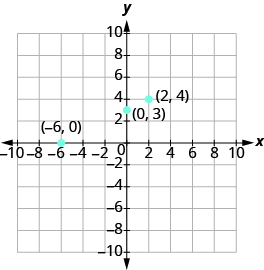
    На графіку показана координатна площина x y. По осі x і y кожна проходить від -10 до 10. Три мічені точки показані на «впорядкована пара -6, 0», «впорядкована пара 0, 3» та «впорядкована пара 2, 4».

    Чи вибудовуються точки? Так, тому проведіть лінію через точки.

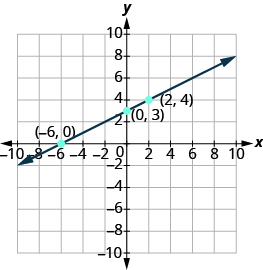
    На графіку показана координатна площина x y. По осі x і y кожна проходить від -10 до 10. Три мічені точки показані на «впорядкована пара -6, 0», «впорядкована пара 0, 3» та «впорядкована пара 2, 4». Через три позначені точки проходить лінія.

    Вправа\(\PageIndex{4A}\)

    Графік рядка за допомогою перехоплень: x−2y = 4.

    Відповідь
    На графіку показана координатна площина x y. По осі x і y кожна проходить від -12 до 12. Через точки «впорядкована пара 0, -2» і «впорядкована пара 4, 0» проходить лінія.
    Вправа\(\PageIndex{4B}\)

    Графік рядка за допомогою перехоплень: −x + 3y = 6.

    Відповідь

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -12 до 12. Через точки «впорядкована пара 0, 2» і «впорядкована пара -6, 0» проходить лінія.

    ЯК: ГРАФІК ЛІНІЇ ЗА ДОПОМОГОЮ ПЕРЕХОПЛЕНЬ

    Крок 1. Знайдіть x - і y-перехоплення рядка.

    • Нехай y = 0 і вирішити для х.
    • Нехай x = 0 і вирішити для y.

    Крок 2. Знайдіть третій розв'язок рівняння.

    Крок 3. Побудуйте три точки, а потім перевірте, щоб вони вишикувалися.

    Крок 4. Намалюйте лінію.

    Приклад\(\PageIndex{5}\)

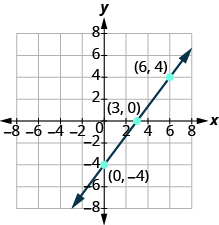
    Графік 4x−3y = 12 за допомогою перехоплень.

    Рішення

    Знайдіть перехоплення і третю точку.

    $\ почати {спліт} х перехоплення,\; &нехай\; y = 0\\ 4x - 3y &= 12\\ 4x - 3 (\ колір тексту {червоний} {0}) &= 12\\ 4x &= 12\\ x &= 3\ кінець {спліт} $$ $\ почати {спліт} y-перехоплення,\; &нехай\; x = 0\\ 4x - 3y &= 12\\ 4 (\ колір тексту {червоний} {0}) - 3y &= 12\\ 4x - 3 (\ колір тексту {червоний} {4}) &= 12\\ -3y &= 12\ y &= -4\ кінець {спліт} $ $\ почати {спліт} третя\; точка,\; &нехай\; y = 4\\ 4x - 3y &= 12\\ 4x - 12\\ 4x &= 12\\ 4x &= 24\\ x &= 6\ кінець {спліт} $$

    Перерахуємо точки і показуємо графік.

    4х - 3й = 12
    х у (х. у)
    3 0 (3, 0)
    0 -4 (0, −4)
    6 4 (6, 4)

    На графіку показана координатна площина x y. Обидві осі проходять від -7 до 7. Три немічені точки намальовані на «впорядкована пара 0, -4», «впорядкована пара 3, 0» та «впорядкована пара 6, 4». Через точки проходить лінія.

    Вправа\(\PageIndex{5A}\)

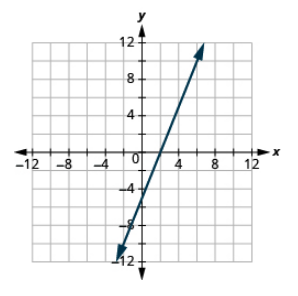
    Графік рядка за допомогою перехоплень: 5x−2y = 10.

    Відповідь

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Лінія проходить через точки «впорядкована пара 0, -5» і «впорядкована пара 2, 0».

    Вправа\(\PageIndex{5B}\)

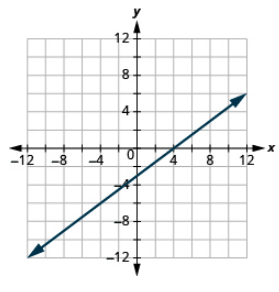
    Графік рядка за допомогою перехоплень: 3x−4y = 12.

    Відповідь

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Через точки «впорядкована пара 0, -3» і «впорядкована пара 4, 0» проходить лінія.

    Приклад\(\PageIndex{6}\)

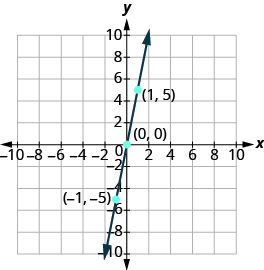
    Графік\(y = 5x\) за допомогою перехоплень.

    Рішення

    $$\ почати {спліт} х перехоплення;\; &Нехай\; y = 0\ ldotp\\ y &= 5x\\\ textcolor {червоний} {0} &= 5x\\ 0 &= x\\ x &= 0\\\ x\\\ Перехоплення\; x\; &is\; (0, 0)\ ldotp\ end {спліт} $ $\ почати {спліт} y-перехоплення;\; &Нехай\; x = 0\ ldotp\\ y &= 5x\\ y &= 5 (\ textcolor {червоний} {0})\\ y &= 0\\\ y-перехоплення\; і є\; (0, 0)\ ldotp\ end {спліт} $

    Ця лінія має тільки один перехоплення! Це точка (0, 0).

    Щоб забезпечити точність, нам потрібно намітити три точки. Оскільки перехоплення - це одна і та ж точка, нам потрібно ще дві точки для графіка лінії. Як завжди, ми можемо вибрати будь-які значення для x, тому ми дозволимо x дорівнювати 1 та −1.

    $\ почати {спліт} х &= 1\\ y &= 5x\\ y &= 5 (\ колір тексту {червоний} {1})\\ y &= 5\\ (1, &-5)\ кінець {спліт} $$ $\ почати {спліт} х &= -1\\ y &= 5x\\ y &= 5 (\ колір тексту {червоний} {-1})\\ y &= -5\\ (-1, &-5)\ кінець {спліт} $$

    Організуйте точки в таблиці.

    у = 5х
    х у (х, у)
    0 0 (0, 0)
    1 5 (1, 5)
    -1 -5 (−1, −5)

    Намалюйте три точки, перевірте, щоб вони вишикувалися, і проведіть лінію.

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -10 до 10. Лінія проходить через три мічені точки: «впорядкована пара -1, -5», «впорядкована пара 0, 0» та впорядкована пара 1, 5».

    Вправа\(\PageIndex{6A}\)

    Графік з використанням перехоплень:\(y = 3x\).

    Відповідь

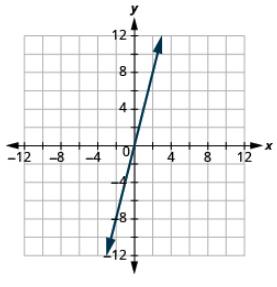
    На графіку показана координатна площина x y. По осі x і y кожна проходить від -12 до 12. Через точки «впорядкована пара 0, 0» і «впорядкована пара 1, 3» проходить лінія.

    Вправа\(\PageIndex{6B}\)

    Графік з використанням перехоплень:\(y = − x\).

    Відповідь

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -12 до 12. Через точки «впорядкована пара 0, 0» і «впорядкована пара 1, -1» проходить лінія.

    Автори та атрибуція