6.1: Функції поліномів

• Ми бачили в попередніх розділах, що мономіал - це добуток числа та одного або декількох змінних факторів, кожен з яких піднімається до позитивної інтегральної сили, як у\(-3 x^{2}\) або 4\(x^{3} y^{4}\).
• Ми також бачили, що біноміал - це сума або різниця двох мономіальних членів, як у\(3 x+5, x^{2}+4,\) або\(3 x y^{2}=2 x^{2} y\).
• Ми також бачили, що триноміал - це сума або різниця трьох мономіальних членів, як у\(x^{2}-2 x-3\) або\(x^{2}-4 x y+5 y^{2}\).

Кореневе слово «полі» означає «багато», як у багатокутник (багато сторін) або поліглот (говорячи багатьма мовами - багатомовний).

• В алгебрі слово поліном означає «багато термінів», де фраза «багато термінів» може тлумачитися як означає від одного до довільного, але кінцевого числа членів. Отже, мономіал можна вважати поліномом, як і біноми та тріноми. У нашій роботі ми зосередимося здебільшого на многочленах однієї змінної. Далі йде більш формальне визначення многочлена в одній змінній\(x\).

Визначення: Поліноми

Функція p, визначена

\[p(x)=a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} \label{1}\]

називається поліном в\(x\).

Є кілька важливих моментів, які слід зробити з приводу цього визначення.

Примітка

1. Многочлен у нашому визначенні в Equation\ ref {1} розташований у висхідних степенях\(x\). Ми могли б так само легко організувати наш многочлен в спадних степенях\(x\), як і в\[p(x)=a_{n} x^{n}+\cdots+a_{2} x^{2}+a_{1} x+a_{0}\]
2. Числа\(a_{0}, a_{1}, a_{2}, \dots, a_{n}\) називаються коефіцієнтами полінома p. − Якщо всі коефіцієнти цілі, то ми говоримо, що «\(p\)є поліномом з цілими коефіцієнтами». - Якщо всі коефіцієнти є раціональними числами, то ми говоримо, що «\(p\)є поліномом з раціональними коефіцієнтами. » - Якщо всі коефіцієнти є дійсними числами, то ми говоримо, що «\(p\)є поліном з дійсними коефіцієнтами».
3. Ступінь многочлена\(p\) є\(n\), найвища сила\(x\).
4. Провідним терміном многочлена\(p\) є термін з найвищою силою\(x\). У випадку Equation\ ref {2} провідним терміном є a\(x^n\).

Давайте розглянемо приклад.

Приклад\(\PageIndex{1}\)

Розглянемо многочлен

\[p(x)=3-4 x^{2}+5 x^{3}-6 x\nonumber\]

Знайдіть ступінь, провідний член, і зробіть заяву про коефіцієнти p, посилаючись на Примітку вище, щоб визначити цілі або раціональні коефіцієнти.

Рішення

Спочатку розставляємо поліноміальні члени по порядку. Незалежно від того, чи використовуєте ви висхідні або спадні сили x, не має різниці. Вибирайте ту чи іншу. У спадних степенях х,

\[p(x)=5 x^{3}-4 x^{2}-6 x+3 \label{5}\]

але в висхідних силах\(x\),

\[p(x)=3-6 x-4 x^{2}+5 x^{3} \label{6}\]

У будь-якому випадку, Equation\ ref {5} або Equation\ ref {6}, ступінь полінома дорівнює 3. Також в будь-якому випадку провідний член многочлена дорівнює 5\(x^{3}\). Оскільки всі коефіцієнти цього многочлена є цілими числами, ми говоримо, що «p - многочлен з цілими коефіцієнтами». Однак всі коефіцієнти також є раціональними числами, тому можна сказати, що p - поліном з раціональними коефіцієнтами. З цього приводу, всі коефіцієнти р є дійсними числами, так що ми могли б також сказати, що р є поліном з дійсними коефіцієнтами.

Давайте розглянемо інший приклад.

Приклад\(\PageIndex{2}\)

Розглянемо многочлен

\[p(x)=3-\frac{4}{3} x+\frac{2}{5} x^{2}-9 x^{3}+12 x^{4}.\]

Знайдіть ступінь, провідний термін, і зробіть заяву про коефіцієнти\(p\).

Рішення

На щастя, многочлен p вже влаштований в висхідних ступенях х Ступінь p дорівнює 4, а провідний член - 12\(x^{4}\). Не всі коефіцієнти є цілими числами, тому ми не можемо сказати, що «p - поліном з цілими коефіцієнтами». Однак всі коефіцієнти є раціональними числами, тому можна сказати, що «р - поліном з раціональними коефіцієнтами». Оскільки всі коефіцієнти р є дійсними числами, ми могли б також сказати, що «\(p\)є поліном з дійсними коефіцієнтами».

Приклад\(\PageIndex{3}\)

Розглянемо многочлен\[p(x)=3-\frac{4}{3} x+\sqrt{2} x^{2}-9 x^{3}+\pi x^{5}\]. Знайдіть ступінь, провідний член, і зробіть заяву про коефіцієнти р.

Рішення

На щастя, многочлен p вже влаштований в висхідних ступенях х Ступінь p дорівнює 5, а провідний член -\(\pi x^{5}\). Не всі коефіцієнти є цілими числами, тому ми не можемо сказати, що «p - поліном з цілими коефіцієнтами». Не всі коефіцієнти є раціональними числами, тому не можна сказати, що «p - поліном з раціональними коефіцієнтами». Однак, оскільки всі коефіцієнти p є дійсними числами, можна сказати, що «p - поліном з дійсними коефіцієнтами».

Графік\(y=x^{n}\)

Основна мета в цьому розділі полягає в обговоренні кінцевої поведінки довільних поліномів. Під «поведінкою кінця» ми маємо на увазі поведінку многочлена для дуже малих значень x (наприклад, −1 000, −10 000, −100 000 тощо) або дуже великих значень x (наприклад, 1 000, 10 000, 100 000 тощо). Перш ніж ми зможемо дослідити кінцеву поведінку довільних поліномів, ми повинні спочатку вивчити кінцеву поведінку деяких дуже основних мономів. Зокрема, нам потрібно дослідити кінцеву поведінку графів\(y=x^{n}\), де n = 1, 2, 3,...

Давайте спочатку розглянемо графік\(y=x^{n}\), коли n парне. Графіки досить прості для малювання, або створивши таблицю точок, або за допомогою графічного калькулятора. На малюнку\(\PageIndex{1}\) (a), (b) і (c) ми намалювали графіки\(y=x^{2}, y=x^{4},\) і\(y=x^{6}\), відповідно.

Малюнок\(\PageIndex{1}\). Приклади графа\(y=x^{n}\), коли n - парне ціле число.

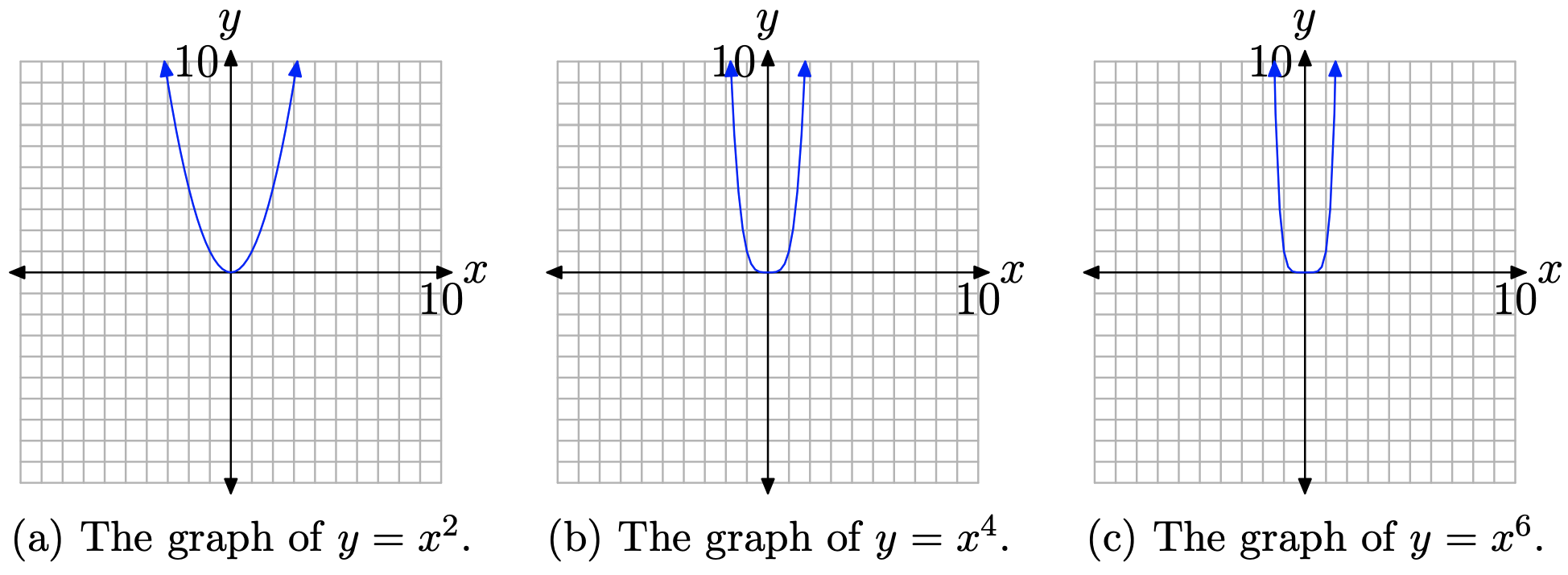
Графіки на малюнку\(\PageIndex{1}\) мають важливу рису. Коли ви змітаєте очі зліва направо, кожен графік падає з позитивної нескінченності, коливається через початок, а потім піднімається назад до позитивної нескінченності.

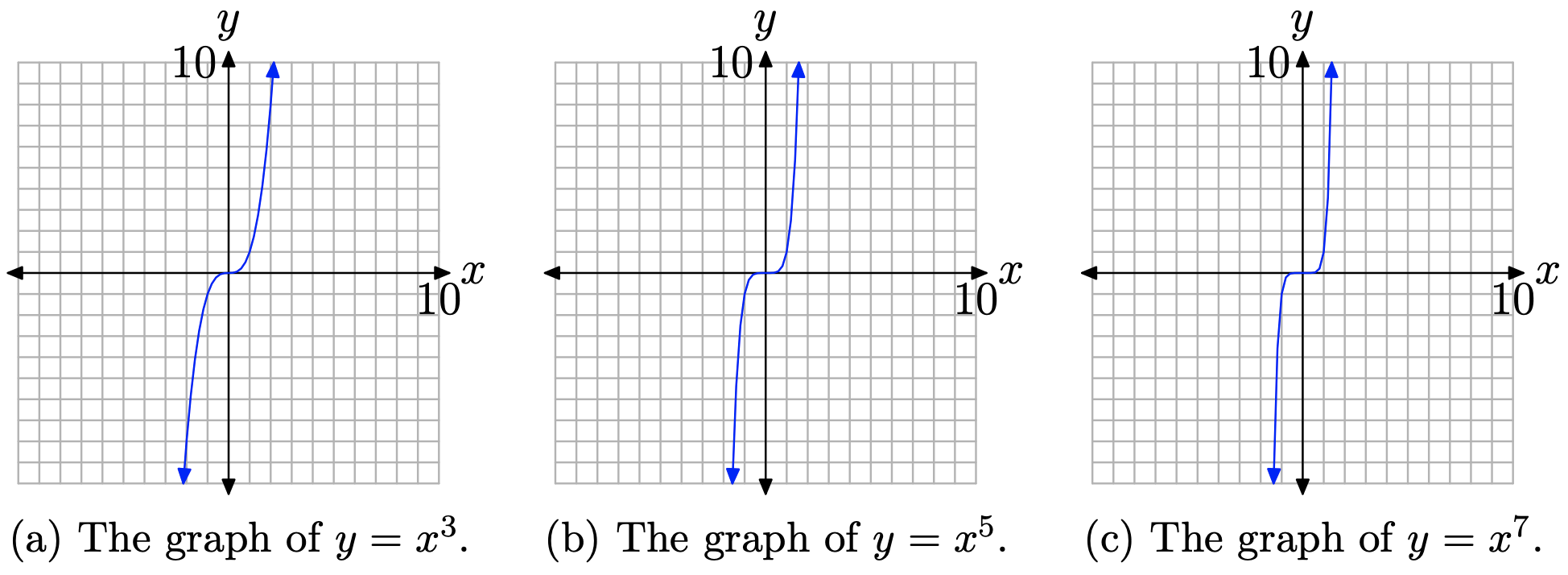
Далі розглянемо графік\(y=x^{n}\), коли n непарне. Знову ж таки, таблиця точок або графічний калькулятор допоможуть скласти графіки\(y=x^{3}, y=x^{5},\) і\(y=x^{7}\), як показано на малюнку\(\PageIndex{2}\) (а), (b) і (c) відповідно.

Графіки на малюнку\(\PageIndex{2}\) мають важливу рису. Коли ви змітаєте очі зліва направо, кожен графік піднімається з негативної нескінченності, коливається через початок, потім піднімається до позитивної нескінченності.

Поведінка, показана на малюнку\(\PageIndex{1}\) та малюнку\(\PageIndex{2}\), є типовою.

Малюнок\(\PageIndex{2}\). Приклади графа\(y=x^{n}\), коли n - непарне ціле число.

Нерухомість 9

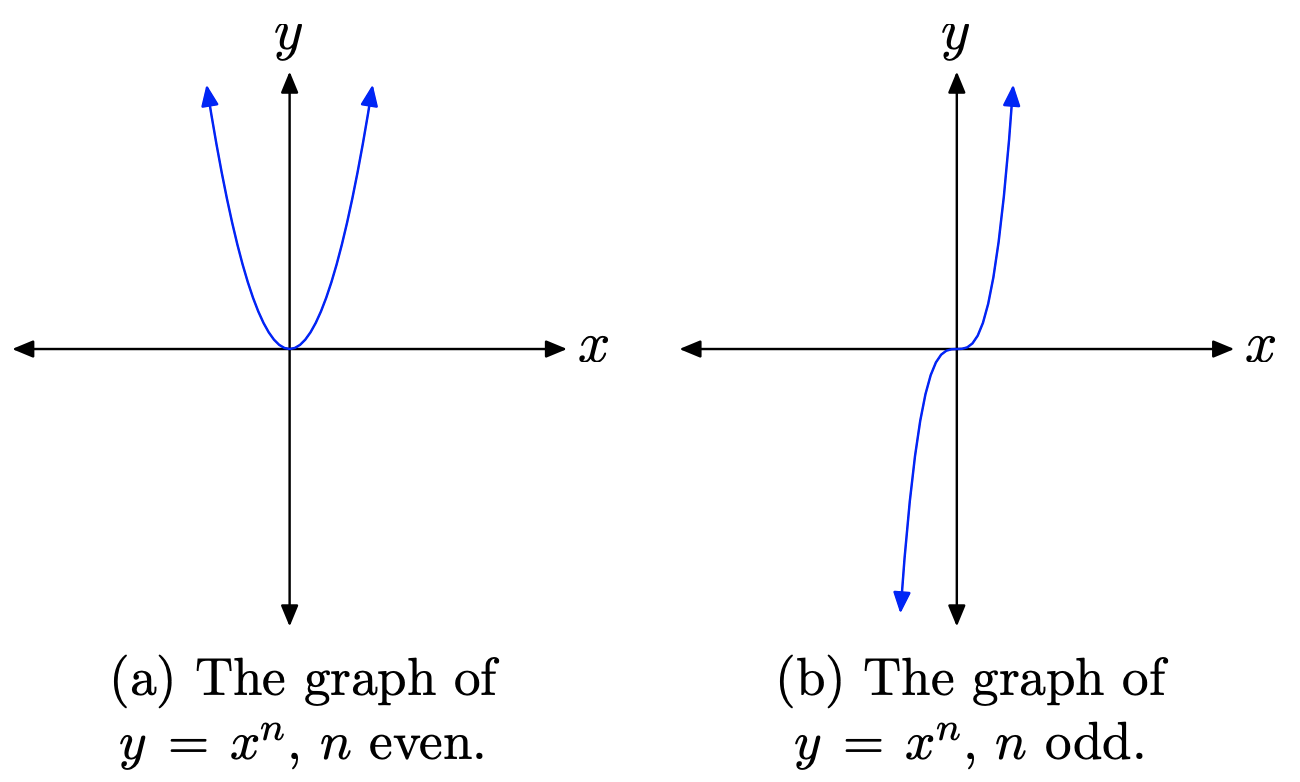
Коли n - парне натуральне число, графік\(y=x^{n}\) буде виглядати так, як показано на малюнку\(\PageIndex{3}\) (a). Якщо n - непарне натуральне число, то графік\(y=x^{n}\) буде аналогічним показаному на малюнку\(\PageIndex{3}\) (b).

1. Коли n парний, як ви змітаєте очі зліва направо, графік\(y=x^{n}\) падає з позитивної нескінченності, коливається через початок, потім піднімається назад до позитивної нескінченності.
2. Якщо n непарне, як ви змітаєте очі зліва направо, графік\(y=x^{n}\) піднімається з негативної нескінченності, коливається через початок, потім піднімається до позитивної нескінченності.

Малюнок\(\PageIndex{3}\)

Графік\(y=a x^{n}\)

Тепер, коли ми знаємо загальну форму графіка\(y=x^{n}\), давайте масштабувати цю функцію шляхом множення на константу, як в\(y=a x^{n}\).

У нашому дослідженні параболи ми дізналися, що якщо помножити на множник a, де a > 1, то розтягнемо графік у вертикальному напрямку на множник a. навпаки, якщо помножити графік на коефіцієнт a, де 0 < a < 1, то будемо стискати графік у вертикальному напрямку на коефіцієнт 1/a. якщо a < 0, то ми не тільки масштабуємо графік, але множення на цей коефіцієнт також відображатиме графік по горизонтальній осі.

Давайте розглянемо кілька прикладів.

Приклад\(\PageIndex{4}\)

Намалюйте графік\(y=-2 x^{3}\).

Рішення

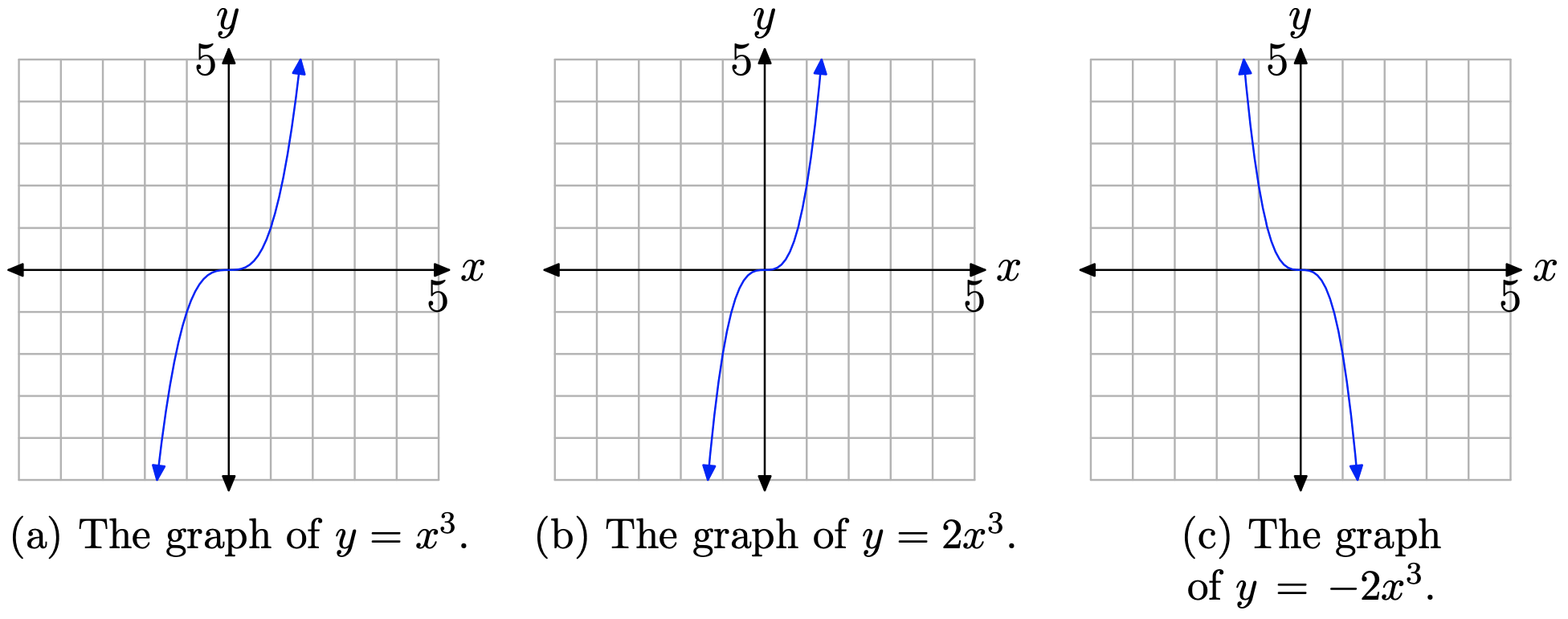
Ми знаємо, як\(y=x^{3}\) виглядає графік. Коли ми змітаємо очі зліва направо, графік піднімається з негативної нескінченності, коливається через початок, потім піднімається до позитивної нескінченності. Така поведінка показана на малюнку\(\PageIndex{4}\) (а).

Якщо помножити на коефіцієнт 2, то розтягуємо вихідний графік на коефіцієнт 2 у вертикальному напрямку. Графік\(y=2 x^{3}\) показаний на малюнку\(\PageIndex{4}\) (б). Зверніть увагу на розтягування у вертикальному напрямку.

Нарешті, якщо ми заперечуємо множенням на −2, це розтягне графік у 2 коефіцієнт, як на малюнку\(\PageIndex{4}\) (b), але він також відображатиме графік по осі x. Графік\(y=-2 x^{3}\) показаний на малюнку\(\PageIndex{4}\) (в).

Малюнок\(\PageIndex{4}\). Масштабування на −2 розтягується вертикально в 2 рази, а потім відображає графік по осі x.

Давайте розглянемо інший приклад.

Приклад\(\PageIndex{5}\)

Намалюйте графік\(y=-\frac{1}{2} x^{4}\)

Рішення

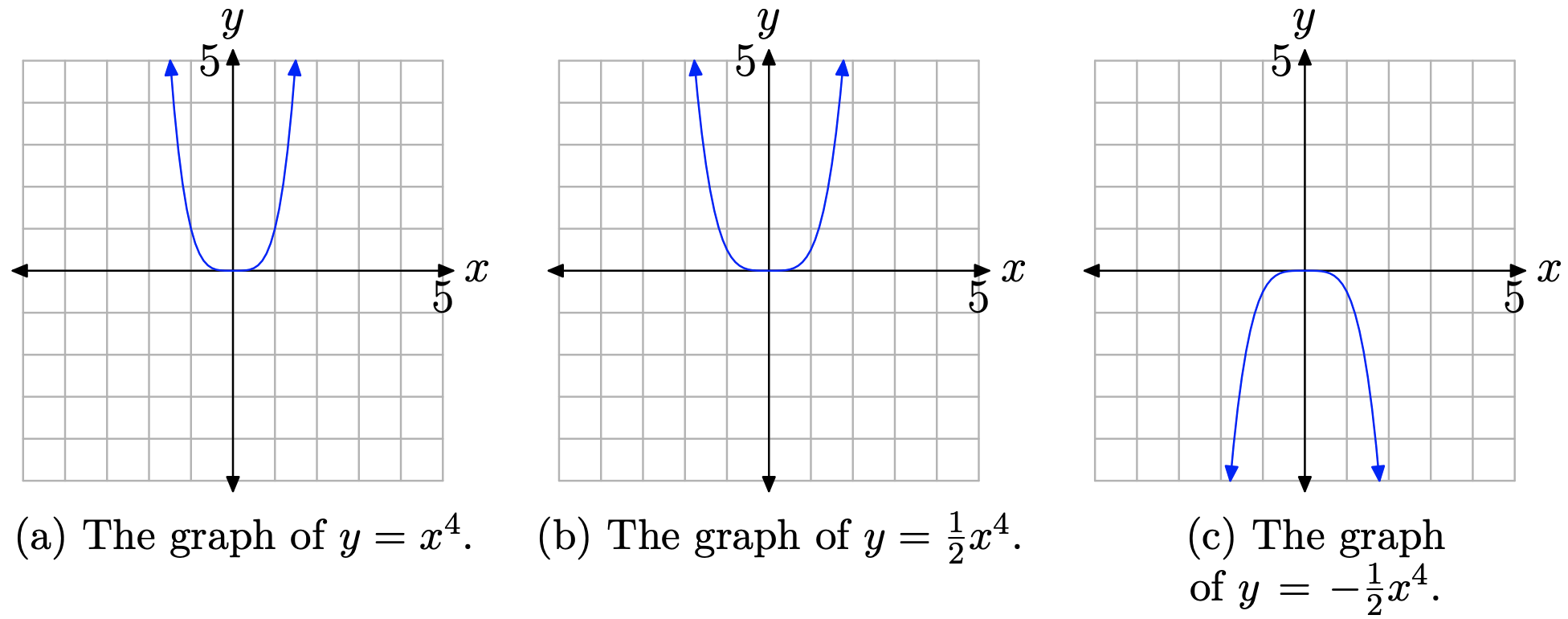
Ми знаємо, як\(y=x^{4}\) виглядає графік. Коли ми змітаємо очі зліва направо, графік падає з позитивної нескінченності, коливається через початок, потім піднімається назад до позитивної нескінченності. Така поведінка показана на малюнку\(\PageIndex{5}\) (а).

Якщо помножити на 1/2, то будемо стискати графік в 2 рази. Зверніть увагу, що графік\(y=\frac{1}{2} x^{4}\) на малюнку\(\PageIndex{5}\) (b) стискається в 2 рази у вертикальному напрямку.

Нарешті, якщо ми помножимо на −1/2, ми не тільки стиснемо графік у 2 рази, ми також відобразимо графік по осі x. Графік\(y=-\frac{1}{2} x^{4}\) показаний на малюнку\(\PageIndex{5}\) (в).

Малюнок\(\PageIndex{5}\). Масштабування на −1/2 стискає вертикально в 2 рази, а потім відображає графік по осі x.

Сподіваюся, в цей момент ви можете накидати графік\(y=a x^{n}\) для будь-якого дійсного числа а і будь-якого натурального числа n, парного або непарного, без використання калькулятора. Давайте використаємо ці новознайдені знання для дослідження кінцевої поведінки поліномів.

Поведінка кінця

Розглянемо многочлен\[p(x)=x^{3}-7 x^{2}+7 x+15\] Ось ключовий факт, який ми будемо використовувати для визначення кінцевої поведінки будь-якого полінома.

Нерухомість 13

Кінцева поведінка полінома повністю визначається його провідним терміном. Тобто кінцева поведінка графа полінома буде відповідати кінцевій поведінці графа його провідного члена.

Через мить ми покажемо, чому це властивість вірно. А поки приймемо правдивість цього твердження і застосуємо його до полінома, визначеного рівнянням (12). Провідним терміном многочлена\(p(x)=x^{3}-7 x^{2}+7 x+15\) є\(x^{3}\). Ми знаємо кінцеву поведінку графа\(y=x^{3}\). Коли ми змітаємо очі зліва направо, графік\(y=x^{3}\) буде підніматися з негативної нескінченності, погойдуватися через початок, а потім продовжувати підніматися до позитивної нескінченності. Ми зобразили цю поведінку раніше на малюнку\(\PageIndex{4}\) (а).

Властивість 13 говорить нам, що графік многочлена\(p(x)=x^{3}-7 x^{2}+7 x+15\) буде демонструвати таку ж кінцеву поведінку, що і графік його провідного члена,\(y=x^{3}\). Ми можемо передбачити, що, коли ми змітаємо очі зліва направо, графік многочлена\(p(x)=x^{3}-7 x^{2}+7 x+15\) підніметься з негативної нескінченності, трохи похитується, а потім підніметься до позитивної нескінченності. Ми не знаємо, що відбувається між ними, але ми знаємо, що відбувається на крайніх лівих і правих кінцях.

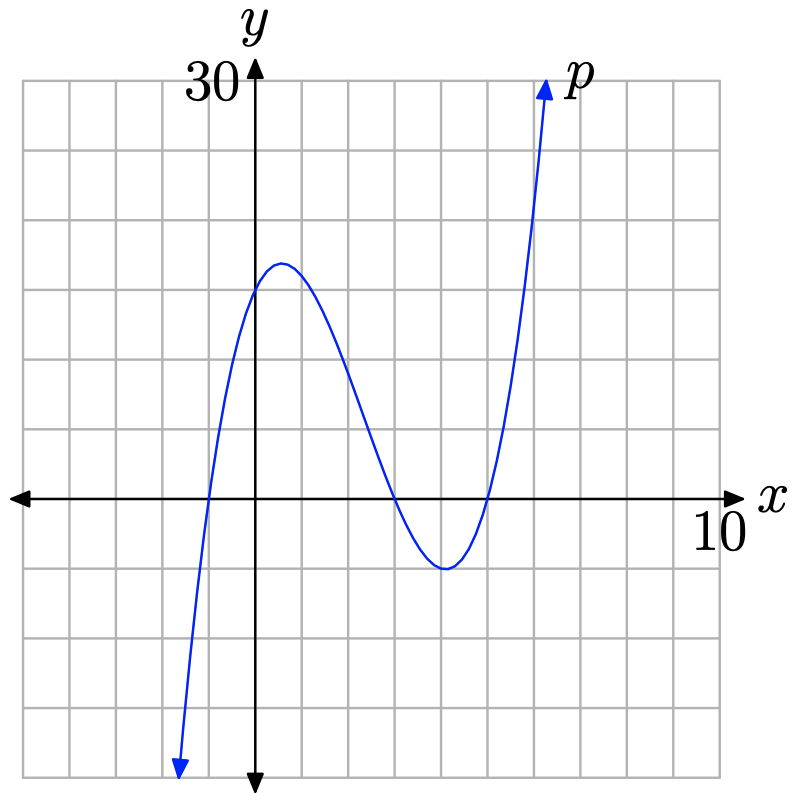
Наша здогадка перевіряється шляхом малювання графіка (використовуйте графічний калькулятор). Графік многочлена\(p(x)=x^{3}-7 x^{2}+7 x+15\) наведено на малюнку\(\PageIndex{6}\). Звичайно, коли ми підмітаємо очі зліва направо, графік на малюнку\(\PageIndex{6}\) піднімається з негативної нескінченності, як передбачалося, трохи коливається, а потім продовжує свій підйом до позитивної нескінченності.

Малюнок\(\PageIndex{6}\). Зауважте, що цей графік\(p(x)=x^{3}-7 x^{2}+7 x+15\) має таку ж поведінку кінця, що і графік\(y=x^{3}\).

Чому це працює? Чому Property 13 так точно прогнозує кінцеву поведінку цього многочлена?

\[p(x)=x^{3}-7 x^{2}+7 x+15\]

Ми можемо продемонструвати, чому спочатку перерахувавши провідний термін.

\[p(x)=x^{3}\left(1-\frac{7}{x}+\frac{7}{x^{2}}+\frac{15}{x^{3}}\right)\]

Тепер задайте наступне питання. Що відбувається з многочленом, коли ми рухаємося до правого кінця? Тобто, що відбувається з поліномом, коли ми використовуємо великі значення x, такі як 1 000, 10 000 або навіть 100 000?

Розглянемо дріб 7/х. оскільки чисельник зафіксований на рівні 7, а знаменник стає все більше і більше (зростає без кордону), дріб все ближче і ближче до нуля. Обчислення студенти використовували б позначення

\[\lim _{x \rightarrow \infty} \frac{7}{x}=0\]

Не відкладайте позначення. Ми використовуємо складні математичні позначення для дуже простої ідеї, яка говорить: «Коли х наближається до нескінченності, дріб 7/x наближається до нуля».

Використовуючи подібні міркування, кожен з дробів у рівнянні (14) йде до нуля, оскільки x переходить до нескінченності (збільшується без обмежень). Таким чином, як х стає все більше і більше (як ми рухаємося все далі і далі вправо),

\[\lim _{x \rightarrow \infty} p(x)=\lim _{x \rightarrow \infty} x^{3}\left(1-\frac{7}{x}+\frac{7}{x^{2}}+\frac{15}{x^{3}}\right) \approx x^{3}(1-0+0+0+0) \approx x^{3}\]

Тобто, оскільки x збільшується без обмежень, графік\(p(x)=x^{3}-7 x^{2}+7 x+15\) повинен наближатися до графіка\(y=x^{3}\).

Використовуючи подібні міркування, кожен з дробів у рівнянні (14) йде до нуля, оскільки x переходить до мінус нескінченності. Тобто, якщо ви ставите числа для x, такі як −1 000, −10 000, −100 000 тощо, дроби у рівнянні (14) зберуться до нуля. Отже, многочлен p (x) все ще повинен наближатися до свого провідного члена x 3 для дуже малих значень x (як підхід x\(-\infty\)).

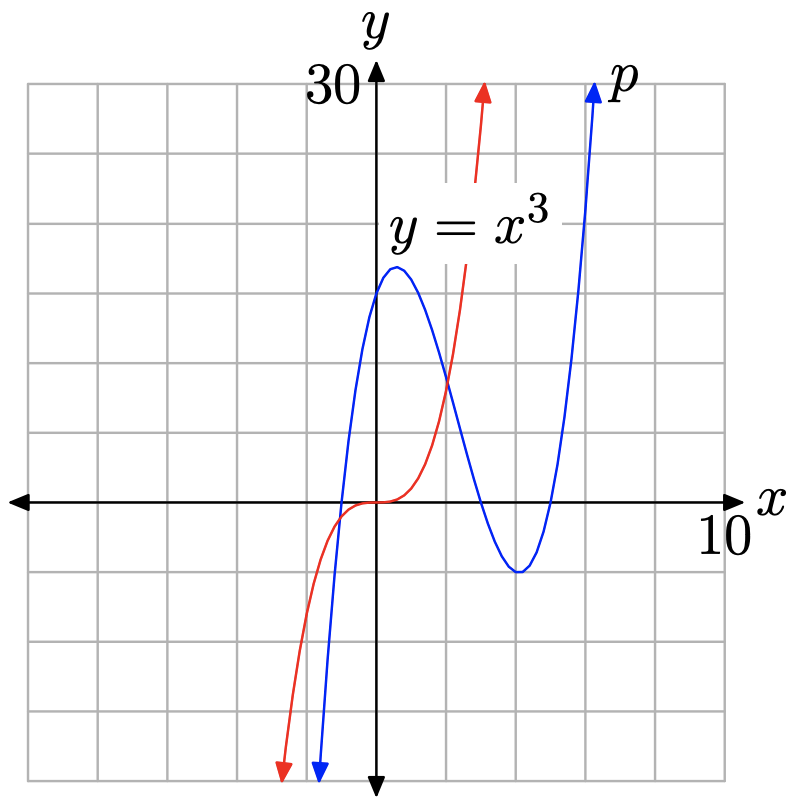
Якщо накласти графік на графік\(p(x)=x^{3}-7 x^{2}+7 x+15\), як\(y=x^{3}\) на малюнку, то зрозуміло\(\PageIndex{7}\), що поліном p має таку ж кінцеву поведінку, як і графік його провідного члена\(y=x^{3}\).

Малюнок\(\PageIndex{7}\). У міру переміщення в крайній лівий або правий графік\(p(x)=x^{3}-7 x^{2}+7 x+15\) наближається до графіка його провідного члена\(y=x^{3}\).

Ви можете забезпечити більш яскраву демонстрацію обґрунтованості претензії в рівнянні (15) шляхом побудови як полінома p, так і його провідного члена\(y=x^{3}\) на вашому калькуляторі, а потім зменшивши масштаб, скоригувавши параметри вікна, як показано на малюнку\(\PageIndex{8}\) (b). Зверніть увагу на те, як графік\(p(x)=x^{3}-7 x^{2}+7 x+15\) більше нагадує графік його провідного члена\(y=x^{3}\), хоча б на правому і лівому краях оглядового вікна. Коли ми зменшуємо масштаб, регулюючи параметри вікна, як показано на малюнку\(\PageIndex{8}\) (d), зверніть увагу на те, як цей графік p наближається до графіка його початкового члена\(y=x^{3}\) ще ближче на кожному краї вікна перегляду.

Малюнок\(\PageIndex{8}\). Зменшення масштабу чітко демонструє, що кінцева поведінка\(p(x)=x^{3}-7 x^{2}+7 x+15\) відповідає поведінці його провідного терміну\(y=x^{3}\).

Давайте розглянемо інший приклад.

Приклад\(\PageIndex{6}\)

Розглянемо многочлен\[p(x)=-x^{4}+37 x^{2}+24 x-180\]. Прокоментуйте кінцеву поведінку p і використовуйте графічний калькулятор, щоб намалювати його графік.

Рішення

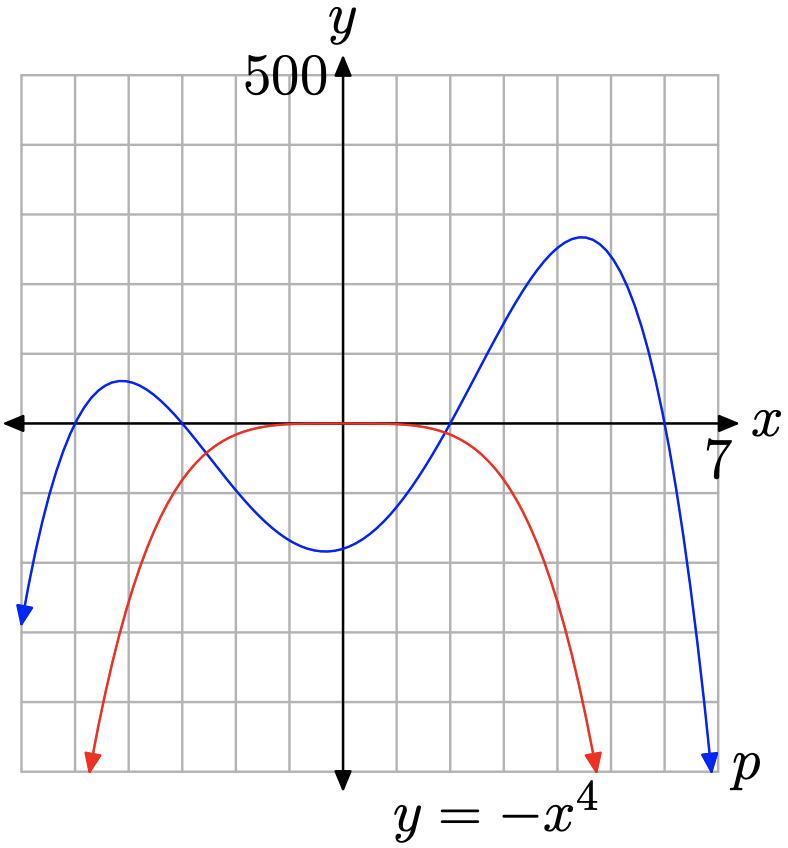
Провідним терміном\(p(x)=-x^{4}+37 x^{2}+24 x-180\) є\(y=-x^{4}\). Ми знаємо кінцеву поведінку графіка провідного терміна. Коли ми змітаємо очі зліва направо, графік\(y=-x^{4}\) піднімається з негативної нескінченності, коливається через початок, потім падає назад до мінус нескінченності. Графік p повинен демонструвати однакову кінцеву поведінку. Дійсно, на малюнку зверніть увагу\(\PageIndex{9}\), що графік\(y=-x^{4}\) і\(y=-x^{4}+37 x^{2}+24 x-180\) обидва мають однакову кінцеву поведінку.

Малюнок\(\PageIndex{9}\). Поліном\(p(x)=-x^{4}+37 x^{2}+24 x-180\) має таку ж кінцеву поведінку, що і графік його провідного члена\(y=-x^{4}\).

Вправа

У вправах 1 - 8 розташуйте кожен многочлен в спадних ступенях x, вкажіть ступінь многочлена, визначте провідний член, потім зробіть заяву про коефіцієнти заданого многочлена, посилаючись на Примітку вище Приклад\(\PageIndex{1}\)  для визначення цілого числа або раціональні коефіцієнти.

Вправа\(\PageIndex{1}\)

\(p(x) = 3x−x^2+4−x^3\)

Відповідь

\(p(x) = −x^3−x^2+3x+4\), ступінь = 3, провідний член =\(−x^3\), «p - многочлен з цілими коефіцієнтами, поліном з раціональними коефіцієнтами» або «p -

многочлен з дійсними коефіцієнтами».

Вправа\(\PageIndex{2}\)

\(p(x) = 4+3x^2−5x+x^3\)

Вправа\(\PageIndex{3}\)

\(p(x) = 3x^2+x^4−x−4\)

Відповідь

\(p(x) = x^4+3x^2−x−4\), ступінь = 4, провідний член =\(x^4\), «p - многочлен з цілими коефіцієнтами», «p - поліном з раціональними коефіцієнтами», або «p -

многочлен з дійсними коефіцієнтами».

Вправа\(\PageIndex{4}\)

\(p(x) = −3+x^2−x^3+5x^4\)

Вправа\(\PageIndex{5}\)

\(p(x) = 5x−\frac{3}{2}x^3+4−\frac{2}{3}x^5\)

Відповідь

\(p(x) = −\frac{2}{3}x^5−\frac{3}{2}x^3+5x+4\), ступінь = 5, провідний член =\(−\frac{2}{3}x^5\), «p - поліном з раціональними коефіцієнтами», або p - многочлен з дійсними коефіцієнтами».

Вправа\(\PageIndex{6}\)

\(p(x) = −\frac{3}{2}x+5−\frac{7}{3}x^5+\frac{4}{3}x^3\)

Вправа\(\PageIndex{7}\)

\(p(x) = −x+\frac{2}{3}x^3−\sqrt{2}x^2+\pi x^6\)

Відповідь

\(p(x) = \pi x^6+\frac{2}{3}x^3−\sqrt{2}x^2−x\), ступінь = 6, провідний член =\(\pi x^6\), «р - многочлен з дійсними коефіцієнтами».

Вправа\(\PageIndex{8}\)

\(p(x) = 3+\sqrt{2}x^4+\sqrt{3}x−2x^2+\sqrt{5}x^6\)

У вправах 9 - 14 вам представлений графік\(y = ax^{n}\). У кожному випадку вкажіть, чи є ступінь парною чи непарною, а потім вкажіть, чи є a позитивним чи негативним числом.

Вправа\(\PageIndex{9}\)

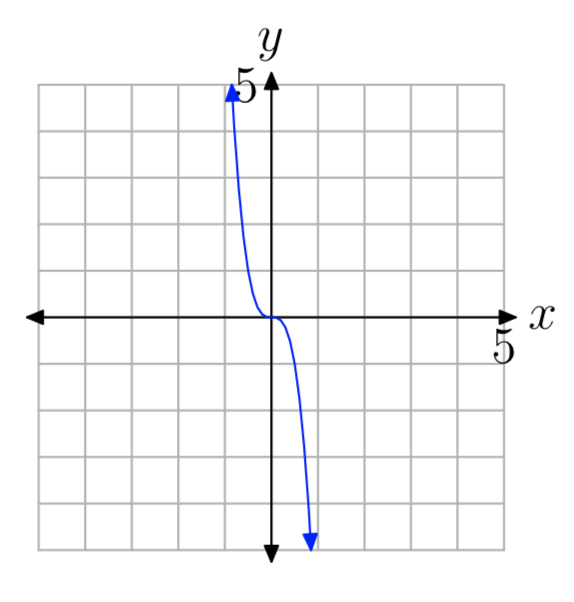
Відповідь

\(y=ax^{n}\), n непарних, a < 0.

Вправа\(\PageIndex{10}\)

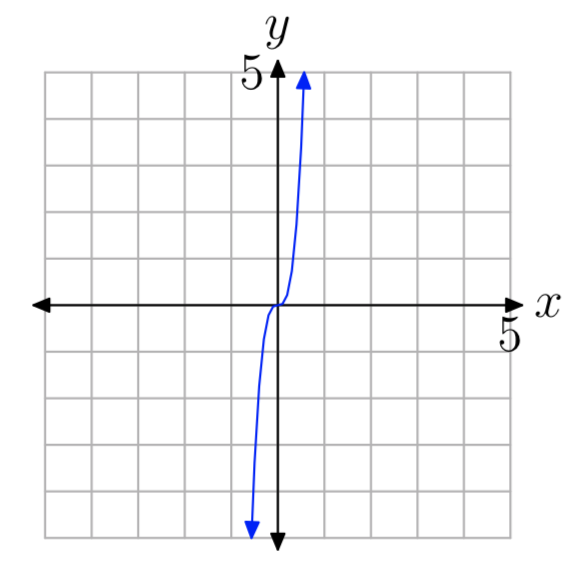
Вправа\(\PageIndex{11}\)

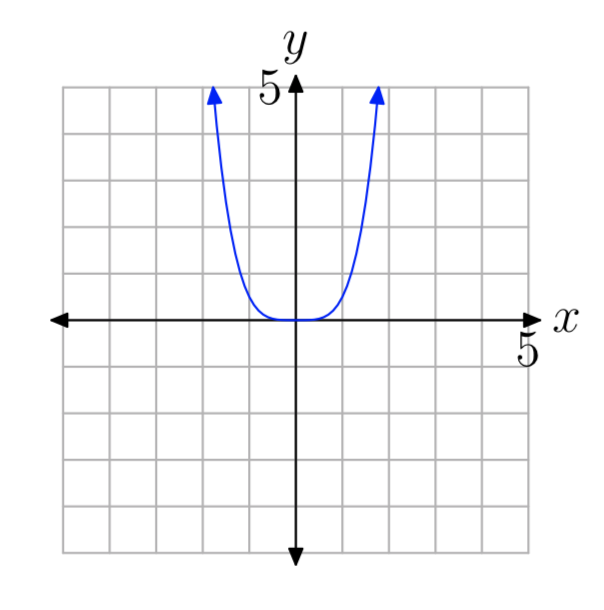
Відповідь

\(y=ax^{n}\), п навіть, а > 0.

Вправа\(\PageIndex{12}\)

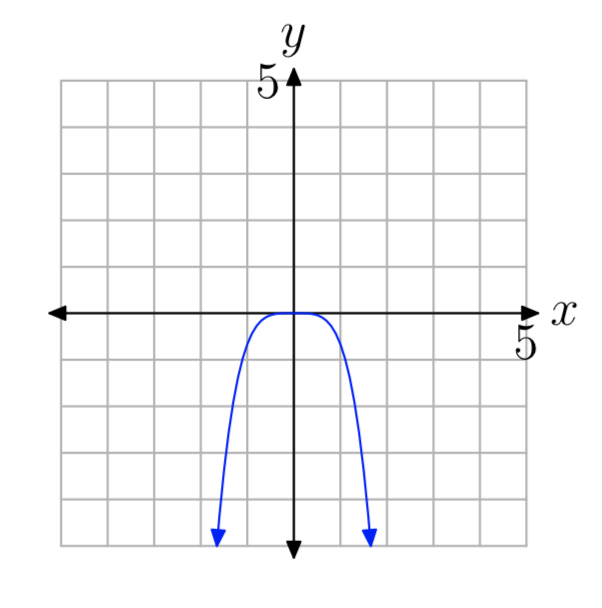
Вправа\(\PageIndex{13}\)

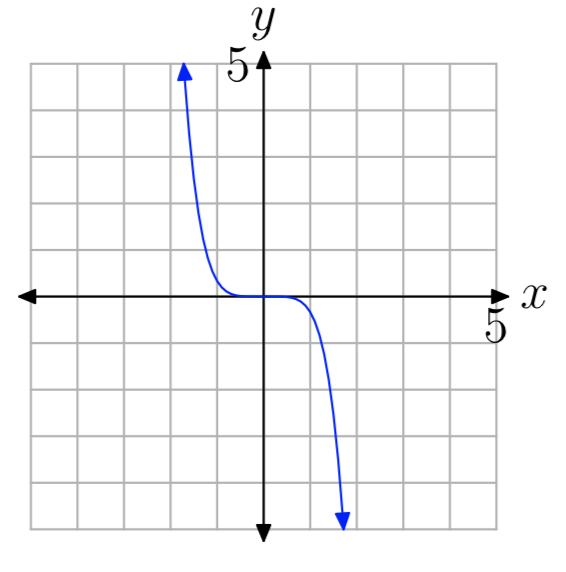
Відповідь

\(y=ax^{n}\), n непарних, a < 0.

Вправа\(\PageIndex{14}\)

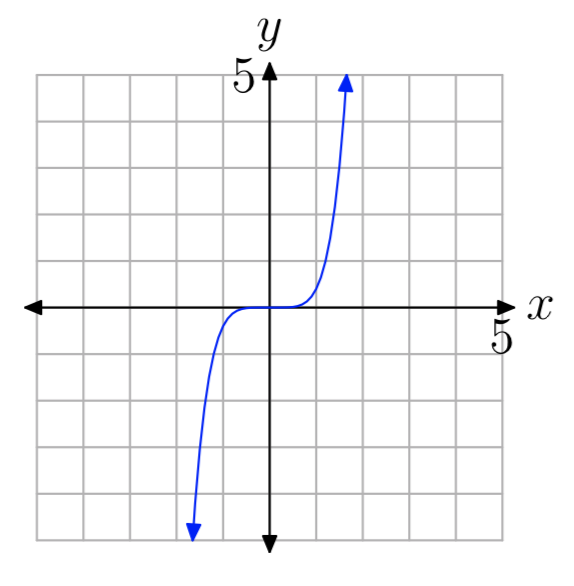
У вправах 15 - 20 вам представлений графік многочлена\(p(x) = a_{n}x^n +···+a_{1}x+a_{0}\). У кожному випадку вкажіть, чи є ступінь многочлена парною чи непарною, а потім вкажіть, чи є провідний коефіцієнт a позитивним чи негативним.

Вправа\(\PageIndex{15}\)

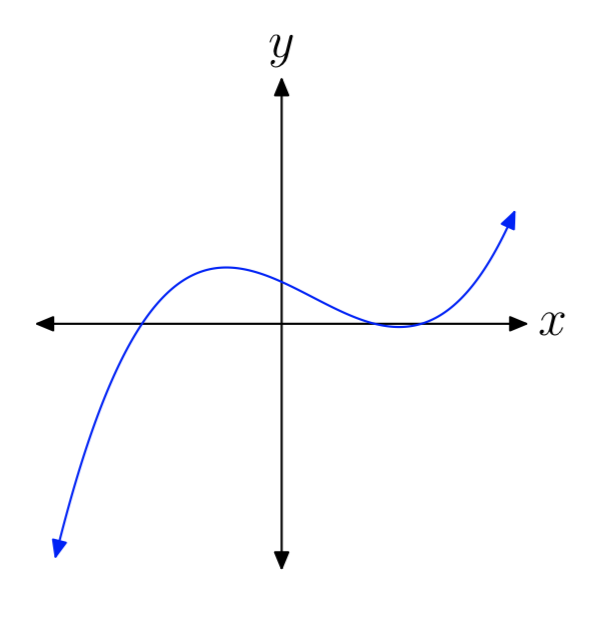
Відповідь

непарний, позитивний

Вправа\(\PageIndex{16}\)

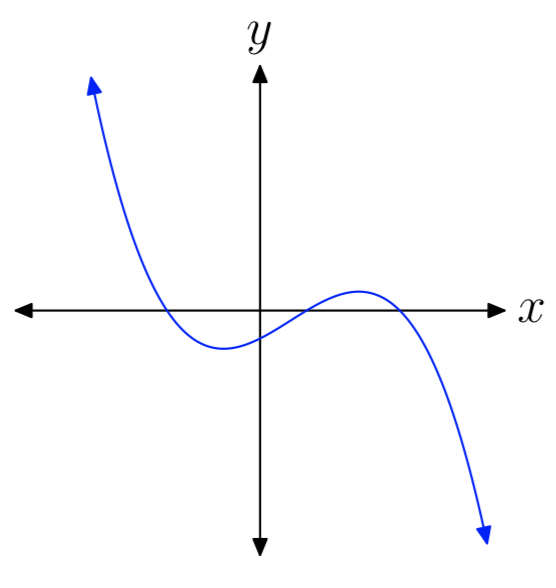
Вправа\(\PageIndex{17}\)

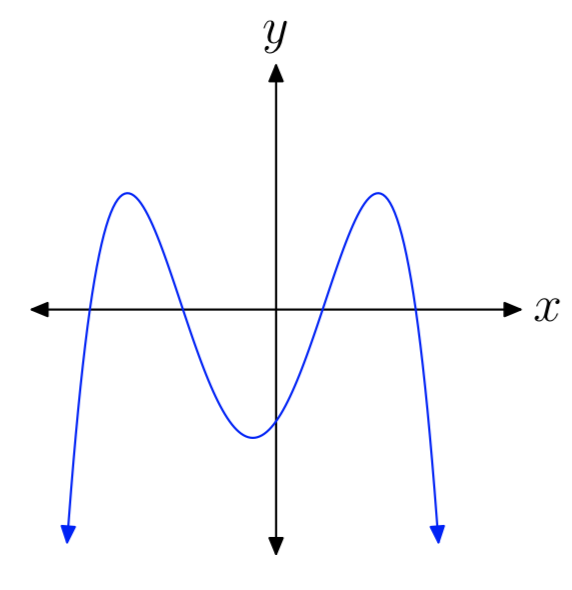
Відповідь

парний, негативний

Вправа\(\PageIndex{18}\)

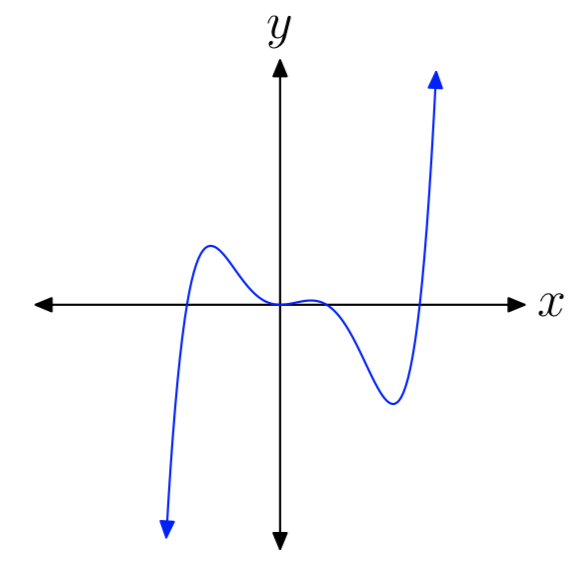
Вправа\(\PageIndex{19}\)

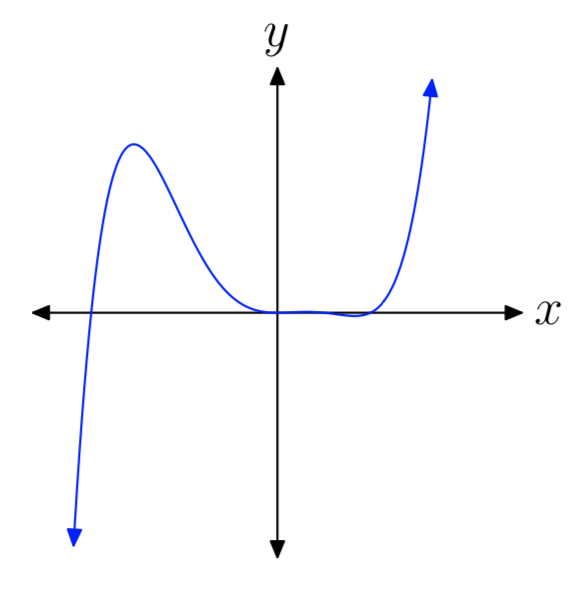
Відповідь

непарний, позитивний

Вправа\(\PageIndex{20}\)

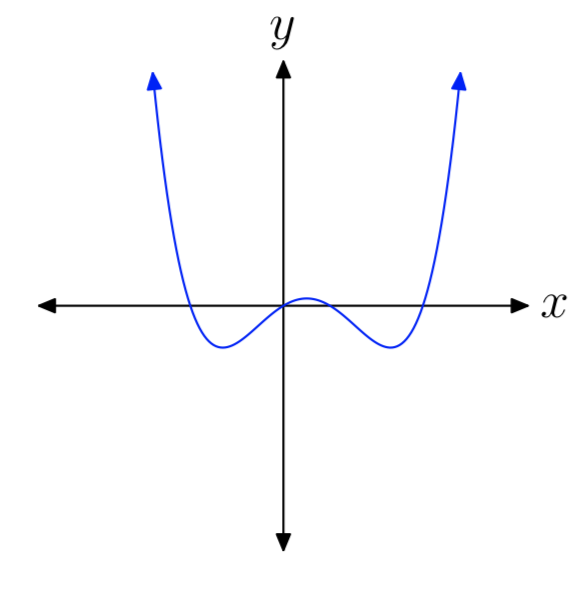
Для кожного полінома у Вправах 21 - 30 виконайте кожне з наступних завдань.

1. Передбачте кінцеву поведінку многочлена, намалювавши дуже грубий ескіз многочлена. Робити це можна без допомоги калькулятора. Єдине занепокоєння тут полягає в тому, що ваш графік показує правильну поведінку кінця.
2. Намалюйте графік на калькуляторі, налаштуйте оглядове вікно так, щоб у вікні перегляду були видні всі «поворотні точки» многочлена, і скопіюйте результат на домашній папір. Як завжди, позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax. Чи згодна фактична кінцева поведінка з вашим прогнозованим кінцевим поведінкою?

Вправа\(\PageIndex{21}\)

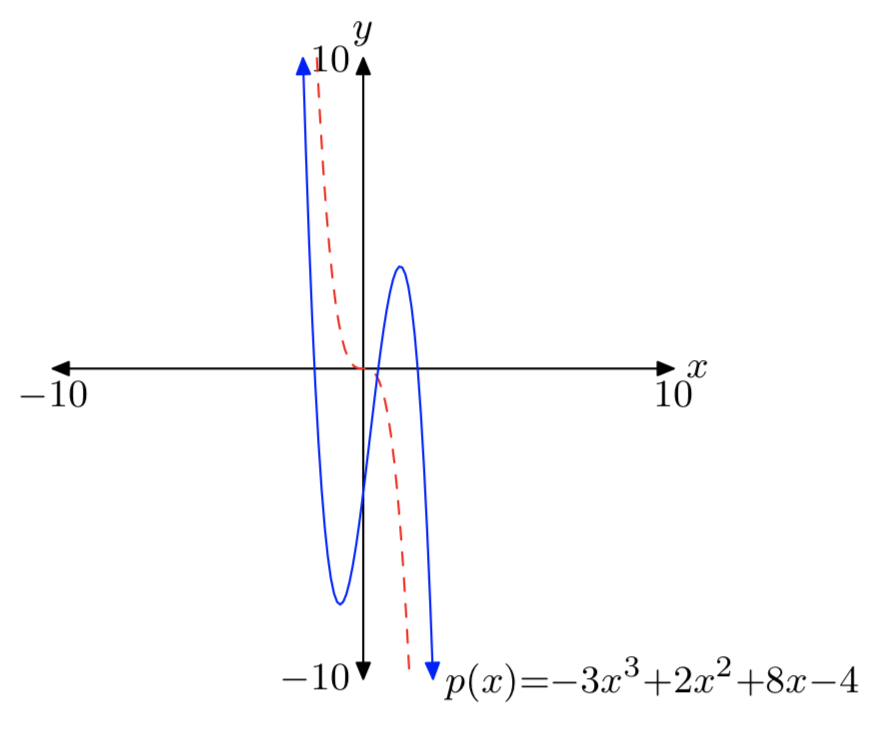
\(p(x) = −3x^3+2x^2+8x−4\)

Відповідь

Зауважте, що провідний термін\(−3x^3\) (пунктирний) має таку ж кінцеву поведінку, що і многочлен p.

Вправа\(\PageIndex{22}\)

\(p(x) = 2x^3−3x^2+4x−8\)

Вправа\(\PageIndex{23}\)

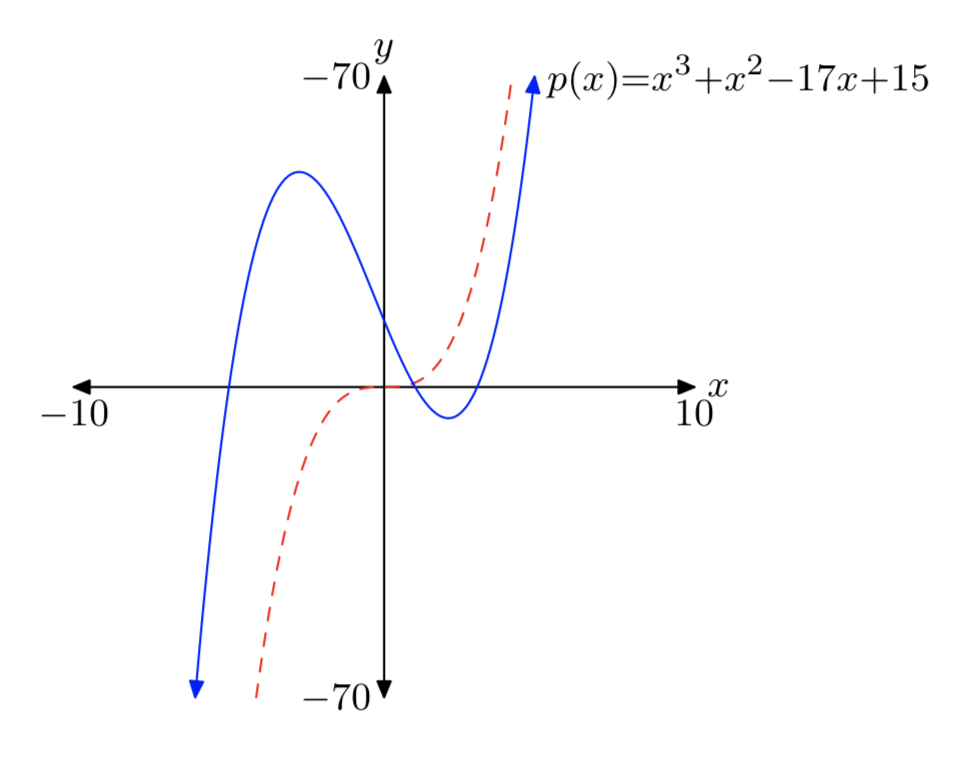
\(p(x) = x^3+x^2−17x+15\)

Відповідь

Зауважте, що провідний термін\(x^3\) (пунктирний) має таку ж кінцеву поведінку, що і многочлен p.

Вправа\(\PageIndex{24}\)

\(p(x) = −x^4+2x^2+29x−30\)

Вправа\(\PageIndex{25}\)

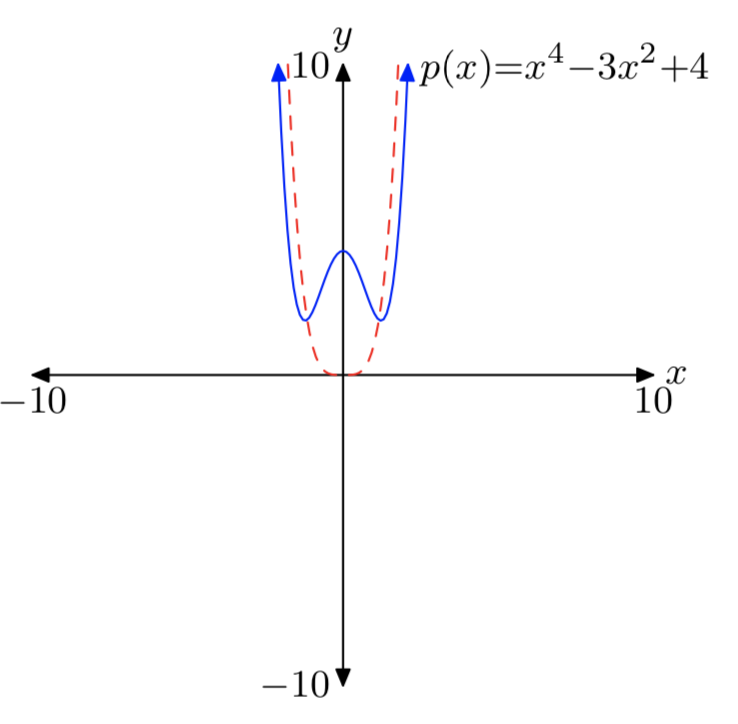
\(p(x) = x^4−3x^2+4\)

Відповідь

Зауважте, що провідний термін\(x^4\) (пунктирний) має таку ж кінцеву поведінку, що і многочлен p.

Вправа\(\PageIndex{26}\)

\(p(x) = −x^4+8x^2−12\)

Вправа\(\PageIndex{27}\)

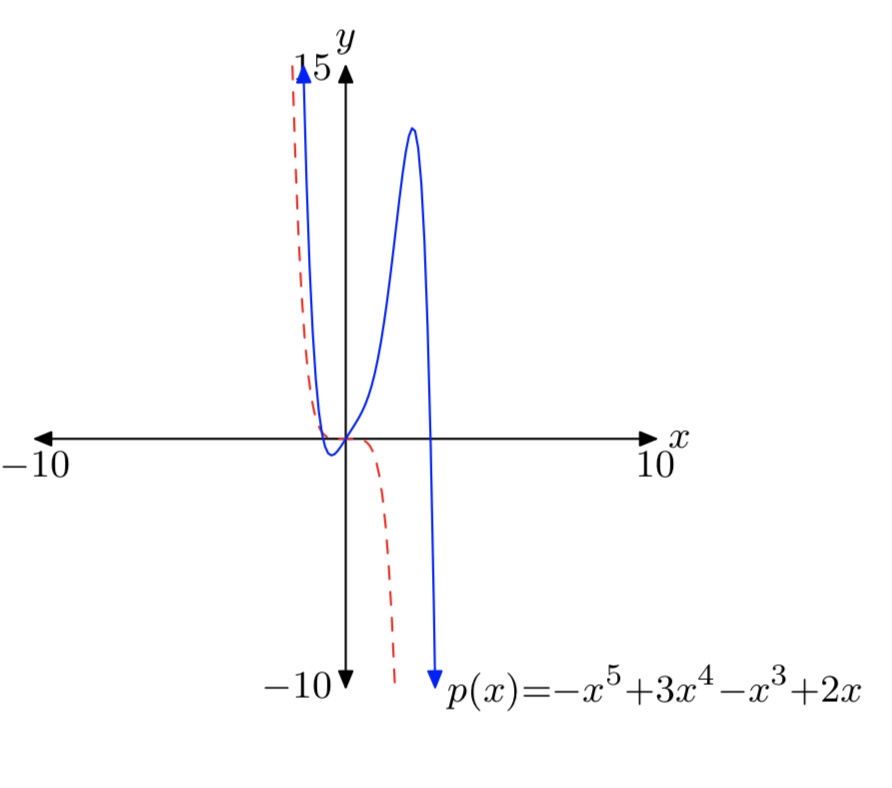
\(p(x) = −x^5+3x^4−x^3+2x\)

Відповідь

Зауважте, що провідний термін\(−x^5\) (пунктирний) має таку ж кінцеву поведінку, що і многочлен p.

Вправа\(\PageIndex{28}\)

\(p(x) = 2x^4−3x^3+x−10\)

Вправа\(\PageIndex{29}\)

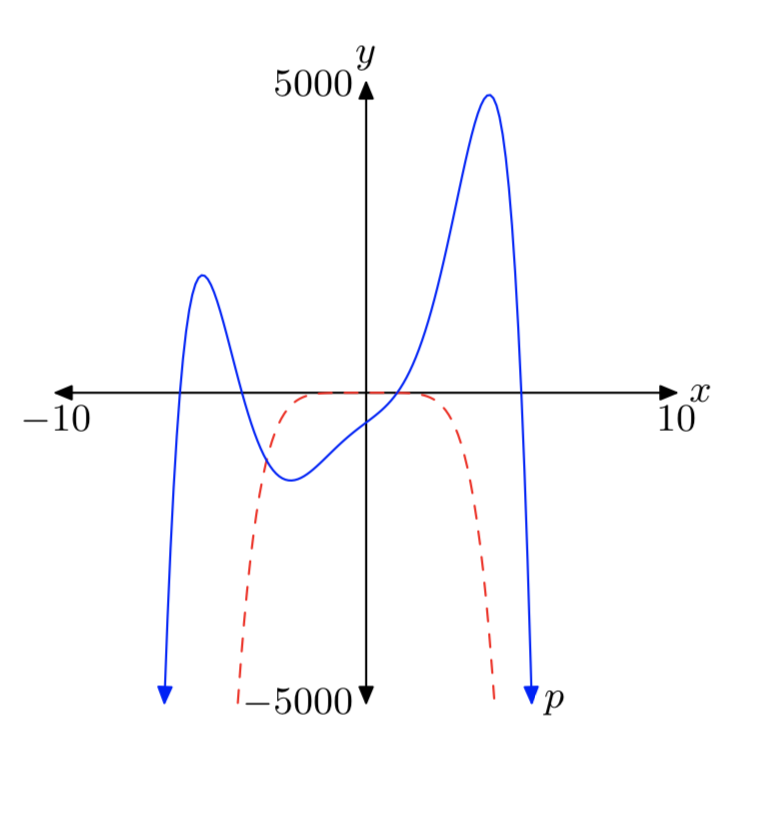
\(p(x) = −x^6−4x^5+27x^4+78x^3+4x^2+376x−480\)

Відповідь

Зауважте, що провідний термін\(−x^6\) (пунктирний) має таку ж кінцеву поведінку, що і многочлен p.

Вправа\(\PageIndex{30}\)

\(p(x) = x^5−27x^3+30x^2−124x+120\)