6.3: Екстрема і моделі

Last updated
Save as PDF

Page ID: 58124

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

В останньому розділі ми використовували кінцеву поведінку та нулі для накреслення графа заданого многочлена. Ми також згадували, що потрібно семестр обчислення, щоб вивчити аналітичну техніку, яка використовується для обчислення «поворотних точок» полінома. Тим не менш, ми все ще будемо переслідувати координати «поворотних точок» в цьому розділі, але ми будемо використовувати графічний калькулятор, щоб допомогти нам у цьому квесті; і тоді ми будемо використовувати цю техніку з деякими додатками.

Екстрема

Перш ніж ми почнемо, ми спочатку хотіли б розрізнити локальні екстреми та абсолютні екстреми. Це найкраще зробити за допомогою прикладу. Розглянемо, якщо хочете, графіки трьох поліноміальних функцій на малюнку 1.

На першому малюнку, Рисунок$\PageIndex{1a}$, точка А - це «абсолютна» найнижча точка на графіку. Тому значення y точки А є абсолютним мінімальним значенням функції.

На другому малюнку, Рисунок$\PageIndex{1b}$, немає «абсолютної» найвищої точки на графіку (графік йде вгору до позитивної нескінченності), а також немає «абсолютної» найнижчої точки на графіку (графік опускається до негативної нескінченності). Тому дана функція не має ні абсолютного мінімуму, ні абсолютного максимуму.

Однак точка Б на малюнку$\PageIndex{1b}$ є найвищою точкою в її безпосередньому сусідстві. Якщо ви блукаєте занадто далеко вправо, на графіку є точки вище точки B, але локально точка B є найвищою точкою. Тому значення y точки B називається локальним максимальним значенням функції.

Точно так само точка С на малюнку$\PageIndex{1b}$ є найнижчою точкою в її безпосередньому сусідстві. Якщо ви заблукаєте занадто далеко вліво, на графіку є точки нижче точки С, але, по сусідству, точка С є найнижчою точкою. Тому значення y точки С називається локальним мінімумом функції.

Малюнок$\PageIndex{1}$: Диференціювання локальних і абсолютних екстрем.

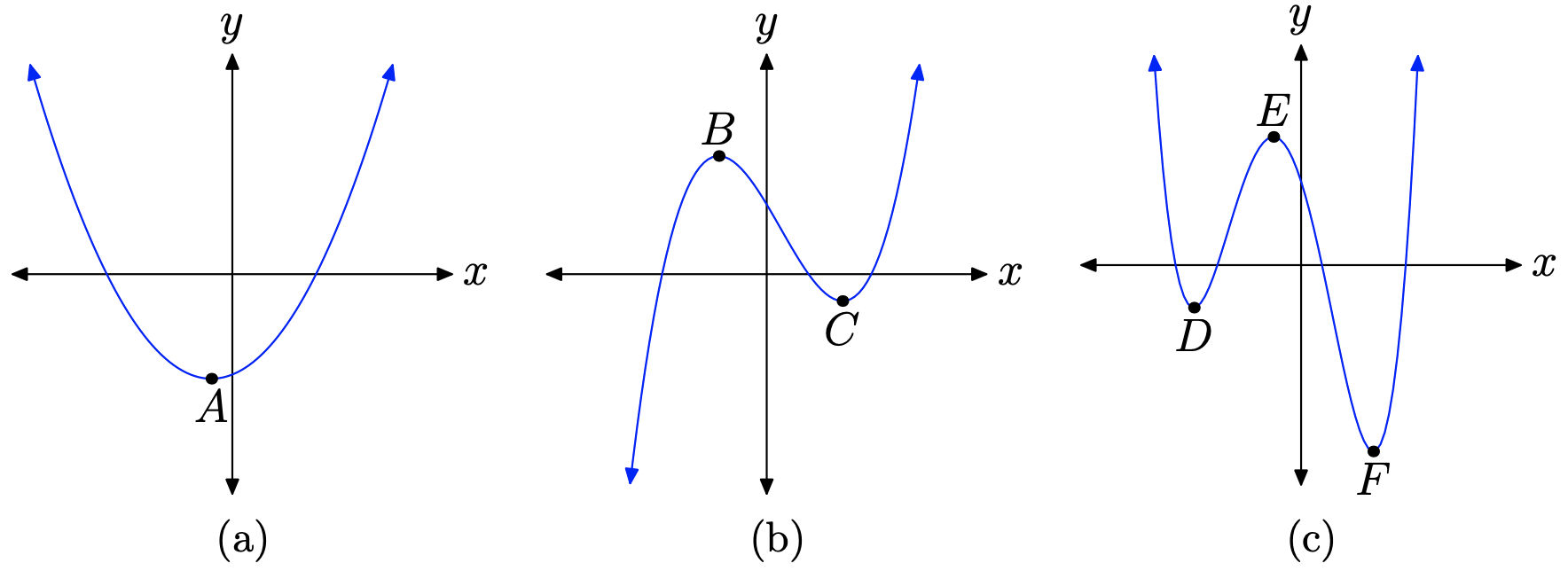
Нарешті, погляньте на графік на малюнку$\PageIndex{1c}$. Точка F - «абсолютна» найнижча точка на графіку, тому значення y точки F є абсолютним мінімумом функції. З іншого боку, на графіку на малюнку$\PageIndex{1}$ (c) немає найвищої точки, оскільки кожен кінець графіка збігає до позитивної нескінченності. Значить, функція не має абсолютного максимуму.

Локально точка D на малюнку$\PageIndex{1}$ (c) є найнижчою точкою, тому значення y точки D є локальним мінімумом функції. Аналогічно, в безпосередньому сусідстві точка Е є найвищою точкою, тому значення y точки Е є локальним максимумом.

Наведемо тепер формальні визначення.

Визначення: Абсолютний максимум

Припустимо, що$c$ знаходиться в області функції$f$ і$f(c) \geq f(x)$ для всіх$x$ в області$f$. Тоді ми говоримо, що$f(c)$ це абсолютний максимум функції$f$. Аналогічно, якщо$f(c) \leq f(x)$ для всіх$x$ в області$f$, то$f(c)$ це абсолютний мінімум функції$f$.

Визначення локальної крайності менш обмежувальне.

Визначення: Локальний максимум

Дозвольте c бути в домені$f$. Якщо$f(c) \geq f(x)$ для всіх$x$ в районі, що містить c, то ми говоримо, що f (c) є локальним максимумом функції f З іншого боку, якщо$f(c) \leq f(x)$ для всіх$x$ в околицях, що містять$c$, то ми говоримо, що f (c) є локальним мінімумом функції f.

Коли математики говорять «сусідство$c$, що містить», вони зазвичай мають на увазі невеликий відкритий інтервал$(a, b)$, який містить$c$.

Давайте вивчимо використання графічного калькулятора при пошуку екстремумів.

Приклад$\PageIndex{1}$

Розглянемо поліноміальну функцію, визначену рівнянням

\[p(x)=2(x-6)(x+2)(x+4). \nonumber\]

Використовуйте графічний калькулятор, щоб знайти та класифікувати всі екстремуми цієї функції.

Рішення

По-перше, скільки графіка можна намалювати без використання калькулятора? Лінійними факторами$p(x)$ є x − 6, x + 2 та x + 4, отже нулями є 6, −2 та −4 відповідно. Отже, ми тепер знаємо, де графік р (х) перетинає вісь x.

Щоб визначити кінцеву поведінку$p(x)$, нам потрібно визначити провідний термін. Не потрібно повністю розширювати многочлен за допомогою розподільної властивості.3 Маленька думка швидко виявляє, що якби ми зробили саме це, провідним терміном у цьому випадку був би$2x^{3}$. Отже, коли ми змітаємо очі зліва направо, кінцева поведінка полінома повинна відповідати поведінці його провідного члена$2x^{3}$, піднімаючись з негативної нескінченності, переміщаючись через його x-перехоплення, а потім піднімаючись до позитивної нескінченності. Єдиний вибір - це графік, подібний до графіка на малюнку$\PageIndex{2}$.

Малюнок$\PageIndex{2}$: Графік$p(x) = 2(x− 6)(x + 2)(x + 4)$ піднімається з негативної нескінченності, коливається через свої x-перехоплення, потім продовжує підніматися до позитивної нескінченності.

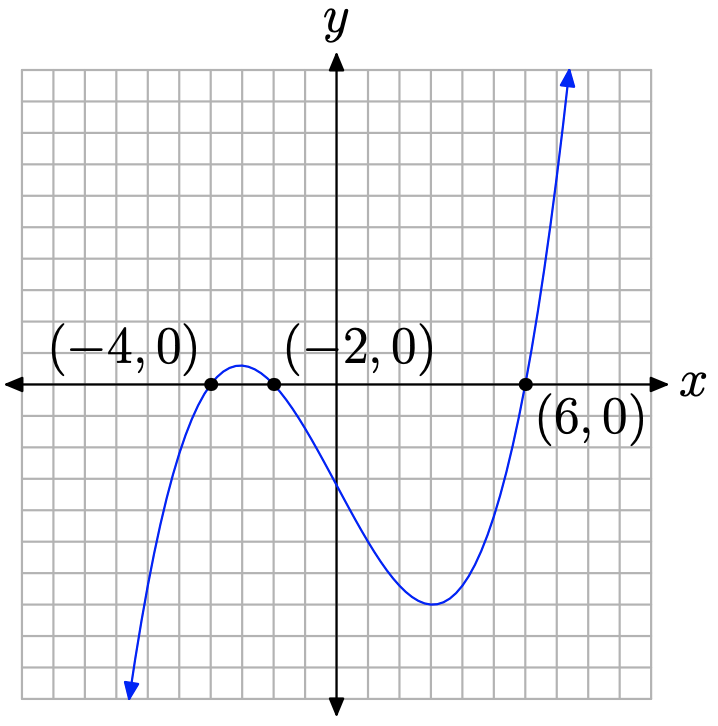
Зауважте, що графік досягає локального максимуму десь поблизу x = −3 та локального мінімуму приблизно x = 3. Ми можемо знайти кращі наближення локальної екстреми, використовуючи максимальні та мінімальні утиліти в меню CALC графічного калькулятора.

Спочатку побудуйте графік многочлена p (x) = 2 (x − 6) (x + 2) (x + 4), як показано на малюнку$\PageIndex{3}$ (a), використовуючи параметри вікна, наведені на малюнку$\PageIndex{3}$ (b).
Відкрийте меню РОЗРАХУВАТИ, натиснувши 2nd CALC. Це відкриває меню вибору, як показано на малюнку$\PageIndex{3}$ (c). Щоб запустити програму, яка допоможе знайти локальний максимум біля x = −3 (див. Рис.$\PageIndex{2}$), натисніть 4:maximum у меню.
Утиліта відповідає, запитуючи «Ліва межа». За допомогою клавіш зі стрілками перемістіть курсор трохи ліворуч від локального максимуму поблизу x = −3, як показано на малюнку$\PageIndex{3}$ (d), потім натисніть клавішу ENTER.

Малюнок$\PageIndex{3}$. За допомогою графічного калькулятора для визначення локального максимуму.

Утиліта відповідає, запитуючи «Right Bound». За допомогою клавіш зі стрілками перемістіть курсор трохи праворуч від локального максимуму біля x = −3, як показано на малюнку$\PageIndex{4}$ (e), потім натисніть клавішу ENTER.
Утиліта відповідає, запитуючи «Вгадайте». Перемістіть курсор так, щоб він лежав між зробленими раніше «Left Bound» і «Right Bound», як показано на малюнку$\PageIndex{4}$ (f), потім натисніть клавішу ENTER. Будь-де між лівою та правою прив'язкою (примітки у верхній частині екрана на малюнку$\PageIndex{4}$ (f)) буде робити.

Малюнок$\PageIndex{4}$. За допомогою графічного калькулятора визначити локальний максимум (продовження).

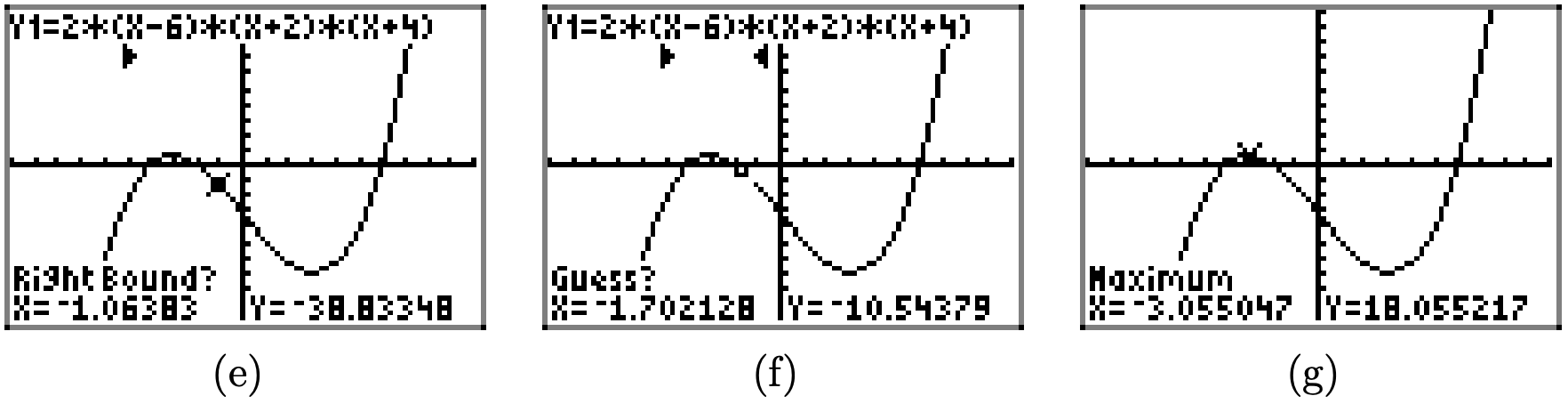
Калькулятор реагує розміщенням курсора в точці, де відбувається локальний максимум, і повідомляє його координати в нижній частині екрана, як показано на малюнку$\PageIndex{4}$ (g).

Координати точки, де відбувається локальний максимум, приблизно\[(-3.055047,18.055217)\]

Ми говоримо, що функція досягає локального максимального значення 18.05217 і що максимум відбувається при$x \approx-3.055047$.

Аналогічним чином можна скористатися мінімальною утилітою в меню CALC, щоб знайти локальний мінімум, який зустрічається біля x = 3, як показано на малюнку$\PageIndex{5}$.

Малюнок$\PageIndex{5}$. Використовуйте мінімальну утиліту, щоб знайти локальний мінімум.

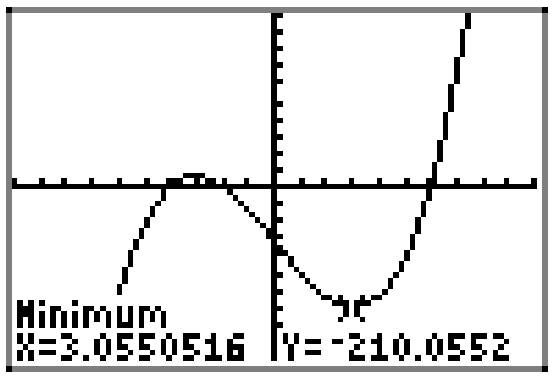
Координати точки, де відбувається локальний мінімум, приблизно\[(3.0550516,-210.0552)\]

Ми скажемо, що функція досягає локального мінімального значення −210.0552 і що мінімум відбувається при$x \approx 3.0550516$.

Додатки

У цьому розділі ми розглянемо деякі програми, які моделюються поліномами.

Приклад$\PageIndex{2}$

Квадратний шматок картону вимірює 24 дюйми на кожну сторону. Джон вирізає чотири менших квадрата з кожного кута картону, відкидаючи матеріал в сторону. Потім він загинає вгору по сторонам залишився картону, щоб сформувати відкриту коробку без верху. Знайдіть розміри квадратів, вирізаних з кожного кута вихідного шматка картону так, щоб Джон максимально збільшив отриманий обсяг коробки.

Рішення

Нехай х представляють довжину сторони квадрата, вирізаного з кожного кута більшого квадрата (див.$\PageIndex{6}$ Рис. Оскільки кожна сторона вихідного квадрата має розміри 24 дюйми, і ми вирізаємо дві довжини х дюймів від кожного кінця, отримана довжина та ширина коробки становить 24 − 2x дюйми (див. Рисунок$\PageIndex{6}$ (a) та/або (b)). Коли відкидаємо квадратні кути, потім складаємо бічні сторони, отримуємо коробку з розмірами, показаними на малюнку$\PageIndex{6}$ (б).

Малюнок$\PageIndex{6}$: Матеріал і вийшла коробка.

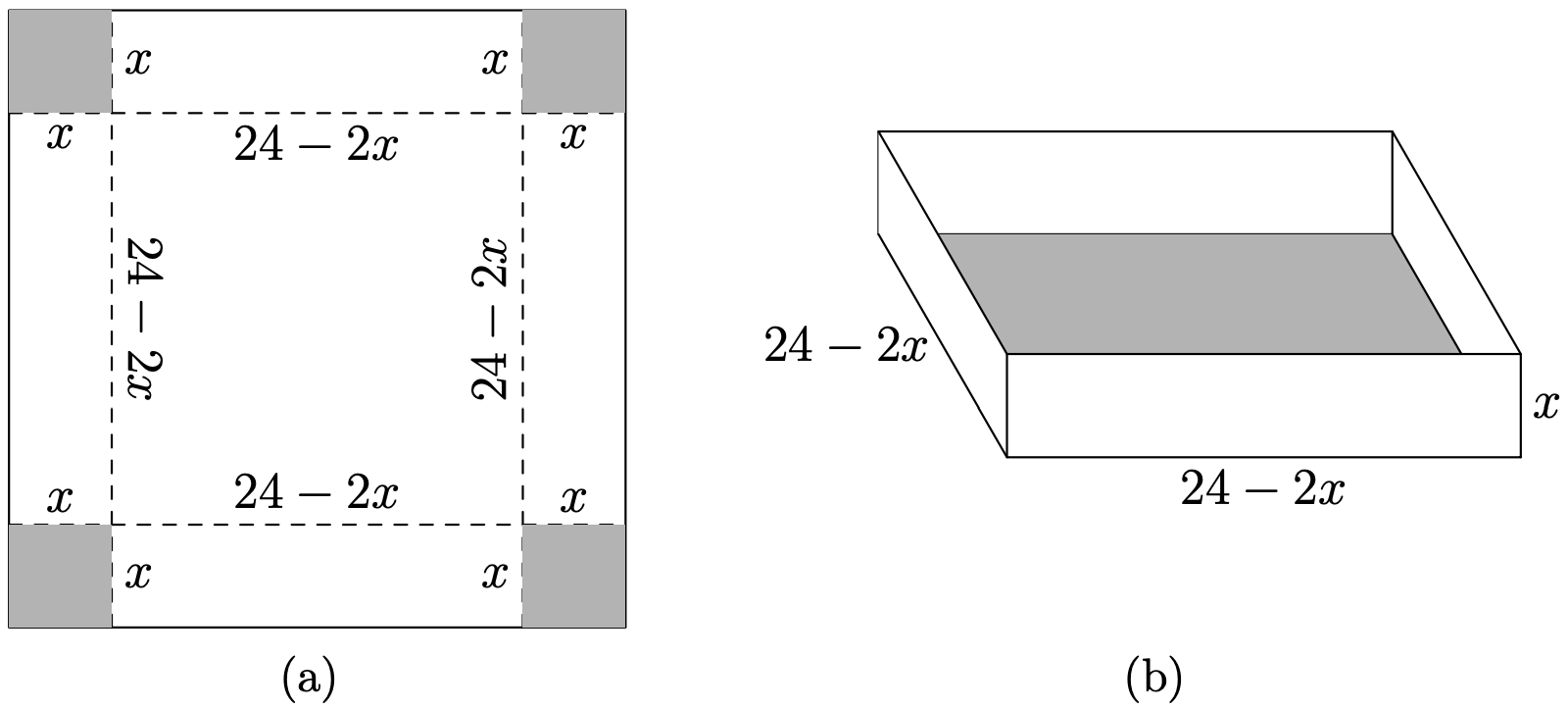
Оскільки обсяг коробки обчислюється шляхом взяття добутку довжини і ширини підстави, помноженого на висоту коробки, обсяг коробки задається за формулою

\[V=x(24-2 x)(24-2 x) \nonumber\]

Ми можемо дещо спростити рівняння (6). Візьміть коефіцієнт 2 від кожного фактора 24−2x, як у

\[V=x(2)(12-x)(2)(12-x) \nonumber\]

потім об'єднати фактори, щоб написати

\[V=4 x(12-x)^{2} \nonumber\]

Ми бачимо, що$x$ і$12 − x$ є лінійними факторами$V$. Значить, нулі V дорівнюють 0 і 12 відповідно. Оскільки 12−x використовується як множник двічі, 2 є «подвійним коренем», отже граф має бути дотичним до осі x$x = 2$.

Якби ми розгорнули рівняння (7) повністю, ми б отримали многочлен з провідним терміном$4x^{3}$. Отже, кінцева поведінка нашого об'ємного полінома повинна відповідати кінцевій поведінці його провідного члена, піднімаючись від негативної нескінченності, переміщаючись через неї нулями, а потім піднімаючись до позитивної нескінченності. Однак, оскільки у нас є «подвійний корінь» при x = 2, ми очікуємо, що графік «поцілує» горизонтальну вісь у цьому нулі, а не проходить через цей нуль.

Таким чином, єдина можлива форма, яку може припустити об'ємний многочлен, - це та, яка показана на малюнку$\PageIndex{7}$.

Малюнок$\PageIndex{7}$: Обсяг коробки в залежності від довжини краю знятих квадратів.

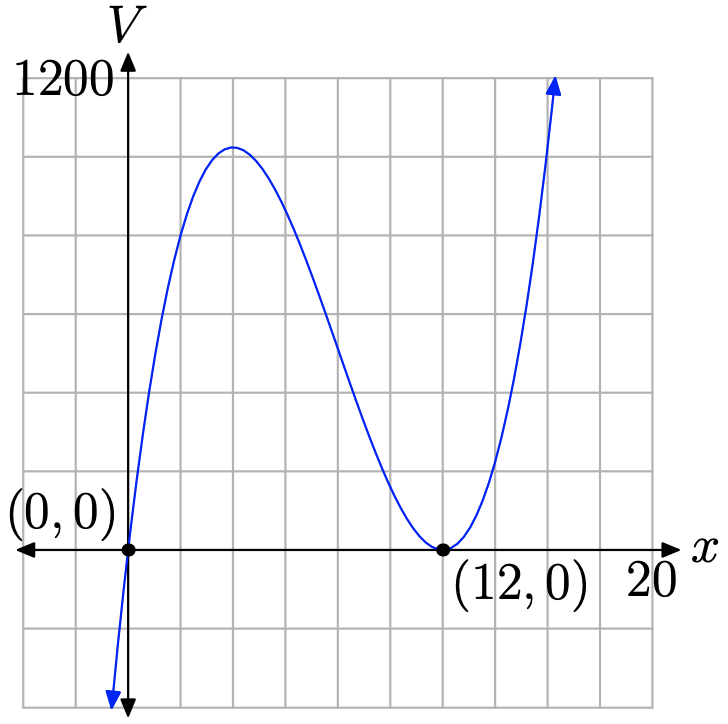
Область многочлена, визначеного рівнянням (7), є множиною всіх дійсних чисел, або, в інтервальному позначенні,$(-\infty, \infty)$. На малюнку$\PageIndex{7}$, якщо ви проектуєте всі точки на графіку на вісь x, вся вісь x буде затінена, що ще більше вказує на те, що область функції гучності - це всі дійсні числа.

Однак ця математична область$(-\infty, \infty)$ ігнорує той факт, що x являє собою довжину квадрата, вирізаного з кожного кута вихідного квадрата картону$\PageIndex{6}$ (див. Рис. Ви не можете вирізати квадрат, що має сторону негативної довжини. При подальшому огляді найбільший квадрат, який можна було б вирізати з кожного кута, матиме край розміром 12 дюймів. Пам'ятайте, ви повинні вирізати чотири квадрати, по одному з кожного кута, а край оригінального квадратного шматка картону розміром всього 24 дюйми. Таким чином, задача обмежує x інтервалом [0, 12]. Цей домен називається емпіричним доменом, або, якщо хочете, практичним доменом.

Визначення: Емпірична область

Емпірична область функції є підмножиною математичної області, обмеженою таким чином, щоб задовольнити обмеження моделі.

Таким чином, лише частина графіка на малюнку має$\PageIndex{7}$ сенс для цього застосування— частина, яка намальована над емпіричною областю [0, 12], як показано на малюнку$\PageIndex{8}$.

Рисунок$\PageIndex{8}$: Ескіз функції гучності над емпіричною областю [0, 12].

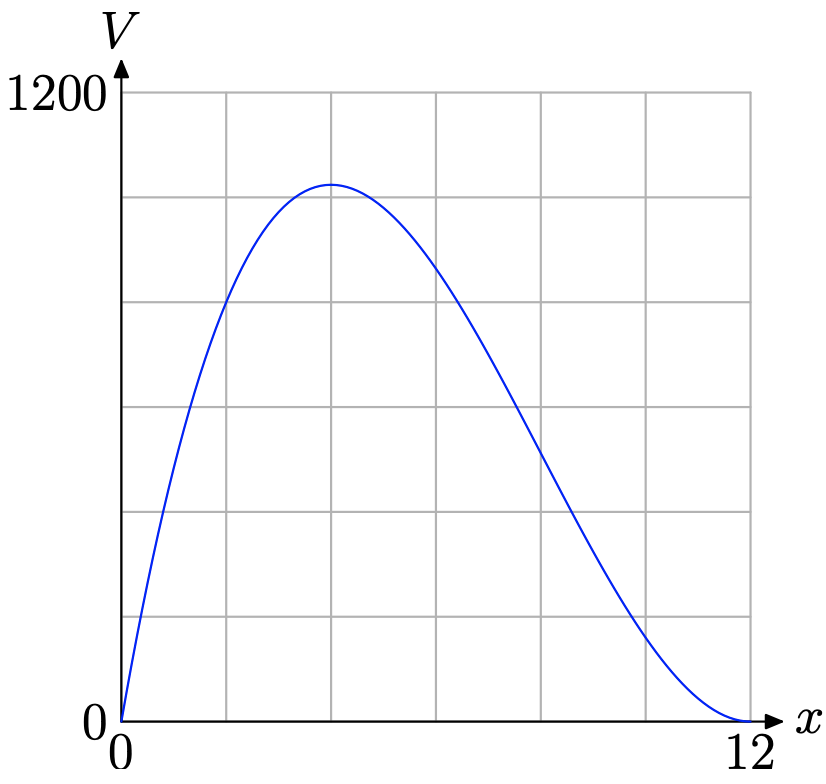
Пам'ятайте, початкова мета полягала в тому, щоб знайти значення x, яке б максимально збільшило обсяг коробки. Швидкий погляд на графік на малюнку$\PageIndex{8}$ показує, що існує абсолютний максимум (принаймні на емпіричній області [0, 12]) поблизу x = 4. Щоб отримати краще наближення, використовуйте максимальну корисність у меню CALC на вашому калькуляторі, як ми це зробили, щоб отримати наближення, показане на малюнку$\PageIndex{9}$ (b).

Малюнок$\PageIndex{9}$. Знаходження довжини краю, який максимізує обсяг коробки.

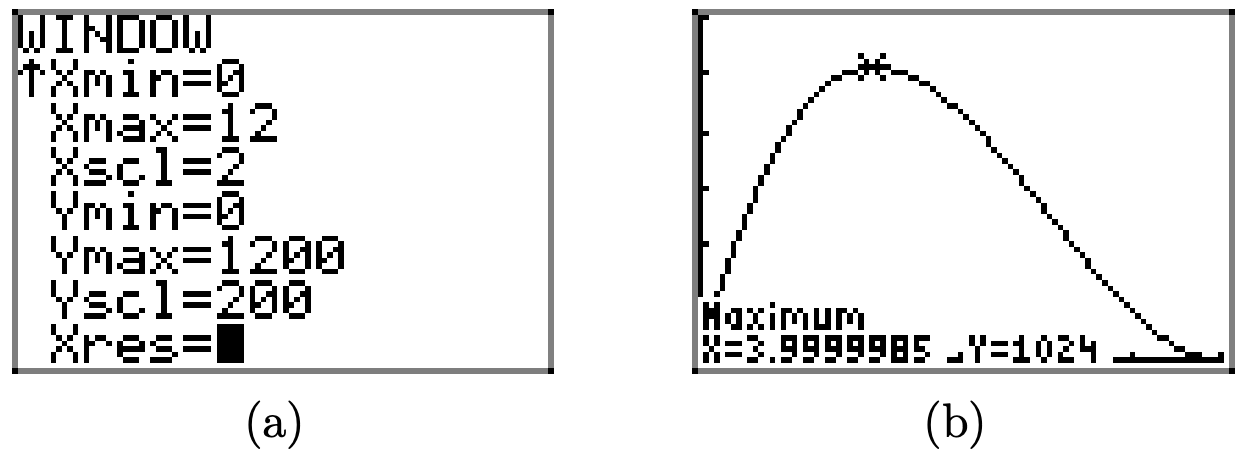
Дійсно, здавалося б, що максимальний обсяг 1024 кубічних дюймів ($V=1024 \mathrm{in}^{3}$) досягається при$x \approx 3.9999985$. Ймовірно, можна з упевненістю сказати, що максимальний обсяг виникає, якщо з кутів оригінального шматка картону вирізати квадрати, що мають сторони довжиною 4 дюйми. 3.9999985 ймовірно містить трохи помилки через помилку округлення на калькуляторі. Дійсно, дуже ймовірно, що деякі читачі отримають рівно x = 4, коли вони використовують максимальну корисність, залежно від використовуваних меж та початкового припущення, тому не турбуйтеся, якщо ваше наближення калькулятора трохи відрізняється від нашого.

Давайте розглянемо інший приклад.

Приклад$\PageIndex{3}$

Знайдіть розміри прямокутника найбільшої площі, який має свою основу на осі x, а дві інші його вершини над віссю x і лежить на графіку параболи$y=4-x^{2}$.

Рішення

Графік$y=4-x^{2}$ являє собою параболу, яка відкривається вниз і зміщується вгору на 4 одиниці. Права частина цього рівняння коефіцієнти

\[y=(2+x)(2-x) \nonumber\]

отже нулями цієї функції є −2 і 2. Оскільки прямокутник має свою основу на осі x, а інші його вершини - на параболі, що лежить над віссю x, нам потрібно лише намалювати параболу на області [−2, 2] (див. Рис.$\PageIndex{10}$).

Малюнок$\PageIndex{10}$: Прямокутник, вписаний під параболу.

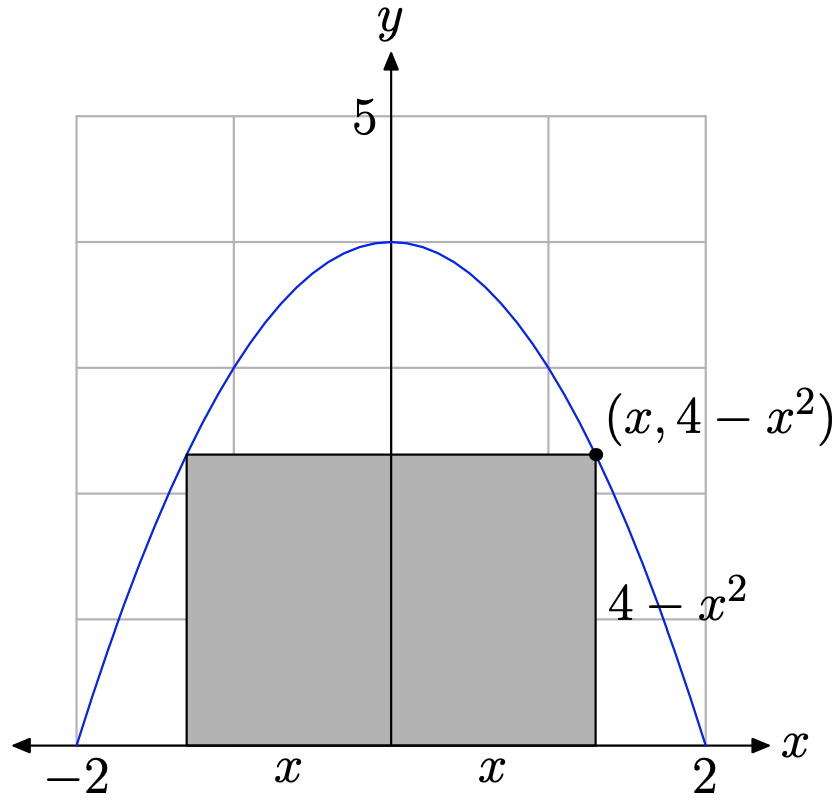
Через симетрію ми можемо обмежити x емпіричним доменом [0, 2]. На малюнку зауважте$\PageIndex{10}$, що ми вибрали значення x з [0, 2], а потім побудували точку, що має це значення x на параболі. Звичайно, значення y цієї точки є$y=4-x^{2}$. Таким чином, висота прямокутника дорівнює$4-x^{2}$ і основа (або ширина) прямокутника двічі x, або 2x. Площа прямокутника задається

\[A=\text { width } \cdot \text { height }\]

Значить, площа А як функція x задається многочленом

\[A=2 x\left(4-x^{2}\right)\]

Зверніть увагу, що рівняння (10) є поліном третього ступеня, що має провідний член$-2 x^{3}$. Таким чином, графік многочлена, коли ми змітаємо очі зліва направо, повинен впасти з позитивної нескінченності, погойдуватися через його х-перехоплення, потім продовжити падіння до негативної нескінченності.

Ми можемо факторне рівняння (10) для отримання

\[A=2 x(2+x)(2-x)\]

Отже, нулі многочлена дорівнюють 0, −2 і 2 відповідно. Таким чином, многочлен повинен мати форму, подібну до тієї, що зображена на малюнку$\PageIndex{11}$. Зауважте, що граф має x-перехоплення за значеннями (−2, 0), (0, 0) та (2, 0).

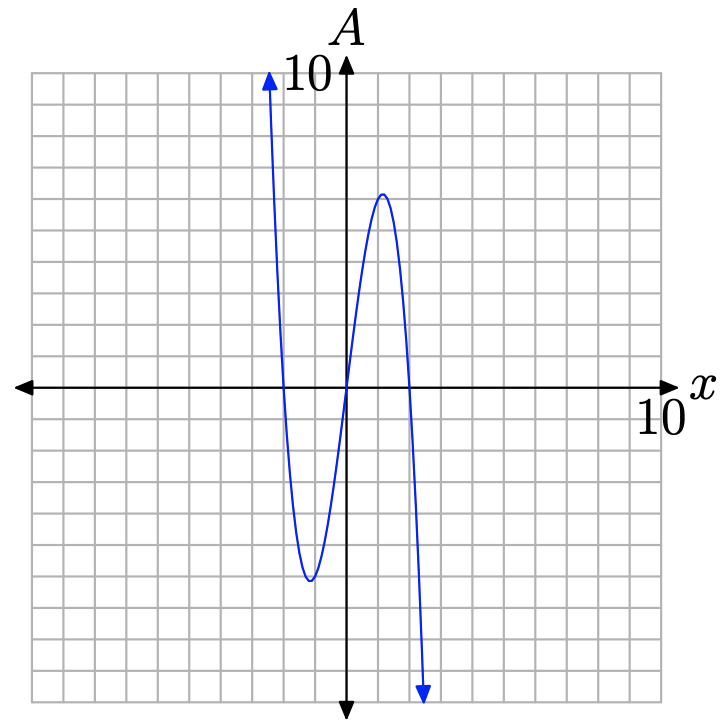
Через практичну природу цієї проблеми нам потрібно обмежити x емпіричною областю [0, 2], про що говорилося вище (див$\PageIndex{10}$. Рис. Графік A = 2x (2 + x) (2 − x), обмежений доменом [0, 2], показаний на рис$\PageIndex{12}$.

Малюнок$\PageIndex{12}$. Графік многочлена A = 2x (2+ x) (2 − x) обмежений емпіричною областю [0, 2].

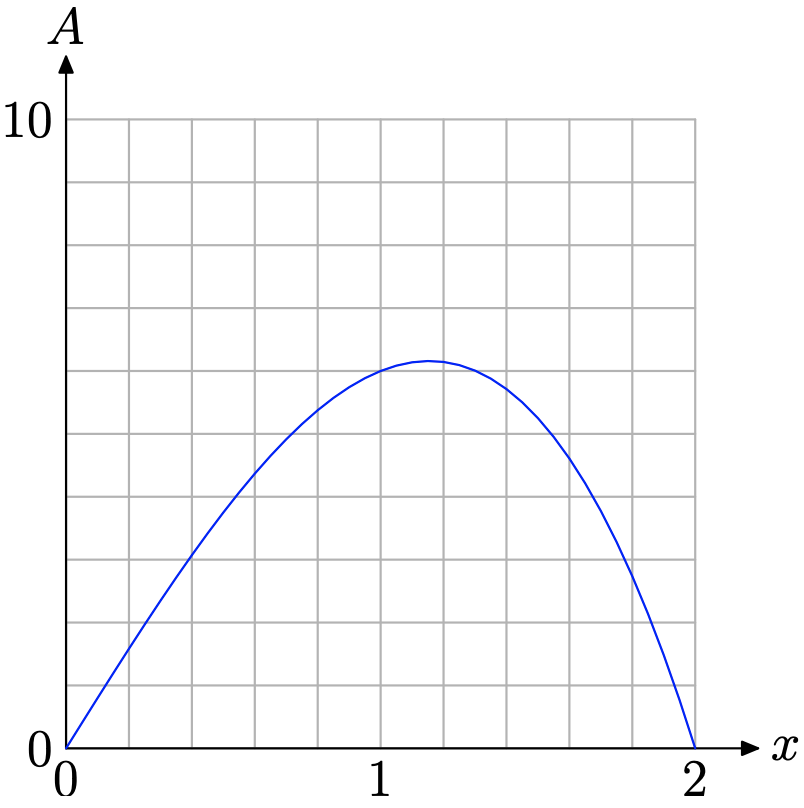
Виявляється (див. Рисунок$\PageIndex{12}$), що A досягає абсолютного максимуму (принаймні в емпіричній області [0, 2]) поблизу$x \approx 1.2$. Щоб отримати краще наближення, використовуйте максимальну утиліту в меню CALC графічного калькулятора, як ми це зробили для отримання наближення, показаного на малюнку$\PageIndex{13}$ (b).

Малюнок$\PageIndex{13}$. Використовуйте максимальну корисність для отримання наближення максимального значення А.

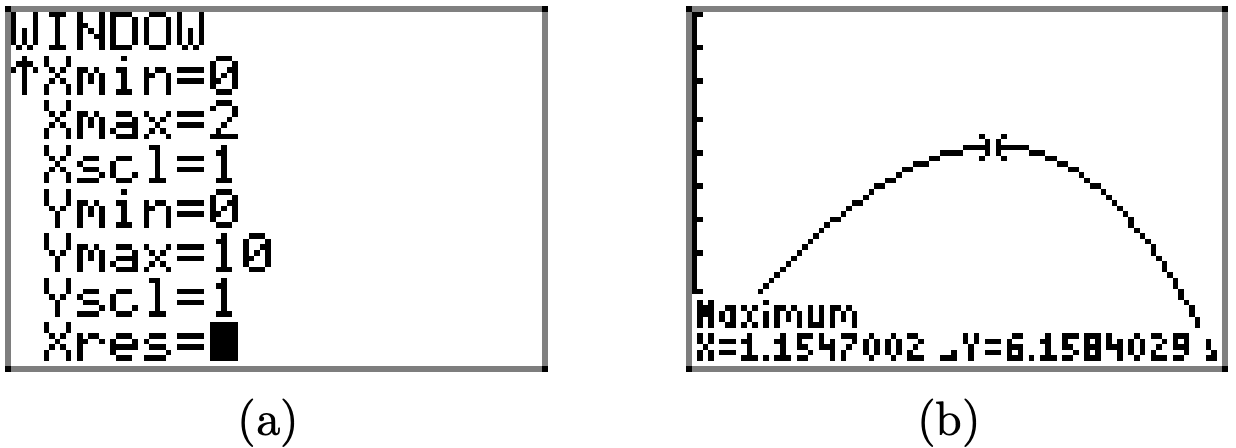
Результат на малюнку$\PageIndex{13}$ (b) показує, що ми досягаємо прямокутника максимальної площі,$A \approx 6.1584029$ якщо ми виберемо$x \approx 1.1547002$. Пам'ятайте, що ваші відповіді можуть дещо відрізнятися залежно від обраної вами лівої та правої меж, вашої здогадки, а також через властиву помилку округлення у всіх калькуляторах.

Вправа

У вправах 1 - 8 виконайте кожне з наступних завдань для даного полінома.

Без допомоги калькулятора використовуйте алгебраїчну техніку для ідентифікації нулів заданого полінома. Фактор при необхідності.
На графічному папері налаштуйте систему координат. Позначте кожну вісь, але масштабуйте лише вісь x. Використовуйте нулі та кінцеву поведінку, щоб намалювати «грубий графік» заданого полінома з допомогою калькулятора.
Класифікуйте кожну локальну крайність як відносний мінімум або відносний максимум.Примітка: Не потрібно знаходити координати відносної екстреми. Дійсно, це було б важко з калькулятором. Все, що потрібно, це позначити кожну крайність як відносний максимум або мінімум

Вправа$\PageIndex{1}$

р (х) = (х+6) (х−1) (х−5)

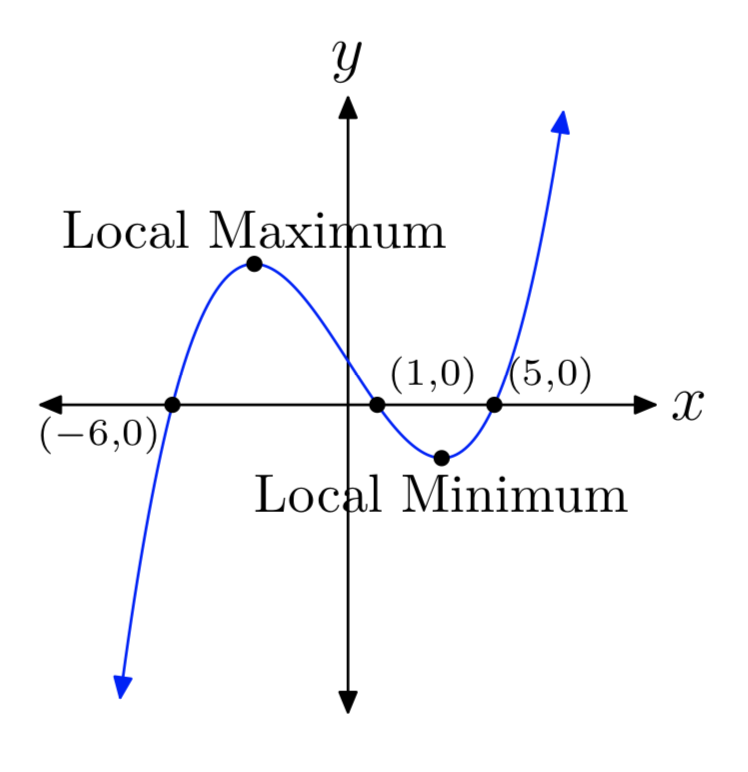
Відповідь: $Знімок екрана 2019-09-02 о 9.01.27 AM.png$

Вправа$\PageIndex{2}$

р (х) = (х+2) (х−4) (х−7)

Вправа$\PageIndex{3}$

$p(x) = x^3−6x^2−4x+24$

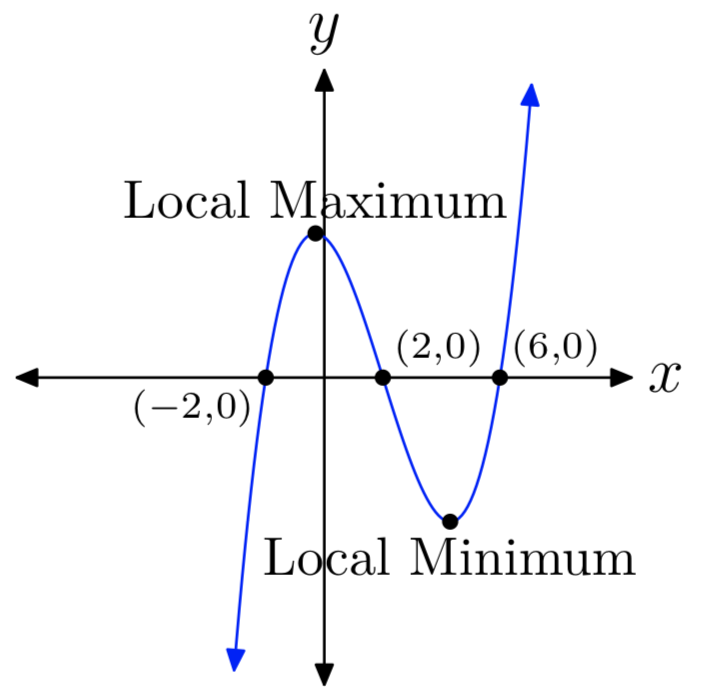
Відповідь: $Знімок екрана 2019-09-02 о 9.02.10 AM.png$

Вправа$\PageIndex{4}$

$p(x) = x^3+x^2−36x−36$

Вправа$\PageIndex{5}$

$p(x) = 2x^3+5x^2−42x$

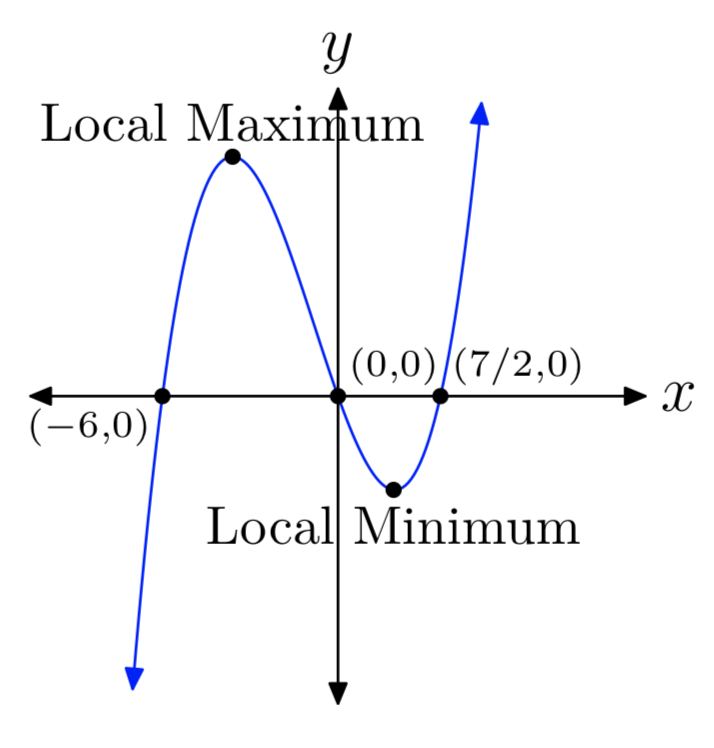
Відповідь: $Знімок екрана 2019-09-02 о 9.02.45 AM.png$

Вправа$\PageIndex{6}$

$p(x) = 2x^3−3x^2−44x$

Вправа$\PageIndex{7}$

$p(x) = −2x^3+4x^2+70x$

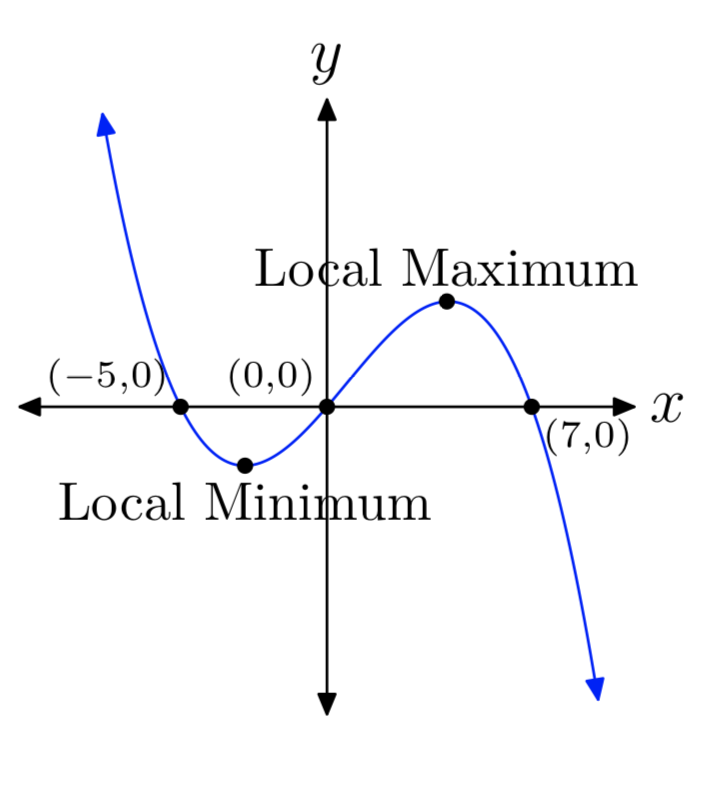
Відповідь: $Знімок екрана 2019-09-02 о 9.03.27 AM.png$

Вправа$\PageIndex{8}$

$p(x) = −6x^3−21x^2+90x$

У вправах 9 - 16 виконайте кожне з наступних завдань для даного полінома.

Використовуйте графічний калькулятор, щоб намалювати графік многочлена. Налаштуйте оглядове вікно так, щоб в оглядовому вікні були видні крайності або «точки повороту» многочлена. Скопіюйте отримане зображення на домашній робочий папір. Позначте та масштабуйте кожну вісь за допомогою xmin , xmax, ymin та ymax.
Використовуйте максимальну і/ або мінімальну утиліту в меню CALC вашого калькулятора, щоб знайти координати екстреми. Позначте кожен екстремум на копії домашнього завдання з його координатами та вкажіть, чи є екстремум відносним або абсолютним максимумом або міні-мамою.

Вправа$\PageIndex{9}$

$p(x) = x^3−8x^2−5x+84$

Відповідь

Відносний макс: (−0,2960664, 84.753138)

Відносний мін: (5.6293978, −19.27166)

Відповіді можуть дещо відрізнятися через помилку округлення.

$Знімок екрана 2019-09-02 о 9.05.38 AM.png$

Вправа$\PageIndex{10}$

$p(x) = x^3+3x^2−33x−35$

Вправа$\PageIndex{11}$

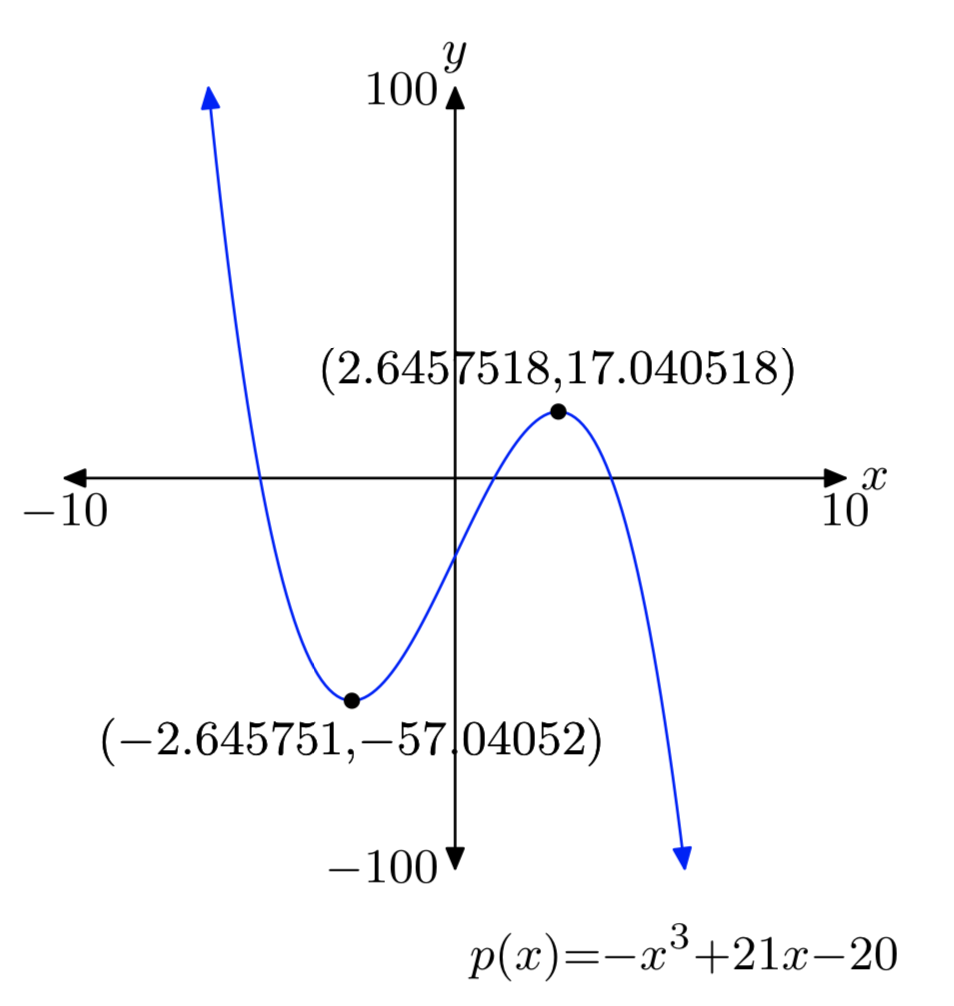
$p(x) = −x^3+21x−20$

Відповідь

Відносна хв: (− 2. 645751, − 57. 04052)

Відносний макс: (2. 6457518, 17. 040518)

Відповіді можуть дещо відрізнятися через помилку округлення.

$Знімок екрана 2019-09-02 о 9.06.51 AM.png$

Вправа$\PageIndex{12}$

$p(x) = −x^3+5x^2+12x−36$

Вправа$\PageIndex{13}$

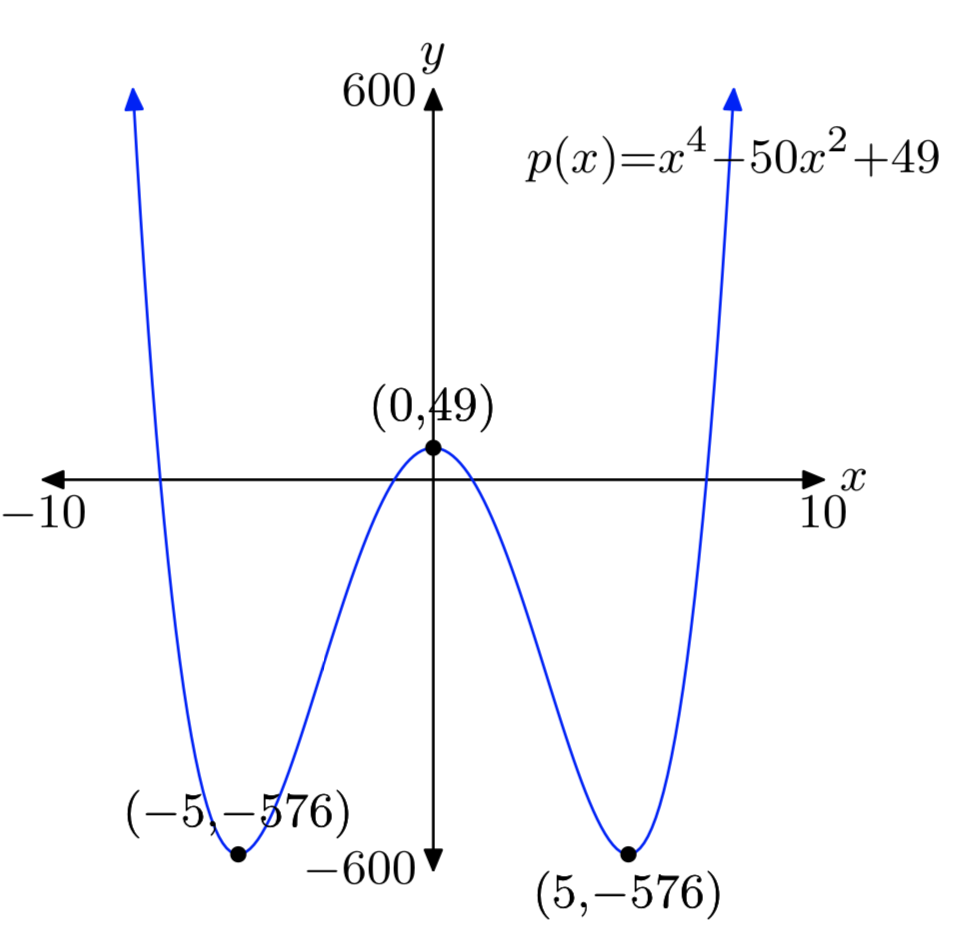
$p(x) = x^4−50x^2+49$

Відповідь

Абсолютна хв: (−5, −576)

Відносний макс: (0, 49)

Абсолютна хв: (5, −576)

Відповіді можуть дещо відрізнятися через помилку округлення.

$Знімок екрана 2019-09-02 о 9.08.17 AM.png$

Вправа$\PageIndex{14}$

$p(x) = x^4−29x^2+100$

Вправа$\PageIndex{15}$

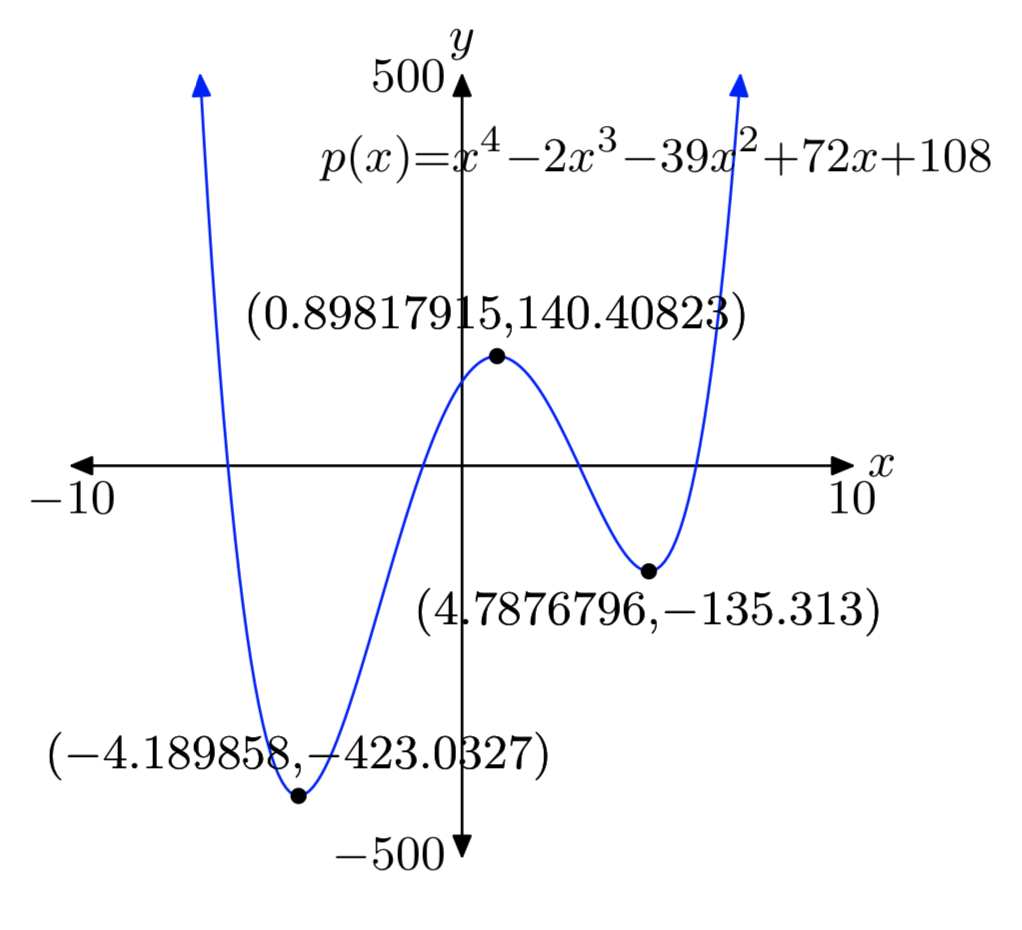
$p(x) = x^4−2x^3−39x^2+72x+108$

Відповідь

Абсолютна хв: (−4,189858, −423.0327)

Відносний макс: (0.89817915, 140.40823)

Відносний хв: (4.7876796, −135.313)

Відповіді можуть дещо відрізнятися через помилку округлення.

$Знімок екрана 2019-09-02 о 9.09.20 AM.png$

Вправа$\PageIndex{16}$

$p(x) = x^4−3x^3−31x^2+63x+90$

Вправа$\PageIndex{17}$

Квадратний шматок картону вимірює 12 дюймів на кожну сторону. Чері вирізає чотири менших квадрата з кожного кута картонного квадрата, відкидаючи матеріал в сторону. Потім вона загинає вгору по сторонам залишився картону, щоб сформувати відкриту коробку без верху. Знайдіть розміри квадратів, вирізаних з кожного кута вихідного шматка картону так, щоб Чері максимально збільшила обсяг отриманої коробки. Виконайте кожен з наступних кроків у своєму аналізі.

Встановіть рівняння, яке визначає обсяг коробки як функція x, довжина краю кожного квадрата, вирізаного з чотирьох кутів картону. Включіть будь-які зображення, які використовуються для визначення цієї функції гучності.
Створіть емпіричну область функції, створеної в частині (а). Скористайтеся калькулятором, щоб намалювати графік функції над цією емпіричною областю. Налаштуйте вікно перегляду так, щоб у вікні перегляду були видні всі крайності.
Скопіюйте зображення у вікні перегляду на домашній папір. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax. Використовуйте утиліту maximum, щоб знайти координати абсолютного максимуму в емпіричній області функції.
Які міри чотирьох квадратів, вирізаних з кожного кута оригінального картону? Який максимальний обсяг коробки?

Відповідь

$V = x(12−2x)^2$
[0, 6]
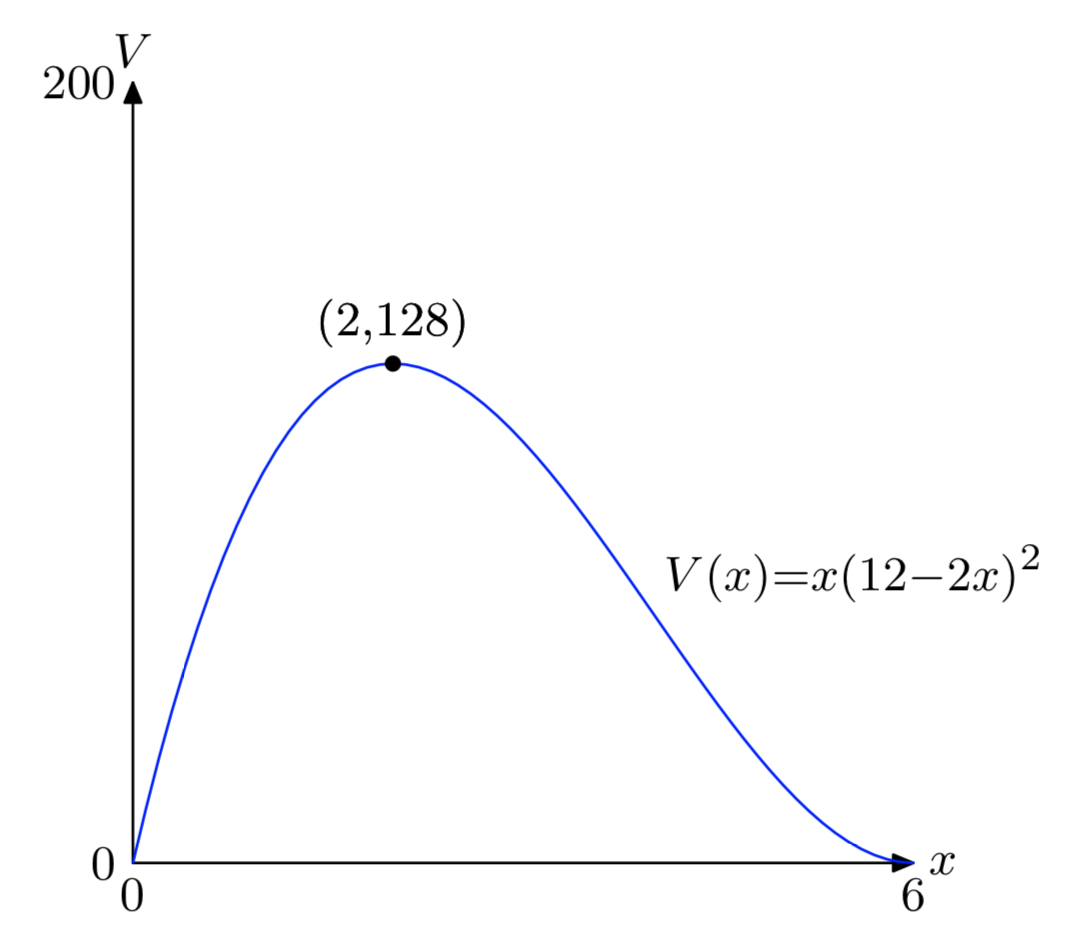
Абсолютний макс: (2, 128) $Знімок екрана 2019-09-02 о 9.11.48 AM.png$
Виріжте квадрат 2 дюйми збоку, щоб виготовити коробку, що має значення 128$in^3$.

Вправа$\PageIndex{18}$

Прямокутний шматок картону розміром 8 дюймів на 12 дюймів. Шуйлер вирізає чотири менших квадрата з кожного кута картонного квадрата, відкидаючи матеріал в сторону. Потім він загинає вгору по сторонам залишився картону, щоб сформувати відкриту коробку без верху. Знайдіть розміри квадратів, вирізаних з кожного кута вихідного шматка картону так, щоб Шуйлер максимально збільшив обсяг отриманої коробки. Виконайте кожен з наступних кроків у своєму аналізі.

Встановіть рівняння, яке визначає обсяг коробки як функція x, довжина краю кожного квадрата, вирізаного з чотирьох кутів картону. Включіть будь-які зображення, які використовуються для визначення цієї функції гучності.
Створіть емпіричну область функції, створеної в частині (а). Скористайтеся калькулятором, щоб намалювати графік функції над цією емпіричною областю. Налаштуйте вікно перегляду так, щоб у вікні перегляду були видні всі крайності.
Скопіюйте зображення у вікні перегляду на домашній папір. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax. Використовуйте утиліту maximum, щоб знайти координати абсолютного максимуму в емпіричній області функції.
Які міри чотирьох квадратів, вирізаних з кожного кута оригінального картону? Який максимальний обсяг коробки?

Вправа$\PageIndex{19}$

Обмежте графік параболи$y = 4−\frac{x^2}{4}$ першим квадрантом, потім впишіть прямокутник всередину параболи, як показано на наступному малюнку.

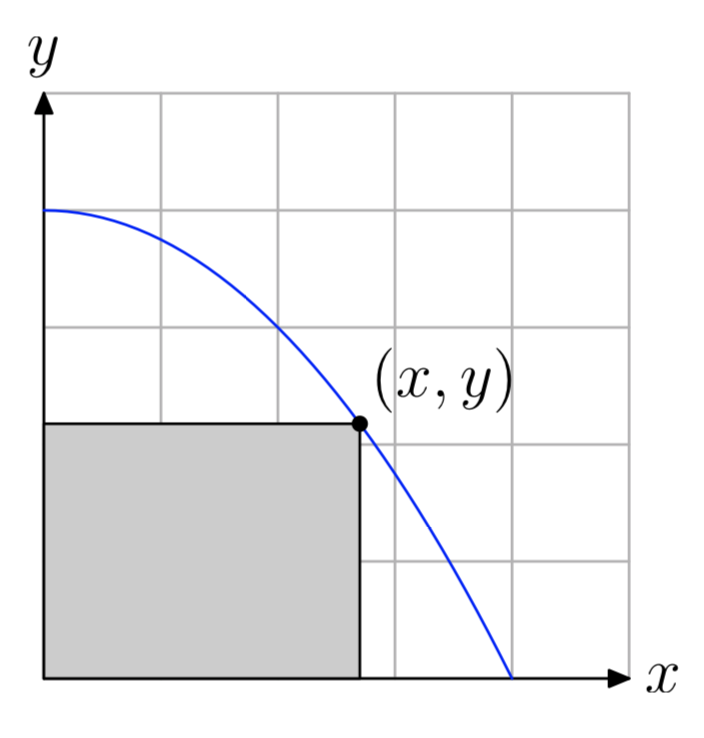
$Знімок екрана 2019-09-02 в 8.55.44 AM.png$

Висловіть площу вписаного прямокутника як функцію x.
Створіть емпіричну область функції, визначеної в частині (1). Використовуйте калькулятор для графіка функції області над її емпіричною областю. Налаштуйте параметри вікна так, щоб всі крайності були видні у вікні перегляду.
Скопіюйте зображення у вікні перегляду на домашній папір. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax. Використовуйте утиліту maximum, щоб знайти координати абсолютного максимуму в емпіричній області функції. Позначте свій графік цим результатом.
Які розміри прямокутника максимальної площі?

Відповідь

$A = x(4−\frac{x^2}{4})$
[0, 4]
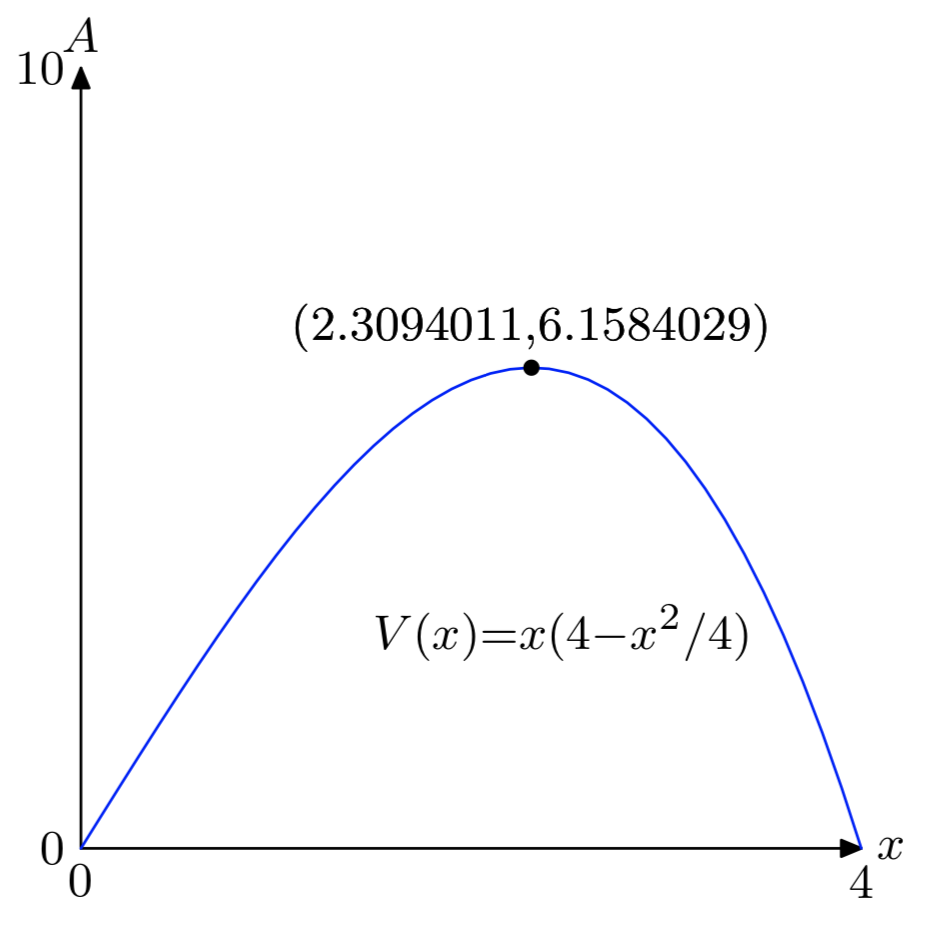
Абсолютний макс: (2.3094011, 6.1584029) $Знімок екрана 2019-09-02 в 9.13.14 AM.png$
х = 2. 3094011, у = 2. 666666

Вправа$\PageIndex{20}$

Обмежте графік параболи$y = 4−\frac{x^2}{4}$ першим квадрантом, потім впишіть трикутник всередину параболи, як показано на наступному малюнку.

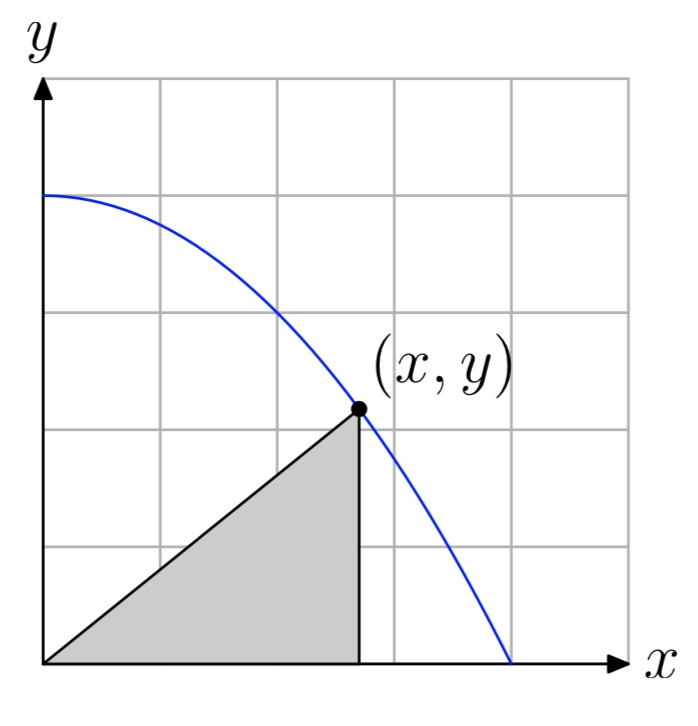
$Знімок екрана 2019-09-02 в 8.59.33 AM.png$

Висловіть площу вписаного три-кута як функцію x.
Створіть емпіричну область функції, визначеної в частині (а). Використовуйте калькулятор для графіка функції області над її емпіричною областю. Налаштуйте параметри вікна так, щоб всі крайності були видні у вікні перегляду.
Скопіюйте зображення у вікні перегляду на домашній папір. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax. Використовуйте утиліту maximum, щоб знайти координати абсолютного максимуму в емпіричній області функції. Позначте свій графік цим результатом.
Яка довжина підстави і висота трикутника максимальної площі?