3.5: Лінія найкращої підгонки

Збираючи дані в реальному світі, графік даних часто виявляє «лінійний тренд», але дані не потрапляють точно на одну лінію. У цьому випадку ми прагнемо знайти лінійну модель, яка наближає дані. Давайте почнемо з розгляду розширеного прикладу.

Aditya і Tami є партнерами лабораторії в класі фізики доктора Міллса. Вони звисають маси з пружини і вимірюють отримане розтягнення в пружині. Див. Таблицю\(\PageIndex{1}\) для їх даних.

Таблиця\(\PageIndex{1}\). Набір даних Адітья і Тамі.

m (маса в грамах)	10	20	30	40	50
x (розтяжка в см)	6.8	10.2	13,9	21.2	24.2

Мета полягає в тому, щоб знайти модель, яка описує дані, як у вигляді графіка, так і рівняння. Першим кроком є побудова даних. Згадаймо деякі рекомендації, надані в першому розділі поточної глави.

Рекомендації

При побудові реальних даних ми дотримуємося цих рекомендацій.

1. Ви не хочете дрібних графіків. Найкраще масштабувати графік так, щоб він заповнив повний аркуш графічного паперу. Це значно полегшить читання і інтерпретацію графіка.
2. У вас можуть бути різні масштаби на кожній осі, але після вибору ви повинні залишатися послідовними.
3. Ви хочете вибрати масштаб, який полегшує нашу першу мету, але також робить дані легкими для побудови графіків.

Адітья і Тамі вільні вибирати маси, які вони висять на пружині. Значить, маса m є незалежною змінною. Отже, ми масштабуємо горизонтальну вісь для розміщення маси. Відстань, яку пружина розтягує, залежить від кількості маси, яка звисає з пружини, тому відстань розтягнута x є залежною змінною. Ми масштабуємо вертикальну вісь, щоб вмістити розтягнуту відстань.

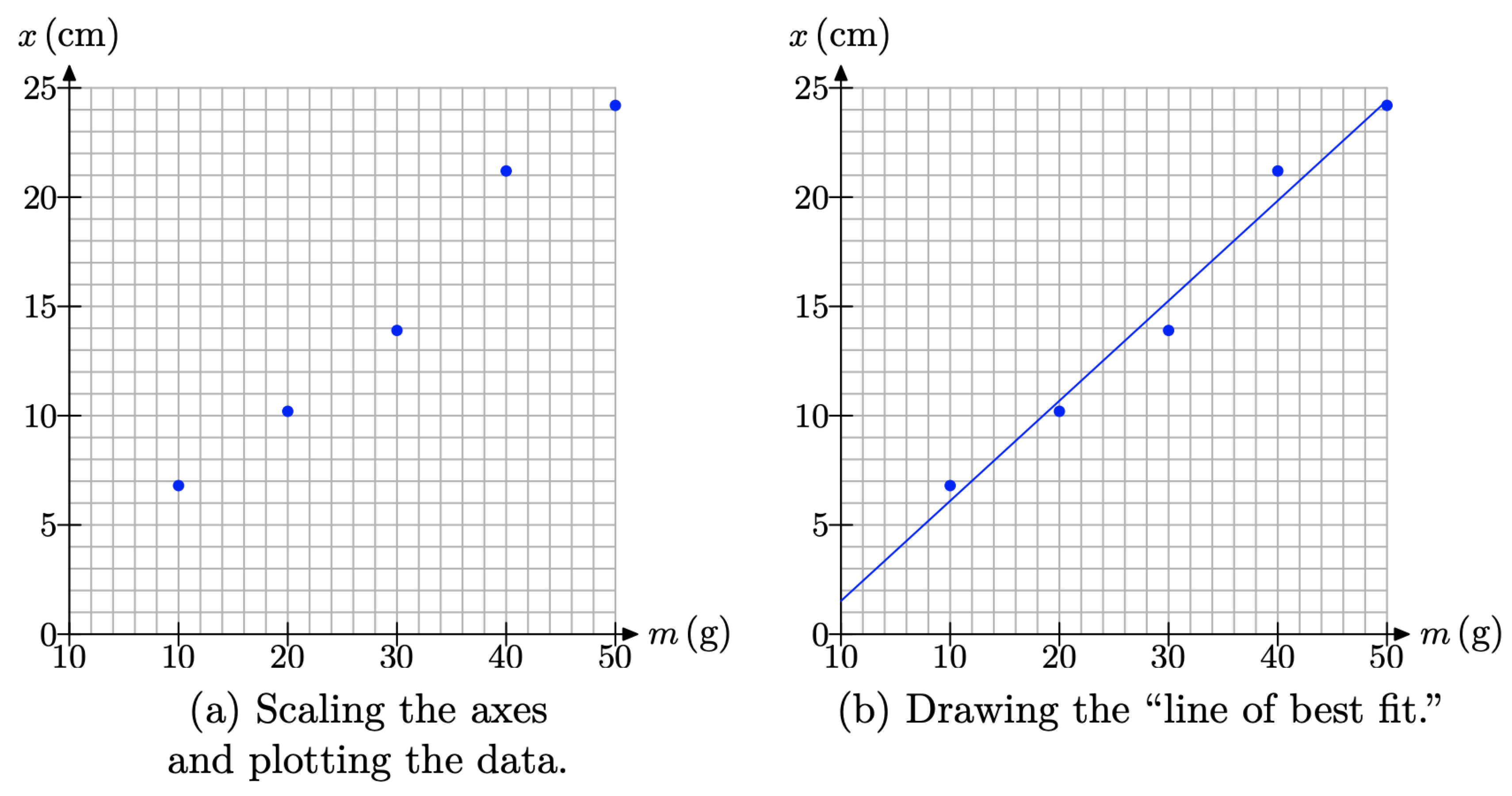
На горизонтальну вісь нам потрібно підігнати маси 10, 20, 30, 40 і 50 грам. Щоб уникнути невеликого графіка, ми дозволимо кожні 5 коробок представляти 10 грам. На вертикальній осі нам потрібно підігнати відстані від 6,8 сантиметрів до 24, 2 сантиметрів включно. Роблячи кожне поле представляти 1 см дає хороший розмір графіка і дозволить легко побудувати наші точки даних, що ми зробили на малюнку\(\PageIndex{1}\) (а).

Зверніть увагу на лінійний тренд, який відображається даними на малюнку\(\PageIndex{1}\) (а). Неможливо намалювати одну лінію, яка буде проходити через кожну з точок даних, тому лінійна модель не буде точно «відповідати» даними. Однак дані є «приблизно лінійними», тому давайте спробуємо провести лінію, яка «майже відповідає» даними.

Тут не наша мета намагатися намалювати лінію, яка проходить через якомога більше точок даних. Якщо ми це зробимо, то ми по суті говоримо, що точки, через які лінія не проходить, не мають ніякого впливу на загальну модель, а також не впливають на будь-які прогнози, які ми могли б зробити з нашою моделлю. Це не є розумним припущенням.

Дійсно, мета полягає в тому, щоб провести лінію, яка максимально наближається до якомога більшої кількості точок. Деякі моменти будуть лежати вище лінії, деякі будуть лежати нижче, і те, що ми спробуємо зробити, це «збалансувати» завищені і занижені в спробі мінімізувати загальну похибку. Найкращий спосіб зробити це - взяти чітку пластикову лінійку, щось, що ви можете побачити, і обертати та зміщувати лінійку, поки ви не думаєте, що у вас є лінія, яка врівноважує завищені та занижені. Ми зробили це для вас на малюнку\(\PageIndex{1}\) (b). Отримана лінія називається «лінією найкращого прилягання».

Малюнок\(\PageIndex{1}\).

Ми можемо використовувати «лінію найкращої посадки» на малюнку\(\PageIndex{1}\) (b) для прогнозування. Наприклад, якби ми хотіли передбачити, наскільки пружина розтягнеться, коли Адітя та Тамі прикріплять 22 грами маси, то ми б розташували 22 грами на горизонтальній осі, проведемо вертикальну лінію вгору до «лінії найкращого прилягання», а потім горизонтальну лінію до вертикальної осі, як показано на малюнку\(\PageIndex{2}\) (а). Зверніть увагу, що значення x на вертикальній осі, здається, становить приблизно 11,6 сантиметра.

Як варіант, ми розробимо модель рівняння. Спочатку виділіть дві точки на «лінії найкращого прилягання», використовуючи наступні рекомендації.

Примітка

1. Виберіть дві точки на «лінії найкращого прилягання», які не є точками даних.
2. Намагайтеся підбирати точки, що проходять через точку решітки сітки. Це значно полегшує інтерпретацію координат точки.
3. Чим далі розділені дві вибрані точки, тим краще точність. Не вибирайте точки, які занадто близько один до одного.

Малюнок\(\PageIndex{2}\).

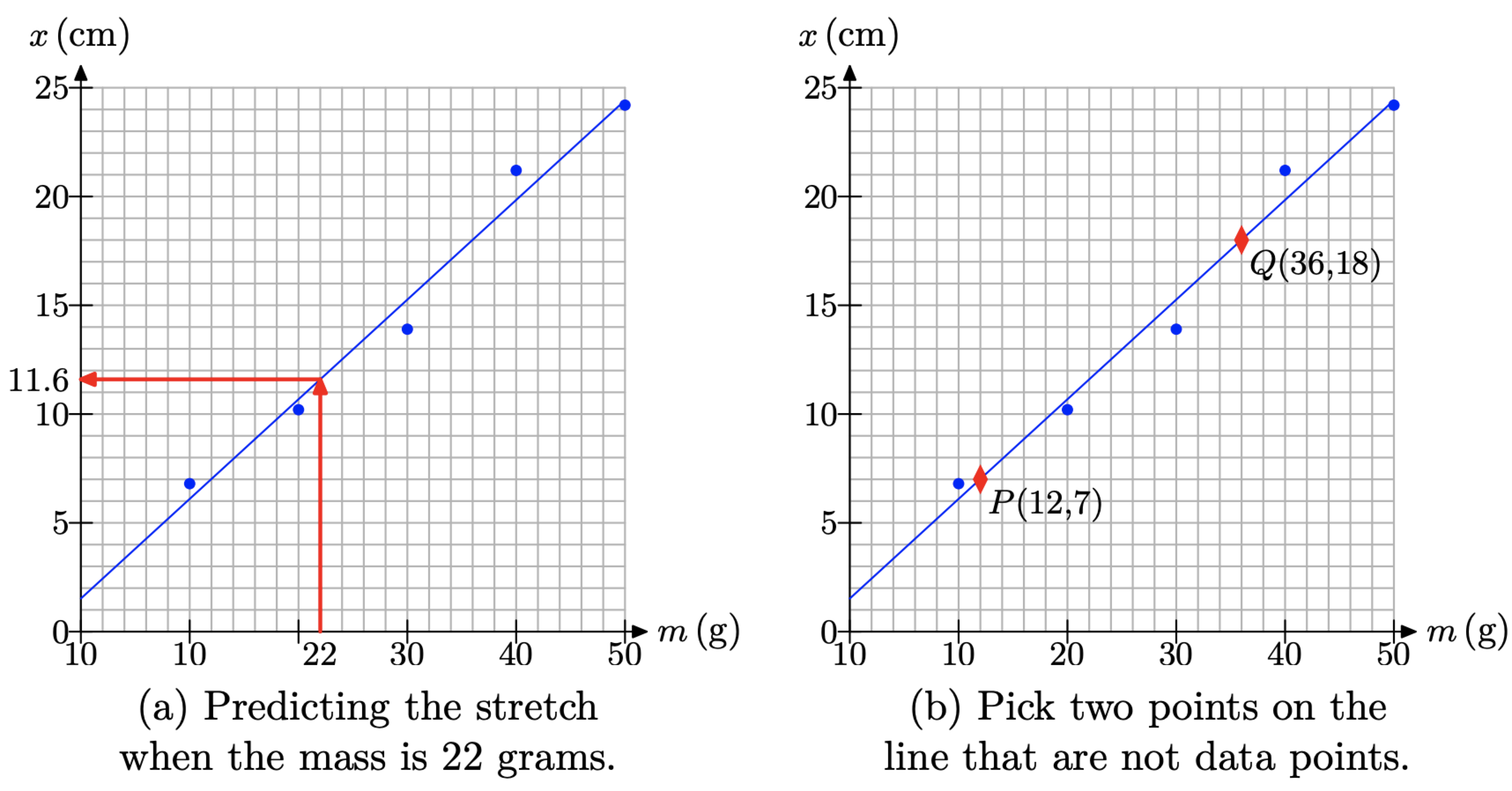
На малюнку\(\PageIndex{2}\) (b) ми вибрали точки P (12, 7) і Q (36, 18). Перший пункт вказує на те, що маса в 12 грам розтягує пружину на 7 сантиметрів. Тлумачення для другого пункту аналогічне. Ми можемо знайти нахил прямої через точки P і Q за формулою нахилу.

\[m=\frac{\Delta x}{\Delta m}=\frac{18 \mathrm{cm}-7 \mathrm{cm}}{36 \mathrm{g}-12 \mathrm{g}}=\frac{11}{24} \frac{\mathrm{cm}}{\mathrm{g}}\]

Нахил лінії - це швидкість, з якою змінюється протягнута відстань щодо того, як змінюється маса. При цьому на кожні додаткові 24 грами маси, яка висівається, пружина тягнеться додаткові 11 сантиметрів.

Наступним кроком є використання формули точка-нахил для визначення рівняння прямої.

\[y-y_{0}=m\left(x-x_{0}\right)\]

Використовуємо точку Р (12, 7). Тобто набір\(\left(x_{0}, y_{0}\right)=(12,7)\). Підставити\(m=11 / 24, x_{0}=12\), і\(y_{0}=7\) в рівняння (1) отримати

\[y-7=\frac{11}{24}(x-12)\]

У застосуванні пружинної маси залежна змінна дорівнює x, а не y, а незалежна змінна m, а не x Замініть y ліворуч рівняння (2) на x, а потім замініть x праворуч рівняння (2) на m, щоб отримати

\[x-7=\frac{11}{24}(m-12)\]

Розв'яжіть рівняння (3) для x

\[\begin{aligned} x-7 &=\frac{11}{24} m-\frac{132}{24} \\ x &=\frac{11}{24} m-\frac{132}{24}+7 \\ x &=\frac{11}{24} m-\frac{132}{24}+\frac{168}{24} \\ x &=\frac{11}{24} m+\frac{36}{24} \end{aligned}\]

Зменшіть 36/24 до 3/2, щоб отримати

\[x=\frac{11}{24} m+\frac{3}{2}\]

Нагадаємо, що х являє собою розтягнуту відстань, а m - кількість маси, підвішеної з пружини. Тобто x є функцією m. Ми можемо використовувати позначення функції, щоб записати останнє рівняння наступним чином.

\[x(m)=\frac{11}{24} m+\frac{3}{2}\]

Ми можемо використовувати модель в рівнянні (4) для визначення кількості розтягування, коли до пружини прикріплюється маса 22 грами. Підставте m = 22 в рівняння (4), потім скористайтеся калькулятором, щоб наблизити розтягнення навесні.

\[x(22)=\frac{11}{24}(22)+\frac{3}{2} \approx 11.6 \mathrm{cm}\]

Зверніть увагу на згоду з графічним рішенням, знайденим на малюнку\(\PageIndex{2}\) (а). Читачі повинні розуміти, що такого роду точність не є звичайною нормою. Існує ряд факторів, які можуть внести помилку.

• Адітья і Тамі, можливо, не зробили точних вимірювань в лабораторії, тому дані можуть бути помилковими для початку.
• Можуть бути помилки, коли ми масштабуємо осі і будуємо дані.
• Лінія «очного яблука» найкращої посадки, яку ми намалювали, була дуже суб'єктивною. Невелике обертання або переклад лінійки під час малювання передбачуваної «лінії найкращого прилягання» може дати різні результати.
• Наші розрахунки можуть містити помилки та помилки округлення.

Використання графічного калькулятора для пошуку лінії найкращого підходу

Статисти розробили певний метод, званий «методом найменших квадратів», який використовується для пошуку «лінії найкращого підгонки» для набору даних, що показує лінійний тренд. Алгоритм прагне знайти рядок, який мінімізує загальну похибку. Ці алгоритми запрограмовані в графічний калькулятор і доступні для використання студентом.

Щоб використовувати графічний калькулятор для визначення лінії найкраще підходить, перше, що вам потрібно дізнатися, як це зробити, це завантажити дані з таблиці\(\PageIndex{1}\) в калькулятор.

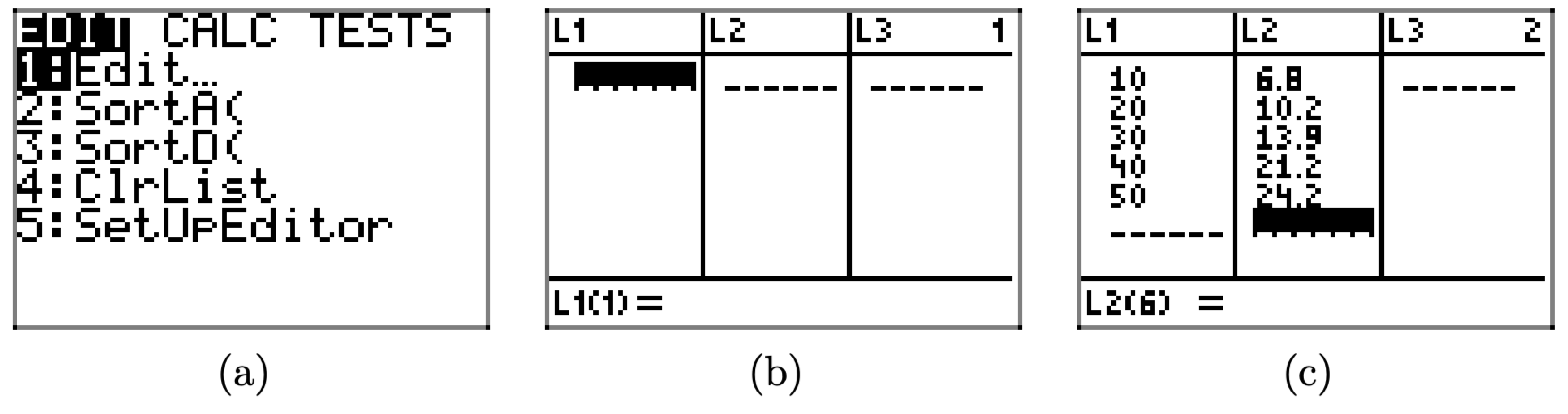
• Знайдіть і натисніть кнопку STAT на клавіатурі, яка відкриє меню, показане на малюнку\(\PageIndex{3}\) (а).

• Виберіть 1: Редагувати з цього меню, яке відкриє вікно редагування, показане на малюнку\(\PageIndex{3}\) (b).

• Введіть дані з таблиці\(\PageIndex{1}\) в списки\(L_{1}\) і\(L_{2}\), як показано на малюнку\(\PageIndex{3}\) (c)

Малюнок\(\PageIndex{3}\). Введіть дані з таблиці\(\PageIndex{1}\) в списки\(L_{1}\) і\(L_{2}\) в графічний калькулятор.

Наступним кроком буде побудова даних, які ви ввели в списки\(L_{1}\) і\(L_{2}\).

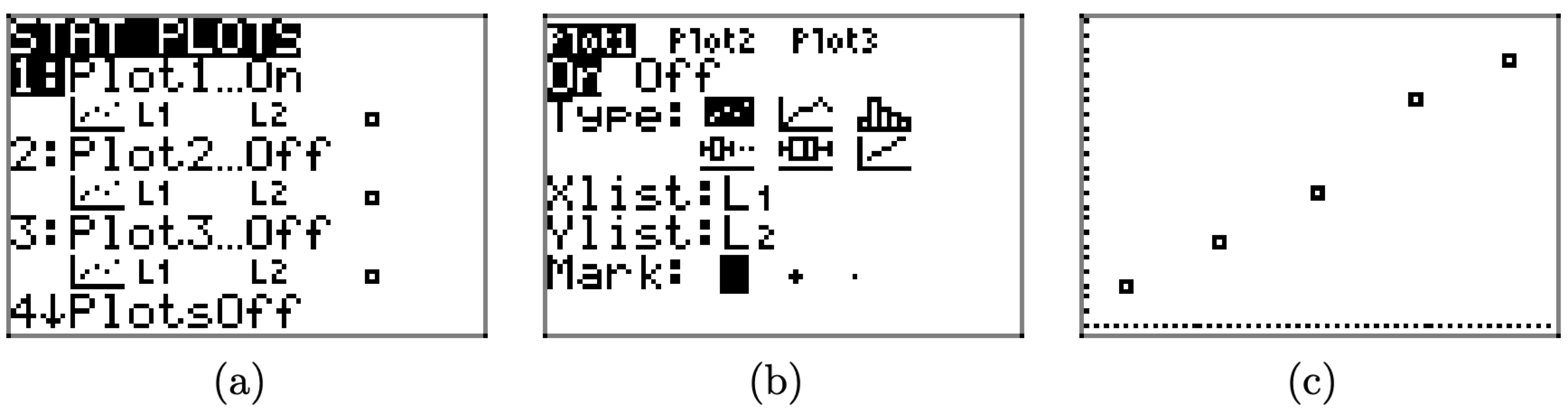
• Натискаємо 2ND клавішу, а потім STAT PLOT (розташований над меню Y =). Відкриється вікно, показане на малюнку\(\PageIndex{4}\) (а).
• Виберіть 1: Plot1, щоб відкрити вікно вибору графіка, показане на малюнку\(\PageIndex{4}\) (b).
• У вікні вибору графіка на малюнку\(\PageIndex{4}\) (b) є кілька речей, які потрібно перевірити.

1. За допомогою клавіш зі стрілками наведіть курсор на слово «On» і натисніть клавішу ENTER, щоб виділити це виділення.
2. Існує шість «типів» ділянок: розсіювач, лінійний плот, гістограма, модифікований графік коробки, графік коробки та графік нормальної ймовірності. Ці варіанти розташовуються в два ряди по три ділянки. Наведіть курсор на перший графік першого рядка, розсіювач, а потім натисніть клавішу ENTER, щоб виділити виділення.
3. Наступним вибором буде XList. Це список, який йде по горизонтальній осі. У випадку з Таблицею 1 ми хочемо розмістити масові дані на горизонтальній осі. Масові дані ми ввели в список L1, тому вводимо 2ND L1 (L1 знаходиться над 1 на клавіатурі).
4. Наступний вибір - Ylist. Введіть 2ND L2 (L2 розташований над 2 на клавіатурі). Тут вказано відстань, розтягнуте і буде розміщено на вертикальній осі.
5. Останній пункт - маркер. Виберіть першу клавішами зі стрілками (це найпростіше побачити) і натисніть клавішу ENTER, щоб виділити цей вибір.

• Натисніть кнопку ZOOM на першому рядку клавіш на клавіатурі. Використовуйте клавіші зі стрілками для прокрутки меню вниз, поки не зможете вибрати 9:ZoomStat. Це призведе до отримання зображення, показаного на малюнку\(\PageIndex{4}\) (c).

Малюнок\(\PageIndex{4}\). Побудова точок даних з таблиці\(\PageIndex{1}\)

Завершальним етапом є розрахунок і побудова лінії найкращого підгонки.

• Знову натисніть кнопку STAT, але потім за допомогою стрілки вправо виберіть підменю CALC, виділене на малюнку\(\PageIndex{5}\) (а).
• Виберіть 4:LinReg (ax+b) у підменю CALC. Це розміщує команду LinReg (ax+b) на головному екрані, як показано на малюнку\(\PageIndex{5}\) (b). Потім необхідно набрати 2ND\(L_{1}\), кому (знаходиться на власній клавіші трохи вище клавіші 7), потім 2-ю\(L_{2}\), як показано на малюнку\(\PageIndex{5}\) (b).
• Натисніть клавішу ENTER, щоб виконати команду LinReg\(L_{1}\)\(L_{2}\), яка виробляє рівняння лінії найкращого прилягання, показаного на малюнку\(\PageIndex{5}\) (c).

Малюнок\(\PageIndex{5}\). Знаходження рівняння лінії найкращого прилягання.

Екран на малюнку\(\PageIndex{5}\) (в) досить інформативний. Це говорить нам дві речі.

1. Рівняння лінії найкращого прилягання дорівнює y = ax + b.
2. Ухил дорівнює a = .458, а y-перехоплення - b = 1,52.

Підставляючи a = 0,458 і b = 1,52 в рівняння y = ax + b дає нам рівняння лінії найкращого прилягання.

\[y=0.458 x+1.52\]

Ми можемо накласти графік лінії найкращої відповідності на наш набір даних у два простих кроки.

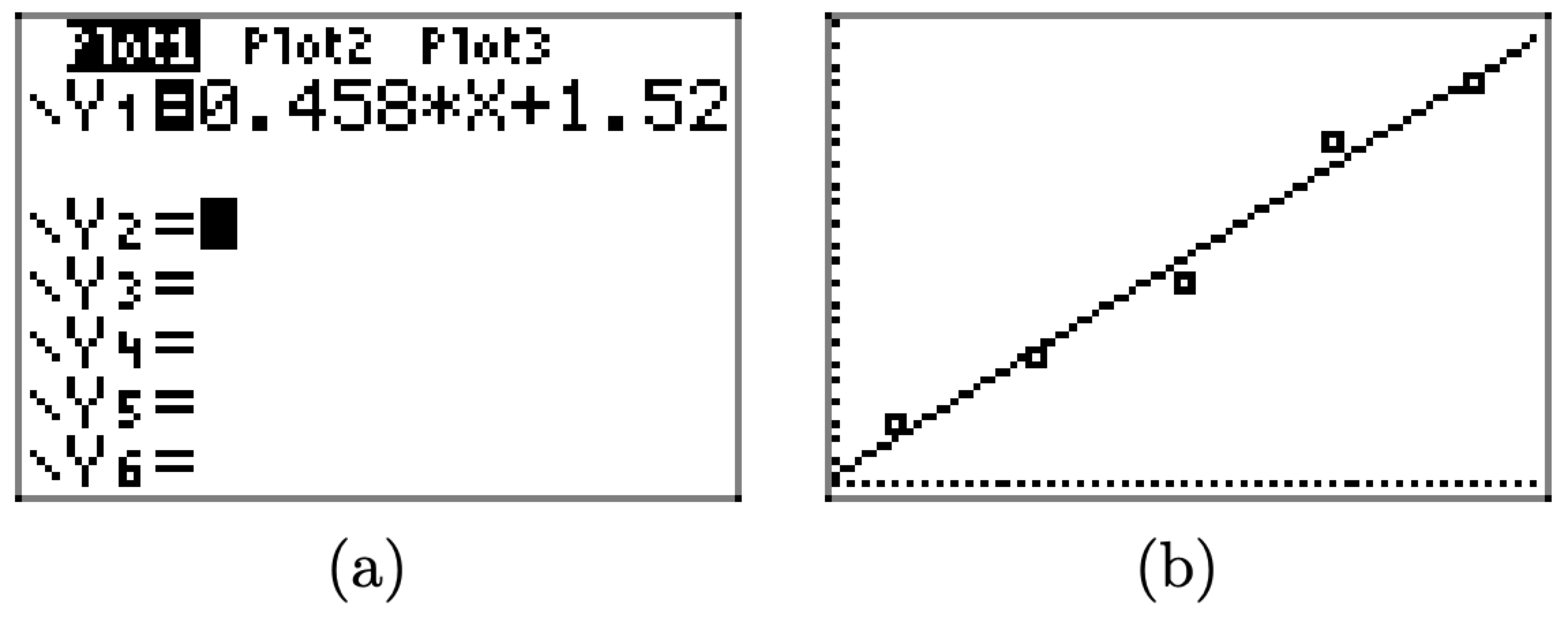
• Натисніть клавішу Y = і введіть рівняння 0.458* X+1.52 в\(\boldsymbol{Y}_{1}\), як показано на малюнку\(\PageIndex{6}\) (а).
• Натисніть кнопку GRAPH у верхньому рядку клавіш на клавіатурі, щоб створити рядок, який найкраще підходить на малюнку\(\PageIndex{6}\) (b).

Малюнок\(\PageIndex{6}\). Накладіть лінію найкращого прилягання на розсіювач даних з таблиці\(\PageIndex{1}\).

У лівій частині рівняння (5) замініть y на x (відстань розтягнуто); праворуч замініть x на m (кількість маси). Це призводить до результату.\[x=0.458 m+1.52\]

Ви можете згадати, що наш ручний розрахунок виробляв рівняння (4), яке ми повторюємо тут для зручності.

\[x=\frac{11}{24} x+\frac{3}{2}\]

Зверніть увагу, що 11\(/ 24 \approx 0.4583\) і 3/2 = 1,5, тому рівняння (6) тісно узгоджується з нашим ручним обчисленим рівнянням лінії найкращого прилягання.

Досить незвично мати ручну обчислену лінію найкращої відповідності так тісно узгоджується зі складним і дуже точним результатом, отриманим графічним калькулятором. Отже, не розчаровуйтеся, коли ваші результати домашнього завдання не збігаються так добре, як у цьому прикладі. Якщо ви перебуваєте в ballpark з ручним обчисленим рівнянням для лінії найкраще підходить, це, як правило, буде досить добре. Однак, якщо ваше обчислене вручну рівняння навіть не близьке до того, що виробляє ваш калькулятор, це «назад до креслярської дошки». Перевірте свій сюжет і свої розрахунки. Будьте вперті! Не будьте задоволені своїми результатами, поки у вас не буде розумної згоди.