3.3: Рівняння ліній
- Page ID
- 58081
У цьому розділі ми розробимо ухил-перехоплення форму лінії. Коли ви закінчите роботу в цьому розділі, ви повинні мати можливість подивитися на графік прямої і визначити її рівняння у формі нахилу-перехоплення.
Форма перехоплення нахилу
У попередньому розділі ми розробили формулу нахилу лінії. Припустимо, що залежна змінна y, а незалежна змінна x і у нас є лінія, що проходить через точки\(P\left(x_{1}, y_{1}\right)\) і\(Q\left(x_{2}, y_{2}\right)\), як показано на малюнку\(\PageIndex{1}\).
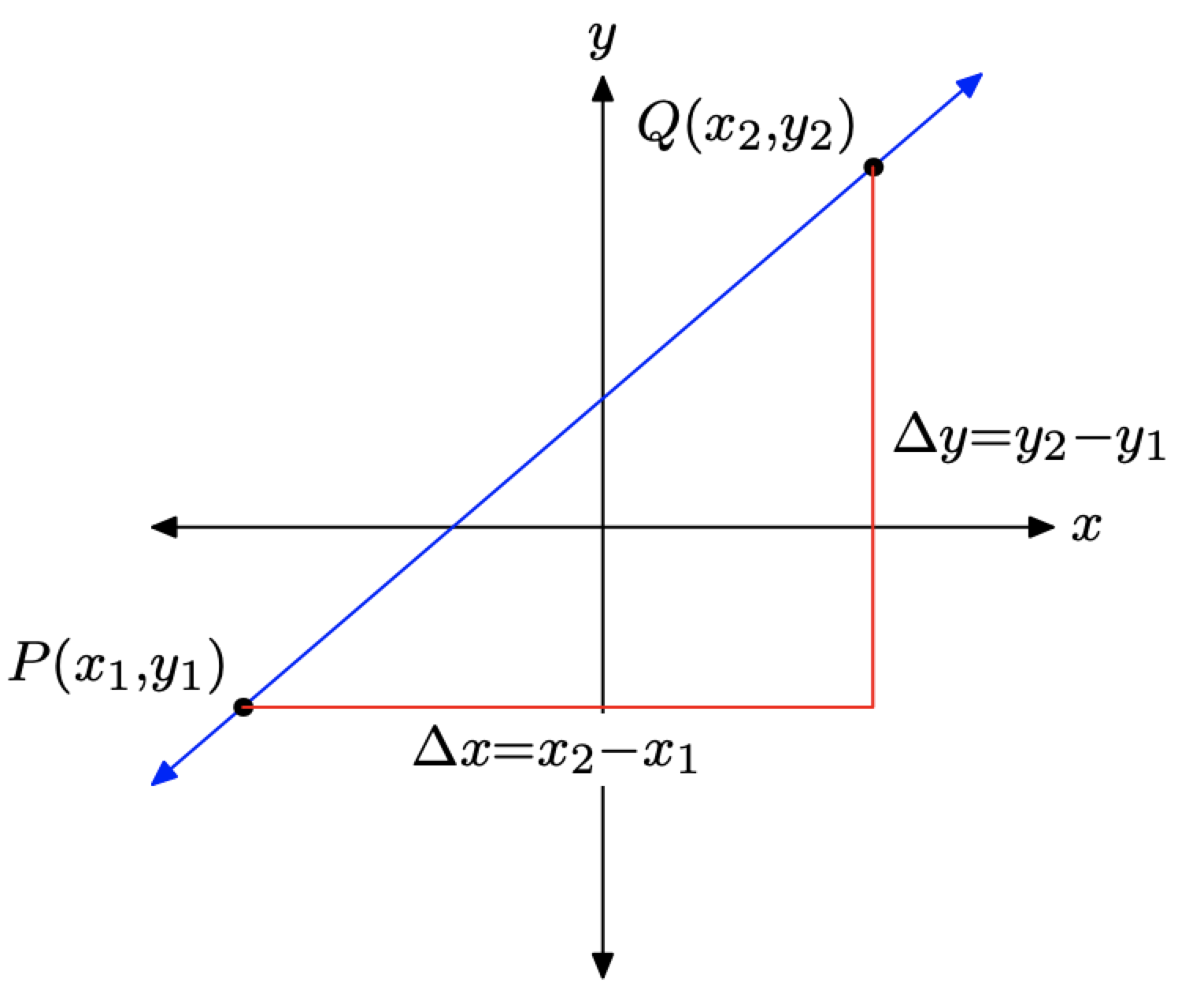
Коли ми підмітаємо очі зліва направо, зверніть увагу, що зміна х є\(\Delta x=x_{2}-x_{1}\) і зміна у є\(\Delta y=y_{2}-y_{1}\). Таким чином, нахил лінії визначається за формулою
\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\]
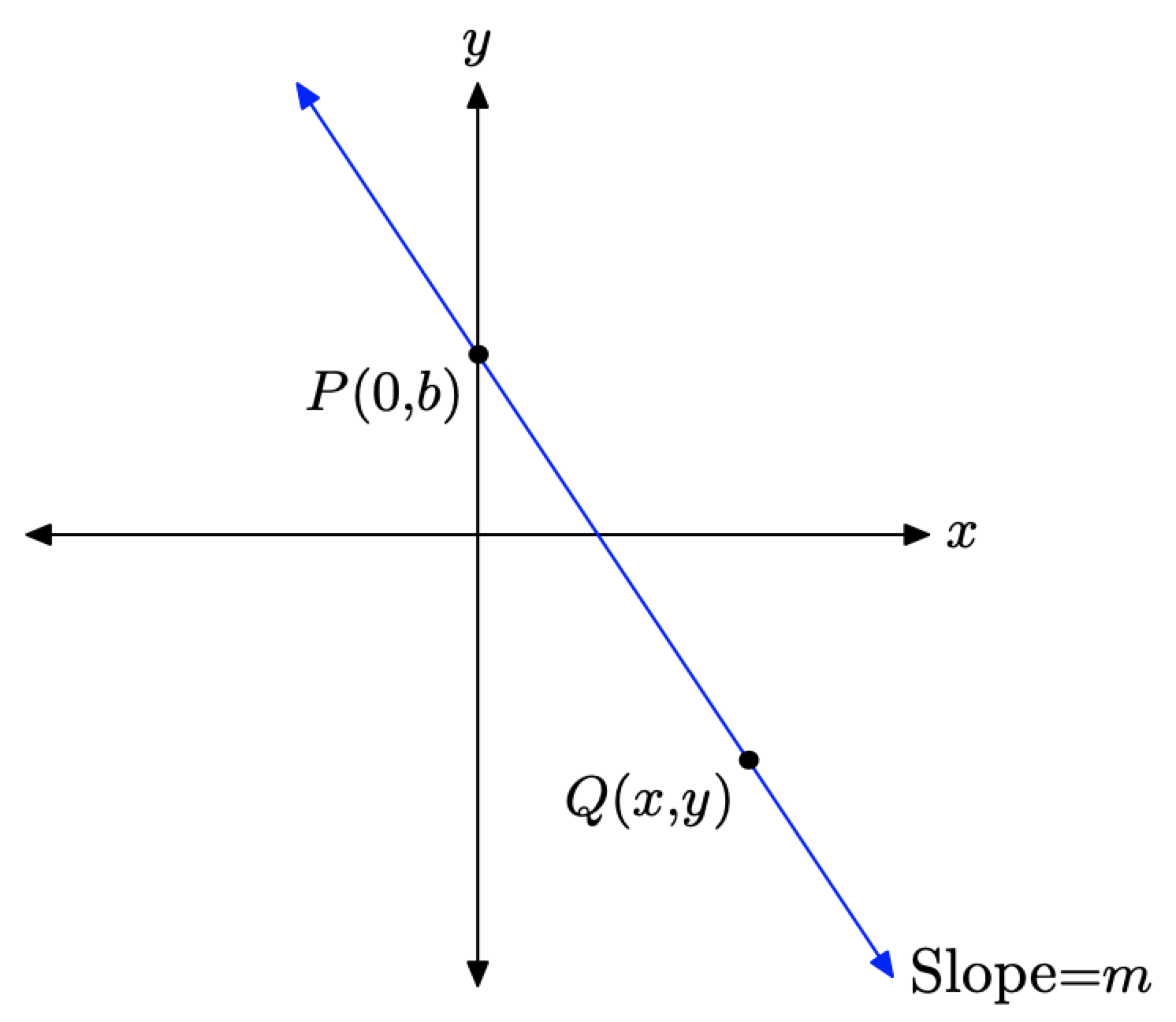
Тепер розглянемо рядок на малюнку\(\PageIndex{2}\). Припустимо, що нам наводяться два факти про цей рядок:
- Точка, де пряма перетинає вісь y (перехоплення y), дорівнює (0, b).
- «Ухил» лінії - деяке число m.
Щоб знайти рівняння лінії, зображеної на малюнку\(\PageIndex{2}\), виберіть довільну точку Q (x, y) на прямій, потім обчислите нахил прямої, використовуючи\(\left(x_{1}, y_{1}\right)=P(0, b)\) і\(\left(x_{2}, y_{2}\right)=Q(x, y)\) в формулі нахилу (1).
\[\text { Slope }=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{y-b}{x-0}\]
Спростити.
\[\text { Slope }=\frac{y-b}{x}\]
Ми отримали, що нахил є числом m, так що замініть це число на слово «схил» в останньому результаті.
\[m=\frac{y-b}{x}\]
Помножте обидві сторони останнього рівняння на\(x\).
\[m x=y-b\]
Додайте b до обох сторін останнього рівняння, щоб отримати
\[m x+b=y\]
або при обміні сторонами рівняння,
\[y=m x+b\]
Вищевикладене обговорення призводить до наступного результату.
Визначення: Форма перехоплення нахилу лінії
Якщо пряма\(L\) перехоплює вісь y в точці (0, b) і має нахил m, то рівняння прямої дорівнює
\[y=m x+b. \label{slopeintercept eq}\]
Така форма рівняння прямої називається формою нахилу-перехоплення. Функція, визначена рівнянням\[f(x)=m x+b\], називається лінійною функцією.
Важливо відзначити два ключових факту про ухил-перехоплення формі y = mx + b.
- Коефіцієнт х (m в y = mx + b) - це ухил лінії.
- Постійний член (b в y = mx+b) - y-координата y-перехоплення (0, b).
Порядок використання форми перехоплення ухилу лінії
Якщо задано нахил прямої та y-перехоплення лінії, використовуйте форму ухил-перехоплення наступним чином:
- Підставляємо заданий ухил на m у формулу\(y = mx + b\).
- Підставте у формулу y-координату перехоплення для b\(y = mx + b\).
Наприклад, якщо лінія має нахил −2, а перехоплення y (точка, де пряма перетинає вісь y) дорівнює (0, 3), тоді підставити m = −2 та b = 3 на Equation\ ref {slopeintercept eq}, щоб отримати
\[y = −2x + 3\].
Давайте розглянемо кілька прикладів використання цієї найважливішої формули.
Приклад\(\PageIndex{1}\)
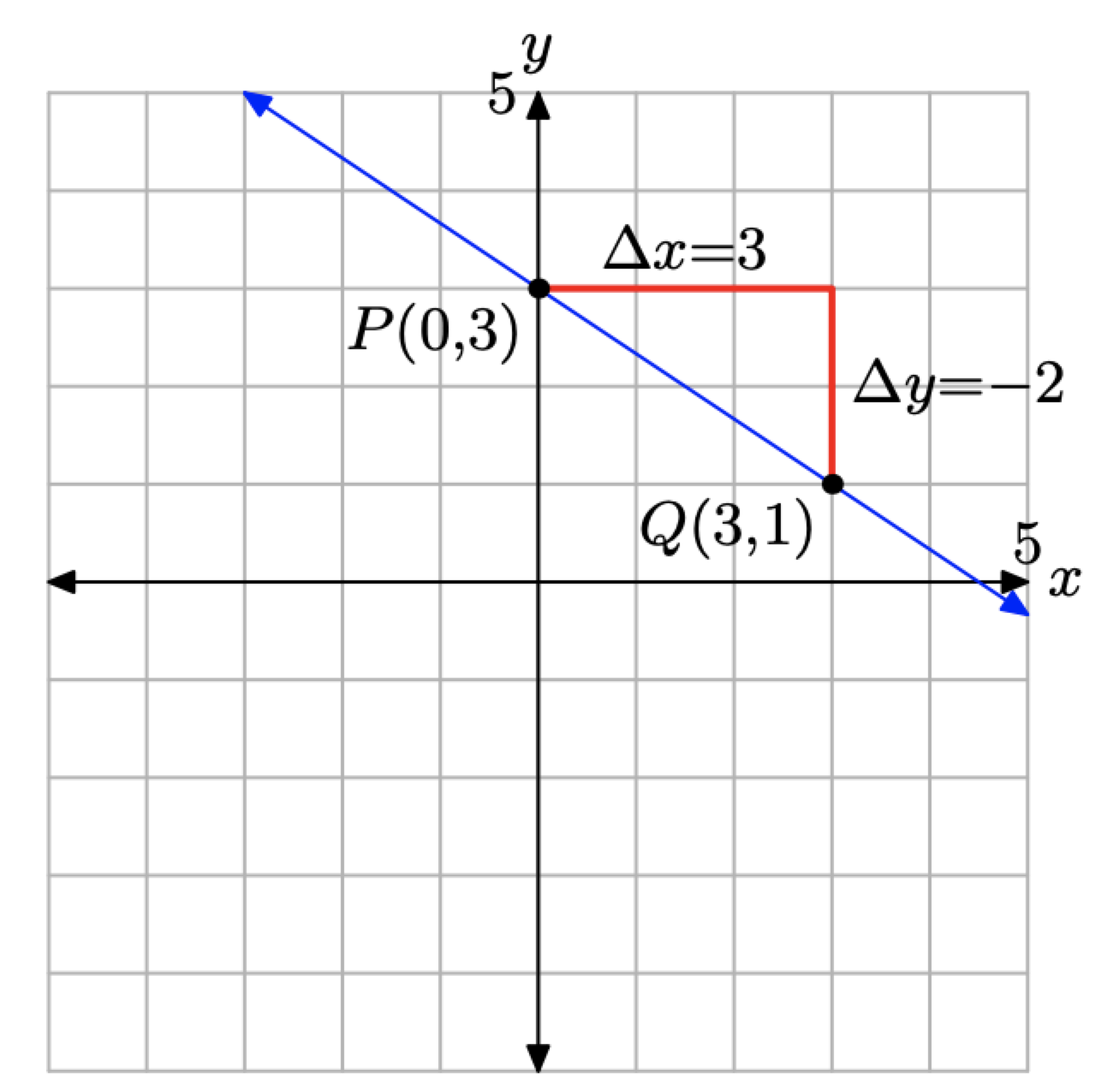
Яке рівняння прямої має нахил −2/3 та перехоплення y (0, 3)? Намалюйте лінію на графічному папері.
Рішення
Рівняння прямої
\[y=m x+b\]
Наведено, що нахил дорівнює −2/3. Значить, m = −2/3. По-друге, ми отримали, що лінія перехоплює вісь y в точці (0, 3). У формі нахилу-перехоплення y = mx + b нагадаємо, що b представляє y-координату y-перехоплення. Значить, b = 3. Підставляємо m = −2/3 і b = 3 в рівнянні (4), отримавши
\[y=-\frac{2}{3} x+3\]
Щоб намалювати графік лінії, спочатку знайдіть y-перехоплення на P (0, 3), як показано на малюнку\(\PageIndex{3}\). Починаючи з y-перехоплення на P (0, 3), перемістіть 3 одиниці вправо і 2 одиниці вниз до точки Q (3, 1). Необхідна лінія проходить через точки Р і Q.
Зверніть увагу, що лінія «перехоплює» вісь y на 3 і нахиляється вниз, відповідно до того, що нахил негативний в даному прикладі.
Приклад\(\PageIndex{2}\)
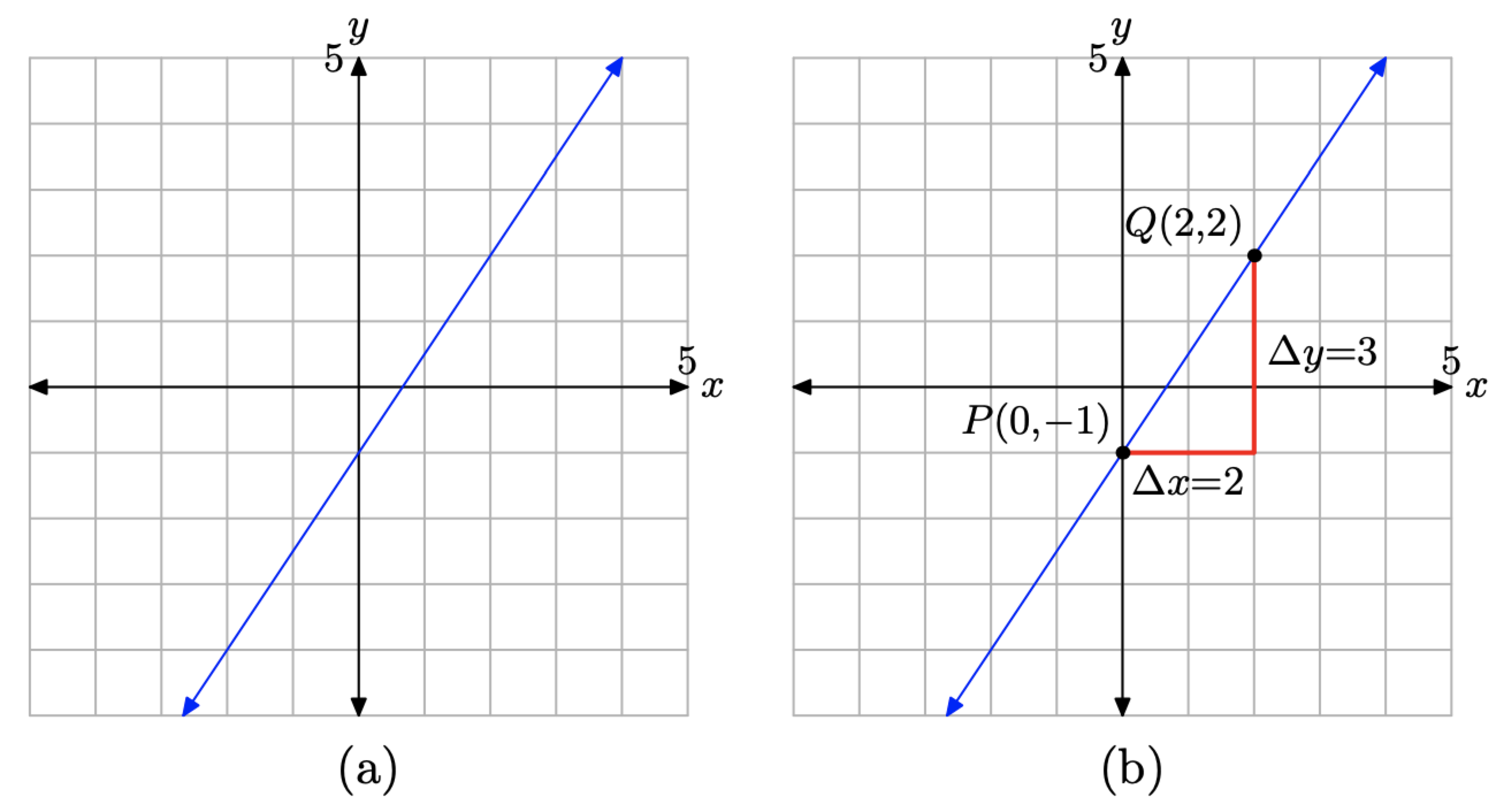
З огляду на графік прямої на малюнку\(\PageIndex{4}\) (а), визначте рівняння прямої.
Рішення
Спочатку знайдіть y-перехоплення рядка, який ми позначили P (0, −1) на малюнку\(\PageIndex{4}\) (b). У формулі y = mx + b нагадаємо, що b представляє y-координату y-перехоплення. Таким чином, b = −1.
По-друге, нам потрібно визначити нахил лінії. На малюнку\(\PageIndex{4}\) (б) почніть з точки Р, перемістіть 2 одиниці вправо, потім на 3 одиниці вгору до точки Q (2, 2). Це робить ухил\[m=\frac{\Delta y}{\Delta x}=\frac{3}{2}\]
Підставляємо m = 3/2 і b = −1 у форму ухил-перехоплення y = mx + b для отримання
\[y=\frac{3}{2} x-1\]
яка є бажаним рівнянням прямої.
Здійснення з'єднань
Якщо зв'язок між швидкістю і нахилом все ще не зрозуміла, згадаємо приклад, який ми робили раніше в розділі.
Себастьян прощається зі своїм братом, який розмовляє з групою своїх друзів приблизно в 20 футах. Потім Себастьян починає відходити від брата з постійною швидкістю 4 фути в секунду.
Відстань між братами залежить від кількості часу, яке пройшло, тому ставимо відстань d на вертикальній осі і час t на горизонтальній осі, як показано на малюнку\(\PageIndex{5}\). Зверніть увагу, що d і t займають «звичайне» місце y та x відповідно. Відстань, що розділяє братів в момент t = 0, дорівнює d = 20 футів. Це вказується при «d-перехопленні» при P (0, 20) на рис\(\PageIndex{5}\).
Далі відстань між братами збільшується зі швидкістю 4 фути в секунду. Починаючи з точки Р (0, 20), перемістіть на 1 секунду вправо (2 коробки) і 4 одиниці вгору (1 коробка) до точки Q (1, 24), як показано на малюнку\(\PageIndex{5}\). Лінія через точки P і Q потім моделює відстань між братами як функцію часу.
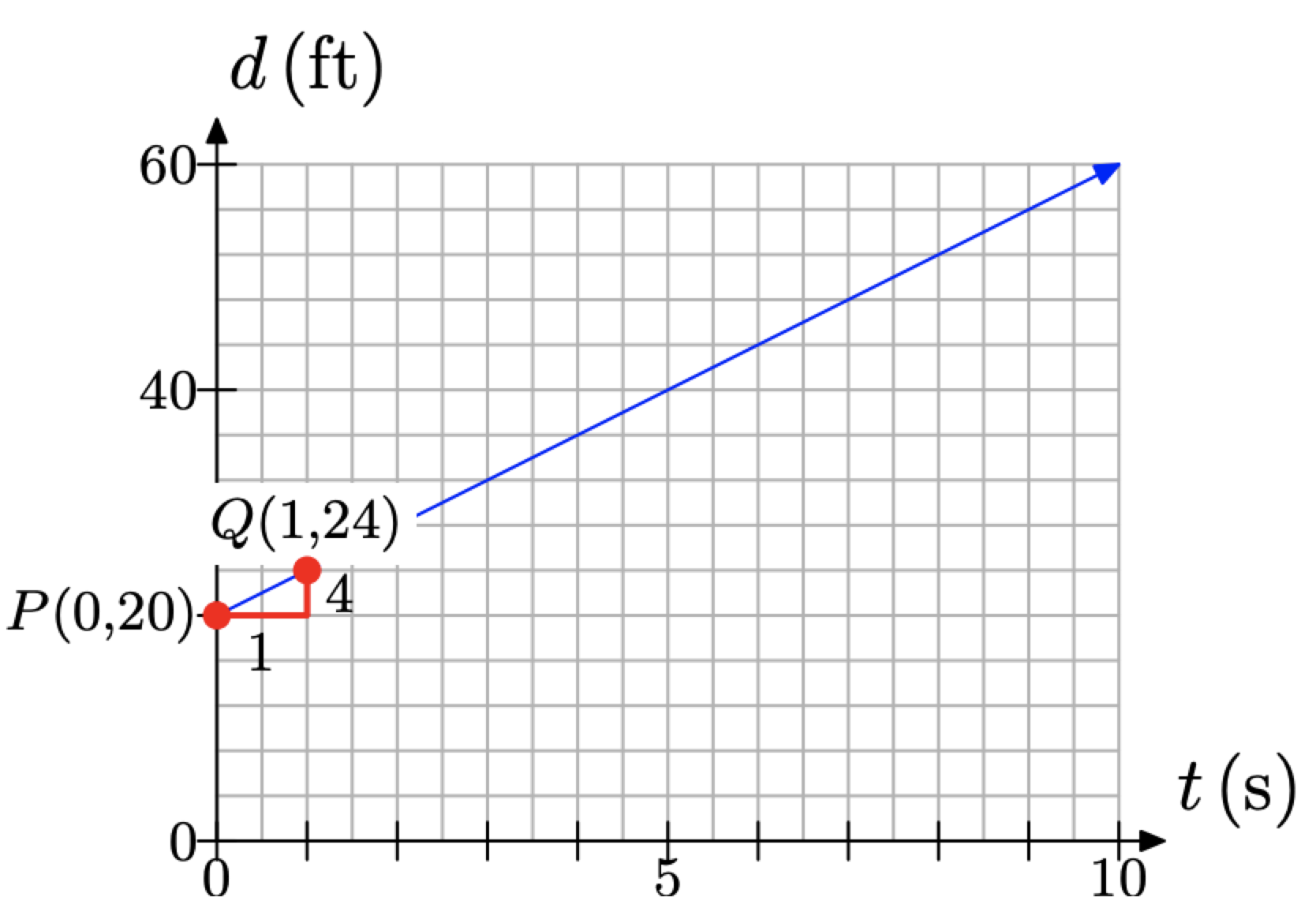
Якщо згадати, то ми визначили співвідношення між відстанню d і часом t, вивчивши відстань між братами в рази t = 0, 1, 2 і 3, і підсумовуючи результати в табл\(\PageIndex{1}\).
| т | d |
|---|---|
| 0 | 20 |
| 1 | 20+4 (1) |
| 2 | 20+4 (2) |
| 3 | 20+4 (3) |
Інтуїція тоді привела до наступної моделі, яка забезпечує відстань d між братами як функцію часу t.
\[d=20+4 t\]
Знову ж таки, читачі повинні перевірити, що рівняння (6) дає результати в таблиці\(\PageIndex{1}\) при t = 0, 1, 2 та 3.
Крім того, з теорією, розробленою в цьому розділі, ми б розробили рівняння прямої, використовуючи форму нахилу-перехоплення лінії; тобто
\[y=m x+b\]
Однак в даному випадку залежною змінною є d, а не y, а незалежна змінна t, а не х. так, замініть y і x в рівнянні (7) на d і t відповідно, отримуючи
\[d=m t+b\]
Далі рядок перехоплює вісь d при P (0, 20), тому b = 20. Крім того, нахил лінії становить 4 фути в секунду, тому m = 4. Підставляємо m = 4 і b = 20 в рівняння (8), щоб отримати
\[d=4 t+20\]
або використовуючи позначення функцій,\(d(t) = 4t + 20\). Зауважте, що рівняння (9) ідентичне інтуїтивно створеній моделі рівняння (6).
Сподіваємось, цей розвиток повинен зацементувати на весь час ідею про те, що нахил лінії - це швидкість, з якою залежна змінна змінюється щодо незалежної змінної.
Стандартна форма лінії
Тепер ми знаємо, що якщо наше рівняння має форму\(y=m x+b\) (або можна маніпулювати в цій формі), графік буде лінією. Візьмемо момент, щоб продемонструвати, що графік рівняння\(A x+B y=C\), де A, B і C є константами, є лінією.
Якщо ми можемо помістити\(A x+B y=C\) форму у формі нахилу перехоплення\(y=m x+b\), то це продемонструє, що графік\(A x+B y=C\) є лінією. Отже, почніть з\(A x+B y=C\) і відніміть Ax з обох сторін рівняння.
\[B y=-A x+C\]
Розділіть обидві сторони цього останнього рівняння на Б. Зверніть увагу, що тут є припущення, що\(B \neq 0\). Ми будемо обробляти випадок, коли B = 0 окремо, в кінці цього розділу.
\[\begin{aligned} \frac{B y}{B} &=\frac{-A x+C}{B} \\ y &=-\frac{A}{B} x+\frac{C}{B} \end{aligned}\]
Коли ми порівнюємо\(y=-(A / B) x+(C / B)\) з y = mx + b, ми зауважимо, що нахил m = −A/B, а y-координата y-перехоплення дорівнює b = C/B. Оскільки нам вдалося розмістити рівняння\(A x+B y=C\) у формі перехоплення нахилу, ми тепер знаємо, що граф\(A x+B y=C\) є лінією (цей результат нам знадобиться в подальшій роботі).
Стандартна форма лінії
Графік рівняння Ax+ By = C є лінією. Форма\[A x+B y=C\] називається стандартною формою лінії.
Давайте розглянемо приклад.
Приклад\(\PageIndex{3}\)
Рівняння 3х+4у = 12 знаходиться в стандартному вигляді. Помістіть це рівняння у формі нахилу-перехоплення, визначте нахил і y-перехоплення, потім використовуйте ці результати, щоб намалювати графік прямої.
Рішення
Спочатку вирішуємо рівняння 3х+ 4y = 12 для y.
\[\begin{aligned} 3 x+4 y &=12 \\ 4 y &=-3 x+12 \\ y &=-\frac{3}{4} x+3 \end{aligned}\]
Зверніть увагу на останньому кроці, як розподільна властивість вступила в гру. Коли ми розділили −3x + 12 на 4, ми розділимо кожен член на 4, отримавши (−3/4) x + 3.
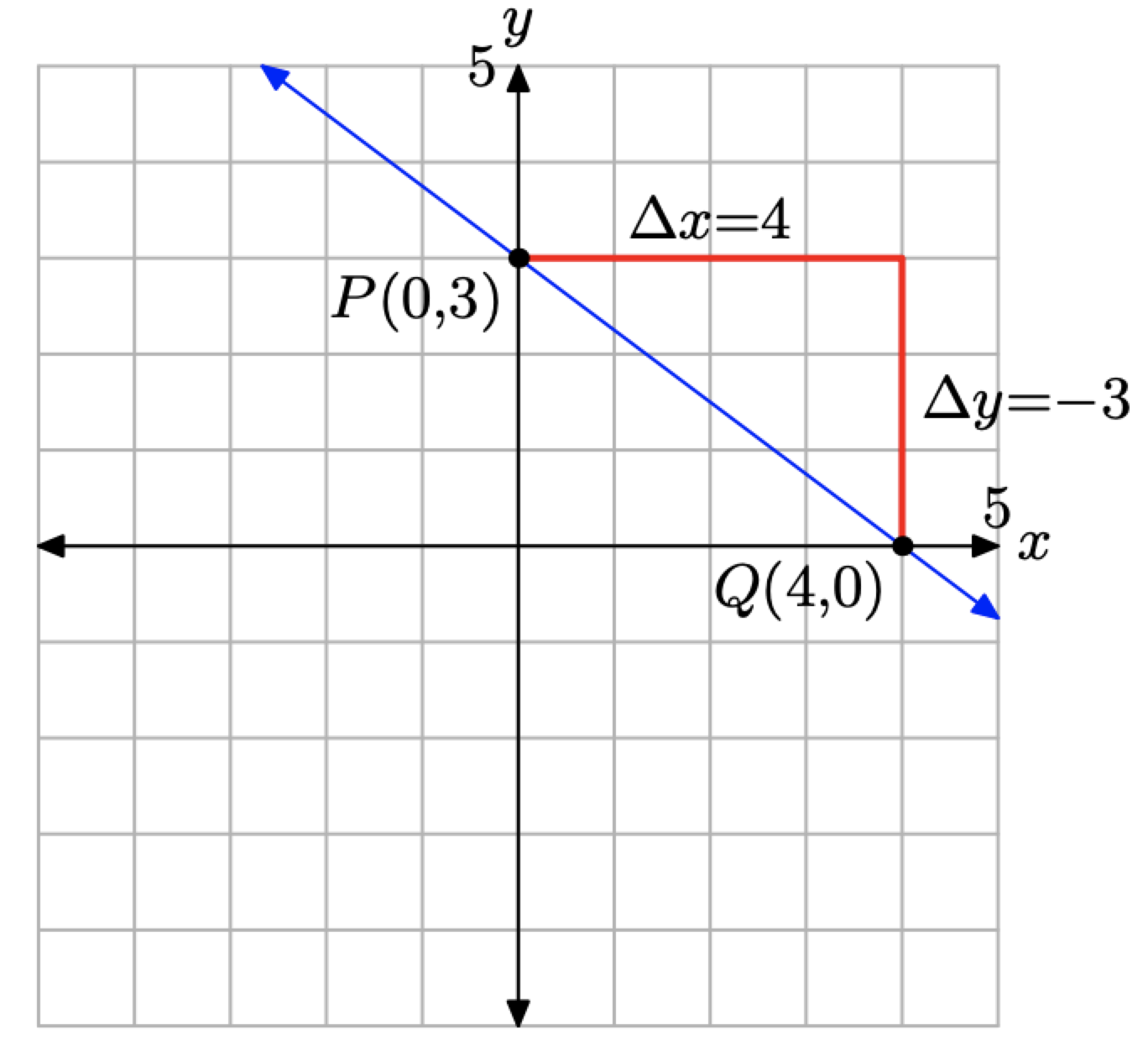
Коли ми порівнюємо y = (−3/4) x+3 із загальною формою ухил-перехоплення y = mx+b, ми визначаємо, що нахил дорівнює m = −3/4, а y-координата y-перехоплення дорівнює b = 3. Щоб намалювати графік лінії, як ми зробили на малюнку\(\PageIndex{6}\), побудуйте y-перехоплення на P (0, 3), потім перемістіть 4 одиниці вправо і 3 одиниці вниз до точки Q (4, 0). Лінія, що проходить через точки Р і Q, є необхідною лінією.
Зауважте ще раз, що нахил дорівнює m = −3/4, а лінія нахиляється «вниз». Також b = 3 і рядок «перехоплює» вісь y при P (0, 3).
Давайте розглянемо інший приклад.
Приклад\(\PageIndex{4}\)
У прикладі\(\PageIndex{1}\) ми визначили, що даний рядок має рівняння
\[y=\frac{3}{2} x-1\]
Помістіть це рівняння в стандартний з\(Ax + By = C\), де A, B і C - цілі числа і\(A > 0\).
Рішення
Нас просять помістити рівняння\(y = (3/2)x − 1\) у вигляді\(Ax + By = C\), де A, B і C є цілими числами, так що давайте почнемо з очищення дробів від рівняння. Помножте обидві сторони рівняння на загальний знаменник 2.
\[\begin{aligned} y &=\frac{3}{2} x-1 \\ 2 y &=2\left(\frac{3}{2} x-1\right) \\ 2 y &=3 x-2 \end{aligned}\]
Тепер відніміть 2y з обох сторін рівняння, а потім додайте 2 до обох сторін рівняння, щоб отримати
\[2=3 x-2 y\]
або еквівалентно,
\[3 x-2 y=2\]
Зауважте, що цей останній результат знаходиться в стандартному вигляді\(Ax + By = C\), де A, B і C є цілими числами, а A > 0.
Перехоплює
Тепер ми знаємо, що графік рівняння\(Ax + By = C\), де A, B і C є константами, є лінією. Оскільки графік\(Ax + By = C\) є лінією, щоб намалювати графік прямої, нам потрібно знайти лише дві точки, які задовольняють рівнянню, побудувати їх, а потім провести лінію через них. Наші два улюблені моменти для роботи - це x- і y-перехоплення, тому що кожен включає в себе число нуль, легке число для роботи.
Розглянемо графік на малюнку\(\PageIndex{7}\) (а). Зверніть увагу, що графік проходить через вісь x три рази. Точки, де графік перехоплює вісь x, називаються x-перехопленнями. Зверніть увагу, що кожна з цих точок має спільне визначальне значення: значення y кожного з цих x-перехоплень дорівнює нулю.
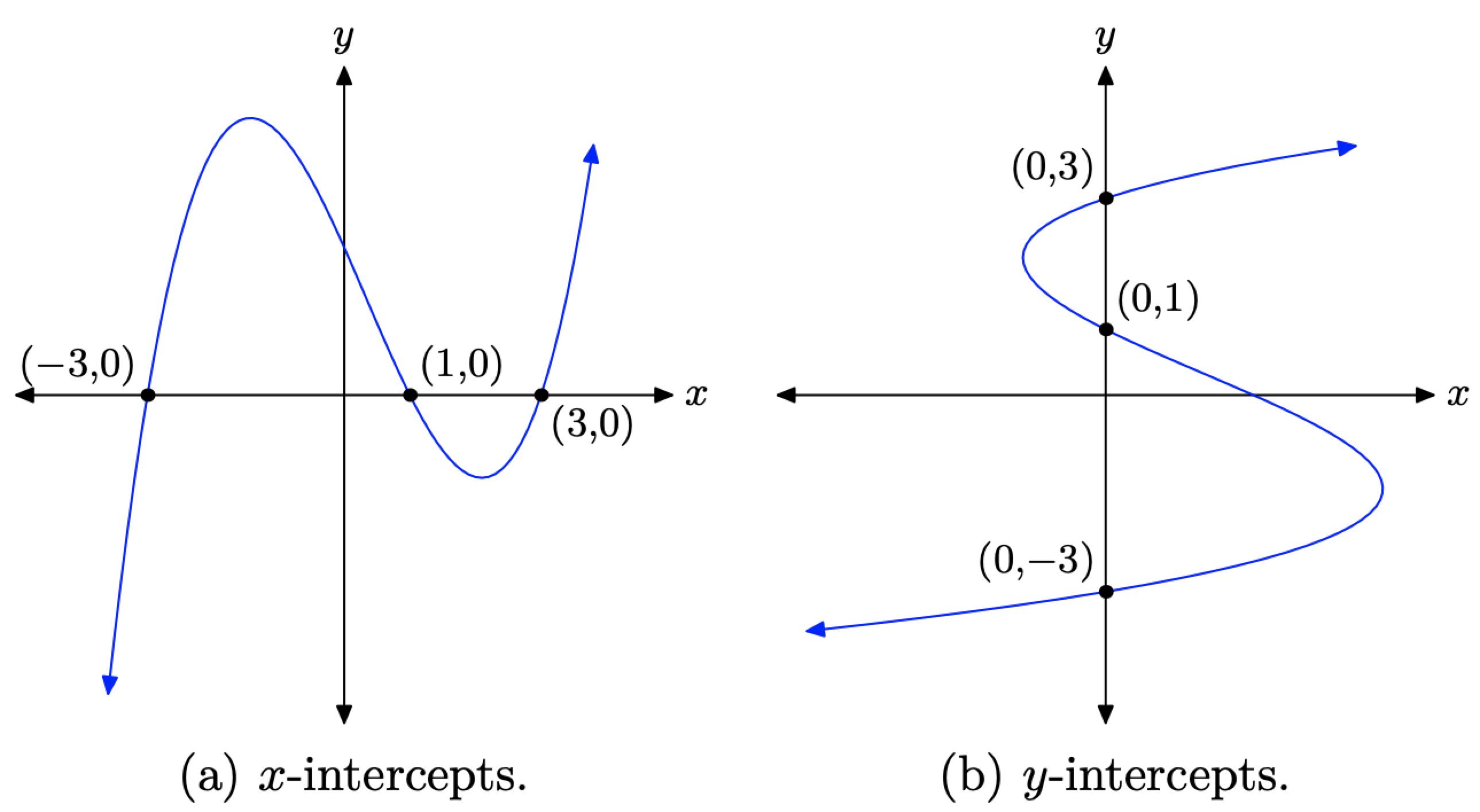
Як знайти X-перехоплення
Щоб знайти перехоплення x, нехай y = 0 в рівнянні і вирішите для x.
З іншого боку, розглянемо графік на малюнку\(\PageIndex{7}\) (b). Зауважте, що це не функція (не виконується тест вертикальної лінії), але графік тричі перехоплює вісь y. Точки, де графік перехоплює вісь y, називаються y-перехопленнями. Зауважте, що кожен з y-перехоплень на рис.\(\PageIndex{7}\) (b) має спільне визначальне значення: значення x кожного з y-перехоплень дорівнює нулю.
Як знайти y-перехоплення
Щоб знайти y-перехоплення, нехай x = 0 в рівнянні і вирішите для y.
Давайте втілимо те, що ми дізналися, на практиці.
Приклад\(\PageIndex{5}\)
Намалюйте графік 3х+ 4у = 12.
Рішення
Ми намалювали графік рівняння 3x + 4y = 12 на рис\(\PageIndex{6}\). Там ми вирішили рівняння для y, щоб визначити нахил і y-перехоплення. Вони, в свою чергу, були використані для малювання графіка 3x + 4y = 12 на малюнку\(\PageIndex{6}\).
Тут наш підхід буде іншим. Ми спочатку визначимо x- і y-перехоплення, намітимо їх, потім проведемо лінію через ці перехоплення. Сподіваємось, ми отримаємо результат, який відповідає тому, що на малюнку\(\PageIndex{6}\).
Щоб знайти x-перехоплення,\(y = 0\) впустіть\(3x + 4y = 12\) і вирішіть для x.
\[\begin{aligned} 3 x+4 y &=12 \\ 3 x+4(0) &=12 \\ 3 x &=12 \\ x &=4 \end{aligned}\]
Значить, x-перехоплення - це точка Q (4, 0). Щоб знайти y-перехоплення, нехай x = 0 in\(3x + 4y = 12\) і вирішіть для y.
\[\begin{aligned} 3 x+4 y &=12 \\ 3(0)+4 y &=12 \\ 4 y &=12 \\ y &=3 \end{aligned}\]
Значить, y-перехоплення - це точка Р (0, 3). На малюнку\(\PageIndex{8}\) ми намалювали як x-, так і y-перехоплення і провели лінію через них. Зверніть увагу, що отримана лінія на малюнку\(\PageIndex{8}\) збігається з тією ж лінією, намальованою на малюнку\(\PageIndex{6}\) (де ми використовували інший метод).
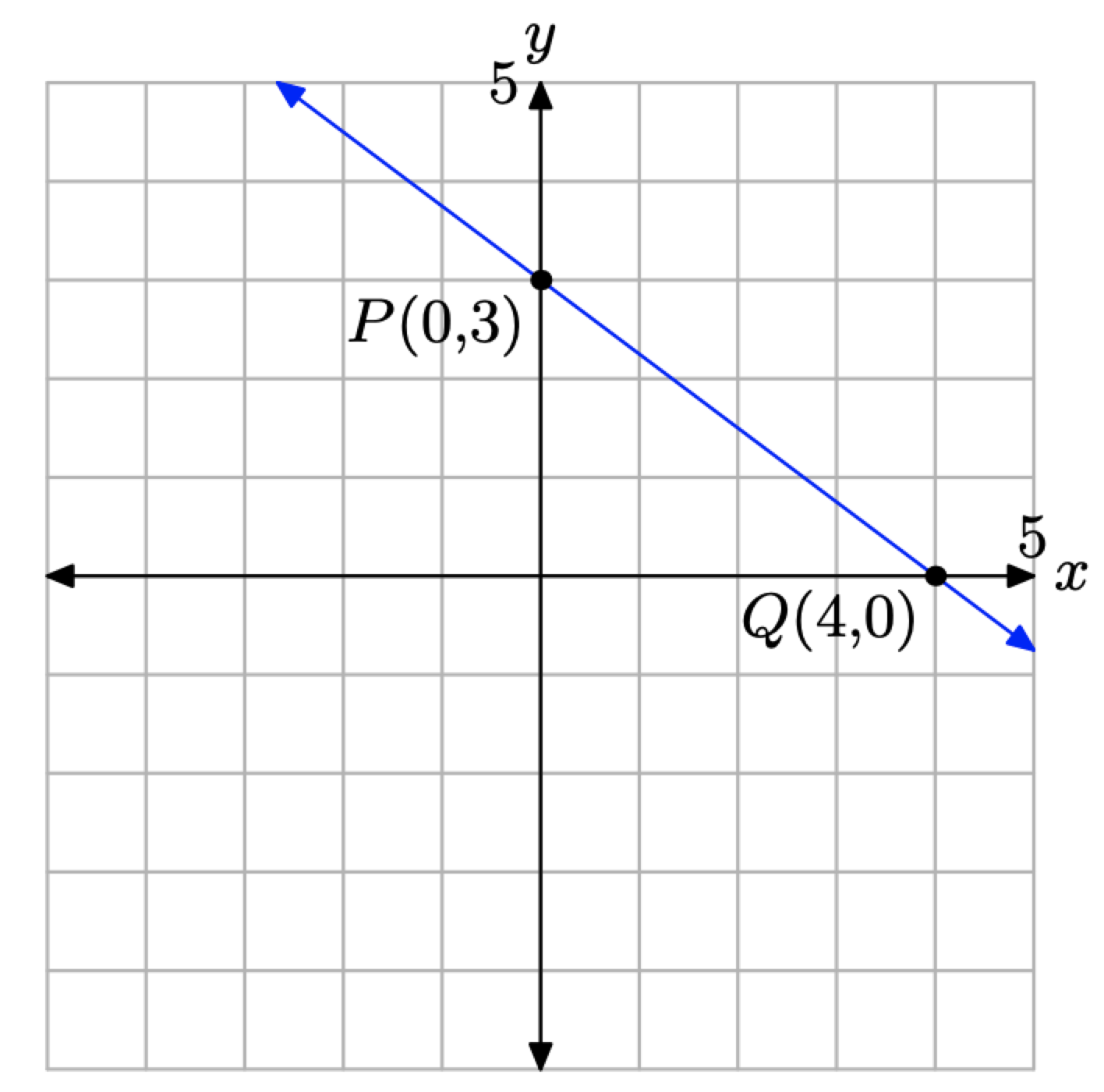
Малюнок\(\PageIndex{8}\). Побудова x- і y-перехоплень.
Ми рекомендуємо щоразу, коли лінія задана в стандартній формі\(Ax + By = C\), знайти x- і y-перехоплення, побудувати їх, а потім провести лінію через них. Дана методика досить ефективна, оскільки робота з числом нуль значно спрощує розрахунки.
Горизонтальні та вертикальні лінії
Ми ввели стандартну форму лінії\(Ax + By = C\). Випадок, коли A і B одночасно рівні нулю, не дуже цікавий.4 Однак цікаві наступні два випадки.
- Якщо ми пустимо A = 0 і B 6= 0 в стандартному вигляді\(Ax + By = C\), то By = C, або еквівалентно y = C/B. зверніть увагу, що це має вигляд y = b, де b - якась константа.
- Аналогічно, якщо ми дозволимо B = 0 і A 6= 0 в стандартному вигляді\(Ax + By = C\), то Ax = C, або еквівалентно, x = C/A. зверніть увагу, що це має вигляд x = a, де a є деякою константою.
Лінії, що мають вигляд x = a та y = b, є двома найпростішими лініями для побудови. Давайте розглянемо на прикладі кожного.
Приклад\(\PageIndex{6}\)
Намалюйте графік рівняння х = 3.
Рішення
Напрямок «ескіз графіка рівняння х = 3» може бути досить неприємним, якщо не згадати, що графік рівняння - це сукупність всіх точок, які задовольняють рівнянню. Таким чином, напрямок краще поставити, якщо ми скажемо «ескіз множини всіх точок (x, y), які задовольняють x = 3,» або еквівалентно, «ескіз множини всіх точок (x, y), які мають значення x 3». Тоді нескладно намалювати вертикальну лінію, показану на малюнку\(\PageIndex{9}\).
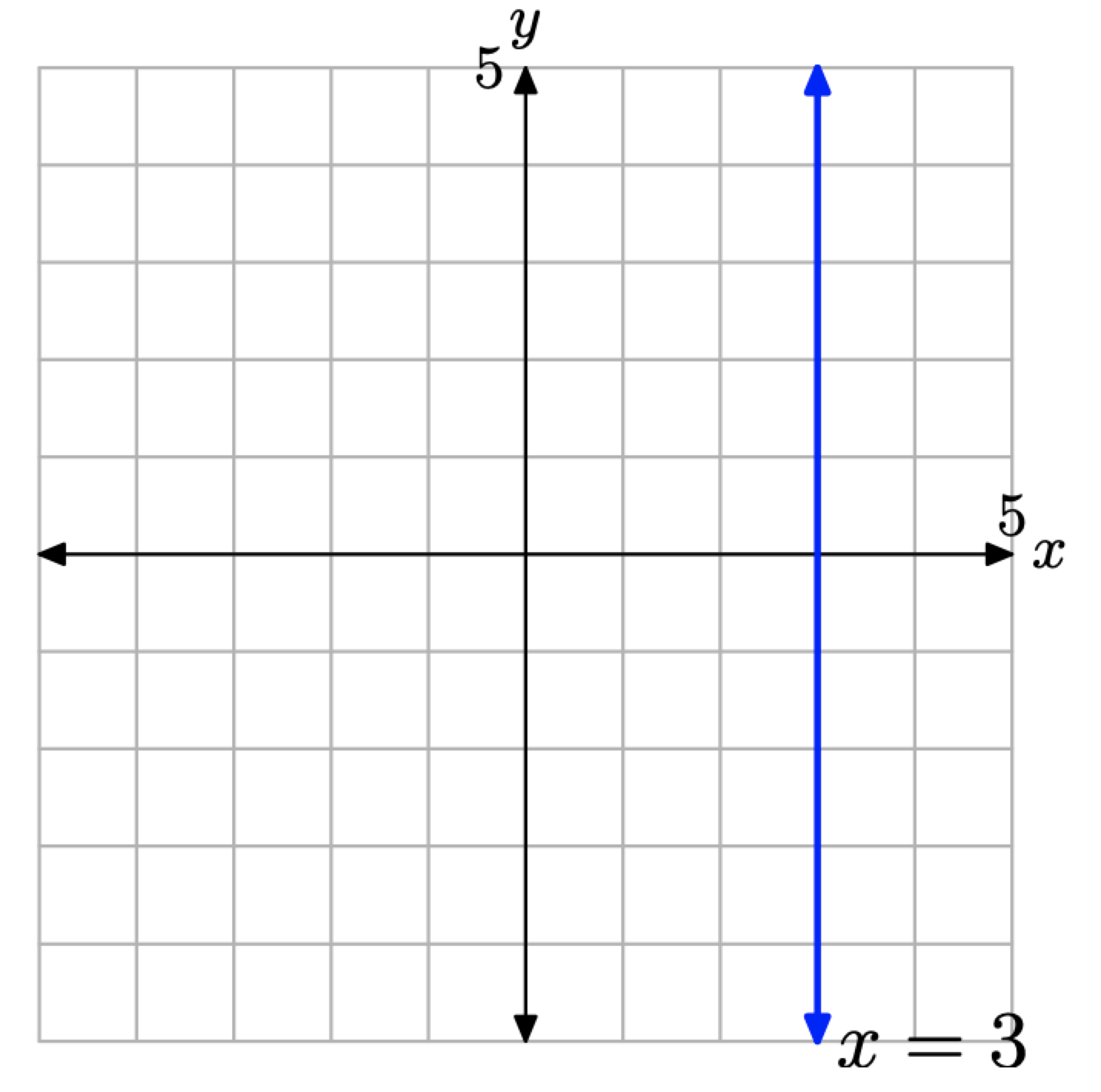
Зверніть увагу, що кожна точка на лінії має значення x, рівне 3. Також зверніть увагу, що нахил цієї вертикальної лінії невизначений.
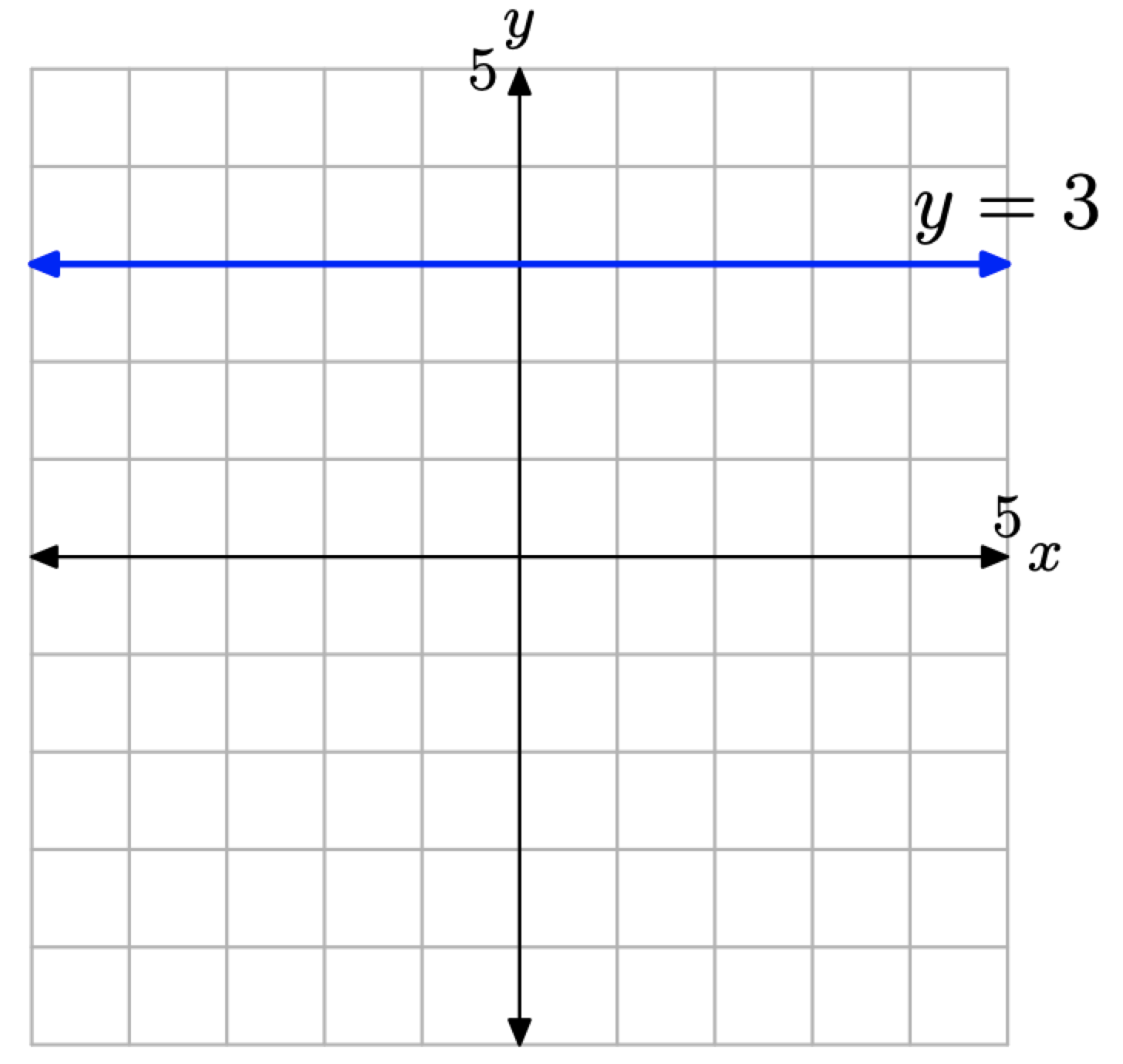
Приклад\(\PageIndex{7}\)
Намалюйте графік рівняння y = 3.
Рішення
Цей напрямок краще поставити, якщо ми скажемо «ескіз множини всіх точок (x, y), які задовольняють y = 3,» або еквівалентно, «ескіз множини всіх точок (x, y), які мають значення y 3». Тоді нескладно намалювати горизонтальну лінію, зображену на малюнку\(\PageIndex{10}\).
Зверніть увагу, що кожна точка на лінії має значення y, рівне 3. Також зверніть увагу, що ця горизонтальна лінія має ухил нуль.
Два остаточних зауваження по порядку. Оскільки лінія на малюнку 10 має нульовий нахил і y-перехоплення (0, 3), ми можемо вставити m = 0 і b = 3 у форму перехоплення нахилу y = mx + b і отримати
\[y=0 x+3\]
що, звичайно, еквівалентно y = 3. Однак вертикальна лінія, показана на малюнку,\(\PageIndex{9}\) має «невизначений» нахил, тому такий підхід недоступний. Ми повинні просто визнати, що вертикальна лінія на малюнку\(\PageIndex{9}\) складається з усіх точок, що мають значення x, рівне 3, а потім зрозуміти, що її рівняння дорівнює x = 3.
