Skip to main content
LibreTexts - Ukrayinska

3.4: Точка-нахил форми лінії

  1. Last updated
  2. Save as PDF
  • Page ID
    58085

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    В останньому розділі ми розробили форму ухил-перехоплення лінії (y = mx + b). Форма перехоплення нахилу лінії застосовується, коли вам задано нахил та перехоплення y-перехоплення лінії. Однак будуть випадки, коли y-перехоплення невідомо.

    Припустимо, наприклад, що вас попросять знайти рівняння прямої, яка проходить через певну точку\(P\left(x_{0}, y_{0}\right)\) з ухилом = m\(\PageIndex{1}\).

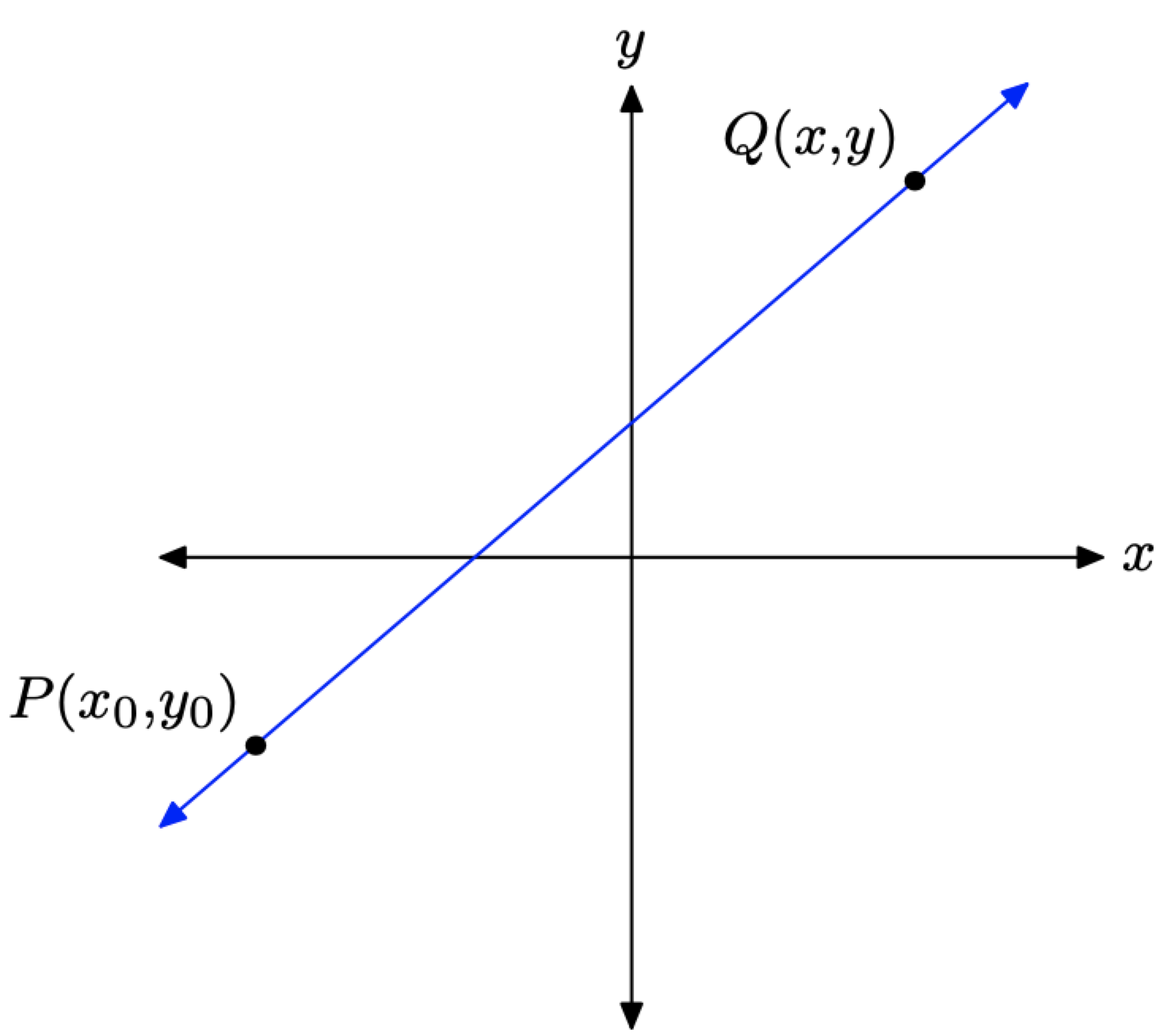
    WeChat7ae165dfc8321137635b442d6de2add0.png
    Малюнок\(\PageIndex{1}\). Лінія наскрізна\(\left(x_{0}, y_{0}\right)\) з ухилом м.

    Нехай точка Q (x, y) буде довільною точкою на прямій. Ми можемо визначити рівняння прямої за допомогою формули нахилу з точками Р і Q. отже,

    \[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{y-y_{0}}{x-x_{0}}\]

    Оскільки нахил дорівнює m, ми можемо встановити нахил = m в цьому останньому результаті, щоб отримати

    \[m=\frac{y-y_{0}}{x-x_{0}}\]

    Якщо помножити обидві сторони цього останнього рівняння на\(x-x_{0}\), отримаємо

    \[m\left(x-x_{0}\right)=y-y_{0}\]

    або обмінюючись сторонами цього останнього рівняння,

    \[y-y_{0}=m\left(x-x_{0}\right)\]

    Цей останній результат є рівнянням прямої.

    Точка-нахил форми прямої

    Якщо лінія L проходить через точку\(\left(x_{0}, y_{0}\right)\) і має нахил m, то рівняння прямої -\[y-y_{0}=m\left(x-x_{0}\right)\] це така форма рівняння прямої називається точково-нахилом форми.

    Щоб використовувати точково-нахильну форму лінії, виконайте наступні дії.

    Порядок використання точково-нахильної форми лінії

    Коли задано нахил прямої та точки на лінії, використовуйте форму точка-нахил наступним чином:

    1. Підставляємо заданий ухил на m у формулу\(y-y_{0}=m\left(x-x_{0}\right)\).
    2. Підставляємо координати заданої точки на x0 і y0 у формулу\(y-y_{0}=m\left(x-x_{0}\right)\).

    Наприклад, якщо пряма має нахил −2 і проходить через точку (3, 4), то підставляємо\(m=-2, x_{0}=3,\) і\(y_{0}=4\)\(y-y_{0}=m\left(x-x_{0}\right)\) в формулу отримуємо\[y-4=-2(x-3)\].

    Приклад\(\PageIndex{1}\)

    Намалюйте лінію, яка проходить через точку Р (−3, −2) і має ухил m = 1/2. Використовуйте форму точка-нахил для визначення рівняння прямої.

    Рішення

    Спочатку нанесіть точку P (−3, −2), як показано на малюнку\(\PageIndex{2}\) (a). Починаючи з точки Р (−3, −2), перемістіть 2 одиниці вправо і на 1 одиницю вгору до точки Q (−1, −1). Лінія через точки P і Q на малюнку\(\PageIndex{2}\) (а) тепер має нахил m = 1/2.

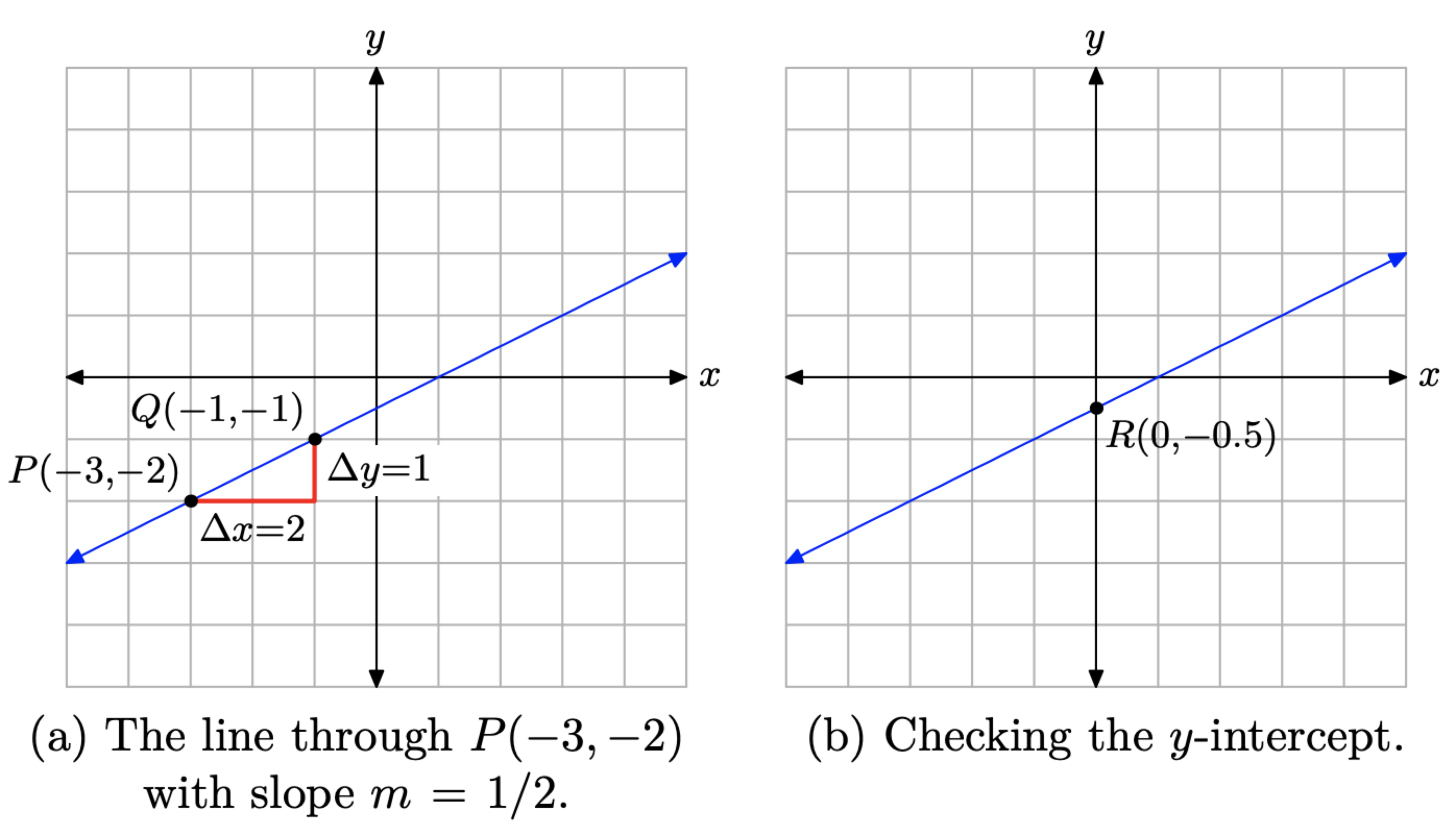
    WeChatb11c39993f9ab17a0098dc9991df0cb7.png
    Малюнок\(\PageIndex{2}\)

    Для визначення рівняння прямої на малюнку\(\PageIndex{2}\) (а) будемо використовувати точково-похилу форму лінії

    \[y-y_{0}=m\left(x-x_{0}\right)\]

    Нахил прямої дорівнює m = 1/2, а задана точка - P (−3, −2), отже\(\left(x_{0}, y_{0}\right)=(−3, −2)\). У рівнянні (3)\(m=1 / 2, x_{0}=-3,\) множиться і\(y_{0}=-2\), отримання

    \[y-(-2)=\frac{1}{2}(x-(-3))\]

    або еквівалентно,

    \[y+2=\frac{1}{2}(x+3)\]

    Це рівняння прямої на малюнку\(\PageIndex{2}\) (а).

    Як перевірка, ми оцінили перехоплення y рядка на малюнку\(\PageIndex{2}\) (b) як R (0, −0.5). Помістимо рівняння (4) у формі нахилу перехоплення, щоб визначити точне значення y-перехоплення. Спочатку розподіліть 1/2, щоб отримати

    \[y+2=\frac{1}{2} x+\frac{3}{2}\]

    Відніміть 2 з обох сторін цього останнього рівняння.

    \[y=\frac{1}{2} x+\frac{3}{2}-2\]

    Зробити еквівалентні дроби з загальним знаменником і спростити.

    \[\begin{array}{l}{y=\frac{1}{2} x+\frac{3}{2}-\frac{4}{2}} \\ {y=\frac{1}{2} x-\frac{1}{2}}\end{array}\]

    Порівняння рівняння (5) з y = mx+b дає нам b = −1/2. Це точне значення y перехоплення y-перехоплення. Зауважте, що цей результат точно порівнюється зі значенням y точки R на малюнку\(\PageIndex{2}\) (b). Це трохи пощастило. Не очікуйте щоразу отримати точне порівняння. Однак, якщо порівняння не близьке, шукайте помилку у вашій роботі, або в ваших обчисленнях, або у вашому графіку.

    Давайте розглянемо інший приклад.

    Приклад\(\PageIndex{2}\)

    Знайти рівняння прямої, що проходить через точки P (−3, 2) та Q (2, −1). Розмістіть остаточну відповідь у стандартній формі.

    Рішення

    Знову ж таки, щоб допомогти зберегти фокус, ми проводимо лінію, що проходить через точки P (−3, 2) та Q (2, −1) на малюнку\(\PageIndex{3}\).

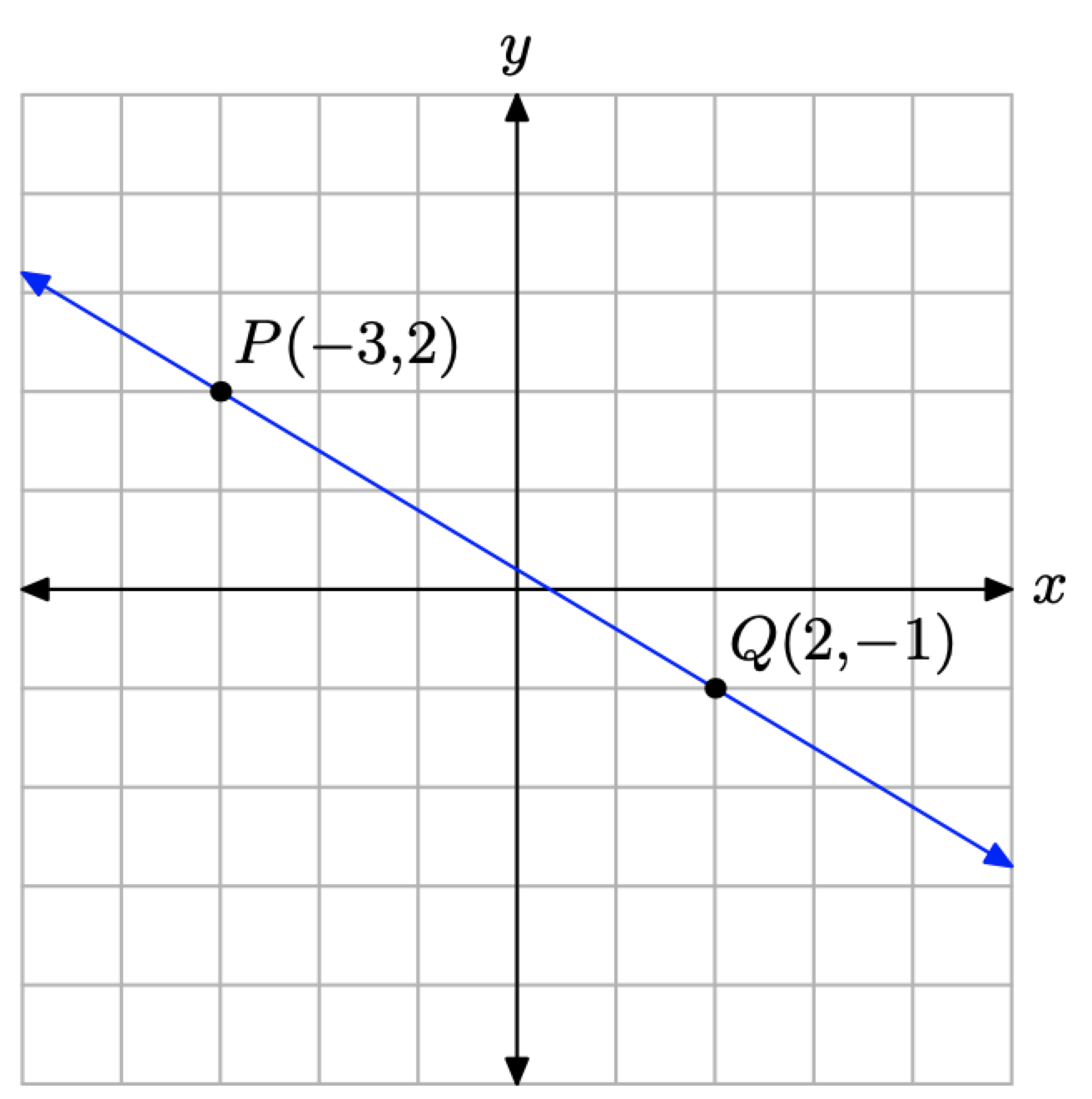
    WeChata0d7e316a7412734afa037efaf06e7b9.png
    Малюнок\(\PageIndex{3}\). Пряма через точки P (−3, 2) та Q (2, −1).

    Використовуйте формулу нахилу для визначення нахилу прямої через точки Р (−3, 2) і Q (2, −1).

    \[m=\frac{\Delta y}{\Delta x}=\frac{-1-2}{2-(-3)}=-\frac{3}{5}\]

    Ми будемо використовувати точку-нахил форми лінії

    \[y-y_{0}=m\left(x-x_{0}\right)\]

    Давайте використаємо точку P (−3, 2) як задану точку\(\left(x_{0}, y_{0}\right)\). Тобто,\(\left(x_{0}, y_{0}\right)=(-3,2)\). \(m=-3 / 5, x_{0}=-3,\)Підставляємо і\(y_{0}=2\) в рівнянні (7), отримання

    \[y-2=-\frac{3}{5}(x-(-3))\]

    Це рівняння прямої, що проходить через точки Р і Q.

    Крім того, ми також можемо використати точку Q (2, −1) як задану точку\(\left(x_{0}, y_{0}\right)\). Тобто,\(\left(x_{0}, y_{0}\right)=(2,-1)\). \(m=-3 / 5, x_{0}=2,\)Підставляємо і\(y_{0}=-1\) в точково-ухил формі (7), отримання

    \[y-(-1)=-\frac{3}{5}(x-2)\]

    Це теж рівняння прямої, що проходить через точки Р і Q.

    Як рівняння (8) і (9) можуть бути рівнянням прямої через P і Q, але виглядати настільки чітко різними? Помістимо кожне рівняння в стандартному вигляді\(Ax + By = C\) і порівняємо результати.

    Якщо ми почнемо з рівняння (8) і розподіляємо нахил,

    \[\begin{array}{l}{y-2=-\frac{3}{5}(x-(-3))} \\ {y-2=-\frac{3}{5} x-\frac{9}{5}}\end{array}\]

    Помножте обидві сторони на спільний знаменник 5, щоб очистити дроби.

    \[\begin{aligned} 5(y-2) &=5\left(-\frac{3}{5} x-\frac{9}{5}\right) \\ 5 y-10 &=-3 x-9 \end{aligned}\]

    Додайте 3x до обох сторін рівняння, а потім додайте 10 до обох сторін рівняння, щоб отримати

    \[3 x+5 y=1\]

    Помістіть рівняння (9) у стандартній формі аналогічним чином. Спочатку почніть з рівняння (9) і розподіліть нахил,

    \[\begin{aligned} y-(-1) &=-\frac{3}{5}(x-2) \\ y+1 &=-\frac{3}{5} x+\frac{6}{5} \end{aligned}\]

    Далі помножте обидві сторони цього останнього результату на 5, щоб очистити дроби з рівняння.

    \[\begin{aligned} 5(y+1) &=5\left(-\frac{3}{5} x+\frac{6}{5}\right) \\ 5 y+5 &=-3 x+6 \end{aligned}\]

    Нарешті, додайте 3x до обох сторін рівняння, потім відніміть 5 з обох сторін рівняння, щоб отримати

    \[3 x+5 y=1\]

    Зверніть увагу, що рівняння (11) ідентичне рівнянню (10). Таким чином, не має значення, яку точку ви використовуєте у формі точки-нахилу. Обидва призводять до однакового результату.

    Паралельні лінії

    Нагадаємо, що нахил контролює «крутизну» лінії. Отже, якщо дві лінії паралельні, вони повинні мати однакову «крутизну» або ухил. Давайте розглянемо на прикладі паралельних ліній.

    Приклад\(\PageIndex{3}\)

    Знайти рівняння прямої, яка проходить через точку Р (−2, 2), яка паралельна прямій, що проходить через точки Q (−3, −1) та R (2, 1).

    Рішення

    Спочатку, щоб допомогти нам залишатися зосередженими, ми проводимо лінію через точки Q (−3, −1) та R (2, 1), потім будуємо точку P (−2, 2), як показано на малюнку\(\PageIndex{4}\) (a).

    Ми можемо використовувати формулу нахилу нахилу прямої, що проходить через точки Q (−3, −1) та R (2, 1).

    \[m=\frac{\Delta y}{\Delta x}=\frac{1-(-1)}{2-(-3)}=\frac{2}{5}\]

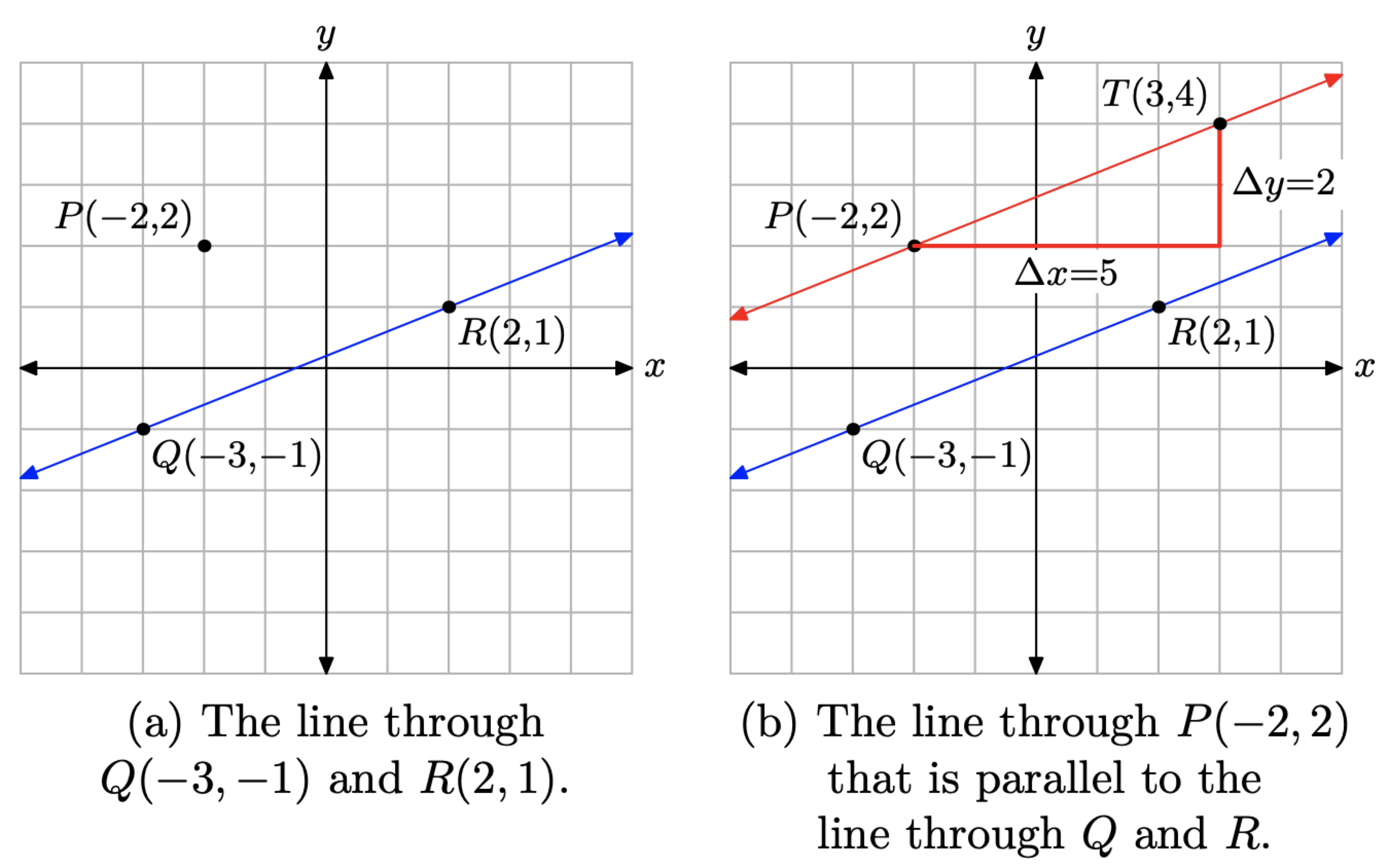
    WeChatf91e04129da47aa1d1b93440e15a29bd.png
    Малюнок\(\PageIndex{4}\).

    Тепер проводимо лінію через точку Р (−2, 2), яка паралельна прямій через точки Q і R. Паралельні лінії повинні мати однаковий нахил, тому починаємо в точці Р (−2, 2), «пробігаємо» 5 одиниць вправо, потім «піднімаємося» на 2 одиниці вгору до точки Т (3, 4), як показано на малюнку\(\PageIndex{4}\) (б).

    Шукаємо рівняння прямої через точки Р і Т. Ми будемо використовувати точкоподібну форму прямої.

    \[y-y_{0}=m\left(x-x_{0}\right)\]

    Ми будемо використовувати точку P (−2, 2) як задану точку\(\left(x_{0}, y_{0}\right)\). Тобто,\(\left(x_{0}, y_{0}\right) = (−2, 2)\). Лінія через П має нахил 2/5. Підставити\(m=2 / 5, x_{0}=-2,\) і\(y_{0}=2\) в рівнянні (13) отримати

    \[y-2=\frac{2}{5}(x-(-2))\]

    Помістимо рівняння (14) в стандартному вигляді. Розподіліть нахил, потім очистіть дроби, помноживши обидві сторони отриманого рівняння на 5.

    \[\begin{aligned} y-2 &=\frac{2}{5} x+\frac{4}{5} \\ 5(y-2) &=5\left(\frac{2}{5} x+\frac{4}{5}\right) \\ 5 y-10 &=2 x+4 \end{aligned}\]

    Нарешті, відніміть 5y з обох сторін останнього рівняння, потім відніміть 4 з обох сторін рівняння, отримавши

    \[-14=2 x-5 y\]

    або еквівалентно,

    \[2 x-5 y=-14\]

    Це стандартна форма рівняння прямої, що проходить через точку Р і паралельної лінії, що проходить через точки Q і R.

    Перпендикулярні лінії

    Припустимо, що дві лінії\(L_{1}\) і\(L_{2}\) мають ухили\(m_{1}\) і\(m_{2}\), відповідно. Нагадаємо (див. Розділ на схилі), що якщо\(L_{1}\) і\(L_{2}\) знаходяться перпендикулярно, то твором їх укосів є\(m_{1} m_{2}=-1\). Як варіант, нахил першої лінії - негативний зворотний другої лінії, і навпаки; т. Е\(m_{2}=-1 / m_{1}\).\(m_{1}=-1 / m_{2}\) Давайте розглянемо приклад перпендикулярних ліній.

    Приклад\(\PageIndex{4}\)

    Знайти рівняння прямої, що проходить через точку Р (−4, −4), яка перпендикулярна прямій 4x + 3y = 12.

    Рішення

    Це допоможе нашому фокусу, якщо ми намалюємо задану лінію 4x + 3y = 12. Найпростіший спосіб побудови лінії в стандартному вигляді Ax+ By = C - знайти x- і y-перехоплення.

    \[\begin{array}{rlrrll}{4 x+3 y} & {=}&{12} & {4 x+3 y} & {=}&{12} \\ {4 x+3(0)} & {=}&{12} & {4(0)+3 y} & {=}&{12} \\ {4 x} & {=}&{12} & {3 y} & {=}&{12} \\ {x} & {=}&{3} & {y} & {=}&{4}\end{array}\]

    Побудувати x- і y-перехоплює R (3, 0) і S (0, 4), як показано на малюнку\(\PageIndex{5}\) (а). Пряма через точки R і S - це графік рівняння 4х + 3y = 12.

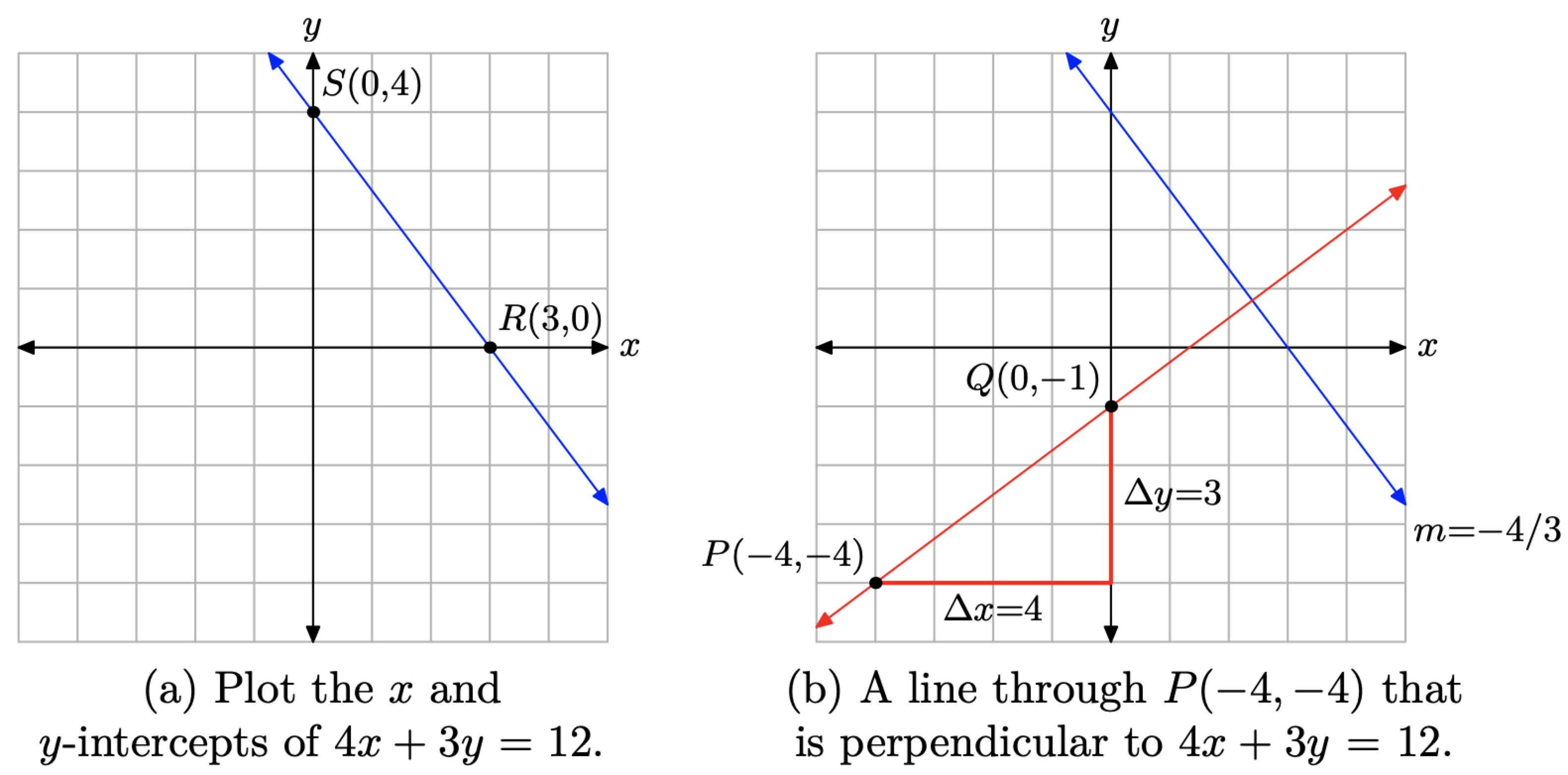
    WeChatf5a79539226b56f42d05801aae5a4375.png
    Малюнок\(\PageIndex{5}\)

    Далі визначаємо нахил прямої 4х + 3y = 12, помістивши це рівняння в ухил-перехоплення вигляді (тобто вирішити рівняння 4х + 3y = 12 для y)

    \[\begin{aligned} 4 x+3 y &=12 \\ 3 y &=-4 x+12 \\ y &=-\frac{4}{3} x+4 \end{aligned}\]

    Якщо дві лінії перпендикулярні, то їх нахили негативні взаємні один одному. Тому нахил лінії, яка перпендикулярна лінії 4х + 3y = 12 (яка має ухил −4/3) дорівнює m = 3/4. Наша друга лінія повинна пройти через точку Р (−4, −4). Щоб намалювати цю другу лінію, спочатку нанесіть точку P (−4, −4), потім перемістіть 4 одиниці вправо і на 3 одиниці вгору до точки Q (0, −1), як показано на малюнку\(\PageIndex{5}\) (b). Лінія через точки Р і Q перпендикулярна лінії 4х + 3у = 12.

    Для визначення рівняння прямої через точки Р і Q скористаємося точково-похилою формою лінії, а саме

    \[y-y_{0}=m\left(x-x_{0}\right)\]

    Ухил лінії через точки Р і Q дорівнює m = 3/4. Якщо використовувати точку P (−4, −4), то\(\left(x_{0}, y_{0}\right)=(-4,-4)\). Множина\(m=3 / 4, x_{0}=-4,\) і\(y_{0}=-4\) в рівнянні (16), отримання

    \[y-(-4)=\frac{3}{4}(x-(-4))\]

    або еквівалентно,

    \[y+4=\frac{3}{4}(x+4)\]

    Крім того, ми могли б використовувати форму перехоплення нахилу лінії. Ми знаємо, що лінія через точки P і Q на малюнку\(\PageIndex{5}\) (b) перетинає вісь y на Q (0, −1). Отже, при нахилі m = 3/4 і y-координаті y-перехоплення b = −1 форма нахилу-перехоплення y = mx + b стає

    \[y=\frac{3}{4} x-1\]

    З іншого боку, якщо ми вирішимо рівняння (17) для y,

    \[\begin{aligned} y+4 &=\frac{3}{4}(x+4) \\ y+4 &=\frac{3}{4} x+3 \\ y &=\frac{3}{4} x-1 \end{aligned}\]

    Зауважте, що це ідентично результату, знайденому за допомогою форми перехоплення нахилу вище.

    Втішно відзначити, що дві форми (точка-нахил і схил-перехоплення) дають однаковий результат, але як визначити найбільш ефективну форму для використання для конкретної проблеми? Ось хороший натяк.

    Визначення форми рядка для використання

    Ось кілька здорових порад, коли ви намагаєтеся визначити, чи використовувати форму нахилу перехоплення або точку нахилу лінії.

    • Якщо вам задано нахил і y-перехоплення, використовуйте форму ухил-перехоплення y = mx + b.
    • Якщо вам задана точка (відмінна від перетину y) і нахил, використовуйте форму точка-нахил\(y-y_{0}=m\left(x-x_{0}\right)\).

    Застосування лінійних функцій

    У цьому розділі ми розглянемо деякі програми лінійних функцій. Ми починаємо з розробки функції, що стосується температури за Фаренгейтом і Цельсієм.

    Приклад\(\PageIndex{5}\)

    Вода замерзає при\(32^{\circ} F\) і\(0^{\circ} \mathrm{C}\). Вода закипає при\(212^{\circ} F\) і\(100^{\circ} \mathrm{C}\). F і C - це скорочення для шкал температури за Фаренгейтом і Цельсієм відповідно. Припускаючи лінійну залежність, розробити модель, що стосується температури за Фаренгейтом і Цельсієм.

    Рішення

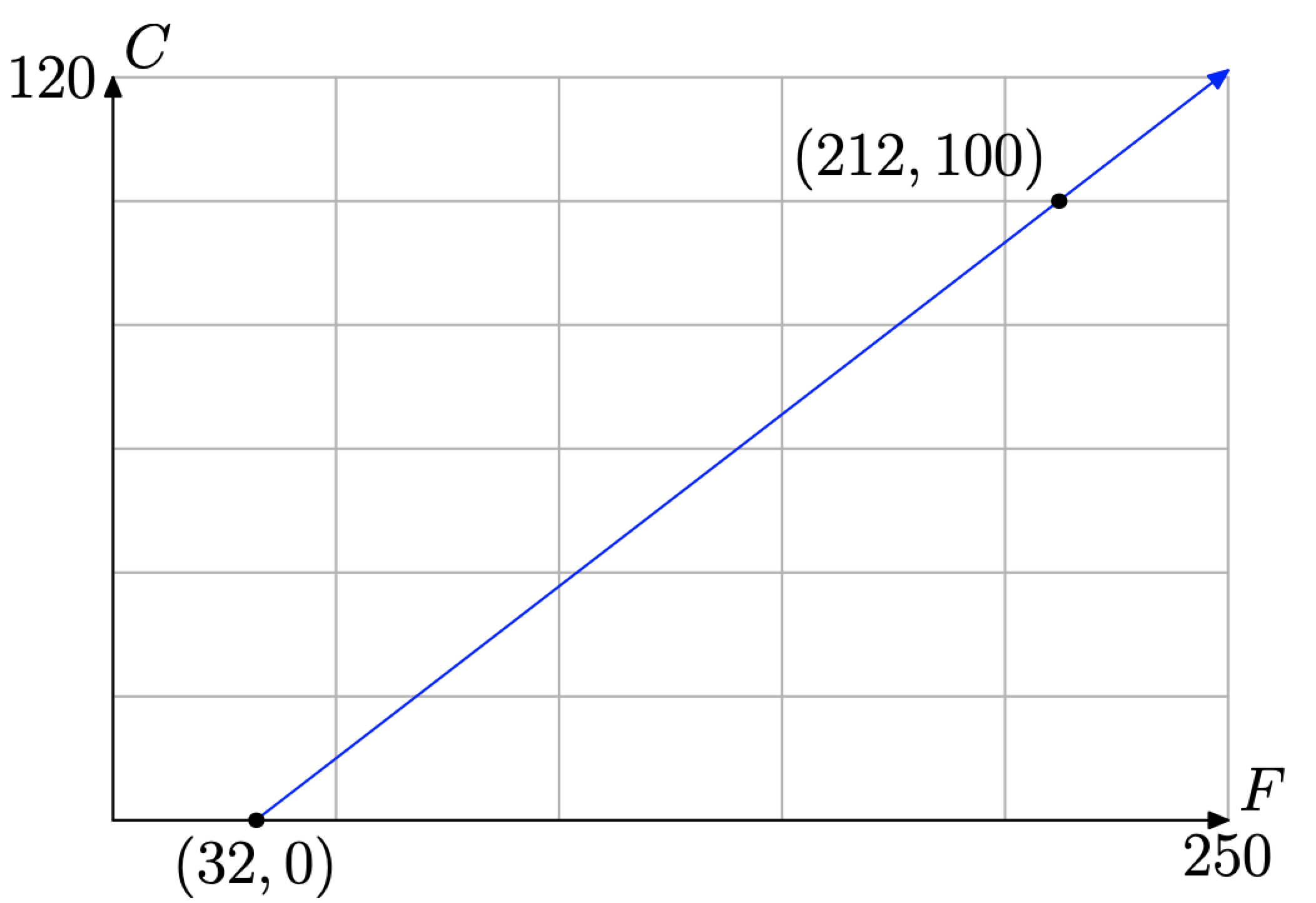
    По-перше, щоб допомогти зберегти нашу увагу, ми створили систему координат на аркуші графічного паперу. На малюнку\(\PageIndex{6}\) ми вирішили зробити температуру Цельсія залежною змінною і присвоїли температуру Цельсія вертикальній осі. Аналогічно, ми оголосили температуру Фаренгейта незалежною змінною і присвоїли її горизонтальній осі.

    Інтерпретувати дані дані:

    • Вода замерзає при\(32^{\circ} F\) і\(0^{\circ} C\). Це дає нам точку (F, C) = (32, 0), яку ми будуємо на малюнку\(\PageIndex{6}\).
    • Вода закипає при\(212^{\circ} F\) і\(100^{\circ} C\). Це дає нам точку (F, C) = (212, 100), яку ми будуємо на малюнку\(\PageIndex{6}\).

    Тепер ми знаходимося на знайомій землі. Ми хочемо знайти рівняння прямої через ці дві точки, що є тим самим типом проблеми, яку ми розглянули в прикладі 6. Спочатку використовуйте точки (32, 0) і (212, 100), щоб визначити нахил лінії.

    \[m=\frac{\Delta C}{\Delta F}=\frac{100-0}{212-32}=\frac{100}{180}=\frac{5}{9}\]

    Тепер будемо використовувати точково-ухил форму лінії,\(y-y_{0}=m\left(x-x_{0}\right)\) при m = 5/9 і\(\left(x_{0}, y_{0}\right)=(32,0)\). \(m=5 / 9, x_{0}=32,\)Замінити і\(y_{0}=0\)\(y-y_{0}=m\left(x-x_{0}\right)\) в отримати

    WeChat592ee9ac052697196b626cb1b26fab84.png
    Малюнок\(\PageIndex{6}\). Графік температури за Цельсієм проти температури Фаренгейта

    \[y-0=\frac{5}{9}(x-32)\]

    Однак наша залежна вісь позначена C, а не y, а наша незалежна вісь позначена F, а не x. так, ми повинні замінити y і x в рівнянні (20) на C і F відповідно, отримавши

    \[C=\frac{5}{9}(F-32)\]

    Цей результат у рівнянні (21) виражає температуру Цельсія як функцію температури Фаренгейта. Крім того, ми могли б також використовувати позначення функцій і писати

    \[C(F)=\frac{5}{9}(F-32)\]

    Припустимо, що ми знаємо, що температура Фаренгейта зовні є,\(80^{\circ} \mathrm{F}\) і ми хочемо висловити це за допомогою шкали Цельсія. Для цього ми просто оцінюємо C (80), як у

    \[C(80)=\frac{5}{9}(80-32) \approx 26.6\]

    Значить, температура за Цельсієм приблизно\(26.6^{\circ} \mathrm{C}\).

    З іншого боку, припустимо, що ми знаємо температуру Цельсія на металевому даху,\(80^{\circ} \mathrm{C}\) і ми хочемо знайти температуру за Фаренгейтом. Для цього нам потрібно вирішити

    \[C(F)=80\]

    для F, або еквівалентно,

    \[\frac{5}{9}(F-32)=80\]

    Помножте обидві сторони на 9, щоб отримати

    \[5(F-32)=720\]

    потім розділіть обидві сторони результату на 5, щоб отримати

    \[F-32=144\]

    Додавання 32 до обох сторін цього останнього результату призводить до температури Фаренгейта\(F = 176^{\circ} \mathrm{F}\). Нічого собі, це гаряче!