3.2: Нахил
- Page ID
- 58080
У попередньому розділі, присвяченому лінійним моделям, ми бачили, що якщо залежна змінна змінювалася з постійною швидкістю щодо незалежної змінної, то графік був рядком. Якщо ставка була позитивною, то в міру того, як ми прокотилися очі зліва направо, лінія піднімалася вгору, залежна змінна збільшувалася зі збільшенням змін незалежної змінної. Якщо ставка була негативною, то графік падав вниз, залежна змінна зменшується зі збільшенням змін незалежної змінної. Можливо, ви також дізналися, що більш високі ставки призвели до більш крутих ліній (ліній, які росли швидше), а більш низькі ставки призвели до ліній, які були менш крутими.
У цьому розділі ми пов'яжемо інтуїтивну концепцію швидкості, розроблену в попередньому розділі, з формальним визначенням нахилу лінії. Для початку давайте заявимо наперед, що мається на увазі під нахилом лінії.
Визначення
Нахил - це число, яке говорить нам, як швидко лінія піднімається або падає.
Якщо ухил - це число, яке безпосередньо пов'язане з «крутизною» лінії, то у нас повинні бути певні очікування.
Очікування
- Лінії з позитивним нахилом повинні нахилятися в гору (як наші очі змітаються зліва направо).
- Лінії з негативним нахилом повинні нахилятися вниз (так як наші очі змітаються зліва направо).
- Оскільки будь-яка горизонтальна лінія не нахиляється ні в гору, ні під гору, ми очікуємо, що вона повинна мати нахил рівний нулю.
- Лінії з більшим позитивним нахилом повинні підніматися швидше, ніж лінії з меншим позитивним ухилом.
- Якщо дві лінії мають негативний нахил, то лінія, що має нахил з більшим абсолютним значенням, повинна падати швидше, ніж інша лінія.
Залишилося визначитися з тим, як обчислити нахил тієї чи іншої лінії. Яке б визначення ми не вибрали, воно повинно відповідати очікуванням, викладеним вище. Ми також хотіли б, щоб визначення нахилу відповідало концепції швидкості, розробленої в попередньому розділі. Таким чином, зробимо наступне визначення.
Визначення: Нахил
Нахил лінії - це швидкість, з якою залежна змінна змінюється відносно незалежної змінної.
Зверніть увагу, як слово «змінити» використовується Визначення. Важливо розуміти, що зміна в деякій кількості може бути позитивним, негативним або нульовим. Наприклад, якщо температура на вулиці - це\(40^{\circ} \mathrm{F}\) коли я виходжу з дому о 6 ранку, а опівдні температура 65◦ F, то зміна температури позитивна\(25^{\circ} \mathrm{F}\). З іншого боку, якщо температура на вулиці опівдні, а температура -\(50^{\circ} \mathrm{F}\) коли я повертаюся додому ввечері, то зміна температури становить негативний 15 градусів за Фаренгейтом.\(65^{\circ} \mathrm{F}\)
При розрахунку зміни кількості дотримуйтесь цього правила.
Визначення: Зміна кількості
Зміна кількості = останнє вимірювання - Колишнє вимірювання.
Таким чином, якщо Т\(\Delta T\) являє собою температуру і являє собою зміну температури, то в нашому першому випадку (приймаючи температуру вранці, потім пізніше опівдні) зміна температури становить\[\Delta T=\text { Latter }-\text { Former }=65^{\circ} \mathrm{F}-40^{\circ} \mathrm{F}=25^{\circ} \mathrm{F}\]
Цей позитивний результат являє собою підвищення температури\(25^{\circ} \mathrm{F}\).
У другому випадку (приймаючи температуру опівдні, потім пізніше ввечері) зміна температури становить
\[\begin{align*} \Delta T &= \text{Latter} - \text{Former} \\[4pt] &=50^{\circ} \mathrm{F}-65^{\circ} \mathrm{F} \\[4pt] &=-15^{\circ} \mathrm{F} \end{align*}\]
Цей негативний результат являє собою зниження температури\(15^{\circ} \mathrm{F}\)
Рада 3
Читачам варто відзначити, що напрямок віднімання вкрай важливо. Щоб виявити зміну кількості, завжди віднімайте перше (попереднє) вимірювання з останнього (пізнішого) вимірювання.
Приклад\(\PageIndex{1}\)
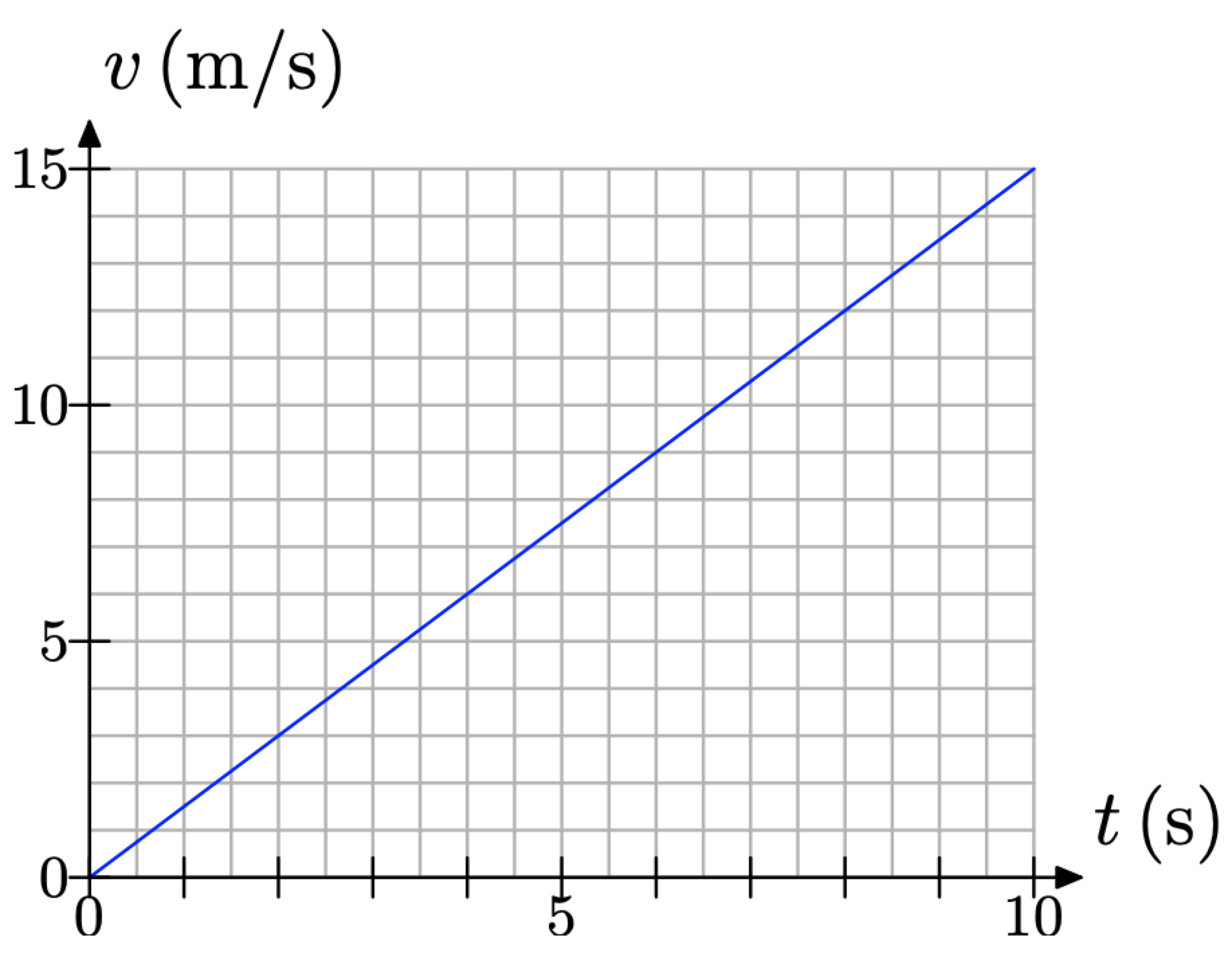
М'яч сидить у спокої у верхній частині довгого пандуса. Йому дається невеликий кран і він починає котитися вниз по рампі. Швидкість v кулі (в метрах в секунду) побудована проти часу t (у секундах) на рис\(\PageIndex{1}\).
Визначаємо ухил лінії.
Рішення
Ми визначили нахил як швидкість, з якою залежна змінна змінюється щодо незалежної змінної. При цьому швидкість v кулі «залежить» від кількості часу t, що минув. Отже, v є залежною змінною і була розміщена на вертикальній осі.3 З іншого боку, t є незалежною змінною і їй присвоюється горизонтальна вісь.
Щоб визначити швидкість, з якою v змінюється щодо t (нахил прямої), спочатку виділяємо дві точки Р (2, 3) і Q (8, 12) на лінії, як показано на малюнку\(\PageIndex{2}\). Коли ми підмітаємо очі зліва направо (угода, яку ми завжди будемо дотримуватися при роботі з нахилом), точка P виникає перед точкою Q. отже, ми вважаємо P «колишнім» вимірюванням, а точку Q - «останнім» вимірюванням.
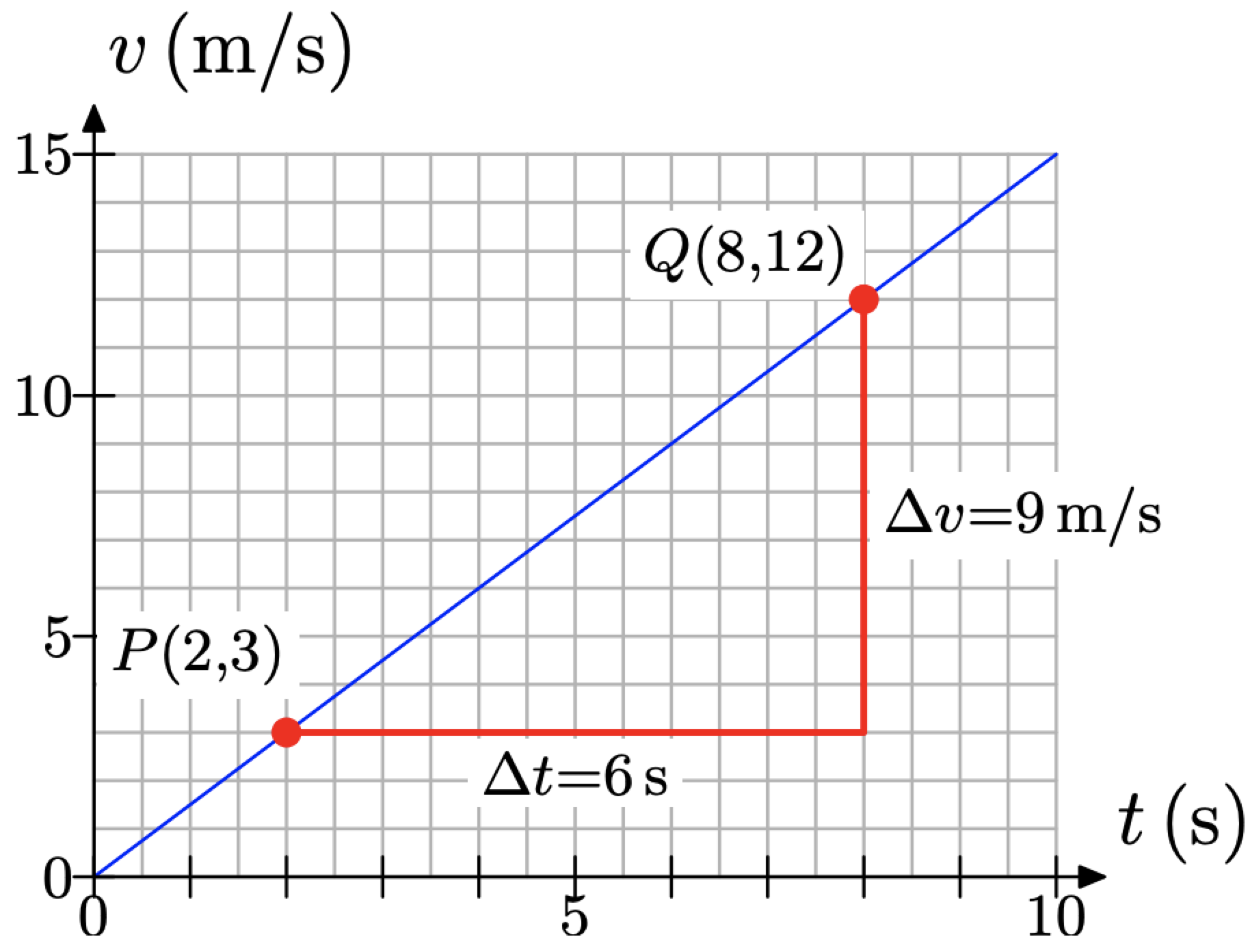
У точці Р час t = 2 секунди, потім в точці Q час t = 8 секунд. Зміна t знаходять шляхом віднімання першого вимірювання з останнього вимірювання.
\[\Delta t=8 s-2 s=6 s \nonumber\]
У точці Р швидкість v = 3 метри в секунду, тоді в точці Q швидкість v = 12 метрів в секунду. Значить, зміна в v
\[\Delta v=12 \mathrm{m} / \mathrm{s}-3 \mathrm{m} / \mathrm{s}=9 \mathrm{m} / \mathrm{s} \nonumber\]
Нарешті, нахил прямої визначається як швидкість, з якою залежна змінна v змінюється щодо незалежної змінної t.
\[\text { Slope }=\frac{\Delta v}{\Delta t}=\frac{9 \mathrm{m} / \mathrm{s}}{6 \mathrm{s}}=\frac{3 \mathrm{m} / \mathrm{s}}{\mathrm{s}} \nonumber\]
Вчені вважають за краще писати це як 1.5\(\mathrm{m} / \mathrm{s}^{2}\), але це може бути не настільки інтуїтивно зрозумілим, як написання 1.5 (м/с) /с, що вказує на те, що швидкість збільшується зі швидкістю 1,5 м/с щосекунди. Це має сенс, оскільки м'яч, що котиться по рампі, набирає швидкість з плином часу. Ухил забезпечує точний числовий опис того, як швидкість збільшується по відношенню до часу.
Відзначимо, що наше визначення ухилу лінії задовольняє одній з наших цілей: нахил точно такий же, як і поняття швидкості, описане в попередньому розділі. Дійсно, зверніть увагу на прямокутний трикутник ми намалювали на малюнку\(\PageIndex{2}\). Нижній край трикутника має довжину 12 коробок, але кожні 2 коробки представляють одну секунду, тому це зміщення в напрямку часу t становить 6 секунд. Вертикальна сторона прямокутного трикутника - це 9 коробок у висоту, де кожна коробка представляє 1 метр в секунду. Отже, цей вертикальний край прямокутного трикутника являє собою позитивне зміщення в 9 метрів в секунду. Таким чином, кожні 6 секунд відбувається збільшення швидкості на 9 метрів в секунду. Отже, м'яч набирає швидкість зі швидкістю 9 метрів в секунду кожні 6 секунд, або еквівалентно 1,5 метра в секунду кожну секунду.
Примітка
На малюнку швидкість\(\PageIndex{2}\), з якою швидкість збільшується по відношенню до часу, еквівалентна нахилу лінії.
Припустимо, що ми позначили наші точки\(P\left(t_{\text { initial }}, v_{\text { initial }}\right)\) і\(Q\left(t_{\text { final }}, v_{\text { final }}\right)\) як показано на малюнку\(\PageIndex{3}\).
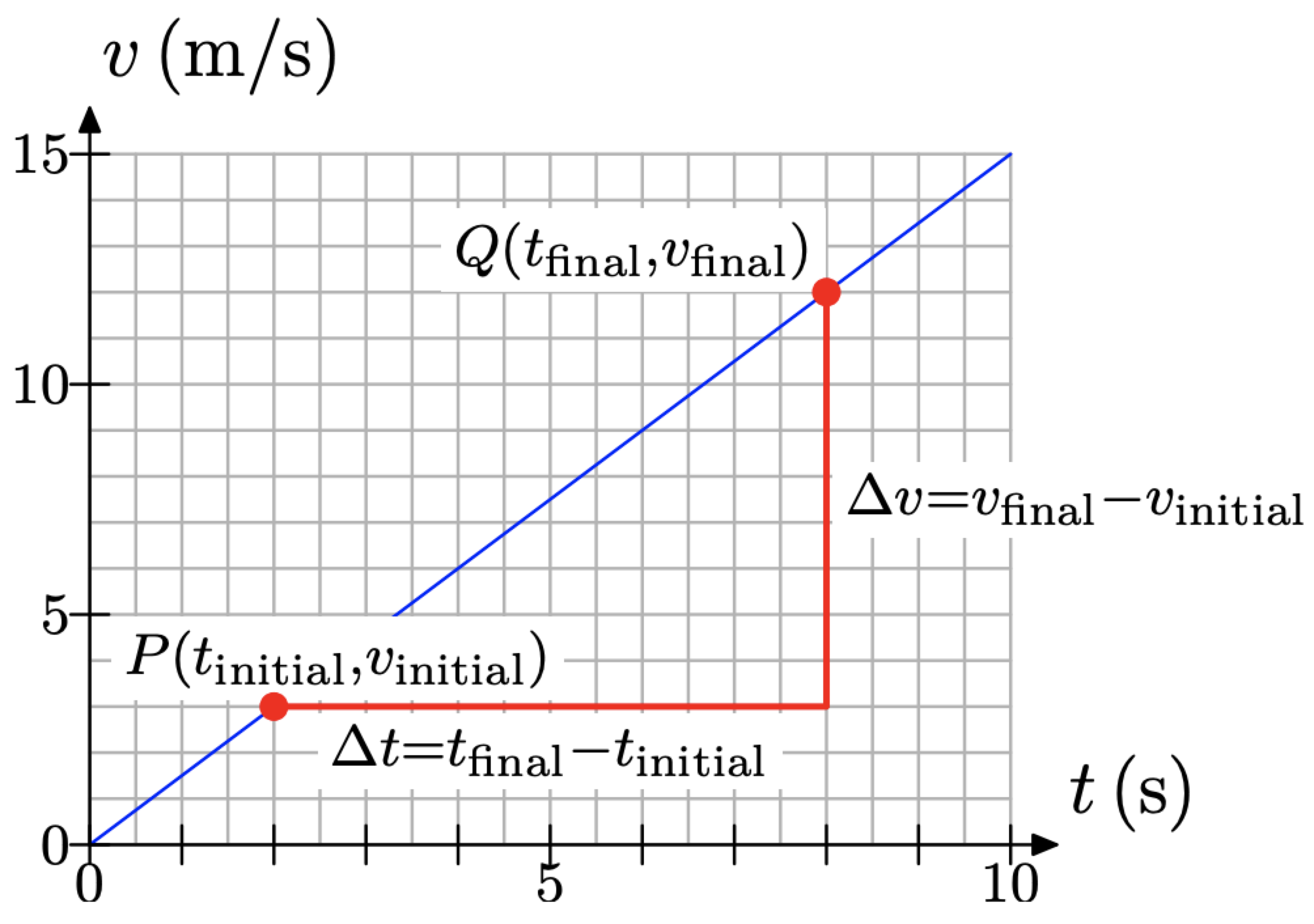
Тепер зміна швидкості v буде
\[\Delta v=v_{\text { final }}-v_{\text { initial }} \nonumber\]
і зміна часу t буде
\[\Delta t=t_{\text { final }}-t_{\text { initial }} \nonumber\]
Тому нахил лінії буде обчислюватися за наступною формулою.
\[\text { Slope }=\frac{\Delta v}{\Delta t}=\frac{v_{\text { final }}-v_{\text { initial }}}{t_{\text { final }}-t_{\text { initial }}}\nonumber\]
З\(P\left(t_{\text { initial }}, v_{\text { initial }}\right)=(2 \mathrm{s}, 3 \mathrm{m} / \mathrm{s})\) і\(Q\left(t_{\text { final }}, v_{\text { final }}\right)=(8 \mathrm{s}, 12 \mathrm{m} / \mathrm{s}),\) це стає
\[\text { Slope }=\frac{12 \mathrm{m} / \mathrm{s}-3 \mathrm{m} / \mathrm{s}}{8 \mathrm{s}-2 \mathrm{s}}=\frac{9 \mathrm{m} / \mathrm{s}}{6 \mathrm{s}}=1.5 \mathrm{m} / \mathrm{s}^{2} \nonumber\]
Формула нахилу
Останній розрахунок у прикладі\(\PageIndex{1}\) дозволяє обговорити нахил лінії як чисто математичне поняття, яке не вкорінюється в допоміжній програмі, як у прикладі\(\PageIndex{1}\). Візьмемо, наприклад, лінію, зображену на малюнку\(\PageIndex{4}\), яка проходить через точки\(P(−3, −3)\) і\(Q(2, 1)\).
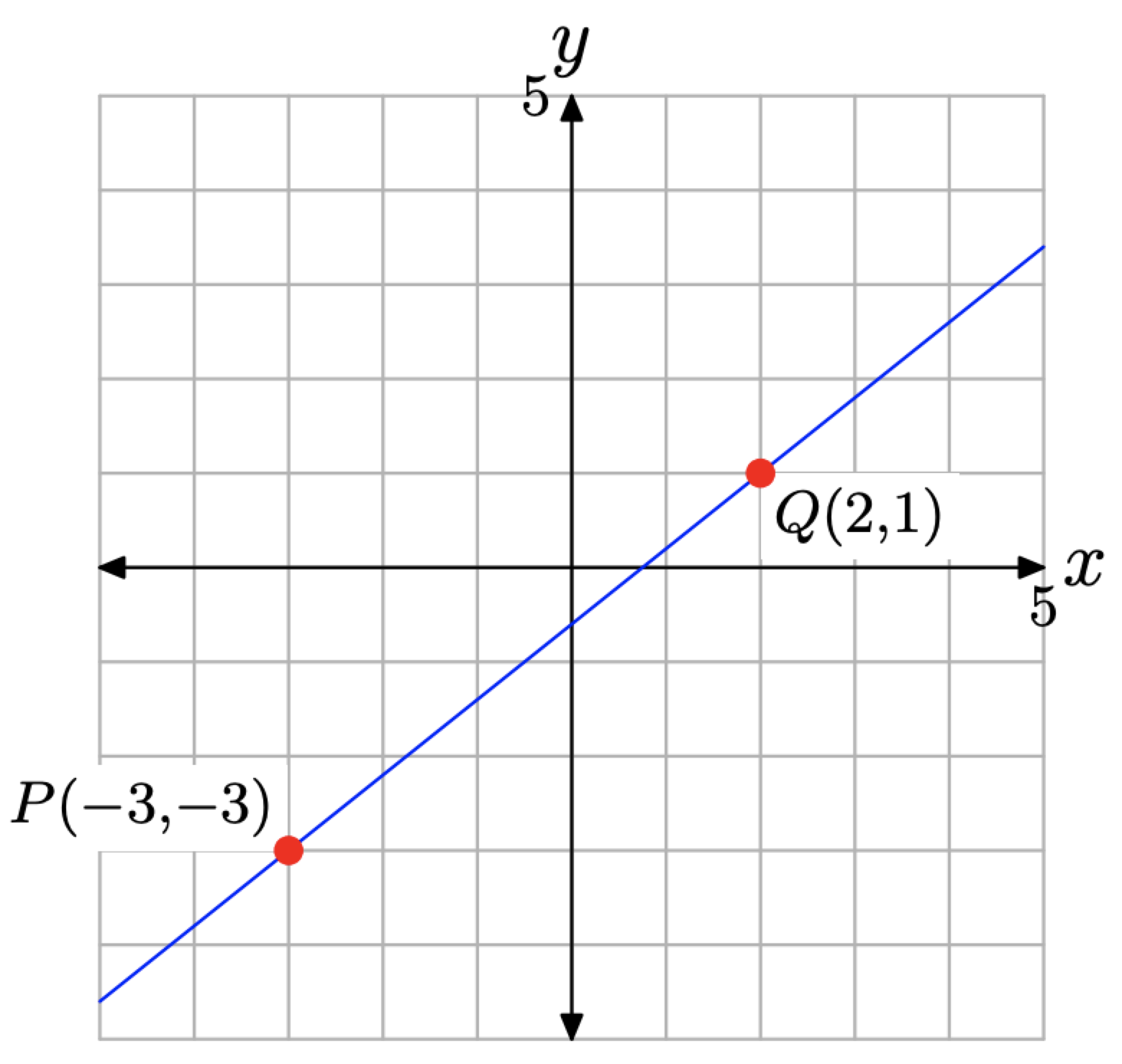
У цьому прикладі залежною змінною є y, а незалежна змінна - x, тому нахил лінії\(\Delta y\) (зміна у) ділиться на\(\Delta x\) (зміна x).
\[\text { Slope }=\frac{\Delta y}{\Delta x}\]
Підмітаючи очі зліва направо, точка P стоїть на першому місці, а потім точка Q. зберігаючи на увазі «останній мінус колишній», зміна у обчислюється шляхом віднімання значення y точки P з y-значення точки Q. тобто
\[\Delta y=1-(-3)=4\]
Аналогічно, зміна x обчислюється шляхом віднімання значення x точки P з значення x точки Q. тобто
\[\Delta x=2-(-3)=5\]
Таким чином, нахил лінії дорівнює
\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{4}{5}\]
Крім того, ми можемо використовувати точки P і Q як вершини прямокутного трикутника зі сторонами, паралельними осям (показано на малюнку\(\PageIndex{5}\) (а)). Горизонтальний край прямокутного трикутника становить 5 коробок (кожна представляє 1 одиницю), тому зміщення в х дорівнює 5 одиницям. Вертикальний край - 4 коробки (кожна представляє 1 одиницю), тому зміщення у дорівнює 4 одиницям. Отже, кожен раз, коли x збільшується на 5 одиниць, y відчуває збільшення на 4 одиниці. Тому нахил лінії знову 4/5.
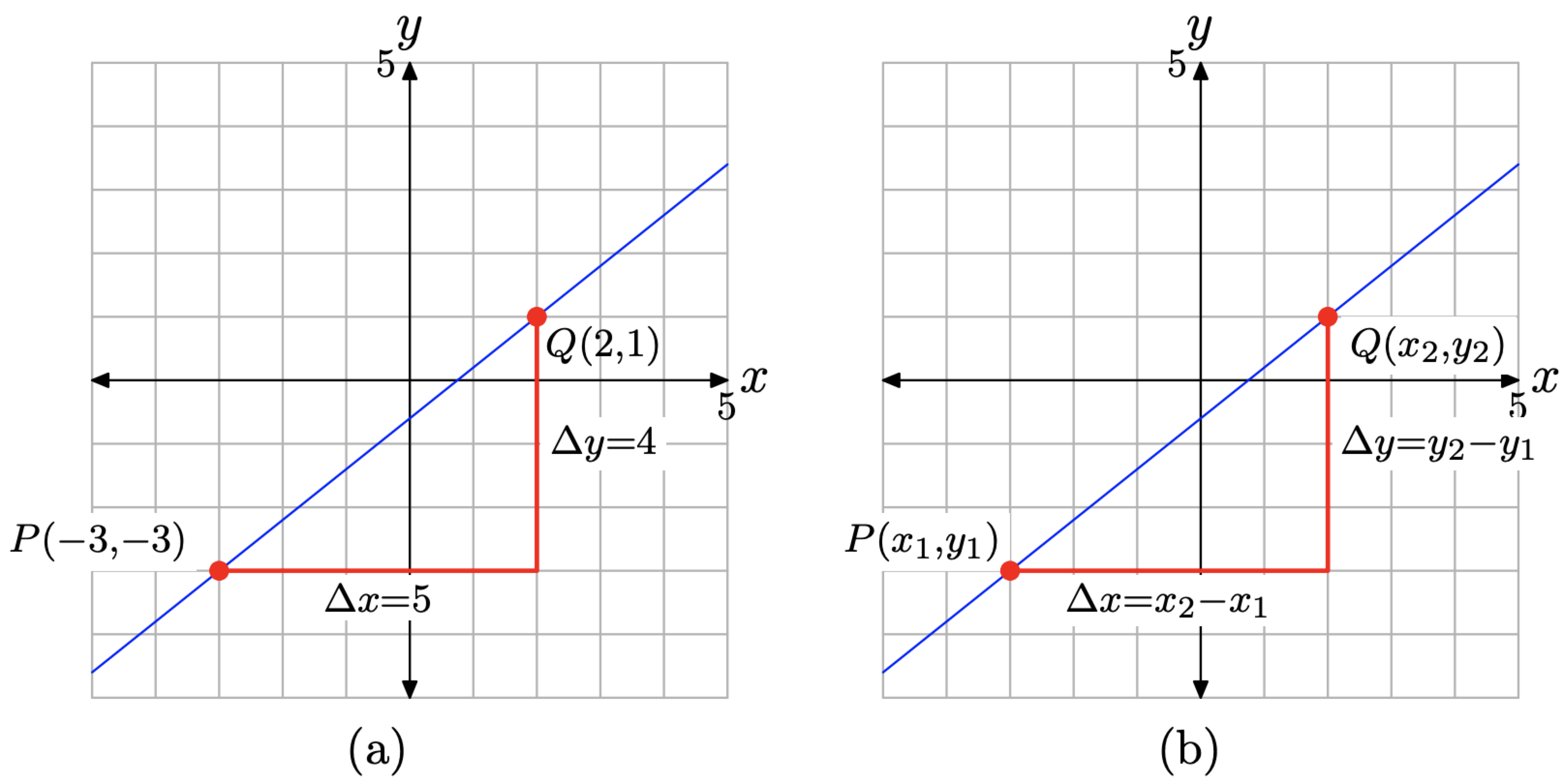
Припустимо, що ми позначили наші точки\(P\left(x_{1}, y_{1}\right)\) і\(Q\left(x_{2}, y_{2}\right)\) як показано на малюнку\(\PageIndex{5}\) (b). Тепер зміна у буде
\[\Delta y=y_{2}-y_{1}\]
і зміна х буде
\[\Delta x=x_{2}-x_{1}\]
Тому нахил лінії буде обчислюватися за наступною формулою.
\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\]
З\(P\left(x_{1}, y_{1}\right)=(-3,-3)\) і\(Q\left(x_{2}, y_{2}\right)=(2,1),\) це стає
\[\text { Slope }=\frac{1-(-3)}{2-(-3)}=\frac{4}{5}\]
Формулу нахилу варто підсумувати у визначенні.
Визначення 5
Нахил лінії, яка проходить через точки\(P\left(x_{1}, y_{1}\right)\) і\(Q\left(x_{2}, y_{2}\right)\) задається за формулою
\[\text {Slope }=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\]
Давайте розглянемо ще кілька прикладів.
Приклад\(\PageIndex{2}\)
Знайти нахил прямої, що проходить через точки P (−3, −2) і Q (3, 1).
Рішення
Ми можемо використовувати формулу нахилу у Визначенні 5 для визначення нахилу. З\(\left(x_{1}, y_{1}\right)=P(-3,-2)\) і\(\left(x_{2}, y_{2}\right)=Q(3,1)\),
\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{1-(-2)}{3-(-3)}=\frac{3}{6}=\frac{1}{2}\]
Читачі іноді запитують: «Який момент повинен бути,\(\left(x_{1}, y_{1}\right)\) а який повинен бути\(\left(x_{2}, y_{2}\right)\)?» Коротка відповідь: «Це не має значення!» Припустимо замість цього, що ми дозволяємо\(\left(x_{1}, y_{1}\right)=Q(3,1)\) і\(\left(x_{2}, y_{2}\right)=P(-3,-2)\). Потім,
\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-2-1}{-3-3}=\frac{-3}{-6}=\frac{1}{2}\]
Оскільки зміна будь-якої кількості виявляється шляхом віднімання попереднього вимірювання з пізнішого вимірювання, ми продовжуватимемо підкреслювати перший порядок. Однак, якщо ми перевернемо точки, як ми зробили в нашому другому обчисленні, обидва чисельник і знаменник зворотний знак з цим обміну, так що ми отримуємо ту ж відповідь.
Звичайно, ми також можемо визначити нахил шляхом побудови P (−3, −2) та Q (3, 1) та лінії, яка проходить через P та Q, як ми зробили на малюнку\(\PageIndex{6}\).
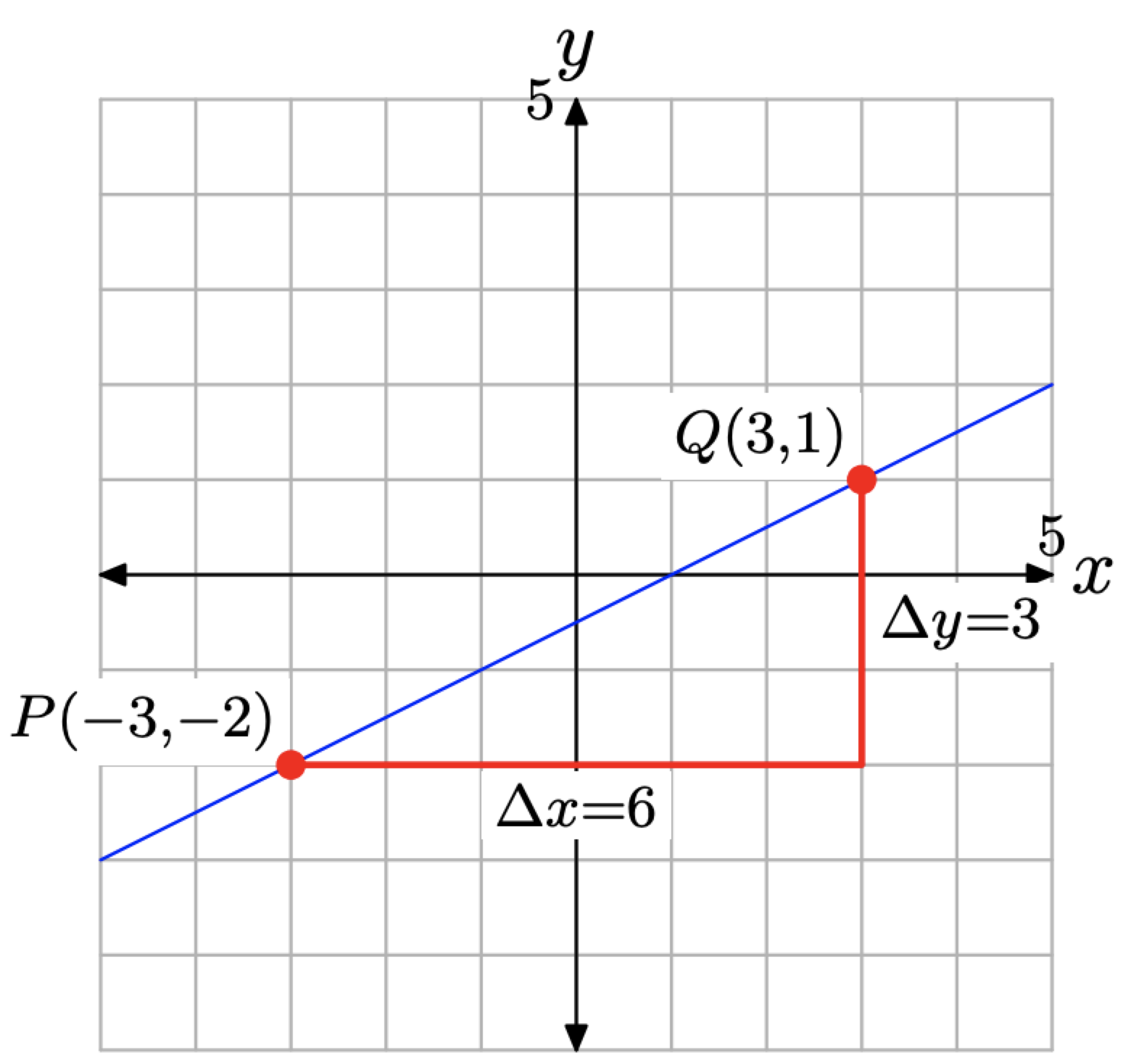
Починаючи з точки Р, щоб дістатися до точки Q, переміщаємо 6 коробок вправо, потім 3 ящика вгору, як показано на малюнку\(\PageIndex{6}\). Значить, нахил лінії дорівнює
\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{3}{6}=\frac{1}{2}\]
Зверніть увагу, що два наші очікування щодо нахилу лінії відповідають цьому прикладі.
- Лінія через P (−3, −2) та Q (3, 1) на рисунку\(\PageIndex{6}\) має нахил 1/2. Це позитивне число, і лінія нахиляється вгору (як очікувалося), коли ми підмітаємо очі зліва направо.
- Нахил в цьому прикладі дорівнює 1/2, що менше нахилу лінії на малюнку\(\PageIndex{5}\) (а), який становив 4/5. Зверніть увагу, що лінія на малюнку\(\PageIndex{6}\) менш крута, ніж лінія на малюнку\(\PageIndex{5}\) (а), що було ще одним із наших попередніх очікувань щодо нахилу лінії.
Приклад\(\PageIndex{3}\)
Знайти нахил прямої, що проходить через точки P (−4, 4) і Q (4, −2).
Рішення
Ми можемо використовувати формулу нахилу у Визначенні 5 для визначення нахилу. З\(\left(x_{1}, y_{1}\right)=P(-4,4)\) і\(\left(x_{2}, y_{2}\right)=Q(4,-2)\),
\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-2-4}{4-(-4)}=\frac{-6}{8}=-\frac{3}{4}\]
Ми також можемо отримати нахил лінії з графіка на малюнку\(\PageIndex{7}\). Починаючи з точки Р (−4, 4), перемістіть 8 одиниць вправо, потім на 6 одиниць вниз, як показано на малюнку\(\PageIndex{7}\).
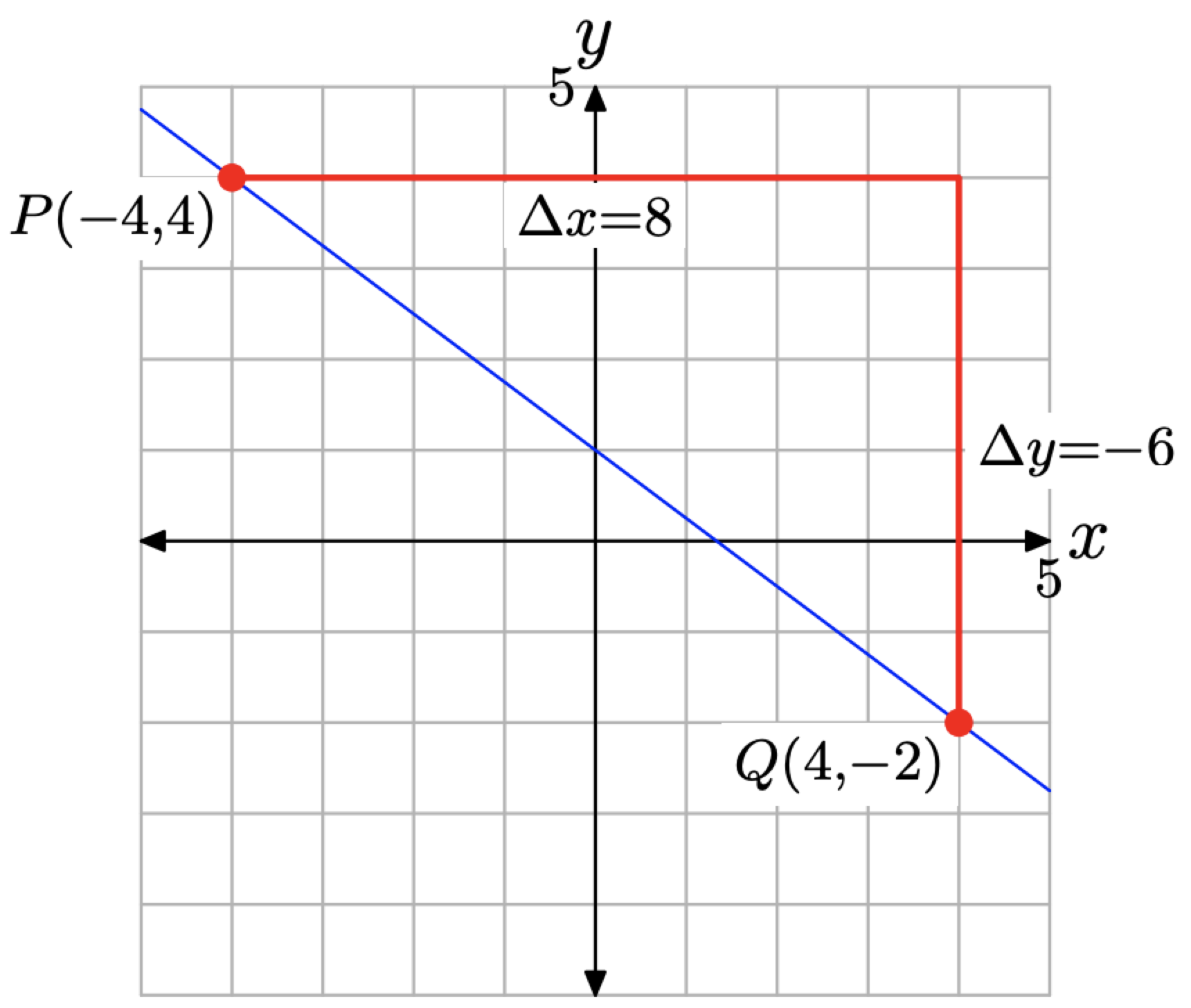
Таким чином, нахил лінії дорівнює
\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{-6}{8}=-\frac{3}{4}\]
Знову ж таки, одне з наших попередніх очікувань щодо нахилу лінії виправдано в цьому прикладі. Нахил дорівнює −3/4, що є від'ємним числом, а лінія на малюнку\(\PageIndex{7}\) нахиляється вниз (коли ми змітаємо очі зліва направо).
Приклад\(\PageIndex{4}\)
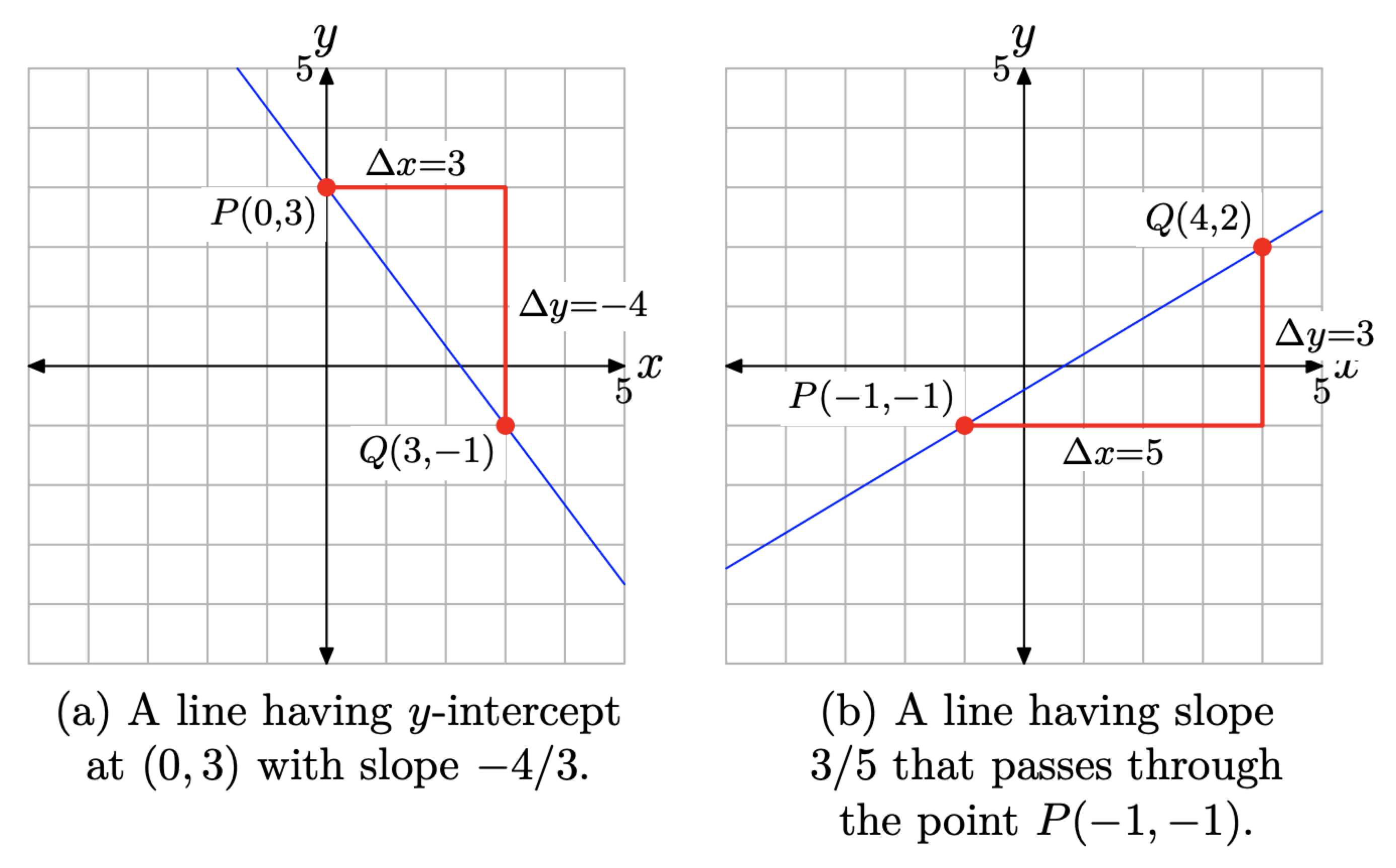
Намалюйте лінію, яка перехоплює вісь y (0, 3) так, щоб лінія мала нахил −4/3. Намалюйте другу лінію, яка проходить через точку Р (−1, −1) з нахилом 3/5.
Рішення
Ухил першої лінії дорівнює −4/3. Це означає, що наша лінія повинна нахилятися вниз (як ми змітаємо очі зліва направо). Нахил - це зміна y над зміною x Тому кожен раз, коли x збільшується на 3 одиниці, y повинен зменшуватися на 4 одиниці. Покладіть точку Р (0, 3), як показано на малюнку\(\PageIndex{8}\) (а). Потім, починаючи з P, перемістіть 3 одиниці вправо, а потім 4 одиниці вниз до точки Q (3, −1), як показано на малюнку\(\PageIndex{8}\) (а). Намалюйте необхідну лінію, яка повинна проходити через точки Р і Q.
Щоб намалювати другу лінію, спочатку нанесіть точку P (−1, −1), як показано на малюнку\(\PageIndex{8}\) (b). Починаючи з точки Р, перемістіть 5 одиниць вправо, потім вгору на 3 одиниці до точки Q (4, 2), як показано на малюнку\(\PageIndex{8}\) (б). Намалюйте необхідну лінію, що проходить через точки Р і Q.
Паралельні лінії
Оскільки нахил контролює «крутизну» лінії, просто зрозуміти, що паралельні лінії повинні мати однаковий нахил.
властивість
\(\boldsymbol{L}_{1}\)Дозволяти лінії, що мають нахил\(m_{1}\). \(\boldsymbol{L}_{2}\)Дозволяти лінії, що мають нахил\(m_{2}\). Якщо\(\boldsymbol{L}_{1}\) і\(\boldsymbol{L}_{2}\) паралельні, то
\[m_{1}=m_{2}\]
Тобто будь-які дві паралельні лінії мають однаковий нахил.
Приклад\(\PageIndex{5}\)
Що таке ухил будь-якої горизонтальної лінії? Що таке ухил будь-якої вертикальної лінії?
Рішення
Можна було б очікувати, що наше визначення перевірить, що нахил будь-якої горизонтальної лінії дорівнює нулю. Виберіть, наприклад, горизонтальну лінію, показану на малюнку 9 (а). Виділіть точки (−3, 3) та (3, 3) на цьому рядку.
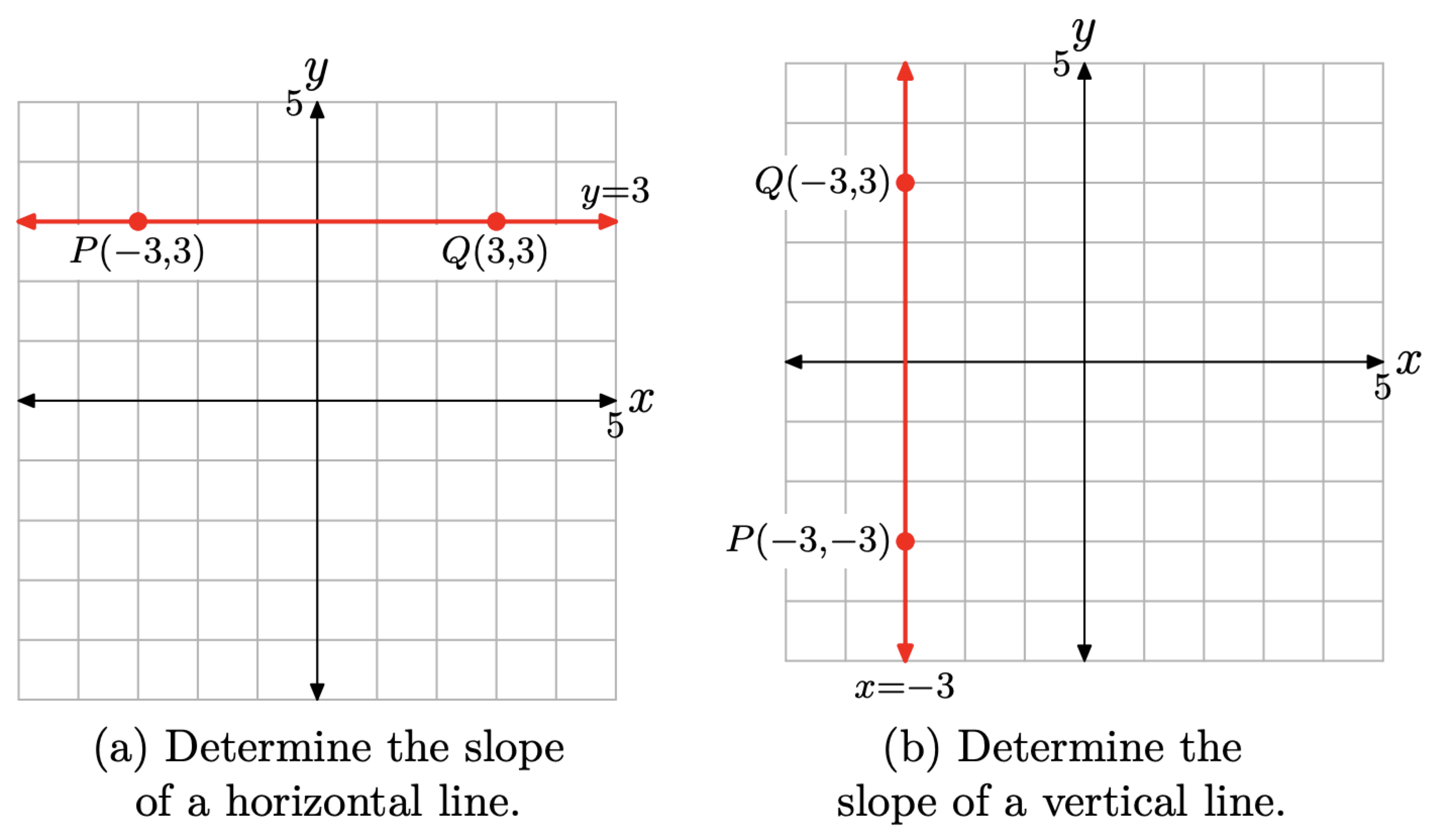
З\(\left(x_{1}, y_{1}\right)=(-3,3)\) і\(\left(x_{2}, y_{2}\right)=(3,3)\)
\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{3-3}{3-(-3)}=\frac{0}{6}=0\]
Таким чином, горизонтальна лінія на малюнку\(\PageIndex{9}\) (а) має нахил рівний нулю, точно так, як очікувалося. Далі всі горизонтальні лінії паралельні цій горизонтальній лінії і мають однаковий нахил. Тому всі горизонтальні лінії мають ухил нульовий.
Ми б припустили, що вертикальна лінія на малюнку\(\PageIndex{9}\) (b) має невизначений нахил (ми вивчимо це більш повно у вправах). На малюнку\(\PageIndex{9}\) (b) ми вибрали точки P (−3, −3) та Q (−3, 3) на вертикальній лінії. З\(\left(x_{1}, y_{1}\right)=P(-3,-3)\) і\(\left(x_{2}, y_{2}\right)=Q(-3,-3)\),\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{3-(-3)}{-3-(-3)}=\frac{6}{0}, \text { which is undefined. }\]
Нахил вертикальної лінії на малюнку\(\PageIndex{9}\) (b) невизначений, оскільки ділення на нуль безглуздо. Далі всі вертикальні лінії паралельні цій вертикальній лінії і мають невизначений нахил.
Приклад\(\PageIndex{6}\)
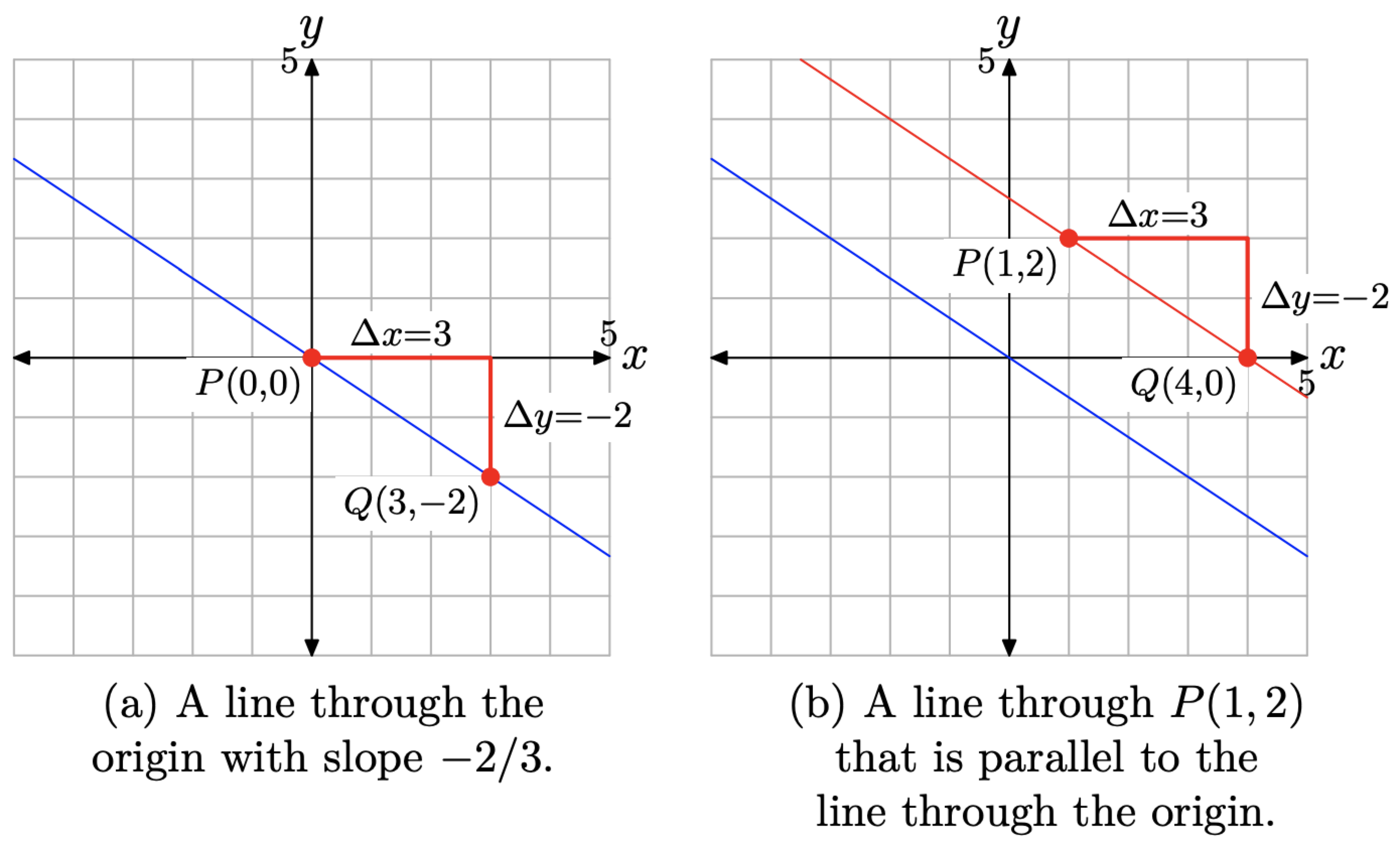
Проведіть лінію через точку Р (1, 2), яка паралельна лінії, що проходить через початок з нахилом −2/3.
Рішення
Спочатку ми проведемо лінію через початок з нахилом −2/3. Покладіть точку P (0, 0), потім перемістіть 3 одиниці вправо і 2 одиниці вниз до точки Q (3, −2), як показано на малюнку\(\PageIndex{10}\) (а). Проведіть лінію через точки P і Q, як показано на малюнку\(\PageIndex{10}\) (а).
Далі намічаємо точку Р (1, 2), як показано на малюнку\(\PageIndex{10}\) (б). Щоб провести лінію через цю точку, паралельну лінії через початок, ця друга лінія повинна мати такий же нахил, як і перша лінія. Тому почніть з точки Р (1, 2), як показано на малюнку\(\PageIndex{10}\) (б), потім перемістіть 3 одиниці вправо і 2 одиниці вниз до точки Q (4, 0). Проведіть лінію через точки P і Q, як показано на малюнку\(\PageIndex{10}\) (b). Зверніть увагу, що ця друга лінія паралельна першій.
Перпендикулярні лінії
Співвідношення між нахилами двох перпендикулярних ліній не так прямолінійно, як відношення між нахилами двох паралельних ліній. Почнемо з констатації відповідного властивості.
Нерухомість 13
\(L_{1}\)Дозволяти лінії, що мають нахил\(m_{1}\). \(L_{2}\)Дозволяти лінії, що мають нахил\(m_{2}\). Якщо\(L_{1}\) і\(L_{2}\) перпендикулярні, то
\[m_{1} m_{2}=-1\]
Тобто добуток нахилів двох перпендикулярних ліній дорівнює −1.
Ми можемо вирішити рівняння (14)\(m_{1}\) за термінами\(m_{2}\).
\[m_{1}=-\frac{1}{m_{2}}\]
Рівняння (15) говорить нам, що нахил першої лінії є негативним зворотним нахилу другої лінії.
Наприклад, припустимо, що\(L_{1}\) і\(L_{2}\) є перпендикулярними лініями з нахилами\(m_{1}\) і\(m_{2}\), відповідно
- Якщо\(m_{2}=2,\) тоді\(m_{1}=-\frac{1}{2}\)
- Якщо\(m_{2}=\frac{3}{5},\) тоді\(m_{1}=-\frac{5}{3}\)
- Якщо\(m_{2}=-\frac{2}{3},\) тоді\(m_{1}=\frac{3}{2}\)
Зауважте, що в кожному маркованому елементі добуток нахилів дорівнює −1.
Ми не будемо надавати докази рівняння (15), але наведемо деякі мотивуючі докази у вигляді графіка.
Приклад\(\PageIndex{7}\)
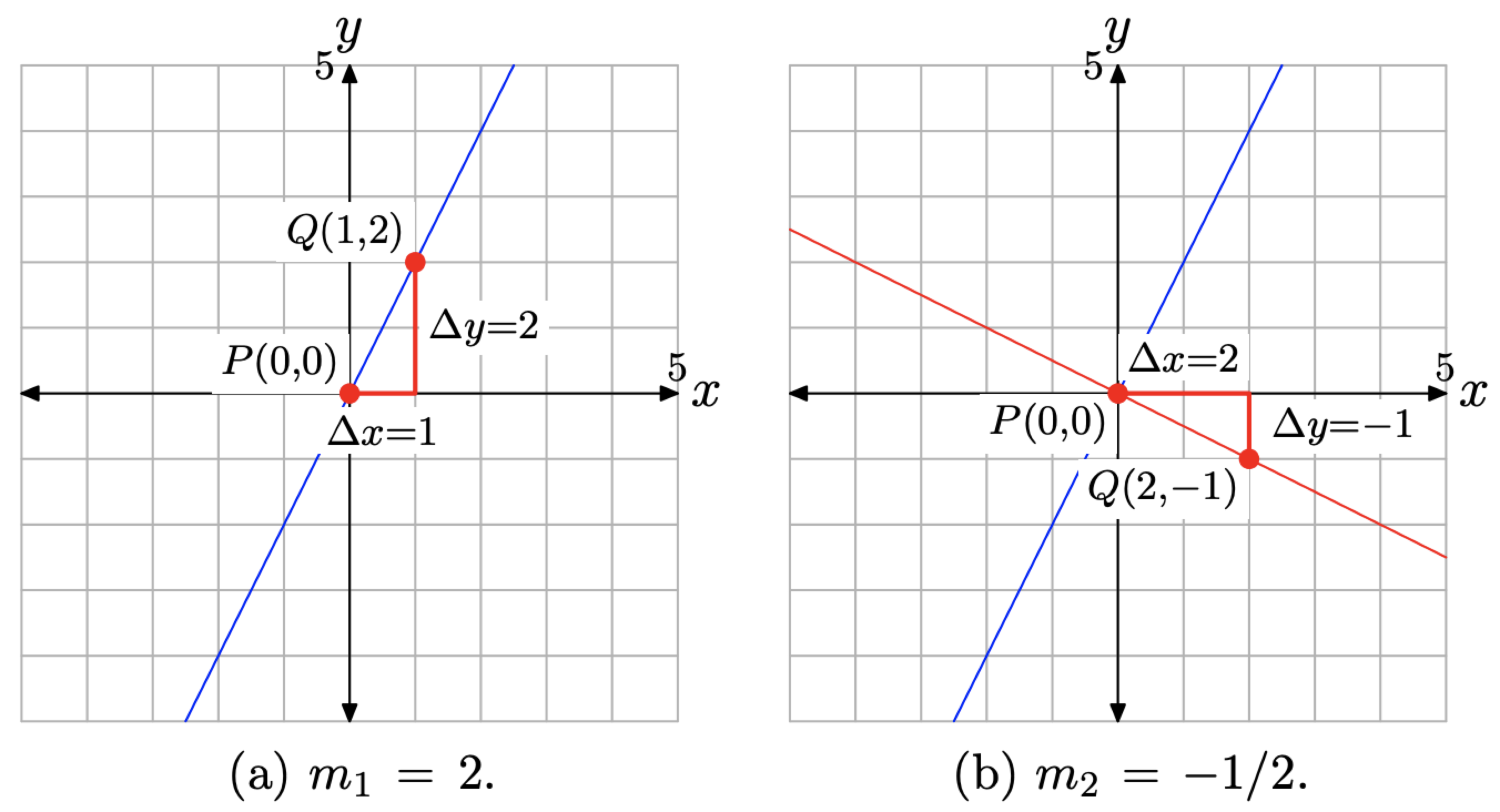
Намалюйте графіки ліній, що проходять через початок координат, що мають нахили 2 та −1/2.
Рішення
На малюнку\(\PageIndex{11}\) (a) ми побудували точку P (0, 0) біля початку, потім перемістили 1 одиницю вправо і 2 одиниці вгору до точки Q (1, 2). Отримана лінія проходить через початок і має нахил\(m_{1}=2\) (альтернативно,\(m_{1}=2 / 1\)).
На малюнку\(\PageIndex{11}\) (b) ми знову побудували точку P (0, 0) біля початку, потім перемістили 2 одиниці вправо і 1 одиницю вниз до точки Q (2, −1). Отримана лінія проходить через початок і має нахил\(m_{2}=-1 / 2\).
Є два важливих моменти, які потрібно зробити щодо ліній на малюнку\(\PageIndex{11}\) (б).
Дві лінії на малюнку\(\PageIndex{11}\) (b) перпендикулярні. Вони зустрічаються і утворюють прямий кут\(90^{\circ}\). Якщо у вас є транспортир, ви можете виміряти кут між двома лініями і зауважте, що міра кута є\(90^{\circ}\).
Твір двох укосів
\[m_{1} m_{2}=2 \cdot\left(-\frac{1}{2}\right)=-1\]