3.1: Лінійні моделі

Себастьян прощається зі своїм братом, який розмовляє з групою своїх друзів приблизно в 20 футах. Потім Себастьян починає відходити від брата з постійною швидкістю 4 фути в секунду. Давайте змоделюємо відстань, що розділяє двох братів, як функцію часу.

Наш перший підхід буде графічним. Ми дозволимо змінній d представляти відстань (у футах) між братами, а змінна t представляє кількість часу (у секундах), що минуло з тих пір, як Себастьян помахав до побачення зі своїм братом. Оскільки відстань, що розділяє братів, залежить від кількості часу, який пройшов, ми скажемо, що відстань d - залежна змінна, а час t - незалежна змінна.

Дещо традиційно в процесі моделювання розміщувати незалежну змінну на горизонтальній осі та залежну змінну на вертикальній осі. Це не жорстке і швидке правило, більше питання особистого смаку, але ми все ж будемо слідувати цьому правилу в нашому прикладі. Таким чином, ми розмістимо відстань по вертикальній осі і час на горизонтальній осі, як показано на малюнку\(\PageIndex{1}\). Зверніть увагу, що ми позначили кожну вісь з її змінним представленням і включили одиниці, важлива практика.

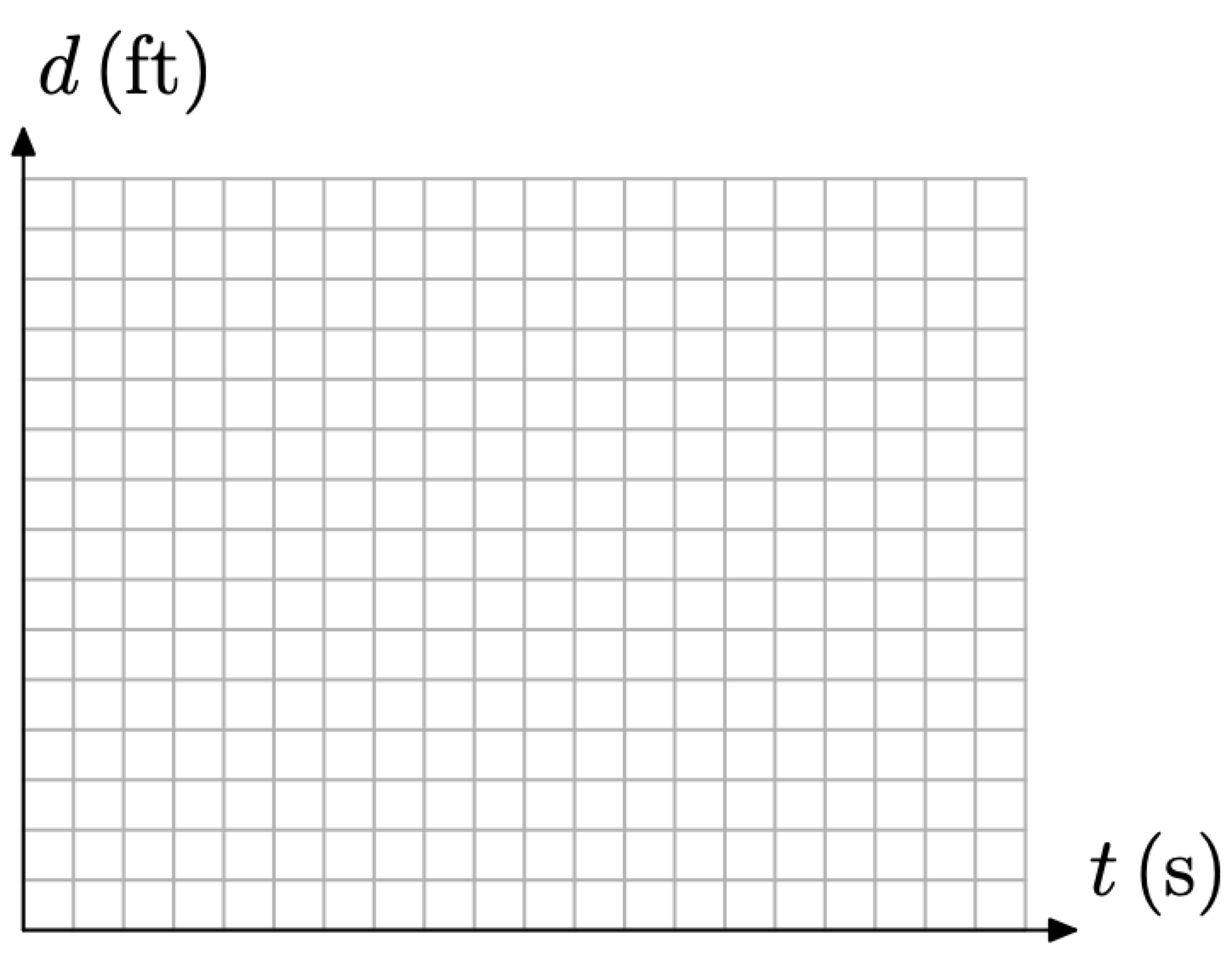
Малюнок\(\PageIndex{1}\). Відстань залежить від часу.

Попередження

Мітка на горизонтальній осі, t (s), може виглядати як позначення функцій для деяких читачів. Це не так. Швидше, змінна t представляє час, а (и) у дужках, що слідують, представляє секунди, стандартну абревіатуру у фізиці. Аналогічні коментарі є по порядку і для етикетки d (ft). Змінна d представляє відстань, а (ft) у дужках, що слідують, представляють фути, ще одна стандартна абревіатура у фізиці.

Існує кілька різних способів, за допомогою яких ви можете позначити осі вашого графіка одиницями, відповідними для проблеми під рукою. Для прикладу розглянемо техніку, представлену на малюнку\(\PageIndex{2}\), де мітки розміщуються зліва від вертикальної осі і під горизонтальною віссю. Ще одна відмінність полягає в тому, що скорочення одиниць на малюнку 1 прописані повністю на рис\(\PageIndex{2}\).

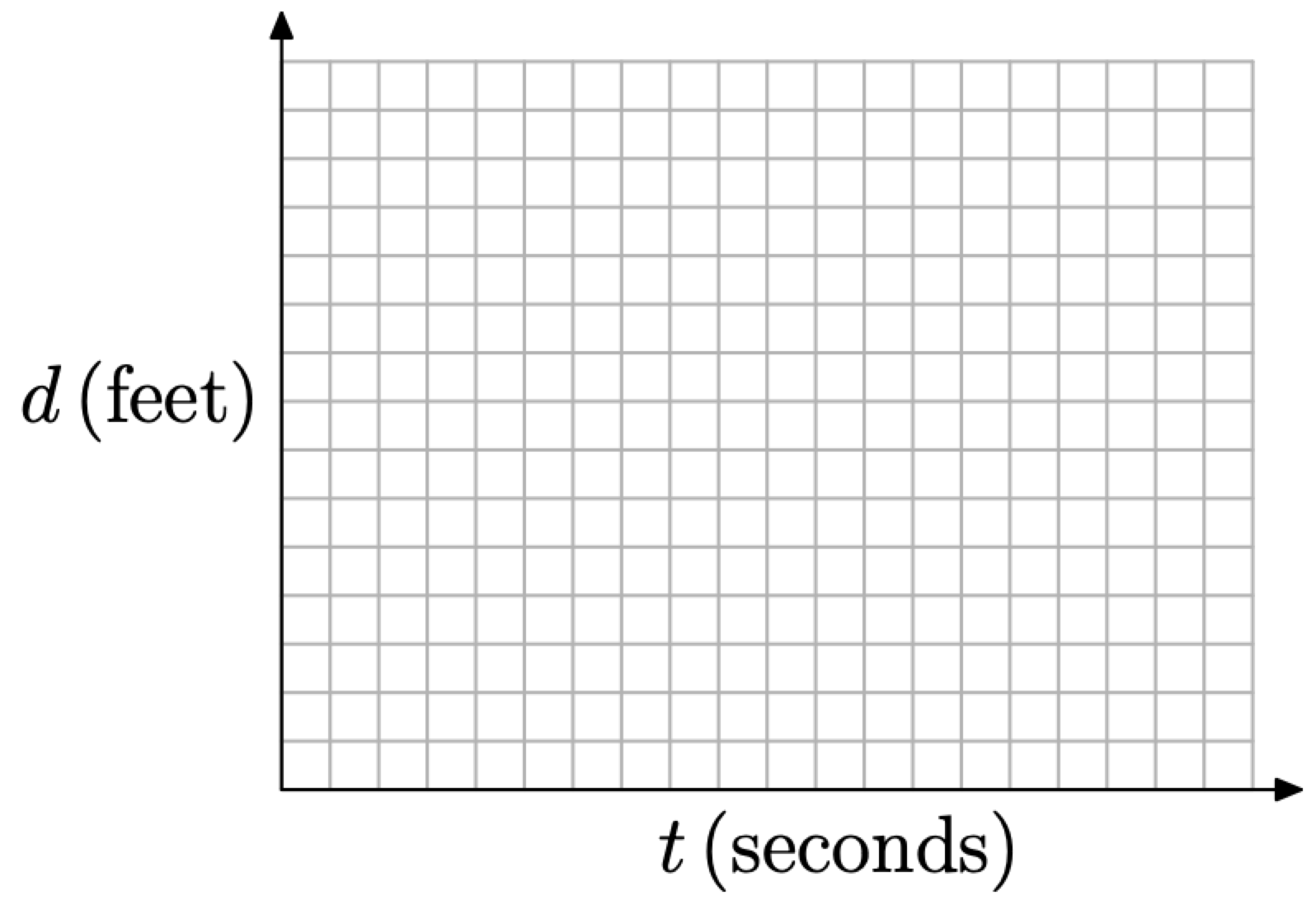
Малюнок\(\PageIndex{2}\). Відстань залежить від часу.

Деякі інструктори вважають за краще, щоб ви повернули мітку відстані на вертикальній осі на дев'яносто градусів, щоб вона з'являлася вбік. Інші вважають за краще, щоб ви позначали кінці кожної осі зі змінною, як ми зробили на малюнку\(\PageIndex{1}\), але викладіть одиниці в повному обсязі поряд з кожною віссю, як ми зробили на малюнку\(\PageIndex{2}\). Список переваг можна продовжувати і далі.

Примітка

Важливо мати розмову з інструктором для того, щоб визначити, що очікування вашого інструктора, коли справа доходить до маркування осей і вказуючи одиниць на графіках.

Ми вважаємо за краще позначити осі\(\PageIndex{1}\), як показано на малюнку, і ми намагатимемося відповідати цьому стандарту протягом решти тексту, хоча час від часу ми можемо відхилятися від альтернативних форм маркування.

Тепер ми повинні масштабувати кожну вісь належним чином, завдання, яке складніше, ніж здається спочатку. Поганий вибір масштабу може зробити завдання попереду складніше, ніж потрібно. Ми підберемо шкалу для кожної осі з урахуванням наступних думок.

Рекомендації щодо масштабування осей

Ось кілька хороших порад, яких слід дотримуватися при масштабуванні залежних і незалежних осей.

1. Ми хочемо уникати графіків розміром з поштові штампи. Великий графік легше інтерпретувати, ніж той, який тісно в маленькому куточку нашої графічного паперу.
2. Не обов'язково мати однакову шкалу на кожній осі, але після вибору шкали ви повинні залишатися послідовними.
3. Ми хочемо вибрати шкалу, яка легко корелює з заданою ставкою.

Себастьян відходить від брата з постійною швидкістю 4 фути в секунду. Давайте нехай кожна коробка на вертикальній осі представляють 4 фути, а кожні дві коробки на горизонтальній осі представляють 1 секунду, як показано на малюнку\(\PageIndex{3}\).

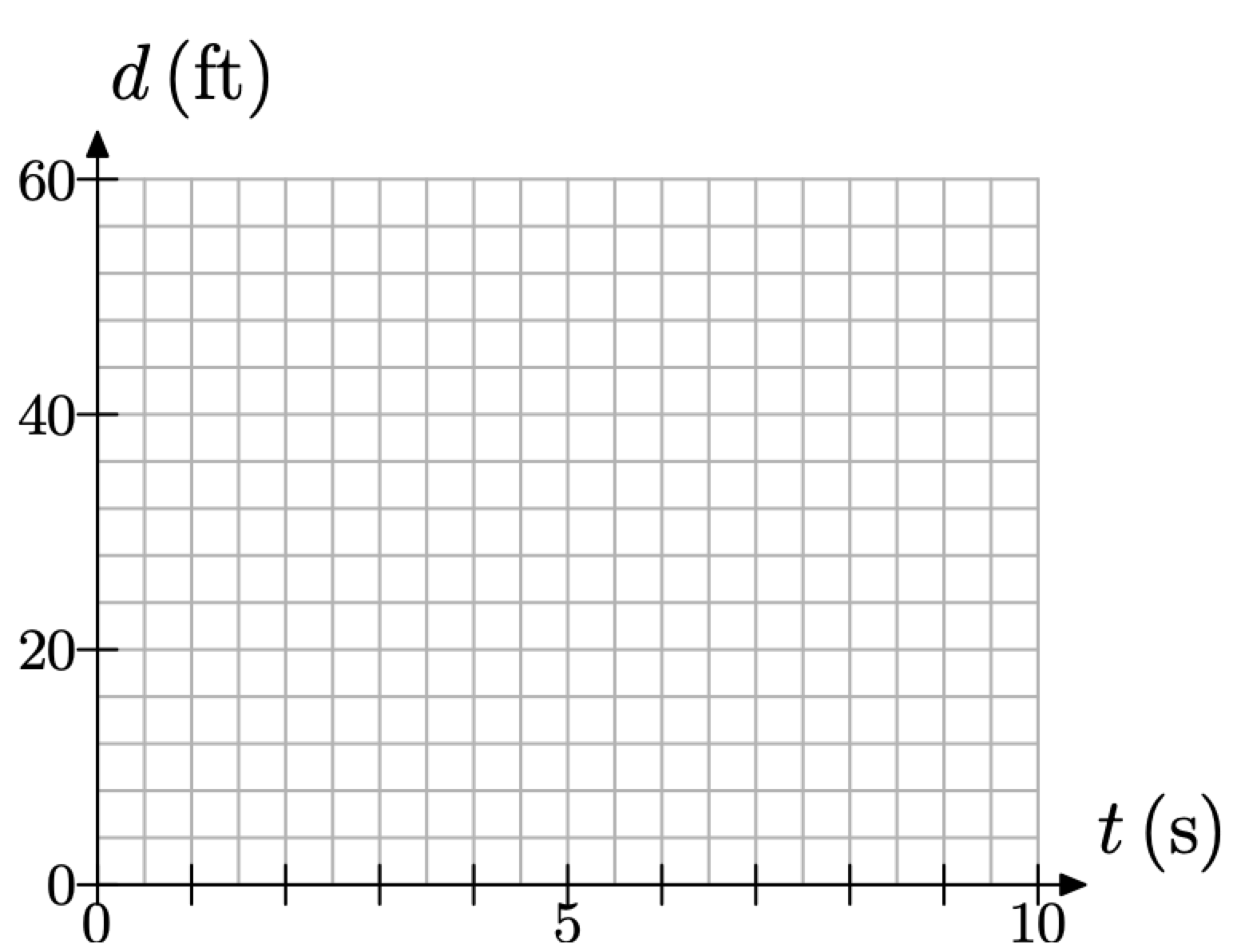
Малюнок\(\PageIndex{3}\). Масштабування кожної осі для розміщення швидкості.

У момент t = 0 Себастьян відділяється від брата на відстані d = 20 футів. Це відповідає точці (t, d) = (0, 20), показаної на малюнку\(\PageIndex{4}\) (а).

Далі Себастьян відходить від брата з постійною швидкістю 4 фути в секунду. Це означає, що за кожну секунду часу, що минає, відстань між братами збільшується на 4 фути. Починаючи з точки (0, 20), перемістіть на 1 секунду (дві коробки) вправо і 4 фути (1 коробка) вгору до точки (1, 24), як показано на малюнку\(\PageIndex{4}\) (b).

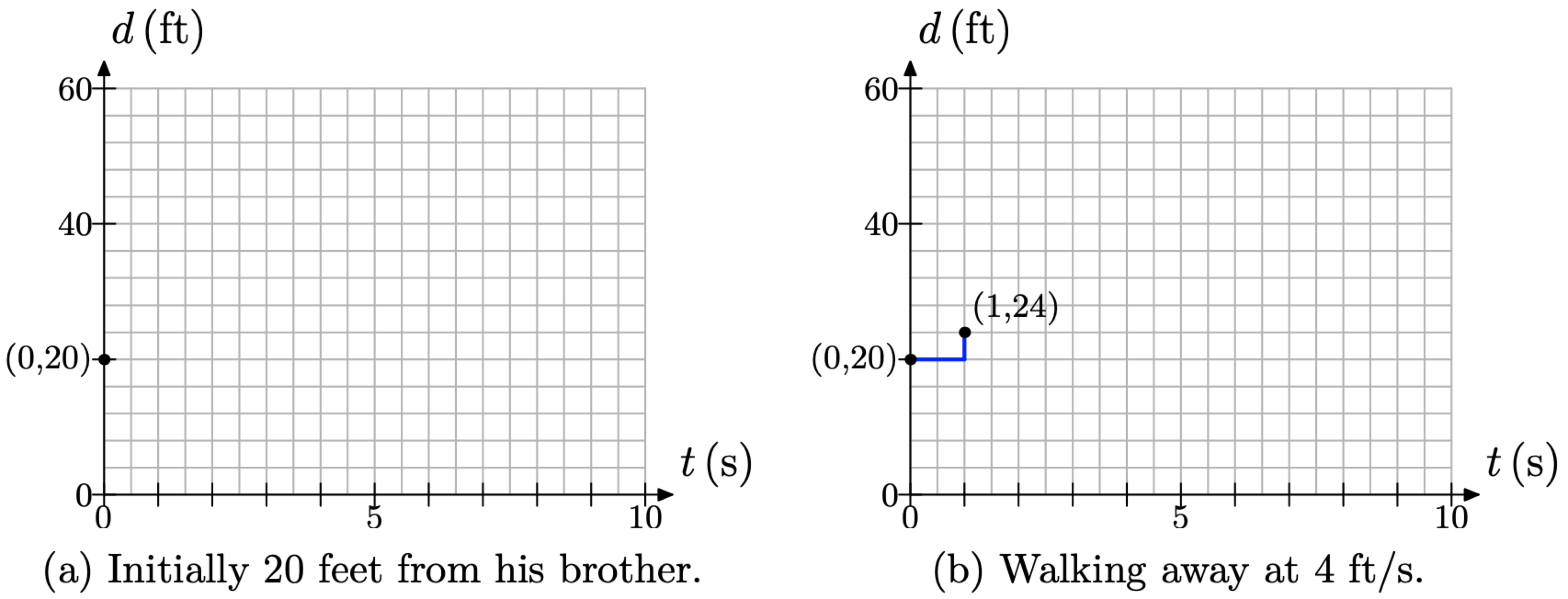
Малюнок\(\PageIndex{4}\).

Швидкість поділу - постійна 4 фути в секунду. Отже, продовжуйте нескінченно в порядку малюнка\(\PageIndex{4}\) (b), рухаючись на 1 секунду (2 коробки) вправо, потім на 4 фути вгору (1 коробка). Це створить лінійну залежність між відстанню та часом, запропоновану на малюнку\(\PageIndex{5}\) (а).

Якщо припустити, що відстань є безперервною функцією часу, законним припущенням через те, що відстань збільшується безперервно з постійною швидкістю 4 фути в секунду, то ми можемо замінити дискретний набір точок даних на малюнку\(\PageIndex{5}\) (а) лінією, показаною на малюнку\(\PageIndex{5}\) (b).

Лінія на малюнку\(\PageIndex{5}\) (б) являє собою суцільну модель. Його можна намалювати простим штрихом олівця, без того, щоб кінчик олівця ніколи не залишав контакту з нашим графічним папером. З іншого боку, множина точок на малюнку\(\PageIndex{4}\) (а) є дискретною моделлю. Після побудови точки наш олівець повинен розірвати контакт з нашим графічним папером, перш ніж малювати наступну точку. Це суттєва відмінність дискретної моделі від неперервної моделі.

При цьому суцільна модель являє собою більш точне уявлення про відстань між братами. Ми говоримо це тому, що відстань між ними збільшується з постійною швидкістю 4 фути в секунду, або 2 фути кожні половину секунди, або 1 фут кожну чверть секунди, і т.д. коротко, ми покажемо приклад, де такого роду безперервна модель є нерозумною.

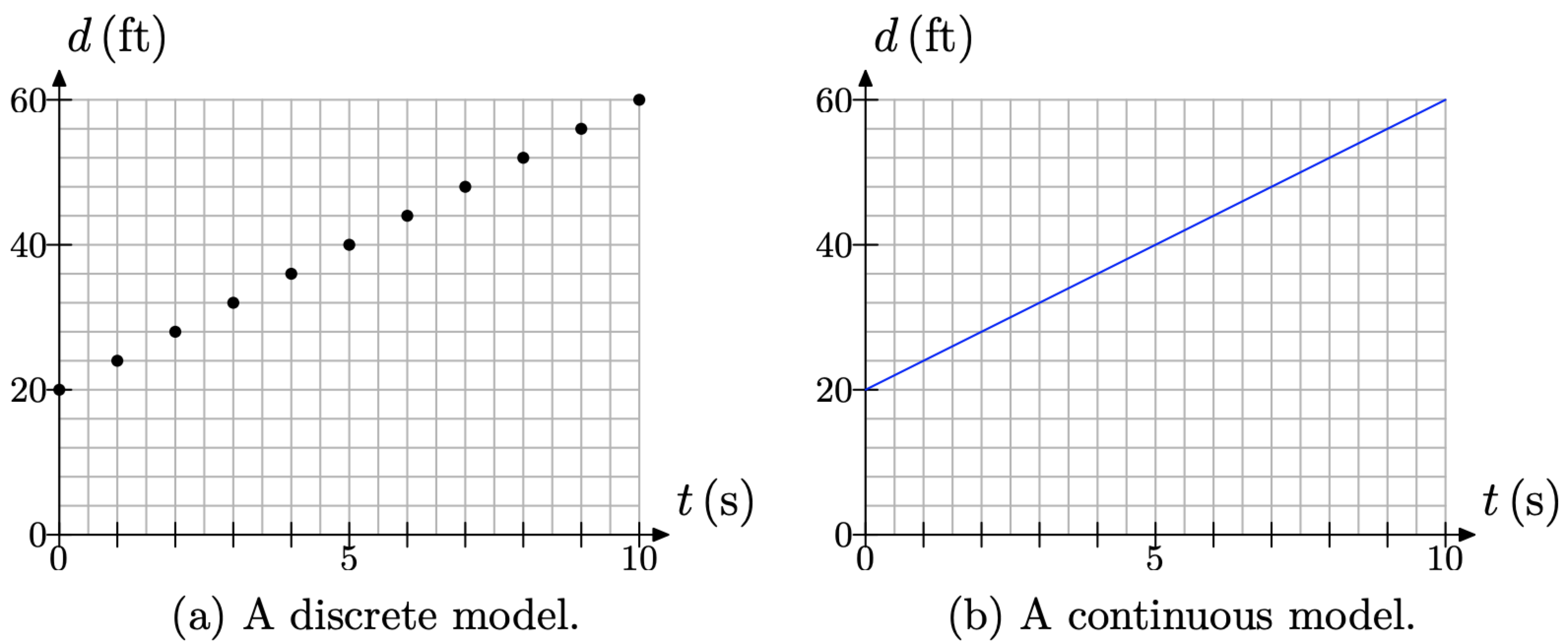
Малюнок\(\PageIndex{5}\). Постійна швидкість дає лінійну залежність.

Тепер, коли ми змоделювали відстань між братами за допомогою графіка, ми можемо використовувати графік для прогнозування. Наприклад, щоб визначити відстань між братами через 8 секунд, знайдіть 8 секунд на осі часу, проведіть вертикальну стрілку до лінії, потім горизонтальну стрілку до осі відстані, як показано на малюнку\(\PageIndex{6}\).

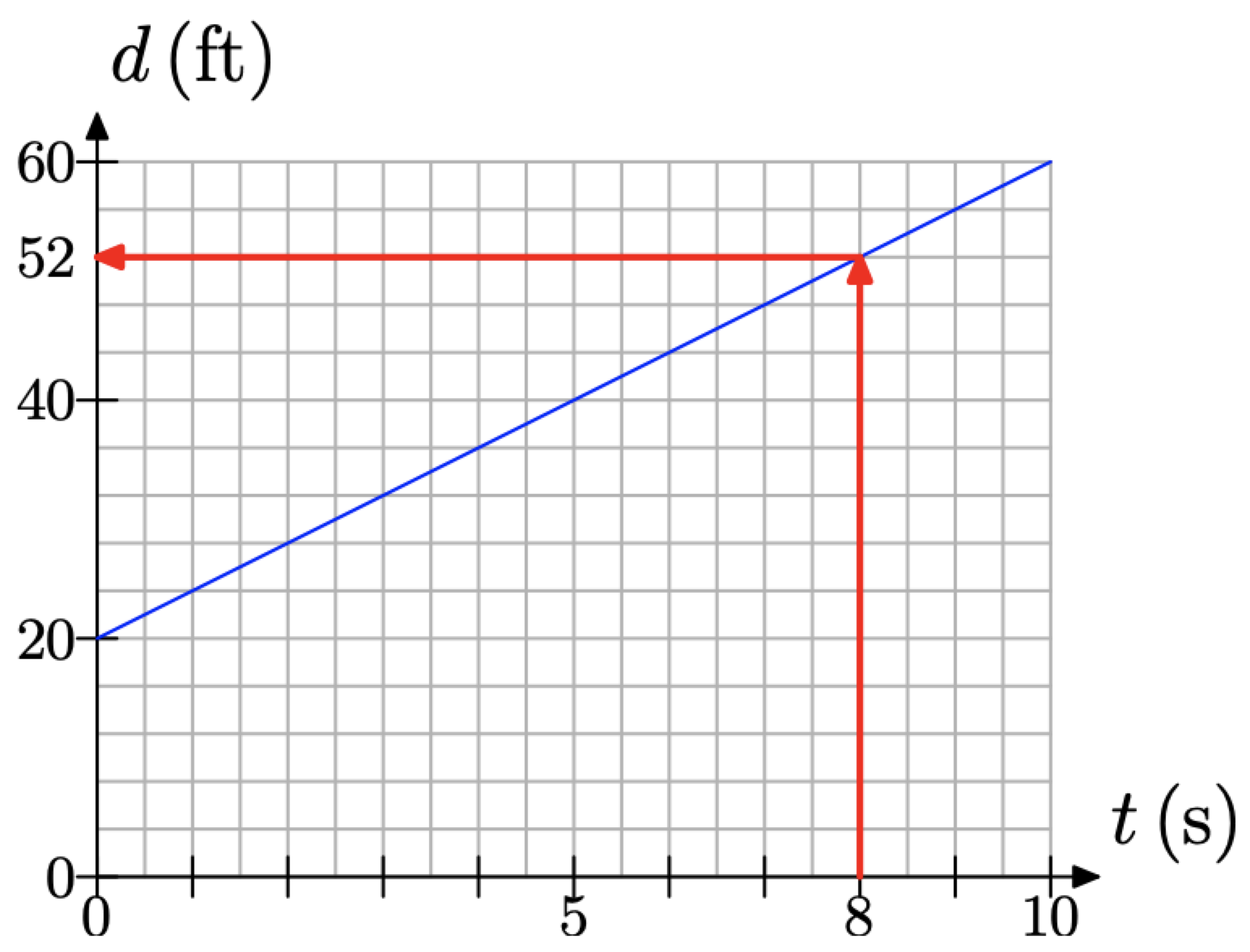
Малюнок\(\PageIndex{6}\). Прогнозування відстані між братами через 8 секунд.

Однак припустимо, що ми хочемо визначити відстань між братами через 2 хвилини. Оскільки графік на малюнку\(\PageIndex{5}\) (b) моделює лише відстань протягом перших 10 секунд, нам доведеться перемалювати графік протягом перших 2 хвилин (120 секунд), щоб визначити відповідь. Ми не планували заздалегідь цю непередбачену ситуацію, тому, можливо, ми зможемо змоделювати відстань між братами іншим способом, таким, який буде легше передбачити відстань між братами через довільну кількість часу t.

Для цього ми шукаємо закономірність, яка описує відстань d між братами як функцію часу t Оскільки відстань між братами збільшується зі швидкістю 4 фути в секунду, відзначимо, що:

• При t = 0 секунд відстань між братами d = 20 футів.
• При t = 1 секунда відстань між братами d = 24 фути.
• При t = 2 секунди відстань між братами d = 28 футів.
• При t = 3 секунди відстань між братами d = 32 фути.

Підсумовуємо ці результати в таблиці\(\PageIndex{1}\) (а).

Однак ви не хочете спрощувати відстані, як ми маємо в таблиці\(\PageIndex{1}\) (а), оскільки ви приховуєте закономірність або зв'язок між відстанню d та часом t Більш ефективно шукати зв'язок між відстанню та часом наступним чином. Після t = 1 секунда відстань збільшується на 1 крок 4 фути, тому d = 20 + 4 (1). Через t = 2 секунди відстань збільшується на 2 кроки в 4 фути, тому d = 20 + 4 (2). Продовжуючи таким чином, ми маємо:

• При t = 3 секунди відстань між братами d = 20 + 4 (3) ноги.

• При t = 4 секунди відстань між братами d = 20 + 4 (4) ноги.

Ці результати зведені в табл.\(\PageIndex{1}\) (b).

т	d
0	20
1	24
2	28
3	32

Таблиця\(\PageIndex{1}\) (а) Визначення модельного рівняння.

т	d
0	20
1	20 + 4 (1)
2	20 + 4 (2)
3	20 + 4 (3)

Таблиця\(\PageIndex{1}\) (b) Визначення модельного рівняння.

На відміну від таблиці\(\PageIndex{1}\) (a), таблиця\(\PageIndex{1}\) (b) виявляє зв'язок між відстанню d та часом t, яку можна описати рівнянням

\[d=20+4 t\]

Уважний читач перевірить, що рівняння (3) виявляє правильні відстані для t = 0, 1, 2 та 3 секунди, як записано в таблиці\(\PageIndex{1}\) (a). Можна зробити два важливих спостереження щодо рівняння (3).

1. 20 в d = 20 + 4t - початкова відстань між братами і відповідає точці (0, 20) на малюнку\(\PageIndex{4}\) (а).
2. 4 в N = 20 + 4t - швидкість, з якою відстань між братами збільшується (4 фути в секунду).

Більш того, рівняння (3) можна використовувати для прогнозування відстані між братами за 2 хвилини. Спочатку перетворіть t = 2 хвилини в t = 120 секунд, потім підставляємо це число в наше модельне рівняння (3).

\[d=20+4(120)=500\]

Таким чином, відстань між братами через 2 хвилини становить d = 500 футів.

Ми також можемо записати рівняння d = 20+ 4t, використовуючи позначення функції.

\[d(t)=20+4 t\]

Потім, щоб знайти відстань між братами в кінці 2 хвилин, ми б виконали наступний розрахунок.

\[\begin{array}{l}{d(120)=20+4(120)} \\ {d(120)=500}\end{array}\]

На відміну від позначення функції, коли в результаті пишеться d = 500 футів, зверніть увагу, як прихований один фрагмент інформації, а саме час. За допомогою позначення функції ми інтерпретуємо d (120) = 500 як «відстань між двома братами через 120 секунд становить 500 футів». Зверніть увагу, як і відстань, і час доступні в позначеннях d (120) = 500.

Моделювання дискретного з неперервним

Дженні будує кролячу Хатч за її сараєм. Вона поміщає в хату 25 кроликів, потім замикає двері і виходить. На жаль, є недолік в конструкції хатки і кролики починають рятуватися з постійною швидкістю 5 кроликів кожні 2 години. Знову ми змоделюємо число N кроликів, що залишилися в хатчі, як функція часу t Спочатку ми пропонуємо графічну модель.

Зверніть увагу, що кількість кроликів, що залишилися в хатці, залежить від кількості часу, яке пройшло. Це робить число N кроликів, що залишилися в хатчі, залежною змінною, яку ми розмістимо на вертикальній осі на малюнку\(\PageIndex{7}\) (а). Час t є незалежною змінною і розміщується на горизонтальній осі.

Ми знову виберемо шкалу для наших сокир, яка вміщує той факт, що популяція кроликів зменшується з постійною швидкістю 5 кроликів кожні 2 години. На малюнку\(\PageIndex{7}\) (b) ми дозволяємо кожній коробці на вертикальній осі представляти 1 кролика, тоді як дві коробки на горизонтальній осі - 1 годину. Ми могли б так само легко дозволити кожній коробці на горизонтальній осі представляти одну годину, але наш вибір робить графік, який трохи більше. Більші графіки трохи легше читати та інтерпретувати.

За часом t = 0 годин популяція кроликів становить N = 25 кроликів. Цей факт представлений точкою (t, N) = (0, 25) на малюнку\(\PageIndex{8}\) (а). Оскільки популяція кроликів зменшується з постійною швидкістю 5 кроликів кожні 2 години, починаємо з точки (0, 25), потім рухаємося на 2 години (4 ящика) вправо, і 5 кроликів (5 коробок) вниз до точки (2, 20), також показаної на малюнку\(\PageIndex{8}\) (а).

Швидкість, з якою кролики знижуються, постійна при 5 кроликів кожні 2 години, тому продовжуйте нескінченно в порядку малюнка\(\PageIndex{8}\) (а), рухаючись на 2 години (4 ящика) вправо, потім 5 кроликів (5 коробок) вниз. Це дасть лінійну залежність між кількістю кроликів N та часом t, показаним на малюнку\(\PageIndex{8}\) (b).

Малюнок\(\PageIndex{7}\).

 

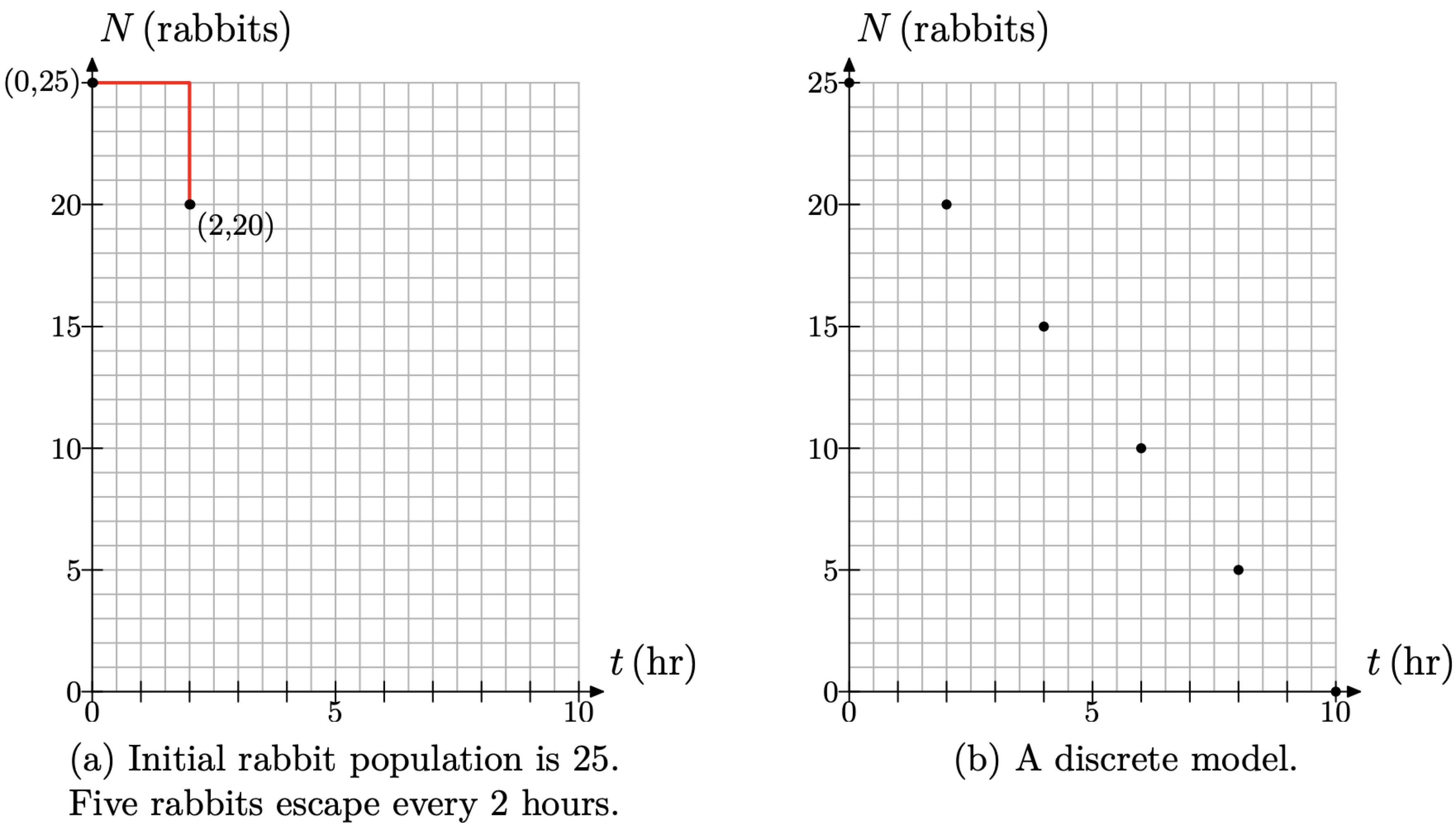
Малюнок\(\PageIndex{8}\).

Ми можемо провести лінію через точки даних на малюнку\(\PageIndex{8}\) (b), щоб створити безперервну модель на малюнку\(\PageIndex{9}\) (а). Однак нам потрібно усвідомлювати недолік, який накладає це безперервне наближення. Наприклад, розглянемо прогноз на малюнку\(\PageIndex{9}\) (б). Чи розумно говорити про те, що 7,5 кроликів залишаються в будці через 7 годин?

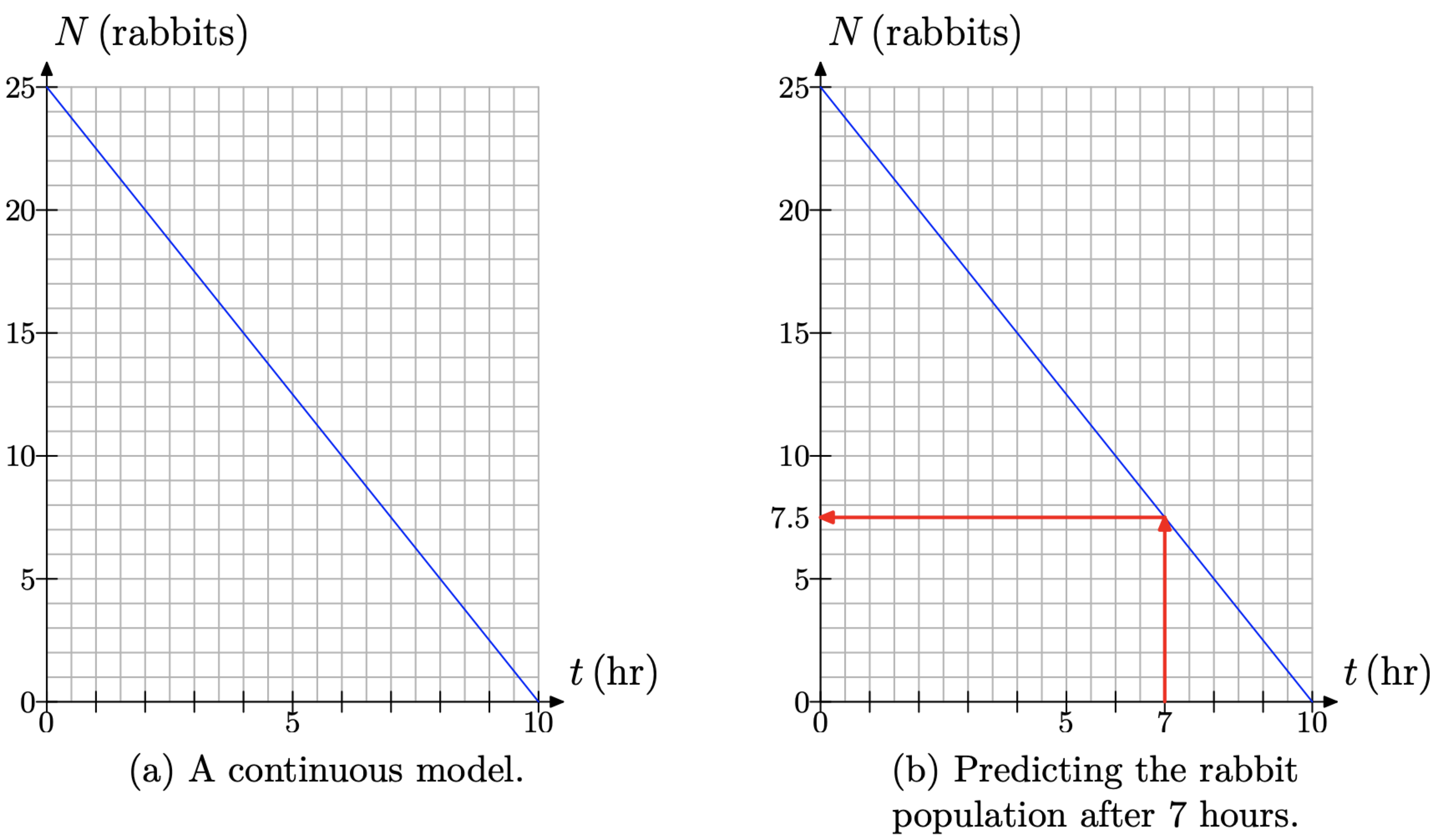
Малюнок\(\PageIndex{9}\).

У нашій першій моделі відстань між братами може бути будь-яким дійсним числом, тому суцільна модель була доречною. Однак у випадку з кролячою хаткою Дженні, що залишилася популяція повинна бути цілою кількістю кроликів (якщо не потрапляє лисиця), тому моделювання популяції з безперервною лінією на малюнку 9 (b) є в кращому випадку наближенням реальності. Однак математики часто моделюють дискретну ситуацію з неперервною моделлю. Поки ми усвідомлюємо її обмеження, ми все ще можемо використовувати модель, щоб робити розумні прогнози. Наприклад, можна сказати, що через 7 годин в хатці залишилося приблизно 7 кроликів.

Ми побачили перевагу використання позначення функцій в кінці нашої попередньої моделі, так що давайте використовувати позначення функцій трохи раніше в цій моделі. Ми дозволимо

\[N(t)=\text { the number of rabbits remaining after } t \text { hours. }\]

Спочатку, на час t = 0, в хутчі 25 кроликів. Таким чином, пишемо

\[N(0)=25\]

Можливо, легше думати про втрату 5 кроликів кожні 2 години як еквівалентну втраті «в середньому» 2,5 кроликів щогодини. Таким чином, по закінченню 1 години кількість кроликів зменшується на один приріст 2,5 кроликів, і пишемо

\[N(1)=25-2.5(1)\]

Наприкінці 2 годин популяція кроликів зменшується на 2 приросту кроликів 2,5, і ми можемо писати

\[N(2)=25-2.5(2)\]

Наприкінці 3 годин популяція кроликів зменшується на 3 приросту 2,5 кроликів, і ми можемо писати

\[N(3)=25-2.5(3)\]

Розвивається чітка закономірність, особливо коли ми підсумовуємо ці результати в табл\(\PageIndex{2}\).

т	Н (т)
0	25
1	25 − 2.5 (1)
2	25 − 2.5 (2)
3	25 − 2,5 (3)

Таблиця\(\PageIndex{2}\) Визначення модельного рівняння.

Таблиця\(\PageIndex{2}\) розкриває зв'язок між числом кроликів N і часом t, яку можна описати рівнянням\[N(t)=25-2.5 t\]

\[N(t)=25-2.5 t\]

Уважний читач знову перевірить, що рівняння (4) повертає правильну кількість кроликів часом t = 0, 1, 2 та 3, як записано в табл\(\PageIndex{2}\).

Є два важливих спостереження, які ми можемо зробити щодо рівняння (4).

1. 25 in\(N(t) = 25 − 2.5t\) - початкова популяція кроликів і відповідає точці (0, 25) на малюнку\(\PageIndex{8}\) (а).
2. −2,5 дюйма\(N(t) = 25−2.5t\) - це швидкість, з якою популяція кроликів зменшується «в середньому» (2,5 кроликів на годину).

Рівняння (4) можна використовувати для прогнозування кількості кроликів, що залишилися в хатці після t = 7 годин. Просто підставити t = 7 в рівняння (4).

\[N(7)=25-2.5(7)=7.5\]

Важливо зазначити, що прогноз, зроблений модельним рівнянням, ідентичний прогнозу, зробленому графіком моделі на малюнку\(\PageIndex{9}\) (b).

Однак знову зауважте, що це рівняння є безперервною моделлю, і його прогноз, що 7,5 кроликів залишаються в хатці, нереально (якщо тільки ця лисиця знову розгубилася). Однак, якщо нам відомо про недоліки моделі, рівняння все ще можна використовувати як хороший інструмент прогнозування. Наприклад, ми можемо знову сказати, що приблизно 7 кроликів залишаються в хатці через 7 годин. Це можна написати\(N(7) \approx 7\), а це означає, що «через 7 годин в хатці залишається приблизно 7 кроликів».

Визначення моделі рівняння з графа

Місіс Берк встановлює детектор руху перед своїм класом, потім позиціонує одного зі своїх учнів на фіксованій відстані від детектора і просить учня підійти до детектора з постійною швидкістю. Детектор вимірює відстань d (у метрах) учня від датчика як функція часу t (у секундах). Графік відстані d проти часу t наведено на рисунку\(\PageIndex{10}\).

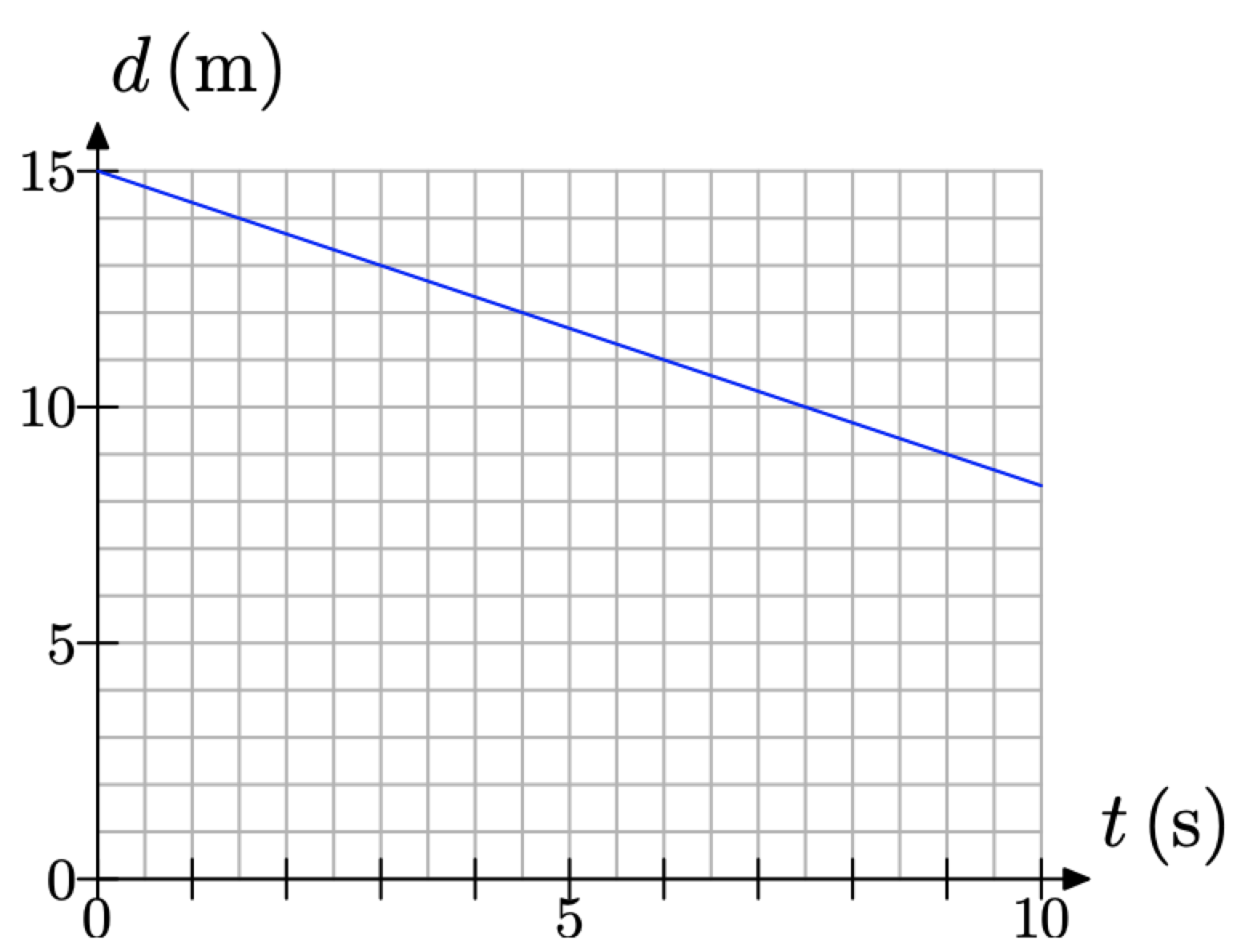
Малюнок\(\PageIndex{10}\). Детектор вимірює відстань між учнем і детектором в залежності від часу.

Визначити початкову відстань учня від детектора нескладно. Нам потрібно лише визначити значення d за часом t = 0 секунд. Результат розташовується в точці (0, 15), як показано на малюнку\(\PageIndex{11}\) (а). Таким чином, студент встановлює на початковій відстані 15 метрів від детектора.

Щоб визначити швидкість, з якою студент наближається до детектора, потрібно зробити трохи більше роботи. Вивчіть графік і виберіть дві точки на лінії. Це трохи полегшує ситуацію, якщо ви вибираєте точки на лінії, які розташовані на перетині двох ліній сітки, але, як ми покажемо, це не обов'язково. Маючи на увазі цю думку, ми вибрали точки P (3, 13) та Q (6, 11) на лінії, як показано на малюнку\(\PageIndex{11}\) (b).

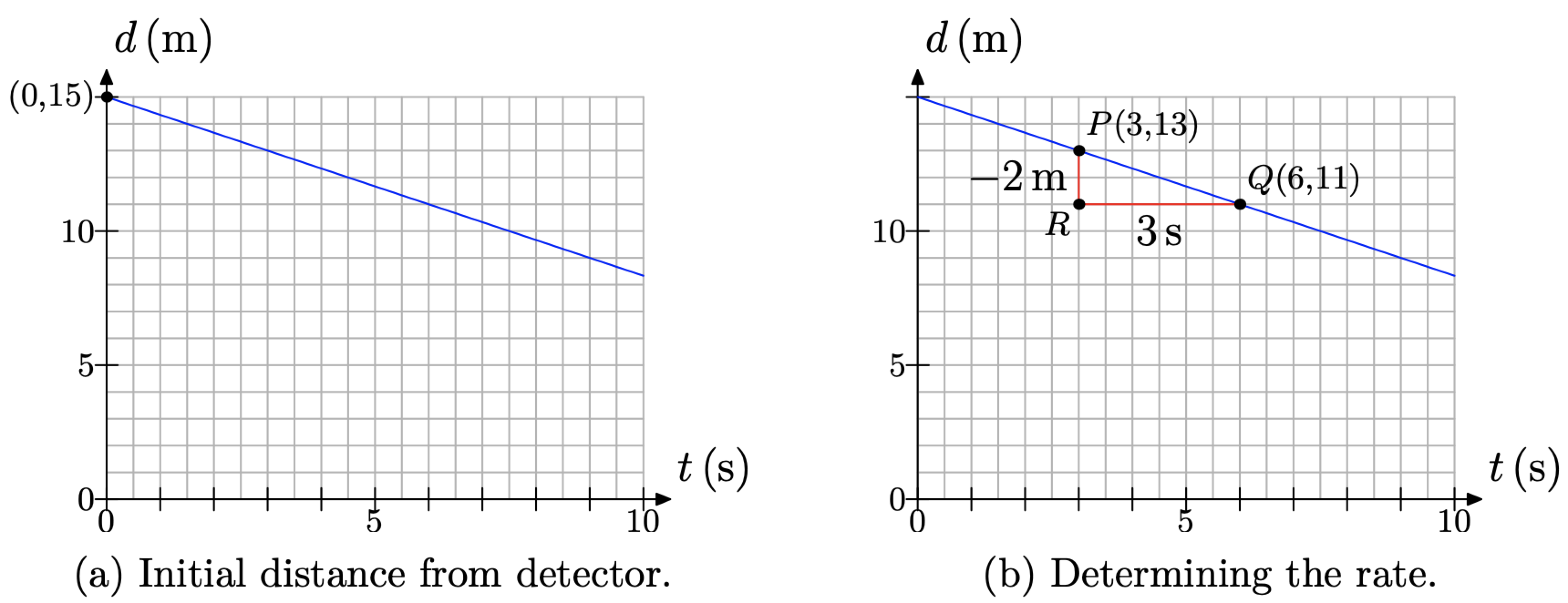
Малюнок\(\PageIndex{11}\). Визначення початкової відстані і швидкості.

Намалюйте прямокутний трикутник\(\triangle P Q R\) зі сторонами, паралельними осям, як показано на малюнку\(\PageIndex{11}\) (б). Визначте довжину кожної сторони прямокутного трикутника.

• Бічний PR має довжину 2 коробки, але кожна коробка представляє 1 метр, тому сторона P R являє собою зменшення відстані на 2 метри від детектора. Ось чому ми використали знак мінус при маркуванні бічного PR за допомогою −2m на малюнку\(\PageIndex{11}\) (b).
• Бічний RQ має довжину 6 коробок, але 2 коробки представляють 1 секунду, тому бічний RQ являє собою збільшення на 3 секунди в часі. Ось чому ми позначили бічний RQ з 3 s на малюнку\(\PageIndex{11}\) (b).

Таким чином, відстань між учнем і детектором зменшується зі швидкістю 2 метри кожні 3 секунди.

Що станеться, якби ми вибрали дві різні точки на лінії? Розглянемо випадок на малюнку\(\PageIndex{12}\), де ми підібрали точки на лінії P (3, 13) та Q (9, 9). Ми також вирішили намалювати прямокутний трикутник\(\triangle P Q R\) на протилежній стороні лінії. Однак ще раз зверніть увагу, що сторони прямокутного трикутника\(\triangle P Q R\) паралельні горизонтальній і вертикальній осях.

 

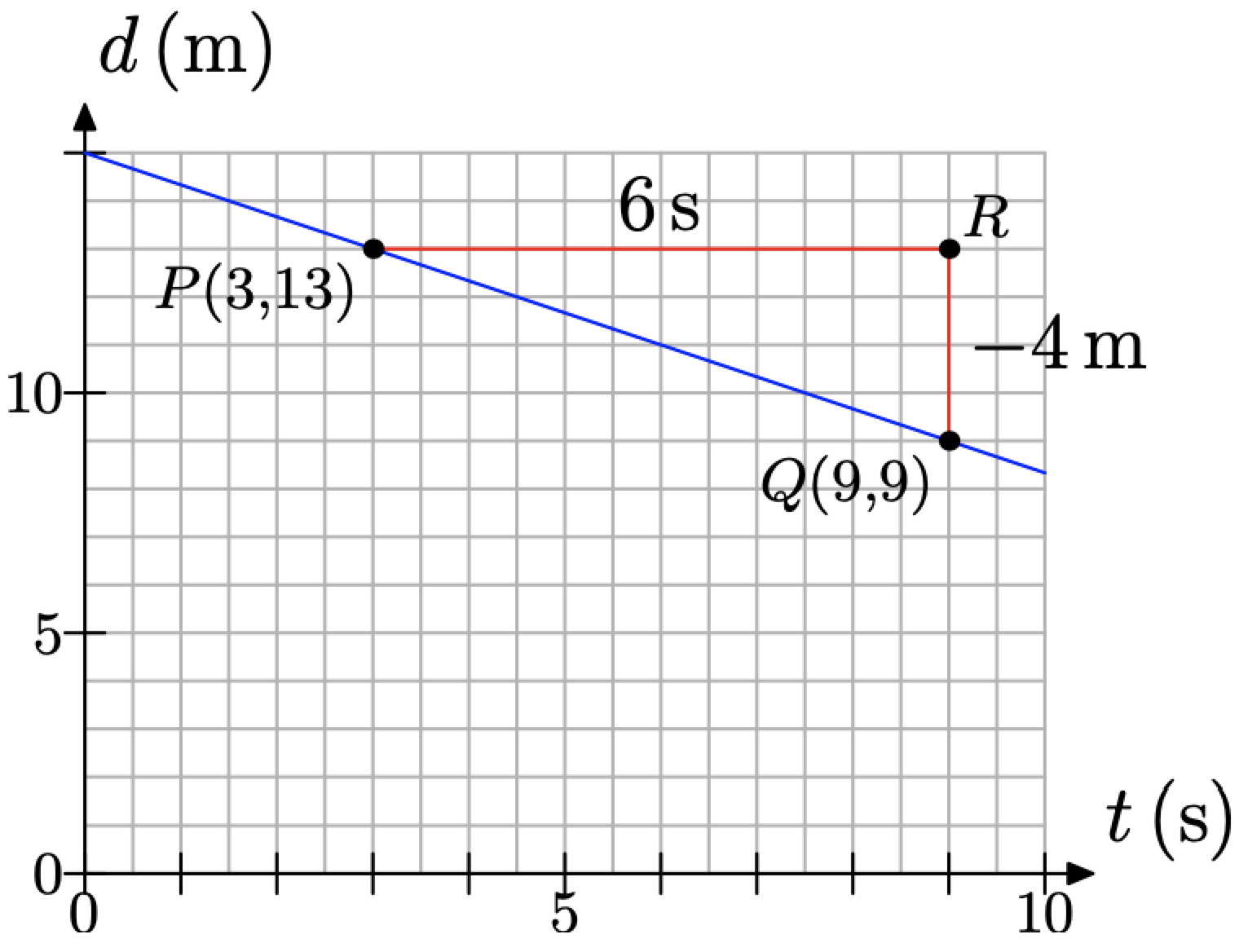
Малюнок\(\PageIndex{12}\). Визначення ставки.

Визначте довжину кожної сторони трикутника\(\triangle P Q R\).

• Бічний PR має довжину 12 коробок, але 2 коробки представляють 1 секунду, тому бічний PR являє собою збільшення на 6 секунд за часом. Ось чому ми позначили сторону P R з 6 s на малюнку\(\PageIndex{12}\).
• Бічний RQ має довжину 4 коробки, але кожна коробка становить 1 метр, тому бічний RQ являє собою зменшення відстані на 4 метри від детектора. Ось чому ми використали знак мінус при маркуванні бічного RQ −4 m на рис\(\PageIndex{12}\).

Таким чином, відстань між учнем і детектором зменшується зі швидкістю 4 метри кожні 6 секунд. У символах ми б написали, що ставка

\[\text { Rate }=\frac{-4 \mathrm{m}}{6 \mathrm{s}}=-\frac{4}{6} \mathrm{m} / \mathrm{s}\]

Зверніть увагу, однак, що це зменшує, до\[\text { Rate }=-\frac{2}{3} \mathrm{m} / \mathrm{s}\] якого ідентична швидкості, знайденої раніше при використанні точок P і Q на малюнку\(\PageIndex{11}\) (b).

Той факт, що ці показники еквівалентні, пояснюється тим, що трикутники (\ трикутник P Q R\) на малюнку\(\PageIndex{11}\) (b) і малюнку\(\PageIndex{12}\) є подібними трикутниками, тому їх сторони пропорційні. Таким чином, не має значення, які дві точки ви вибираєте на лінії, і не має значення, на якій стороні лінії ви розміщуєте свій прямокутний трикутник. Таким чином, єдина вимога полягає в тому, щоб ви намалювали прямокутний трикутник зі сторонами, паралельними осям координат.

Нарешті, давайте подивимося, чи зможемо ми розробити модельне рівняння. Визначимо\[d(t)=\text { the distance from the detector at time } t\]

Спочатку студент знаходиться в 15 метрах від детектора. Тобто в момент t = 0 відстань від детектора становить 15 метрів. В символах пишемо

\[d(0)=15\]

Відстань зменшується зі швидкістю 2 метри кожні 3 секунди. Це еквівалентно тому, що відстань зменшується на 2/3 метра щосекунди. В кінці 1 секунди відстань зменшилася на 1 крок 2/3 метра, тому відстань від детектора задається

\[d(1)=15-\frac{2}{3}(1)\]

В кінці 2 секунд відстань зменшилася на 2 кроку 2/3 метра, тому відстань від детектора задається

\[d(2)=15-\frac{2}{3}(2)\]

В кінці 3 секунд відстань зменшилася на 3 кроку 2/3 метра, тому відстань від детектора задається

\[d(3)=15-\frac{2}{3}(3)\]

Виникає чітка закономірність, особливо якщо підсумувати результати, як ми маємо в табл\(\PageIndex{3}\).

т	д (т)
0	15
1	15 − (2/3) (1)
2	15 − (2/3) (2)
3	15 − (2/3) (3)

Таблиця\(\PageIndex{3}\) Визначення модельного рівняння.

Таблиця\(\PageIndex{3}\) показує, що лінійна залежність (див. Рис.\(\PageIndex{10}\)) між відстанню d від детектора в момент t може бути змодельована рівнянням\[d(t)=15-\frac{2}{3} t\]

Знову ж таки, уважний читач перевірить, що рівняння (5) повертає правильну відстань d у часи t = 0, 1, 2 та 3, записані в табл\(\PageIndex{3}\).

Існує два важливих спостереження щодо рівняння (5).

1. 15 in d (t) = 15− (2/3) t - початкова відстань від детектора і відповідає точці (0, 15) на малюнку\(\PageIndex{11}\) (а).

2. −2/3 в d (t) = 15− (2/3) t - швидкість, з якою змінюється відстань між учнем та детектором, як визначено на малюнку\(\PageIndex{11}\) (b). Він негативний, оскільки відстань зменшується з часом.

Рівняння (5) можна використовувати для прогнозування. Наприклад, щоб визначити відстань між учнем і детектором в кінці 9 секунд, вставте t = 9 в рівняння (5).

\[d(9)=15-\frac{2}{3}(9)=15-6=9\]

Звичайно, позначення d (9) = 9 інтерпретується як «відстань між учнем і детектором через 9 секунд становить 9 метрів.