8.5: Розв'язування нелінійних систем

Last updated
Save as PDF

Page ID: 58374

Anonymous
LibreTexts

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Визначте нелінійні системи.
Розв'язуйте нелінійні системи за допомогою методу заміщення.

Нелінійні системи

Система рівнянь, де хоча б одне рівняння не є лінійним, називається нелінійною системою ³². У цьому розділі ми будемо використовувати метод підстановки для розв'язання нелінійних систем. Нагадаємо, що розв'язки системи з двома змінними є впорядкованими парами\((x,y)\), які задовольняють обом рівнянням.

Приклад\(\PageIndex{1}\):

Вирішити:\(\left\{\begin{array}{l}{x+2 y=0} \\ {x^{2}+y^{2}=5}\end{array}\right.\).

Рішення

У цьому випадку ми починаємо з розв'язання для x у першому рівнянні.

\(\left\{\begin{array}{c}{x+2 y=0} \\ {x^{2}+y^{2}=5}\end{array}\Longrightarrow x=-2y \right.\)

\(x=−2y\)Підставляємо в друге рівняння, а потім вирішуємо для\(y\).

\(\begin{aligned}(\color{Cerulean}{-2y }\color{black}{)}^{2}+y^{2} &=5 \\ 4 y^{2}+y^{2} &=5 \\ 5 y^{2} &=5 \\ y^{2} &=1 \\ y &=\pm 1 \end{aligned}\)

Тут є дві відповіді для\(y\); використовуйте\(x=−2y\) для пошуку відповідних\(x\) -значень.

Таблиця\(\PageIndex{1}\)
Використання\(y=-1\)	Використання\(y=1\)
\ (y=-1\) ">\(\begin{aligned} x &=-2 y \\ &=-2(-1) \\ &=2 \end{aligned}\)	\ (y=1\) ">\(\begin{aligned} x &=-2 y \\ &=-2(1) \\ &=-2 \end{aligned}\)

Це дає нам два впорядкованих парних рішення,\((2,−1)\) і\((−2,1)\).

Відповідь:

\((2,−1), (−2,1)\)

У попередньому прикладі дана система складалася з лінії і кола. Графікуючи ці рівняння на одному і тому ж наборі осей, ми бачимо, що два впорядкованих парних рішення відповідають двом точкам перетину.

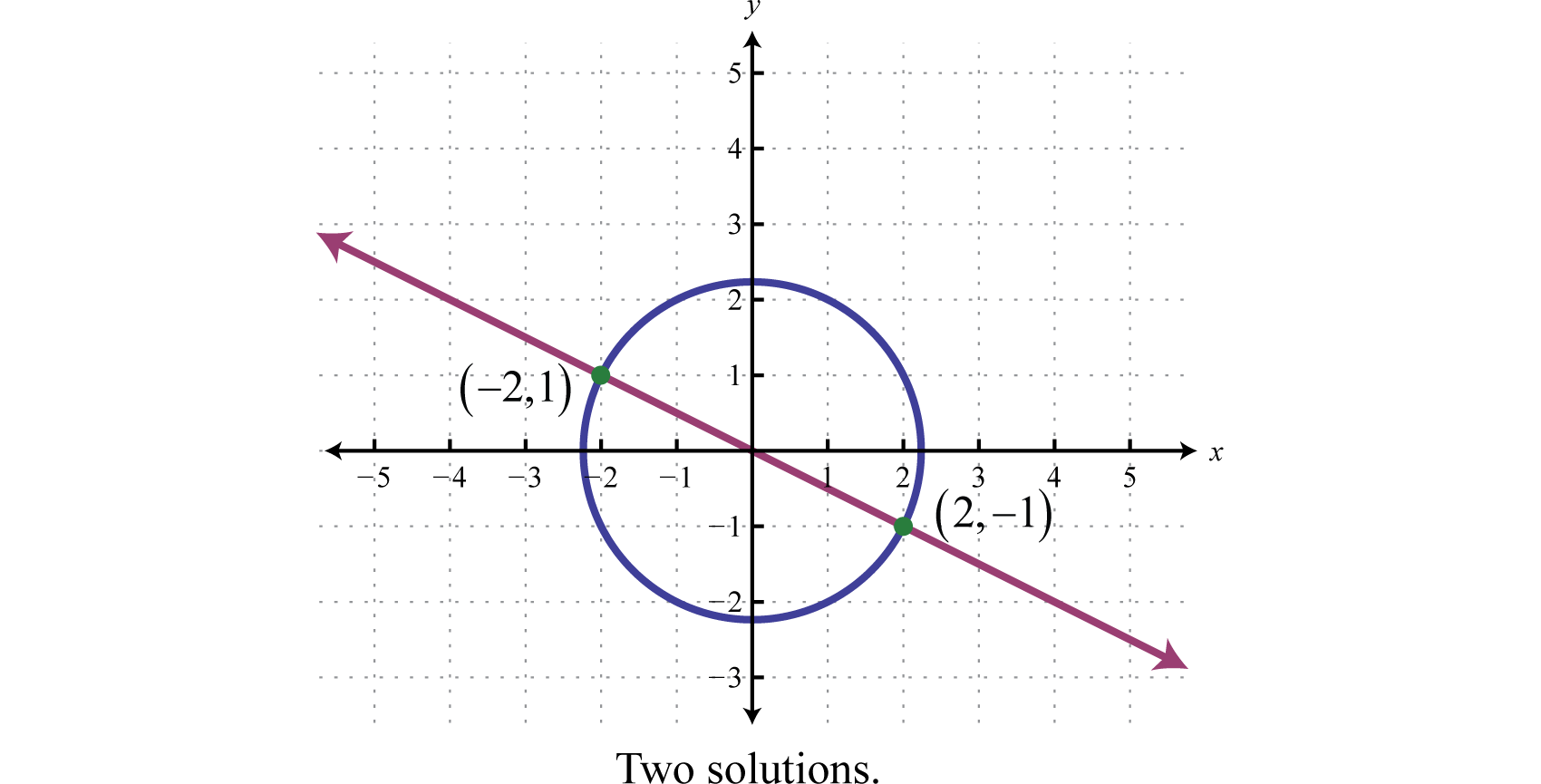
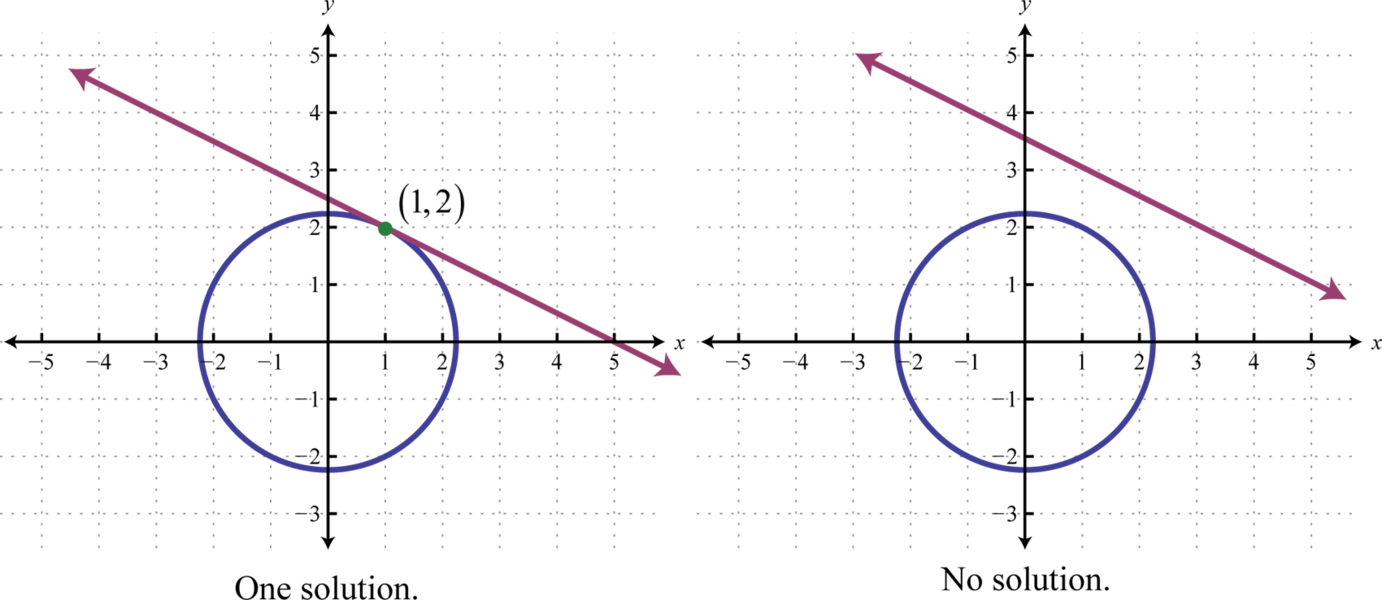
Якщо нам задано систему, що складається з кола і лінії, то є\(3\) можливості для реальних рішень - два рішення, як на малюнку вище, одне рішення або відсутність рішення.

Приклад\(\PageIndex{2}\)

Вирішити:\(\left\{\begin{array}{c}{x+y=3} \\ {x^{2}+y^{2}=2}\end{array}\right.\).

Рішення

Вирішити для\(y\) в першому рівнянні.

\(\left\{\begin{array}{c}{x+y} \\ {x^{2}+y^{2}}\end{array}\right.\)

Далі\(y=3−x\) підставляємо в друге рівняння, а потім вирішуємо для\(x\).

\(\begin{array}{r}{x^{2}+(\color{Cerulean}{3-x}\color{black}{)}^{2}=2} \\ {x^{2}+9-6 x+x^{2}=2} \\ {2 x^{2}-6 x+9=2} \\ {2 x^{2}-6 x+7=0}\end{array}\)

Отримане рівняння не коефіцієнт. Крім того, використовуючи\(a=2\)\( b=−6\), і\(c=7\) ми можемо побачити, що дискримінант є негативним:

\(\begin{aligned} b^{2}-4 a c &=(-6)^{2}-4(2)(7) \\ &=36-56 \\ &=-20 \end{aligned}\)

Ми робимо висновок, що немає реальних розв'язків цього рівняння і, отже, немає розв'язку системи.

Відповідь:

\(Ø\)

Вправа\(\PageIndex{1}\)

Вирішити:\(\left\{\begin{aligned} x-y &=5 \\ x^{2}+(y+1)^{2} &=8 \end{aligned}\right.\)

Відповідь

\((2,−3)\)

www.youtube.com/В/тур JW-8СНА

Якщо задано коло і параболу, то є\(5\) можливості для вирішення.

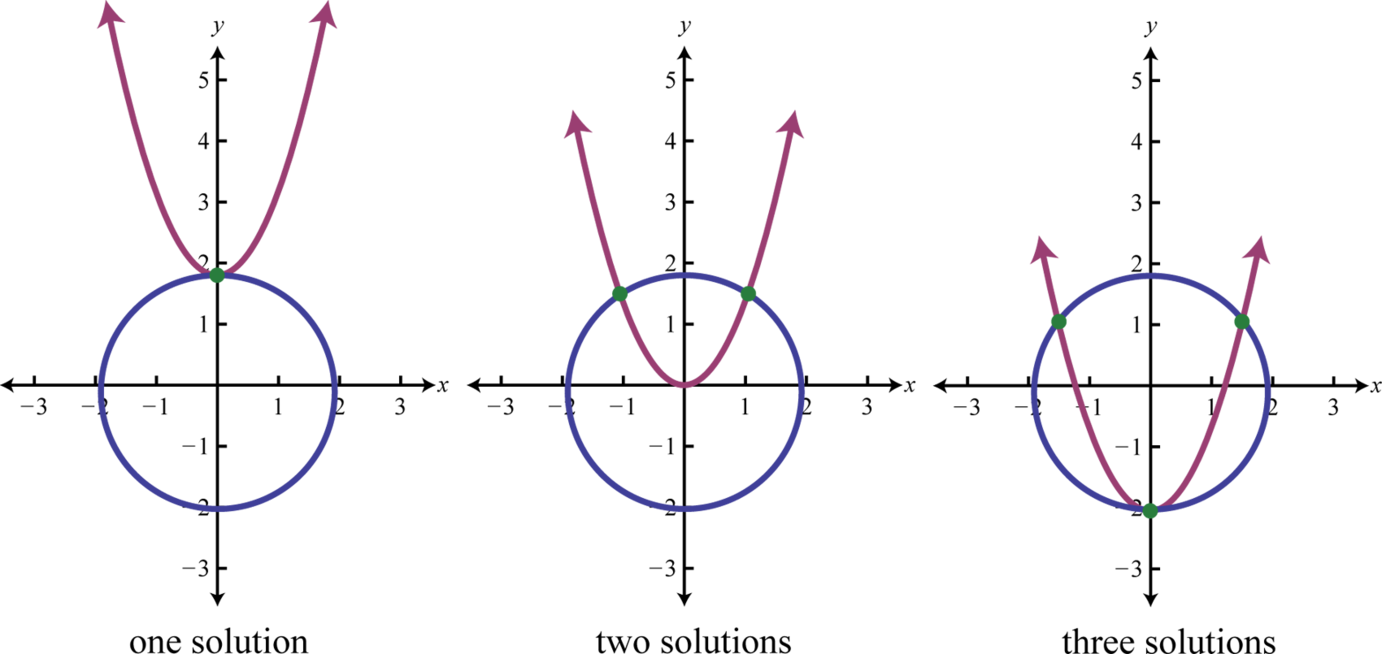
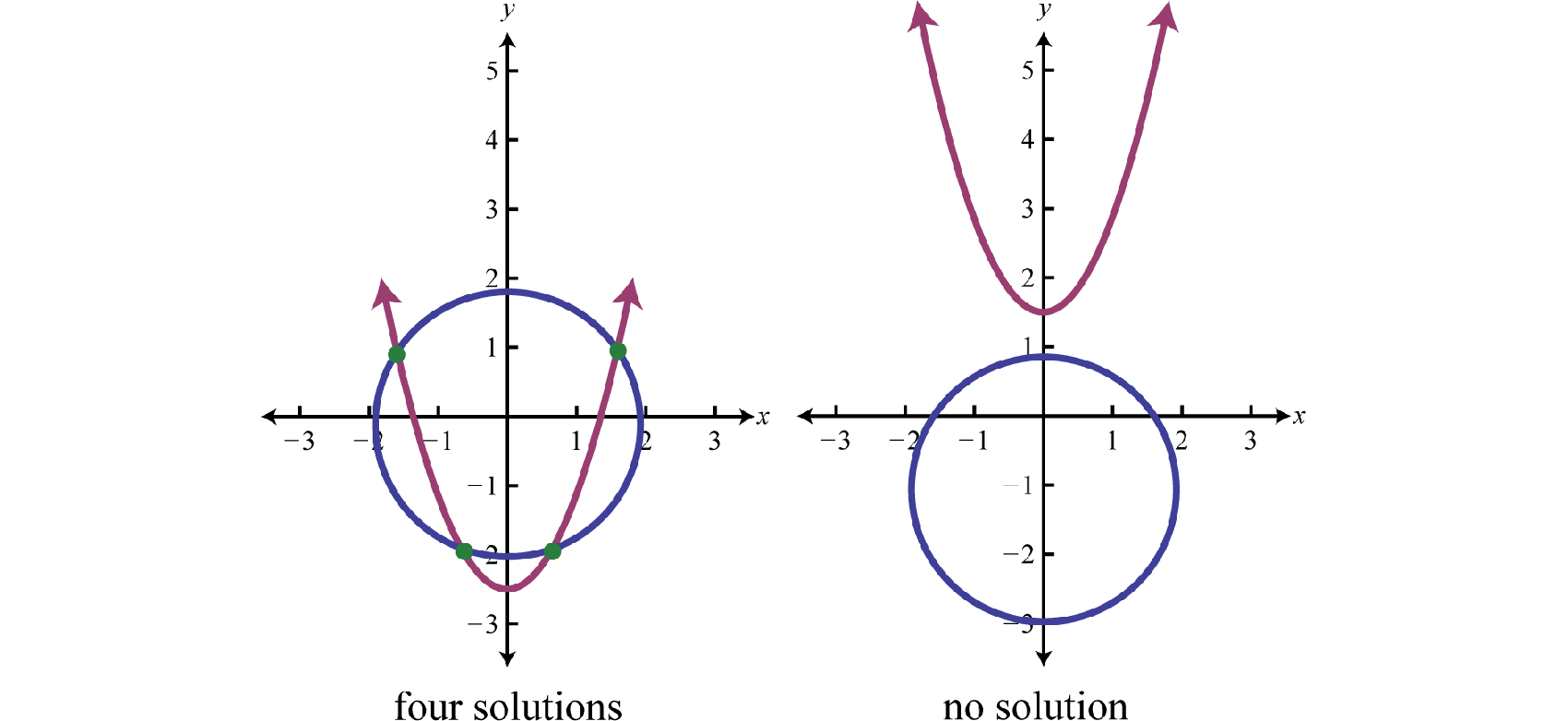
При використанні методу підстановки ми можемо виконати крок підстановки за допомогою цілих алгебраїчних виразів. Мета полягає в тому, щоб створити єдине рівняння в одній змінній, яке можна вирішити за допомогою методів, вивчених до цього моменту в нашому вивченні алгебри.

Приклад\(\PageIndex{3}\):

Вирішити:\(\left\{\begin{array}{c}{x^{2}+y^{2}=2} \\ {y-x^{2}=-2}\end{array}\right.\).

Рішення

Ми можемо вирішити for\(x^{2}\) у другому рівнянні.

\(\left\{\begin{array}{l}{x^{2}+y^{2}=2} \\ {y-x^{2}=-2 \quad \Rightarrow \quad y+2=x^{2}}\end{array}\right.\)

\(x^{2}=y+2\)Підставляємо в перше рівняння, а потім вирішуємо для\(y\).

\(\begin{aligned} \color{Cerulean}{y+2}\color{black}{+}y^{2} &=2 \\ y^{2}+y &=0 \\ y(y+1) &=0 \\ y &=0 \quad \text { or } \quad y=-1 \end{aligned}\)

Назад підставляємо\(x^{2}=y+2\) в, щоб знайти відповідні\(x\) -значення.

Таблиця\(\PageIndex{2}\)
Використання\(y=-1\)	Використання\(y=0\)
\ (y=-1\) ">\(\begin{aligned} x^{2} &=y+2 \\ x^{2} &=\color{Cerulean}{-1}\color{black}{+}2 \\ x^{2} &=1 \\ x &=\pm 1 \end{aligned}\)	\ (y=0\) ">\(\begin{aligned} x^{2} &=y+2 \\ x^{2} &=\color{Cerulean}{0}\color{black}{+}2 \\ x^{2} &=2 \\ x &=\pm \sqrt{2} \end{aligned}\)

Це призводить нас до чотирьох рішень,\((±1,−1)\) і\((\pm \sqrt{2}, 0)\).

Відповідь:

\((\pm 1,-1),(\pm \sqrt{2}, 0)\)

Приклад\(\PageIndex{4}\)

Вирішити:\(\left\{\begin{aligned}(x-1)^{2}-2 y^{2} &=4 \\ x^{2}+y^{2} &=9 \end{aligned}\right.\)

Рішення

Ми можемо вирішити for\(y^{2}\) у другому рівнянні,

\(\left\{\begin{array}{r}{(x-1)^{2}-2 y^{2}=4} \\ {x^{2}+y^{2}=9}\end{array}\right. \Longrightarrow y^{2}=9-x^{2}\)

\(y^{2}=9−x^{2}\)Підставляємо в перше рівняння, а потім вирішуємо для\(x\).

\(\begin{aligned}(x-1)^{2}-2\color{black}{\left(\color{Cerulean}{9-x^{2}}\right) }&=4 \\ x^{2}-2 x+1-18+2 x^{2} &=0 \\ 3 x^{2}-2 x-21 &=0 \\(3 x+7)(x-3) &=0 \\ 3 x+7 &=0 \text { or } x-3=0 \\ x &=-\frac{7}{3} \quad x=3 \end{aligned}\)

Назад підставляємо\(y^{2}=9−x^{2}\) в, щоб знайти відповідні\(y\) -значення.

Таблиця\(\PageIndex{3}\)
Використання\(x=-\frac{7}{3}\)	Використання\(x=3\)
\ (x=-\ гідророзриву {7} {3}\) ">\(\begin{array}{l}{y^{2}=9-\color{black}{\left(\color{Cerulean}{-\frac{7}{3}}\right)^{2}}} \\ {y^{2}=\frac{9}{1}-\frac{49}{9}} \\ {y^{2}=\frac{32}{9}} \\ {y=\pm \frac{\sqrt{32}}{3}=\pm \frac{4 \sqrt{2}}{3}}\end{array}\)	\ (x = 3\) ">\(\begin{aligned} y^{2} &=9-(\color{Cerulean}{3}\color{black}{)}^{2} \\ y^{2} &=0 \\ y &=0 \end{aligned}\)

Це призводить до трьох рішень,\(\left(-\frac{7}{3}, \pm \frac{4 \sqrt{2}}{3}\right)\) і\((3,0)\).

Відповідь:

\((3,0),\left(-\frac{7}{3}, \pm \frac{4 \sqrt{2}}{3}\right)\)

Приклад\(\PageIndex{5}\)

Вирішити:\(\left\{\begin{aligned} x^{2}+y^{2} &=2 \\ x y &=1 \end{aligned}\right.\).

Рішення

\(y\)Розв'яжіть для у другому рівнянні.

\(\left\{\begin{array}{r}{x^{2}+y^{2}=2} \\ {x y=1}\end{array}\right.\Longrightarrow y=\frac{1}{x}\)

\(y=\frac{1}{x}\)Підставляємо в перше рівняння, а потім вирішуємо для\(x\).

\(x^{2}+\left(\frac{1}{x}\right)^{2}=2\)
\(x^{2}+\frac{1}{x^{2}}=2\)

Це залишає нам раціональне рівняння. Зробіть позначку, що\(x≠0\) і помножте обидві сторони на\(x^{2}\).

\(\begin{aligned} \color{Cerulean}{x^{2}}\color{black}{\left(x^{2}+\frac{1}{x^{2}}\right)} &=2 \cdot \color{Cerulean}{x^{2}} \\ x^{4}+1 &=2 x^{2} \\ x^{4}-2 x^{2}+1 &=0 \\\left(x^{2}-1\right)\left(x^{2}-1\right) &=0 \end{aligned}\)

На цьому етапі ми бачимо, що обидва фактори однакові. Застосувати властивість нульового продукту.

\(\begin{aligned} x^{2}-1 &=0 \\ x^{2} &=1 \\ x &=\pm 1 \end{aligned}\)

Назад підставляємо\(y=\frac{1}{x}\) в, щоб знайти відповідні\(y\) -значення.

Використання\(x=-1\)	Використання\(x=1\)
\ (x = -1\) ">\(\begin{aligned} y &=\frac{1}{x} \\ &=\frac{1}{\color{Cerulean}{-1}} \\ &=-1 \end{aligned}\)	\ (x = 1\) ">\(\begin{aligned} y &=\frac{1}{x} \\ &=\frac{1}{\color{Cerulean}{1}} \\ &=1 \end{aligned}\)

Це призводить до двох рішень.

Відповідь:

\((1,1),(-1,-1)\)

Вправа\(\PageIndex{2}\)

Вирішити:\(\left\{\begin{array}{r}{\frac{1}{x}+\frac{1}{y}=4} \\ {\frac{1}{x^{2}}+\frac{1}{y^{2}}=40}\end{array}\right.\)

Відповідь

\(\left(-\frac{1}{2}, \frac{1}{6}\right)\left(\frac{1}{6},-\frac{1}{2}\right)\)

www.youtube.com/В/N8JJ_Ібегкм

Ключові виноси

Використовувати метод заміщення для розв'язання нелінійних систем.
Оптимізуйте процес розв'язання, використовуючи цілі алгебраїчні вирази на етапі підстановки для отримання єдиного рівняння з однією змінною.
Розуміння геометричної інтерпретації системи може допомогти в пошуку реальних рішень.

Вправа\(\PageIndex{3}\)

Вирішити.

\(\left\{\begin{array}{c}{x^{2}+y^{2}=10} \\ {x+y=4}\end{array}\right.\)
\(\left\{\begin{array}{c}{x^{2}+y^{2}=5} \\ {x-y=-3}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=30} \\ {x-3 y=0}\end{array}\right.\)
\(\left\{\begin{array}{c}{x^{2}+y^{2}=10} \\ {2 x-y=0}\end{array}\right.\)
\(\left\{\begin{array}{c}{x^{2}+y^{2}=18} \\ {2 x-2 y=-12}\end{array}\right.\)
\(\left\{\begin{aligned}(x-4)^{2}+y^{2} &=25 \\ 4 x-3 y &=16 \end{aligned}\right.\)
\(\left\{\begin{array}{c}{3 x^{2}+2 y^{2}=21} \\ {3 x-y=0}\end{array}\right.\)
\(\left\{\begin{aligned} x^{2}+5 y^{2} &=36 \\ x-2 y &=0 \end{aligned}\right.\)
\(\left\{\begin{array}{c}{4 x^{2}+9 y^{2}=36} \\ {2 x+3 y=6}\end{array}\right.\)
\(\left\{\begin{array}{c}{4 x^{2}+y^{2}=4} \\ {2 x+y=-2}\end{array}\right.\)
\(\left\{\begin{array}{c}{2 x^{2}+y^{2}=1} \\ {x+y=1}\end{array}\right.\)
\(\left\{\begin{array}{c}{4 x^{2}+3 y^{2}=12} \\ {2 x-y=2}\end{array}\right.\)
\(\left\{\begin{aligned} x^{2}-2 y^{2} &=35 \\ x-3 y &=0 \end{aligned}\right.\)
\(\left\{\begin{array}{c}{5 x^{2}-7 y^{2}=39} \\ {2 x+4 y=0}\end{array}\right.\)
\(\left\{\begin{array}{c}{9 x^{2}-4 y^{2}=36} \\ {3 x+2 y=0}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {x-2 y=-12}\end{array}\right.\)
\(\left\{\begin{array}{l}{2 x^{2}+3 y=9} \\ {8 x-4 y=12}\end{array}\right.\)
\(\left\{\begin{array}{l}{2 x-4 y^{2}=3} \\ {3 x-12 y=6}\end{array}\right.\)
\(\left\{\begin{aligned} 4 x^{2}+3 y^{2} &=12 \\ x-\frac{3}{2} &=0 \end{aligned}\right.\)
\(\left\{\begin{aligned} 5 x^{2}+4 y^{2} &=40 \\ y-3 &=0 \end{aligned}\right.\)
Сума квадратів двох натуральних чисел дорівнює\(10\). Якщо перше ціле число додається в два рази більше другого, сума дорівнює\(7\). Знайти цілі числа.
Діагональ прямокутника вимірює\(\sqrt{5}\) одиниці виміру і має периметр, рівний\(6\) одиницям. Знайдіть розміри прямокутника.
Для яких значень\(b\) буде наступна система мати реальні рішення? \(\left\{\begin{array}{c}{x^{2}+y^{2}=1} \\ {y=x+b}\end{array}\right.\)
Для яких значень\(m\) буде наступна система має реальні рішення? \(\left\{\begin{array}{c}{x^{2}-y^{2}=1} \\ {y=m x}\end{array}\right.\)

Відповідь

1. \((1,3),(3,1)\)

3. \((-3 \sqrt{3},-\sqrt{3}),(3 \sqrt{3}, \sqrt{3})\)

5. \((-3,3)\)

7. \((-1,-3),(1,3)\)

9. \((0,2),(3,0)\)

11. \((0,1),\left(\frac{2}{3}, \frac{1}{3}\right)\)

13. \((-3 \sqrt{5},-\sqrt{5}),(3 \sqrt{5}, \sqrt{5})\)

15. \(\emptyset\)

17. \(\left(\frac{-3+3 \sqrt{5}}{2},-6+3 \sqrt{5}\right) ,\left(\frac{-3-3 \sqrt{5}}{2},-6-3 \sqrt{5}\right)\)

19. \(\left(\frac{3}{2},-1\right),\left(\frac{3}{2}, 1\right)\)

21. \(1,3\)

23. \(b \in[-\sqrt{2}, \sqrt{2}]\)

Вправа\(\PageIndex{4}\)

Вирішити.

\(\left\{\begin{array}{c}{x^{2}+y^{2}=4} \\ {y-x^{2}=2}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {y-x^{2}=-2}\end{array}\right.\)
\(\left\{\begin{array}{c}{x^{2}+y^{2}=4} \\ {y-x^{2}=3}\end{array}\right.\)
\(\left\{\begin{array}{c}{x^{2}+y^{2}=4} \\ {4 y-x^{2}=-4}\end{array}\right.\)
\(\left\{\begin{array}{c}{x^{2}+3 y^{2}=9} \\ {y^{2}-x=3}\end{array}\right.\)
\(\left\{\begin{array}{c}{x^{2}+3 y^{2}=9} \\ {x+y^{2}=-4}\end{array}\right.\)
\(\left\{\begin{aligned} 4 x^{2}-3 y^{2} &=12 \\ x^{2}+y^{2} &=1 \end{aligned}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=1} \\ {x^{2}-y^{2}=1}\end{array}\right.\)
\(\left\{\begin{aligned} x^{2}+y^{2} &=1 \\ 4 y^{2}-x^{2}-4 y &=0 \end{aligned}\right.\)
\(\left\{\begin{aligned} x^{2}+y^{2} &=4 \\ 2 x^{2}-y^{2}+4 x &=0 \end{aligned}\right.\)
\(\left\{\begin{aligned} 2(x-2)^{2}+y^{2} &=6 \\(x-3)^{2}+y^{2} &=4 \end{aligned}\right.\)
\(\left\{\begin{array}{c}{x^{2}+y^{2}-6 y=0} \\ {4 x^{2}+5 y^{2}+20 y=0}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+4 y^{2}=25} \\ {4 x^{2}+y^{2}=40}\end{array}\right.\)
\(\left\{\begin{array}{c}{x^{2}-2 y^{2}=-10} \\ {4 x^{2}+y^{2}=10}\end{array}\right.\)
\(\left\{\begin{array}{c}{2 x^{2}+y^{2}=14} \\ {x^{2}-(y-1)^{2}=6}\end{array}\right.\)
\(\left\{\begin{array}{c}{3 x^{2}-(y-2)^{2}=12} \\ {x^{2}+(y-2)^{2}=1}\end{array}\right.\)
Різниця квадратів двох натуральних чисел дорівнює\(12\). Сума більшого цілого числа і квадрата меншого дорівнює\(8\). Знайти цілі числа.
Різниця між довжиною та шириною прямокутника є\(4\) одиницями та діагональними\(8\) вимірами одиниць. Знайдіть розміри прямокутника. Округлити до найближчої десятої.
Діагональ прямокутника вимірює\(p\) одиниці виміру і має периметр, рівний\(2q\) одиницям. Знайдіть розміри прямокутника в перерахунку на\(p\) і\(q\).
Площа прямокутника -\(p\) квадратні одиниці, а його периметр -\(2q\) одиниці. Знайдіть розміри прямокутника в перерахунку на\(p\) і\(q\).

Відповідь

1. \((0,2)\)

3. \(\emptyset\)

5. \((-3,0),(0,-\sqrt{3}),(0, \sqrt{3})\)

7. \(\emptyset\)

9. \((0,1),\left(-\frac{2 \sqrt{5}}{5},-\frac{1}{5}\right),\left(\frac{2 \sqrt{5}}{5},-\frac{1}{5}\right)\)

11. \((3,-2),(3,2)\)

13. \((-3,-2),(-3,2),(3,-2),(3,2)\)

15. \((-\sqrt{7}, 0),(\sqrt{7}, 0),\left(-\frac{\sqrt{55}}{3}, \frac{4}{3}\right),\left(\frac{\sqrt{55}}{3}, \frac{4}{3}\right)\)

17. \(2,4\)

19. \(\frac{q+\sqrt{2 p^{2}-q^{2}}}{2}\)одиниць за\(\frac{q-\sqrt{2 p^{2}-q^{2}}}{2}\) одиницями

Вправа\(\PageIndex{5}\)

Вирішити.

\(\left\{\begin{aligned} x^{2}+y^{2} &=26 \\ x y &=5 \end{aligned}\right.\)
\(\left\{\begin{aligned} x^{2}+y^{2} &=10 \\ x y &=3 \end{aligned}\right.\)
\(\left\{\begin{aligned} 2 x^{2}-3 y^{2} &=5 \\ x y &=1 \end{aligned}\right.\)
\(\left\{\begin{array}{c}{3 x^{2}-4 y^{2}=-11} \\ {x y=1}\end{array}\right.\)
\(\left\{\begin{array}{c}{x^{2}+y^{2}=2} \\ {x y-2=0}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=1} \\ {2 x y-1=0}\end{array}\right.\)
\(\left\{\begin{aligned} 4 x-y^{2} &=0 \\ x y &=2 \end{aligned}\right.\)
\(\left\{\begin{array}{c}{3 y-x^{2}=0} \\ {x y-9=0}\end{array}\right.\)
\(\left\{\begin{aligned} 2 y-x^{2} &=0 \\ x y-1 &=0 \end{aligned}\right.\)
\(\left\{\begin{aligned} x-y^{2} &=0 \\ x y &=3 \end{aligned}\right.\)
Діагональ прямокутника вимірює\(2\sqrt{10}\) одиниці виміру. Якщо площа прямокутника дорівнює\(12\) квадратним одиницям, знайдіть його розміри.
Площа прямокутника -\(48\) квадратні метри, а периметр вимірює\(32\) метри. Знайдіть розміри прямокутника.
Добуток двох натуральних чисел -\(72\) і їх сума дорівнює\(18\). Знайти цілі числа.
Сума квадратів двох натуральних чисел дорівнює\(52\) і їх добуток дорівнює\(24\). Знайти цілі числа.

Відповідь

1. \((-5,-1),(5,1),(-1,-5),(1,5)\)

3. \(\left(-\sqrt{3},-\frac{\sqrt{3}}{3}\right),\left(\sqrt{3}, \frac{\sqrt{3}}{3}\right)\)

5. \(\emptyset\)

7. \((1,2)\)

9. \(\left(\sqrt[3]{2}, \frac{\sqrt[3]{4}}{2}\right)\)

11. \(2\)одиниць за\(6\) одиницями

13. \(6,12\)

Вправа\(\PageIndex{6}\)

Вирішити.

\(\left\{\begin{array}{l}{\frac{1}{x}+\frac{1}{y}=4} \\ {\frac{1}{x}-\frac{1}{y}=2}\end{array}\right.\)
\(\left\{\begin{array}{l}{\frac{2}{x}-\frac{1}{y}=5} \\ {\frac{1}{x}+\frac{1}{y}=2}\end{array}\right.\)
\(\left\{\begin{array}{l}{\frac{1}{x}+\frac{2}{y}=1} \\ {\frac{3}{x}-\frac{1}{y}=2}\end{array}\right.\)
\(\left\{\begin{array}{l}{\frac{1}{x}+\frac{1}{y}=6} \\ {\frac{1}{x^{2}}+\frac{1}{y^{2}}=20}\end{array}\right.\)
\(\left\{\begin{array}{l}{\frac{1}{x}+\frac{1}{y}=2} \\ {\frac{1}{x^{2}}+\frac{1}{y^{2}}=34}\end{array}\right.\)
\(\left\{\begin{array}{l}{x y-16=0} \\ {2 x^{2}-y=0}\end{array}\right.\)
\(\left\{\begin{array}{l}{x+y^{2}=4} \\ {y=\sqrt{x}}\end{array}\right.\)
\(\left\{\begin{array}{c}{y^{2}-(x-1)^{2}=1} \\ {y=\sqrt{x}}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=2^{x}} \\ {y=2^{2 x}-56}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=3^{2 x}-72} \\ {y-3^{x}=0}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=e^{4 x}} \\ {y=e^{2 x}+6}\end{array}\right.\)
\(\left\{\begin{array}{l}{y-e^{2 x}=0} \\ {y-e^{x}=0}\end{array}\right.\)

Відповідь

1. \(\left(\frac{1}{3}, 1\right)\)

3. \(\left(\frac{7}{5}, 7\right)\)

5. \(\left(-\frac{1}{3}, \frac{1}{5}\right),\left(\frac{1}{5},-\frac{1}{3}\right)\)

7. \((2, \sqrt{2})\)

9. \((3,8)\)

11. \(\left(\frac{\ln 3}{2}, 9\right)\)

Вправа\(\PageIndex{7}\)

Скільки реальних рішень можна отримати з системи, яка складається з кола і гіперболи? Поясніть.
Складіть власну нелінійну систему, вирішіть її та надайте відповідь. Також надайте графік і обговоріть геометричну інтерпретацію розв'язків.

Відповідь: 1. Відповідь може відрізнятися

Виноски

³² Система рівнянь, де принаймні одне рівняння не є лінійним.