8.E: Конічні секції (вправи)
- Page ID
- 58373
Вправа\(\PageIndex{1}\)
Обчисліть відстань і середину між заданими двома точками.
- \((0,2)\)і\((-4,-1)\)
- \((6,0)\)і\((-2,-6)\)
- \((-2,4)\)і\((-6,-8)\)
- \(\left(\frac{1}{2},-1\right)\)і\(\left(\frac{5}{2},-\frac{1}{2}\right)\)
- \((0,-3 \sqrt{2})\)і\((\sqrt{5},-4 \sqrt{2})\)
- \((-5 \sqrt{3}, \sqrt{6})\)і\((-3 \sqrt{3}, \sqrt{6})\)
- Відповідь
-
1. Відстань:\(5\) одиниці виміру; середина:\(\left(-2, \frac{1}{2}\right)\)
3. Відстань:\(4\sqrt{10}\) одиниці виміру; середина:\((-4,-2)\)
5. Відстань:\(\sqrt{7}\) одиниці виміру; середина:\(\left(\frac{\sqrt{5}}{2},-\frac{7 \sqrt{2}}{2}\right)\)
Вправа\(\PageIndex{2}\)
Визначте площу кола, діаметр якої визначається заданими двома точками.
- \((-3,3)\)і\((3,-3)\)
- \((-2,-9)\)і\((-10,-15)\)
- \(\left(\frac{2}{3},-\frac{1}{2}\right)\)і\(\left(-\frac{1}{3}, \frac{3}{2}\right)\)
- \((2 \sqrt{5},-2 \sqrt{2})\)і\((0,-4 \sqrt{2})\)
- Відповідь
-
1. \(18\pi\)квадратні одиниці
3. \(\frac{5 \pi}{4}\)квадратні одиниці
Вправа\(\PageIndex{3}\)
Перепишіть в стандартному вигляді і дайте вершину.
- \(y=x^{2}-10 x+33\)
- \(y=2 x^{2}-4 x-1\)
- \(y=x^{2}-3 x-1\)
- \(y=-x^{2}-x-2\)
- \(x=y^{2}+10 y+10\)
- \(x=3 y^{2}+12 y+7\)
- \(x=-y^{2}+8 y-3\)
- \(x=5 y^{2}-5 y+2\)
- Відповідь
-
1. \(y=(x-5)^{2}+8 ;\)вершина:\((5,8)\)
3. \(y=\left(x-\frac{3}{2}\right)^{2}-\frac{13}{4} ;\)вершина:\(\left(\frac{3}{2},-\frac{13}{4}\right)\)
5. \(x=(y+5)^{2}-15 ;\)вершина:\((-15,-5)\)
7. \(x=-(y-4)^{2}+13 ;\)вершина:\((13,4)\)
Вправа\(\PageIndex{4}\)
Перепишіть в стандартній формі і графі. Обов'язково знайдіть вершину і все перехоплення.
- \(y=x^{2}-20 x+75\)
- \(y=-x^{2}-10 x+75\)
- \(y=-2 x^{2}-12 x-24\)
- \(y=4 x^{2}+4 x+6\)
- \(x=y^{2}-10 y+16\)
- \(x=-y^{2}+4 y+12\)
- \(x=-4 y^{2}+12 y\)
- \(x=9 y^{2}+18 y+12\)
- \(x=-4 y^{2}+4 y+2\)
- \(x=-y^{2}-5 y+2\)
- Відповідь
-
1. \(y=(x-10)^{2}-25\);
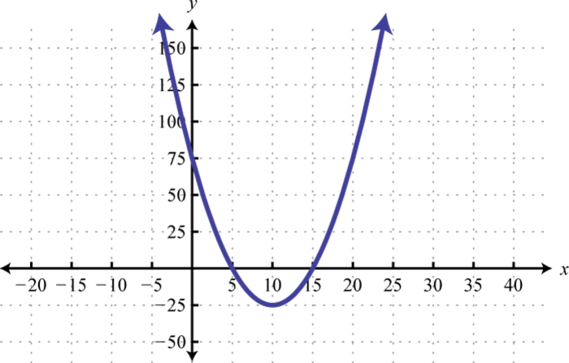
Малюнок 8.E.1 3. \(y=-2(x+3)^{2}-6\);
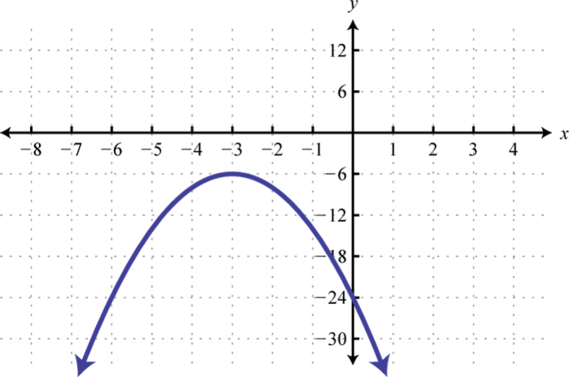
Малюнок 8.E.2 5. \(x=(y-5)^{2}-9\);

Малюнок 8.E.3 7. \(x=-4\left(y-\frac{3}{2}\right)^{2}+9\);
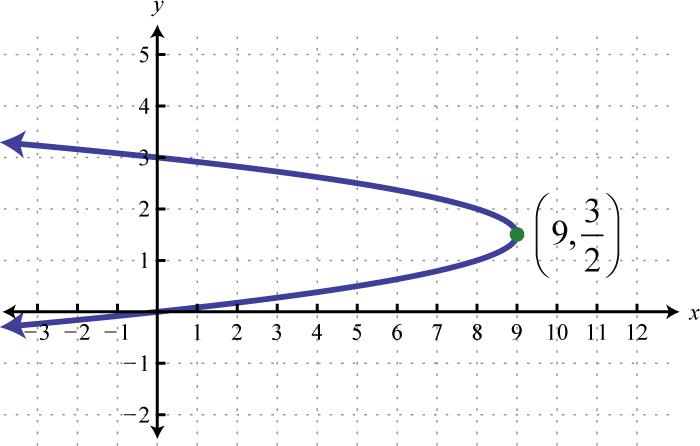
Малюнок 8.E.4 9. \(x=-4\left(y-\frac{1}{2}\right)^{2}+3\);
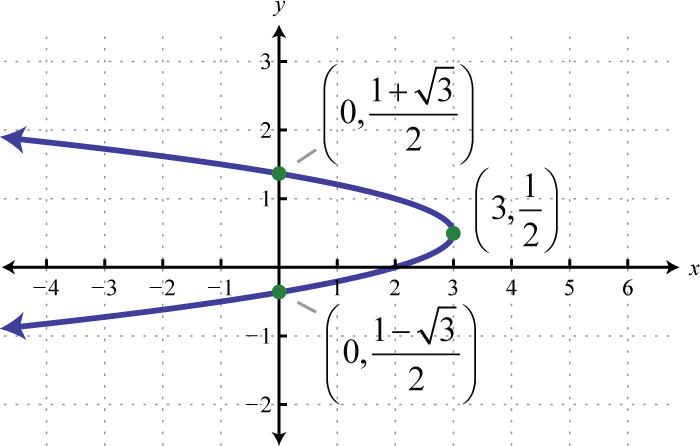
Малюнок 8.E.5
Вправа\(\PageIndex{5}\)
Визначте центр і радіус за даними рівняння окружності в стандартному вигляді.
- \((x-6)^{2}+y^{2}=9\)
- \((x+8)^{2}+(y-10)^{2}=1\)
- \(x^{2}+y^{2}=5\)
- \(\left(x-\frac{3}{8}\right)^{2}+\left(y+\frac{5}{2}\right)^{2}=\frac{1}{2}\)
- Відповідь
-
1. Центр:\((6,0) ;\) радіус:\(r=3\)
3. Центр:\((0,0) ;\) радіус:\(r=\sqrt{5}\)
Вправа\(\PageIndex{6}\)
Визначаємо стандартну форму для рівняння кола:
- Центр\((-7,2)\) з радіусом\(r=10\)
- Центр\(\left(\frac{1}{3},-1\right)\) з радіусом\(r=\frac{2}{3}\)
- Центр\((0,-5)\) з радіусом\(r=2 \sqrt{7}\)
- Центр\((1,0)\) з радіусом\(r=\frac{5 \sqrt{3}}{2}\)
- Коло, діаметр якого визначається\((-4,10)\) і\((-2,8)\)
- Коло, діаметр якого визначається\((3,-6)\) і\((0,-4)\)
- Відповідь
-
1. \((x+7)^{2}+(y-2)^{2}=100\)
3. \(x^{2}+(y+5)^{2}=28\)
5. \((x+3)^{2}+(y-9)^{2}=2\)
Вправа\(\PageIndex{7}\)
Знайдіть\(x\) - і\(y\) -перехоплює.
- \((x-3)^{2}+(y+5)^{2}=16\)
- \((x+5)^{2}+(y-1)^{2}=4\)
- \(x^{2}+(y-2)^{2}=20\)
- \((x-3)^{2}+(y+3)^{2}=8\)
- \(x^{2}+y^{2}-12 y+27=0\)
- \(x^{2}+y^{2}-4 x+2 y+1=0\)
- Відповідь
-
1. \(x\)-перехоплює: немає;\(y\) -перехоплює:\((0,-5 \pm \sqrt{7})\)
3. \(x\)-перехоплює:\((\pm 4,0)\);\(y\) -перехоплює:\((0,2 \pm 2 \sqrt{5})\)
5. \(x\)-перехоплює: немає;\(y\) -перехоплює:\((0,3),(0,9)\)
Вправа\(\PageIndex{8}\)
Графік.
- \((x+8)^{2}+(y-6)^{2}=4\)
- \((x-20)^{2}+\left(y+\frac{15}{2}\right)^{2}=\frac{225}{4}\)
- \(x^{2}+y^{2}=24\)
- \((x-1)^{2}+y^{2}=\frac{1}{4}\)
- \(x^{2}+(y-7)^{2}=27\)
- \((x+1)^{2}+(y-1)^{2}=2\)
- Відповідь
-
1.

Малюнок 8.E.6 3.
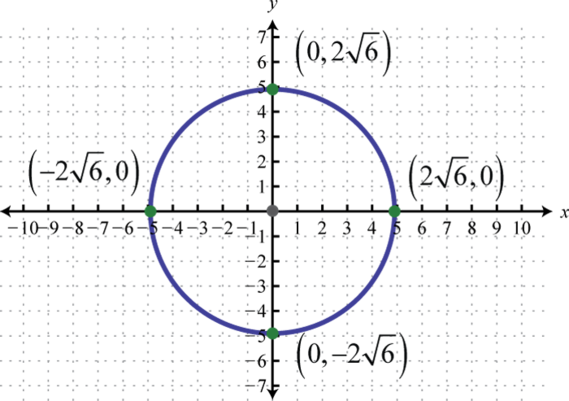
Малюнок 8.E.7 5.
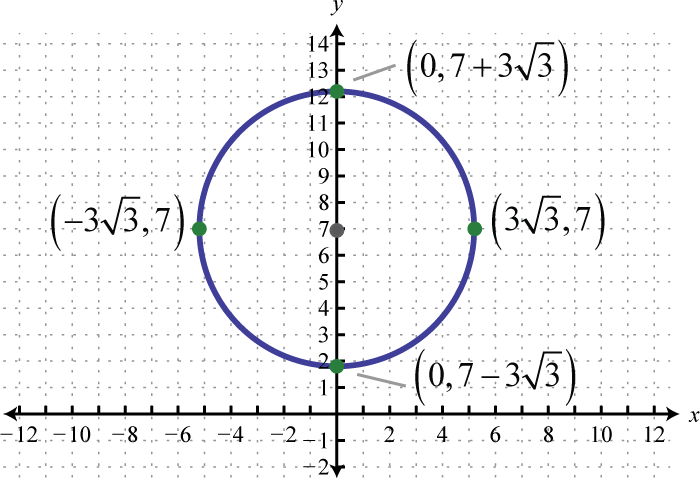
Малюнок 8.E.8
Вправа\(\PageIndex{9}\)
Перепишіть в стандартній формі і графі.
- \(x^{2}+y^{2}-6 x+4 y-3=0\)
- \(x^{2}+y^{2}+8 x-10 y+16=0\)
- \(2 x^{2}+2 y^{2}-2 x-6 y-3=0\)
- \(4 x^{2}+4 y^{2}+8 y+1=0\)
- \(x^{2}+y^{2}-5 x+y-\frac{1}{2}=0\)
- \(x^{2}+y^{2}+12 x-8 y=0\)
- Відповідь
-
1. \((x-3)^{2}+(y+2)^{2}=16\);

Малюнок 8.E.9 3. \(\left(x-\frac{1}{2}\right)^{2}+\left(y-\frac{3}{2}\right)^{2}=4\);
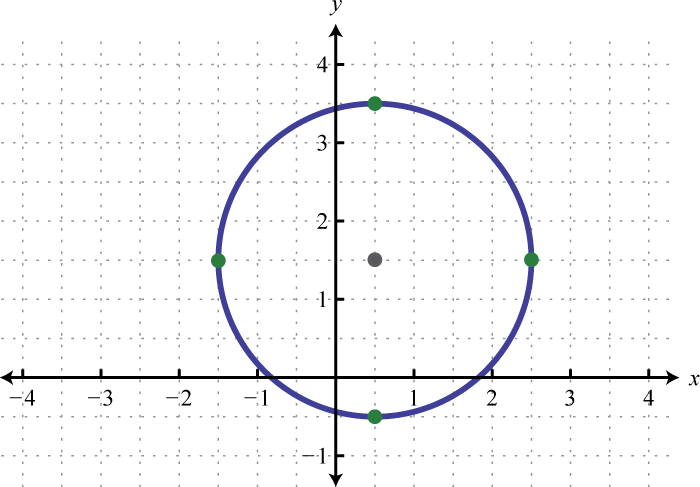
Малюнок 8.E.10 5. \(\left(x-\frac{5}{2}\right)^{2}+\left(y+\frac{1}{2}\right)^{2}=7\);

Малюнок 8.E.11
Вправа\(\PageIndex{10}\)
Враховуючи рівняння еліпса в стандартній формі, визначте його центр, орієнтацію, великий радіус і малий радіус.
- \(\frac{(x+12)^{2}}{16}+\frac{(y-10)^{2}}{4}=1\)
- \(\frac{(x+3)^{2}}{3}+\frac{y^{2}}{25}=1\)
- \(x^{2}+\frac{(y-5)^{2}}{12}=1\)
- \(\frac{(x-8)^{2}}{5}+\frac{(y+8)}{18}=1\)
- Відповідь
-
1. Центр:\((−12, 10)\); орієнтація: горизонтальна; великий радіус:\(4\) одиниці виміру; малий радіус:\(2\) одиниці
3. Центр:\((0, 5)\); орієнтація: вертикальна; великий радіус:\(2\sqrt{3}\) одиниці виміру; малий радіус:\(1\) одиниця
Вправа\(\PageIndex{11}\)
Визначити стандартну форму для рівняння еліпса дано наступну інформацію.
- Центр\((0,-4)\) з\(a=3\) і\(b=4\)
- Центр\((3,8)\) з\(a=1\) і\(b=\sqrt{7}\)
- Центр\((0,0)\) з\(a=5\) і\(b=\sqrt{2}\)
- Центр\((-10,-30)\) з\(a=10\) і\(b=1\)
- Відповідь
-
1. \(\frac{x^{2}}{9}+\frac{(y+4)^{2}}{16}=1\)
3. \(\frac{x^{2}}{25}+\frac{y^{2}}{2}=1\)
Вправа\(\PageIndex{12}\)
Знайдіть\(x\) - і\(y\) -перехоплює.
- \(\frac{(x+2)^{2}}{4}+\frac{y^{2}}{9}=1\)
- \(\frac{(x-1)^{2}}{2}+\frac{(y+1)^{2}}{3}=1\)
- \(5 x^{2}+2 y^{2}=20\)
- \(5(x-3)^{2}+6 y^{2}=120\)
- Відповідь
-
1. \(x\)-перехоплює:\((-4,0),(0,0) ; y\) -перехоплює:\((0,0)\)
3. \(x\)-перехоплює:\((\pm 2,0) ; y\) -перехоплює:\((0, \pm \sqrt{10})\)
Вправа\(\PageIndex{13}\)
Графік.
- \(\frac{(x-10)^{2}}{25}+\frac{(y+5)^{2}}{4}=1\)
- \(\frac{(x+6)^{2}}{9}+\frac{(y-8)^{2}}{36}=1\)
- \(\frac{\left(x-\frac{3}{2}\right)^{2}}{4}+\left(y-\frac{7}{2}\right)^{2}=1\)
- \(\left(x-\frac{2}{3}\right)^{2}+\frac{y^{2}}{4}=1\)
- \(\frac{x^{2}}{2}+\frac{y^{2}}{5}=1\)
- \(\frac{(x+2)^{2}}{8}+\frac{(y-3)^{2}}{12}=1\)
- Відповідь
-
1.
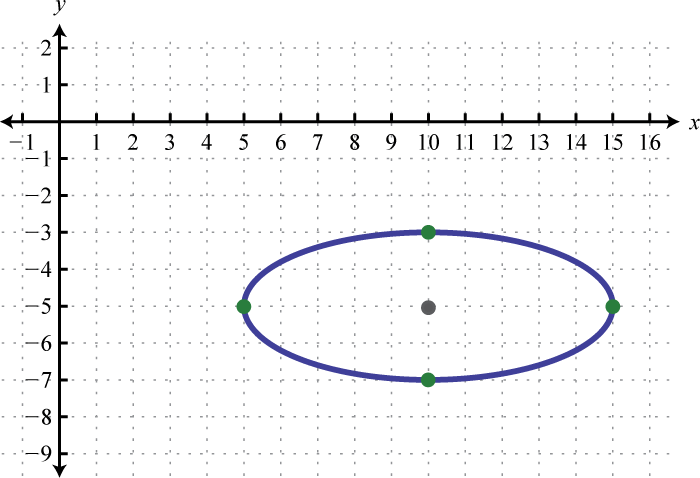
Малюнок 8.E.12 3.
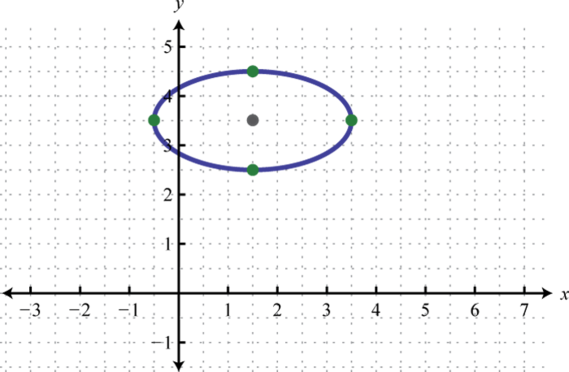
Малюнок 8.E.13 5.
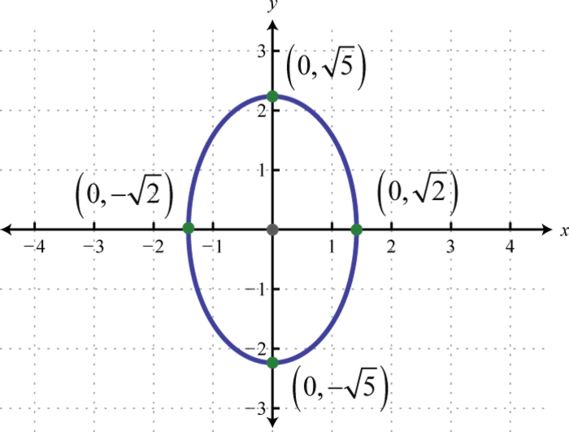
Малюнок 8.E.14
Вправа\(\PageIndex{14}\)
Перепишіть в стандартній формі і графі.
- \(4 x^{2}+9 y^{2}-8 x+90 y+193=0\)
- \(9 x^{2}+4 y^{2}+108 x-80 y+580=0\)
- \(x^{2}+9 y^{2}+6 x+108 y+324=0\)
- \(25 x^{2}+y^{2}-350 x-8 y+1,216=0\)
- \(8 x^{2}+12 y^{2}-16 x-36 y-13=0\)
- \(10 x^{2}+2 y^{2}-50 x+14 y+7=0\)
- Відповідь
-
1. \(\frac{(x-1)^{2}}{9}+\frac{(y+5)^{2}}{4}=1\);
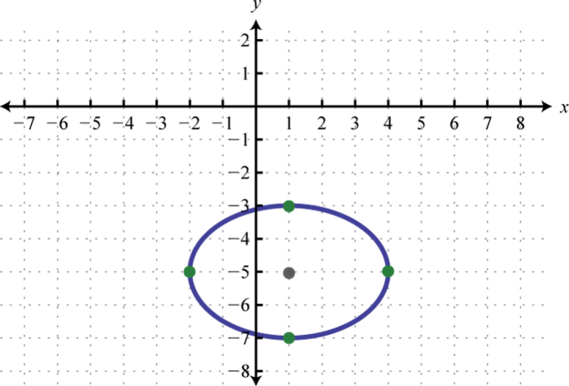
Малюнок 8.E.15 3. \(\frac{(x+3)^{2}}{9}+(y+6)^{2}=1\);

Малюнок 8.E.16 5. \(\frac{(x-1)^{2}}{6}+\frac{\left(y-\frac{3}{2}\right)^{2}}{4}=1\);

Малюнок 8.E.17
Вправа\(\PageIndex{15}\)
З огляду на рівняння гіперболи в стандартній формі, визначають її центр, в який бік відкривається граф, і вершини.
- \(\frac{(x-10)^{2}}{4}-\frac{(y+5)^{2}}{16}=1\)
- \(\frac{(x+7)^{2}}{2}-\frac{(y-8)^{2}}{8}=1\)
- \(\frac{(y-20)^{2}}{3}-(x-15)^{2}=1\)
- \(3 y^{2}-12(x-1)^{2}=36\)
- Відповідь
-
1. Центр:\((10,-5)\); відкриває вліво і вправо; вершини:\((8,-5),(12,-5)\)
3. Центр:\((15,20)\); відкривається вгору і вниз; вершини:\((15,20-\sqrt{3}),(15,20+\sqrt{3})\)
Вправа\(\PageIndex{16}\)
Визначте стандартну форму для рівняння гіперболи.
- Центр\((-25,10), a=3, b=\sqrt{5},\) відкривається вгору і вниз.
- Центр\((9,-12), a=5 \sqrt{3}, b=7,\) відкривається вліво і вправо.
- Центр\((-4,0), a=1, b=6,\) відкривається вліво і вправо.
- Центр\((-2,-3), a=10 \sqrt{2}, b=2 \sqrt{3},\) відкривається вгору і вниз.
- Відповідь
-
1. \(\frac{(y-10)^{2}}{5}-\frac{(x+25)^{2}}{9}=1\)
3. \((x+4)^{2}-\frac{y^{2}}{36}=1\)
Вправа\(\PageIndex{17}\)
Знайдіть\(x\) - і\(y\) -перехоплює.
- \(\frac{(x-1)^{2}}{4}-\frac{(y+3)^{2}}{9}=1\)
- \(\frac{(x+4)^{2}}{8}-\frac{(y-2)^{2}}{12}=1\)
- \(4(y-2)^{2}-x^{2}=16\)
- \(6(y+1)^{2}-3(x-1)^{2}=18\)
- Відповідь
-
1. \(x\)-перехоплює:\((1 \pm 2 \sqrt{2}, 0) ; y\) -перехоплює: немає
3. \(x\)-перехоплює:\((0,0) ; y\) -перехоплює:\((0,0),(0,4)\)
Вправа\(\PageIndex{18}\)
Графік.
- \(\frac{(x-10)^{2}}{25}-\frac{(y+5)^{2}}{100}=1\)
- \(\frac{(x-4)^{2}}{4}-\frac{(y-8)^{2}}{16}=1\)
- \(\frac{(y-3)^{2}}{9}-\frac{(x-6)^{2}}{81}=1\)
- \(\frac{(y+1)^{2}}{4}-\frac{(x+1)^{2}}{25}=1\)
- \(\frac{y^{2}}{27}-\frac{(x-3)^{2}}{9}=1\)
- \(\frac{x^{2}}{2}-\frac{y^{2}}{3}=1\)
- Відповідь
-
1.
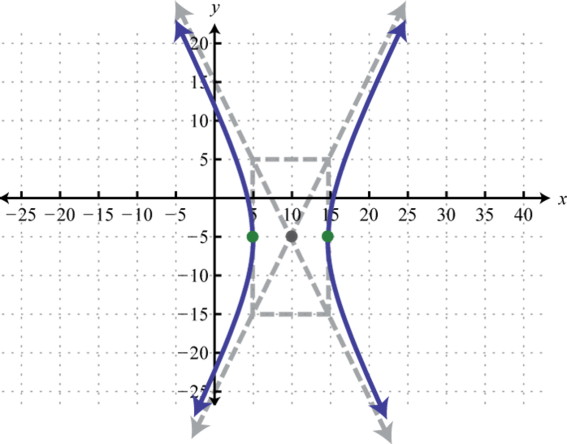
Малюнок 8.E.18 3.
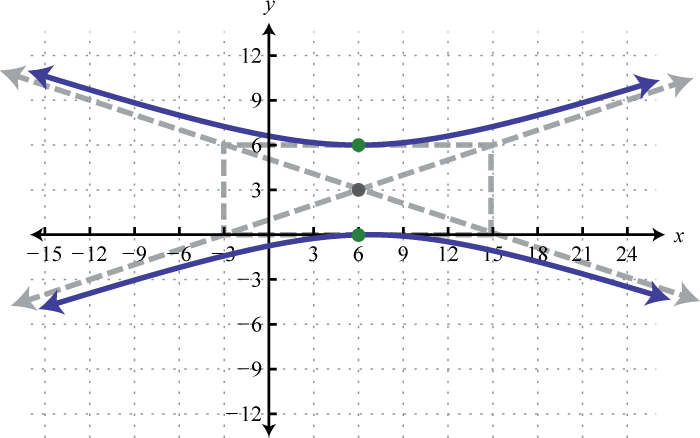
Малюнок 8.E.19 5.
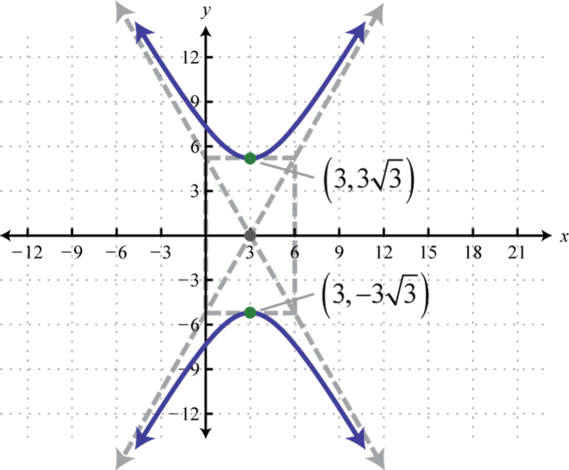
Малюнок 8.E.20
Вправа\(\PageIndex{19}\)
Перепишіть в стандартній формі і графі.
- \(4 x^{2}-9 y^{2}-8 x-90 y-257=0\)
- \(9 x^{2}-y^{2}-108 x+16 y+224=0\)
- \(25 y^{2}-2 x^{2}-100 y+50=0\)
- \(3 y^{2}-x^{2}-2 x-10=0\)
- \(8 y^{2}-12 x^{2}+24 y-12 x-33=0\)
- \(4 y^{2}-4 x^{2}-16 y-28 x-37=0\)
- Відповідь
-
1. \(\frac{(x-1)^{2}}{9}-\frac{(y+5)^{2}}{4}=1\);
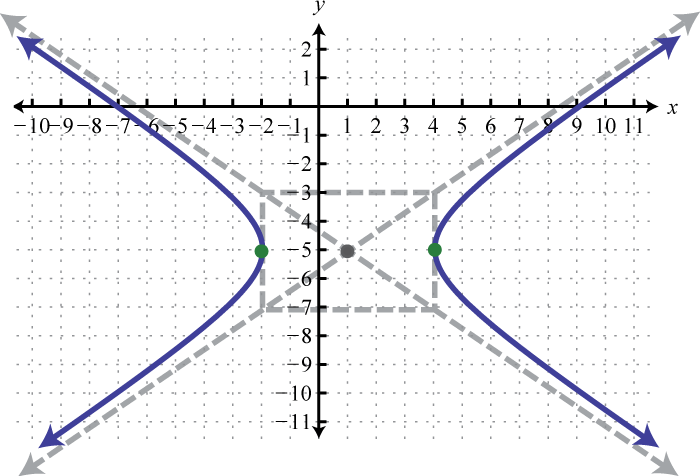
Малюнок 8.E.21 3. \(\frac{(y-2)^{2}}{2}-\frac{x^{2}}{25}=1\);
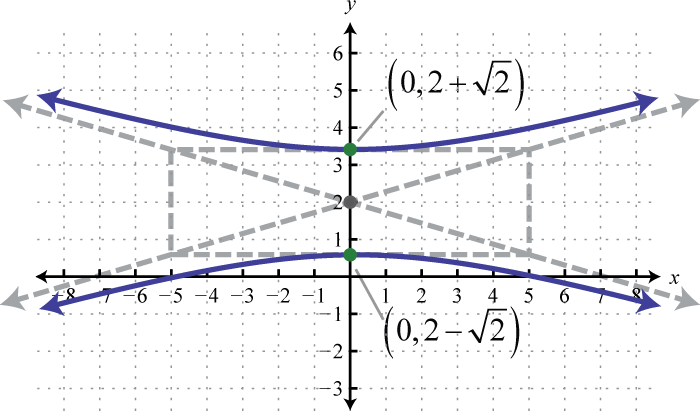
Малюнок 8.E.22 5. \(\frac{\left(y+\frac{3}{2}\right)^{2}}{6}-\frac{\left(x+\frac{1}{2}\right)^{2}}{4}=1\)

Малюнок 8.E.23
Вправа\(\PageIndex{20}\)
Визначте конічні перетину і перепишіть в стандартному вигляді.
- \(x^{2}+y^{2}-2 x-8 y+16=0\)
- \(x^{2}+2 y^{2}+4 x-24 y+74=0\)
- \(x^{2}-y^{2}-6 x-4 y+3=0\)
- \(x^{2}+y-10 x+22=0\)
- \(x^{2}+12 y^{2}-12 x+24=0\)
- \(x^{2}+y^{2}+10 y+22=0\)
- \(4 y^{2}-20 x^{2}+16 y+20 x-9=0\)
- \(16 x-16 y^{2}+24 y-25=0\)
- \(9 x^{2}-9 y^{2}-6 x-18 y-17=0\)
- \(4 x^{2}+4 y^{2}+4 x-8 y+1=0\)
- Відповідь
-
1. коло;\((x-1)^{2}+(y-4)^{2}=1\)
3. гіпербола;\(\frac{(x-3)^{2}}{2}-\frac{(y+2)^{2}}{2}=1\)
5. Еліпс;\(\frac{(x-6)^{2}}{12}+y^{2}=1\)
7. гіпербола;\(\frac{(y+2)^{2}}{5}-\left(x-\frac{1}{2}\right)^{2}=1\)
9. гіпербола;\(\left(x-\frac{1}{3}\right)^{2}-(y+1)^{2}=1\)
Вправа\(\PageIndex{21}\)
З огляду на графік, запишіть рівняння в загальному вигляді.
1.
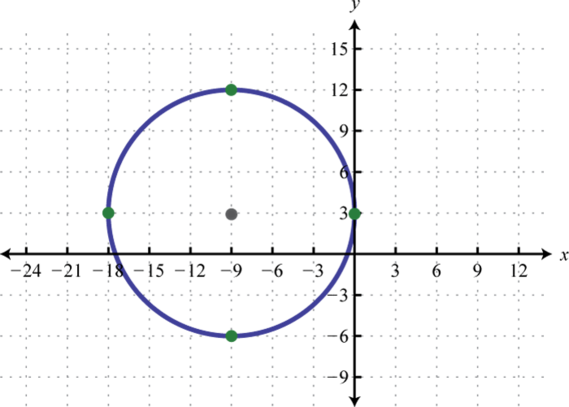
2.
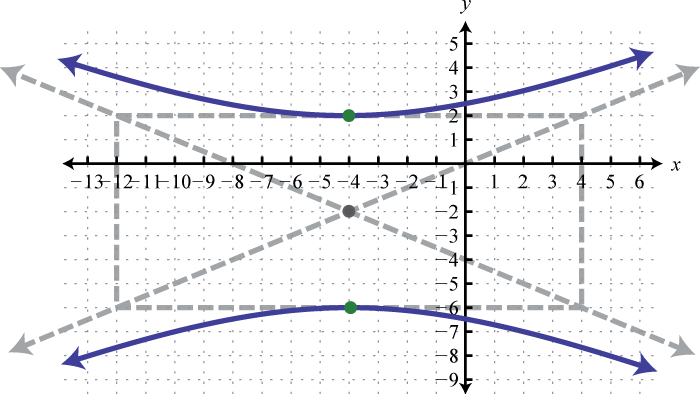
3.

4.

5.
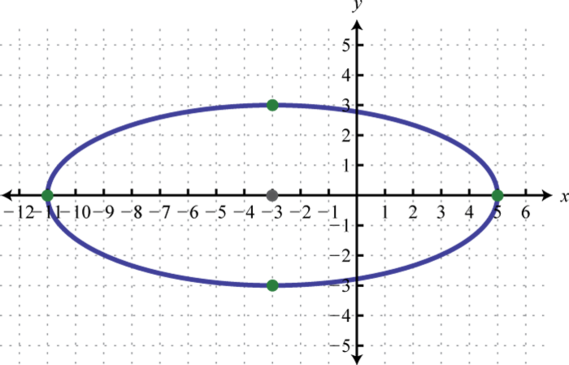
6.

- Відповідь
-
1. \(x^{2}+y^{2}+18 x-6 y+9=0\)
3. \(9 x^{2}-y^{2}+72 x-12 y+72=0\)
5. \(9 x^{2}+64 y^{2}+54 x-495=0\)
Вправа\(\PageIndex{22}\)
Вирішити.
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=8} \\ {x-y=4}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=1} \\ {x+2 y=1}\end{array}\right.\)
- \(\left\{\begin{array}{c}{x^{2}+3 y^{2}=4} \\ {2 x-y=1}\end{array}\right.\)
- \(\left\{\begin{array}{c}{2 x^{2}+y^{2}=5} \\ {x+y=3}\end{array}\right.\)
- \(\left\{\begin{array}{c}{3 x^{2}-2 y^{2}=1} \\ {x-y=2}\end{array}\right.\)
- \(\left\{\begin{array}{c}{x^{2}-3 y^{2}=10} \\ {x-2 y=1}\end{array}\right.\)
- \(\left\{\begin{array}{c}{2 x^{2}+y^{2}=11} \\ {4 x+y^{2}=5}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+4 y^{2}=1} \\ {2 x^{2}+4 y=5}\end{array}\right.\)
- \(\left\{\begin{array}{c}{5 x^{2}-y^{2}=10} \\ {x^{2}+y=2}\end{array}\right.\)
- \(\left\{\begin{array}{l}{2 x^{2}+y^{2}=1} \\ {2 x-4 y^{2}=-3}\end{array}\right.\)
- \(\left\{\begin{array}{c}{x^{2}+4 y^{2}=10} \\ {x y=2}\end{array}\right.\)
- \(\left\{\begin{array}{l}{y+x^{2}=0} \\ {x y-8=0}\end{array}\right.\)
- \(\left\{\begin{array}{l}{\frac{1}{x}+\frac{1}{y}=10} \\ {\frac{1}{x}-\frac{1}{y}=6}\end{array}\right.\)
- \(\left\{\begin{array}{l}{\frac{1}{x}+\frac{1}{y}=1} \\ {y-x=2}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x-2 y^{2}=3} \\ {y=\sqrt{x-4}}\end{array}\right.\)
- \(\left\{\begin{array}{c}{(x-1)^{2}+y^{2}=1} \\ {y-\sqrt{x}=0}\end{array}\right.\)
- Відповідь
-
1. \((2,-2)\)
3. \(\left(-\frac{1}{13},-\frac{15}{13}\right),(1,1)\)
5. \((-9,-11),(1,-1)\)
7. \((-1,-3),(-1,3)\)
9. \((-\sqrt{2}, 0),(\sqrt{2}, 0),(-\sqrt{7},-5),(\sqrt{7},-5)\)
11. \((\sqrt{2}, \sqrt{2}) \cdot(-\sqrt{2},-\sqrt{2}) \cdot\left(2 \sqrt{2}, \frac{\sqrt{2}}{2}\right) \cdot\left(-2 \sqrt{2},-\frac{\sqrt{2}}{2}\right)\)
13. \(\left(\frac{1}{8}, \frac{1}{2}\right)\)
15. \((5,1)\)
Зразок іспиту
Вправа\(\PageIndex{23}\)
- З огляду на два пункти\((-4,-6)\) і\((2,-8)\):
- Обчисліть відстань між ними.
- Знайдіть середню точку між ними.
- Визначте площу кола, діаметр якої визначається точками\((4, −3)\) і\((−1, 2)\).
- Відповідь
-
1. (1)\(2\sqrt{10}\) одиниці; (2)\((-1,-7)\)
Вправа\(\PageIndex{24}\)
Перепишіть в стандартній формі і графі. Знайдіть вершину і всі перехоплення, якщо такі є.
- \(y=-x^{2}+6 x-5\)
- \(x=2 y^{2}+4 y-6\)
- \(x=-3 y^{2}+3 y+1\)
- Знайдіть рівняння кола в стандартній формі з\(2 \sqrt{5}\) одиницями центру\((−6, 3)\) і радіуса.
- Відповідь
-
1. \(y=-(x-3)^{2}+4\);
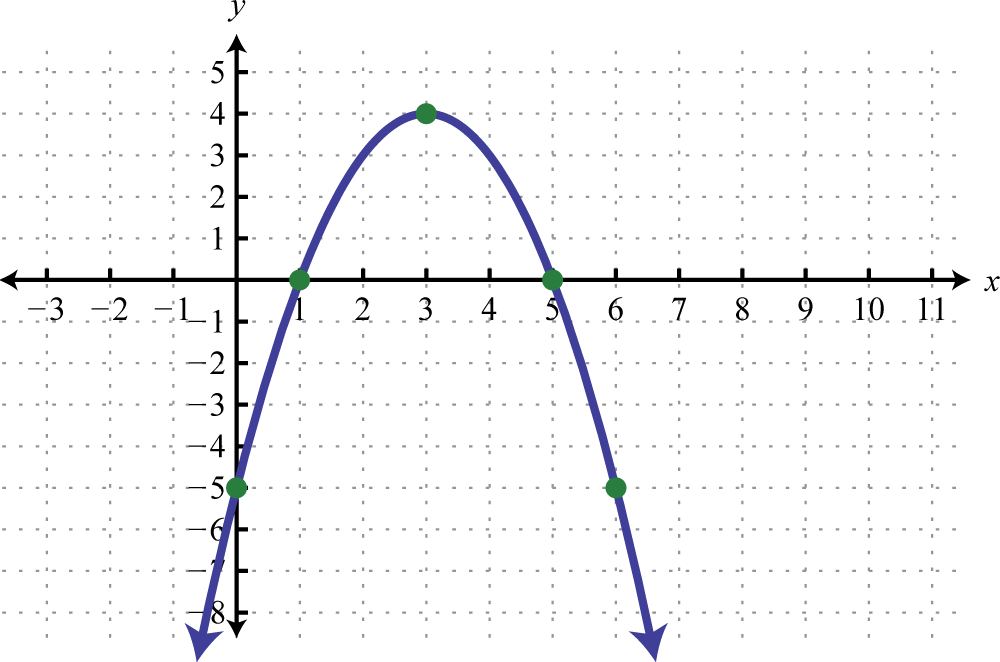
Малюнок 8.E.30 3. \(x=-3\left(y-\frac{1}{2}\right)^{2}+\frac{7}{4}\);
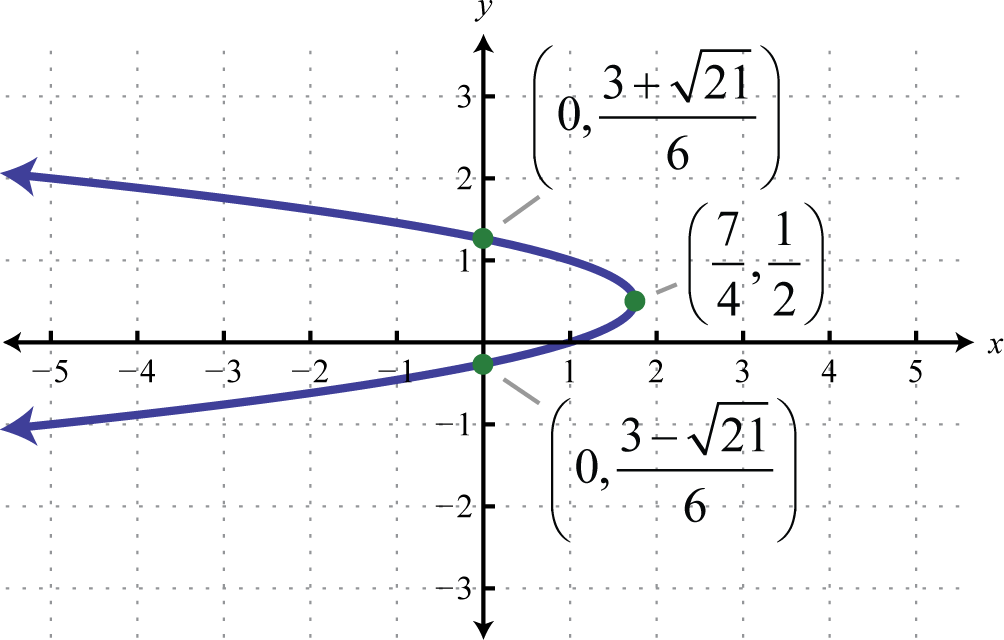
Малюнок 8.E.31
Вправа\(\PageIndex{25}\)
Намалюйте графік конічного перерізу з урахуванням його рівняння в стандартному вигляді.
- \((x-4)^{2}+(y+1)^{2}=45\)
- \(\frac{(x+3)^{2}}{4}+\frac{y^{2}}{9}=1\)
- \(\frac{y^{2}}{3}-\frac{x^{2}}{9}=1\)
- \(\frac{x^{2}}{16}-(y-2)^{2}=1\)
- Відповідь
-
1.

Малюнок 8.E.32 3.
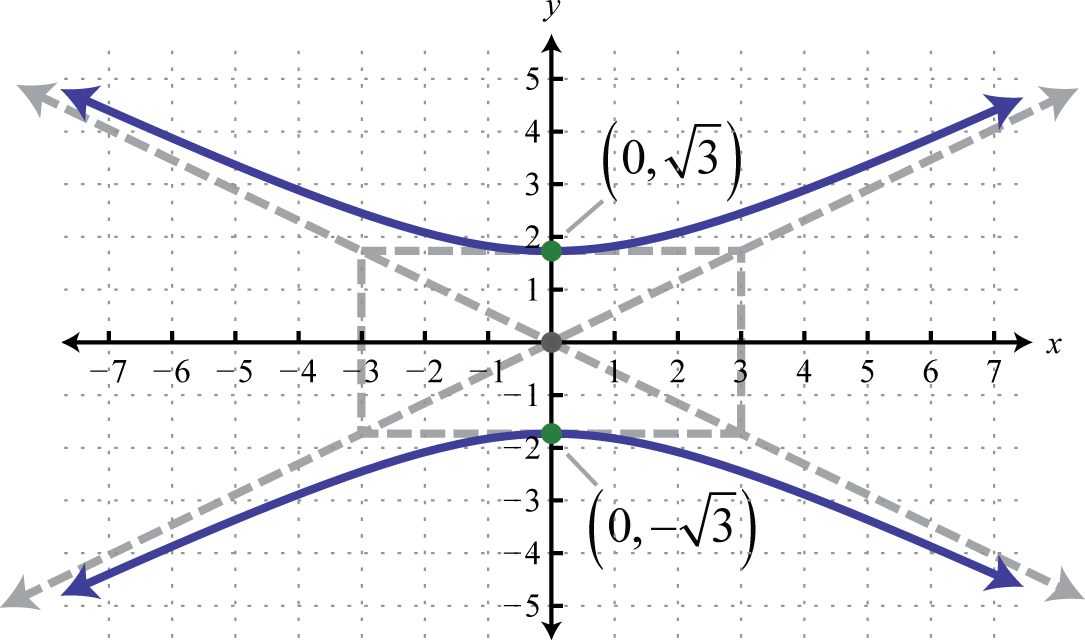
Малюнок 8.E.33
Вправа\(\PageIndex{26}\)
Перепишіть в стандартній формі і графі.
- \(9 x^{2}+4 y^{2}-144 x+16 y+556=0\)
- \(x-y^{2}+6 y+7=0\)
- \(x^{2}+y^{2}+20 x-20 y+100=0\)
- \(4 y^{2}-x^{2}+40 y-30 x-225=0\)
- Відповідь
-
1. \(\frac{(x-8)^{2}}{4}+\frac{(y+2)^{2}}{9}=1\);
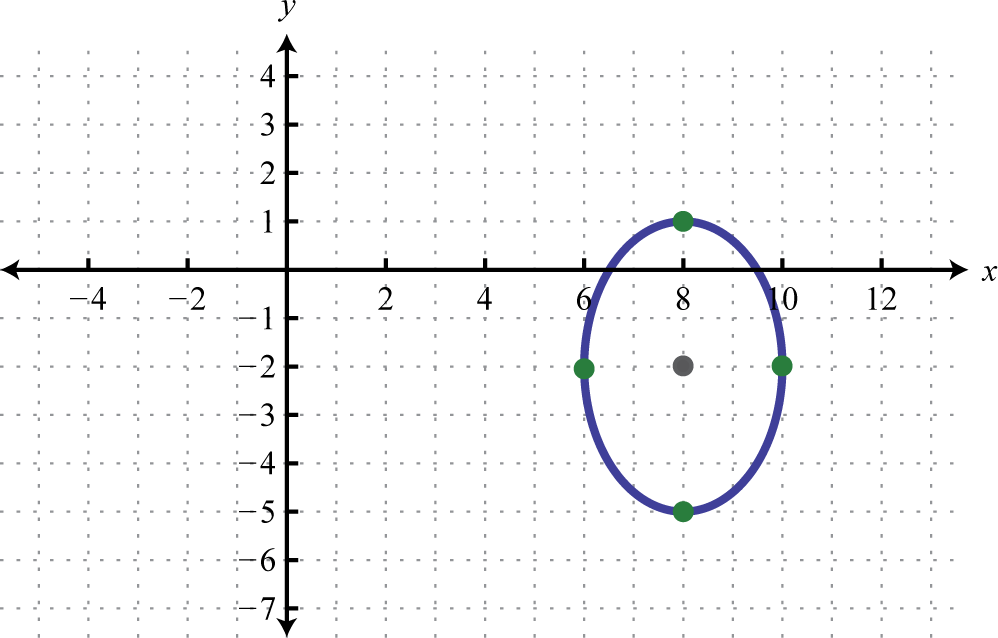
Малюнок 8.E.34 3. \((x+10)^{2}+(y-10)^{2}=100\);
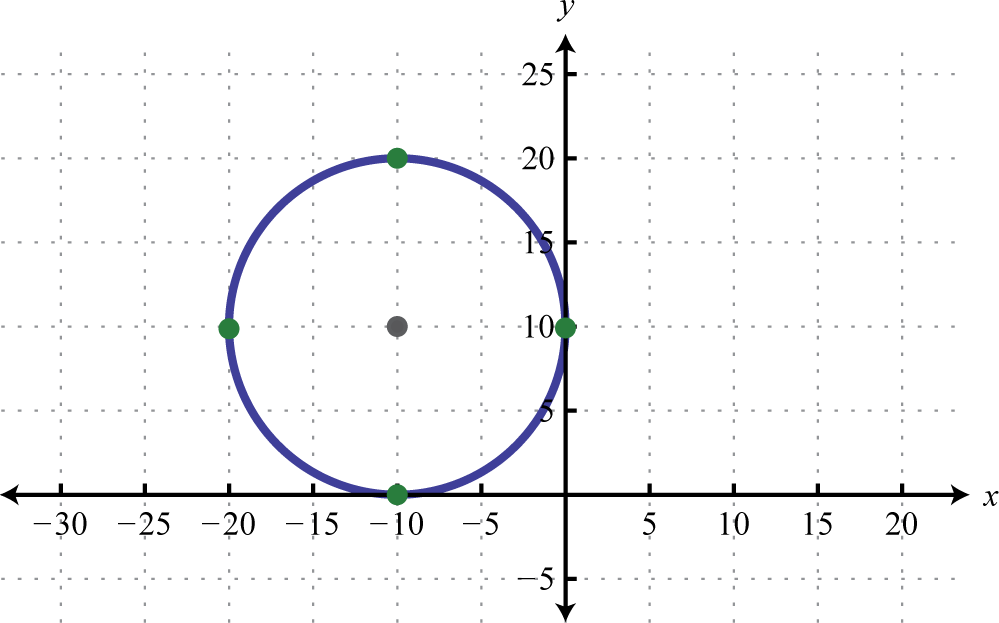
Малюнок 8.E.35
Вправа\(\PageIndex{27}\)
Знайдіть\(x\) - і\(y\) -перехоплює.
- \(x=-2(y-4)^{2}+9\)
- \(\frac{(y-1)^{2}}{12}-(x+1)^{2}=1\)
- Відповідь
-
1. \(x\)-перехоплення:\((-23,0) ; y\) -перехоплює:\(\left(0, \frac{8 \pm 3 \sqrt{2}}{2}\right)\)
Вправа\(\PageIndex{28}\)
Вирішити.
- \(\left\{\begin{array}{l}{x+y=2} \\ {y=-x^{2}+4}\end{array}\right.\)
- \(\left\{\begin{array}{l}{y-x^{2}=-3} \\ {x^{2}+y^{2}=9}\end{array}\right.\)
- \(\left\{\begin{array}{c}{2 x-y=1} \\ {(x+1)^{2}+2 y^{2}=1}\end{array}\right.\)
- \(\left\{\begin{array}{c}{x^{2}+y^{2}=6} \\ {x y=3}\end{array}\right.\)
- Відповідь
-
1. \((-1,3),(2,0)\)
3. \(\emptyset\)
Вправа\(\PageIndex{29}\)
- Знайдіть рівняння еліпса в стандартній формі з вершинами\((−3, −5)\)\((5, −5)\) та малими\(2\) одиницями радіуса в довжину.
- Знайдіть рівняння гіперболи в стандартній формі, що відкриває вліво і вправо з вершинами\((\pm \sqrt{5}, 0)\) і сполученою віссю, яка вимірює\(10\) одиниці виміру.
- З огляду на графік еліпса, визначте його рівняння в загальному вигляді.
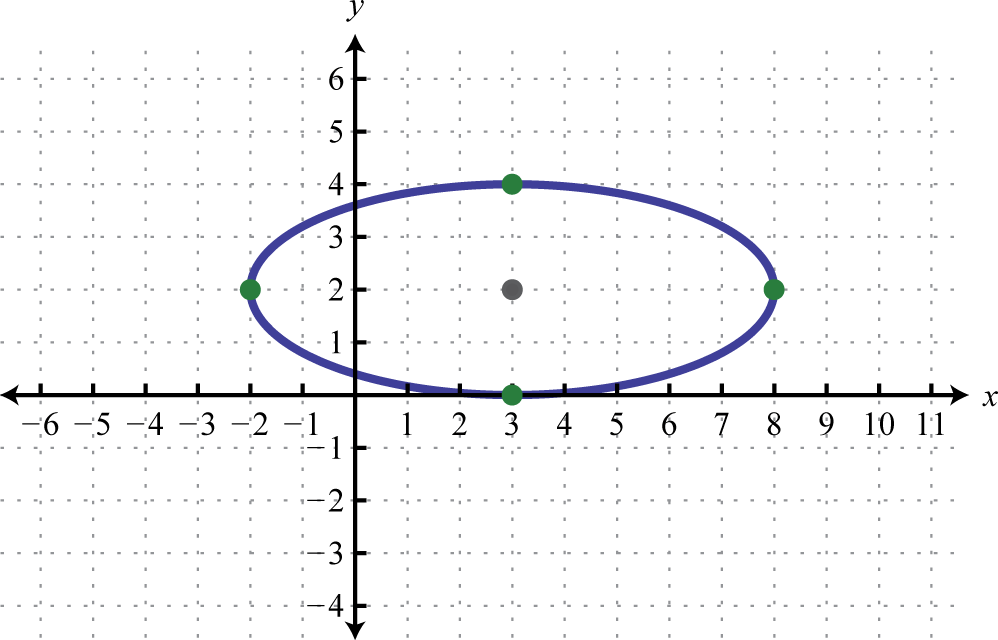
4. Прямокутна палуба має площу\(80\) квадратних футів і периметр, який вимірює\(36\) ноги. Знайдіть розміри колоди.
5. Діагональ прямокутника вимірює\(2\sqrt{13}\) сантиметри, а периметр вимірює\(20\) сантиметри. Знайдіть розміри прямокутника.
- Відповідь
-
1. \(\frac{(x-1)^{2}}{16}+\frac{(y+5)^{2}}{4}=1\)
3. \(4 x^{2}+25 y^{2}-24 x-100 y+36=0\)
5. \(6\)сантиметри по\(4\) сантиметрам
