8.2: Кола

Цілі навчання

• Графік кола в стандартній формі.
• Визначити рівняння кола за заданим її графіком.
• Перепишіть рівняння кола в стандартному вигляді.

Коло в стандартній формі

Коло ⁸ - це сукупність точок в площині, які лежать на фіксованій відстані, званому радіусом ⁹, від будь-якої точки, званої центром. Діаметр ¹⁰ - довжина відрізка лінії, що проходить через центр, кінцеві точки якого знаходяться на колі. Крім того, коло може бути утворений перетином конуса і площини, перпендикулярної осі конуса:

Малюнок$\PageIndex{1}$

У прямокутній координатній площині, де центр кола з$r$ радіусом$(h,k)$, ми маємо

Малюнок$\PageIndex{2}$

Обчисліть відстань між$(h,k)$ і$(x,y)$ використовуючи формулу відстані,

$\sqrt{(x-h)^{2}+(y-k)^{2}}=r$

Квадратування обох сторін призводить нас до рівняння кола в стандартному вигляді ¹¹,

$(x-h)^{2}+(y-k)^{2}=r^{2}$

У такому вигляді видно центр і радіус. Наприклад, враховуючи рівняння,$(x-2)^{2}+(y+5)^{2}=16$ яке ми маємо,

$\begin{array}{l}{(x-h)^{2}\:+\:(x\:-k)^{2}=r^{2}} \\ \quad\quad\color{Cerulean}{\downarrow}\quad\quad\quad\quad\:\color{Cerulean}{\downarrow}\quad\quad\color{Cerulean}{\downarrow} \\ {(x-\color{Cerulean}{2}\color{black}{)}^{2}+[y-(\color{Cerulean}{-5}\color{black}{)}]^{2}=\color{Cerulean}{4}^{\color{black}{2}}}\end{array}$

В даному випадку центром є$(2,−5)$ і$r=4$. Далі наведено додаткові приклади:

Таблиця$\PageIndex{1}$

Рівняння	Центр	Радіус
$(x-3)^{2}+(y-4)^{2}=25$	$(3,4)$	$r=5$
$(x-1)^{2}+(y+2)^{2}=7$	$(1,-2)$	$r=\sqrt{7}$
$(x+4)^{2}+(y-3)^{2}=1$	$(-4,3)$	$r=1$
$x^{2}+(y+6)^{2}=8$	$(0,-6)$	$r=2 \sqrt{2}$

Графік кола повністю визначається його центром і радіусом.

Приклад$\PageIndex{1}$:

Графік:$(x-2)^{2}+(y+5)^{2}=16$.

Рішення

Написано в цій формі ми бачимо, що центр є$(2,−5)$ і що радіус$r=4$ одиниць. Від центру відзначте точки$4$ одиниць вгору і вниз, а також$4$ одиниць вліво і вправо.

Малюнок$\PageIndex{3}$

Потім проведіть по колу через ці чотири точки.

Відповідь:

Малюнок$\PageIndex{4}$

Як і в будь-якому графіку, ми зацікавлені в пошуку$x$ - і$y$ -перехоплення.

Приклад$\PageIndex{2}$:

Знайдіть перехоплення:$(x-2)^{2}+(y+5)^{2}=16$.

Рішення

Щоб знайти набір$y$ -incepts$x=0$:

$\begin{aligned}(x-2)^{2}+(y+5)^{2} &=16 \\(\color{Cerulean}{0}\color{black}{-}2)^{2}+(y+5)^{2} &=16 \\ 4+(y+5)^{2} &=16 \end{aligned}$

Для цього рівняння ми можемо вирішити шляхом вилучення квадратних коренів.

$\begin{aligned}(y+5)^{2} &=12 \\ y+5 &=\pm \sqrt{12} \\ y+5 &=\pm 2 \sqrt{3} \\ y &=-5 \pm 2 \sqrt{3} \end{aligned}$

Тому$y$ -перехоплення є$(0,-5-2 \sqrt{3})$ і$(0,-5+2 \sqrt{3})$. Щоб знайти набір$x$ -incepts$y=0$:

$\begin{aligned}(x-2)^{2}+(y+5)^{2} &=16 \\(x-2)^{2}+(\color{Cerulean}{0}\color{black}{+}5)^{2} &=16 \\(x-2)^{2}+25 &=16 \\(x-2)^{2} &=-9 \\ x-2 &=\pm \sqrt{-9} \\ x &=2 \pm 3 i \end{aligned}$

А оскільки рішення складні, ми робимо висновок, що реальних$x$ -перехоплень немає. Зауважте, що це має сенс, враховуючи графік.

Малюнок$\PageIndex{5}$

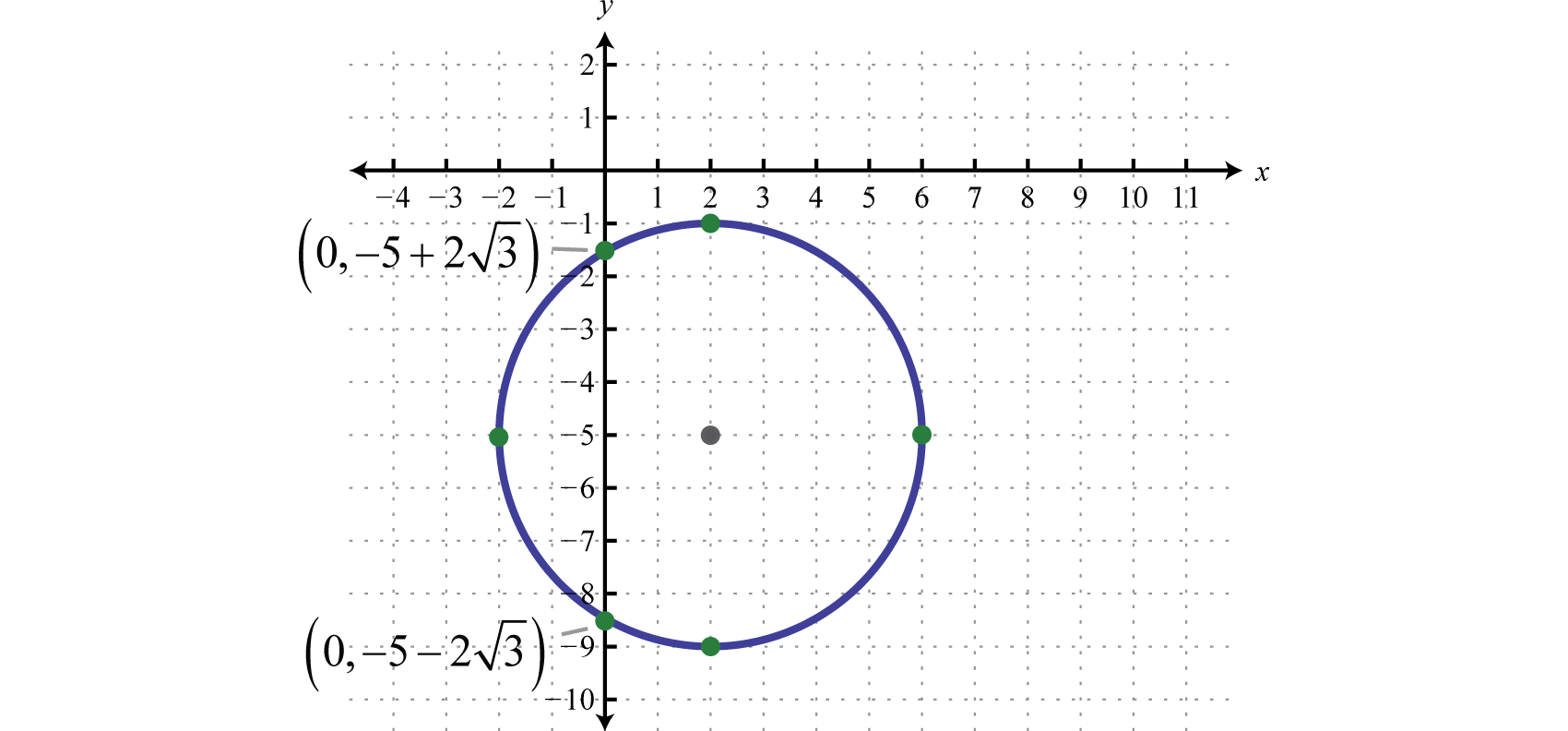
Відповідь:

$x$-перехоплює: немає;$y$ -перехоплює:$(0,-5-2 \sqrt{3})$ і$(0,-5+2 \sqrt{3})$

З огляду на центр і радіус кола, ми можемо знайти його рівняння.

Приклад$\PageIndex{3}$:

Графік кола з радіусними$r=3$ одиницями, зосередженими на$(−1,0)$. Дайте її рівняння в стандартній формі і визначте перехоплення.

Рішення:

Враховуючи, що центр є$(−1,0)$ і радіус є,$r=3$ ми накидаємо графік наступним чином:

Малюнок$\PageIndex{6}$

Підставити$h, k$, і$r$ знайти рівняння в стандартному вигляді. Так як$(h,k)=(−1,0)$ і у$r=3$ нас,

$\begin{aligned} (x-h)^{2}+(y-k)^{2}&=r^{2}\\ [x-(\color{Cerulean}{-1}\color{black}{)}]^{2}+(y-\color{Cerulean}{0}\color{black}{)}^{2}&=\color{Cerulean}{3}\color{black}{^{2}} \\ (x+1)^{2}+y^{2}&=9 \end{aligned}$

Рівняння кола є$(x+1)^{2}+y^{2}=9$, використовуйте це для визначення$y$ -перехоплення.

$\begin{aligned}(x+1)^{2}+y^{2} &=9 \quad \color{Cerulean} { Set\:x=0\: to\: and\: solve\: for\: y. } \\(\color{Cerulean}{0}\color{black}{+}1)^{2}+y^{2} &=9 \\ 1+y^{2} &=9 \\ y^{2} &=8 \\ y &=\pm \sqrt{8} \\ y &=\pm 2 \sqrt{2} \end{aligned}$

Тому y-перехоплення є$(0,-2 \sqrt{2})$ і$(0,2 \sqrt{2})$. Знайти$x$ -перехоплює алгебраїчно, встановити$y=0$ і вирішити для$x$; це залишається для читача як вправа.

Малюнок$\PageIndex{7}$

Відповідь:

Рівняння:$(x+1)^{2}+y^{2}=9$;$y$ -перехоплює:$(0,-2 \sqrt{2})$ і$(0,2 \sqrt{2})$;$x$ -перехоплює:$(−4,0)$ і$(2,0)$

Особливе значення має одиниця окружності ¹²,

$x^{2}+y^{2}=1$

Або,

$(x-0)^{2}+(y-0)^{2}=1^{2}$

У такому вигляді повинно бути зрозуміло, що центр є$(0,0)$ і що радіус -$1$ одиниця. Крім того, якщо ми вирішимо для,$y$ ми отримаємо дві функції:

$\begin{aligned} x^{2}+y^{2} &=1 \\ y^{2} &=1-x^{2} \\ y &=\pm \sqrt{1-x^{2}} \end{aligned}$

Функція,$y=\sqrt{1-x^{2}}$ визначена, є верхньою половиною кола, а функція, визначена,$y=-\sqrt{1-x^{2}}$ є нижньою половиною одиничного кола:

Малюнок$\PageIndex{8}$

Вправа$\PageIndex{1}$:

Графік і позначення перехоплень:$x^{2}+(y+2)^{2}=25$.

Відповідь:

Малюнок$\PageIndex{9}$

www.youtube.com/В/КЕКТ9К6

Коло в загальній формі

Ми бачили, що графік кола повністю визначається центром і радіусом, які можна прочитати з його рівняння в стандартній формі. Однак рівняння не завжди дається в стандартній формі. Рівняння кола в загальному вигляді ¹³ виглядає наступним чином:

$x^{2}+y^{2}+c x+d y+e=0$

Тут$c, d$ і$e$ знаходяться дійсні числа. Наступні кроки для побудови графіка кола, заданого його рівняння в загальній формі.

Приклад$\PageIndex{4}$:

Графік:$x^{2}+y^{2}+6 x-8 y+13=0$.

Рішення

Почніть з перезапису рівняння в стандартному вигляді.

Крок 1: Згрупуйте терміни з однаковими змінними і перемістіть константу в праву сторону. У цьому випадку відніміть з обох$13$ сторін і згрупуйте терміни за участю$x$ та терміни, що стосуються$y$, наступним чином.

$\begin{aligned} x^{2}+y^{2}+6 x-8 y+13 &=0 \\ \left(x^{2}+6 x+\_\_\_\right)+\left(y^{2}-8 y+\_\_\_\right)&=-13 \end{aligned}$

Крок 2: Заповніть квадрат для кожного угруповання. Ідея полягає в тому, щоб додати значення, яке завершує квадрат$\left(\frac{b}{2}\right)^{2}$, до обох сторін для обох груп, а потім коефіцієнт. Для термінів, що передбачають$x$ використання,$\left(\frac{6}{2}\right)^{2}=3^{2}=9$ і для термінів, пов'язаних з$y$ використанням$\left(\frac{-8}{2}\right)^{2}=(-4)^{2}=16$.

$\begin{array}{c}{\color{black}{\left(x^{2}+6 x\color{Cerulean}{+9}\right)+}\color{black}{\left(y^{2}-8 y\color{OliveGreen}{+16}\right)=}-13\color{Cerulean}{+9}\color{OliveGreen}{+16}} \\ {(x+3)^{2}+(y-4)^{2}=12}\end{array}$

Крок 3: Визначте центр і радіус з рівняння в стандартній формі. В даному випадку центром є$(−3,4)$ і радіус$r=\sqrt{12}=2 \sqrt{3}$.

Крок 4: Від центру відзначте радіус вертикально і горизонтально, а потім намалюйте коло через ці точки.

Малюнок$\PageIndex{10}$

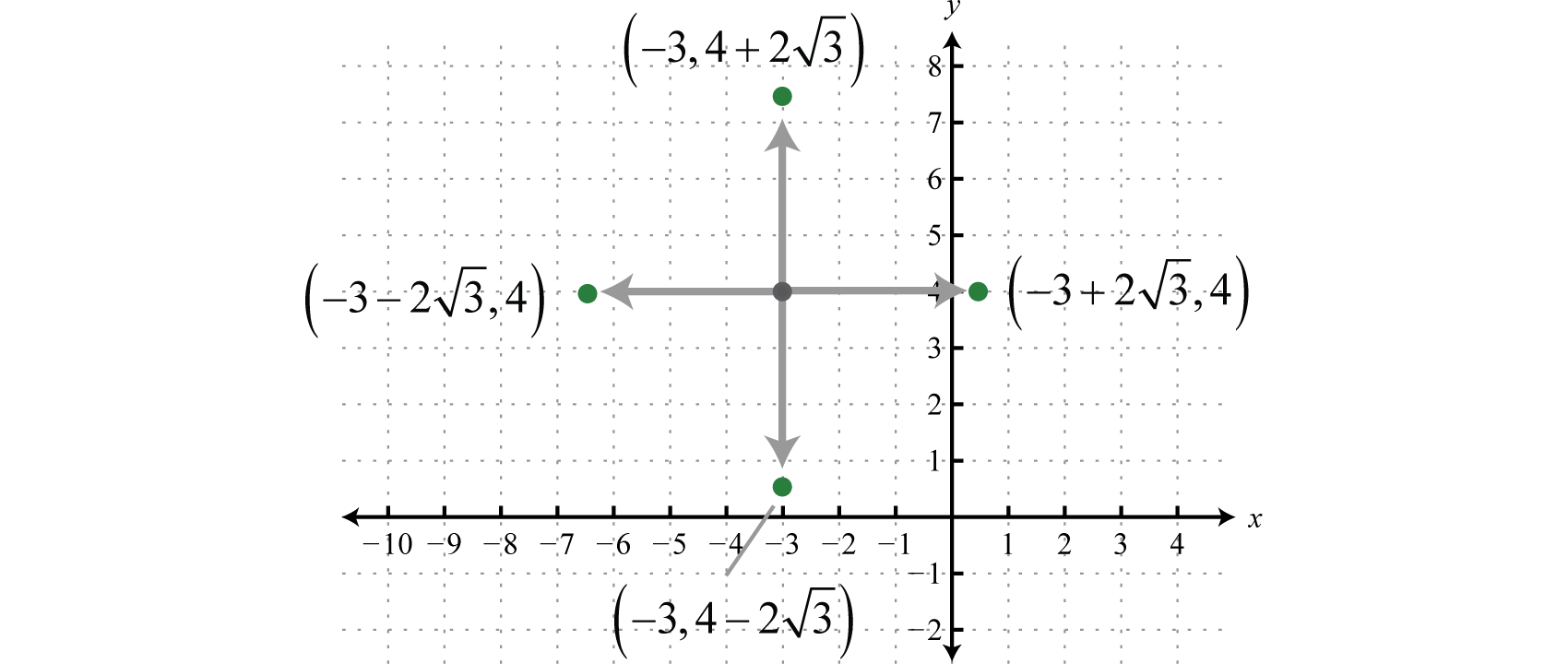
Відповідь:

Малюнок$\PageIndex{11}$

Приклад$\PageIndex{5}$:

Визначаємо центр і радіус:$4 x^{2}+4 y^{2}-8 x+12 y-3=0$.

Рішення

Ми можемо отримати загальну форму, попередньо розділивши обидві сторони на$4$.

$\frac{4 x^{2}+4 y^{2}-8 x+12 y-3}{4}=\frac{0}{4}$
$x^{2}+y^{2}-2 x+3 y-\frac{3}{4}=0$

Тепер, коли ми маємо загальну форму для кола, де обидва терміни ступеня два мають провідний коефіцієнт$1$, ми можемо використовувати кроки для перезапису його в стандартному вигляді. Почніть з додавання$\frac{3}{4}$ до обох сторін і групи змінних, які є однаковими.

$\left(x^{2}-2 x+\_\_\_\right)+\left(y^{2}+3 y+\_\_\_\right)=\frac{3}{4}$

Далі завершити квадрат для обох угруповань. $\left(\frac{-2}{2}\right)^{2}=(-1)^{2}=1$Використовується для першого угруповання і$\left(\frac{3}{2}\right)^{2}=\frac{9}{4}$ для другого групування.

$\begin{aligned}\color{black}{\left(x^{2}-2 x\color{Cerulean}{+1}\right)+}\color{black}{\left(y^{2}+3 y\color{OliveGreen}{+\frac{9}{4}}\right)}&=\frac{3}{4}\color{Cerulean}{+1}\color{OliveGreen}{+\frac{9}{4}} \\ (x-1)^{2}+\left(y+\frac{3}{2}\right)^{2} &=\frac{16}{4} \\ (x-1)^{2}+\left(y+\frac{3}{2}\right)^{2}&=4\end{aligned}$

Відповідь:

Центр:$\left(1,-\frac{3}{2}\right)$; радіус дії:$r=2$

Підсумовуючи, для перетворення зі стандартної форми в загальну форму ми множимо, а для перетворення із загальної форми в стандартну форму ми заповнюємо квадрат.

Малюнок$\PageIndex{12}$

Вправа$\PageIndex{2}$:

Графік:$x^{2}+y^{2}-10 x+2 y+21=0$.

Відповідь:

Малюнок$\PageIndex{13}$

www.youtube.com/В/MS8NQS6S

Ключові винос

• Графік кола повністю визначається його центром і радіусом.
• Стандартною формою рівняння кола є$(x-h)^{2}+(y-k)^{2}=r^{2}$. Центр є$(h,k)$ і радіус вимірює$r$ одиниці.
• Для графіка кола позначте$r$ точки вгору, вниз, вліво і праворуч від центру. Намалюйте коло через ці чотири точки.
• Якщо рівняння кола задано в загальному вигляді$x^{2}+y^{2}+c x+d y+e=0$, згрупуйте терміни з однаковими змінними і заповніть квадрат для обох групувань. Це призведе до стандартної форми, з якої ми зможемо зчитувати центр і радіус кола.
• Ми визнаємо рівняння кола, якщо воно квадратичне в обох$x$ і$y$ де коефіцієнт квадратних членів однаковий.

Вправа$\PageIndex{3}$

Визначте центр і радіус за даними рівняння окружності в стандартному вигляді.

1. $(x-5)^{2}+(y+4)^{2}=64$
2. $(x+9)^{2}+(y-7)^{2}=121$
3. $x^{2}+(y+6)^{2}=4$
4. $(x-1)^{2}+y^{2}=1$
5. $(x+1)^{2}+(y+1)^{2}=7$
6. $(x+2)^{2}+(y-7)^{2}=8$

Відповідь

1. Центр:$(5, −4)$; радіус дії:$r = 8$

3. Центр:$(0, −6)$; радіус дії:$r = 2$

5. Центр:$(−1, −1)$; радіус дії:$r = \sqrt{7}$

Вправа$\PageIndex{4}$

Визначте стандартну форму для рівняння окружності, заданої її центром і радіусом.

1. Центр$(5, 7)$ з радіусом$r = 7$.
2. Центр$(−2, 8)$ з радіусом$r = 5$.
3. Центр$(6, −11)$ з радіусом$r = \sqrt{2}$.
4. Центр$(−4, −5)$ з радіусом$r = \sqrt{6}$.
5. Центр$(0, −1)$ з радіусом$r = 2\sqrt{5}$.
6. Центр$(0, 0)$ з радіусом$r = 3\sqrt{10}$.

Відповідь

1. $(x-5)^{2}+(y-7)^{2}=49$

3. $(x-6)^{2}+(y+11)^{2}=2$

5. $x^{2}+(y+1)^{2}=20$

Вправа$\PageIndex{5}$

Графік.

1. $(x-1)^{2}+(y-2)^{2}=9$
2. $(x+3)^{2}+(y-3)^{2}=25$
3. $(x-2)^{2}+(y+6)^{2}=4$
4. $(x+6)^{2}+(y+4)^{2}=36$
5. $x^{2}+(y-4)^{2}=1$
6. $(x-3)^{2}+y^{2}=4$
7. $x^{2}+y^{2}=12$
8. $x^{2}+y^{2}=8$
9. $(x-7)^{2}+(y-6)^{2}=2$
10. $(x+2)^{2}+(y-5)^{2}=5$
11. $(x+3)^{2}+(y-1)^{2}=18$
12. $(x-3)^{2}+(y-2)^{2}=15$

Відповідь

1.

Малюнок$\PageIndex{14}$

3.

Малюнок$\PageIndex{15}$

5.

Малюнок$\PageIndex{16}$

7.

Малюнок$\PageIndex{17}$

9.

Малюнок$\PageIndex{18}$

11.

Малюнок$\PageIndex{19}$

Вправа$\PageIndex{6}$

Знайдіть$x$ - і$y$ -перехоплює.

1. $(x-1)^{2}+(y-2)^{2}=9$
2. $(x+5)^{2}+(y-3)^{2}=25$
3. $x^{2}+(y-4)^{2}=1$
4. $(x-3)^{2}+y^{2}=18$
5. $x^{2}+y^{2}=50$
6. $x^{2}+(y+9)^{2}=20$
7. $(x-4)^{2}+(y+5)^{2}=10$
8. $(x+10)^{2}+(y-20)^{2}=400$

Відповідь

1. $x$-перехоплює:$(1 \pm \sqrt{5}, 0)$;$y$ -перехоплює:$(0,2 \pm 2 \sqrt{2})$

3. $x$-перехоплює: немає;$y$ -перехоплює:$(0, 3), (0, 5)$

5. $x$-перехоплює:$(\pm 5 \sqrt{2}, 0)$;$y$ -перехоплює:$(0, \pm 5 \sqrt{2})$

7. $x$-перехоплює: немає;$y$ -перехоплює: ніхто

Вправа$\PageIndex{7}$

Знайдіть рівняння кола.

1. Коло з центром,$(1, −2)$ що проходить через$(3, −4)$.
2. Коло з центром,$(−4, −1)$ що проходить через$(0, −3)$.
3. Коло, діаметр якого визначається$(5, 1)$ і$(−1, 7)$.
4. Коло, діаметр якого визначається$(−5, 7)$ і$(−1, −5)$.
5. Коло з центром$(5, −2)$ і площею$9π$ квадратних одиниць.
6. Коло з центром$(−8, −3)$ і окружністю$12π$ квадратних одиниць.
7. Знайдіть площу кола за допомогою рівняння$(x+12)^{2} \pm(x-5)^{2}=7$.
8. Знайдіть окружність кола за допомогою рівняння$(x+1)^{2}+(y+5)^{2}=8$.

Відповідь

1. $(x-1)^{2}+(y+2)^{2}=8$

3. $(x-2)^{2}+(y-4)^{2}=18$

5. $(x-5)^{2}+(y+2)^{2}=9$

7. $7π$квадратні одиниці

Вправа$\PageIndex{8}$

Перепишіть в стандартній формі і графі.

1. $x^{2}+y^{2}+4 x-2 y-4=0$
2. $x^{2}+y^{2}-10 x+2 y+10=0$
3. $x^{2}+y^{2}+2 x+12 y+36=0$
4. $x^{2}+y^{2}-14 x-8 y+40=0$
5. $x^{2}+y^{2}+6 y+5=0$
6. $x^{2}+y^{2}-12 x+20=0$
7. $x^{2}+y^{2}+8 x+12 y+16=0$
8. $x^{2}+y^{2}-20 x-18 y+172=0$
9. $4 x^{2}+4 y^{2}-4 x+8 y+1=0$
10. $9 x^{2}+9 y^{2}+18 x+6 y+1=0$
11. $x^{2}+y^{2}+4 x+8 y+14=0$
12. $x^{2}+y^{2}-2 x-4 y-15=0$
13. $x^{2}+y^{2}-x-2 y+1=0$
14. $x^{2}+y^{2}-x+y-\frac{1}{2}=0$
15. $4 x^{2}+4 y^{2}+8 x-12 y+5=0$
16. $9 x^{2}+9 y^{2}+12 x-36 y+4=0$
17. $2 x^{2}+2 y^{2}+6 x+10 y+9=0$
18. $9 x^{2}+9 y^{2}-6 x+12 y+4=0$

Відповідь

1. $(x+2)^{2}+(y-1)^{2}=9$;

Малюнок$\PageIndex{20}$

3. $(x+1)^{2}+(y+6)^{2}=1$;

Малюнок$\PageIndex{21}$

5. $x^{2}+(y+3)^{2}=4$;

Малюнок$\PageIndex{22}$

7. $(x+4)^{2}+(y+6)^{2}=36$;

Малюнок$\PageIndex{23}$

9. $\left(x-\frac{1}{2}\right)^{2}+(y+1)^{2}=1$;

Малюнок$\PageIndex{24}$

11. $(x+2)^{2}+(y-4)^{2}=6$;

Малюнок$\PageIndex{25}$

13. $\left(x-\frac{1}{2}\right)^{2}+(y-1)^{2}=\frac{1}{4}$;

Малюнок$\PageIndex{26}$

15. $(x+1)^{2}+\left(y-\frac{3}{2}\right)^{2}=2$;

Малюнок$\PageIndex{27}$

17. $\left(x+\frac{3}{2}\right)^{2}+\left(y+\frac{5}{2}\right)^{2}=4$;

Малюнок$\PageIndex{28}$

Вправа$\PageIndex{9}$

Задано коло в загальному вигляді, визначають перехоплення.

1. $x^{2}+y^{2}-5 x+3 y+6=0$
2. $x^{2}+y^{2}+x-2 y-7=0$
3. $x^{2}+y^{2}-6 y+2=2$
4. $x^{2}+y^{2}-6 x-8 y+5=0$
5. $2 x^{2}+2 y^{2}-3 x-9=0$
6. $3 x^{2}+3 y^{2}+8 y-16=0$
7. Визначте площу кола, рівняння якої є$x^{2}+y^{2}-2 x-6 y-35=0$.
8. Визначте площу кола, рівняння якої є$4 x^{2}+4 y^{2}-12 x-8 y-59=0$.
9. Визначте окружність кола, рівняння якого є$x^{2}+y^{2}-5 x+1=0$.
10. Визначте окружність кола, рівняння якого є$x^{2}+y^{2}+5 x-2 y+3=0$.
11. Знайти загальний вигляд рівняння окружності з центром при$(−3, 5)$ проходженні$(1, −2)$.
12. Знайти загальний вигляд рівняння окружності з центром при$(−2, −3)$ проходженні$(−1, 3)$.

Відповідь

1. $x$-перехоплює:$(2, 0), (3, 0)$;$y$ -перехоплює: немає

3. $x$-перехоплює:$(0, 0)$;$y$ -перехоплює:$(0, 0), (0, 6)$

5. $x$-перехоплює:$(−\frac{3}{2}, 0), (3, 0)$;$y$ -перехоплює:$\left(0, \pm \frac{3 \sqrt{2}}{2}\right)$

7. $45π$квадратні одиниці

9. $π\sqrt{21}$одиниць

11. $x^{2}+y^{2}+6 x-10 y-31=0$

Вправа$\PageIndex{10}$

З огляду на графік кола, визначають його рівняння в загальному вигляді.

1.

Малюнок$\PageIndex{29}$

2.

Малюнок$\PageIndex{30}$

3.

Малюнок$\PageIndex{31}$

4.

Малюнок$\PageIndex{32}$

Відповідь

1. $x^{2}+y^{2}-6 x+10 y+18=0$

3. $x^{2}+y^{2}+2 y=0$

Вправа$\PageIndex{11}$

1. Центр кола є частиною графіка? Поясніть.
2. Складіть своє коло, напишіть його в загальному вигляді, і зробіть графік.
3. Поясніть, як ми можемо визначити різницю між рівнянням параболи в загальному вигляді і рівнянням кола в загальному вигляді. Наведемо приклад.
4. Чи всі кола мають перехоплення? Які можливі номери перехоплень? Проілюструйте своє пояснення графіками.

Відповідь

1. Відповідь може відрізнятися

3. Відповідь може відрізнятися

Виноски

⁸ Коло - це сукупність точок на площині, які лежать на фіксованій відстані від заданої точки, яка називається центром.

⁹ Фіксована відстань від центру кола до будь-якої точки на колі.

¹⁰ Довжина відрізка лінії, що проходить через центр кола, кінцеві точки якого знаходяться на колі.

¹¹ Рівняння кола записано у вигляді$(x-h)^{2}+(y-k)^{2}=r^{2}$ де$(h, k)$ центр і$r$ є радіусом.

¹² Коло, центроване на початку з радіусом$1$; його рівняння є$x^{2} + y^{2} = 1$.

¹³ Рівняння кола записано у вигляді$x^{2} + y^{2} + cx + dy + e = 0$.