8.1: Відстань, середина та парабола

Цілі навчання

• Застосуйте формули відстані та середини.
• Графік параболи, використовуючи її рівняння, наведене в стандартній з.
• Визначити стандартну форму для рівняння параболи заданої загальної форми.

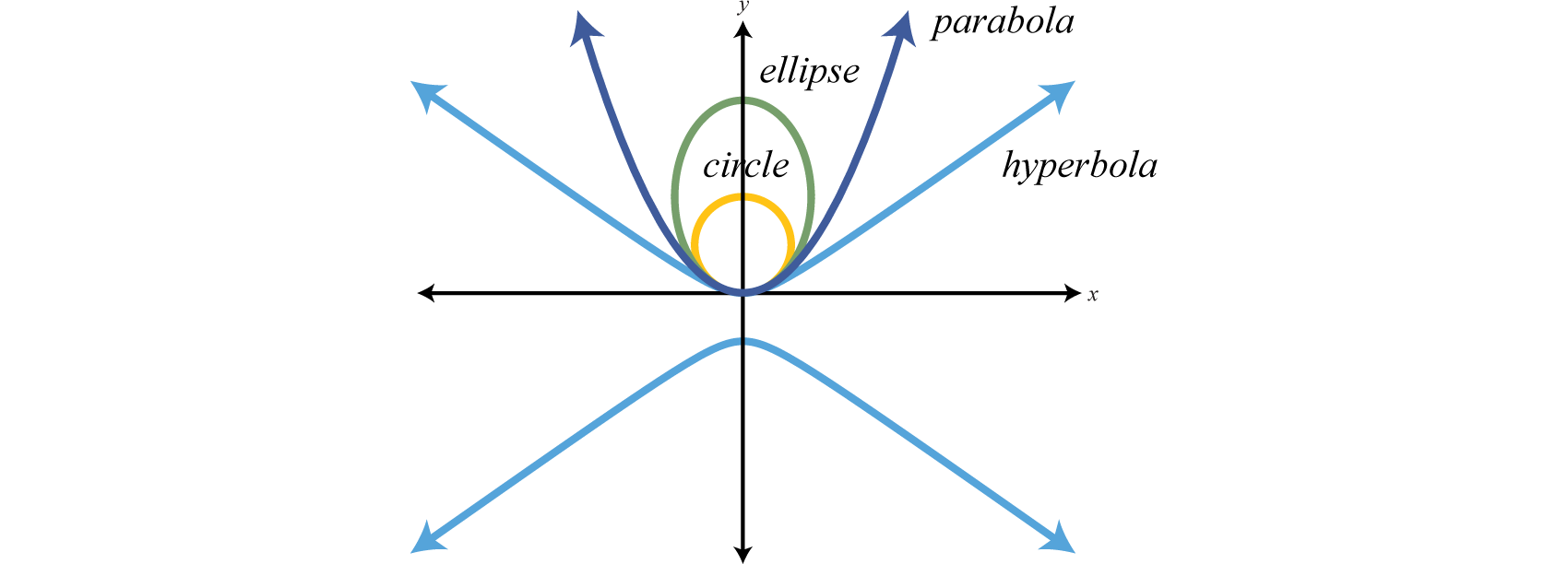
Конічні перерізи

Конічний перетин ¹ - це крива, отримана від перетину прямого кругового конуса і площини. Конічні перерізи - це парабола, коло, еліпс та гіпербола.

Малюнок$\PageIndex{1}$

Мета полягає в тому, щоб накидати ці графіки на прямокутній координатній площині.

Малюнок$\PageIndex{2}$

Формули відстані та середини

Починаємо з огляду формули відстані ². За двома точками$(x_{1},  y_{1})$ і$( x_{2},  y_{2})$ в прямокутній координатній площині відстань$d$ між ними задається за формулою відстані,

$d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}$

Крім того, точка, яка перетинає відрізок лінії, утворений цими двома точками, називається середньою точкою ³ і задається формулою,

$\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)$

Середина - це впорядкована пара, утворена середнім значенням$x$ -значень та середнім значенням$y$ -значень.

Приклад$\PageIndex{1}$:

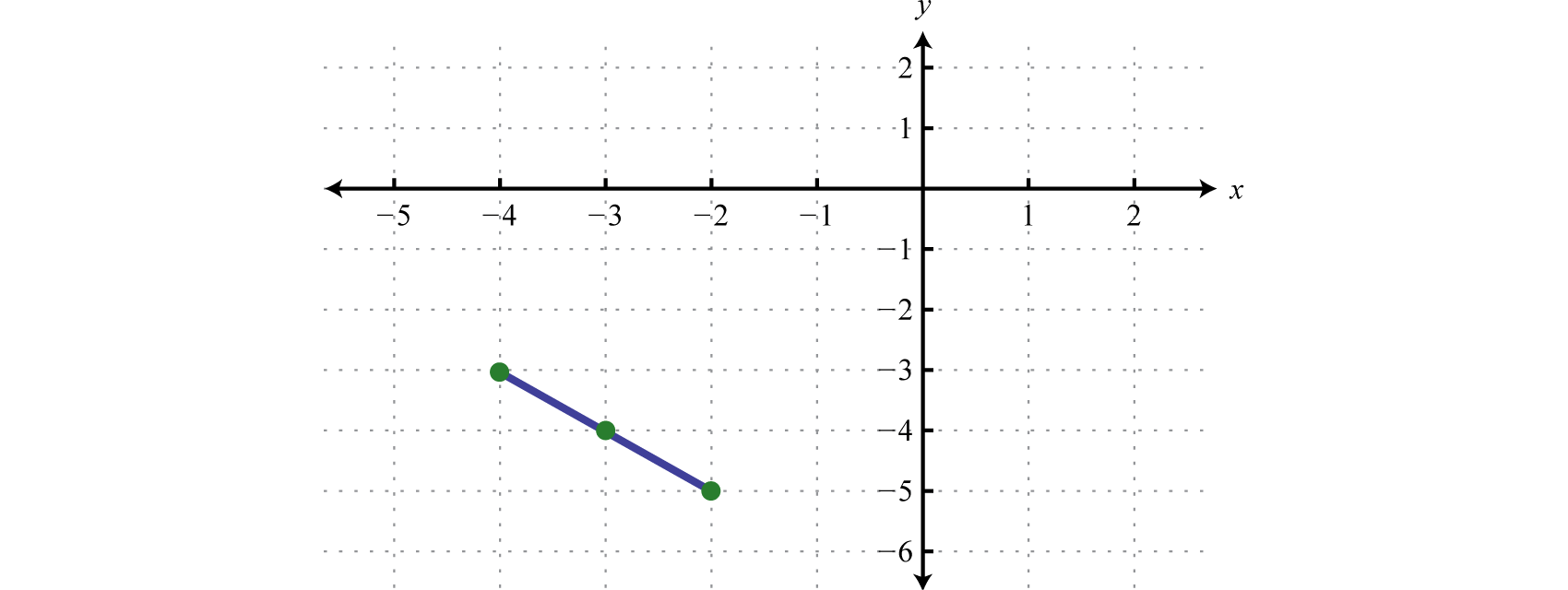
Дано$(−2,−5)$ і$(−4,−3)$ обчислюють відстань і середину між ними.

Рішення:

В цьому випадку ми будемо використовувати формули з наступними пунктами:

$\begin{array}{c c}{\left(x_{1}, y_{1}\right)} &{\left(x_{2}, y_{2}\right)} \\ {\color{black}{(\color{Cerulean}{-2}\color{black}{,}\color{OliveGreen}{-5})}}&{\color{black}{(\color{Cerulean}{-4}\color{black}{,}\color{OliveGreen}{-3})}}\end{array}$

Хорошою практикою є включення формули в загальному вигляді перед підстановкою значень для змінних; це покращує читабельність і зменшує ймовірність помилок.

$\begin{aligned} d &=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}} \\ &=\sqrt{[\color{Cerulean}{-4}\color{black}{-}(\color{Cerulean}{-2}\color{black}{)}]^{2}+[\color{OliveGreen}{-3}\color{black}{-}(\color{OliveGreen}{-5}\color{black}{)}]^{2}} \\ &=\sqrt{(-4+2)^{2}+(-3+5)^{2}} \\ &=\sqrt{(-2)^{2}+(2)^{2}} \\ &=\sqrt{4+4} \\ &=\sqrt{8} \\ &=2 \sqrt{2} \end{aligned}$

Далі визначаємо середню точку.

$\begin{aligned}\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right) &=\left(\frac{-2+(-4)}{2}, \frac{-5+(-3)}{2}\right) \\ &=\left(\frac{-6}{2}, \frac{-8}{2}\right) \\ &=(-3,-4) \end{aligned}$

Розміщуючи ці точки на графіку, який ми маємо,

Малюнок$\PageIndex{3}$

Відповідь:

Відстань:$2\sqrt{2}$ одиниці виміру; середина:$(−3,−4)$

Приклад$\PageIndex{2}$:

Діаметр кола визначається двома точками$(−1,2)$ і$(1,−2)$. Визначте радіус кола і використовуйте його для обчислення його площі.

Рішення

Знайдіть діаметр, використовуючи формулу відстані.

$\begin{aligned} d &=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}} \\ &=\sqrt{\left[\color{Cerulean}{1}\color{black}{-}(\color{Cerulean}{-1}\color{black}{)}^{2}+(\color{OliveGreen}{-2}\color{black}{-}\color{OliveGreen}{2}\color{black}{)}^{2}\right.} \\ &=\sqrt{[2)^{2}+(-4)^{2}} \\&=\sqrt{4+16} \\&=\sqrt{20} \\ &=2 \sqrt{5} \end{aligned}$

Нагадаємо, що радіус кола дорівнює половині діаметра кола. Тому якщо$d=2\sqrt{5}$ одиниці, то

$r=\frac{d}{2}=\frac{2 \sqrt{5}}{2}=\sqrt{5}$

Площа кола задається за формулою$A=πr^{2}$ і ми маємо

$\begin{aligned} A &=\pi(\sqrt{5})^{2} \\ &=\pi \cdot 5 \\ &=5 \pi \end{aligned}$

Площа вимірюється в квадратних одиницях.

Відповідь:

Радіус:$\sqrt{5}$ одиниці; площа:$5π$ квадратні одиниці

Вправа$\PageIndex{1}$

Дано$(0,0)$ і$(9,−3)$ обчислюють відстань і середину між ними.

Відповідь

Відстань:$3\sqrt{10}$ одиниці виміру; середина:$\left(\frac{9}{2},-\frac{3}{2}\right)$

www.youtube.com/В/6 ККК НакоПВ 0

Парабола

Парабола ⁴ - це множина точок на площині, рівновіддаленій від заданої лінії, яка називається директрисою, і точка не на прямій, яка називається фокусом. Іншими словами, якщо дана$L$ пряма директриса, а точка$F$ фокусування, то$(x,y)$ це точка на параболі, якщо найкоротша відстань від неї до фокуса і від неї до лінії дорівнює як на малюнку нижче:

Малюнок$\PageIndex{4}$

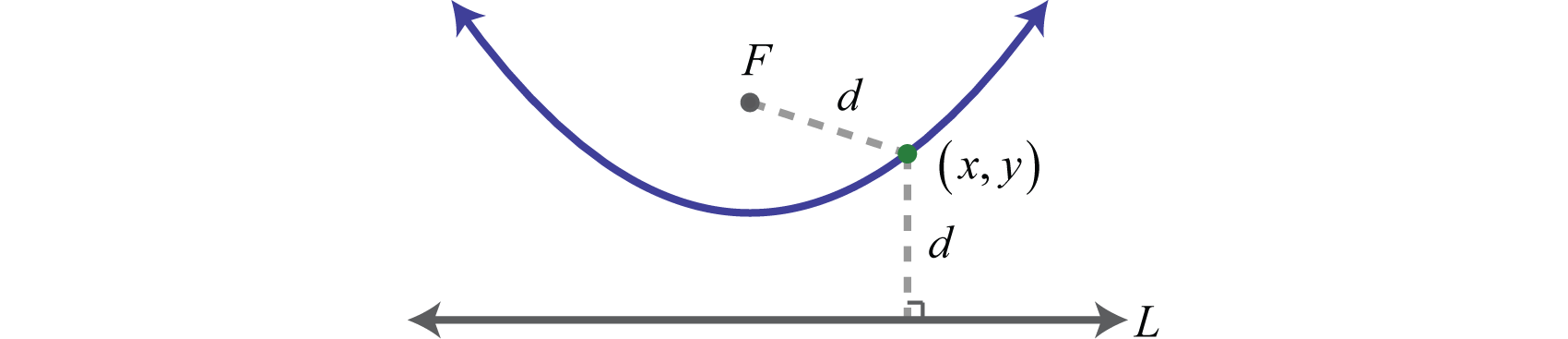
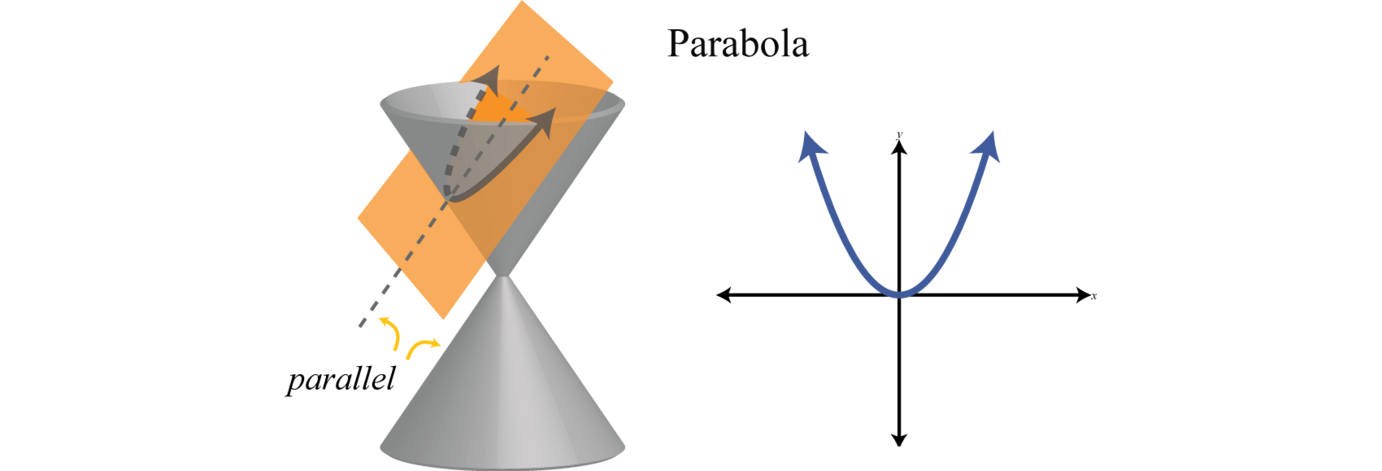
Вершина параболи - точка, де найкоротша відстань до директриси знаходиться на мінімумі. Крім того, парабола утворюється перетином конуса з косою площиною, яка паралельна стороні конуса:

Малюнок$\PageIndex{5}$

Нагадаємо, що графік квадратичної функції, поліноміальної функції 2 ступеня, є параболічним. Ми можемо записати рівняння параболи в загальному вигляді ⁵ або можемо записати рівняння параболи в стандартному вигляді ⁶:

$\begin{array}{cc}{\color{Cerulean} { General\: Form }} & {\color{Cerulean} { Standard\: Form }} \\ {y=a x^{2}+b x+c} & {y=a(x-h)^{2}+k}\end{array}$

Обидві форми корисні при визначенні загальної форми графіка. Однак в цьому розділі мова піде про отримання стандартної форми, яку часто називають вершинної формою ⁷. Задано квадратичну функцію в стандартному вигляді, вершина дорівнює$(h,k)$. Щоб побачити, що це так, розгляньте графіки з$y=(x+3)^{2}+2$ використанням перетворень.

$\begin{array}{ll}{y=x^{2}} & {\color{Cerulean} { Basic\: squaring\: function. }} \\ {y=(x+3)^{2}} & {\color{Cerulean} {Horizontal\: shift\: left\: 3\: units. }} \\ {y=(x+3)^{2}+2} & {\color{Cerulean} { Vertical\: shift\: up\: 2\: units. }}\end{array}$

Використовуйте ці переклади для ескізу графіка,

Малюнок$\PageIndex{6}$

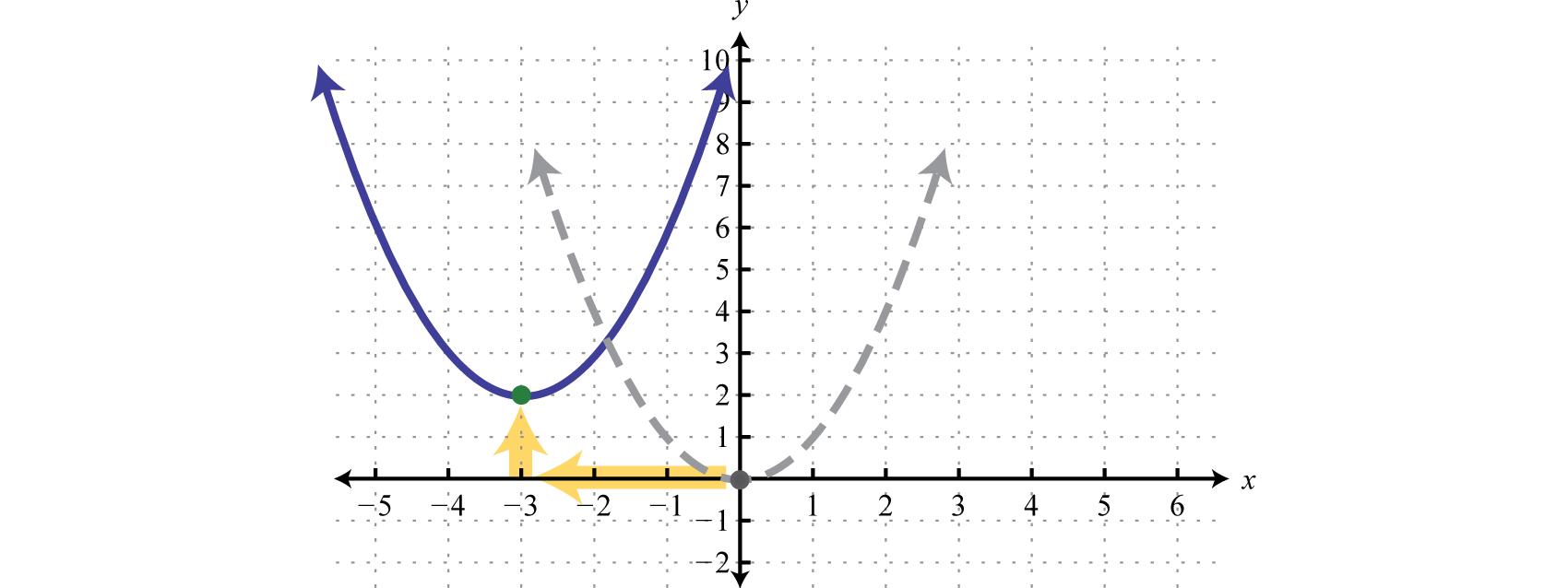
Тут ми бачимо, що вершина є$(−3,2)$. Це можна визначити безпосередньо з рівняння в стандартній формі,

$\begin{array}{l}{y=a(x-h)^{2}\:+\:\:k} \\\color{Cerulean}{\quad\quad\quad\quad\:\downarrow \quad\quad\: \color{Cerulean}{\downarrow}} \\ {y=[x-(-3)]^{2}+2}\end{array}$

Написано в такому вигляді ми бачимо, що вершина є$(−3,2)$. Однак рівняння зазвичай не дається в стандартній формі. Перетворення загальної форми в стандартну форму, шляхом заповнення квадрата, є основним процесом, за допомогою якого ми накидаємо всі конічні перерізи.

Приклад$\PageIndex{3}$:

Перепишіть рівняння в стандартному вигляді і визначте вершину його графа:$y=x^{2}-8 x+15$.

Рішення

Почніть з звільнення місця для постійного терміну, який завершує квадрат.

$\begin{aligned} y &=x^{2}-8 x+15 \\ &=x^{2}-8 x \color{Cerulean}{+ \_\_\_ }\color{black}{+}15 \color{Cerulean}{- \_\_\_}\end{aligned}$

Ідея полягає в тому, щоб додати і відняти значення, яке завершує квадрат$\left(\frac{b}{2}\right)^{2}$, а потім коефіцієнт. В цьому випадку додаємо і віднімаємо$\left(\frac{b}{2}\right)^{2}=\left(\frac{-8}{2}\right)^{2}=(-4)^{2}=16$.

$\begin{aligned} y &=x^{2}-8 x+15 \quad\quad\quad\quad\quad\quad\:\:\color{Cerulean}{Add\:and\:subtract\:16.} \\ &=\color{black}{\left(x^{2}-8 x\color{Cerulean}{+16}\right)}+15\color{Cerulean}{-16}\quad\color{Cerulean}{Factor.} \\ &=(x-4)(x-4)-1 \\ &=(x-4)^{2}-1 \end{aligned}$

Додавання та віднімання одного і того ж значення всередині виразу не змінює його. Робити це еквівалентно додаванню$0$. Як тільки рівняння буде в такому вигляді, ми можемо легко визначити вершину.

$\begin{array}{l}{y=a(x-h)^{2}\:+\:k} \\\quad\quad\quad\quad\:\color{Cerulean}{\downarrow}\quad\quad\color{Cerulean}{\downarrow} \\ {y=(x\:-\:4)^{2}+(-1)}\end{array}$

Тут ми маємо переклад на потрібні$4$ одиниці і вниз$1$ одиниці. Значить,$h = 4$ і$k = −1$.

Відповідь:

$y=(x-4)^{2}-1$; вершина:$(4,−1)$

Якщо є провідний коефіцієнт$1$, крім, то почніть з факторингу цього провідного коефіцієнта з перших двох членів триноміала.

Приклад$\PageIndex{4}$:

Перепишіть рівняння в стандартному вигляді і визначте вершину графа:$y=-2 x^{2}+12 x-16$.

Рішення

Оскільки$a=−2$, враховуйте це з перших двох термінів, щоб завершити квадрат. Залиште місце всередині дужок, щоб додати і відняти значення, яке завершує квадрат.

$\begin{aligned} y &=-2 x^{2}+12 x-16 \\ &=-2\color{black}{\left(x^{2}-6 x\color{Cerulean}{+\_\_\_-\_\_\_}\right)-}16\end{aligned}$

Тепер використовуйте$−6$ для визначення значення, яке завершує квадрат. В даному випадку,$\left(\frac{b}{2}\right)^{2}=\left(\frac{-6}{2}\right)^{2}=(-3)^{2}=9$. Додайте і відніміть$9$ і коефіцієнт наступним чином:

$\begin{aligned} y &=-2 x^{2}+12 x-16 \\ &=-2\color{black}{\left(x^{2}-6 x\color{Cerulean}{+\_\_\_-\_\_\_}\right)}-16\quad\color{Cerulean}{Add\:and\:subtract\:9.} \\ &=-2\color{black}{\left(x^{2}-6 x\color{Cerulean}{+9-9}\right)-}16\quad\quad\:\:\quad\color{Cerulean}{Factor.} \\ &=-2[(x-3)(x-3)-9]-16\ \\ &=-2\left[(x-3)^{2}-9\right]-16\quad\quad\quad\quad\:\:\color{Cerulean}{Distribute\:the\:-2.} \\ &=-2(x-3)^{2}+18-16 \\ &=-2(x-3)^{2}+2 \end{aligned}$

У такому вигляді ми легко можемо визначити вершину.

$\begin{array}{l}{y=a\:(x\:-\:h)^{2}+k}\\\quad\quad\quad\quad\quad\color{Cerulean}{\downarrow}\quad\:\:\color{Cerulean}{\downarrow} \\ {y=-2(x-3)^{2}+2}\end{array}$

Ось$h = 3$ і$k = 2$.

Відповідь:

y=−2 (x−3) 2+2y=−2 (x−3) 2+2; вершина: (3,2) (3,2)

Використовуйте як загальну форму, так і стандартну форму під час ескізу графіка параболи.

Приклад$\PageIndex{5}$:

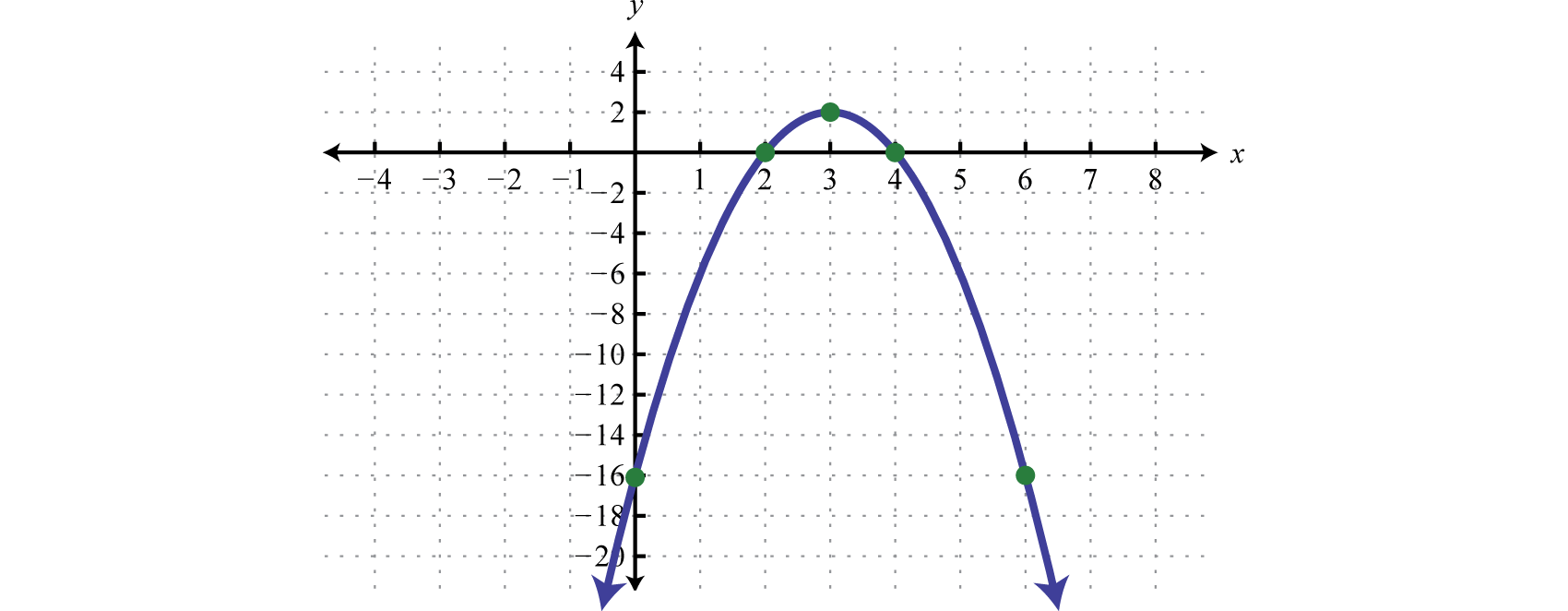
Графік:$y=-2 x^{2}+12 x-16$.

Рішення:

З попереднього прикладу ми маємо дві еквівалентні форми цього рівняння,

$\begin{array}{c} {\color{Cerulean}{General\:Form}}&{\color{Cerulean}{Standard\:Form}}\\{y=-2 x^{2}+12 x-16}&{ y=-2(x-3)^{2}+2}\end{array}$

Нагадаємо, що якщо$a>0$ провідний коефіцієнт парабола відкривається вгору і якщо$a<0$ парабола відкривається вниз. В цьому випадку$a=−2$ і робимо висновок, парабола відкривається вниз. Використовуйте загальну форму для визначення$y$ -перехоплення. Коли$x=0$ ми бачимо, що$y$ -перехоплення є$(0,−16)$. З рівняння в стандартному вигляді ми бачимо, що вершина є$(3,2)$. Щоб знайти$x$ -intercept, ми могли б використовувати будь-яку форму. У цьому випадку ми будемо використовувати стандартну форму для визначення$x$ -values де$y=0$,

$\begin{aligned} y &=-2(x-3)^{2}+2\quad\color{Cerulean}{Set\:y=0\:and\:solve.} \\ 0 &=-2(x-3)^{2}+2 \\-2 &=-2(x-3)^{2} \\ & 1=(x-3)^{2}\quad\quad\quad\:\:\color{Cerulean}{Apply\:the\:square\:root\:property.} \\ \pm 1 &=x-3 \\ 3 \pm 1 &=x \end{aligned}$

Ось$x=3−1=2$ або,$x=3+1=4$ отже,$x$ -перехоплення є$(2,0)$ і$(4,0)$. Використовуйте цю інформацію для ескізу графіка.

Відповідь:

Малюнок$\PageIndex{7}$

Поки ми малювали параболи, які відкриваються вгору або вниз, оскільки ці графіки представляють функції. На цьому етапі ми розширюємо наше дослідження, щоб включити параболи, які відкриваються праворуч або ліворуч. Якщо взяти рівняння, яке визначає параболу в попередньому прикладі,

$y=-2(x-3)^{2}+2$

і перемикають значення x і y, які ми отримуємо

$x=-2(y-3)^{2}+2$

Це створює новий графік з симетрією навколо лінії$y=x$.

Малюнок$\PageIndex{8}$

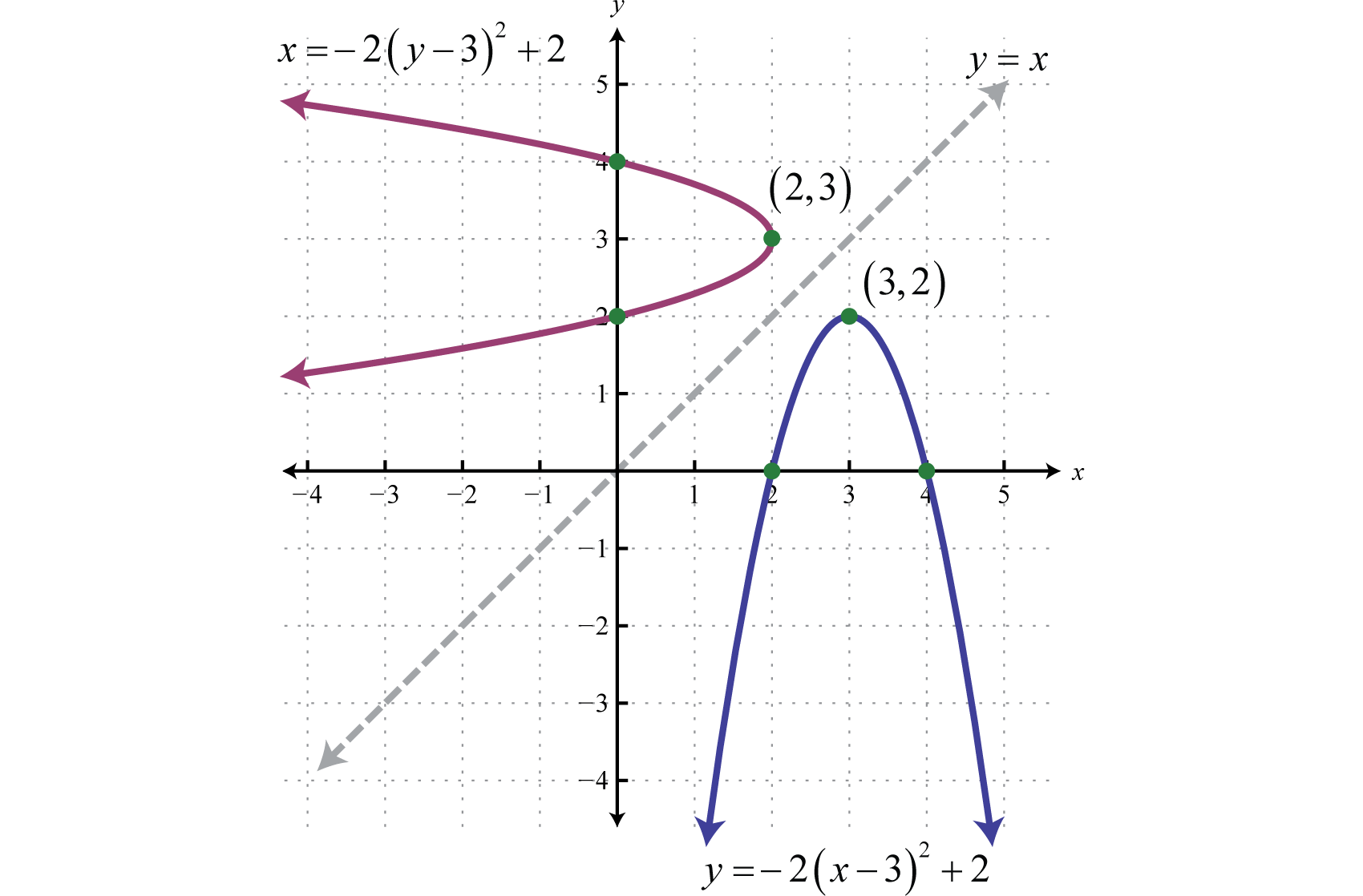
Зверніть увагу, що отриманий графік не є функцією. Однак він має ту саму загальну параболічну форму, яка відкривається ліворуч. Ми можемо розпізнати рівняння парабол, які відкриваються вліво чи вправо, помітивши, що вони квадратичні$y$ замість$x$. Графічні параболи, які відкриваються вліво чи вправо, схоже на графічні параболи, які відкриваються вгору та вниз. Загалом, у нас є

Малюнок$\PageIndex{9}$

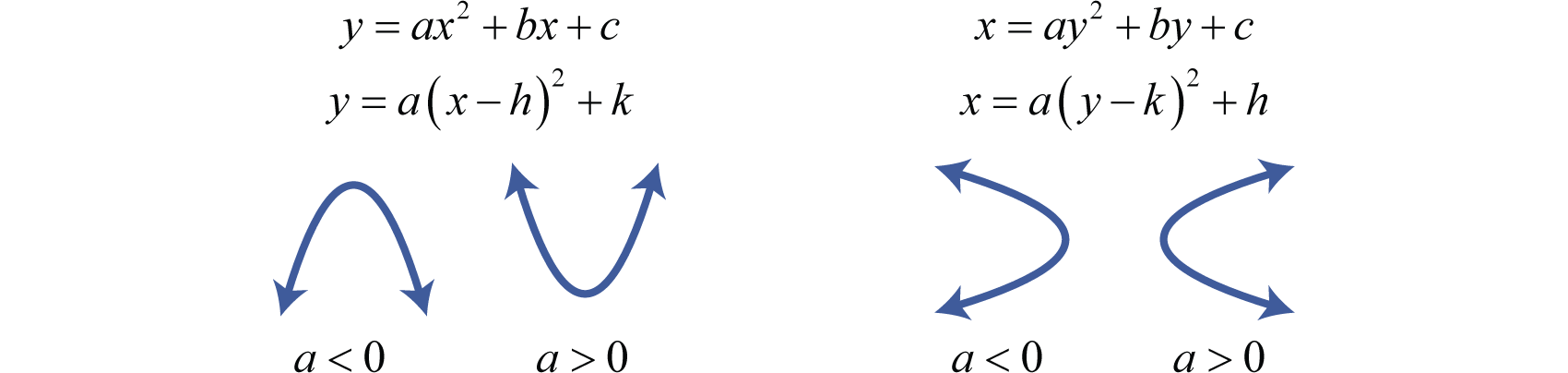
У всіх випадках вершина є$(h,k)$. Подбайте про розміщення$h$ і$k$ в кожному рівнянні.

Приклад$\PageIndex{6}$:

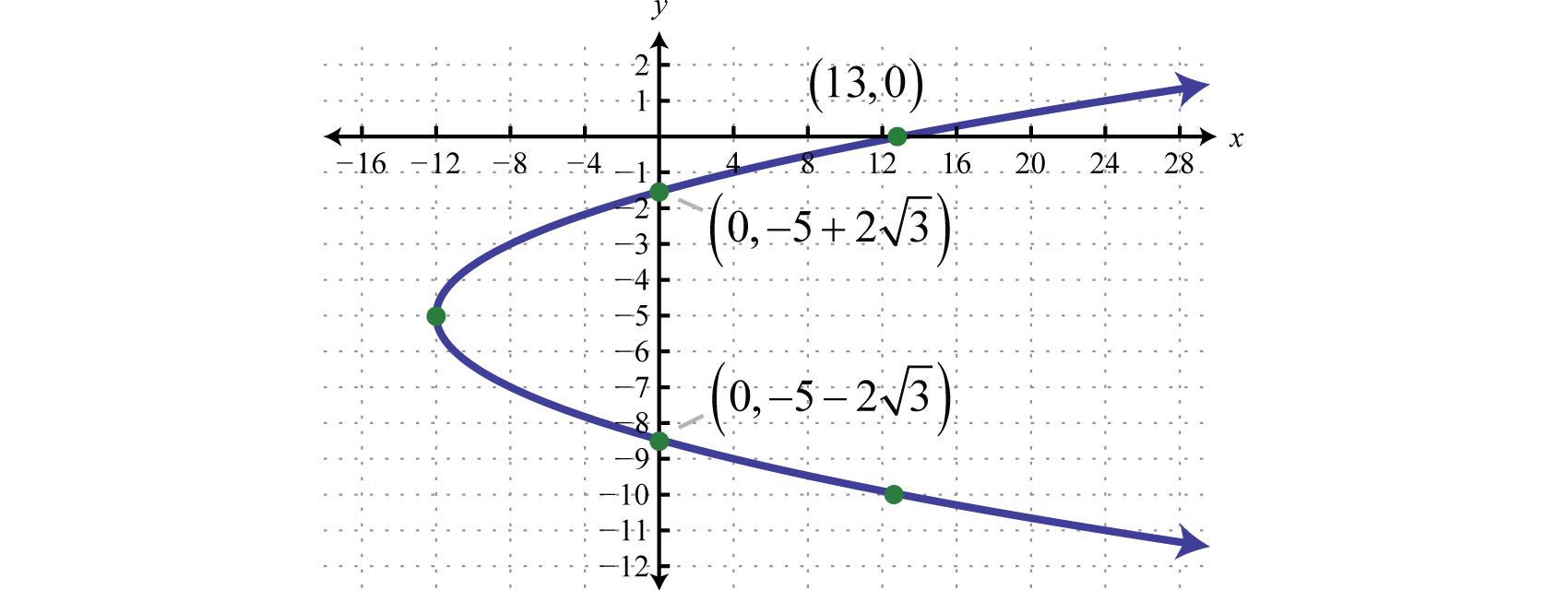
Графік:$x=y^{2}+10 y+13$.

Рішення

Оскільки коефіцієнт$y^{2}$ позитивний$a=1$, то робимо висновок, що графік - це парабола, яка відкривається вправо. Крім того, коли$y=0$ зрозуміло, що$x=13$ і, отже,$x$ -перехоплення є$(13,0)$. Доповніть квадрат, щоб отримати стандартну форму. Тут ми будемо додавати і віднімати$\left(\frac{b}{2}\right)^{2}=\left(\frac{10}{2}\right)^{2}=(5)^{2}=25$.

$\begin{aligned} x &=y^{2}+10 y+13 \\ &=y^{2}+10 y\color{Cerulean}{+25-25}\color{black}{+}13 \\ &=(y+5)(y+5)-12 \\ &=(y+5)^{2}-12 \end{aligned}$

Тому

$\begin{array}{l}{x=a\:(y\:-\:k)^{2}\:\:\:+\:\:\:\:h}\\ \quad\quad\quad\quad\quad\color{Cerulean}{\downarrow}\quad\quad\quad\color{Cerulean}{\downarrow} \\ {x=(y-(-5))^{2}+(-12)}\end{array}$

З цього ми бачимо, що вершина$(h,k)=(−12,−5)$. Далі використовуйте стандартну форму, щоб знайти$y$ -перехоплення за допомогою установки$x=0$.

$\begin{aligned} x &=(y+5)^{2}-12 \\ 0 &=(y+5)^{2}-12 \\ 12 &=(y+5)^{2} \\ \pm \sqrt{12} &=y+5 \\ \pm 2 \sqrt{3} &=y+5 \\-5 \pm 2 \sqrt{3} &=y \end{aligned}$

$y$-перехоплює є$(0,-5-2 \sqrt{3})$ і$(0,-5+2 \sqrt{3})$. Використовуйте цю інформацію для ескізу графіка.

Відповідь

Малюнок$\PageIndex{10}$

Приклад$\PageIndex{7}$

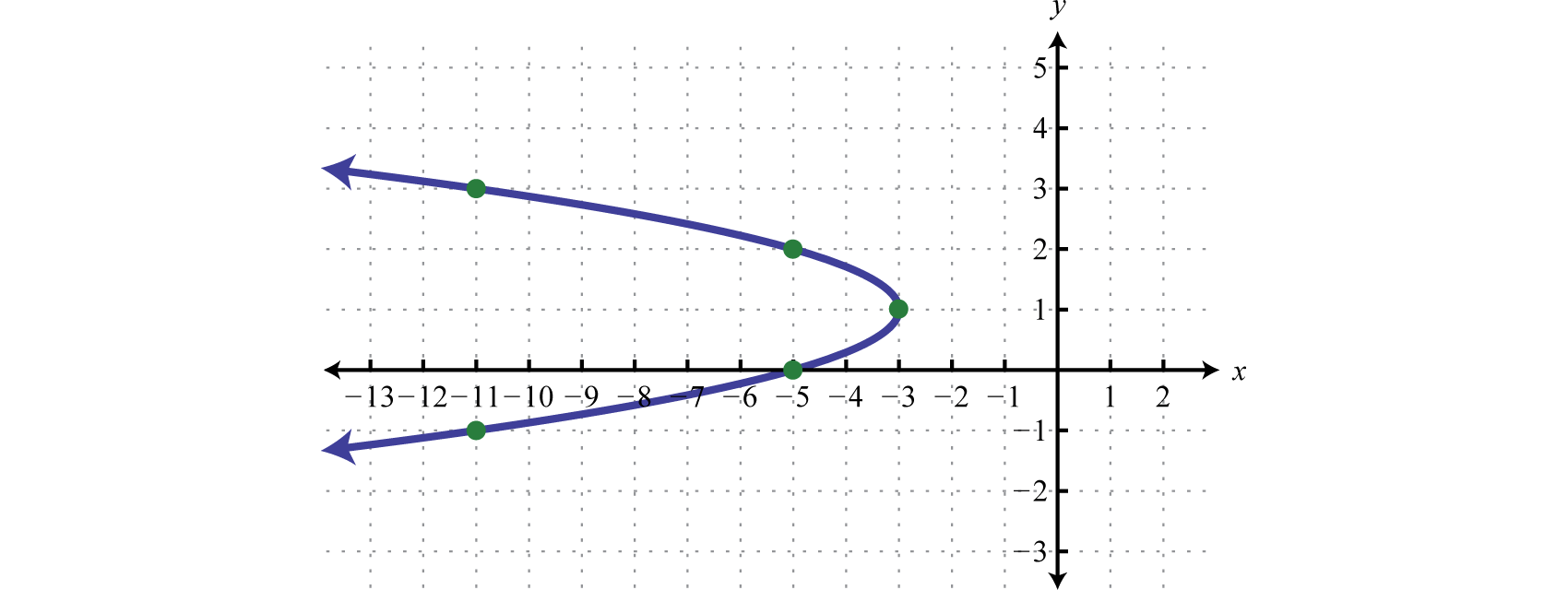
Графік:$x=-2 y^{2}+4 y-5$.

Рішення

Оскільки коефіцієнт$y^{2}$ є$a=−2$, робимо висновок, що графік - це парабола, яка відкривається вліво. Крім того, коли$y=0$ зрозуміло, що$x=−5$ і, отже,$x$ -перехоплення є$(−5,0)$. Почніть з факторингу провідного коефіцієнта наступним чином:

$\begin{aligned} x &=-2 y^{2}+4 y-5 \\ &=-2\left(y^{2}-2 y+\_\_\_-\_\_\_\right)-5\end{aligned}$

Тут ми будемо додавати і віднімати$\left(\frac{b}{2}\right)^{2}=\left(\frac{-2}{2}\right)^{2}=(-1)^{2}=1$.

$\begin{aligned} x &=-2 y^{2}+4 y-5 \\ &=-2\color{black}{\left(y^{2}-2 y\color{Cerulean}{+1-1}\right)-}5 \\ &=-2\left[(y-1)^{2}-1\right]-5 \\ &=-2(y-1)^{2}+2-5 \\ &=-2(y-1)^{2}-3 \end{aligned}$

Тому з вершинної форми ми бачимо$x=-2(y-1)^{2}-3$, що вершина є$(h,k)=(−3,1)$. Оскільки вершина знаходиться в,$(−3,1)$ а парабола відкривається вліво, можна зробити висновок, що немає$y$ -перехоплень. Оскільки у нас всього дві точки, вибираємо деякі$y$ -значення і знаходимо відповідні$x$ -значення.

Таблиця$\PageIndex{1}$

$x$	$y$	$x=-2(y-1)^{2}-3$
$\color{Cerulean}{-11}$	$-1$	$x=-2(-1-1)^{2}-3=-2(-2)^{2}-3=-11$
$\color{Cerulean}{-5}$	$2$	$x=-2(2-1)^{2}-3=-2(1)^{2}-3=-5$
$\color{Cerulean}{-11}$	$3$	$x=-2(3-1)^{2}-3=-2(2)^{2}-3=-11$

Відповідь:

Малюнок$\PageIndex{11}$

Вправа$\PageIndex{2}$:

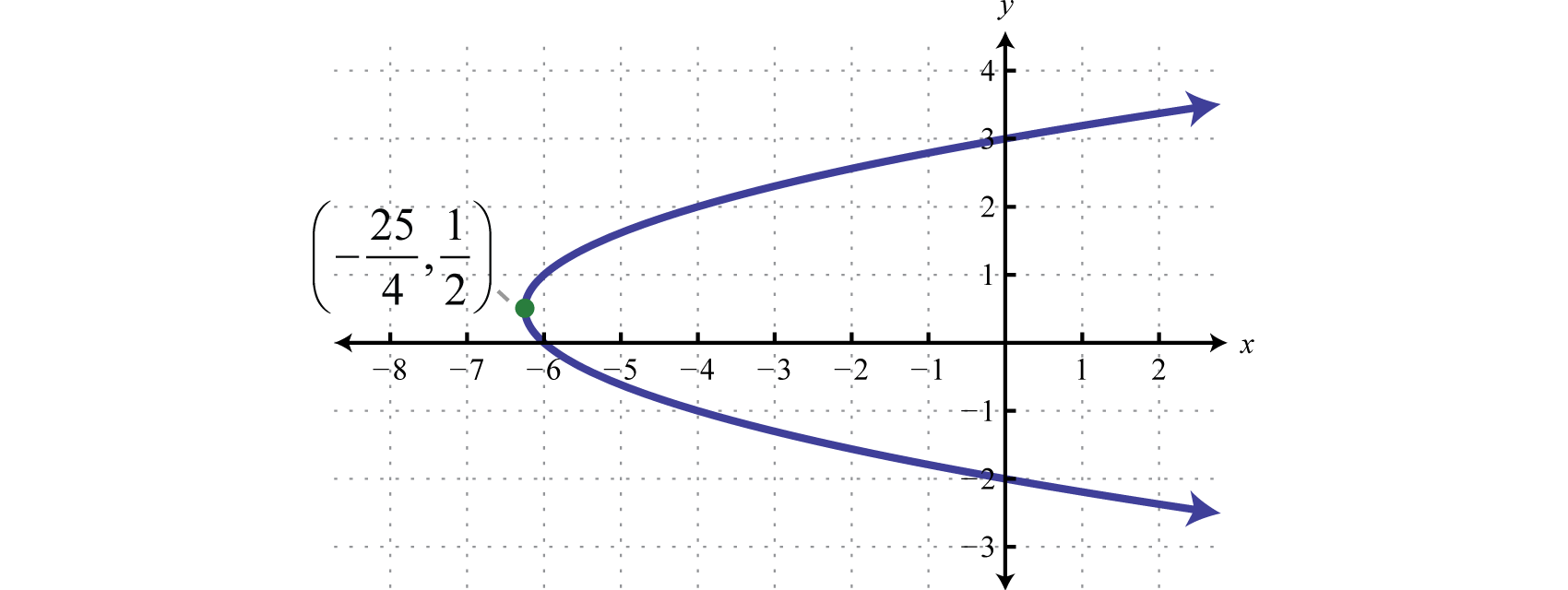
Графік:$x= y^{2}−y−6$.

Відповідь:

Малюнок$\PageIndex{12}$

www.youtube.com/В/PXGE96NHSCI

Ключові виноси

• Використовуйте формулу відстані, щоб визначити відстань між будь-якими двома заданими точками. Використовуйте формулу середньої точки, щоб визначити середину між будь-якими двома заданими точками.
• Парабола може відкриватися вгору або вниз, в цьому випадку це функція. У цьому розділі ми розширюємо наше дослідження парабол, щоб включити ті, які відкриваються вліво чи вправо. Такі графіки не представляють функцій.
• Рівняння параболи, що відкривається вгору або вниз, є квадратичним в$x, y=ax^{2}+bx+c$. Якщо$a>0$, то парабола відкривається вгору, а якщо a<0a<0, то парабола відкривається вниз.
• Рівняння параболи, що відкривається вліво або вправо, є квадратичним в$y, x=ay^{2}+by+c$. Якщо$a>0$, то парабола відкривається вправо і якщо$a<0$, то парабола відкривається вліво.
• Рівняння параболи в загальному вигляді$y=ax^{2}+bx+c$ або$x=ay^{2}+by+c$ може бути перетворено в стандартну форму$y=a(x−h)^{2}+k$ або$x=a(y−k)^{2}+h$ заповнивши квадрат.
• При заповненні квадрата переконайтеся, що провідний коефіцієнт угруповання змінних є$1$ перед додаванням та відніманням значення, яке завершує квадрат.
• Як загальні, так і стандартні форми корисні при графікуванні парабол. При стандартній формі вершина очевидна$(h,k)$. Щоб знайти набір$x$ -intercept$y=0$ і вирішити для$x$ і знайти набір$y$ -перехоплення$x=0$ і вирішити для$y$.

Вправа$\PageIndex{3}$

Обчисліть відстань і середину між заданими двома точками.

1. $(-1,-3)$і$(5,-11)$
2. $(-3,2)$і$(1,-1)$
3. $(4,-2)$і$(-2,-6)$
4. $(-5,-6)$і$(-3,-4)$
5. $(10,-1)$і$(9,6)$
6. $(-6,-4)$і$(-12,1)$
7. $(0,0)$і$(\sqrt{2}, \sqrt{3})$
8. $(0,0)$і$(2 \sqrt{2},-\sqrt{3})$
9. $(\sqrt{5},-\sqrt{3})$і$(2 \sqrt{5},-\sqrt{3})$
10. $(3 \sqrt{10}, \sqrt{6})$і$(\sqrt{10},-5 \sqrt{6})$
11. $\left(\frac{1}{2},-1\right)$і$\left(-2, \frac{3}{2}\right)$
12. $\left(-\frac{4}{3}, 2\right)$і$\left(-\frac{1}{3},-\frac{1}{2}\right)$
13. $\left(\frac{1}{5},-\frac{9}{5}\right)$і$\left(\frac{3}{10},-\frac{5}{2}\right)$
14. $\left(-\frac{1}{2}, \frac{4}{3}\right)$і$\left(-\frac{2}{3}, \frac{5}{6}\right)$
15. $(a, b)$і$(0,0)$
16. $(0,0)$і$(a \sqrt{2}, 2 \sqrt{a})$

Відповідь

1. Відстань:$10$ одиниці виміру; середина:$(2, −7)$

3. Відстань:$2\sqrt{13}$ одиниці виміру; середина:$(1, −4)$

5. Відстань:$5\sqrt{2}$ одиниці виміру; середина:$(\frac{19}{2},\frac{5}{2})$

7. Відстань:$\sqrt{5}$ одиниці виміру; середина:$\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{3}}{2}\right)$

9. Відстань:$\sqrt{5}$ одиниці виміру; середина:$\left(\frac{3 \sqrt{5}}{2},-\sqrt{3}\right)$

11. Відстань:$\frac{5 \sqrt{2}}{2}$ одиниці виміру; середина:$(−\frac{3}{4}, \frac{1}{4})$

13. Відстань:$\frac{\sqrt{2}}{2}$ одиниці виміру; середина:$\left(\frac{1}{4},-\frac{43}{20}\right)$

15. Відстань:$\sqrt{a^{2}+b^{2}}$ одиниці виміру; середина:$\left(\frac{a}{2}, \frac{b}{2}\right)$

Вправа$\PageIndex{4}$

Визначте площу кола, діаметр якої визначається заданими двома точками.

1. $(-8,12)$і$(-6,8)$
2. $(9,5)$і$(9,-1)$
3. $(7,-8)$і$(5,-10)$
4. $(0,-5)$і$(6,1)$
5. $(\sqrt{6}, 0)$і$(0,2 \sqrt{3})$
6. $(0, \sqrt{7})$і$(\sqrt{5}, 0)$

Відповідь

1. $5π$квадратні одиниці

3. $2π$квадратні одиниці

5. $\frac{9}{2} π$квадратні одиниці

Вправа$\PageIndex{5}$

Визначте периметр трикутника, задавши координати вершин.

1. $(5,3),(2,-3),$і$(8,-3)$
2. $(-3,2),(-4,-1),$і$(-1,0)$
3. $(3,3),(5,3-2 \sqrt{3}),$і$(7,3)$
4. $(0,0),(0,2 \sqrt{2}),$і$(\sqrt{2}, 0)$

Відповідь

1. $6+6 \sqrt{5}$одиниць

3. $12$одиниць

Вправа$\PageIndex{6}$

Знайдіть$a$ так, щоб відстань$d$ між точками дорівнювало заданій величині.

1. $(1,2)$і$(4, a) ; d=5$ одиниць
2. $(-3, a)$і$(5,6) ; d=10$ одиниць
3. $(3,1)$і$(a, 0) ; d=\sqrt{2}$ одиниць
4. $(a, 1)$і$(5,3) ; d=\sqrt{13}$ одиниць

Відповідь

1. $-2,6$

3. $2,4$

Вправа$\PageIndex{7}$

Графік. Обов'язково знайдіть вершину і все перехоплення.

1. $y=x^{2}+3$
2. $y=\frac{1}{2}(x-4)^{2}$
3. $y=-2(x+1)^{2}-1$
4. $y=-(x-2)^{2}+1$
5. $y=-x^{2}+3$
6. $y=-(x+1)^{2}+5$
7. $x=y^{2}+1$
8. $x=y^{2}-4$
9. $x=(y+2)^{2}$
10. $x=(y-3)^{2}$
11. $x=-y^{2}+2$
12. $x=-(y+1)^{2}$
13. $x=\frac{1}{3}(y-3)^{2}-1$
14. $x=-\frac{1}{3}(y+3)^{2}-1$

Відповідь

1.

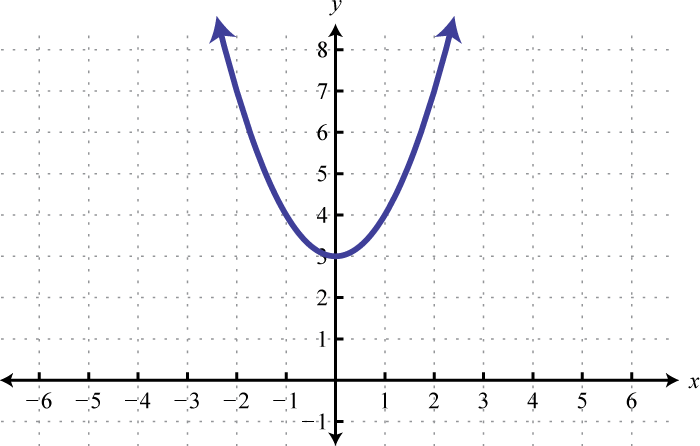
Малюнок$\PageIndex{13}$

3.

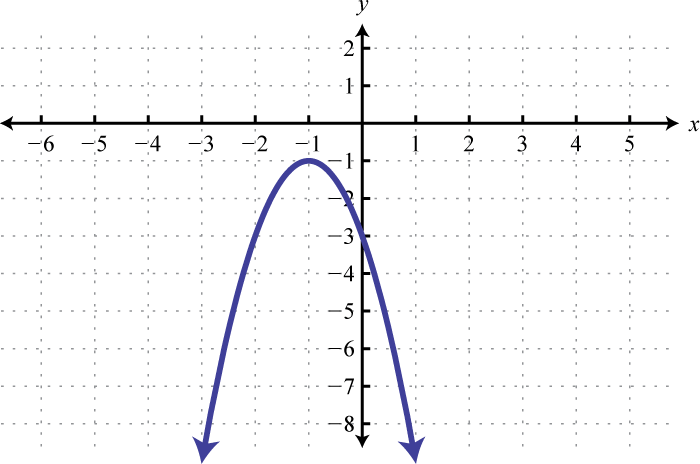
Малюнок$\PageIndex{14}$

5.

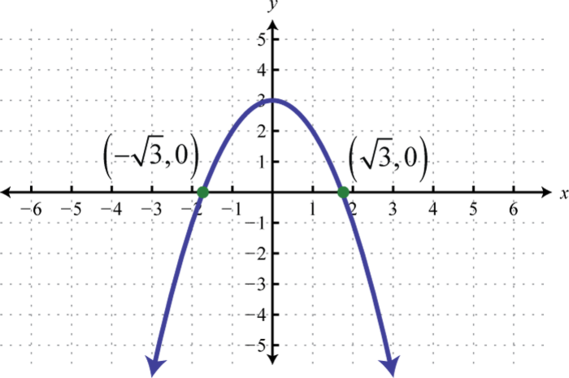
Малюнок$\PageIndex{15}$

7.

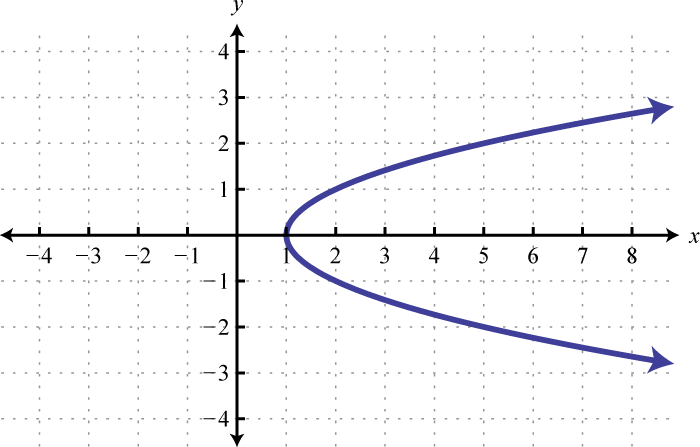
Малюнок$\PageIndex{16}$

9.

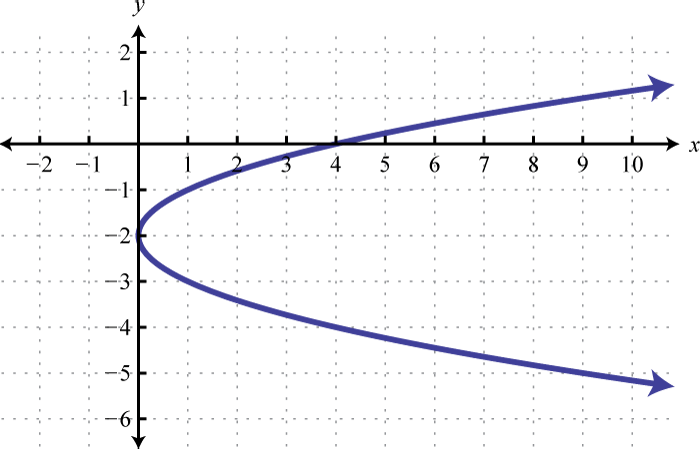
Малюнок$\PageIndex{17}$

11.

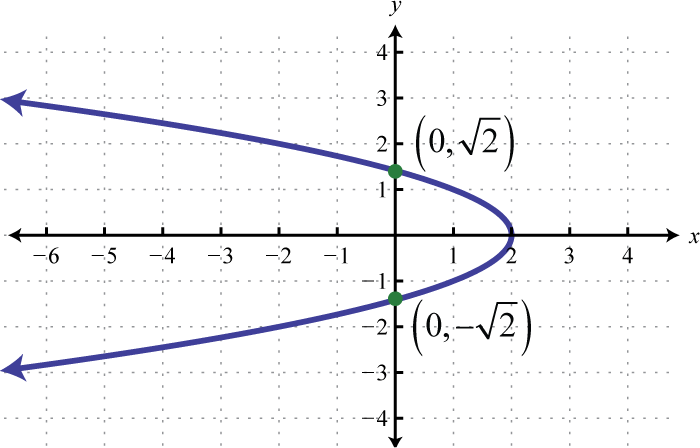
Малюнок$\PageIndex{18}$

13.

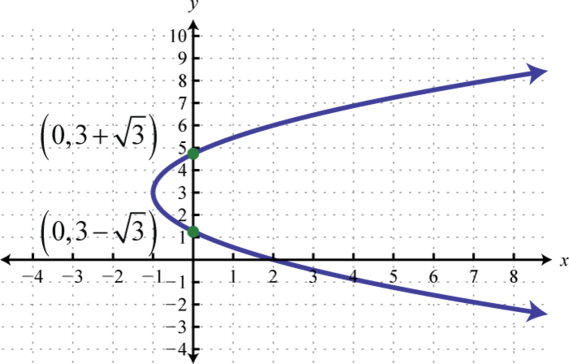
Малюнок$\PageIndex{19}$

Вправа$\PageIndex{8}$

Перепишіть в стандартному вигляді і дайте вершину.

1. $y=x^{2}-6 x+18$
2. $y=x^{2}+8 x+36$
3. $x=y^{2}+20 y+87$
4. $x=y^{2}-10 y+21$
5. $y=x^{2}-14 x+49$
6. $x=y^{2}+16 y+64$
7. $x=2 y^{2}-4 y+5$
8. $y=3 x^{2}-30 x+67$
9. $y=6 x^{2}+36 x+54$
10. $x=3 y^{2}+6 y-1$
11. $y=2 x^{2}-2 x-1$
12. $x=5 y^{2}+15 y+9$
13. $x=-y^{2}+5 y-5$
14. $y=-x^{2}+9 x-20$

Відповідь

1. $y=(x-3)^{2}+9 ;$вершина:$(3,9)$

3. $x=(y+10)^{2}-13 ;$вершина:$(-13,-10)$

5. $y=(x-7)^{2} ;$вершина:$(7,0)$

7. $x=2(y-1)^{2}+3 ;$вершина:$(3,1)$

9. $y=6(x+3)^{2} ;$вершина:$(-3,0)$

11. $y=2\left(x-\frac{1}{2}\right)^{2}-\frac{3}{2} ;$вершина:$\left(\frac{1}{2},-\frac{3}{2}\right)$

13. $x=-\left(y-\frac{5}{2}\right)^{2}+\frac{5}{4} ;$вершина:$\left(\frac{5}{4}, \frac{5}{2}\right)$

Вправа$\PageIndex{9}$

Перепишіть в стандартній формі і графі. Обов'язково знайдіть вершину і все перехоплення.

1. $y=x^{2}-4 x-5$
2. $y=x^{2}+6 x-16$
3. $y=-x^{2}+12 x-32$
4. $y=-x^{2}-10 x$
5. $y=2 x^{2}+4 x+9$
6. $y=3 x^{2}-6 x+4$
7. $y=-5 x^{2}+30 x-45$
8. $y=-4 x^{2}-16 x-16$
9. $x=y^{2}-2 y-8$
10. $x=y^{2}+4 y+8$
11. $x=y^{2}-2 y-3$
12. $x=y^{2}+6 y-7$
13. $x=-y^{2}-10 y-24$
14. $x=-y^{2}-12 y-40$
15. $x=3 y^{2}+12 y+12$
16. $x=-2 y^{2}+12 y-18$
17. $x=y^{2}-4 y-3$
18. $x=y^{2}+6 y+1$
19. $x=-y^{2}+2 y+5$
20. $y=2 x^{2}-2 x+1$
21. $y=-3 x^{2}+2 x+1$
22. $y=-x^{2}+3 x+10$
23. $x=-4 y^{2}-4 y-5$
24. $x=y^{2}-y+2$
25. $y=x^{2}+5 x-1$
26. $y=2 x^{2}+6 x+3$
27. $x=2 y^{2}+10 x+12$
28. $x=y^{2}+y-1$

Відповідь

1. $y=(x-2)^{2}-9$;

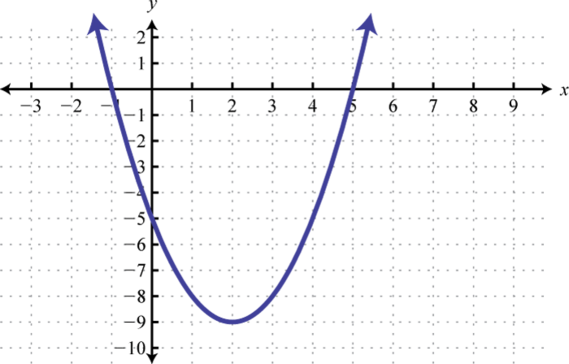
Малюнок$\PageIndex{20}$

3. $y=-(x-6)^{2}+4$;

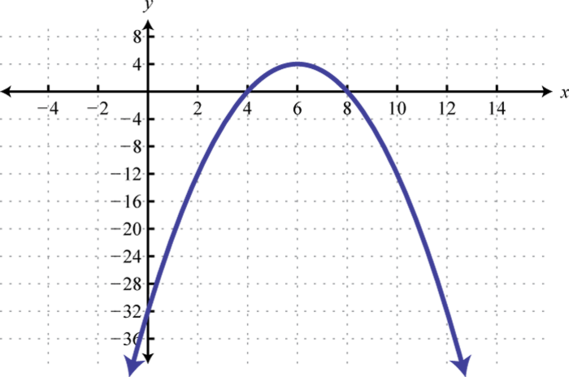
Малюнок$\PageIndex{21}$

5. $y=2(x+1)^{2}+7$;

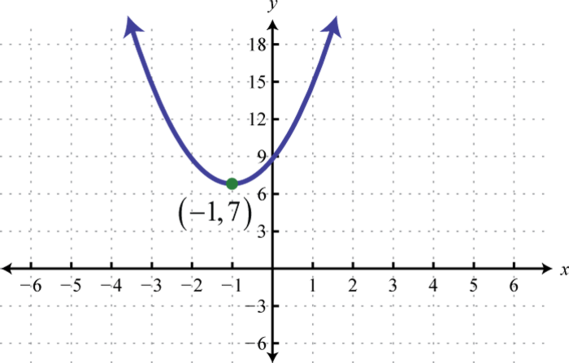
Малюнок$\PageIndex{22}$

7. $y=-5(x-3)^{2}$;

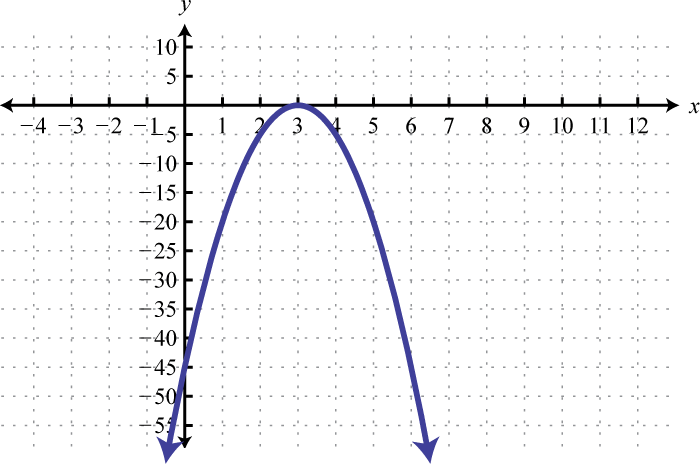
Малюнок$\PageIndex{23}$

9. $x=(y-1)^{2}-9$;

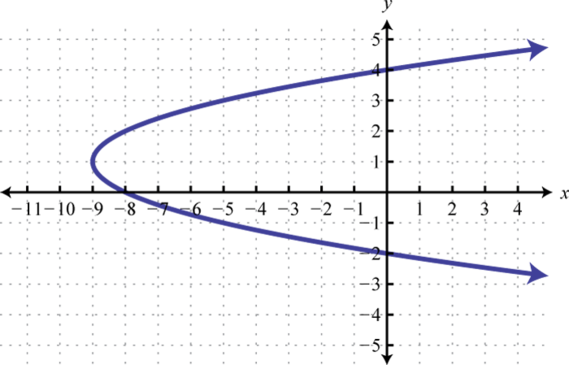
Малюнок$\PageIndex{24}$

11. $x=(y-1)^{2}-4$;

Малюнок$\PageIndex{25}$

13. $x=-(y+5)^{2}+1$;

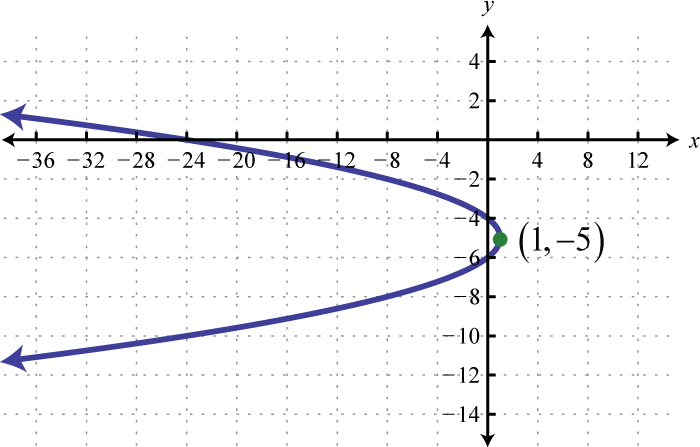
Малюнок$\PageIndex{26}$

15. $x=3(y+2)^{2}$;

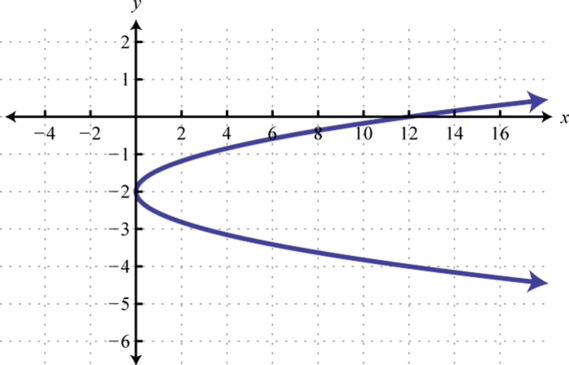
Малюнок$\PageIndex{27}$

17. $x=(y-2)^{2}-7$;

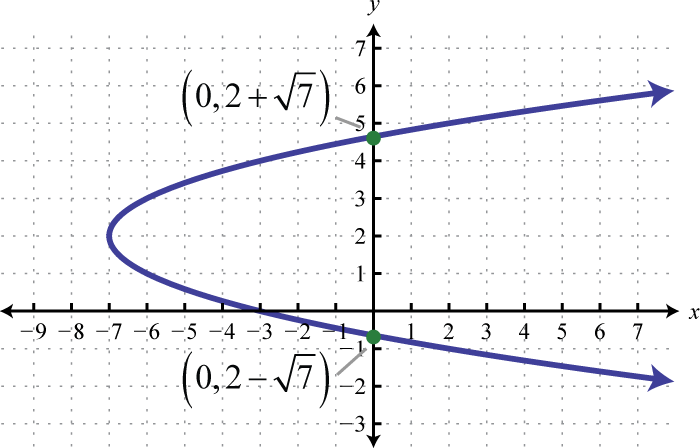
Малюнок$\PageIndex{28}$

19. $x=-(y-1)^{2}+6$;

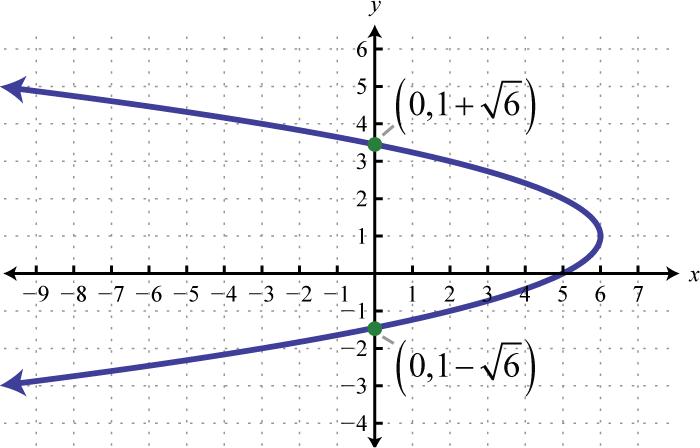
Малюнок$\PageIndex{29}$

21. $y=-3\left(x-\frac{1}{3}\right)^{2}+\frac{4}{3}$;

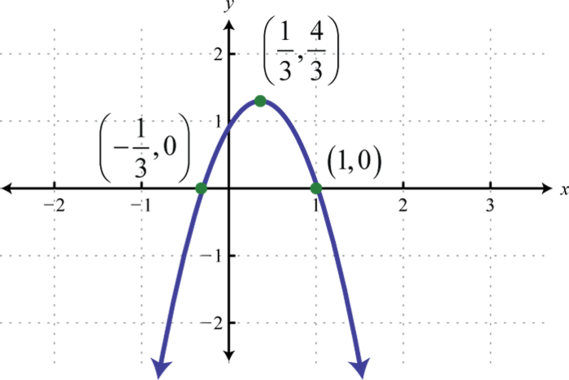
Малюнок$\PageIndex{30}$

23. $x=-4\left(y+\frac{1}{2}\right)^{2}-4$;

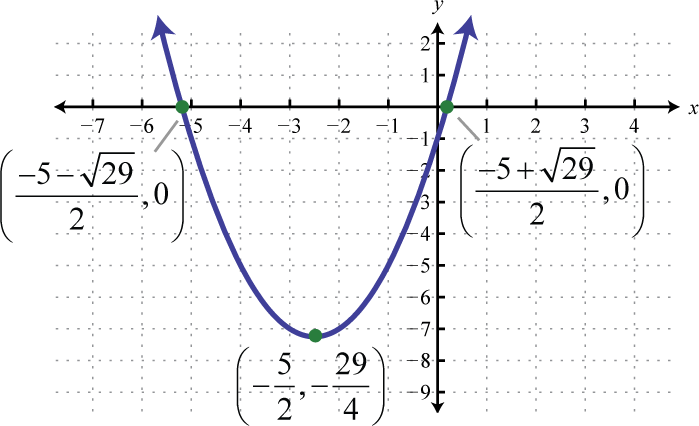
Малюнок$\PageIndex{31}$

25. $y=\left(x+\frac{5}{2}\right)^{2}-\frac{29}{4}$;

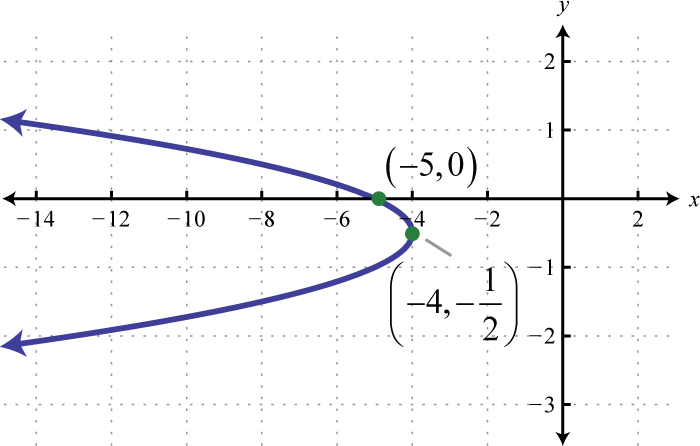
Малюнок$\PageIndex{32}$

27. $x=2\left(y+\frac{5}{2}\right)^{2}-\frac{1}{2}$;

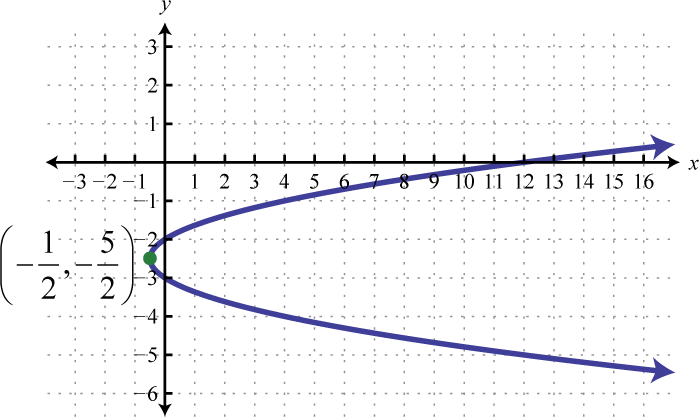
Малюнок$\PageIndex{33}$

Вправа$\PageIndex{10}$

1. Досліджуйте та обговоріть реальні програми, які передбачають параболу.
2. Чи всі параболи мають$x$ -перехоплення? Поясніть.
3. Чи всі параболи мають$y$ -перехоплення? Поясніть.
4. Складіть власну параболу, яка відкривається вліво або вправо, напишіть її в загальному вигляді, і зробіть графік.

Відповідь

1. Відповідь може відрізнятися

3. Відповідь може відрізнятися

Виноски

¹ Крива, отримана від перетину прямого кругового конуса і площини.

² З огляду на дві точки$(x_{1} , y_{1})$ і$(x_{2}, y_{2})$, відстань$d$ між ними задається$d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}$.

³ З огляду на дві точки$(x_{1}, y_{1})$ і$(x_{2}, y_{2})$, середина - це впорядкована пара, задана$\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)$.

⁴ Множина точок на площині, рівновіддаленій від заданої лінії, називається директрисою, і точка не на прямій, називається фокусом.

⁵ Рівняння параболи записано у вигляді$y=a x^{2}+b x+c$ або$x=a y^{2}+b y+c$, де$a, b$, і$c$ є дійсними числами і$a ≠ 0$.

⁶ Рівняння параболи записано у вигляді$y=a(x-h)^{2}+k$ або$x=a(y-k)^{2}+h$.

⁷ Рівняння параболи, записане в стандартній формі, часто називають вершиною форми. У такому вигляді вершина очевидна:$(h, k)$.