8.4: Гіперболи

Цілі навчання

• Графік гіперболи в стандартній формі.
• Визначте рівняння гіперболи за заданим її графіком.
• Перепишіть рівняння гіперболи в стандартній формі.
• Визначте конічний переріз із заданням його рівняння.

Гіпербола в стандартній формі

Гіпербола ²³ - це сукупність точок на площині, відстані яких від двох нерухомих точок, званих вогнищами, має абсолютну різницю, яка дорівнює позитивній константі. Іншими словами, якщо точки$F_{1}$ і$F_{2}$ є осередками і$d$ є деякою заданою позитивною константою, то$(x,y)$ це точка на гіперболі, якщо$d=\left|d_{1}-d_{2}\right|$ як на малюнку нижче:

Малюнок$\PageIndex{1}$

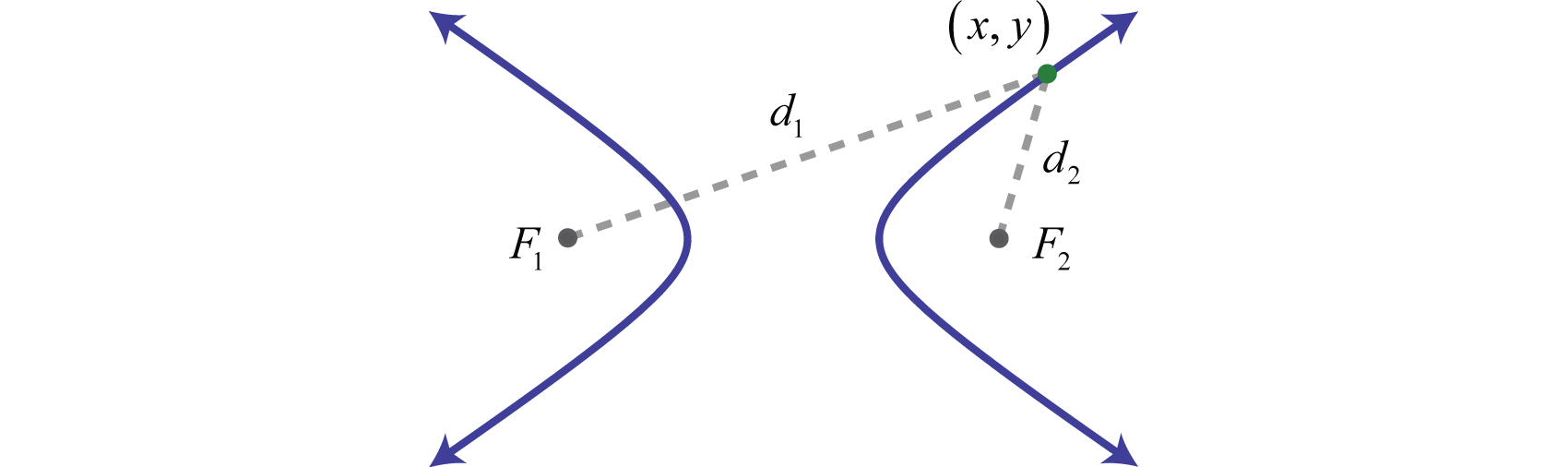
Крім того, гіпербола утворюється перетином конуса з косою площиною, яка перетинає підставу. Він складається з двох окремих кривих, званих гілками ²⁴. Точки на окремих гілках графа, де відстань знаходиться на мінімумі, називаються вершинами ²⁵. Серединою між вершинами гіперболи є її центр. На відміну від параболи, гіпербола асимптотична до певних ліній, проведених через центр. У цьому розділі ми зупинимося на графіку гіпербол, які відкриваються вліво і вправо або вгору і вниз.

Малюнок$\PageIndex{2}$

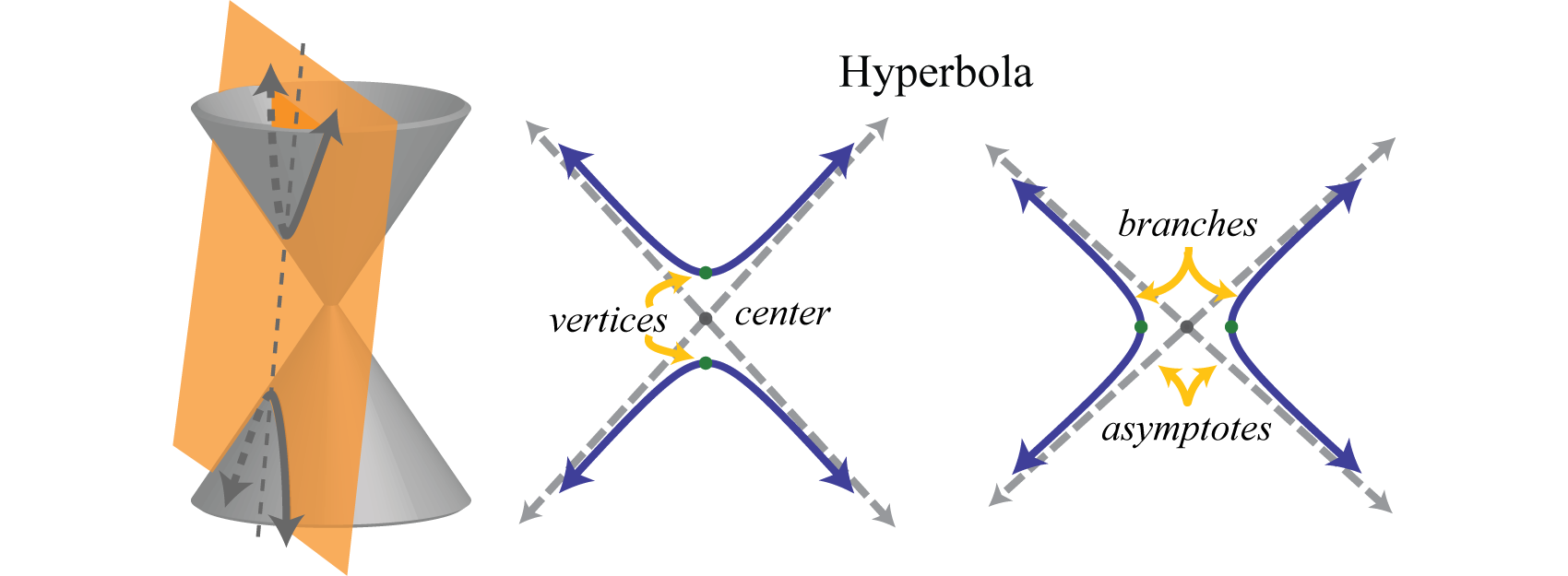
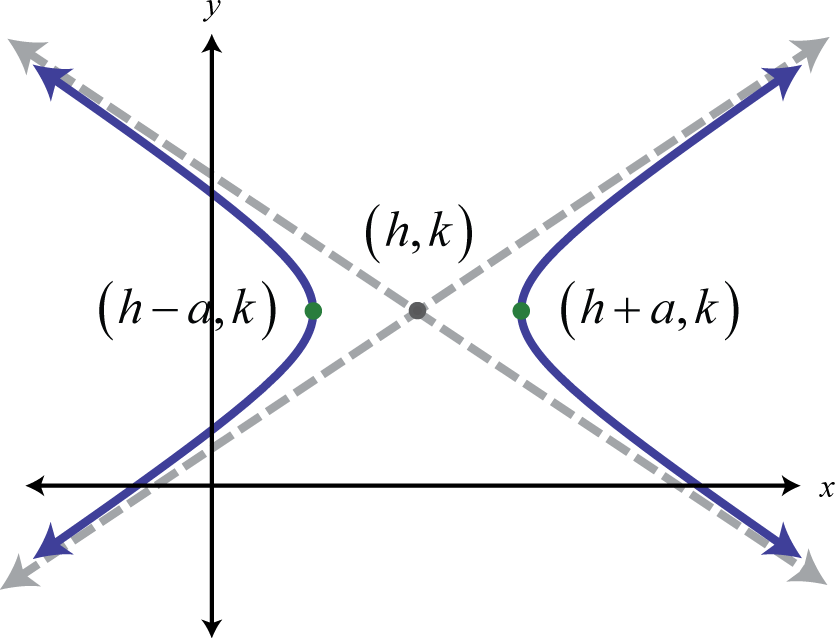
Асимптоти малюються пунктирними, оскільки вони не є частиною графіка; вони просто вказують на кінцеву поведінку графіка. Рівняння гіперболи, що відкривається вліво і вправо в стандартному вигляді ²⁶, виглядає наступним чином:

$$\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1 \nonumber$$

Малюнок$\PageIndex{3}$

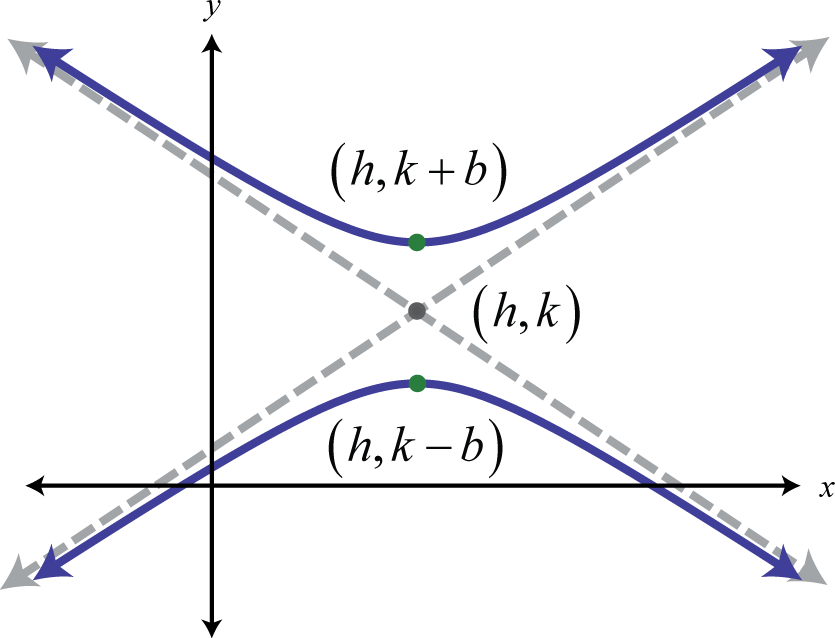
Тут центр є$(h,k)$ і вершини$(h±a,k)$. Рівняння гіперболи, що відкривається вгору і вниз в стандартній формі ²⁷, виглядає наступним чином:

$$\frac{(y-k)^{2}}{b^{2}}-\frac{(x-h)^{2}}{a^{2}}=1 \nonumber$$

Малюнок$\PageIndex{4}$

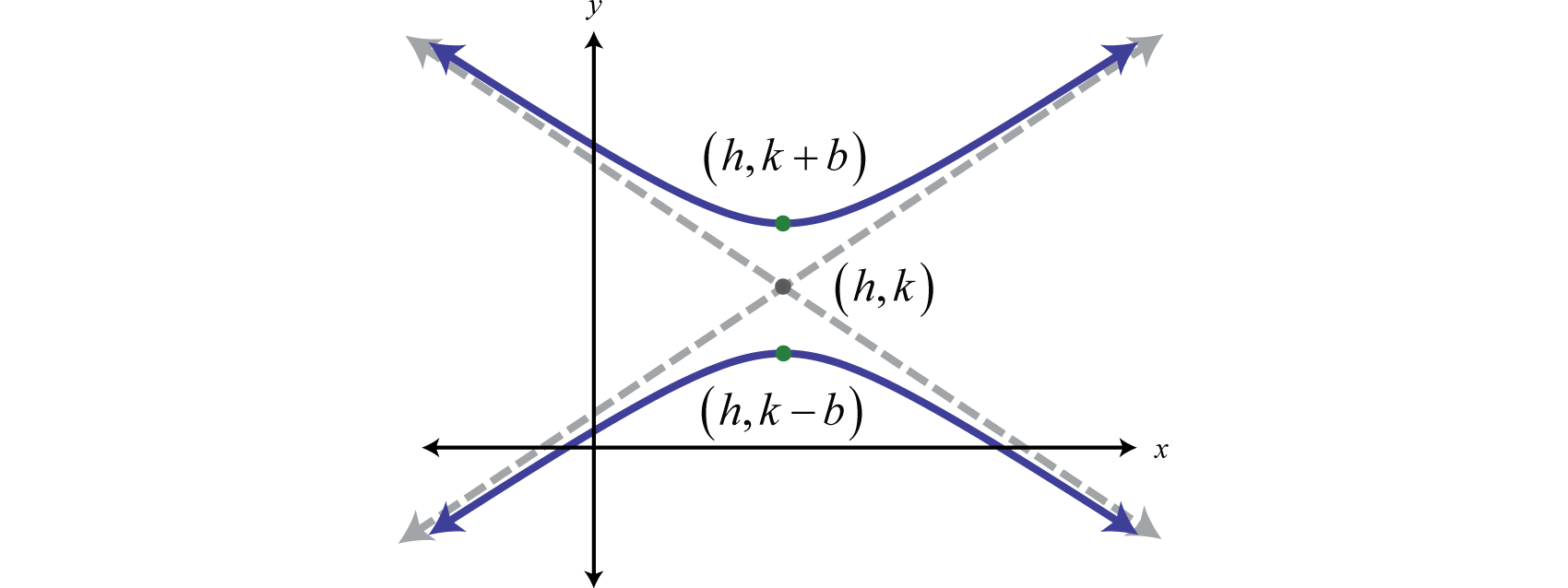
Тут центр є$(h,k)$ і вершини$(h,k±b)$.

Асимптоти мають важливе значення для визначення форми будь-якої гіперболи. За стандартною формою асимптоти є лінії, що проходять через центр$(h,k)$ з нахилом$m=\pm \frac{b}{a}$. Щоб легко намалювати асимптоти, ми використовуємо два спеціальні відрізки лінії через центр за допомогою$a$ і$b$. З огляду на будь-яку гіперболу, поперечна вісь ²⁸ - це відрізок лінії, утворений її вершинами. Сполучений вісь ²⁹ - це відрізок лінії через центр, перпендикулярний поперечній осі, як показано нижче:

Малюнок$\PageIndex{5}$

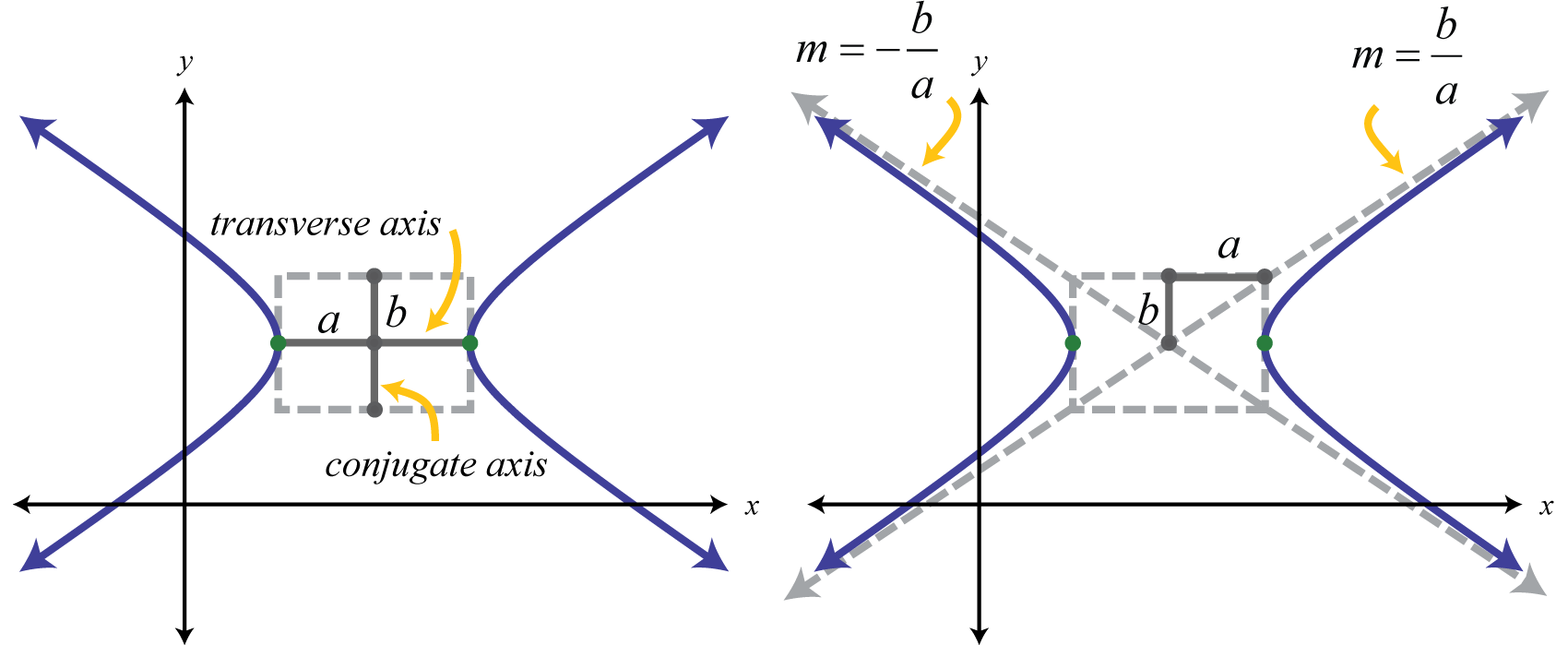
Прямокутник, який визначається поперечною і сполученою осями, називається основним прямокутником ³⁰. Лінії через кути цього прямокутника мають ухили$m=\pm \frac{b}{a}$. Ці лінії є асимптотами, які визначають форму гіперболи. Тому, з огляду на стандартну форму, багато властивостей гіперболи очевидні.

Таблиця$\PageIndex{1}$

Рівняння	Центр	$a$	$b$	Відкриває
$\frac{(x-3)^{2}}{25}-\frac{(y-5)^{2}}{16}=1$	$(3,5)$	\ (a\) ">$a=5$	\ (b\) ">$b=4$	Ліворуч і праворуч
$\frac{(y-2)^{2}}{36}-\frac{(x+1)^{2}}{9}=1$	$(-1,2)$	\ (a\) ">$a=3$	\ (b\) ">$b=6$	Вгору і вниз
$\frac{(y+2)^{2}}{3}-(x-5)^{2}=1$	$(5,-2)$	\ (a\) ">$a=1$	\ (b\) ">$b=\sqrt{3}$	Вгору і вниз
$\frac{x^{2}}{49}-\frac{(y+4)^{2}}{8}=1$	$(0,-4)$	\ (a\) ">$a=7$	\ (b\) ">$b=2 \sqrt{2}$	Ліворуч і праворуч

Графік гіперболи повністю визначається її центром, вершинами та асимптотами.

Приклад$\PageIndex{1}$:

Графік:$\frac{(x-5)^{2}}{9}-\frac{(y-4)^{2}}{4}=1$.

Рішення:

При цьому вираз за участю$x$ має позитивний провідний коефіцієнт; отже, гіпербола відкривається вліво і вправо. Ось$a=\sqrt{9}=3$ і$b=\sqrt{4}=2$. Від центру$(5,4)$ відзначте точки$3$ одиниць вліво і вправо, а також$2$ одиниці вгору і вниз. З'єднайте ці точки прямокутником наступним чином:

Малюнок$\PageIndex{6}$

Лінії через кути цього прямокутника визначають асимптоти.

Малюнок$\PageIndex{7}$

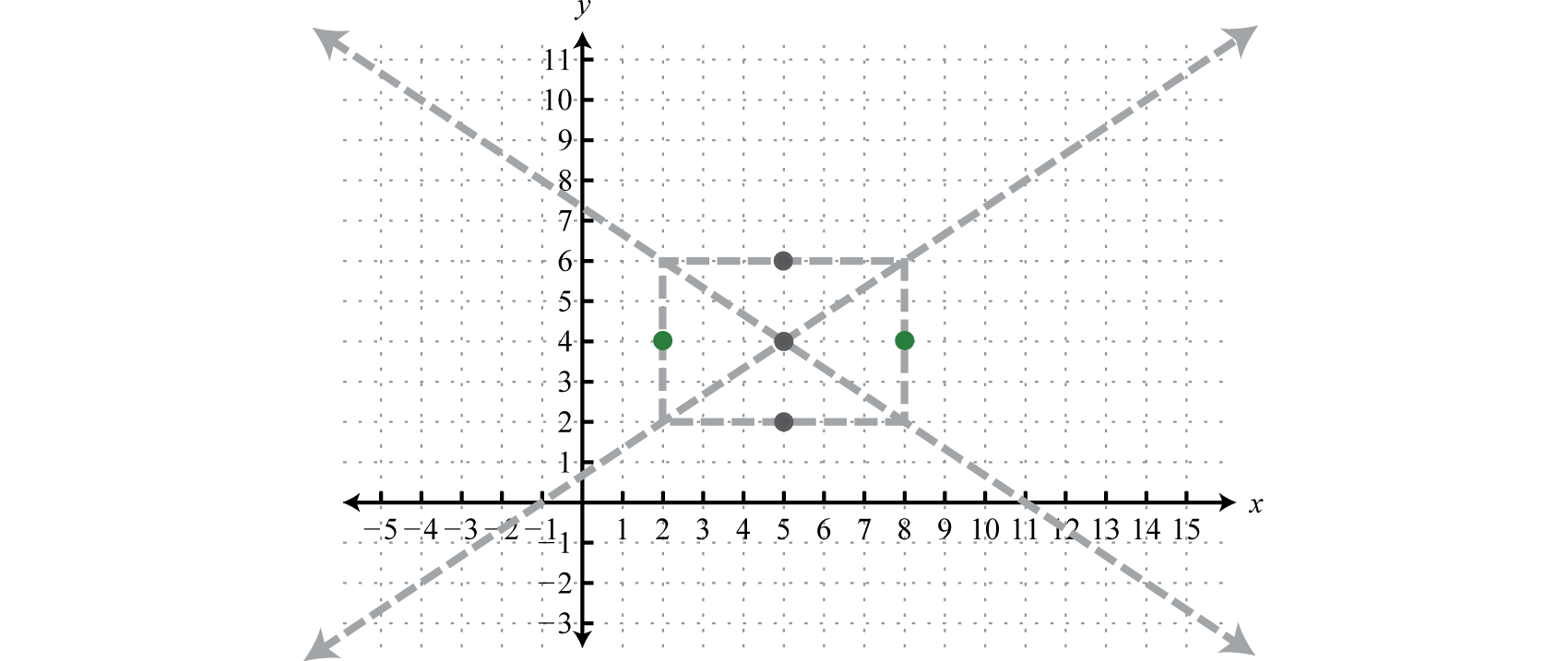
Використовуйте ці пунктирні лінії як орієнтир для графіка гіперболи, що відкриваються вліво і вправо, що проходять через вершини.

Відповідь

Малюнок$\PageIndex{8}$

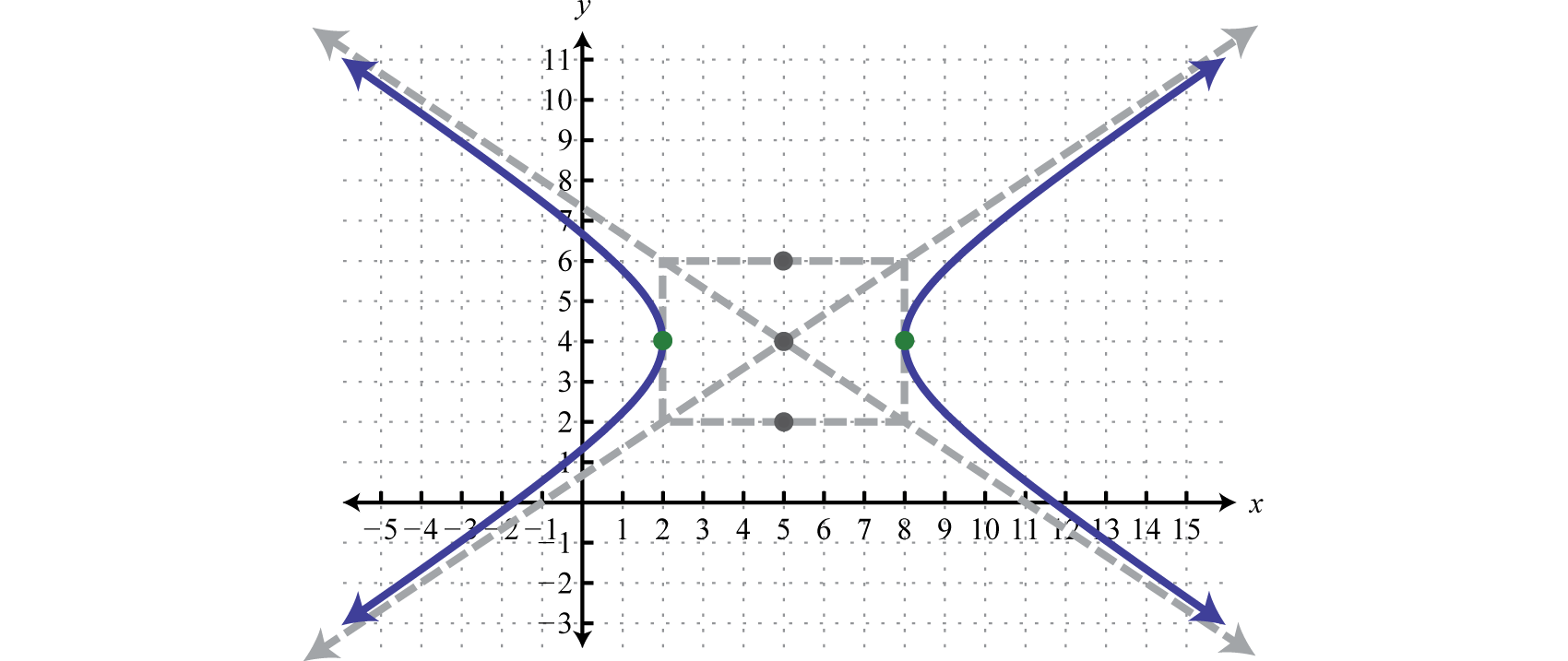
Приклад$\PageIndex{2}$:

Графік:$\frac{(y-2)^{2}}{4}-\frac{(x+1)^{2}}{36}=1$.

Рішення

При цьому вираз за участю$y$ має позитивний провідний коефіцієнт; отже, гіпербола відкривається вгору і вниз. Ось$a=\sqrt{36}=6$ і$b=\sqrt{4}=2$. Від центру$(−1,2)$ відзначте точки$6$ одиниць вліво і вправо, а також$2$ одиниці вгору і вниз. З'єднайте ці точки прямокутником. Лінії через кути цього прямокутника визначають асимптоти.

Малюнок$\PageIndex{9}$

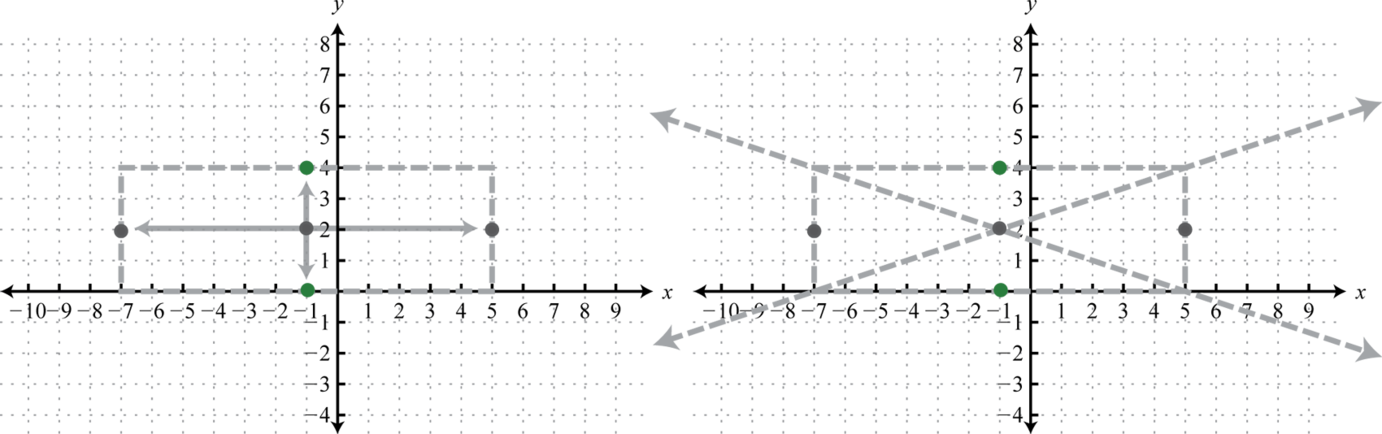
Використовуйте ці пунктирні лінії як орієнтир для графіка гіперболи, що відкривається вгору і вниз, що проходить через вершини.

Відповідь:

Малюнок$\PageIndex{10}$

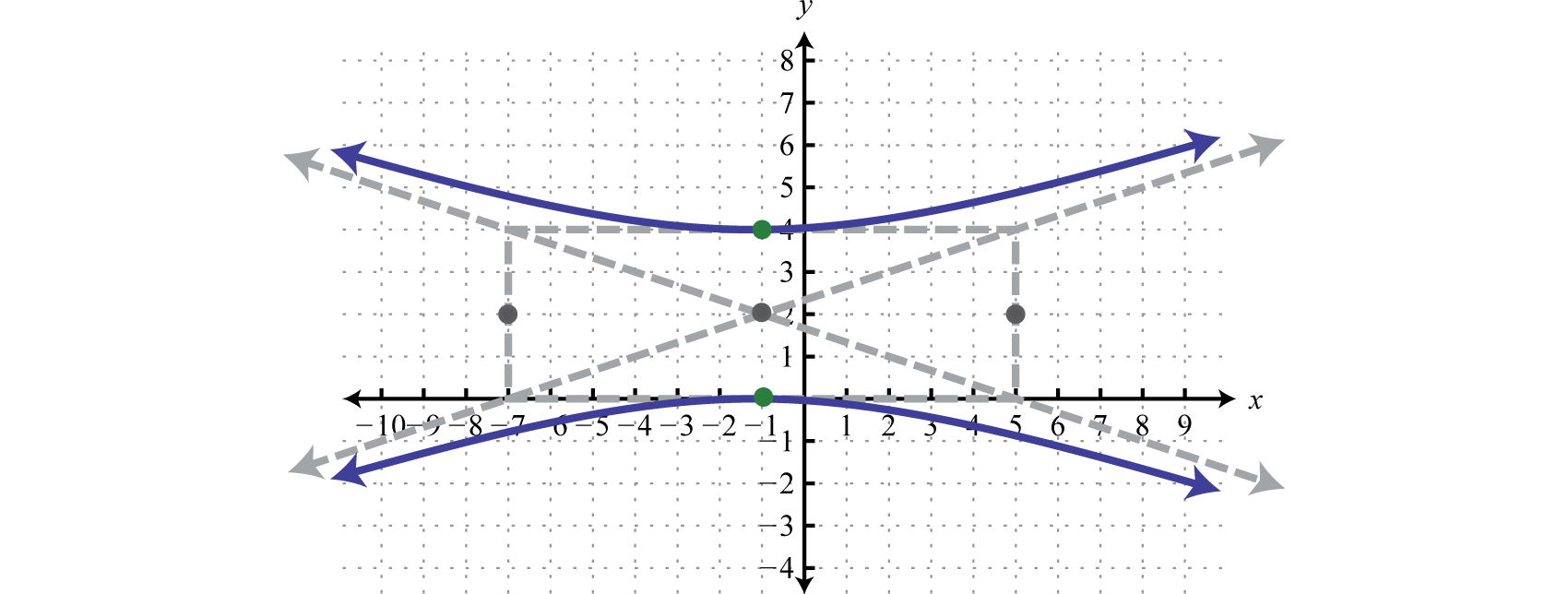
Примітка

Коли дана гіпербола, що відкривається вгору і вниз, як і в попередньому прикладі, це поширена помилка обміну значеннями для центру,$h$ і$k$. Це відбувається тому, що кількість, що включає змінну,$y$ зазвичай з'являється спочатку у стандартній формі. Подбайте про те, щоб$y$ -значення центру походить від величини, що включає змінну,$y$ і що$x$ -значення центру отримується з кількості, що включає змінну$x$.

Як і в будь-якому графіку, ми зацікавлені в пошуку$x$ - і$y$ -перехоплення.

Приклад$\PageIndex{3}$:

Знайдіть перехоплення:$\frac{(y-2)^{2}}{4}-\frac{(x+1)^{2}}{36}=1$.

Рішення

Щоб знайти$x$ -перехоплення встановити$y=0$ і вирішити для$x$.

$$\begin{align*} \frac{(\color{Cerulean}{0}\color{black}{-}2)^{2}}{4}-\frac{(x+1)^{2}}{36} &=1 \\[4pt] 1-\frac{(x+1)^{2}}{36} &=1 \\[4pt] -\frac{(x+1)^{2}}{36} &=0 \\[4pt] (x+1)^{2} &=0 \\[4pt] x+1 &=0 \\[4pt] x &=-1 \end{align*}$$

Тому є тільки один$x$ -перехоплення,$(−1,0)$. Щоб знайти набір$y$ -intercept$x=0$ і вирішити для$y$.

$$\begin{align*} \frac{(y-2)^{2}}{4}-\frac{(\color{Cerulean}{0}\color{black}{+}1)^{2}}{36} &=1 \\[4pt] \frac{(y-2)^{2}}{4}-\frac{1}{36} &=1 \\[4pt] \frac{(y-2)^{2}}{4} &=\frac{37}{36} \\[4pt] \frac{(y-2)}{2} &=\frac{\sqrt{37}}{36} \\[4pt] y-2 &=\pm \frac{\sqrt{37}}{3} \\[4pt] y &=2 \pm \frac{\sqrt{37}}{3}=\frac{6 \pm \sqrt{37}}{3} \end{align*}$$

Тому є два$y$ -перехоплення,$\left(0, \frac{6-\sqrt{37}}{3}\right) \approx(0,-0.03)$$\left(0, \frac{6+\sqrt{37}}{3}\right) \approx(0,4.03)$ і.Візьміть хвилинку, щоб порівняти їх з ескізом графіка в попередньому прикладі.

Відповідь:

$x$-перехоплення:$(−1,0)$;$y$ -перехоплює:$\left(0, \frac{6-\sqrt{37}}{3}\right)$ і$\left(0, \frac{6+\sqrt{37}}{3}\right)$.

Розглянемо гіперболу, зосереджену на початку,

$$9 x^{2}-5 y^{2}=45\nonumber$$

Стандартна форма вимагає, щоб одна сторона була рівною$1$. В цьому випадку ми можемо отримати стандартну форму, розділивши обидві сторони на$45$.

$$\begin{align*} \frac{9 x^{2}-5 y^{2}}{45} &=\frac{45}{45} \\[4pt] \frac{9 x^{2}}{45}-\frac{5 y^{2}}{45} &=\frac{45}{45} \\[4pt] \frac{x^{2}}{5}-\frac{y^{2}}{9} &=1 \end{align*}$$

Це можна записати наступним чином:

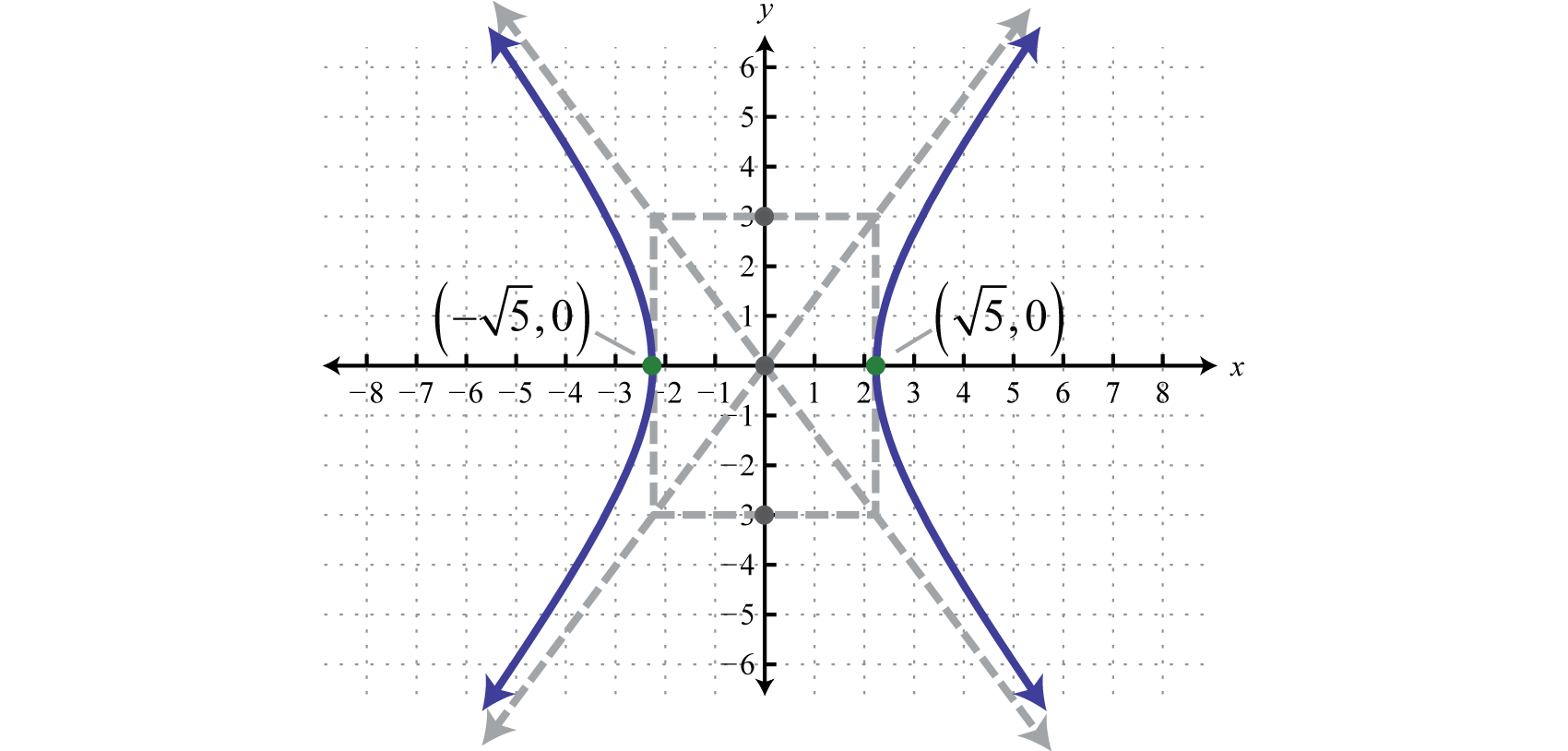
$$\frac{(x-0)^{2}}{5}-\frac{(y-0)^{2}}{9}=1\nonumber$$

У такому вигляді зрозуміло, що центр є$(0,0)$$a=\sqrt{5}$, і$b=3$. Далі йде графік.

Малюнок$\PageIndex{11}$

Вправа$\PageIndex{1}$:

Графік:$\frac{y^{2}}{25}-\frac{(x-5)^{2}}{9}=1$:

Відповідь:

Малюнок$\PageIndex{12}$

www.youtube.com/В/ІІТ1К

Гіпербола в загальній формі

Ми бачили, що граф гіперболи повністю визначається його центром, вершинами та асимптотами; що можна прочитати з його рівняння в стандартній формі. Однак рівняння не завжди дається в стандартній формі. Рівняння гіперболи в загальному вигляді ³¹ виглядає наступним чином:

$\begin{array}{l}{p x^{2}-q y^{2}+c x+d y+e=0\quad \color{Cerulean} { Hyperbola \:opens\: left\: and\: right.}} \\[4pt] {q y^{2}-p x^{2}+c x+d y+e=0\quad \color{Cerulean} { Hyperbola \:opens\: upward\: and\: downward.}}\end{array}$

де$p,q>0$. Етапи побудови графіка гіперболи з урахуванням її рівняння в загальному вигляді викладені в наступному прикладі.

Приклад$\PageIndex{4}$:

Графік:$4 x^{2}-9 y^{2}+32 x-54 y-53=0$.

Рішення

Почніть з перезапису рівняння в стандартному вигляді.

Крок 1: Згрупуйте терміни з однаковими змінними і перемістіть константу в праву сторону. Фактор так, що провідний коефіцієнт кожної угруповання є$1$.

$\begin{aligned} 4 x^{2}-9 y^{2}+32 x-54 y-53 &=0 \\[4pt] \left(4 x^{2}+32 x+\_\_\_\right )+\left(-9 y^{2}-54 y+\_\_\_\right)&=53 \\[4pt] 4\left(x^{2}+8x+\_\_\_ \right)-9\left(y^{2}+6y+\_\_\_ \right)&=53 \end{aligned}$

Крок 2: Заповніть квадрат для кожного угруповання. У цьому випадку для термінів, що передбачають$x$ використання,$\left(\frac{8}{2}\right)^{2}=4^{2}=16$ і для термінів, пов'язаних з$y$ використанням$\left(\frac{6}{2}\right)^{2}=(3)^{2}=9$. Коефіцієнт перед кожним угрупованням впливає на значення, яке використовується для збалансування рівняння праворуч,

$4\color{black}{\left(x^{2}+8 x\color{Cerulean}{+16}\right)-}9\color{black}{\left(y^{2}+6 y\color{OliveGreen}{+9}\right)=}53\color{Cerulean}{+64}\color{OliveGreen}{-81}$

Через властивість distributive додавання$16$ всередині першого групування еквівалентно додаванню$4⋅16=64$. Аналогічно, додавання$9$ всередині другого групування еквівалентно додаванню$−9⋅9=−81$. Тепер коефіцієнт, а потім ділимо, щоб отримати$1$ на правій стороні.

$\begin{aligned} 4(x+4)^{2}-9(y+3)^{2} &=36 \\[4pt] \frac{4(x+4)^{2}-9(y+3)^{2}}{\color{Cerulean}{36}} &\color{black}{=}\frac{36}{\color{Cerulean}{36}} \\[4pt] \frac{4(x+4)^{2}}{36}-\frac{9(y+3)^{2}}{36} &=\frac{36}{36} \\[4pt] \frac{(x+4)^{2}}{9}-\frac{(y+3)^{2}}{4} &=1 \end{aligned}$

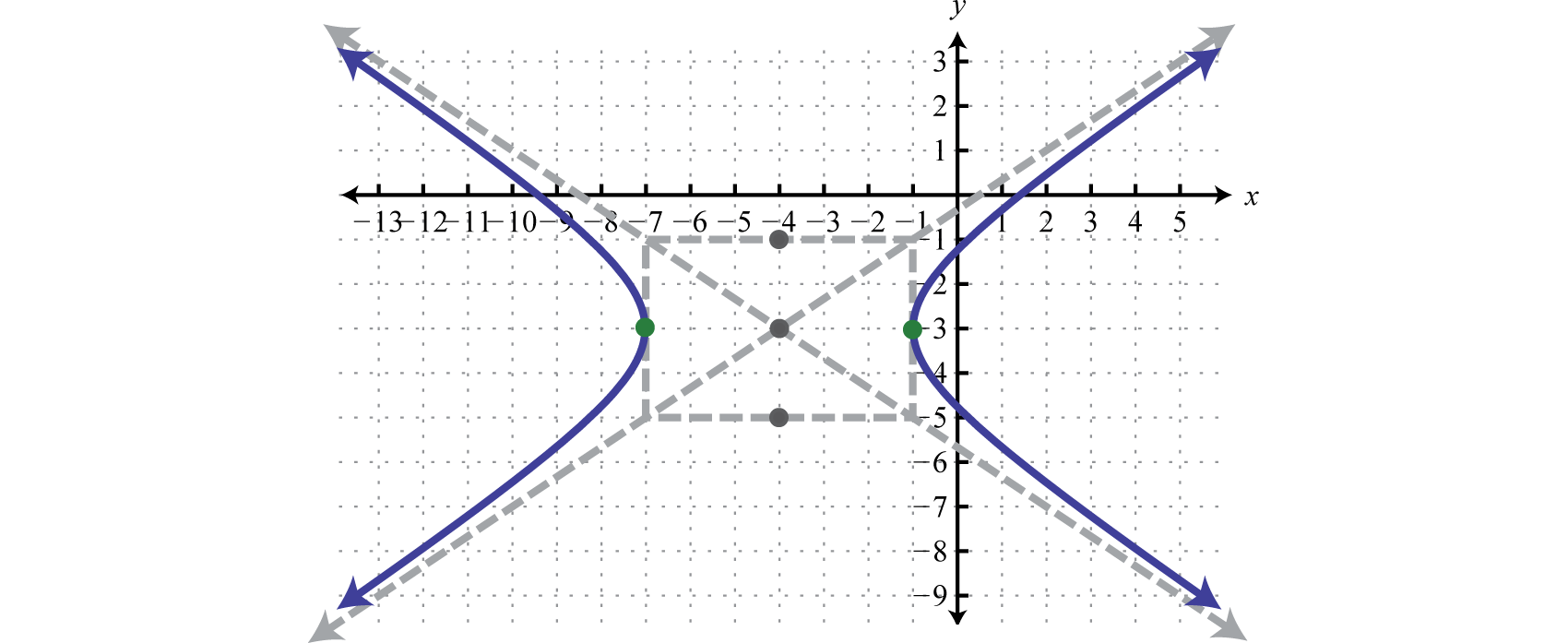
Крок 3: Визначте центр, a та b, а потім використовуйте цю інформацію для ескізу графіка. При цьому центр - це$(−4,−3)$$a=\sqrt{9}=3$, і$b=\sqrt{4}=2$. Оскільки провідний коефіцієнт виразу за участю$x$ є позитивним, а коефіцієнт виразу, що включає$y$ негативний, ми графуємо гіперболу, що відкривається вліво і вправо.

Відповідь:

Малюнок$\PageIndex{13}$

Вправа$\PageIndex{2}$:

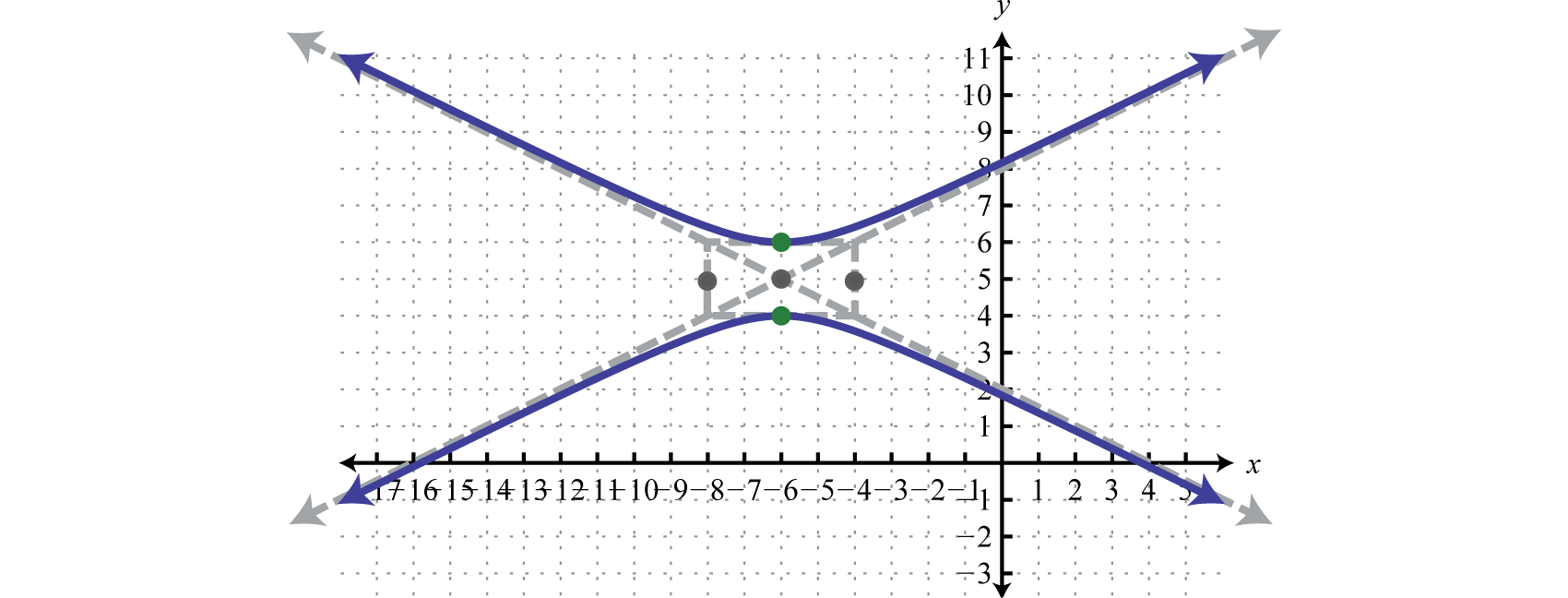
Графік:$4 y^{2}-x^{2}-40 y-12 x+60=0$.

Відповідь:

Малюнок$\PageIndex{14}$

www.youtube.com/В/С4Ф6ІЗЛГВГС

Визначення конічних перерізів

У цьому розділі завдання полягає у визначенні конічного перерізу з урахуванням його рівняння в загальному вигляді. Для розрізнення конічних перерізів використовують показники і коефіцієнти. Якщо рівняння квадратичне тільки в одній змінній і лінійне в іншій, то його графік буде параболою.

Таблиця$\PageIndex{2}$

Парабола:$a>0$
\ (a>0\) ">$y=a(x-h)^{2}+k$ $y=a x^{2}+b x+c$	$x=a(y-k)^{2}+h$ $x=a y^{2}+b y+c$
\ (a>0\) "> Малюнок$\PageIndex{15}$	Малюнок$\PageIndex{16}$

Таблиця$\PageIndex{3}$

Парабола:$a<0$
\ (a<0\) ">$y=a(x-h)^{2}+k$ $y=a x^{2}+b x+c$	$x=a(y-k)^{2}+h$ $x=a y^{2}+b y+c$
\ (a<0\) "> Малюнок$\PageIndex{17}$	Малюнок$\PageIndex{18}$

Якщо рівняння квадратичне в обох змінних, де коефіцієнти квадратних членів однакові, то його графік буде колом.

Таблиця$\PageIndex{4}$

Коло:
$\begin{aligned}(x-h)^{2}+(y-k)^{2} &=r^{2} \\[4pt] x^{2}+y^{2}+c x+d y+e &=0 \end{aligned}$	Малюнок$\PageIndex{19}$

Якщо рівняння квадратичне в обох змінних, де коефіцієнти квадратних членів різні, але мають однаковий знак, то його графік буде еліпсом.

Таблиця$\PageIndex{5}$

Еліпс:$a, b>0$ і$p, q>0$
\ (a, b>0\) і$p, q>0$ «>$\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$ $p x^{2}+q y^{2}+c x+d y+e=0$	Малюнок$\PageIndex{20}$

Якщо рівняння квадратичне в обох змінних, де коефіцієнти квадратних членів мають різні ознаки, то його графік буде гіперболою.

Таблиця$\PageIndex{6}$

Гіпербола:$a, b>0$ і$p, q>0$
$\begin{aligned} \frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}} &=1 \\[4pt] p x^{2}-q y^{2}+c x+d y+e &=0 \end{aligned}$	$\begin{aligned} \frac{(y-k)^{2}}{b^{2}}-\frac{(x-h)^{2}}{a^{2}} &=1 \\[4pt] q y^{2}-p x^{2}+c x+d y+e &=0 \end{aligned}$
Малюнок$\PageIndex{21}$	Малюнок$\PageIndex{22}$

Приклад$\PageIndex{5}$:

Визначте графік кожного рівняння як параболу, коло, еліпс або гіперболу.

1. $4 x^{2}+4 y^{2}-1=0$
2. $3 x^{2}-2 y^{2}-12=0$
3. $x-y^{2}-6 y+11=0$

Рішення

1. Рівняння квадратичне в обох$x$ і$y$ де провідні коефіцієнти для обох змінних однакові,$4$.

$\begin{aligned} 4 x^{2}+4 y^{2}-1 &=0 \\[4pt] 4 x^{2}+4 y^{2} &=1 \\[4pt] x^{2}+y^{2} &=\frac{1}{4} \end{aligned}$

Це рівняння окружності з центром у початку координат з радіусом$1/2$.

2. Рівняння квадратичне в обох$x$ і$y$ де провідні коефіцієнти для обох змінних мають різні ознаки.

$3 x^{2}-2 y^{2}-12=0$
$\frac{3 x^{2}-2 y^{2}}{12}=\frac{12}{12}$
$\frac{x^{2}}{4}-\frac{y^{2}}{6}=1$

Це рівняння гіперболи, що відкривається вліво і вправо по центру у початку.

3. Рівняння є квадратичним$y$ тільки в.

$\begin{aligned} x-y^{2}+6 y-11 &=0 \\[4pt] x &=y^{2}-6 y+\quad+11 \\[4pt] x &=\color{black}{\left(y^{2}-6 y\color{Cerulean}{+9}\right)+}11\color{Cerulean}{-9} \\[4pt] x &=(y-3)^{2}+2 \end{aligned}$

Це рівняння параболи, що відкривається праворуч з вершиною$(2,3)$.

Відповідь:

1. Коло

2. Гіпербола

3. Парабола

Ключові винос

• Графік гіперболи повністю визначається її центром, вершинами та асимптотами.
• Центр, вершини та асимптоти очевидні, якщо рівняння гіперболи дано в стандартній формі:$\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1$ або$\frac{(y-k)^{2}}{b^{2}}-\frac{(x-h)^{2}}{a^{2}}=1$.
• Щоб намалювати гіперболу, позначте точки$a$ одиниці ліворуч і праворуч від центру і точки$b$ одиниць вгору і вниз від центру. Використовуйте ці точки, щоб намалювати основний прямокутник; лінії через кути цього прямокутника є асимптотами. Якщо коефіцієнт$x^{2}$ позитивний, проведіть гілки гіперболи, що відкриваються вліво і вправо, через визначені точки$a$. Якщо коефіцієнт$y^{2}$ позитивний, проведіть гілки гіперболи, що відкриваються вгору і вниз через визначені точки$b$.
• Орієнтація поперечної осі залежить від коефіцієнта$x^{2}$ і$y^{2}$.
• Якщо рівняння гіперболи дано в загальному вигляді$p x^{2}-q y^{2}+c x+d y+e=0$ або$q y^{2}-p x^{2}+c x+d y+e=0$ де$p,q>0$, згрупуйте члени з однаковими змінними та заповніть квадрат для обох груп, щоб отримати стандартну форму.
• Ми визнаємо рівняння гіперболи, якщо воно квадратичне в обох$x$ і$y$ де коефіцієнти квадратних членів протилежні за знаком.

Вправа$\PageIndex{3}$

З огляду на рівняння гіперболи в стандартній формі, визначають її центр, в який бік відкривається граф, і вершини.

1. $\frac{(x-6)^{2}}{16}-\frac{(y+4)^{2}}{9}=1$
2. $\frac{(y-3)^{2}}{25}-\frac{(x+1)^{2}}{64}=1$
3. $\frac{(y+9)^{2}}{5}-x^{2}=1$
4. $\frac{(x-5)^{2}}{12}-y^{2}=1$
5. $4(y+10)^{2}-25(x+1)^{2}=100$
6. $9(x-1)^{2}-5(y+10)^{2}=45$

Відповідь

1. Центр:$(6,-4) ; a=4 ; b=3$; відкриває вліво і вправо; вершини:$(2, −4), (10, −4)$

3. Центр:$(0,-9) ; a=1, b=\sqrt{5}$; відкривається вгору і вниз; вершини:$(0,-9-\sqrt{5}),(0,-9+\sqrt{5})$

5. Центр:$(−1, −10); a = 2, b = 5$; відкривається вгору і вниз; вершини:$(−1, −15) , (−1, −5)$

Вправа$\PageIndex{4}$

Визначити стандартну форму для рівняння гіперболи дано наступну інформацію.

1. Центр$(2,7), a=6, b=3,$ відкривається вліво і вправо.
2. Центр$(-9,1), a=7, b=2,$ відкривається вгору і вниз.
3. Центр$(10,-3), a=\sqrt{7}, b=5 \sqrt{2},$ відкривається вгору і вниз.
4. Центр$(-7,-2), a=3 \sqrt{3}, b=\sqrt{5},$ відкривається вліво і вправо.
5. Центр$(0,-8), a=\sqrt{2} b=1,$ відкривається вгору і вниз.
6. Центр$(0,0), a=2 \sqrt{6}, b=4,$ відкривається вліво і вправо.

Відповідь

1. $\frac{(x-2)^{2}}{36}-\frac{(y-7)^{2}}{9}=1$

3. $\frac{(y+3)^{2}}{50}-\frac{(x-10)^{2}}{7}=1$

5. $\frac{(y+8)^{2}}{1}-\frac{x^{2}}{2}=1$

Вправа$\PageIndex{5}$

Графік.

1. $\frac{(x-3)^{2}}{9}-\frac{(y+1)^{2}}{16}=1$
2. $\frac{(x+3)^{2}}{4}-\frac{(y-1)^{2}}{25}=1$
3. $\frac{(x-2)^{2}}{16}-\frac{(y+3)^{2}}{1}=1$
4. $\frac{(y+2)^{2}}{9}-\frac{(x+2)^{2}}{36}=1$
5. $\frac{(y-1)^{2}}{4}-\frac{(x-2)^{2}}{16}=1$
6. $(y+2)^{2}-\frac{(x+3)^{2}}{9}=1$
7. $4(x+3)^{2}-9(y-3)^{2}=36$
8. $16 x^{2}-4(y-1)^{2}=64$
9. $4(y-1)^{2}-25 x^{2}=100$
10. $9 y^{2}-16 x^{2}=144$
11. $\frac{(x-2)^{2}}{12}-\frac{(y-4)^{2}}{9}=1$
12. $\frac{(x+2)^{2}}{4}-\frac{(y-1)^{2}}{8}=1$
13. $\frac{(y+1)^{2}}{5}-\frac{(x-3)^{2}}{2}=1$
14. $\frac{(y-4)^{2}}{3}-\frac{(x+6)^{2}}{18}=1$
15. $4 x^{2}-3(y-3)^{2}=12$
16. $7(x+1)^{2}-2 y^{2}=14$
17. $6 y^{2}-3 x^{2}=18$
18. $10 x^{2}-3 y^{2}=30$

Відповідь

1.

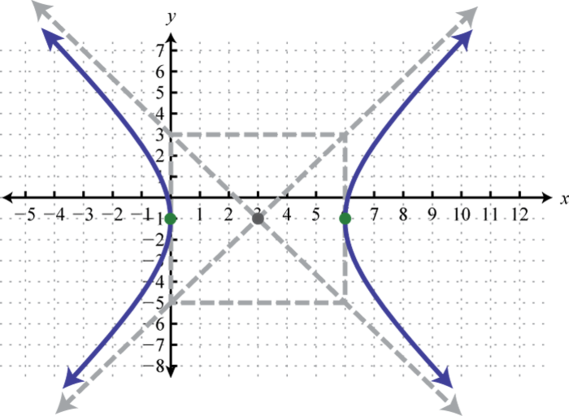
Малюнок$\PageIndex{23}$

3.

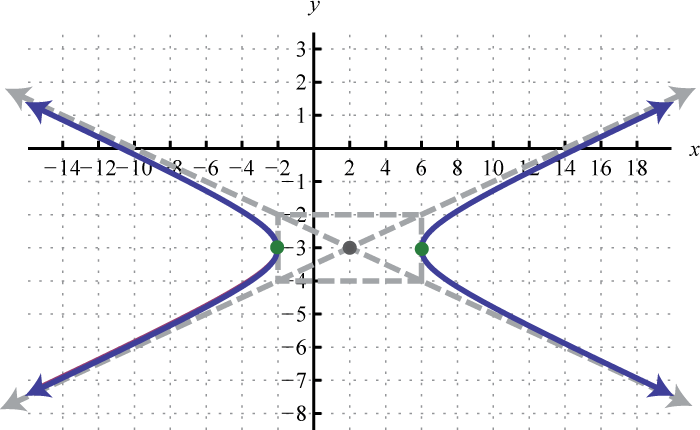
Малюнок$\PageIndex{24}$

5.

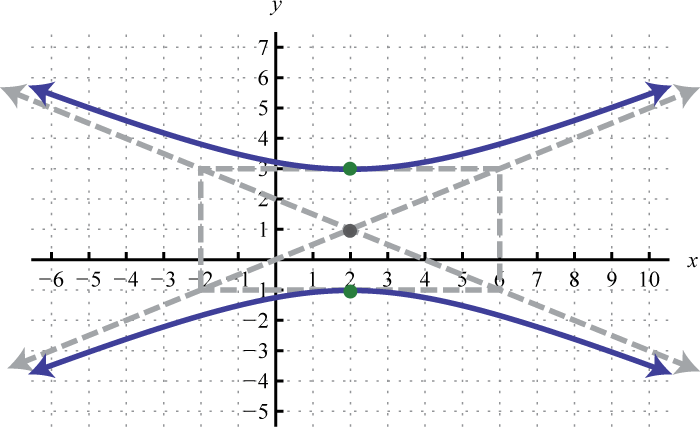
Малюнок$\PageIndex{25}$

7.

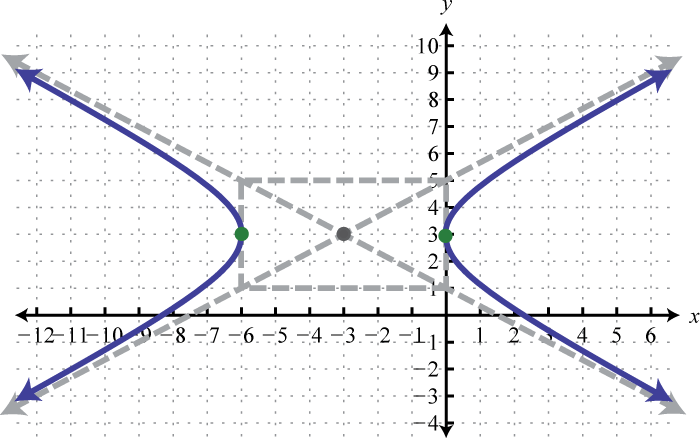
Малюнок$\PageIndex{26}$

9.

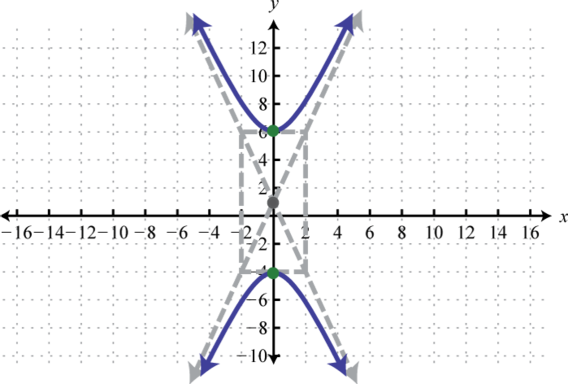
Малюнок$\PageIndex{27}$

11.

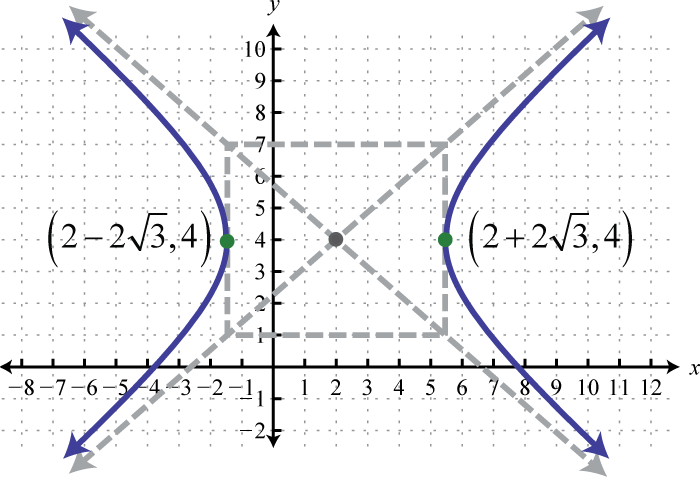
Малюнок$\PageIndex{28}$

13.

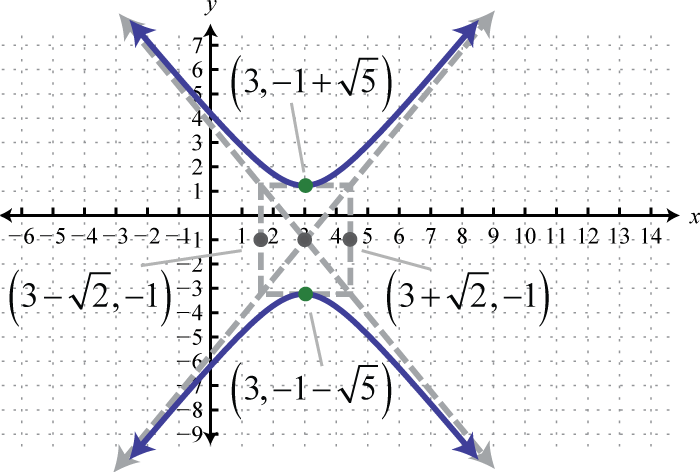
Малюнок$\PageIndex{29}$

15.

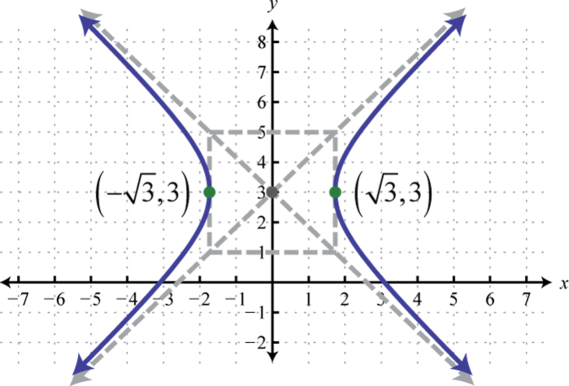
Малюнок$\PageIndex{30}$

17.

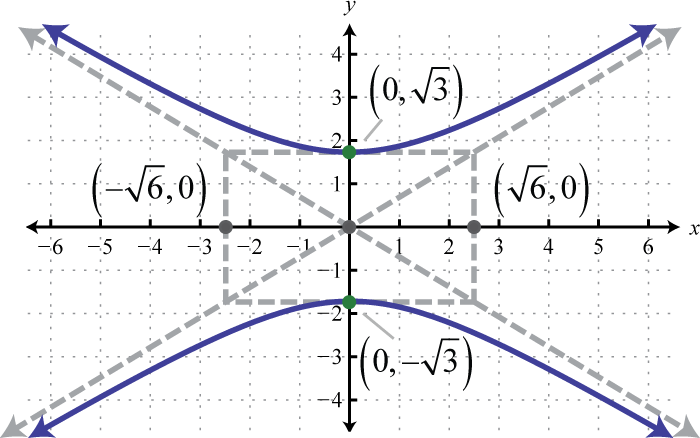
Малюнок$\PageIndex{31}$

Вправа$\PageIndex{6}$

Знайдіть$x$ - і$y$ -перехоплює.

1. $\frac{(x-1)^{2}}{9}-\frac{(y-4)^{2}}{4}=1$
2. $\frac{(x+4)^{2}}{16}-\frac{(y-3)^{2}}{9}=1$
3. $\frac{(y-1)^{2}}{4}-\frac{(x+1)^{2}}{36}=1$
4. $\frac{(y+2)^{2}}{4}-\frac{(x-1)^{2}}{16}=1$
5. $2 x^{2}-3(y-1)^{2}=12$
6. $6(x-5)^{2}-2 y^{2}=12$
7. $36 x^{2}-2 y^{2}=9$
8. $6 y^{2}-4 x^{2}=2$
9. Знайдіть рівняння гіперболи з вершинами$(±2, 3)$ і сполученою віссю, яка вимірює$12$ одиниці виміру.
10. Знайдіть рівняння гіперболи з вершинами$(4, 7)$$(4, 3)$ та сполученою віссю, яка вимірює$6$ одиниці виміру.

Відповідь

1. $x$-перехоплює:$(1 \pm 3 \sqrt{5}, 0)$$y$ -перехоплює: немає

3. $x$-перехоплює: жоден$y$ -перехоплює:$\left(0, \frac{3 \pm \sqrt{37}}{3}\right)$

5. $x$-перехоплює:$\left(\pm \frac{\sqrt{30}}{2}, 0\right)$$y$ -перехоплює: немає

7. $x$-перехоплює:$\left(\pm \frac{1}{2}, 0\right)$$y$ -перехоплює: немає

9. $\frac{x^{2}}{4}-\frac{(y-3)^{2}}{36}=1$

Вправа$\PageIndex{7}$

Перепишіть в стандартній формі і графі.

1. $4 x^{2}-9 y^{2}+16 x+54 y-101=0$
2. $9 x^{2}-25 y^{2}-18 x-100 y-316=0$
3. $4 y^{2}-16 x^{2}-64 x+8 y-124=0$
4. $9 y^{2}-4 x^{2}-24 x-72 y+72=0$
5. $y^{2}-36 x^{2}-72 x-12 y-36=0$
6. $9 y^{2}-x^{2}+8 x-36 y+11=0$
7. $36 x^{2}-4 y^{2}+24 y-180=0$
8. $x^{2}-25 y^{2}-2 x-24=0$
9. $25 x^{2}-64 y^{2}+200 x+640 y-2,800=0$
10. $49 y^{2}-4 x^{2}+40 x+490 y+929=0$
11. $3 x^{2}-2 y^{2}+24 x+8 y+34=0$
12. $4 x^{2}-8 y^{2}-24 x+80 y-196=0$
13. $3 y^{2}-x^{2}-2 x-6 y-16=0$
14. $12 y^{2}-5 x^{2}+40 x+48 y-92=0$
15. $4 x^{2}-16 y^{2}+12 x+16 y-11=0$
16. $4 x^{2}-y^{2}-4 x-2 y-16=0$
17. $4 y^{2}-36 x^{2}+108 x-117=0$
18. $4 x^{2}-9 y^{2}+8 x+6 y-33=0$

Відповідь

1. $\frac{(x+2)^{2}}{9}-\frac{(y-3)^{2}}{4}=1$;

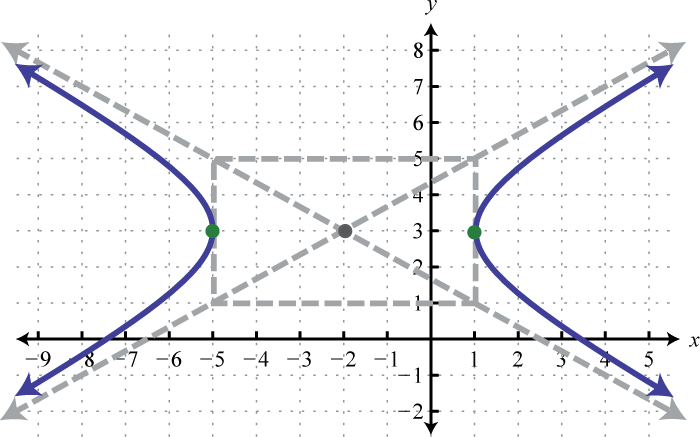
Малюнок$\PageIndex{32}$

3. $\frac{(y+1)^{2}}{16}-\frac{(x+2)^{2}}{4}=1$;

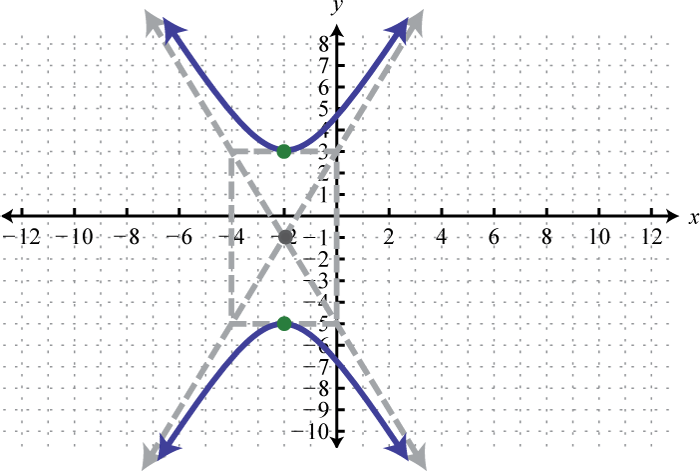
Малюнок$\PageIndex{33}$

5. $\frac{(y-6)^{2}}{36}-(x+1)^{2}=1$;

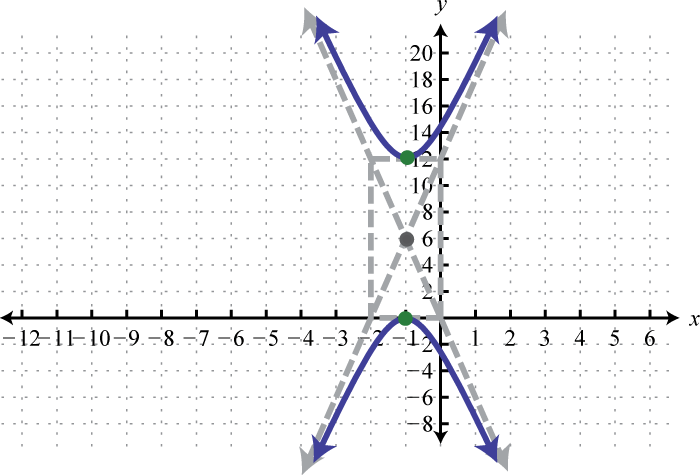
Малюнок$\PageIndex{34}$

7. $\frac{x^{2}}{4}-\frac{(y-3)^{2}}{36}=1$;

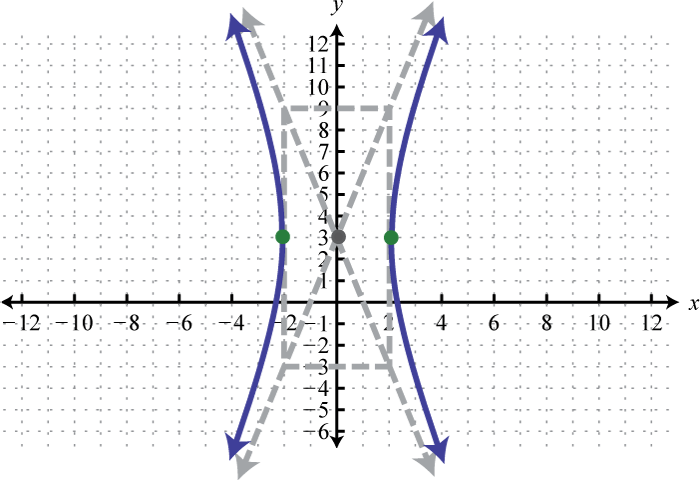
Малюнок$\PageIndex{35}$

9. $\frac{(x+4)^{2}}{64}-\frac{(y-5)^{2}}{25}=1$;

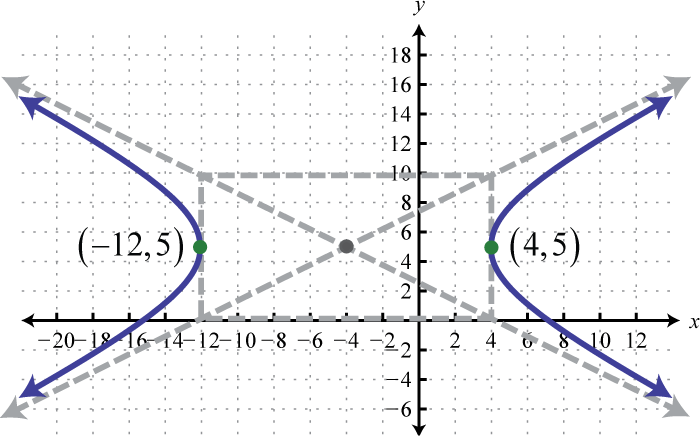
Малюнок$\PageIndex{36}$

11. $\frac{(x+4)^{2}}{2}-\frac{(y-2)^{2}}{3}=1$;

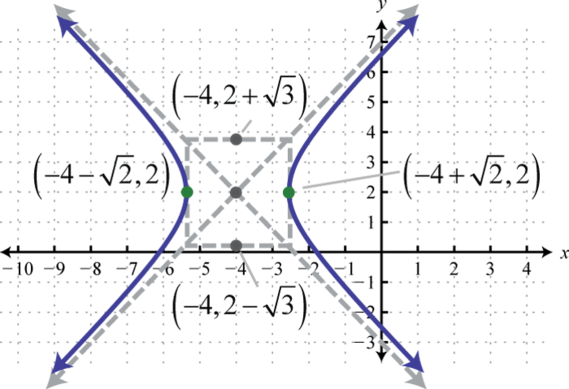
Малюнок$\PageIndex{37}$

13. $\frac{(y-1)^{2}}{6}-\frac{(x+1)^{2}}{18}=1$;

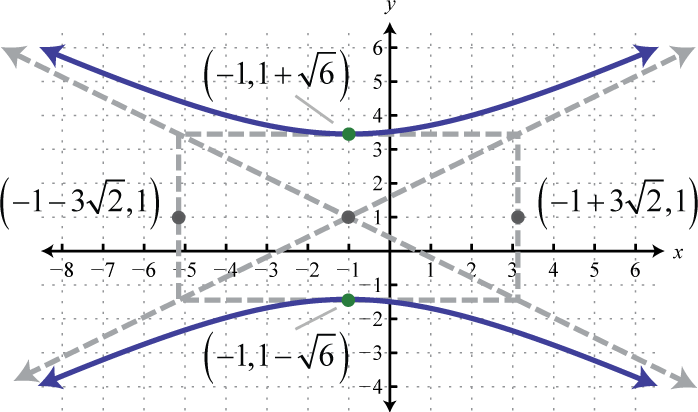
Малюнок$\PageIndex{38}$

15. $\frac{\left(x+\frac{3}{2}\right)^{2}}{4}-\frac{\left(y-\frac{1}{2}\right)^{2}}{1}=1$

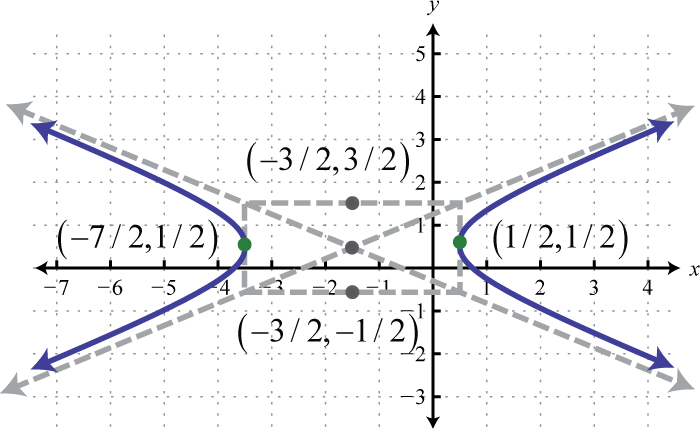
Малюнок$\PageIndex{39}$

17. $\frac{y^{2}}{9}-\left(x-\frac{3}{2}\right)^{2}=1$;

Малюнок$\PageIndex{40}$

Вправа$\PageIndex{8}$

З огляду на загальну форму, визначають перехоплення.

1. $3 x^{2}-y^{2}-11 x-8 y-4=0$
2. $4 y^{2}-8 x^{2}+2 x+9 y-9=0$
3. $x^{2}-y^{2}+2 x+2 y-4=0$
4. $y^{2}-x^{2}+6 y-8 x-16=0$
5. $5 x^{2}-2 y^{2}-4 x-3 y=0$
6. $2 x^{2}-3 y^{2}-4 x-5 y+1=0$

Відповідь

1. $x$-перехоплює:$\left(-\frac{1}{3}, 0\right),(4,0) ; y$ -перехоплює:$(0,-4 \pm 2 \sqrt{3})$

3. $x$-перехоплює:$(-1 \pm \sqrt{5}, 0) ; y$ -перехоплює: немає

5. $x$-перехоплює:$(0,0),\left(\frac{4}{5}, 0\right) ; y$ -перехоплює:$(0,0),\left(0,-\frac{3}{2}\right)$

Вправа$\PageIndex{9}$

Знайдіть рівняння асимптотів заданої гіперболи.

1. $\frac{(y-5)^{2}}{9}-\frac{(x+8)^{2}}{16}=1$
2. $\frac{(x+9)^{2}}{36}-\frac{(y-4)^{2}}{4}=1$
3. $16 x^{2}-4 y^{2}-24 y-96 x+44=0$
4. $4 y^{2}-x^{2}-8 y-4 x-4=0$

Відповідь

1. $y=-\frac{3}{4} x-1, y=\frac{3}{4} x+11$

3. $y=-2 x+3, y=2 x-9$

Вправа$\PageIndex{10}$

З огляду на графік гіперболи, визначають її рівняння в загальному вигляді.

1.

Малюнок$\PageIndex{41}$

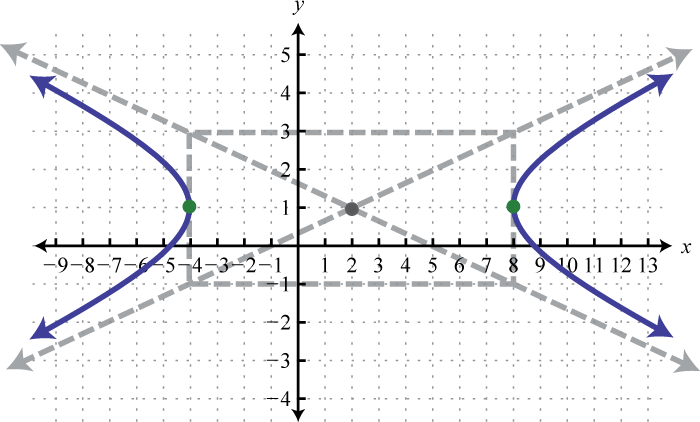
2.

Малюнок$\PageIndex{42}$

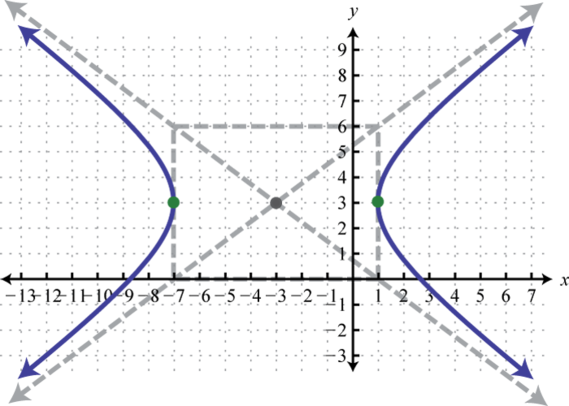
3.

Малюнок$\PageIndex{43}$

4.

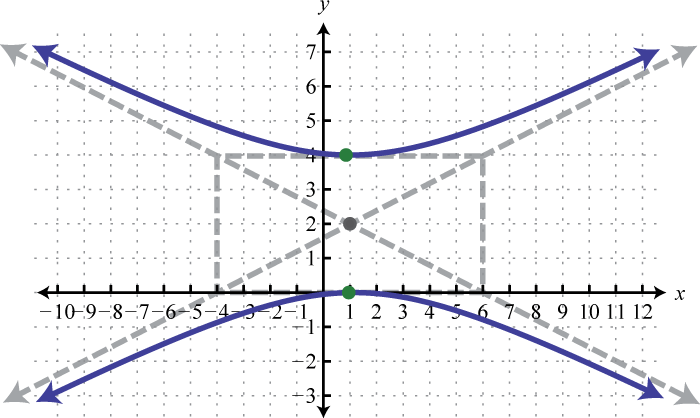
Малюнок$\PageIndex{44}$

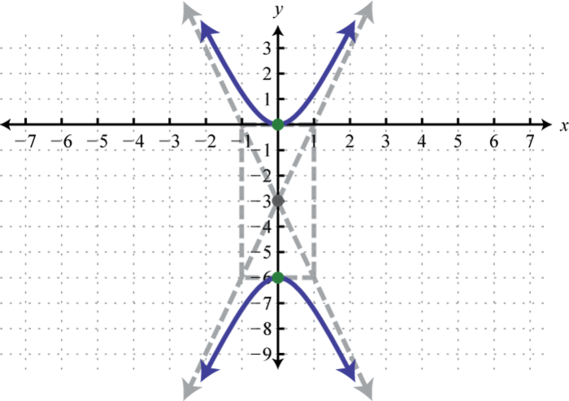
Відповідь

1. $x^{2}-9 y^{2}-4 x+18 y-41=0$

3. $25 y^{2}-4 x^{2}-100 y+8 x-4=0$

Вправа$\PageIndex{11}$

Визначте наступне як рівняння прямої, параболи, кола, еліпса або гіперболи.

1. $x^{2}+y^{2}+10 x-2 y+23=0$
2. $x^{2}+y+2 x-3=0$
3. $2 x^{2}+y^{2}-12 x+14=0$
4. $3 x-2 y=24$
5. $x^{2}-y^{2}+36=0$
6. $4 x^{2}+4 y^{2}-32=0$
7. $x^{2}-y^{2}-2 x+2 y-1=0$
8. $x-y^{2}+2 y+1=0$
9. $3 x+3 y+5=0$
10. $8 x^{2}+4 y^{2}-144 x-12 y+641=0$

Відповідь

1. Коло

3. Еліпс

5. Гіпербола

7. Гіпербола

9. Лінія

Вправа$\PageIndex{12}$

Визначте конічні перетину і перепишіть в стандартному вигляді.

1. $x^{2}-y-6 x+11=0$
2. $x^{2}+y^{2}-12 x-6 y+44=0$
3. $x^{2}-2 y^{2}-4 x-12 y-18=0$
4. $25 y^{2}-2 x^{2}+36 x-50 y-187=0$
5. $7 x^{2}+4 y^{2}-84 x+16 y+240=0$
6. $4 x^{2}+4 y^{2}-80 x+399=0$
7. $4 x^{2}+4 y^{2}+4 x-32 y+29=0$
8. $16 x^{2}-4 y^{2}-32 x+20 y-25=0$
9. $9 x-18 y^{2}+12 y+7=0$
10. $16 x^{2}+12 y^{2}-24 x-48 y+9=0$

Відповідь

1. парабола;$y=(x-3)^{2}+2$

3. гіпербола;$\frac{(x-2)^{2}}{4}-\frac{(y+3)^{2}}{2}=1$

5. Еліпс;$\frac{(x-6)^{2}}{4}+\frac{(y+2)^{2}}{7}=1$

7. коло;$\left(x+\frac{1}{2}\right)^{2}+(y-4)^{2}=9$

9. парабола;$x=2\left(y-\frac{1}{3}\right)^{2}-1$

Вправа$\PageIndex{13}$

1. Розробити формулу рівнянь асимптотів гіперболи. Поділіться ним разом із прикладом на дошці обговорень.
2. Складіть власне рівняння гіперболи, запишіть його в загальному вигляді, і зробіть графік.
3. Чи всі гіперболи мають перехоплення? Які можливі номери перехоплень для гіперболи? Поясніть.
4. Досліджуйте та обговоріть реальні приклади гіпербол.

Відповідь

1. Відповідь може відрізнятися

3. Відповідь може відрізнятися

Виноски

²³ Множина точок на площині, відстані яких від двох нерухомих точок, званих вогнищами, має абсолютну різницю, яка дорівнює позитивній константі.

²⁴ Дві окремі криві гіперболи.

²⁵ Точки на окремих гілках гіперболи, де відстань мінімальна.

²⁶ Рівняння гіперболи записано у$\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1$ вигляді.Центр є$(h, k)$,$a$ визначає поперечну вісь, і$b$ визначає сполучену вісь.

²⁷ Рівняння гіперболи записано у вигляді$\frac{(y-k)^{2}}{b^{2}}-\frac{(x-h)^{2}}{a^{2}}=1$. Центр є$(h, k)$,$b$ визначає поперечну вісь і$a$ визначає сполучену вісь.

²⁸ Відрізок лінії, утворений вершинами гіперболи.

²⁹ Відрізок лінії через центр гіперболи, який перпендикулярний поперечній осі.

³⁰ Прямокутник, утворений за допомогою кінцевих точок гіперболи, поперечних і сполучених осей.

³¹ Рівняння гіперболи записано у вигляді$px^{2} − qy^{2} + cx +dy + e = 0$ або$qy^{2} − px^{2} − cx +dy + e = 0$ де$p, q > 0$.