8.3: Еліпси

Цілі навчання

• Графік еліпса в стандартній формі.
• Визначте рівняння еліпса за заданим його графіком.
• Перепишіть рівняння еліпса в стандартному вигляді.

Еліпс у стандартній формі

Еліпс ¹⁴ - це сукупність точок на площині, відстані яких від двох нерухомих точок, званих вогнищами, мають суму, рівну позитивній константі. Іншими словами, якщо точки$F1$ і$F2$ є осередками (множина фокусу) і$d$ є деякою заданою позитивною константою, то$(x,y)$ це точка на еліпсі, якщо$d=d_{1}+d_{2}$ як показано нижче:

Малюнок$\PageIndex{1}$

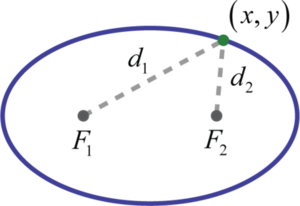
Крім того, еліпс може бути утворений перетином конуса з косою площиною, яка не паралельна стороні конуса і не перетинає підставу конуса. Точки на цій овальній формі, де відстань між ними знаходиться на максимумі, називаються вершинами ¹⁵ і визначають велику вісь ¹⁶. Центром еліпса є середина між вершинами. Мала вісь ¹⁷ - це відрізок лінії через центр еліпса, визначеного двома точками на еліпсі, де відстань між ними мінімально. Кінцеві точки другорядної осі називаються співвершинами ¹⁸.

Малюнок$\PageIndex{2}$

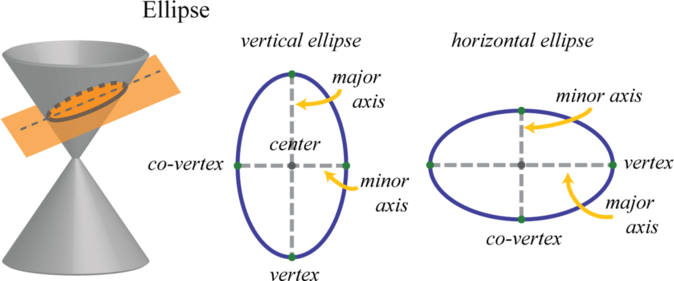
Якщо велика вісь еліпса паралельна$x$ -осі в прямокутній координатній площині, ми говоримо, що еліпс горизонтальний. Якщо велика вісь паралельна$y$ -осі, ми говоримо, що еліпс вертикальний. У цьому розділі ми займаємося лише ескізом цих двох типів еліпсів. Однак еліпс має багато реальних застосувань, і подальші дослідження цього багатого предмета заохочуються. У прямокутній координатній площині, де знаходиться центр горизонтального еліпса$(h,k)$, ми маємо

Малюнок$\PageIndex{3}$

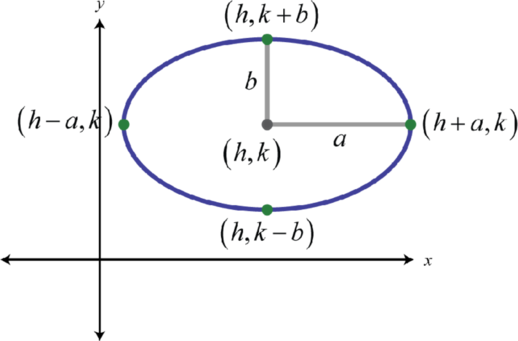
Як на малюнку$a>b$ де$a$, половина довжини великої осі, називається великим радіусом ¹⁹. Причому$b$, одна половина довжини другорядної осі, називається малим радіусом ²⁰. Рівняння еліпса в стандартній формі ²¹ виглядає наступним чином:

$\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$

Вершини є$(h±a,k)$$(h,k±b)$ і орієнтація залежить від$a$ і$b$. Якщо$a>b$, то еліпс горизонтальний, як показано вище, а якщо$a<b$, то еліпс вертикальний і$b$ стає великим радіусом. Як ви думаєте, що відбувається, коли$a=b$?

Таблиця$\PageIndex{1}$

Рівняння	Центр	$a$	$b$	Орієнтація
$\frac{(x-1)^{2}}{4}+\frac{(y-8)^{2}}{9}=1$	$(1,8)$	\ (a\)» style="вертикальне вирівнювання: середина; ">$a=2$	\ (b\)» style="вертикальне вирівнювання: середина; ">$b=3$	Вертикальний
$\frac{(x-3)^{2}}{2}+\frac{(y+5)^{2}}{16}=1$	$(3,-5)$	\ (a\)» style="вертикальне вирівнювання: середина; ">$a=\sqrt{2}$	\ (b\)» style="вертикальне вирівнювання: середина; ">$b=4$	Вертикальний
$\frac{(x+1)^{2}}{1}+\frac{(y-7)^{2}}{8}=1$	$(-1,7)$	\ (a\)» style="вертикальне вирівнювання: середина; ">$a=1$	\ (b\)» style="вертикальне вирівнювання: середина; ">$b=2 \sqrt{2}$	Вертикальний
$\frac{x^{2}}{25}+\frac{(y+6)^{2}}{10}=1$	$(0,-6)$	\ (a\)» style="вертикальне вирівнювання: середина; ">$a=5$	\ (b\)» style="вертикальне вирівнювання: середина; ">$b=\sqrt{10}$	Горизонтальний

Графік еліпса повністю визначається його центром, орієнтацією, великим радіусом і малим радіусом, все це може бути визначено з його рівняння, записаного в стандартній формі.

Приклад$\PageIndex{1}$:

Графік:$\frac{(x+3)^{2}}{4}+\frac{(y-2)^{2}}{25}=1$.

Рішення

Написано в такому вигляді ми бачимо, що центр еліпса є$(−3,2)$$a=\sqrt{4}=2$, і$b=\sqrt{25}=5$. Від центру позначки вказує 2 одиниці вліво і вправо і по 5 одиниць вгору і вниз.

Малюнок$\PageIndex{4}$

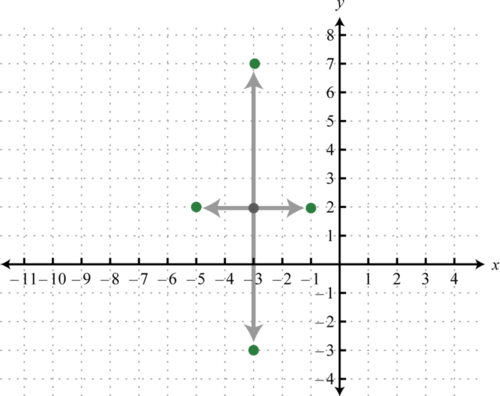
Потім намалюйте еліпс через ці чотири точки.

Відповідь

Малюнок$\PageIndex{5}$

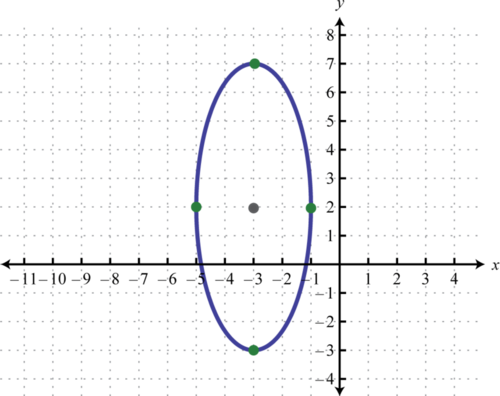
Як і в будь-якому графіку, ми зацікавлені в пошуку$x$ - і$y$ -перехоплення.

Приклад$\PageIndex{2}$

Знайдіть перехоплення:$\frac{(x+3)^{2}}{4}+\frac{(y-2)^{2}}{25}=1$.

Рішення

Щоб знайти набір$x$ -incepts$y=0$:

$\begin{aligned} \frac{(x+3)^{2}}{4}+\frac{(0-2)^{2}}{25} &=1 \\ \frac{(x+3)^{2}}{4}+\frac{4}{25} &=1 \\ \frac{(x+3)^{2}}{4} &=1-\frac{4}{25} \\ \frac{(x+3)^{2}}{4} &=\frac{21}{25} \end{aligned}$

На цьому етапі ми витягуємо корінь, застосовуючи властивість квадратного кореня.

$\begin{aligned} \frac{x+3}{2} &=\pm \sqrt{\frac{21}{25}} \\ x+3 &=\pm \frac{2 \sqrt{21}}{5} \\ x &=-3 \pm \frac{2 \sqrt{21}}{5}=\frac{-15 \pm 2 \sqrt{21}}{5} \end{aligned}$

Установка$x=0$ і рішення для$y$ призводить до складних рішень, отже, немає$y$ -перехоплень. Це залишають як вправу.

Відповідь:

$x$-перехоплює:$\left(\frac{-15 \pm 2 \sqrt{21}}{5}, 0\right)$;$y$ -перехоплює: немає.

На відміну від кола, стандартна форма для еліпса вимагає з одного$1$ боку його рівняння.

Приклад$\PageIndex{3}$:

Графік і позначення перехоплень:$(x-2)^{2}+9(y-1)^{2}=9$.

Рішення

Щоб отримати стандартну форму, з правого$1$ боку розділіть обидві сторони на$9$.

$\begin{aligned} \frac{(x-2)^{2}+9(y-1)^{2}}{\color{Cerulean}{9}} &\color{black}{=}\frac{9}{\color{Cerulean}{9}} \\ \frac{(x-2)^{2}}{9}+\frac{9(y-1)^{2}}{9} &=\frac{9}{9} \\ \frac{(x-2)^{2}}{9}+\frac{(y-1)^{2}}{1} &=1 \end{aligned}$

Тому центр еліпса - це$(2,1)$$a=\sqrt{9}=3$, і$b=\sqrt{1}=1$. Графік виглядає наступним чином:

Малюнок$\PageIndex{6}$

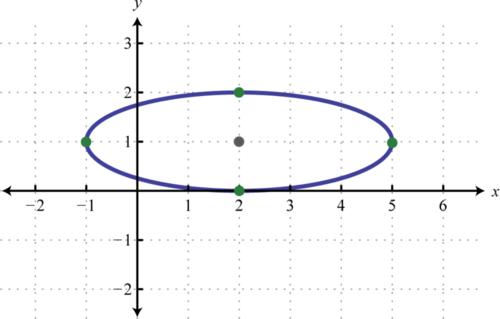
Щоб знайти перехоплення, ми можемо скористатися стандартною формою$\frac{(x-2)^{2}}{9}+(y-1)^{2}=1$:

Таблиця$\PageIndex{2}$

$x$-перехоплює набір$y=0$	$y$-перехоплює набір$x=0$
$\begin{array}{r}{\frac{(x-2)^{2}}{9}+(\color{Cerulean}{0}\color{black}{-}1)^{2}=1} \\ {\frac{(x-2)^{2}}{9}+1=1} \\ {(x-2)^{2}=0} \\ {x-2=0} \\ {x=2}\end{array}$	$\begin{aligned} \frac{(\color{Cerulean}{0}\color{black}{-}2)^{2}}{9}+(y-1)^{2} &=1 \\ \frac{4}{9}+(y-1)^{2} &=1 \\(y-1)^{2} &=\frac{5}{9} \\ y-1 &=\pm \sqrt{\frac{5}{9}} \\ y &=1 \pm \frac{\sqrt{5}}{3}=\frac{3 \pm \sqrt{5}}{3} \end{aligned}$

Тому$x$ -перехоплення є$(2,0)$ і$y$ -перехоплення є$\left(0, \frac{3+\sqrt{5}}{3}\right)$ і$\left(0, \frac{3-\sqrt{5}}{3}\right)$.

Відповідь:

Малюнок$\PageIndex{7}$

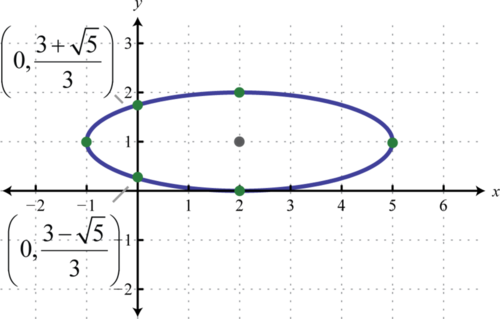
Розглянемо еліпс по центру в початковій точці,

$x^{2}+\frac{y^{2}}{4}=1$

З огляду на це рівняння, ми можемо записати,

$\frac{(x-0)^{2}}{1^{2}}+\frac{(y-0)^{2}}{2^{2}}=1$

У такому вигляді зрозуміло, що центр є$(0,0)$$a=1$, і$b=2$. Крім того, якщо ми вирішимо для,$y$ ми отримаємо дві функції:

$\begin{aligned} x^{2}+\frac{y^{2}}{4} &=1 \\ \frac{y^{2}}{4} &=1-x^{2} \\ y^{2} &=4\left(1-x^{2}\right) \\ y &=\pm \sqrt{4\left(1-x^{2}\right)} \\ y &=\pm 2 \sqrt{1-x^{2}} \end{aligned}$

Функція,$y=2 \sqrt{1-x^{2}}$ визначена, є верхньою половиною еліпса, а функція, визначена,$y=-2 \sqrt{1-x^{2}}$ є нижньою половиною.

Малюнок$\PageIndex{8}$

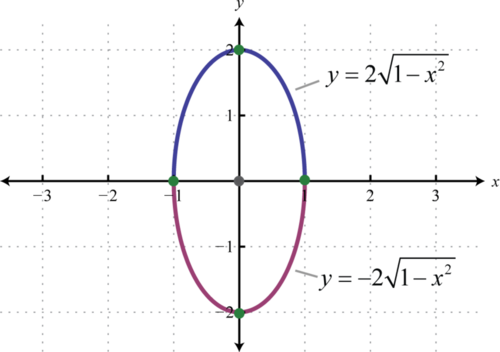
Вправа$\PageIndex{1}$

Графік:$9(x-3)^{2}+4(y+2)^{2}=36$.

Відповідь

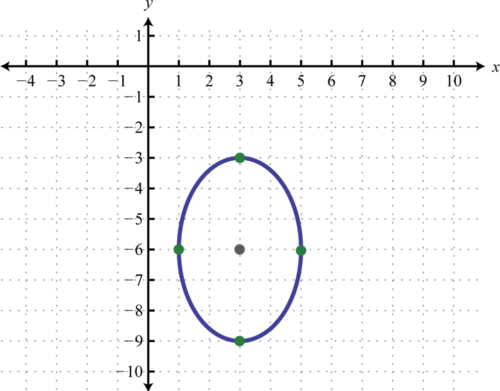
Малюнок$\PageIndex{9}$

Еліпс у загальній формі

Ми бачили, що графік еліпса повністю визначається його центром, орієнтацією, великим радіусом та малим радіусом; що можна прочитати з його рівняння в стандартній формі. Однак рівняння не завжди дається в стандартній формі. Рівняння еліпса в загальному вигляді ²² випливає,

$p x^{2}+q y^{2}+c x+d y+e=0$

де$p,q>0$. Етапи побудови графіка еліпса з урахуванням його рівняння в загальному вигляді викладені в наступному прикладі.

Приклад$\PageIndex{4}$:

Графік$2 x^{2}+9 y^{2}+16 x-90 y+239=0$.

Рішення

Почніть з перезапису рівняння в стандартному вигляді.

Крок 1: Згрупуйте терміни з однаковими змінними і перемістіть константу в праву сторону. Фактор так, що провідний коефіцієнт кожної угруповання є$1$.

$\begin{aligned} 2 x^{2}+9 y^{2}+16 x-90 y+239 &=0 \\ \left(2 x^{2}+16 x+\_\_\_\right.)+\left(9 y^{2}-90 y+\_\_\_\right)&=-239 \\ 2\left(x^{2}+8x+\_\_\_ \right)+9\left(y^{2}-10y+\_\_\_ \right)&=-239 \end{aligned}$

Крок 2: Заповніть квадрат для кожного угруповання. У цьому випадку для термінів, що передбачають$x$ використання,$\left(\frac{8}{2}\right)^{2}=4^{2}=16$ і для термінів, пов'язаних з$y$ використанням$\left(\frac{-10}{2}\right)^{2}=(-5)^{2}=25$. Коефіцієнт перед групуванням впливає на значення, яке використовується для збалансування рівняння з правого боку:

$2\color{black}{\left(x^{2}+8 x\color{Cerulean}{+16}\right)+}9\color{black}{\left(y^{2}-10 y\color{OliveGreen}{+25}\right)=}-239\color{Cerulean}{+32}\color{OliveGreen}{+225}$

Через властивість distributive додавання$16$ всередині першого групування еквівалентно додаванню$2⋅16=32$. Аналогічно, додавання$25$ всередині другого групування еквівалентно додаванню$9⋅25=225$. Тепер коефіцієнт, а потім ділимо, щоб отримати$1$ на правій стороні.

$\begin{aligned}2(x+4)^{2}+9(y-5)^{2}&=18 \\ \frac{2(x+4)^{2}+9(y-5)^{2}}{\color{Cerulean}{18}}&\color{black}{=}\frac{18}{\color{Cerulean}{18}} \\ \frac{2(x+4)^{2}}{18}+\frac{9(y-5)^{2}}{18}&=\frac{18}{18} \\ \frac{(x+4)^{2}}{9}+\frac{(y-5)^{2}}{2}&=1\end{aligned}$

Крок 3: Визначте центр$a$, і$b$. При цьому центр - це$(−4,5)$$a=\sqrt{9}=3$, і$b=\sqrt{2}$.

Крок 4: Використовуйте a, щоб позначити вершини ліворуч і праворуч від центру, використовуйте b, щоб позначити вершини вгору і вниз від центру, а потім намалюйте графік. При цьому вершини уздовж другорядних осей не$(-4,5 \pm \sqrt{2})$ видно і повинні бути марковані.

Малюнок$\PageIndex{10}$

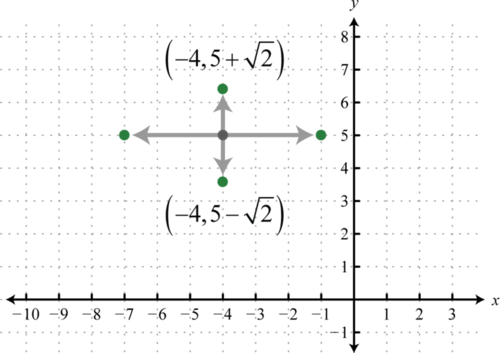
Відповідь:

Малюнок$\PageIndex{11}$

Приклад$\PageIndex{5}$:

Визначте центр еліпса, а також довжини великих і другорядних осей:$5 x^{2}+y^{2}-3 x+40=0$.

Рішення

У цьому прикладі нам потрібно лише заповнити квадрат для термінів, що беруть участь$x$.

$\begin{aligned} 5 x^{2}+y^{2}-30 x+40 &=0 \\ \left(5 x^{2}-30 x+ \_\_\_\right)+y^{2}&=-40 \\5\left(x^{2}-6x+\_\_\_ \right)+y^{2}&=-40 \end{aligned}$

Використовуйте$\left(\frac{-6}{2}\right)^{2}=(-3)^{2}=9$ для першого угруповання, щоб бути збалансованим$5⋅9=45$ на правій стороні.

$\begin{aligned} 5\color{black}{\left(x^{2}-6 x\color{Cerulean}{+9}\right)+}y^{2} &=-40\color{Cerulean}{+45} \\ 5(x-3)^{2}+y^{2} &=5 \\ \frac{5(x-3)^{2}+y^{2}}{\color{Cerulean}{5}} &\color{black}{=}\frac{5}{\color{Cerulean}{5}} \\ \frac{(x-3)^{2}}{1}+\frac{y^{2}}{5} &=1 \end{aligned}$

Тут центр знаходиться$(3,0)$$a=\sqrt{1}=1$, і$b=\sqrt{5}$. $b$Оскільки більше$a$, ніж, довжина великої$2b$ осі є, а довжина другорядної осі є$2a$.

Відповідь

Центр:$(3,0)$; велика вісь: 2$\sqrt{5}$ одиниці; незначна вісь:$2$ одиниці.

Вправа$\PageIndex{2}$

Графік$x^{2}+4 y^{2}+10 x-16 y+25=0$.

Відповідь

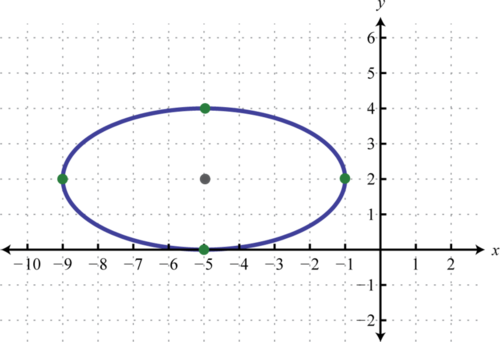
Малюнок$\PageIndex{12}$

www.youtube.com/В/МНП7С5Х2820

Ключові виноси

• Графік еліпса повністю визначається його центром, орієнтацією, великим радіусом і малим радіусом.
• Центр, орієнтація, великий радіус і малий радіус очевидні, якщо рівняння еліпса дано в стандартній формі:$\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$.
• Щоб намалювати еліпс, позначте точки$a$ ліворуч і праворуч від центру та$b$ вказують одиниці вгору та вниз від центру. Намалюйте еліпс через ці точки.
• Орієнтація еліпса визначається$a$ і$b$. Якщо$a>b$ тоді еліпс ширше, ніж він високий і вважається горизонтальним еліпсом. Якщо a<ba<b, то еліпс вищий за ширину і вважається вертикальним еліпсом.
• Якщо рівняння еліпса задано в загальному вигляді$p x^{2}+q y^{2}+c x+d y+e=0$ де$p,q>0$, згрупуйте члени з однаковими змінними і заповніть квадрат для обох групувань.
• Ми визнаємо рівняння еліпса, якщо воно квадратичне в обох$x$ і$y$ і коефіцієнти кожного квадратного члена мають однаковий знак.

Вправа$\PageIndex{3}$

Враховуючи рівняння еліпса в стандартній формі, визначте його центр, орієнтацію, великий радіус і малий радіус.

1. $\frac{(x-1)^{2}}{4}+\frac{(y+2)^{2}}{49}=1$
2. $\frac{(x+3)^{2}}{64}+\frac{(y-2)^{2}}{9}=1$
3. $\frac{x^{2}}{3}+(y+9)^{2}=1$
4. $\frac{(x-1)^{2}}{8}+y^{2}=1$
5. $4(x+5)^{2}+9(y+5)^{2}=36$
6. $16(x-1)^{2}+3(y+10)^{2}=48$

Відповідь

1. Центр:$(1, −2)$; орієнтація: вертикальна; великий радіус:$7$ одиниці виміру; малий радіус:$2$ одиниці;$a = 2; b = 7$

3. Центр:$(0, −9)$; орієнтація: горизонтальна; великий радіус:$\sqrt{3}$ одиниці виміру; малий радіус:$1$ одиниця;$a=\sqrt{3} ; b=1$

5. Центр:$(−5, −5)$; орієнтація: горизонтальна; великий радіус:$3$ одиниці виміру; малий радіус:$2$ одиниці виміру;$a = 3; b = 2$

Вправа$\PageIndex{4}$

Визначити стандартну форму для рівняння еліпса за даними наступної інформації.

1. Центр$(3,4)$ з$a=5$ і$b=2$.
2. Центр$(-1,9)$ з$a=7$ і$b=3$.
3. Центр$(5,-1)$ з$a=\sqrt{6}$ і$b=2 \sqrt{3}$.
4. Центр$(-7,-2)$ з$a=5 \sqrt{2}$ і$b=\sqrt{7}$.
5. Центр$(0,-3)$ з$a=1$ і$b=\sqrt{5}$.
6. Центр$(0,0)$ з$a=\sqrt{2}$ і$b=4$.

Відповідь

1. $\frac{(x-3)^{2}}{25}+\frac{(y-4)^{2}}{4}=1$

3. $\frac{(x-5)^{2}}{6}+\frac{(y+1)^{2}}{12}=1$

5. $x^{2}+\frac{(y+3)^{2}}{5}=1$

Вправа$\PageIndex{5}$

Графік.

1. $\frac{(x-4)^{2}}{4}+\frac{(y+2)^{2}}{9}=1$
2. $\frac{(x+1)^{2}}{25}+\frac{(y-2)^{2}}{4}=1$
3. $\frac{(x-5)^{2}}{16}+\frac{(y+6)^{2}}{1}=1$
4. $\frac{(x+4)^{2}}{4}+\frac{(y+3)^{2}}{36}=1$
5. $\frac{(x-2)^{2}}{9}+\frac{(y-1)^{2}}{64}=1$
6. $\frac{(x+1)^{2}}{49}+(y+3)^{2}=1$
7. $4(x+3)^{2}+9(y-3)^{2}=36$
8. $16 x^{2}+(y-1)^{2}=16$
9. $4(x-2)^{2}+25 y^{2}=100$
10. $81 x^{2}+y^{2}=81$
11. $\frac{(x-2)^{2}}{8}+\frac{(y-4)^{2}}{9}=1$
12. $\frac{(x+1)^{2}}{4}+\frac{(y-1)^{2}}{12}=1$
13. $\frac{(x-6)^{2}}{2}+\frac{(y+2)^{2}}{5}=1$
14. $\frac{(x+3)^{2}}{18}+\frac{(y-5)^{2}}{3}=1$
15. $3 x^{2}+2(y-3)^{2}=6$
16. $5(x+1)^{2}+3 y^{2}=15$
17. $4 x^{2}+6 y^{2}=24$
18. $5 x^{2}+10 y^{2}=50$

Відповідь

1.

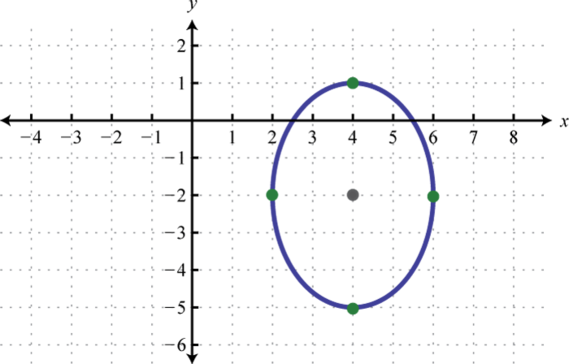
Малюнок$\PageIndex{13}$

3.

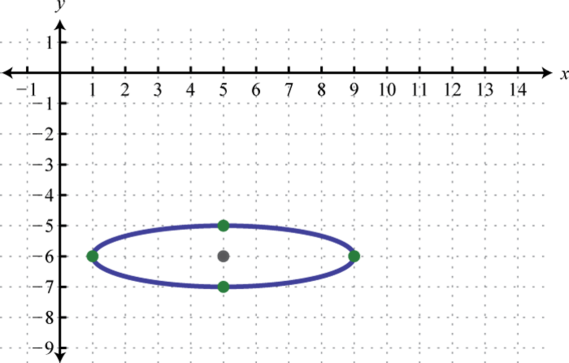
Малюнок$\PageIndex{14}$

5.

Малюнок$\PageIndex{15}$

7.

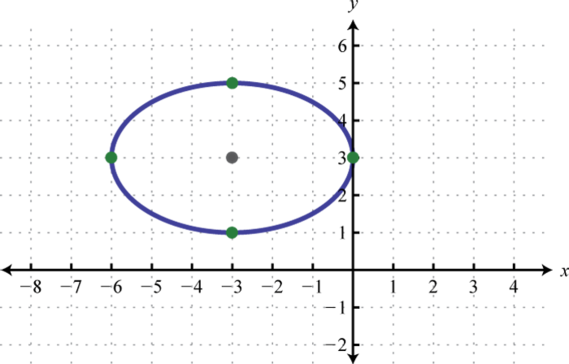
Малюнок$\PageIndex{16}$

9.

Малюнок$\PageIndex{17}$

11.

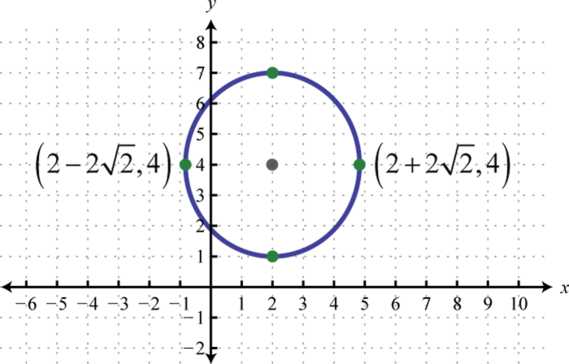
Малюнок$\PageIndex{18}$

13.

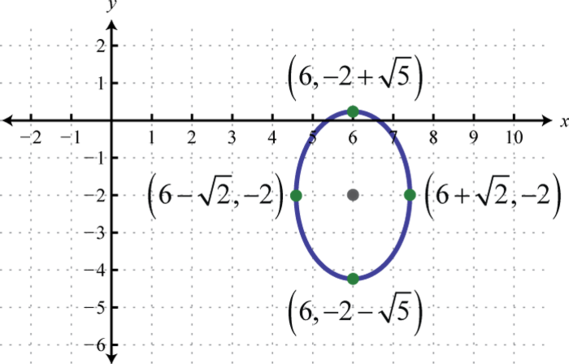
Малюнок$\PageIndex{19}$

15.

Малюнок$\PageIndex{20}$

17.

Малюнок$\PageIndex{21}$

Вправа$\PageIndex{6}$

Знайдіть$x$ - і$y$ -перехоплює.

1. $\frac{(x-3)^{2}}{4}+\frac{(y-2)^{2}}{9}=1$
2. $\frac{(x+3)^{2}}{16}+\frac{(y-7)^{2}}{9}=1$
3. $\frac{(x-2)^{2}}{4}+\frac{(y+6)^{2}}{36}=1$
4. $\frac{(x+1)^{2}}{25}+\frac{(y-1)^{2}}{9}=1$
5. $5 x^{2}+2(y-4)^{2}=20$
6. $4(x-3)^{2}+9 y^{2}=72$
7. $5 x^{2}+2 y^{2}=10$
8. $3 x^{2}+4 y^{2}=24$

Відповідь

1. $x$-перехоплює:$\left(\frac{9 \pm 2 \sqrt{5}}{3}, 0\right)$;$y$ -перехоплює: немає

3. $x$-перехоплює:$(2,0)$;$y$ -перехоплює:$(0,-6$

5. $x$-перехоплює: немає;$y$ -перехоплює:$(0,4 \pm \sqrt{10})$

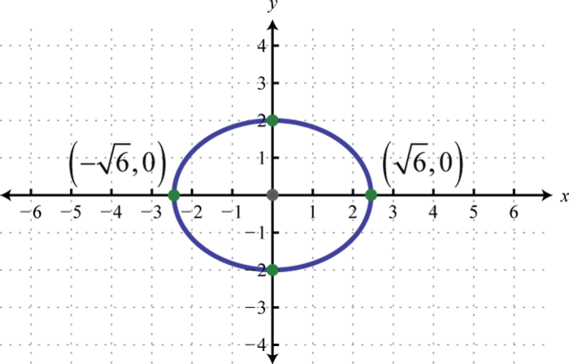
7. $x$-перехоплює:$(\pm \sqrt{2}, 0)$;$y$ -перехоплює:$(0, \pm \sqrt{5})$

Вправа$\PageIndex{7}$

Знайдіть рівняння еліпса.

1. Еліпс з вершинами$(±5, 0)$ і$(0, ±6)$.
2. Еліпс, велика вісь якого має вершини,$(2, 9)$$(2, −1)$ а незначна вісь має вершини$(−2, 4)$ і$(6, 4)$.
3. Еліпс, велика вісь якого має вершини,$(−8, −2)$$(0, −2)$ а незначна вісь має довжину$4$ одиниць.
4. Еліпс, велика вісь якого має вершини,$(−2, 2)$$(−2, 8)$ а незначна вісь має довжину$2$ одиниць.

Відповідь

1. $\frac{x^{2}}{25}+\frac{y^{2}}{36}=1$

3. $\frac{(x+4)^{2}}{16}+\frac{(y+2)^{2}}{4}=1$

Вправа$\PageIndex{8}$

Перепишіть в стандартній формі і графі.

1. $4 x^{2}+9 y^{2}+8 x-36 y+4=0$
2. $9 x^{2}+25 y^{2}-18 x+100 y-116=0$
3. $4 x^{2}+49 y^{2}+24 x+98 y-111=0$
4. $9 x^{2}+4 y^{2}-72 x+24 y+144=0$
5. $x^{2}+64 y^{2}-12 x+128 y+36=0$
6. $16 x^{2}+y^{2}-96 x-4 y+132=0$
7. $36 x^{2}+4 y^{2}-40 y-44=0$
8. $x^{2}+9 y^{2}-2 x-8=0$
9. $x^{2}+9 y^{2}-4 x-36 y-41=0$
10. $16 x^{2}+y^{2}+160 x-10 y+361=0$
11. $4 x^{2}+5 y^{2}+32 x-20 y+64=0$
12. $2 x^{2}+3 y^{2}-8 x-30 y+65=0$
13. $8 x^{2}+5 y^{2}-16 x+10 y-27=0$
14. $7 x^{2}+2 y^{2}+28 x-16 y+46=0$
15. $36 x^{2}+16 y^{2}-36 x-32 y-119=0$
16. $16 x^{2}+100 y^{2}+64 x-300 y-111=0$
17. $x^{2}+4 y^{2}-20 y+21=0$
18. $9 x^{2}+y^{2}+12 x-2 y-4=0$

Відповідь

1. $\frac{(x+1)^{2}}{9}+\frac{(y-2)^{2}}{4}=1$;

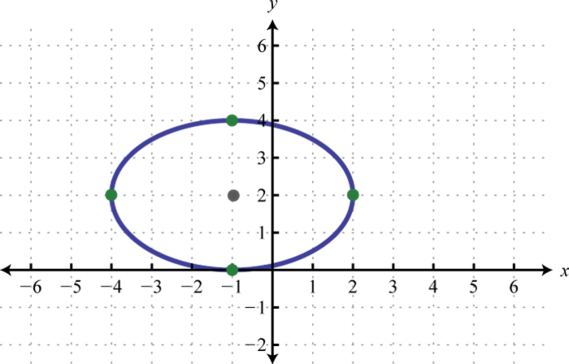
Малюнок$\PageIndex{22}$

3. $\frac{(x+3)^{2}}{49}+\frac{(y+1)^{2}}{4}=1$;

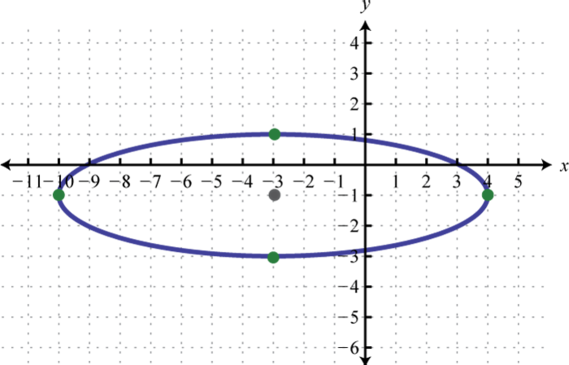
Малюнок$\PageIndex{23}$

5. $\frac{(x-6)^{2}}{64}+(y+1)^{2}=1$;

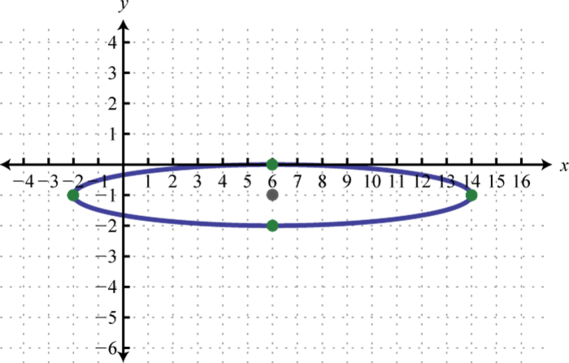
Малюнок$\PageIndex{24}$

7. $\frac{x^{2}}{4}+\frac{(y-5)^{2}}{36}=1$;

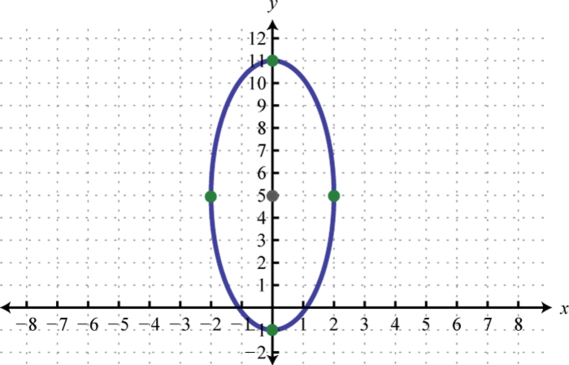
Малюнок$\PageIndex{25}$

9. $\frac{(x-2)^{2}}{81}+\frac{(y-2)^{2}}{9}=1$;

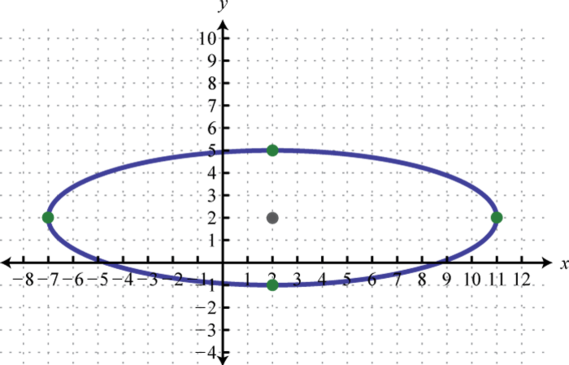
Малюнок$\PageIndex{26}$

11. $\frac{(x+4)^{2}}{5}+\frac{(y-2)^{2}}{4}=1$;

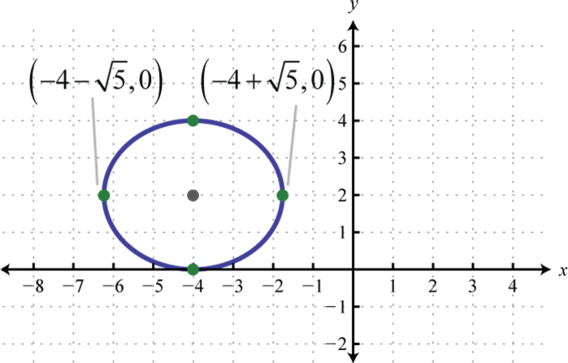
Малюнок$\PageIndex{27}$

13. $\frac{(x-1)^{2}}{5}+\frac{(y+1)^{2}}{8}=1$;

Малюнок$\PageIndex{28}$

15. $\frac{\left(x-\frac{1}{2}\right)^{2}}{4}+\frac{(y-1)^{2}}{9}=1$;

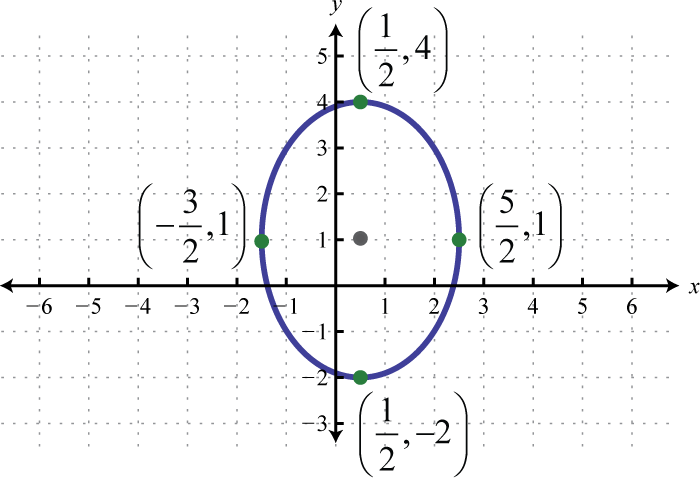
Малюнок$\PageIndex{29}$

17. $\frac{x^{2}}{4}+\left(y-\frac{5}{2}\right)^{2}=1$;

Малюнок$\PageIndex{30}$

Вправа$\PageIndex{9}$

У загальній формі визначають перехоплення.

1. $5 x^{2}+4 y^{2}-20 x+24 y+36=0$
2. $4 x^{2}+3 y^{2}-8 x+6 y-5=0$
3. $6 x^{2}+y^{2}-12 x+4 y+4=0$
4. $8 x^{2}+y^{2}-6 y-7=0$
5. $5 x^{2}+2 y^{2}-20 x-8 y+18=0$
6. $2 x^{2}+3 y^{2}-4 x-5 y+1=0$

Відповідь

1. $x$-перехоплює: немає;$y$ -перехоплює:$(0,-3)$

3. $x$-перехоплює:$\left(\frac{3 \pm \sqrt{3}}{3}, 0\right)$;$y$ -перехоплює:$(0,-2)$

5. $x$-перехоплює:$\left(\frac{10 \pm \sqrt{10}}{5}, 0\right)$;$y$ -перехоплює: немає

Вправа$\PageIndex{10}$

Визначте площу еліпса. (Площа еліпса задається формулою$A = πab$, де$a$ і$b$ є довжинами великого радіуса і малого радіуса.)

1. $\frac{(x-10)^{2}}{25}+\frac{(y+3)^{2}}{5}=1$
2. $\frac{(x+1)^{2}}{18}+\frac{y^{2}}{36}=1$
3. $7 x^{2}+3 y^{2}-14 x+36 y+94=0$
4. $4 x^{2}+8 y^{2}+20 x-8 y+11=0$

Відповідь

1. $5\pi \sqrt{5}$квадратні одиниці

3. $\pi \sqrt{21}$квадратні одиниці

Вправа$\PageIndex{11}$

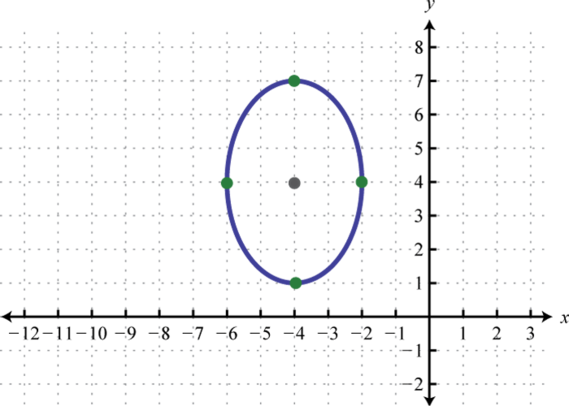
З огляду на графік еліпса, визначте його рівняння в загальному вигляді.

1.

Малюнок$\PageIndex{31}$

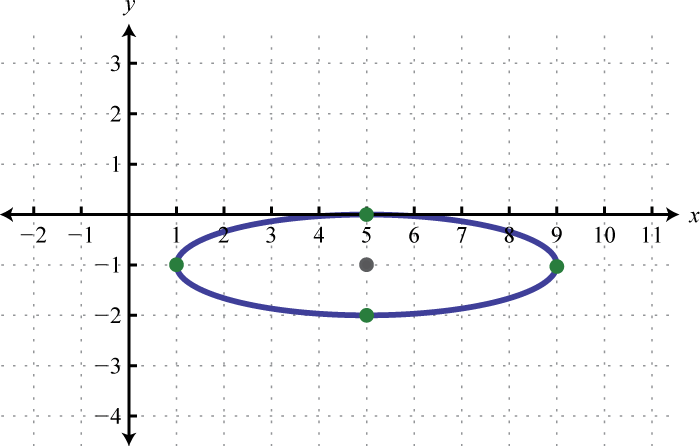
2.

Малюнок$\PageIndex{32}$

3.

Малюнок$\PageIndex{33}$

4.

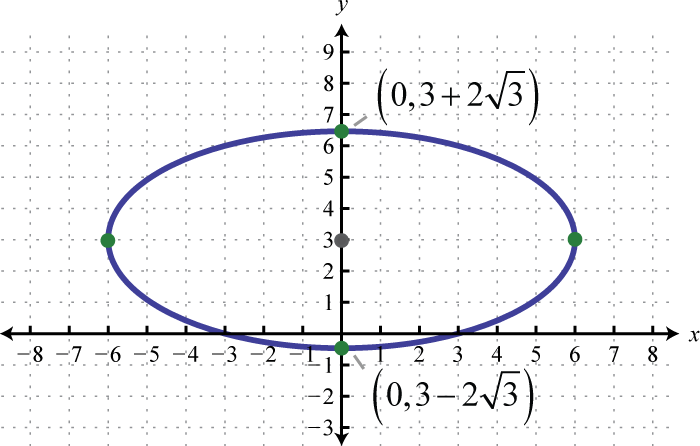
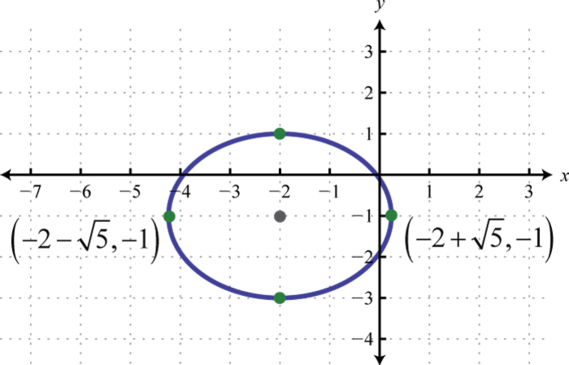
Малюнок$\PageIndex{34}$

Відповідь

1. $9 x^{2}+4 y^{2}+72 x-32 y+172=0$

3. $x^{2}+3 y^{2}-18 y-9=0$

Вправа$\PageIndex{12}$

1. Поясніть, чому коло можна вважати дуже особливим еліпсом.
2. Складіть власне рівняння еліпса, запишіть його в загальному вигляді і зробіть графік.
3. Чи всі еліпси мають перехоплення? Які можливі числа перехоплень для еліпса? Поясніть.
4. Досліджуйте та обговоріть реальні приклади еліпсів.

Відповідь

1. Відповідь може відрізнятися

3. Відповідь може відрізнятися

Виноски

¹⁴ Множина точок на площині, відстані яких від двох нерухомих точок мають суму, рівну позитивній константі.

¹⁵ Точки на еліпсі, які позначають кінцеві точки великої осі.

¹⁶ Відрізок лінії через центр еліпса визначається двома точками на еліпсі, де відстань між ними максимальна.

¹⁷ Відрізок лінії через центр еліпса визначається двома точками на еліпсі, де відстань між ними мінімальна.

¹⁸ Точки на еліпсі, які позначають кінцеві точки другорядної осі.

¹⁹ Одна половина довжини великої осі.

²⁰ Одна половина довжини другорядної осі.

²¹ Рівняння еліпса записано у$\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$ вигляді.Центр є$(h, k)$ і більше$a$ і$b$ є великим радіусом і меншим є малий радіус.

²² Рівняння еліпса записано у вигляді$p x^{2}+q y^{2}+c x+d y+e=0$ де$p, q > 0$.