12.1: Еліпс
- Page ID
- 59453
- Запишіть рівняння еліпсів в стандартній формі.
- Еліпси графа з центром у початковому місці.
- Еліпси графа не зосереджені на початку координат.
- Вирішуємо прикладні завдання за участю еліпсів.
Ви можете собі уявити, що стоїть на одному кінці великої кімнати і все ще можете почути шепіт від людини, що стоїть на іншому кінці? Національний статуарний зал у Вашингтоні, округ Колумбія, показаний на малюнку\(\PageIndex{1}\), є такою кімнатою. Це кімната овальної форми, яку називають шепочної камерою, оскільки форма дозволяє звуку подорожувати вздовж стін. У цьому розділі ми дослідимо форму цієї кімнати та її реальні програми, включаючи те, наскільки далеко один від одного двоє людей у Статуарному залі можуть стояти і все ще чути один одного шепіт.

Ілюстрація\(\PageIndex{1}\): Національний скульптурний зал у Вашингтоні, округ Колумбія (кредит: Грег Палмер, Flickr)
Написання рівнянь еліпсів у стандартній формі
Конічний перетин, або конічний, являє собою форму, отриману в результаті перетину прямого кругового конуса з площиною. Кут, під яким площину перетинає конус, визначає форму, як показано на малюнку\(\PageIndex{2}\).
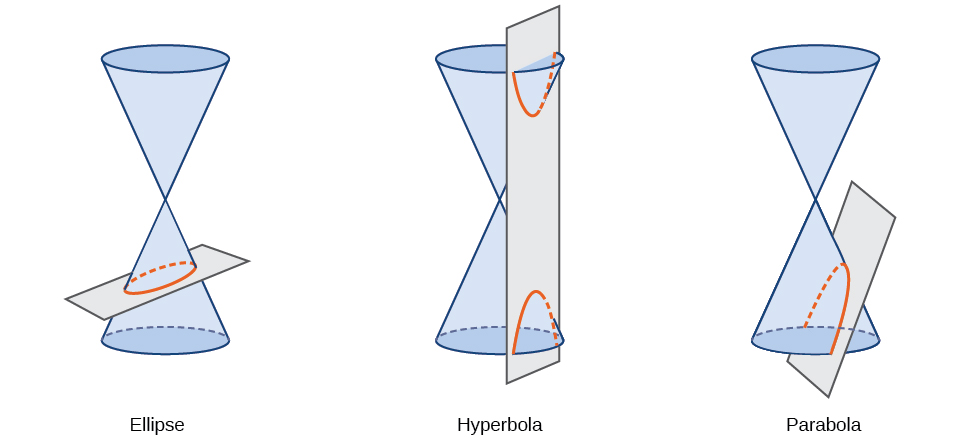
Малюнок\(\PageIndex{2}\)
Конічні перерізи також можуть бути описані множиною точок в координатній площині. Пізніше в цьому розділі ми побачимо, що графік будь-якого квадратного рівняння у двох змінних є конічним перерізом. Ознаки рівнянь і коефіцієнти змінних членів визначають форму. Цей розділ присвячений чотирьом варіаціям стандартної форми рівняння для еліпса. Еліпс - це сукупність всіх точок\((x,y)\) на площині таким чином, що сума їх відстаней від двох нерухомих точок є постійною. Кожна нерухома точка називається фокусом (множина: вогнища).
Ми можемо намалювати еліпс, використовуючи шматок картону, два мініатюри, олівець і рядок. Помістіть мініатюри в картон, щоб сформувати вогнища еліпса. Відріжте шматок рядка довший, ніж відстань між двома мініатюрами (довжина рядка представляє константу у визначенні). Приклейте кожен кінець нитки до картону, і проведіть криву олівцем, натягнутим на нитку. В результаті виходить еліпс. Див\(\PageIndex{3}\). Малюнок.
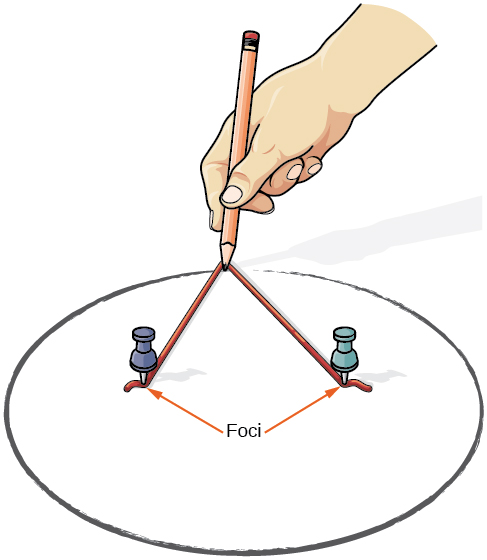
Малюнок\(\PageIndex{3}\)
Кожен еліпс має дві осі симетрії. Довша вісь називається великою віссю, а коротша вісь називається незначною віссю. Кожна кінцева точка великої осі є вершиною еліпса (множина: вершини), а кожна кінцева точка другорядної осі є спільною вершиною еліпса. Центр еліпса - це середина як великої, так і другої осей. Осі розташовуються перпендикулярно по центру. Вогнища завжди лежать на великій осі, а сума відстаней від вогнищ до будь-якої точки на еліпсі (постійна сума) більше відстані між вогнищами (рис.\(\PageIndex{4}\)).
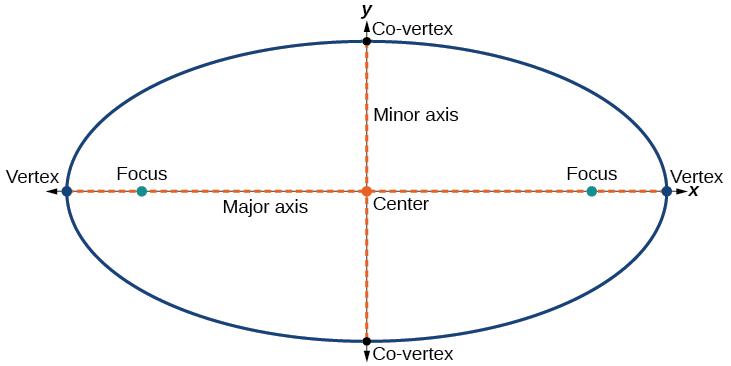
Малюнок\(\PageIndex{4}\)
У цьому розділі ми обмежуємо еліпси тими, які розташовані вертикально або горизонтально в координатній площині. Тобто осі будуть або лежати, або розташовуватися паралельно\(x\) - і\(y\) -осям. Пізніше в розділі ми побачимо еліпси, які обертаються в координатній площині.
Для роботи з горизонтальними і вертикальними еліпсами в координатній площині розглянемо два випадки: ті, які розташовані по центру у початку і ті, які центруються в точці, відмінній від початку. Спочатку навчимося виводити рівняння еліпсів, а потім навчимося писати рівняння еліпсів в стандартному вигляді. Пізніше ми будемо використовувати те, що ми навчимося малювати графіки.
Виведення рівняння еліпса з центром на початку
Щоб вивести рівняння еліпса з центром у початку, починаємо з вогнищ\((−c,0)\) і\((c,0)\). Еліпс - це сукупність всіх точок\((x,y)\) такої, що сума відстаней від\((x,y)\) до вогнищ постійна, як показано на малюнку\(\PageIndex{5}\).
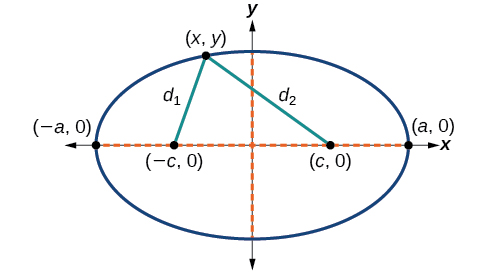
Малюнок\(\PageIndex{5}\)
Якщо\((a,0)\) є вершиною еліпса, відстань від\((−c,0)\) до\((a,0)\) дорівнює\(a−(−c)=a+c\). Відстань від\((c,0)\) до\((a,0)\) є\(a−c\). Сума відстаней від вогнищ до вершини дорівнює
\((a+c)+(a−c)=2a\)
Якщо\((x,y)\) точка на еліпсі, то ми можемо визначити наступні змінні:
- \(d_1=\)відстань від\((−c,0)\) до\((x,y)\)
- \(d_2=\)відстань від\((c,0)\) до\((x,y)\)
За визначенням еліпса,\(d_1+d_2\) є постійною для будь-якої точки\((x,y)\) на еліпсі. Ми знаємо, що сума цих відстаней\(2a\) припадає на вершину\((a,0)\). Звідси випливає, що\(d_1+d_2=2a\) для будь-якої точки на еліпсі. Почнемо виведення з застосування формули відстані. Решта деривація - алгебраїчна.
\[\begin{align*} d_1+d_2&= 2a\\ \sqrt{{(x-(-c))}^2+{(y-0)}^2}+\sqrt{{(x-c)}^2+{(y-0)}^2}&=2a\qquad \text{Distance formula}\\ \sqrt{{(x+c)}^2+y^2}+\sqrt{{(x-c)}^2+y^2}&=2a\qquad \text{Simplify expressions.}\\ \sqrt{{(x+c)}^2+y^2}&=2a-\sqrt{{(x-c)}^2+y^2}\qquad \text{Move radical to opposite side.}\\ {(x+c)}^2+y^2&={\left[2a-\sqrt{{(x-c)}^2+y^2}\right]}^2\qquad \text{Square both sides.}\\ x^2+2cx+c^2+y^2&=4a^2-4a\sqrt{{(x-c)}^2+y^2}+{(x-c)}^2+y^2\qquad \text{Expand the squares.}\\ x^2+2cx+c^2+y^2&=4a^2-4a\sqrt{{(x-c)}^2+y^2}+x^2-2cx+c^2+y^2\qquad \text{Expand remaining squares.}\\ 2cx&=4a^2-4a\sqrt{{(x-c)}^2+y^2}-2cx\qquad \text{Combine like terms.}\\ 4cx-4a^2&=-4a\sqrt{{(x-c)}^2+y^2}\qquad \text{Isolate the radical.}\\ cx-a^2&=-a\sqrt{{(x-c)}^2+y^2}\qquad \text{Divide by 4.}\\ {\left[ cx-a^2\right]}^2&=a^2{\left[ \sqrt{{(x-c)}^2+y^2}\right] }^2\qquad \text{Square both sides.}\\ c^2x^2-2a^2cx+a^4&=a^2(x^2-2cx+c^2+y^2)\qquad \text{Expand the squares.}\\ c^2x^2-2a^2cx+a^4&=a^2x^2-2a^2cx+a^2c^2+a^2y^2\qquad \text{Distribute } a^2\\ a^2x^2-c^2x^2+a^2y^2&=a^4-a^2c^2\qquad \text{Rewrite.}\\ x^2(a^2-c^2)+a^2y^2&=a^2(a^2-c^2)\qquad \text{Factor common terms.}\\ x^2b^2+a^2y^2&=a^2b^2\qquad \text{Set } b^2=a^2-c^2\\ \dfrac{x^2b^2}{a^2b^2}+\dfrac{a^2y^2}{a^2b^2}&=\dfrac{a^2b^2}{a^2b^2}\qquad \text{Divide both sides by } a^2b^2\\ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}&=1\qquad \text{Simplify} \end{align*}\]
Таким чином, стандартне рівняння еліпса\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) є.Це рівняння визначає еліпс, центрований у початку. Якщо\(a>b\), еліпс витягується далі в горизонтальному напрямку, а якщо\(b>a\), то еліпс витягується далі у вертикальному напрямку.
Написання рівнянь еліпсів з центром на початку у стандартній формі
Стандартні форми рівнянь розповідають про ключові особливості графіків. Знайдіть хвилинку, щоб згадати деякі стандартні форми рівнянь, з якими ми працювали в минулому: лінійні, квадратичні, кубічні, експоненціальні, логарифмічні тощо. Навчившись інтерпретувати стандартні форми рівнянь, ми зв'язуємо зв'язок між алгебраїчними та геометричними зображеннями математичних явищ.
Ключовими особливостями еліпса є його центр, вершини, співвершини, вогнища, а також довжини та положення великої та другої осей. Так само, як і в інших рівняннях, ми можемо визначити всі ці особливості, просто дивлячись на стандартну форму рівняння. Існує чотири варіації стандартної форми еліпса. Ці варіації класифікуються спочатку за місцем розташування центру (походження чи не походження), а потім за положенням (горизонтальне або вертикальне). Кожен представлений разом з описом того, як частини рівняння відносяться до графіка. Інтерпретація цих частин дозволяє сформувати уявну картину еліпса.
Стандартна форма рівняння еліпса з центром\((0,0)\) і великою віссю на\(x\) -осі дорівнює
\[\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\]
де
- \(a>b\)
- довжина великої осі\(2a\)
- координати вершин\((\pm a,0)\)
- довжина другорядної осі дорівнює\(2b\)
- координати співвершин\((0,\pm b)\)
- координати вогнищ знаходяться\((\pm c,0)\), де\(c^2=a^2−b^2\). Див\(\PageIndex{6a}\). Малюнок.
Стандартна форма рівняння еліпса з центром\((0,0)\) і великою віссю на\(y\) -осі дорівнює
\[\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\]
де
- \(a>b\)
- довжина великої осі\(2a\)
- координати вершин\((0,\pm a)\)
- довжина другорядної осі дорівнює\(2b\)
- координати співвершин\((\pm b,0)\)
- координати вогнищ знаходяться\((0,\pm c)\), де\(c^2=a^2−b^2\). Див\(\PageIndex{6b}\). Малюнок.
Зверніть увагу, що вершини, співвершини та вогнища пов'язані рівнянням\(c^2=a^2−b^2\). Коли нам задані координати вогнищ і вершин еліпса, ми можемо використовувати це співвідношення, щоб знайти рівняння еліпса в стандартному вигляді.
Малюнок\(\PageIndex{6}\): (a) Горизонтальний еліпс з центром\((0,0)\) (b) Вертикальний еліпс з центром\((0,0)\)
- Визначте, чи лежить велика вісь на осі x - або y.
- Якщо задані координати вершин і осередків мають вигляд\((\pm a,0)\) і\((\pm c,0)\) відповідно, то основною віссю є х -вісь. Використовуйте стандартну форму\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)
- Якщо задані координати вершин і вогнищ мають вигляд\((0,\pm a)\) і\((\pm c,0)\), відповідно, то великою віссю є y -вісь. Використовуйте стандартну форму\(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\)
- Використовуйте\(c^2=a^2−b^2\) рівняння разом із заданими координатами вершин і вогнищ для вирішення для\(b^2\).
- Підставте значення для\(a^2\) і\(b^2\) в стандартну форму рівняння, визначеного в кроці 1.
Що таке стандартне рівняння форми еліпса, що має вершини\((\pm 8,0)\) і вогнища\((\pm 5,0)\)?
Рішення
Вогнища знаходяться на\(x\) -осі, тому велика вісь\(x\) - вісь. Таким чином, рівняння матиме вигляд\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)
Вершини є\((\pm 8,0)\), так\(a=8\) і\(a^2=64\).
Вогнища є\((\pm 5,0)\), так\(c=5\) і\(c^2=25\).
Ми знаємо, що вершини і вогнища пов'язані рівнянням\(c^2=a^2−b^2\). Вирішуючи для\(b^2\), у нас є:
\[\begin{align*} c^2&=a^2-b^2\\ 25&=64-b^2\qquad \text{Substitute for } c^2 \text{ and } a^2\\ b^2&=39\qquad \text{Solve for } b^2 \end{align*}\]
Тепер нам потрібно лише підставити\(a^2=64\) і\(b^2=39\) в стандартну форму рівняння. Рівняння еліпса є\(\dfrac{x^2}{64}+\dfrac{y^2}{39}=1\).
Що таке стандартне рівняння форми еліпса, що має вершини\((0,\pm 4)\) і вогнища\((0,\pm \sqrt{15})\)?
- Відповідь
-
\(x^2+\dfrac{y^2}{16}=1\)
Чи можемо ми записати рівняння еліпса з центром на початку заданих координат тільки одного фокуса і вершини?
Так. Еліпси симетричні, тому координати вершин еліпса з центром навколо початку завжди матимуть форму\((\pm a,0)\) або\((0, \pm a)\). Аналогічно координати вогнищ завжди будуть мати вигляд\((\pm c,0)\) або\((0, \pm c)\). Знаючи це, ми можемо використовувати\(a\) і\(c\) з заданих точок разом з рівнянням\(c^2=a^2−b^2\) знайти\(b^2\).
Написання рівнянь еліпсів, не центрованих на початку
Як і графіки інших рівнянь, графік еліпса можна перекласти. Якщо еліпс перекладається\(h\) одиницями горизонтально, а\(k\) одиниці вертикально, центр еліпса буде\((h,k)\). Цей переклад призводить до стандартної форми рівняння, яке ми бачили раніше,\(x\) замінене на\((x−h)\) і y замінено на\((y−k)\).
Стандартна форма рівняння еліпса з центром\((h, k)\) і великою віссю паралельно\(x\) -осі дорівнює
\[\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1\]
де
- \(a>b\)
- довжина великої осі\(2a\)
- координати вершин\((h\pm a,k)\)
- довжина другорядної осі дорівнює\(2b\)
- координати співвершин\((h,k\pm b)\)
- координати вогнищ знаходяться\((h\pm c,k)\), де\(c^2=a^2−b^2\). Див\(\PageIndex{7a}\). Малюнок.
Стандартна форма рівняння еліпса з центром\((h,k)\) і великою віссю паралельно\(y\) -осі дорівнює
\[\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1\]
де
- \(a>b\)
- довжина великої осі\(2a\)
- координати вершин\((h,k\pm a)\)
- довжина другорядної осі дорівнює\(2b\)
- координати співвершин\((h\pm b,k)\)
- координати вогнищ знаходяться\((h,k\pm c)\), де\(c^2=a^2−b^2\). Див\(\PageIndex{7b}\). Малюнок.
Так само, як і з еліпсами, зосередженими на початку, еліпси, які зосереджені в точці,\((h,k)\) мають вершини, співвершини та фокуси, пов'язані рівнянням\(c^2=a^2−b^2\). Ми можемо використовувати цей зв'язок разом із формулами середньої та відстані, щоб знайти рівняння еліпса в стандартній формі, коли задані вершини та вогнища.
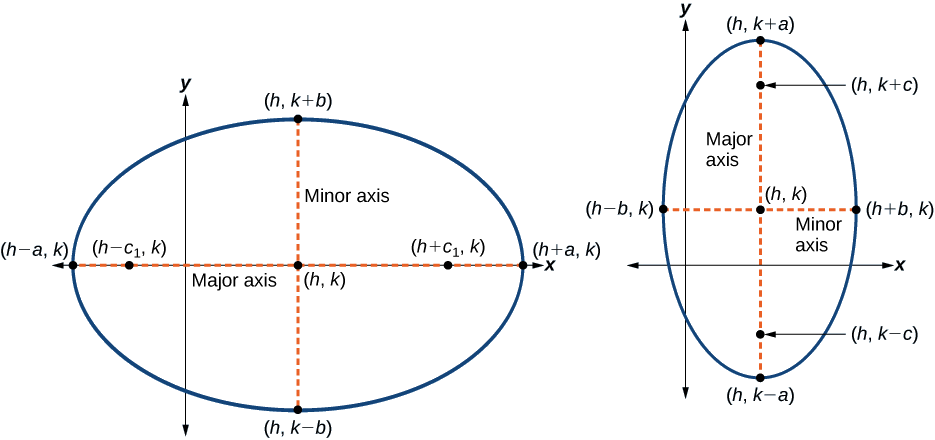
Малюнок\(\PageIndex{7}\): (a) Горизонтальний еліпс з центром\((h,k)\) (b) Вертикальний еліпс з центром\((h,k)\)
- Визначте, чи велика вісь паралельна\(x\) - або\(y\) -осі.
- Якщо y -координати заданих вершин і вогнищ однакові, то велика вісь паралельна\(x\) -осі. Використовуйте стандартну форму\(\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1\)
- Якщо x -координати заданих вершин і вогнищ однакові, то велика вісь паралельна осі y. Використовуйте стандартну форму\(\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1\)
- Визначте центр еліпса\((h,k)\) за допомогою формули середньої точки та заданих координат для вершин.
- Знайти\(a^2\) шляхом вирішення для довжини великої осі\(2a\), яка є відстанню між заданими вершинами.
- Знайдіть\(c^2\) за допомогою\(h\) і\(k\), знайденого в кроці 2, разом із заданими координатами для вогнищ.
- Вирішіть для\(b^2\) використання рівняння\(c^2=a^2−b^2\).
- Підставте значення для\(h\),\(k\),\(a^2\), і\(b^2\) в стандартну форму рівняння, визначеного в кроці 1.
Що таке стандартне рівняння форми еліпса, що має вершини\((−2,−8)\) і\((−2,2)\) і вогнища\((−2,−7)\) і\((−2,1)\)?
Рішення
\(x\)-координати вершин і вогнищ однакові, тому велика вісь паралельна\(y\) -осі. Таким чином, рівняння еліпса матиме вигляд
\(\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1 \nonumber\)
Спочатку визначаємо центр,\((h,k)\). Центр знаходиться на півдорозі між вершинами,\((−2,−8)\) і\((−2,2)\). Застосовуючи формулу середньої точки, ми маємо:
\[\begin{align} (h,k) &=\left(\dfrac{−2+(−2)}{2},\dfrac{−8+2}{2}\right) \nonumber \\ &=(−2,−3) \nonumber \end{align} \nonumber\]
Далі знаходимо\(a^2\). Довжина великої осі\(2a\), обмежена вершинами. Вирішуємо\(a\) for шляхом знаходження відстані між y -координатами вершин.
\[\begin{align} 2a &=2−(−8) \nonumber \\ 2a &=10 \nonumber\\ a&=5 \nonumber \end{align} \nonumber\]
Отже\(a^2=25\).
Тепер знаходимо\(c^2\). Вогнища задаються\((h,k\pm c)\). Отже,\((h,k−c)=(−2,−7)\) і\((h,k+c)=(−2,1)\). Ми підставляємо,\(k=−3\) використовуючи будь-який з цих пунктів для вирішення\(c\).
\[\begin{align} k+c &=1 \nonumber \\ −3+c&=1 \nonumber \\ c&=4 \nonumber \end{align} \nonumber\]
Отже\(c^2=16\).
Далі вирішуємо для\(b^2\) використання рівняння\(c^2=a^2−b^2\).
\[\begin{align} c^2&=a^2−b^2 \nonumber \\ 16&=25−b^2 \nonumber \\ b^2&=9 \nonumber \end{align} \nonumber\]
Нарешті, підставляємо значення, знайдені для\(h\),\(k\)\(a^2\), і\(b^2\) в стандартне рівняння форми для еліпса:
\[\dfrac{{(x+2)}^2}{9}+\dfrac{{(y+3)}^2}{25}=1 \nonumber\]
Що таке стандартне рівняння форми еліпса, що має вершини\((−3,3)\) і\((5,3)\) і вогнища\((1−2\sqrt{3},3)\) і\((1+2\sqrt{3},3)\)?
- Відповідь
-
\(\dfrac{{(x−1)}^2}{16}+\dfrac{{(y−3)}^2}{4}=1 \nonumber\)
Графічні еліпси з центром на початку
Так само, як ми можемо записати рівняння для еліпса з урахуванням його графіка, ми можемо зробити графік еліпса з урахуванням його рівняння. Для графування еліпсів з центром у початковій точці ми використовуємо стандартну форму
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1, a>b\)для горизонтальних еліпсів
і
\(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1, a>b\)для вертикальних еліпсів
- Використовуйте стандартні форми рівнянь еліпса для визначення великої осі, вершин, співвершин і вогнищ.
- Якщо рівняння має вигляд\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\), де\(a>b\), то
- головна вісь\(x\) - вісь
- координати вершин\((\pm a,0)\)
- координати співвершин\((0,\pm b)\)
- координати вогнищ\((\pm c,0)\)
- Якщо рівняння має вигляд\(x^2b^2+y^2a^2=1\), де\(a>b\), то
- головна вісь\(y\) - вісь
- координати вершин\((0,\pm a)\)
- координати співвершин\((\pm b,0)\)
- координати вогнищ\((0,\pm c)\)
- Якщо рівняння має вигляд\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\), де\(a>b\), то
- Вирішіть для\(c\) використання рівняння\(c^2=a^2−b^2\).
- Помістіть центр, вершини, співвершини та вогнища в координатній площині та намалюйте плавну криву, щоб сформувати еліпс.
Графік еліпса, заданого рівнянням,\(\dfrac{x^2}{9}+\dfrac{y^2}{25}=1\). Визначте та позначте центр, вершини, співвершини та вогнища.
Рішення
Спочатку визначаємо положення великої осі. Тому що\(25>9\), велика вісь знаходиться на\(y\) -осі. Тому рівняння знаходиться у вигляді\(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\), де\(b^2=9\) і\(a^2=25\). Звідси випливає, що:
- центр еліпса\((0,0)\)
- координати вершин\((0,\pm a)=(0,\pm \sqrt{25})=(0,\pm 5)\)
- координати співвершин\((\pm b,0)=(\pm 9,0)=(\pm 3,0)\)
- координати вогнищ є\((0,\pm c)\), де\(c^2=a^2−b^2\) Розв'язуючи для\(c\), ми маємо:
\[\begin{align} c&=\pm \sqrt{a^2−b^2} \nonumber \\ &=\pm \sqrt{25−9} \nonumber\\ &=\pm \sqrt{16} \nonumber\\ &=\pm 4 \nonumber \end{align} \nonumber\]
Тому координати вогнищ є\((0,\pm 4)\).
Далі ми розміщуємо та позначимо центр, вершини, співвершини та вогнища, а також намалюємо плавну криву, щоб сформувати еліпс. Див\(\PageIndex{8}\). Малюнок.
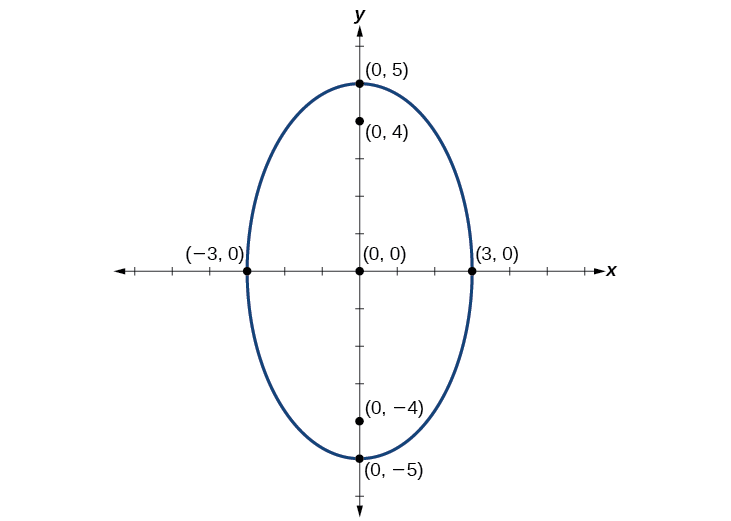
Малюнок\(\PageIndex{8}\)
Графік еліпса, заданого рівнянням\(\dfrac{x^2}{36}+\dfrac{y^2}{4}=1\). Визначте та позначте центр, вершини, співвершини та вогнища.
- Відповідь
-
центр:\((0,0)\); вершини:\((\pm 6,0)\); співвершини:\((0,\pm 2)\); вогнища:\((\pm 4\sqrt{2},0)\)
Малюнок\(\PageIndex{9}\)
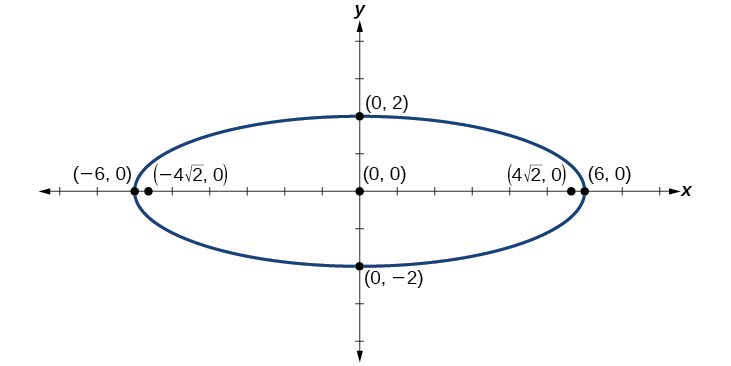
Графік еліпса, заданого рівнянням\(4x^2+25y^2=100\). Перепишіть рівняння в стандартному вигляді. Потім визначте та позначте центр, вершини, співвершини та вогнища.
Рішення
По-перше, використовуйте алгебру, щоб переписати рівняння в стандартній формі.
\[\begin{align} 4x^2+25y^2&=100 \nonumber \\ \dfrac{4x^2}{100}+\dfrac{25y^2}{100}&=\dfrac{100}{100} \nonumber \\ \dfrac{x^2}{25}+\dfrac{y^2}{4}&=1 \nonumber \end{align} \nonumber \]
Далі визначаємо положення великої осі. Тому що\(25>4\), велика вісь знаходиться на\(x\) -осі. Тому рівняння знаходиться у вигляді\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\), де\(a^2=25\) і\(b^2=4\). Звідси випливає, що:
- центр еліпса\((0,0)\)
- координати вершин\((\pm a,0)=(\pm \sqrt{25},0)=(\pm 5,0)\)
- координати співвершин\((0,\pm b)=(0,\pm \sqrt{4})=(0,\pm 2)\)
- координати вогнищ знаходяться\((\pm c,0)\), де\(c^2=a^2−b^2\). Вирішуючи для\(c\), у нас є:
\[\begin{align} c&=\pm \sqrt{a^2−b^2} \nonumber \\ &=\pm \sqrt{25−4} \nonumber \\ &=\pm \sqrt{21} \nonumber \end{align} \nonumber \]
Тому координати вогнищ є\((\pm \sqrt{21},0)\).
Далі ми розміщуємо та позначимо центр, вершини, співвершини та вогнища, а також намалюємо плавну криву, щоб сформувати еліпс.
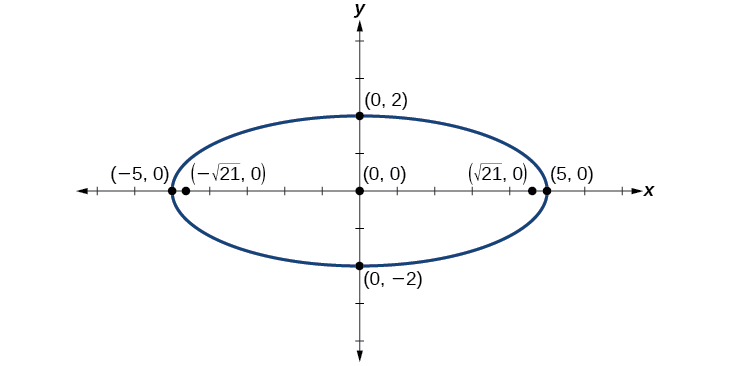
Малюнок\(\PageIndex{10}\)
Графік еліпса, заданого рівнянням\(49x^2+16y^2=784\). Перепишіть рівняння в стандартному вигляді. Потім визначте та позначте центр, вершини, співвершини та вогнища.
- Відповідь
-
Стандартна форма:\(\dfrac{x^2}{16}+\dfrac{y^2}{49}=1\); центр:\((0,0)\); вершини:\((0,\pm 7)\); співвершини:\((\pm 4,0)\); вогнища:\((0,\pm \sqrt{33})\)
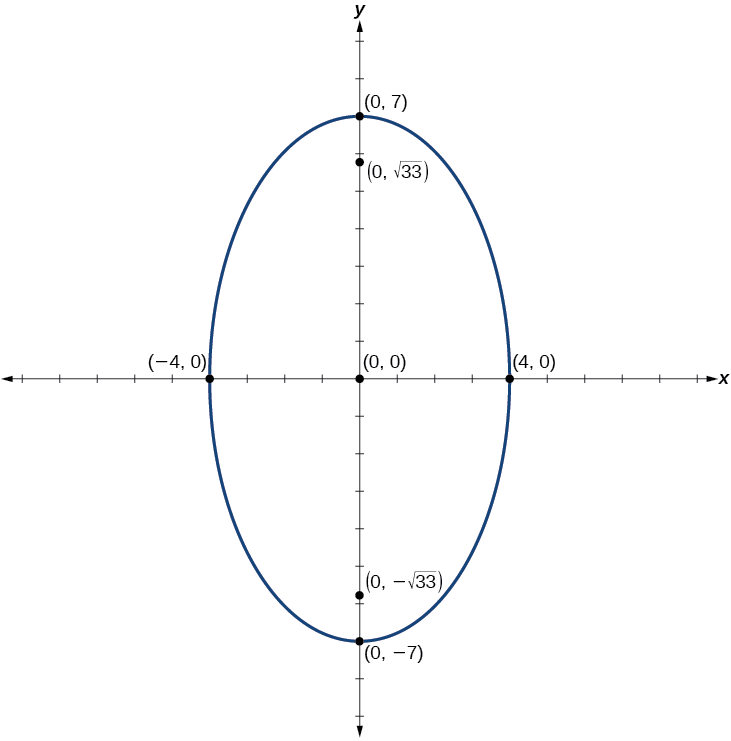
Малюнок\(\PageIndex{11}\)
Графічні еліпси, які не зосереджені на початку
Коли еліпс не зосереджений на початку, ми все ще можемо використовувати стандартні форми, щоб знайти ключові особливості графіка. Коли еліпс центрується в певній точці\((h,k)\), ми використовуємо стандартні форми\(\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1\),\(a>b\) для горизонтальних еліпсів і\(\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1\),\(a>b\) для вертикальних еліпсів. За цими стандартними рівняннями ми можемо легко визначити центр, вершини, співвершини, вогнища та положення великих та другорядних осей.
- Використовуйте стандартні форми рівнянь еліпса для визначення центру, положення великої осі, вершин, співвершин і вогнищ.
- Якщо рівняння має вигляд\(\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1\), де\(a>b\), то
- центр - це\((h,k)\)
- велика вісь паралельна\(x\) -осі
- координати вершин\((h\pm a,k)\)
- координати співвершин\((h,k\pm b)\)
- координати вогнищ\((h\pm c,k)\)
- Якщо рівняння має вигляд\(\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1\), де\(a>b\), то
- центр - це\((h,k)\)
- велика вісь паралельна\(y\) -осі
- координати вершин\((h,k\pm a)\)
- координати співвершин\((h\pm b,k)\)
- координати вогнищ\((h,k\pm c)\)
- Якщо рівняння має вигляд\(\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1\), де\(a>b\), то
- Вирішіть для\(c\) використання рівняння\(c^2=a^2−b^2\).
- Помістіть центр, вершини, співвершини та вогнища в координатній площині та намалюйте плавну криву, щоб сформувати еліпс.
Графік еліпса, заданого рівнянням,\(\dfrac{{(x+2)}^2}{4}+\dfrac{{(y−5)}^2}{9}=1\). Визначте та позначте центр, вершини, співвершини та вогнища.
Рішення
Спочатку визначаємо положення великої осі. Тому що\(9>4\), велика вісь паралельна\(y\) -осі. Тому рівняння знаходиться у вигляді\(\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1\), де\(b^2=4\) і\(a^2=9\). Звідси випливає, що:
- центр еліпса\((h,k)=(−2,5)\)
- координати вершин є\((h,k\pm a)=(−2,5\pm \sqrt{9})=(−2,5\pm 3)\), або\((−2,2)\) і\((−2,8)\)
- координати співвершин є\((h\pm b,k)=(−2\pm \sqrt{4},5)=(−2\pm 2,5)\), або\((−4,5)\) і\((0,5)\)
- координати вогнищ знаходяться\((h,k\pm c)\), де\(c^2=a^2−b^2\). Вирішуючи для\(c\), у нас є:
\[ \begin{align} c&=\pm \sqrt{a^2−b^2} \nonumber \\[4pt] &=\pm \sqrt{9−4} \nonumber \\[4pt] &=\pm \sqrt{5} \nonumber \end{align} \nonumber\]
Тому координати вогнищ -\((−2,5−\sqrt{5})\) і\((−2,5+\sqrt{5})\).
Далі ми розміщуємо та позначимо центр, вершини, співвершини та вогнища, а також намалюємо плавну криву, щоб сформувати еліпс.
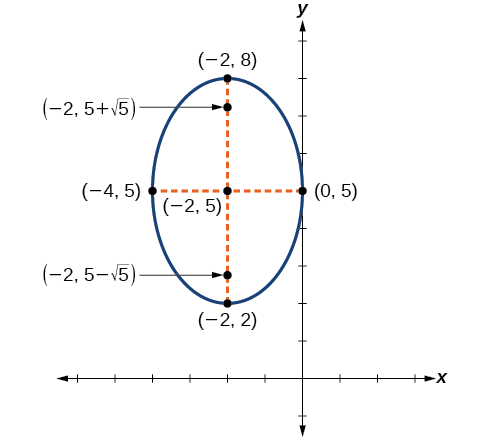
Малюнок\(\PageIndex{12}\)
Графік еліпса, заданого рівнянням\(\dfrac{{(x−4)}^2}{36}+\dfrac{{(y−2)}^2}{20}=1\). Визначте та позначте центр, вершини, співвершини та вогнища.
- Відповідь
-
Центр:\((4,2)\); вершини:\((−2,2)\) і\((10,2)\); співвершини:\((4,2−2\sqrt{5})\) і\((4,2+2\sqrt{5})\); вогнища:\((0,2)\) і\((8,2)\)
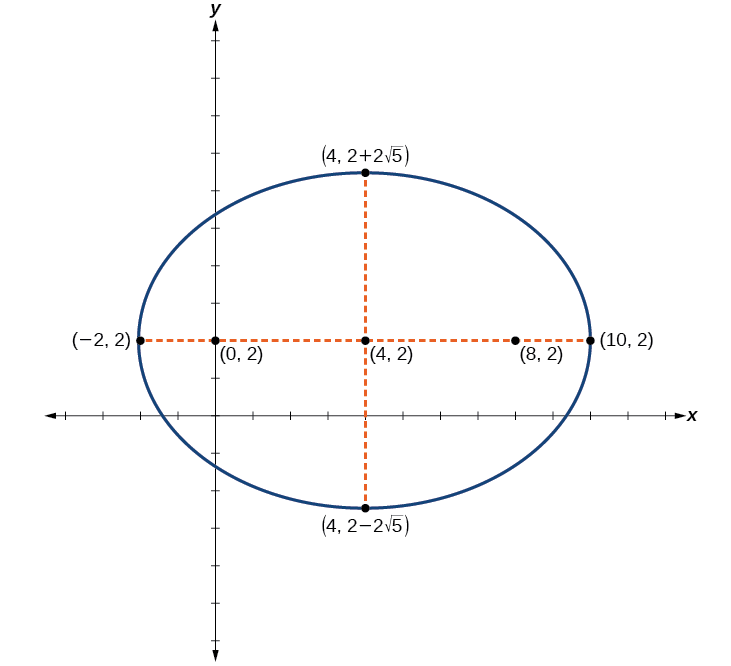
Малюнок\(\PageIndex{13}\)
- Визнайте, що еліпс, описаний рівнянням у формі\(ax^2+by^2+cx+dy+e=0\), є загальною формою.
- Перевпорядкуйте рівняння шляхом групування термінів, які містять ту саму змінну. Перемістіть постійний член в протилежну сторону рівняння.
- Фактор коефіцієнтів\(x^2\) і\(y^2\) термінів при підготовці до заповнення квадрата.
- Доповніть квадрат для кожної змінної, щоб переписати рівняння у вигляді суми кратних двох біноміалів у квадраті множини, рівних константі\(m_1{(x−h)}^2+m_2{(y−k)}^2=m_3\), де\(m_1\)\(m_2\), і\(m_3\) є константами.
- Розділіть обидві сторони рівняння на постійний член, щоб висловити рівняння в стандартному вигляді.
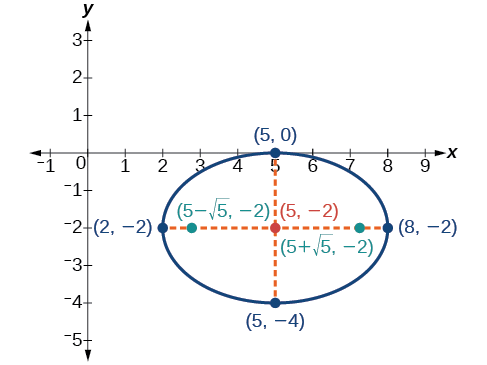
Графік еліпса, заданого рівнянням\(4x^2+9y^2−40x+36y+100=0\). Визначте та позначте центр, вершини, співвершини та вогнища.
Рішення
Почати треба з перезапису рівняння в стандартному вигляді.
\(4x^2+9y^2−40x+36y+100=0\)
Групуйте члени, які містять одну і ту ж змінну, і перемістіть константу в протилежну сторону рівняння.
\((4x^2−40x)+(9y^2+36y)=−100\)
Помножити коефіцієнти квадратних членів.
\(4(x^2−10x)+9(y^2+4y)=−100\)
Завершіть квадрат двічі. Не забудьте збалансувати рівняння, додаючи однакові константи до кожної сторони.
\(4(x^2−10x+25)+9(y^2+4y+4)=−100+100+36\)
Перепишіть як ідеальні квадрати.
\(4{(x−5)}^2+9{(y+2)}^2=36\)
Розділіть обидві сторони на постійний член, щоб розмістити рівняння в стандартній формі.
\(\dfrac{{(x−5)}^2}{9}+\dfrac{{(y+2)}^2}{4}=1\)
Тепер, коли рівняння знаходиться в стандартній формі, ми можемо визначити положення великої осі. Тому що\(9>4\), велика вісь паралельна\(x\) -осі. Тому рівняння знаходиться у вигляді\(\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1\), де\(a^2=9\) і\(b^2=4\). Звідси випливає, що:
- центр еліпса\((h,k)=(5,−2)\)
- координати вершин є\((h\pm a,k)=(5\pm \sqrt{9},−2)=(5\pm 3,−2)\), або\((2,−2)\) і\((8,−2)\)
- координати співвершин є\((h,k\pm b)=(5,−2\pm \sqrt{4})=(5,−2\pm 2)\), або\((5,−4)\) і\((5,0)\)
- координати вогнищ знаходяться\((h\pm c,k)\), де\(c^2=a^2−b^2\). Вирішуючи для\(c\), у нас є:
\[\begin{align*} c&=\pm \sqrt{a^2-b^2}\\ &=\pm \sqrt{9-4}\\ &=\pm \sqrt{5} \end{align*}\]
Тому координати вогнищ -\((5−\sqrt{5},−2)\) і\((5+\sqrt{5},−2)\).
Далі ми розміщуємо та позначимо центр, вершини, співвершини та фокуси та намалюємо плавну криву, щоб сформувати еліпс, як показано на малюнку\(\PageIndex{14}\).

Малюнок\(\PageIndex{14}\)
Висловіть рівняння еліпса, задане в стандартній формі. Визначте центр, вершини, співвершини та вогнища еліпса.
\(4x^2+y^2−24x+2y+21=0\)
- Відповідь
-
\(\dfrac{{(x−3)}^2}{4}+\dfrac{{(y+1)}^2}{16}=1\); центр:\((3,−1)\); вершини:\((3,−5)\) і\((3,3)\); ко-вершини:\((1,−1)\) і\((5,−1)\); вогнища:\((3,−1−2\sqrt{3})\) і\((3,−1+2\sqrt{3})\)
Рішення прикладних задач за участю еліпсів
Багато реальних ситуацій можуть бути представлені еліпсами, включаючи орбіти планет, супутників, супутників і комет, а також форми човнових кілів, рулів і деяких крил літака. Медичний пристрій під назвою літотриптер використовує еліптичні відбивачі для розщеплення каменів у нирках шляхом генерації звукових хвиль. Деякі будівлі, які називаються шепочними камерами, спроектовані з еліптичними куполами так, що людина, що шепоче на одному фокусі, може легко почути хтось, хто стоїть біля іншого вогнища. Це відбувається через акустичних властивостей еліпса. Коли звукова хвиля виникає в одному фокусі шепотіння камери, звукова хвиля буде відбиватися від еліптичного купола і назад до іншого фокусу (рис.\(\PageIndex{15}\)). У камері шепоту в Музеї науки і промисловості в Чикаго двоє людей, що стоять біля фокусу - близько\(43\) ніг один від одного, можуть чути шепіт один одного.
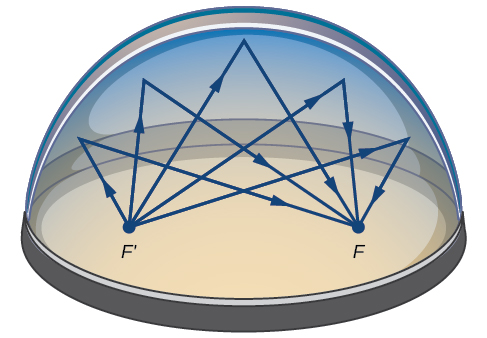
Малюнок\(\PageIndex{15}\): Звукові хвилі відбиваються між осередками в еліптичному приміщенні, званому шепочной камерою.
Статуарний зал у будівлі Капітолію у Вашингтоні, округ Колумбія, є шепотіння палати. Його розміри -\(46\) ноги шириною на\(96\) ноги довжиною, як показано на малюнку\(\PageIndex{16}\).
- Яка стандартна форма рівняння еліпса, що представляє контур кімнати? Підказка: припустимо горизонтальний еліпс, і нехай центр кімнати буде точкою\((0,0)\).
- Якщо два сенатора, що стоять біля вогнищ цієї кімнати, можуть почути шепіт один одного, наскільки далеко один від одного знаходяться сенатори? Округлити до найближчої ноги.
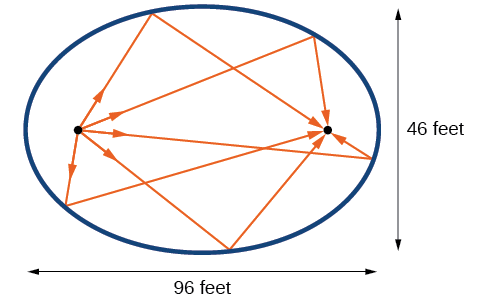
Малюнок\(\PageIndex{16}\)
Рішення
- Ми припускаємо горизонтальний еліпс з центром\((0,0)\), тому нам потрібно знайти рівняння форми\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\), де\(a>b\). Ми знаємо, що довжина великої осі\(2a\), більше, ніж довжина другорядної осі,\(2b\). Так довжина кімнати, 96, представлена великою віссю, а ширина кімнати, 46, представлена другорядної віссю.
Отже, рівняння еліпса дорівнює\ [(dfrac {x^2} {2304} +\ dfrac {y^2} {529} =1\)
- Рішення для\(a\), ми маємо\(2a=96\), значить\(a=48\), і\(a^2=2304\).
- Рішення для\(b\), ми маємо\(2b=46\), значить\(b=23\), і\(b^2=529\).
- Щоб знайти відстань між сенаторами, ми повинні знайти відстань між вогнищами\((\pm c,0)\), де\(c^2=a^2−b^2\). Вирішуючи для\(c\), у нас є:
\[\begin{align*} c^2&=a^2-b^2\\ c^2&=2304-529\qquad \text{Substitute using the values found in part } (a)\\ c&=\pm \sqrt{2304-529}\qquad \text{Take the square root of both sides.}\\ c&=\pm \sqrt{1775}\qquad \text{Subtract.}\\ c&\approx \pm 42\qquad \text{Round to the nearest foot.} \end{align*}\]
Точки\((\pm 42,0)\) представляють вогнища. Таким чином, відстань між сенаторами -\(2(42)=84\) стопи.
Припустимо, що камера шепоту\(480\) ноги довжиною, а\(320\) ноги шириною.
- Яка стандартна форма рівняння еліпса, що представляє кімнату? Підказка: припустимо горизонтальний еліпс, і нехай центр кімнати буде точкою\((0,0)\).
- Якщо двоє людей стоять біля вогнищ цієї кімнати і можуть чути один одному шепіт, наскільки далеко один від одного знаходяться люди? Округлити до найближчої ноги.
- Відповідь на
-
\(\dfrac{x^2}{57,600}+\dfrac{y^2}{25,600}=1\)
- Відповідь б
-
Народ стоїть на\(358\) ногах один від одного.
Отримайте доступ до цих онлайн-ресурсів для додаткової інструкції та практики з еліпсами.
Ключові рівняння
| Горизонтальний еліпс, центр на початку | \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\),\(a>b\) |
| Вертикальний еліпс, центр на початку | \(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\),\(a>b\) |
| Горизонтальний еліпс, центр\((h,k)\) | \(\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1\),\(a>b\) |
| Вертикальний еліпс, центр\((h,k)\) | \(\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1\),\(a>b\) |
Key Concepts
- An ellipse is the set of all points \((x,y)\) in a plane such that the sum of their distances from two fixed points is a constant. Each fixed point is called a focus (plural: foci).
- When given the coordinates of the foci and vertices of an ellipse, we can write the equation of the ellipse in standard form. See Example \(\PageIndex{1}\) and Example \(\PageIndex{2}\).
- When given an equation for an ellipse centered at the origin in standard form, we can identify its vertices, co-vertices, foci, and the lengths and positions of the major and minor axes in order to graph the ellipse. See Example \(\PageIndex{3}\) and Example \(\PageIndex{4}\).
- When given the equation for an ellipse centered at some point other than the origin, we can identify its key features and graph the ellipse. See Example \(\PageIndex{5}\) and Example \(\PageIndex{6}\).
- Real-world situations can be modeled using the standard equations of ellipses and then evaluated to find key features, such as lengths of axes and distance between foci. See Example \(\PageIndex{7}\).
