4.1: Алгебра функцій
- Page ID
- 58250
Навички для розвитку
- Визначте та оцінюйте поліноміальні функції.
- Додавання і віднімання функцій.
- Функції множення і ділення.
- Додайте функції графічно.
Функції поліномів
Будь-поліном з однією змінною є функцією і може бути записаний у вигляді
\(f(x)=a_nx^n+a_{n−1}x^{n−1} + ⋯ +a_1x + a_0.\)
Тут\(a_{n}\) представляє будь-яке дійсне число і\(n\) представляє будь-яке ціле число. Ступінь многочлена з однією змінною є найбільшим показником з усіх членів. Зазвичай ми влаштовуємо терміни многочленів у порядку убування виходячи з їх ступеня і класифікуємо їх наступним чином:
\(\begin{array} { l r } { f ( x ) = 2 } & { \color{Cerulean} { Constant\: function\: (degree }\: 0 ) } \\ { g ( x ) = 3 x + 2 } & { \color{Cerulean} { Linear\: function\: (degree\: } 1 ) } \\ { h ( x ) = 4 x ^ { 2 } + 3 x + 2 } & { \color{Cerulean} { Quadratic\: function\: (degree\: } 2 ) } \\ { r ( x ) = 5 x ^ { 3 } + 4 x ^ { 2 } + 3 x + 2}&{ \color{Cerulean} { Cubic\: function\: (degree\: } 3 ) } \end{array}\)
У цьому підручнику ми називаємо будь-який многочлен зі ступенем вище\(3\)\(n\) полінома th-го ступеня. Наприклад, якщо ступінь є\(4\), ми називаємо це поліном четвертого ступеня; якщо ступінь є\(5\), ми називаємо це поліном п'ятого ступеня, і так далі.
Приклад\(\PageIndex{1}\):
Дано\(f(x)=x^{2}−8x+17\), знайдіть\(f(2)\) і\(f(4)\).
Рішення
Замініть кожен\(x\) екземпляр на значення, вказане всередині дужок.
| \(\begin{aligned} f ( \color{Cerulean}{2}\color{black}{ )} & = ( \color{Cerulean}{2}\color{black}{ )} ^ { 2 } - 8 ( \color{Cerulean}{2}\color{black}{ )} + 17 \\ & = 4 - 16 + 17 \\ & = 4 + 1 \\ & = 5 \end{aligned}\) | \(\begin{aligned} f ( \color{Cerulean}{4}\color{black}{ ) }& = ( \color{Cerulean}{4}\color{black}{ )} ^ { 2 } - 8 ( \color{Cerulean}{4}\color{black}{ )} + 17 \\ & = 16 - 32 + 17 \\ & = - 16 + 17 \\ & = 1 \end{aligned}\) |
Ми можемо написати\(f(2)=5\) і\(f(4)=1\). Пам'ятайте, що\(f(x)=y\) і тому ми можемо інтерпретувати ці результати на графіку наступним чином:
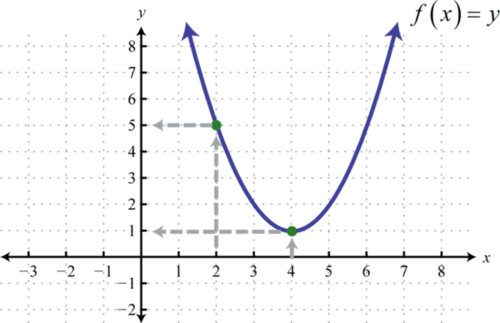
Таблиця\(\PageIndex{1}\)
Відповідь:
\( f(2)=5; f(4)=1\)
Часто нас попросять оцінити поліноми для алгебраїчних виразів.
Приклад\(\PageIndex{2}\):
Дано\(g(x)=x^{3}−x+5\), знайдіть\(g(−2u)\) і\(g(x−2)\).
Рішення
\(x\)Замініть на вирази, вказані всередині дужок.
| \(\begin{aligned} g (\color{Cerulean}{ - 2 u} \color{black}{) }& = (\color{Cerulean}{ - 2 u}\color{black}{ )} ^ { 3 } - ( \color{Cerulean}{- 2 u}\color{black}{ )} + 5 \\ & = - 8 u ^ { 3 } + 2 u + 5 \end{aligned}\) | \(\begin{aligned} g ( \color{Cerulean}{x - 2}\color{black}{ )} & = ( \color{Cerulean}{x - 2}\color{black}{ )} ^ { 3 } - (\color{Cerulean}{ x - 2}\color{black}{)} +5 \\ & = ( x - 2 ) (x-2)(x-2) - ( x -2) + 5 \\ & = ( x - 2 ) ( x^{2} - 4x +4 ) -x +7 \\ & = x ^ { 3 } - 4 x ^ { 2 } + 4 x - 2x^{2} + 8x -8 -x +7 \\ & = x ^ { 3 } - 6 x ^ { 2 } + 11x - 1 \end{aligned}\) |
Відповідь:
\(g(−2u)=−8u^{2}+2u+5\)і\(g(x−2)=x^{3}−6x^{2}+11x−1\)
Висота об'єкта, запущеного вгору, ігноруючи ефекти опору повітря, може бути змодельована за допомогою такої квадратичної функції:
\(h(t)=−\frac{1}{2}gt^2+v_{0}t+s_{0}\)
За допомогою цієї формули висоту\(h(t)\) можна розрахувати в будь-який момент часу\(t\) після запуску об'єкта. Буква\(g\) представляє прискорення за рахунок сили тяжіння на поверхні Землі, яка становить\(32\) фути на секунду в квадраті (або, використовуючи метричні одиниці,\(g = 9.8\) метри на секунду в квадраті). Змінна\(v_{0}\), вимовлена «v-naught», або іноді «v-zero», представляє початкову швидкість об'єкта і\(s_{0}\) представляє початкову висоту, з якої був запущений об'єкт.
Приклад\(\PageIndex{3}\)
Об'єкт запускається з землі зі швидкістю\(64\) футів в секунду. Напишіть функцію, яка моделює висоту об'єкта і використовуйте її для обчислення висоти об'єктів в\(1\) секунду і в\(3.5\) секундах.
Рішення
Ми знаємо, що прискорення через гравітацію становить\(g = 32\) фути на секунду в квадраті, і нам дається початкова швидкість\(v_{0}=64\) футів в секунду. Так як об'єкт запускається з землі, початкова висота -\(s_{0}=0\) ноги. Створіть математичну модель, підставивши ці коефіцієнти в наступну формулу:
\(\begin{array} { l } { h ( t ) = - \frac { 1 } { 2 } g t ^ { 2 } + v _ { 0 } t + s _ { 0 } } \\ { h ( t ) = - \frac { 1 } { 2 } ( \color{Cerulean}{32}\color{black}{ )} t ^ { 2 } + ( \color{Cerulean}{64}\color{black}{ )} t + \color{Cerulean}{0} } \\ { h ( t ) = - 16 t ^ { 2 } + 64 t } \end{array}\)
Використовуйте цю модель для обчислення висоти об'єкта за\(1\) секунду та\(3.5\) секунди.
\(\begin{array} { l } { h ( \color{Cerulean}{1}\color{black}{ )} = - 16 ( \color{Cerulean}{1}\color{black}{ )} ^ { 2 } + 64 ( \color{Cerulean}{1}\color{black}{ )} = - 16 + 64 = 48 } \\ { h ( \color{Cerulean}{3.5}\color{black}{ )} = - 16 ( \color{Cerulean}{3.5}\color{black}{ )} ^ { 2 } + 64 ( \color{Cerulean}{3.5}\color{black}{ )} = - 196 + 224 = 28 } \end{array}\)
Відповідь:
\(h ( t ) = - 16 t ^ { 2 } + 64 t\); У\(1\) секунду об'єкт знаходиться на висоті\(48\) ніг, а в\(3.5\) секундах - на висоті\(28\) ніг.
Вправа\(\PageIndex{1}\)
Об'єкт скидається з висоти 6 метрів. Напишіть функцію, яка моделює висоту об'єкта, і використовуйте її для обчислення висоти об'єкта за\(1\) секунду після його скидання.
- Відповідь
-
\(h ( t ) = - 4.9 t ^ { 2 } + 6\); У\(1\) секунду об'єкт знаходиться на висоті\(1.1\) метрів.
www.youtube.com/В/РРР8КЗК
Додавання та віднімання функцій
Позначення, що використовуються для позначення додавання 1 та віднімання 2 функцій, такі:
Додавання функцій:\((f+g)(x)=f(x)+g(x)\)
Віднімання функцій:\((f−g)(x)=f(x)−g(x)\)
Використовуючи позначення функції, будьте обережні, щоб згрупувати всю функцію і відповідно додати або відняти.
Приклад\(\PageIndex{4}\)
Дано\(f(x)=x^{3}−5x−7\) і\(g(x)=3x^{2}+7x−2\), знайдіть\((f+g)(x)\) і\((f−g)(x)\).
Рішення
Позначення\(f+g\) вказує на те, що ми повинні додати задані вирази.
\(\begin{aligned} ( f + g ) ( x ) & = f ( x ) + g ( x ) \\ & = \left( x ^ { 3 } - 5 x - 7 \right) + \left( 3 x ^ { 2 } + 7 x - 2 \right) \\ & = x ^ { 3 } - 5 x - 7 + 3 x ^ { 2 } + 7 x - 2 \\ & = x ^ { 3 } + 3 x ^ { 2 } + 2 x - 9 \end{aligned}\)
Позначення\(f−g\) вказує на те, що ми повинні відняти дані вирази. При відніманні дужки стають дуже важливими. Нагадаємо, що усунути їх можна після застосування розподільного майна.
\(\begin{aligned} ( f - g ) ( x ) & = f ( x ) - g ( x ) \\ & = \left( x ^ { 3 } - 5 x - 7 \right) - \left( 3 x ^ { 2 } + 7 x - 2 \right) \\ & = x ^ { 3 } - 5 x - 7 - 3 x ^ { 2 } - 7 x + 2 \\ & = x ^ { 3 } - 3 x ^ { 2 } - 12 x - 5 \end{aligned}\)
Відповідь:
\((f+g)(x)=x^{3}+3x^{2}+2x−9\)і\((f−g)(x)=x^{3}−3x^{2}−12x−5\)
Нас можуть попросити оцінити суму або різницю двох функцій. У нас є можливість спочатку знайти суму або різницю в цілому, а потім використовувати результуючу функцію для оцінки для заданої змінної, або спочатку оцінити кожну, а потім знайти суму або різницю.
Приклад\(\PageIndex{5}\)
Оцініть\((f−g)(3)\) дані\(f(x)=5x^{2}−x+4\) і\(g(x)=x^{2}+2x−3\).
Рішення
Спочатку знайдіть\((f−g)(x)\).
\(\begin{aligned} ( f - g ) ( x ) & = f ( x ) - g ( x ) \\ & = \left( 5 x ^ { 2 } - x + 4 \right) - \left( x ^ { 2 } + 2 x - 3 \right) \\ & = 5 x ^ { 2 } - x + 4 - x ^ { 2 } - 2 x + 3 \\ & = 4 x ^ { 2 } - 3 x + 7 \end{aligned}\)
Тому,
\(( f - g ) ( x ) = 4 x ^ { 2 } - 3 x + 7\).
Далі\(3\) підставляємо змінну\(x\).
\(\begin{aligned} ( f - g ) ( \color{OliveGreen}{3}\color{black}{ )} & = 4 ( \color{OliveGreen}{3}\color{black}{ )} ^ { 2 } - 3 (\color{OliveGreen}{ 3}\color{black}{ )} + 7 \\ & = 36 - 9 + 7 \\ & = 34 \end{aligned}\)
Звідси\((f−g)(3)=34\).
Альтернативне рішення
Так як\((f−g)(3)=f(3)−g(3)\), ми можемо знайти,\(f(3)\)\(g(3)\) а потім відняти результати.
| \(\begin{aligned} f ( x ) & = 5 x ^ { 2 } - x + 4 \\ f ( \color{Cerulean}{3}\color{black}{ )} & = 5 ( \color{Cerulean}{3}\color{black}{ )} ^ { 2 } - ( \color{Cerulean}{3}\color{black}{ )} + 4 \\ & = 45 - 3 + 4 \\ & = 46 \end{aligned}\) | \(\begin{aligned} g ( x ) & = x ^ { 2 } + 2 x - 3 \\ g ( \color{Cerulean}{3}\color{black}{ )} & = (\color{Cerulean}{ 3}\color{black}{ )} ^ { 2 } + 2 ( \color{Cerulean}{3}\color{black}{ )} - 3 \\ & = 9 + 6 - 3 \\ & = 12 \end{aligned}\) |
Тому,
\(\begin{aligned} ( f - g ) ( 3 ) & = f ( 3 ) - g ( 3 ) \\ & = 46 - 12 \\ & = 34 \end{aligned}\)
Зверніть увагу, що ми отримуємо таку ж відповідь.
Відповідь:
\((f−g)(3)=34\)
Примітка
Якщо потрібно оцінити декілька значень, найкраще спочатку знайти суму або різницю в цілому, а потім використати її для оцінки.
Вправа\(\PageIndex{2}\)
Оцініть\((f+g)(−1)\) дані\(f(x)=x^{3}+x−8\) і\(g(x)=2x^{2}−x+9\).
- Відповідь
-
\(2\)
www.youtube.com/В/АйКЗЗ9U6XPW
Функції множення та ділення
Позначення, що використовуються для позначення множення 3 та ділення 4 функцій, такі:
| Множення функцій: | \(( f \cdot g ) ( x ) = f ( x ) \cdot g ( x )\) |
|---|---|
| Розподіл функцій: | \(( f / g ) ( x ) = \frac { f ( x ) } { g ( x ) } , \text { where } g ( x ) \neq 0\) |
Приклад\(\PageIndex{6}\):
Дано\(f(x)=15x^{4}−9x^{3}+6x^{2}\) і\(g(x)=3x^{2}\), знайдіть\((f⋅g)(x)\) і\((f/g)(x)\).
Рішення
Позначення\(f⋅g\) вказує на те, що ми повинні множити. Застосовуємо розподільне властивість і спрощуємо.
\(\begin{aligned} ( f \cdot g ) ( x ) & = f ( x ) \cdot g ( x ) \\ & = \left( 15 x ^ { 4 } - 9 x ^ { 3 } + 6 x ^ { 2 } \right) \left( 3 x ^ { 2 } \right) \\ & = 15 x ^ { 4 } \cdot \color{Cerulean}{3 x ^ { 2 }}\color{black}{ -} 9 x ^ { 3 } \cdot \color{Cerulean}{3 x ^ { 2} }\color{black}{ +} 6 x ^ { 2 } \cdot \color{Cerulean}{3 x ^ { 2} } \\ & = 45 x ^ { 6 } - 27 x ^ { 5 } + 18 x ^ { 4 } \end{aligned}\)
Позначення\(f /g\) вказує на те, що ми повинні ділити. Для цього коефіцієнта припустимо\(x ≠ 0\).
\(\begin{aligned} ( f / g ) ( x ) & = \frac { f ( x ) } { g ( x ) } \\ & = \frac { 15 x ^ { 4 } - 9 x ^ { 3 } + 6 x ^ { 2 } } { 3 x ^ { 2 } } \\ & = \frac { 15 x ^ { 4 } } { 3 x ^ { 2 } } - \frac { 9 x ^ { 3 } } { 3 x ^ { 2 } } + \frac { 6 x ^ { 2 } } { 3 x ^ { 2 } } \\ & = 5 x ^ { 2 } - 3 x + 2 \end{aligned}\)
Відповідь:
\((f⋅g)(x)=45x^{6}−27x^{5}+18x^{4}\)і\((f/g)(x)=5x^{2}−3x+2\) де\(x≠0\).
Приклад\(\PageIndex{7}\):
Дано\(f(x)=6x−5\) і\(g(x)=3x^{2}−2x−1\), оцінити\((f⋅g)(0)\) і\((f⋅g)(−1)\)
Рішення
Почніть з пошуку\((f⋅g)(x)\).
\(\begin{aligned} ( f \cdot g ) ( x ) & = f ( x ) \cdot g ( x ) \\ & = ( 6 x - 5 ) \left( 3 x ^ { 2 } - 2 x - 1 \right) \\ & = 18 x ^ { 3 } - 12 x ^ { 2 } - 6 x - 15 x ^ { 2 } + 10 x + 5 \\ & = 18 x ^ { 3 } - 27 x ^ { 2 } + 4 x + 5 \end{aligned}\)
\(( f \cdot g ) ( x ) = 18 x ^ { 3 } - 27 x ^ { 2 } + 4 x + 5\)Тому і у нас є,
| \(\begin{aligned} ( f \cdot g ) ( \color{Cerulean}{0}\color{black}{ )} & = 18 ( \color{Cerulean}{0}\color{black}{ )} ^ { 3 } - 27 ( \color{Cerulean}{0}\color{black}{ )} ^ { 2 } + 4 ( \color{Cerulean}{0}\color{black}{ )} + 5 \\ & = 5 \end{aligned}\) | \(\begin{aligned} ( f \cdot g ) ( \color{Cerulean}{-1}\color{black}{ )} & = 18 ( \color{Cerulean}{-1}\color{black}{ )} ^ { 3 } - 27 ( \color{Cerulean}{-1}\color{black}{ )} ^ { 2 } + 4 ( \color{Cerulean}{-1}\color{black}{ )} + 5 \\ & = -18-27-4+5\\ &=-44 \end{aligned}\) |
Відповідь:
\(( f \cdot g ) ( 0 ) = 5 \text { and } ( f \cdot g ) ( - 1 ) = - 44\)
Вправа\(\PageIndex{3}\)
Оцініть\((f⋅g)(−1)\) дані\(f(x)=x^{3}+x−8\) і\(g(x)=2x^{2}−x+9\).
- Відповідь
-
\(-120\)
www.youtube.com/В/ВизФГКА9CXG
Додавання функцій графічно
Тут ми досліджуємо геометрію додавання функцій. Один із способів зробити це - використовувати той факт, що\((f+g)(x)=f(x)+g(x)\). Додайте функції разом, використовуючи x -значення, для яких визначено як f, так і g.
Приклад\(\PageIndex{8}\)
Використовуйте графіки\(f\) та\(g\) для графування\(f+g\). Крім того, дайте домен\(f+g\).
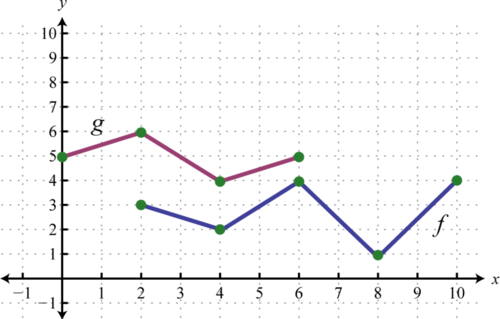
Рішення
У цьому випадку обидві функції визначаються для\(x\) -values між\(2\) і\(6\). Ми будемо використовувати\(2\)\(4\), і\(6\) як репрезентативні значення в області ескізу свого графіка.\(f+g\)
\(\begin{array} { l } { ( f + g ) ( \color{Cerulean}{2}\color{black}{ )} = f ( \color{Cerulean}{2}\color{black}{ )} + g (\color{Cerulean}{ 2}\color{black}{ )} = 3 + 6 = 9 } \\ { ( f + g ) ( \color{Cerulean}{4}\color{black}{ )} = f ( \color{Cerulean}{4}\color{black}{ )} + g ( \color{Cerulean}{4}\color{black}{ )} = 2 + 4 = 6 } \\ { ( f + g ) ( \color{Cerulean}{6}\color{black}{ )} = f ( \color{Cerulean}{6}\color{black}{ )} + g ( \color{Cerulean}{6}\color{black}{ )} = 4 + 5 = 9 } \end{array}\)
Намалюйте графік f+g, використовуючи три впорядковані парні розв'язки\((2,9), (4,6)\), і\((6,9)\).
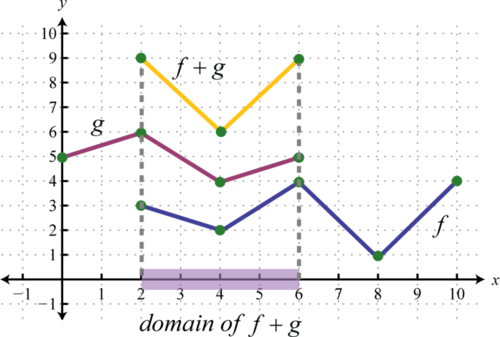
Відповідь:
\(f+g\)на графіку вище має домен\([2,6]\).
Приклад\(\PageIndex{9}\)
Використовуйте графіки\(f\) та\(g\) для графування\(f+g\). Крім того, дайте домен\(f+g\).
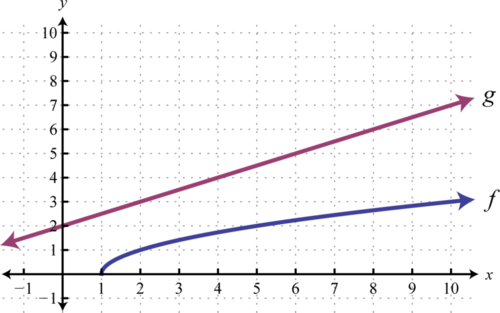
Рішення
Іншим способом графічного додавання невід'ємних функцій є копіювання відрізка лінії, утвореного від\(x\) осі -до однієї з функцій, на іншу, як показано нижче.
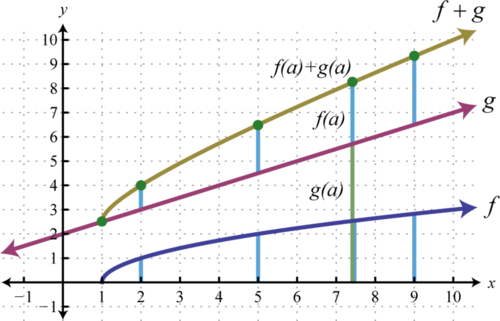
Відрізок лінії від\(x\) -осі до функції\(f\) представляє\(f(a)\). Скопіюйте цей відрізок лінії на іншу функцію над тією ж точкою; кінцева точка представляє\(f(a)+g(a)\). Виконання цього для ряду пунктів дозволяє отримати швидкий ескіз комбінованого графіка. У цьому прикладі домен\(f+g\) обмежується\(x\) значеннями -values, для яких\(f\) визначено.
Відповідь:
Домен:\([1,∞)\)
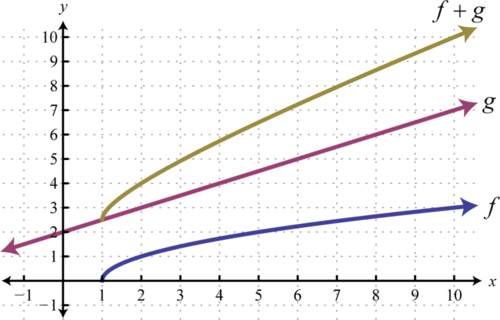
Загалом, домен\(f+g\) - це перетин домену\(f\) з доменом\(g\). Насправді це стосується всіх арифметичних операцій з додатковим врахуванням для ділення. При діленні функцій ми подбаємо про видалення будь-яких значень, які роблять знаменник нулем. Про це буде розглянуто більш докладно в міру просування в алгебрі.
Ключові винос
- Будь-поліном з однією змінною є функцією і може бути записаний у вигляді\(f ( x ) = a _ { n } x ^ { n } + a _ { n - 1 } x ^ { n - 1 } + \ldots + a _ { 1 } x + a _ { 0 }\). Ступінь многочлена є найбільшим показником з усіх членів.
- Використовуйте позначення функцій для впорядкування процесу оцінювання. Підставляйте значення або вираз всередині дужок для кожного екземпляра змінної.
- Позначення\((f+g)(x)\) вказує на те, що ми повинні додати\(f(x)+g(x)\).
- Позначення\((f−g)(x)\) вказує на те, що ми повинні відняти\(f(x)−g(x)\).
- Позначення\((f⋅g)(x)\) вказує на те, що ми повинні множити\(f(x)g(x)\).
- Позначення\((f/g)(x)\) вказує на те, що ми повинні ділити\(\frac{f(x)}{g(x)}\), де\(g(x)≠0\).
- Доменом функції, яка є результатом цих арифметичних операцій, є перетин області кожної функції. Домен частки додатково обмежується значеннями, які не оцінюються нулем у знаменнику.
Вправа\(\PageIndex{4}\)
Оцініть.
- Дано\(f(x)=x^{2}−10x+3\), знайдіть\(f(−3), f(0)\), і\(f(5)\).
- Дано\(f(x)=2x^{2}−x+9\), знайдіть\(f(−1), f(0)\), і\(f(3)\).
- Дано\(g(x)=x^{3}−x^{2}+x+7\), знайдіть\(g(−2), g(0)\), і\(g(3)\).
- Дано\(g(x)=x^{3}−2x+5\), знайдіть\(g(−5), g(0)\), і\(g(3)\).
- Дано\(s(t)=5t^{4}−t^{2}+t−3\), знайдіть\(s(−1), s(0)\), і\(s(2)\).
- Дано\(p(n)=n^{4}−10n^{2}+9\), знайдіть\(p(−3), p(−1)\), і\(p(2)\).
- Дано\(f(x)=x^{6}−64\), знайдіть\(f(−2), f(−1)\), і\(f(0)\).
- Дано\(f(x)=x^{6}−x^{3}+3\), знайдіть\(f(−2), f(−1)\), і\(f(0)\).
- Дано\(f(x)=x^{2}−2x−1\), знайдіть\(f(2t)\) і\(f(2t−1)\).
- Дано\(f(x)=x^{2}−2x+4\), знайдіть\(f(−3t)\) і\(f(2−3t)\).
- Дано\(g(x)=2x^{2}+3x−1\), знайдіть\(g(−5a)\) і\(g(5−2x)\).
- Дано\(g(x)=3x^{2}−5x+4\), знайдіть\(g(−4u)\) і\(g(3x−1)\).
- Дано\(f(x)=x^{3}−1\), знайдіть\(f(2a)\) і\(f(x−2)\).
- Дано\(f(x)=x^{3}−x+1\), знайдіть\(f(−3x)\) і\(f(2x+1)\).
- Дано\(g(x)=x^{3}+x^{2}−1\), знайдіть\(g(x^{2})\) і\(g(x−4)\).
- Дано\(g(x)=2x^{3}−x+1\), знайдіть\(g(−2x^{3})\) і\(g(3x−1)\).
- Відповідь
-
1. \(f ( - 3 ) = 42 ; f ( 0 ) = 3 ; f ( 5 ) = - 22\)
3. \(g ( - 2 ) = - 7 ; g ( 0 ) = 7 ; g ( 3 ) = 28\)
5. \(s ( - 1 ) = 0 ; s ( 0 ) = - 3 ; s ( 2 ) = 75\)
7. \(f ( - 2 ) = 0 ; f ( - 1 ) = - 63 ; f ( 0 ) = - 64\)
9. \(f ( 2 t ) = 4 t ^ { 2 } - 4 t - 1 : f ( 2 t - 1 ) = 4 t ^ { 2 } - 8 t + 2\)
11. \(g ( - 5 a ) = 50 a ^ { 2 } - 15 a - 1 ; g ( 5 - 2 x ) = 8 x ^ { 2 } - 46 x + 64\)
13. \(f ( 2 a ) = 8 a ^ { 3 } - 1 ; f ( x - 2 ) = x ^ { 3 } - 6 x ^ { 2 } + 12 x - 9\)
15. \(g \left( x ^ { 2 } \right) = x ^ { 6 } + x ^ { 4 } - 1 ; g ( x - 4 ) = x ^ { 3 } - 11 x ^ { 2 } + 40 x - 49\)
Вправа\(\PageIndex{5}\)
Дано функцію обчислення\(f(x+h)\).
- \(f(x)=5x−3\)
- \(f(x)=x^{2}−1\)
- \(f(x)=x^{3}−8\)
- \(f(x)=x^{4}\)
- Відповідь
-
1. \(f ( x + h ) = 5 x + 5 h - 3\)
3. \(f ( x + h ) = x ^ { 3 } + 3 h x ^ { 2 } + 3 h ^ { 2 } x + h ^ { 3 } - 8\)
Вправа\(\PageIndex{6}\)
За заданим графіком поліноміальної функції\(f\) знайдіть значення функції.
1. Знайти\(f(0), f(1)\), і\(f(2)\).
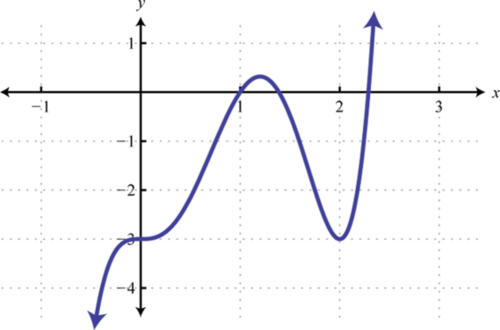
2. Знайти\(f(−1), f(0)\), і\(f(1)\).
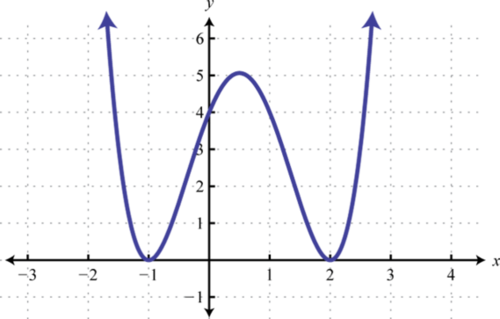
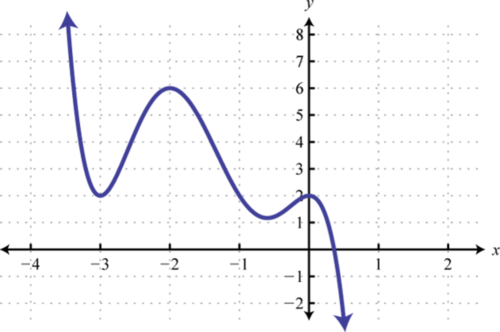
3. Знайти\(f(−2), f(−1)\), і\(f(0)\).
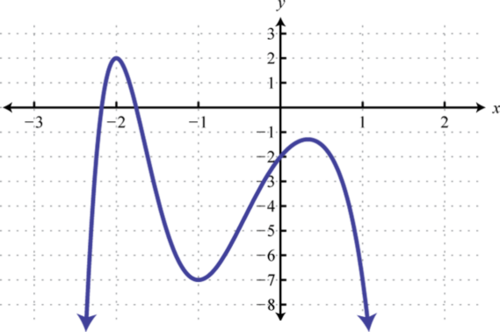
4. Знайти\(f(−3), f(−2)\), і\(f(0)\).
5. Снаряд запускається вгору від землі зі швидкістю\(48\) футів в секунду. Напишіть функцію, яка моделює висоту снаряда і використовуйте її для обчислення висоти\(1/2\) щосекунди після запуску. Намалюйте графік, який показує висоту снаряда по відношенню до часу.
6. Об'єкт кидається вгору з платформи\(48\) -foot зі швидкістю\(32\) футів в секунду. Напишіть функцію, яка моделює висоту об'єкта і використовуйте її для обчислення висоти\(1/2\) щосекунди після кидання об'єкта. Намалюйте графік, який показує висоту об'єкта по відношенню до часу.
7. Об'єкт скидається з\(128\) пішохідного моста. Напишіть функцію, яка моделює висоту об'єкта, і використовуйте її для обчислення висоти в\(1\) секунду та\(2\) секунди після того, як він був скинутий.
8. Об'єкт скидається з будівлі\(500\) -foot. Напишіть функцію, яка моделює висоту об'єкта, і використовуйте її для обчислення відстані, на яку об'єкт потрапляє в\(1\) 1-у секунду,\(2\) і другу, і другу,\(3\) і другу.
9. Куля вистрілюється прямо в повітря зі швидкістю\(320\) метрів в секунду. Ігноруючи наслідки тертя повітря, напишіть функцію, яка моделює висоту кулі, і використовуйте її для обчислення висоти кулі за\(1\) хвилину після того, як вона була випущена в повітря.
10. Книга скидається з висоти\(10\) метрів. Напишіть функцію, яка дає висоту книги, і використовуйте її, щоб визначити, наскільки вона впаде за\(1 \frac{1}{4}\) лічені секунди.
- Відповідь
-
1. \(f ( 0 ) = - 3 ; f ( 1 ) = 0 ; f ( 2 ) = - 3\)
3. \(f ( - 2 ) = 2 ; f ( - 1 ) = - 7 ; f ( 0 ) = - 2\)
5. \(h ( t ) = - 16 t ^ { 2 } + 48 t\)
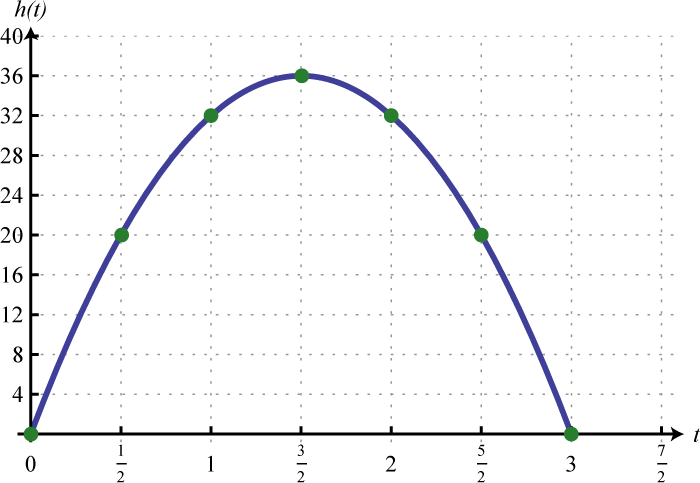
Малюнок\(\PageIndex{11}\) 7. \(h ( t ) = - 16 t ^ { 2 } + 128\); У\(1\) секунду висота об'єкта -\(112\) ноги, а в\(2\) секундах його висота -\(64\) ноги.
9. \(h ( t ) = - 4.9 t ^ { 2 } + 320 t ; 1,560\)метрів
Вправа\(\PageIndex{7}\)
Дано функції\(f\) і\(g\), знайти\((f+g)\) і\((f-g)\).
- \(f(x)=5x−3, g(x)=4x−1\)
- \(f(x)=3x+2, g(x)=7x−5\)
- \(f(x)=2−3x, g(x)=1−x\)
- \(f(x)=8x−5, g(x)=−7x+4\)
- \(f(x)=x^{2}−3x+2, g(x)=x^{2}+4x−7\)
- \(f(x)=2x^{2}+x−3, g(x)=x^{2}−x+4\)
- \(f(x)=x^{2}+5x−3, g(x)=6x+11\)
- \(f(x)=9x+5, g(x)=2x^{2}−5x+4\)
- \(f(x)=9x^{2}−1, g(x)=x^{2}+5x\)
- \(f(x)=10x^{2}, g(x)=5x^{2}−8\)
- \(f(x)=8x^{3}+x−4, g(x)=4x^{3}+x^{2}−1\)
- \(f(x)=x^{3}−x^{2}+x+1, g(x)=x^{3}−x^{2}−x−1\)
- Відповідь
-
1. \(( f + g ) ( x ) = 9 x - 4 ; ( f - g ) ( x ) = x - 2\)
3. \(( f + g ) ( x ) = - 4 x + 3 ; ( f - g ) ( x ) = - 2 x + 1\)
5. \(( f + g ) ( x ) = 2 x ^ { 2 } + x - 5 ; ( f - g ) ( x ) = - 7 x + 9\)
7. \(( f + g ) ( x ) = x ^ { 2 } + 11 x + 8 ; ( f - g ) ( x ) = x ^ { 2 } - x - 14\)
9. \(( f + g ) ( x ) = 10 x ^ { 2 } + 5 x - 1 ; ( f - g ) ( x ) = 8 x ^ { 2 } - 5 x - 1\)
11. \(\begin{array} { l } { ( f + g ) ( x ) = 12 x ^ { 3 } + x ^ { 2 } + x - 5 } \\ { ( f - g ) ( x ) = 4 x ^ { 3 } - x ^ { 2 } + x - 3 } \end{array}\)
Вправа\(\PageIndex{8}\)
З огляду на\(f ( x ) = x ^ { 3 } + 2 x ^ { 2 } - 8\) і\(g ( x ) = 2 x ^ { 2 } - 3 x + 5\), оцініть наступне.
- \((f+g)(−2)\)
- \((f+g)(3)\)
- \((f−g)(−2)\)
- \((f−g)(3)\)
- \((g−f)(−2)\)
- \((g−f)(3)\)
- \((f+f)(1)\)
- \((g+g)(−1)\)
- Відповідь
-
1. \(11\)
3. \(-27\)
5. \(27\)
7. \(-10\)
Вправа\(\PageIndex{9}\)
З огляду на графіки\(f\) і\(g\), оцініть наступне.

- \((f+g)(−4)\)
- \((f−g)(−4)\)
- \((f+g)(−2)\)
- \((f−g)(−2)\)
- \((f+g)(0)\)
- \((f−g)(0)\)
- Відповідь
-
1. \(-4\)
3. \(1\)
5. \(-2\)
Вправа\(\PageIndex{10}\)
Дано\(f\) і\(g\), знайдіть\(f⋅g\).
- \(f(x)=5x, g(x)=x−3\)
- \(f(x)=x−4, g(x)=6x\)
- \(f(x)=2x−3, g(x)=3x+4\)
- \(f(x)=5x−1, g(x)=2x+1\)
- \(f(x)=3x+4, g(x)=3x−4\)
- \(f(x)=x+5, g(x)=x−5\)
- \(f(x)=x−2, g(x)=x^{2}−3x+2\)
- \(f(x)=2x−3, g(x)=x^{2}+2x−1\)
- \(f(x)=2x^{2}, g(x)=x^{2}−7x+5\)
- \(f(x)=5x^{3}, g(x)=x^{2}−3x−1\)
- \(f(x)=x^{2}−3x−2, g(x)=2x^{2}−x+3\)
- \(f(x)=x^{2}+x−1, g(x)=x^{2}−x+1\)
- Відповідь
-
1. \(( f \cdot g ) ( x ) = 5 x ^ { 2 } - 15 x\)
3. \(( f \cdot g ) ( x ) = 6 x ^ { 2 } - x - 12\)
5. \(( f \cdot g ) ( x ) = 9 x ^ { 2 } - 16\)
7. \(( f \cdot g ) ( x ) = x ^ { 3 } - 5 x ^ { 2 } + 8 x - 4\)
9. \(( f \cdot g ) ( x ) = 2 x ^ { 4 } - 14 x ^ { 3 } + 10 x ^ { 2 }\)
11. \(( f \cdot g ) ( x ) = 2 x ^ { 4 } - 7 x ^ { 3 } + 2 x ^ { 2 } - 7 x - 6\)
Вправа\(\PageIndex{11}\)
Дано\(f\) і\(g\), знайдіть\(f/g\). (Припустимо, що всі вирази в знаменнику є ненульовими.)
- \(f ( x ) = 36 x ^ { 3 } - 16 x ^ { 2 } - 8 x , g ( x ) = 4 x\)
- \(f ( x ) = 2 x ^ { 3 } - 6 x ^ { 2 } + 10 x , g ( x ) = 2 x\)
- \(f ( x ) = 20 x ^ { 7 } - 15 x ^ { 5 } + 5 x ^ { 3 } , g ( x ) = 5 x ^ { 3 }\)
- \(f ( x ) = 9 x ^ { 6 } + 12 x ^ { 4 } - 3 x ^ { 2 } , g ( x ) = 3 x ^ { 2 }\)
- \(f ( x ) = x ^ { 3 } + 4 x ^ { 2 } + 3 x - 2 , g ( x ) = x + 2\)
- \(f ( x ) = x ^ { 3 } - x ^ { 2 } - 10 x + 12 , g ( x ) = x - 3\)
- \(f ( x ) = 6 x ^ { 3 } - 13 x ^ { 2 } + 36 x - 45 , g ( x ) = 2 x - 3\)
- \(f ( x ) = 6 x ^ { 3 } - 11 x ^ { 2 } + 15 x - 4 , g ( x ) = 3 x - 1\)
- \(f ( x ) = 3 x ^ { 3 } - 13 x ^ { 2 } - x + 8 , g ( x ) = 3 x + 2\)
- \(f ( x ) = 5 x ^ { 3 } - 16 x ^ { 2 } + 13 x - 6 , g ( x ) = 5 x - 1\)
- Відповідь
-
1. \(( f / g ) ( x ) = 9 x ^ { 2 } - 4 x - 2\)
3. \(( f / g ) ( x ) = 4 x ^ { 4 } - 3 x ^ { 2 } + 1\)
5. \(( f / g ) ( x ) = x ^ { 2 } + 2 x - 1\)
7. \(( f / g ) ( x ) = 3 x ^ { 2 } - 2 x + 15\)
9. \(( f / g ) ( x ) = x ^ { 2 } - 5 x + 3 + \frac { 2 } { 3 x + 2 }\)
Вправа\(\PageIndex{12}\)
Наведено\(f ( x ) = 25 x ^ { 4 } + 10 x ^ { 3 } - 5 x ^ { 2 }\) і\(g(x) = 5x^{2}\) оцінюють наступне.
- \((f⋅g)(−1)\)
- \((f⋅g)(1)\)
- \((f/g)(−2)\)
- \((f/g)(−3)\)
- \((g⋅f)(0)\)
- \((g/f)(1)\)
- \((g⋅g)(−1)\)
- \((f⋅f)(−1)\)
- Відповідь
-
1. \(50\)
3. \(15\)
5. \(0\)
7. \(25\)
Вправа\(\PageIndex{13}\)
Наведено графіки\(f\) і\(g\) оцінюють наступне.

1. \((f⋅g)(3)\)
2. \((f⋅g)(5)\)
3. \((f/g)(5)\)
4. \((f/g)(3)\)
5. \((f⋅g)(1)\)
6. \((f/g)(1)\)
- Відповідь
-
1. \(-2\)
3. \(0\)
5. \(4\)
Вправа\(\PageIndex{14}\)
Дано\(f ( x ) = 5 x ^ { 3 } - 15 x ^ { 2 } + 10 x , g ( x ) = x ^ { 2 } - x + 3\), і\(h(x)=-5x\), знайдіть наступне. (Припустимо, що всі вирази в знаменнику є ненульовими.)
- \((f−g)(x)\)
- \((g−f)(x)\)
- \((g⋅h)(x)\)
- \((f/h)(x)\)
- \((h+g)(x)\)
- \((h⋅f)(x)\)
- \((g/h)(2)\)
- \((g−h)(−3)\)
- Дохід в доларах від продажу MP3-плеєрів дається функцією\(R(n)=125n−0.15n^{2}\), де\(n\) представляє кількість проданих одиниць\((0≤n<833)\). Вартість виробництва MP3-плеєрів у доларах визначається формулою,\(C(n)=1200+42n\) де\(n\) представлена кількість вироблених одиниць. Напишіть функцію, яка моделює прибуток від виробництва та продажу\(n\) MP3-плеєрів. Використовуйте функцію для визначення прибутку, отриманого від виробництва та продажу\(225\) MP3-плеєрів. Нагадаємо, що прибуток дорівнює доходу за вирахуванням витрат.
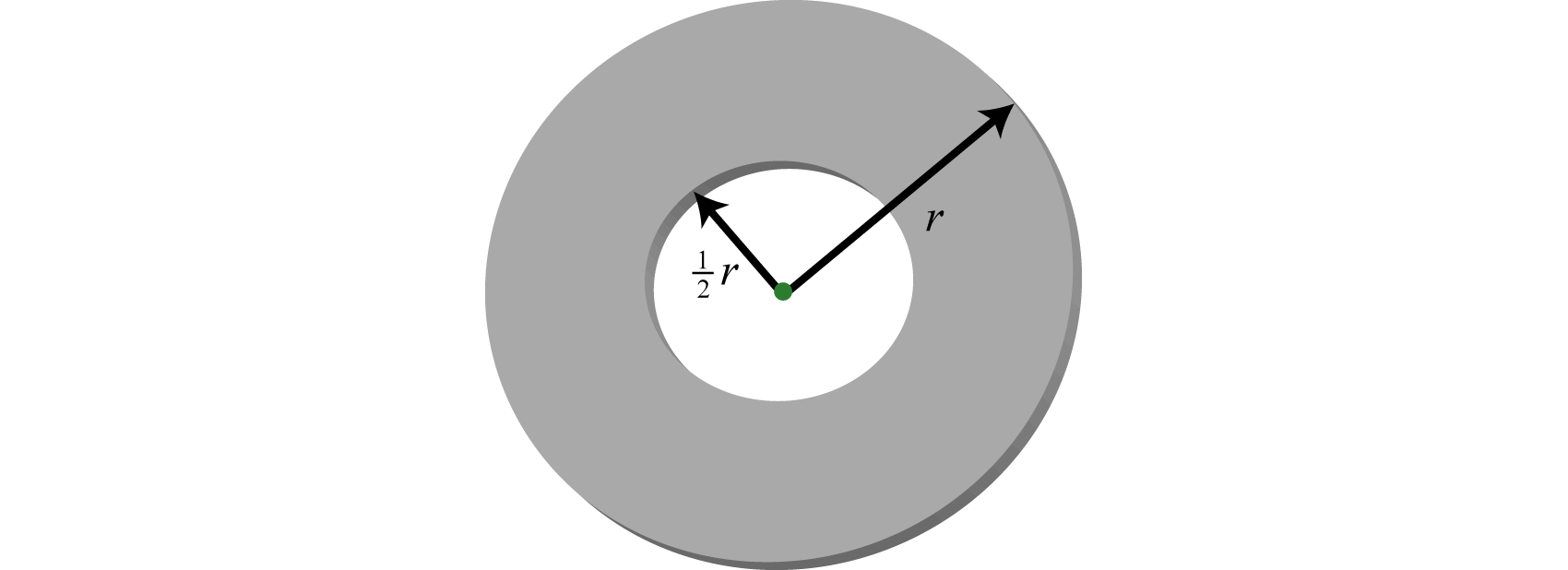
- Внутрішній радіус шайби -\(\frac{1}{2}\) це зовнішній радіус.
- Відповідь
-
1. \(( f - g ) ( x ) = 5 x ^ { 3 } - 16 x ^ { 2 } + 11 x - 3\)
3. \(( g \cdot h ) ( x ) = - 5 x ^ { 3 } + 5 x ^ { 2 } - 15 x\)
5. \(( h + g ) ( x ) = x ^ { 2 } - 6 x + 3\)
7. \(( g / h ) ( 2 ) = - \frac { 1 } { 2 }\)
9. \(P ( n ) = - 0.15 n ^ { 2 } + 83 n - 1200 ; \$ 9,881.25\)
Вправа\(\PageIndex{15}\)
Використовуйте графіки\(f\) та\(g\) для графування\(f+g\). Крім того, дайте домен\(f+g\).
1.

2.

3.

4.

5.
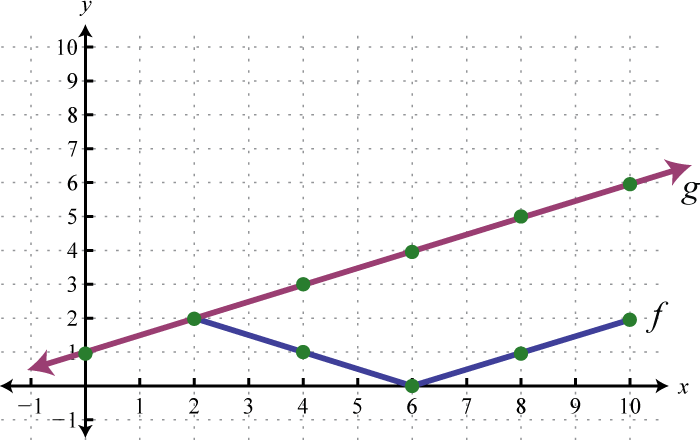
6.
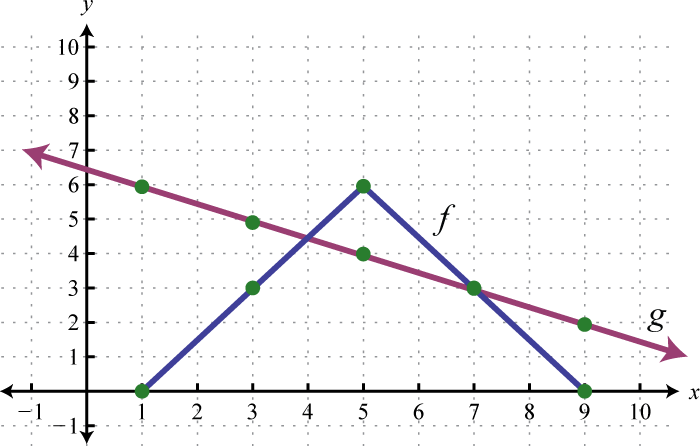
7.

8.

9.

10.

- Відповідь
-
1. \([2,8]\)

Малюнок\(\PageIndex{25}\) 3. \([0,10]\)

Малюнок\(\PageIndex{26}\) 5. \([2,10]\)

Малюнок\(\PageIndex{27}\) 7. \([ - 2 , \infty )\)
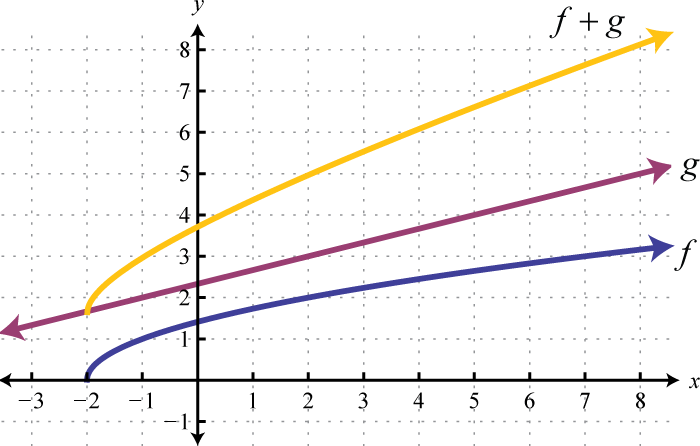
Малюнок\(\PageIndex{28}\) 9. \(( - \infty , \infty )\)

Малюнок\(\PageIndex{29}\)
Вправа\(\PageIndex{16}\)
- Які арифметичні операції над функціями є комутативними? Поясніть.
- Дослідіть способи графічного додавання функцій, якщо вони виявляються негативними.
- Відповідь
-
1. Відповідь може відрізнятися
Виноски
1 Додайте функції, зазначені позначенням:\((f + g) (x) = f (x) + g (x) \).
2 Відніміть функції, як зазначено позначенням:\((f − g) (x) = f (x) − g (x)\).
3 Функції множення, як зазначено позначенням:\((f ⋅ g) (x) = f (x) ⋅ g (x)\).
4 Розділіть функції, як зазначено позначенням:\((f /g) (x) = \frac{f(x)}{ g(x)}\), де\(g (x) ≠ 0\).
