1.4: Поліноми
- Page ID
- 59277
У цьому розділі студенти будуть:
- Визначте ступінь і провідний коефіцієнт многочленів.
- Додайте і відніміть многочлени.
- Множимо многочлени.
- Використовуйте FOIL для множення біноміалів.
- Виконувати операції при поліномії
- ls декількох змінних.
Граф будує собачий будиночок, фронт якого має форму квадрата, увінчаного трикутником. Тут буде прямокутна двері, через яку собака зможе увійти і вийти з будинку. Граф хоче знайти площу передньої частини собачої будки, щоб він міг придбати потрібну кількість фарби. Використовуючи виміри фасаду будинку, показані на малюнку\(\PageIndex{1}\), ми можемо створити вираз, що поєднує в собі кілька змінних термінів, що дозволяють вирішити цю задачу і інші подібні.
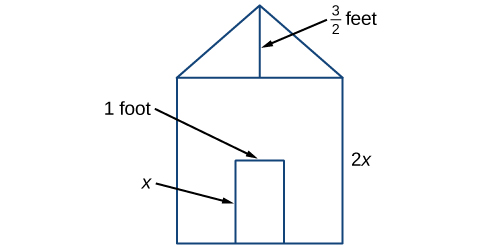
- Спочатку знайдіть площу квадрата в квадратних футах.
\[\begin{align*} A &= s^2\\ &= {(2x)}^2\\ &= 4x^2 \end{align*}\]
- Потім знайдіть площу трикутника в квадратних футах.
\[\begin{align*} A &= \dfrac{1}{2}bh\\ &= \dfrac{1}{2}(2x)\left (\dfrac{3}{2} \right )\\ &= \dfrac{3}{2}x \end{align*}\]
- Далі знаходимо площу прямокутної двері в квадратних футах.
\[\begin{align*} A &= lw\\ &= x\times1\\ &= x \end{align*}\]
Площа передньої частини собачої будки можна знайти, склавши площі квадрата і трикутника, а потім віднімаючи площу прямокутника. Коли ми це робимо, ми отримуємо
\(4x^2+\dfrac{3}{2}x-x\)\(ft^2\)
або
\(4x^2+\dfrac{1}{2}x\)\(ft^2\)
У цьому розділі ми розглянемо такі вирази, як цей, які об'єднують кілька змінних термінів.
Визначення ступеня та провідного коефіцієнта поліномів
Щойно знайдена формула є прикладом многочлена, який є сумою або різницею членів, кожен з яких складається зі змінної, зведеної до невід'ємного цілого степеня. Число, помножене на змінну, підняту до показника\(384\pi\), наприклад, відомо як коефіцієнт. Коефіцієнти можуть бути додатними, негативними або нульовими, а можуть бути цілими числами, десятковими дроби або дроби. Кожен твір\(a_ix^i\)\(384\pi w\), наприклад, є терміном полінома. Якщо термін не містить змінної, він називається константою.
Поліном, що містить тільки один член\(5x^4\), наприклад, називається моном. Поліном, що містить два члени\(2x−9\), такі як, називається біном. Многочлен, що містить три члени\(−3x^2+8x−7\), такі як, називається триноміальним.
Ми можемо знайти ступінь многочлена, ідентифікуючи найвищу потужність змінної, яка зустрічається в многочлені. Термін з найвищим ступенем називається провідним терміном, оскільки він зазвичай пишеться першим. Коефіцієнт провідного члена називається провідним коефіцієнтом. Коли многочлен пишеться так, щоб сили були спадними, ми говоримо, що він в стандартній формі.
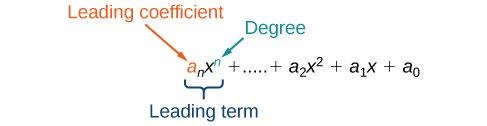
Многочлен - це вираз, яке можна записати у вигляді
Кожне дійсне число ai називається коефіцієнтом. Число\(a_0\), яке не множиться на змінну, називається константою. Кожен\(a_ix^i\) твір є терміном многочлена. Найвища сила змінної, яка зустрічається в многочлені, називається ступенем многочлена. Провідним терміном є термін з найбільшою потужністю, а його коефіцієнт називається провідним коефіцієнтом.
- Знайдіть найвищу потужність x, щоб визначити ступінь.
- Визначте термін, що містить найвищу силу x, щоб знайти провідний термін.
- Визначте коефіцієнт провідного терміну.
Для наступних поліномів визначте ступінь, провідний член та провідний коефіцієнт.
- \(3+2x^2−4x^3\)
- \(5t^5−2t^3+7t\)
- \(6p−p^3−2\)
Рішення
- Найвища сила\(x\) є\(3\), тому ступінь є\(3\). Провідним терміном є термін, що містить цей ступінь,\(−4x^3\). Провідним коефіцієнтом є коефіцієнт цього терміну,\(−4\).
- Найвища сила\(t\) є\(5\), тому ступінь є\(5\). Провідним терміном є термін, що містить цей ступінь,\(5t^5\). Провідним коефіцієнтом є коефіцієнт цього терміну,\(5\).
- Найвища сила\(p\) є\(3\), тому ступінь є\(3\). Провідним терміном є термін, що містить цей ступінь\(−p^3\),, Провідний коефіцієнт є коефіцієнтом цього терміну, −1.
Визначте ступінь, провідний член та провідний коефіцієнт многочлена\(4x^2−x^6+2x−6\).
- Відповідь
-
Ступінь є\(6\), провідним терміном є\(−x^6\), а провідний коефіцієнт є\(−1\).
Додавання та віднімання многочленів
Ми можемо додавати і віднімати поліноми, поєднуючи подібні терміни, які є термінами, які містять ті самі змінні, підняті до тих самих показників. Наприклад,\(5x^2\) і\(−2x^2\) схожі на терміни, і можуть бути додані, щоб отримати\(3x^2\), але\(3x\) і не\(3x^2\) схожі на терміни, а тому не можуть бути додані.
- Поєднуйте подібні терміни.
- Спростити і написати в стандартній формі.
Знайдіть суму.
\((12x^2+9x−21)+(4x^3+8x^2−5x+20)\)
Рішення
\[\begin{align*} &4x^3+(12x^2+8x^2)+(9x-5x)+(-21+20)\qquad \text{Combine like terms} \\ &4x^3+20x^2+4x-1\qquad \qquad \qquad \qquad \qquad \qquad \; \; \; \text{Simplify} \end{align*}\]
Аналіз
Ми можемо перевірити наші відповіді на ці типи проблем за допомогою графічного калькулятора. Щоб перевірити, графуйте задачу як дано разом із спрощеною відповіддю. Два графіки повинні бути рівнозначними. Обов'язково використовуйте одне і те ж вікно для порівняння графіків. Використання різних вікон може змусити вирази здаватися рівнозначними, коли вони не є.
Знайдіть суму.
\((2x^3+5x^2−x+1)+(2x^2−3x−4)\)
- Відповідь
-
\(2x^3+7x^2−4x−3\)
Знайдіть різницю.
\((7x^4−x^2+6x+1)−(5x^3−2x^2+3x+2)\)
Рішення
\(7x^4−5x^3+(−x^2+2x^2)+(6x−3x)+(1−2)\)Поєднуйте подібні терміни
\(7x^4−5x^3+x^2+3x−1\)Спростити
Аналіз
Зверніть увагу, що знаходження різниці між двома многочленами таке ж, як додавання протилежного другого многочлена до першого.
Знайдіть різницю.
\((−7x^3−7x^2+6x−2)−(4x^3−6x^2−x+7)\)
- Відповідь
-
\(−11x^3−x^2+7x−9\)
Множення многочленів
Множення многочленів трохи складніше, ніж додавання та віднімання поліномів. Ми повинні використовувати розподільну властивість, щоб помножити кожен член у першому многочлені на кожен член у другому многочлені. Потім ми поєднуємо як терміни. Ми також можемо використовувати ярлик, який називається методом FOIL при множенні біноміалів. Деякі спеціальні продукти слідують шаблонам, які ми можемо запам'ятовувати та використовувати замість того, щоб щоразу множити многочлени вручну. Ми розглянемо найрізноманітніші способи множення многочленів.
Множення многочленів за допомогою розподільної властивості
Щоб помножити число на многочлен, скористаємося розподільним властивістю. Число необхідно розподілити на кожен член многочлена. Ми можемо розподілити\(2\) in,\(2(x+7)\) щоб отримати еквівалентний вираз\(2x+14\). При множенні многочленів розподільне властивість дозволяє множити кожен член першого многочлена на кожен член другого. Потім ми додаємо продукти разом і поєднуємо подібні терміни, щоб спростити.
- Помножте кожен член першого многочлена на кожен член другого.
- Поєднуйте подібні терміни.
- Спростити.
Знайдіть товар.
\((2x+1)(3x^2−x+4)\)
Рішення
\[\begin{align*} &2x(3x^2-x+4)+1(3x^2-x+4)\qquad \text{ Use the distributive property }\\ &(6x^3-2x^2+8x)+(3x^2-x+4)\qquad \text{ Multiply }\\ &6x^3+(-2x^2+3x^2)+(8x-x)+4\qquad \text{ Combine like terms } \\ &6x^3+x^2+7x+4\qquad \text{ Simplify } \end{align*}\]
Аналіз
Ми можемо використовувати таблицю для відстеження нашої роботи, як показано в табл\(\PageIndex{1}\). Запишіть один многочлен поперек зверху, а інший вниз збоку. Для кожного поля таблиці помножте термін для цього рядка на термін для цього стовпця. Потім додайте всі терміни разом, об'єднайте подібні терміни та спростіть.
| \(3x^2\) | \(−x\) | \(+4\) | |
| \(2x\) | \(6x^3\) | \(−2x^2\) | \(8x\) |
| \(+1\) | \(3x^2\) | \(−x\) | \(4\) |
Знайдіть товар.
\((3x+2)(x^3−4x^2+7)\)
- Відповідь
-
\(3x^4−10x^3−8x^2+21x+14\)
Використання FOIL для множення біноміалів
Ярлик під назвою FOIL іноді використовується для пошуку добутку двох біноміалів. Він називається FOIL, тому що ми множимо перші члени, зовнішні члени, внутрішні члени, а потім останні члени кожного біноміала.

Метод FOIL виникає з розподільної властивості. Ми просто множимо кожен член першого біноміала на кожен член другого двочлена, а потім об'єднуємо подібні терміни.
Задано два біноміали, використовуйте FOIL для спрощення виразу.
- Помножте зовнішні члени біноміалів.
- Помножте останні члени кожного двочлена.
- Поєднуйте подібні терміни і спрощуйте.
Використовуйте FOIL, щоб знайти продукт.
\((2x−10)(3x+3) \nonumber\)
Рішення
Знайдіть твір перших термінів.

Знайдіть добуток зовнішніх термінів.

Знайдіть твір внутрішніх термінів.

Знайдіть твір останніх термінів.

\[\begin{align*} &6x^2+6x-54x-54\qquad \text{Add the products}\\ &6x^2+(6x-54x)-54\qquad \text{Combine like terms} \\ &6x^2-48x-54\qquad \qquad \qquad \text{Simplify} \end{align*}\]
Використовуйте FOIL, щоб знайти продукт.
\((x+7)(3x−5)\)
- Відповідь
-
\(3x^2+16x−35\)
Ідеальні квадратні триноміали
Певні біноміальні вироби мають особливі форми. Коли біноміал знаходиться в квадраті, результат називається ідеальним квадратним тріноміалом. Ми можемо знайти квадрат, помноживши біноміал сам по собі. Однак існує особлива форма, яку приймає кожен з цих ідеальних квадратних триномів, а запам'ятовування форми робить квадратичне біноміали набагато простіше і швидше. Давайте розглянемо кілька ідеальних квадратних тріноманів, щоб ознайомитися з формою.
\({(x+5)}^2=x^2+10x+25\)
\({(x-3)}^2=x^2-6x+9\)
Зверніть увагу, що перший член кожного трічлена є квадратом першого члена двочлена і, аналогічно, останній член кожного триноміалу - квадрат останнього члена біноміалу. Середній термін є подвійним добутком двох термінів. Нарешті, ми бачимо, що перша ознака триноміала така ж, як і знак біноміала.
Коли біноміал у квадраті, результатом є перший член у квадраті, доданий, щоб подвоїти добуток обох термінів і останнього члена в квадраті.
\[{(x+a)}^2=(x+a)(x+a)=x^2+2ax+a^2\]
- Квадратний перший член двочлена.
- Квадратний останній член двочлена.
- Для середнього члена триноміала подвоїти добуток двох членів.
- Додайте і спрощуйте.
Розгорнути\((3x−8)^2\).
Рішення
Почніть з квадрата першого члена і останнього члена. Для середнього члена триноміала подвоїти добуток двох членів.
\[\begin{align*} &{(3x)}^2-2(3x)(8)+{(-8)}^2 \\ &9x^2-48x+64\qquad \qquad \; \; \; \; \text{Simplify} \end{align*}\]
Розгорнути\({(4x−1)}^2\).
- Відповідь
-
\(16x^2−8x+1\)
Різниця квадратів
Ще одним особливим добутком називається різниця квадратів, яка виникає, коли ми множимо біном на інший біном з тими ж долями, але протилежним знаком. Давайте подивимося, що відбувається, коли ми множимо\((x+1)(x−1)\) за допомогою методу FOIL.
\[\begin{align*} (x+1)(x-1) &= x^2-x+x-1\\ &= x^2-1 \end{align*}\]
Середній член випадає, в результаті чого утворюється різниця квадратів. Так само, як ми зробили з ідеальними квадратами, давайте розглянемо кілька прикладів.
\((x+5)(x-5)=x^2-25\)
\((x+11)(x-11)=x^2-121\)
\((2x+3)(2x-3)=4x^2-9\)
Оскільки знак змінюється у другому двочлені, зовнішній і внутрішній члени скасовують один одного, і нам залишається тільки квадрат першого члена мінус квадрат останнього члена.
Чи існує спеціальна форма для суми квадратів?
Ні. Різниця квадратів відбувається тому, що протилежні ознаки біноміалів змушують зникати середні члени. Не існує двох бічленів, які множаться на суму квадратів.
Коли двочлен множиться на біном з тими ж долями, відокремленими протилежним знаком, результатом є квадрат першого члена мінус квадрат останнього члена.
\[(a+b)(a−b)=a^2−b^2\]
- Квадратний перший член двочленів.
- Квадратний останній член біноміалів.
- Відніміть квадрат останнього члена з квадрата першого члена.
Помножити\((9x+4)(9x−4)\).
Рішення
Квадратний перший термін, щоб отримати\({(9x)}^2=81x^2\). Квадратний останній термін, щоб отримати\(4^2=16\). Відніміть квадрат останнього члена з квадрата першого члена, щоб знайти добуток\(81x^2−16\).
Помножити\((2x+7)(2x−7)\).
- Відповідь
-
\(4x^2−49\)
Виконання операцій з поліномами декількох змінних
Ми розглянули многочлени, що містять лише одну змінну. Однак многочлен може містити кілька змінних. Всі ті ж правила застосовуються при роботі з поліномами, що містять кілька змінних. Розглянемо приклад:
\[\begin{align*} &(a+2b)(4a-b-c) a(4a-b-c)+2b(4a-b-c)\qquad \text{ Use the distributive property }\\ &4a^2-ab-ac+8ab-2b^2-2bc\qquad \qquad\qquad\qquad\qquad \text{ Multiply }\\ &4a^2+(-ab+8ab)-ac-2b^2-2bc\qquad \qquad\qquad\qquad \; \text{ Combine like terms } \\ &4a^2+7ab-ac-2bc-2b^2\qquad \qquad \qquad \qquad \qquad \qquad\text{ Simplify } \end{align*}\]
Помножити\((x+4)(3x−2y+5)\).
Рішення
\[\begin{align*} &x(3x-2y+5)+4(3x-2y+5)\qquad \text{ Use the distributive property }\\ &3x^2-2xy+5x+12x-8y+20\qquad \text{ Multiply }\\ &3x^2-2xy+(5x+12x)-8y+20\qquad \text{ Combine like terms } \\ &3x^2-2xy+17x-8y+20\qquad \qquad\text{ Simplify } \end{align*}\]
Помножити\((3x−1)(2x+7y−9)\).
- Відповідь
-
\(6x^2+21xy−29x−7y+9\)
Отримайте доступ до цих онлайн-ресурсів для додаткової інструкції та практики з поліномами.
Ключові рівняння
| ідеальний квадратний триноміал | \({(x+a)}^2=(x+a)(x+a)=x^2+2ax+a^2\) |
| різниця квадратів | \((a+b)(a−b)=a^2−b^2\) |
Ключові концепції
- Многочлен - це сума членів, кожен з яких складається зі змінної, зведеної до невід'ємного цілого степеня. Ступінь - це найвища сила змінної, яка зустрічається в многочлені. Провідним терміном є термін, що містить найвищу ступінь, а провідний коефіцієнт - коефіцієнт цього терміну. Див. Приклад.
- Ми можемо додавати і віднімати поліноми, комбінуючи подібні терміни. Див. Приклад і Приклад.
- Щоб помножити многочлени, використовуйте розподільну властивість, щоб помножити кожен член у першому многочлені на кожен член у другому. Потім додаємо продукти. Див. Приклад.
- FOIL (Перший, Зовнішній, Внутрішній, Останній) - це ярлик, який може бути використаний для множення біноміалів. Див. Приклад.
- Ідеальні квадратні триноми та різниця квадратів - це спеціальні продукти. Див. Приклад і Приклад.
- Дотримуйтесь тих же правил для роботи з поліномами, що містять кілька змінних. Див. Приклад.
