4.2: Факторингові поліноми

Цілі навчання

• Визначте найбільший спільний фактор (ГКФ) мономов.
• Фактор з GCF многочлена.
• Фактор чотиричленного многочлена шляхом групування.
• Фактор спеціальних біноміалів.

Визначення GCF мономів

Процес написання числа або виразу у вигляді продукту називається факторингом ⁵. Якщо ми пишемо мономіал\(8x^{7}=2x^{5}⋅4x^{2}\), ми говоримо, що твір\(2x^{5}⋅4x^{2}\) є факторизацією ⁶\(8x^{7}\) і що\(2x^{5}\) і\(4x^{2}\) є факторами ⁷. Як правило, існує безліч способів фактора мономіала. Деякі факторизації\(8x^{7}\) наступні:

\(\left. \begin{aligned} 8 x ^ { 7 } & = 2 x ^ { 5 } \cdot 4 x ^ { 2 } \\ 8 x ^ { 7 } & = 8 x ^ { 6 } \cdot x \\ 8 x ^ { 7 } & = 2 x \cdot 2 x ^ { 2 } \cdot 2 x ^ { 4 } \end{aligned} \right\} \quad \color{Cerulean} { Factorizations\: of \:} 8 x ^ { 7 }\)

З огляду на два або більше мономи, корисно буде знайти найбільший загальний мономіальний фактор (ГКФ) ⁸ кожного. ГКФ мономов - це добуток загальних змінних факторів і ГКФ коефіцієнтів.

Приклад\(\PageIndex{1}\)

Знайдіть ЗКФ\(25x^{7}y^{2}z\) і\(15x^{3}y^{4}z^{2}\).

Рішення

Почніть з знаходження GCF коефіцієнтів. В даному випадку\(25=5⋅5\) і\(15=3⋅5\). Повинно бути зрозуміло, що

\(\operatorname { GCF } ( 25,15 ) = 5\)

Далі визначають загальні змінні коефіцієнти з найменшими показниками.

\(25 x ^ { 7 } \color{Cerulean}{y ^ { 2 } z} \quad \color{black}{\text { and} } \quad 15\color{Cerulean}{ x ^ { 3} } \color{black}{y ^ { 4 }} z ^ { 2 }\)

Загальними змінними факторами є\(x^{3}, y^{2}\), і\(z\). Тому, враховуючи два мономи,

\(\mathrm { GCF } = 5 x ^ { 3 } y ^ { 2 } z\)

Відповідь:

\(5x^{3}y^{2}z\)

Варто зазначити, що GCF розділяє обидва вирази рівномірно.

\(\frac { 25 x ^ { 7 } y ^ { 2 } z } {\color{Cerulean}{ 5 x ^ { 3 } y ^ { 2 } z} }\color{black}{ =} 5 x ^ { 4 } \quad \text { and } \quad \frac { 15 x ^ { 3 } y ^ { 4 } z ^ { 2 } } {\color{Cerulean}{ 5 x ^ { 3 } y ^ { 2 } z} }\color{black}{ =} 3 y ^ { 2 } z\)

Крім того, ми можемо написати наступне:

\(25 x ^ { 7 } y ^ { 2 } z = \color{Cerulean}{5 x ^ { 3 } y ^ { 2 } z}\color{black}{ \cdot} 5 x ^ { 4 } \quad \text { and } \quad 15 x ^ { 3 } y ^ { 4 } z ^ { 2 } = \color{Cerulean}{5 x ^ { 3 } y ^ { 2 } z}\color{black}{ \cdot} 3 y ^ { 2 } z\)

Фактори\(5x^{4}\) і не\(3y^{2}z\) поділяють загальних мономіальних факторів, крім\(1\); вони є відносно простими ⁹.

Приклад\(\PageIndex{2}\)

Визначити ГКФ можна за такими трьома виразами:\(12a^{5}b^{2}(a+b)^{5}, 60a^{4}b^{3}c (a+b)^{3}\), і\(24a^{2}b^{7}c^{3}(a+b)^{2}\).

Рішення

Почніть з знаходження GCF коефіцієнтів. Для цього визначають просту факторизацію кожного, а потім множать загальні фактори з найменшими показниками.

\(\begin{array} { l } { 12 = 2 ^ { 2 } \cdot 3 } \\ { 60 = 2 ^ { 2 } \cdot 3 \cdot 5 } \\ { 24 = 2 ^ { 3 } \cdot 3 } \end{array}\)

Тому ГКФ коефіцієнтів трьох мономіалів дорівнює

\(\operatorname { GCF } ( 12,60,24 ) = 2 ^ { 2 } \cdot 3 = 12\)

Далі визначаємо загальні чинники змінних.

\(12a^{5}\color{Cerulean}{b^{2}}\color{black}{(}a+b)^{5}\)і\(60a^{4}b^{3}c(a+b)^{3}\) і\(24\color{Cerulean}{a^{2}}\color{black}{b^{7}}c^{3}\color{Cerulean}{(a+b)^{2}}\)

Спільними змінними факторами є\(a^{2}, b^{2}\), і\((a+b)^{2}\). Тому

\(\mathrm { GCF } = 12 \cdot a ^ { 2 } \cdot b ^ { 2 } \cdot ( a + b ) ^ { 2 }\)

Зверніть увагу, що змінна не\(c\) є загальною для всіх трьох виразів і, таким чином, не входить до складу GCF.

Відповідь

\(12a^{2}b^{2}(a+b)^{2}\)

Факторинг GCF

Застосування розподільного властивості є ключем до множення многочленів. Наприклад,

\(\begin{aligned} \color{Cerulean}{6 x y ^ { 2} }\color{black}{ (} 2 x y + 1 ) & = \color{Cerulean}{6 x y ^ { 2} }\color{black}{ \cdot} 2 x y + \color{Cerulean}{6 x y ^ { 2} }\color{black}{ \cdot} 1 \quad \color{Cerulean} { Multiplying } \\ & = 12 x ^ { 2 } y ^ { 3 } + 6 x y ^ { 2 } \end{aligned}\)

Процес факторингу полінома передбачає застосування розподільної властивості у зворотному порядку для запису кожного полінома як добутку поліноміальних факторів.

\(\begin{array} { c c } { \color{Cerulean}{a}\color{black}{ (} b + c ) = \color{Cerulean}{a}\color{black}{ b} + \color{Cerulean}{a}\color{black}{ c} } & { \color{Cerulean} { Multiplying } } \\ {\color{Cerulean}{ a}\color{black}{ b} + \color{Cerulean}{a}\color{black}{ c} = \color{Cerulean}{a}\color{black}{ (} b + c ) } & { \color{Cerulean} { Factoring } } \end{array}\)

Розглянемо факторинг результату відкриття на прикладі:

\(\begin{aligned} 12 x ^ { 2 } y ^ { 3 } + 6 x y ^ { 2 } & = \color{Cerulean}{6 x y ^ { 2} }\color{black}{ \cdot} 2 x y +\color{Cerulean}{ 6 x y ^ { 2} }\color{black}{ \cdot} 1 \quad \color{Cerulean}{Factoring} \\ & =\color{Cerulean}{ 6 x y ^ { 2} } \color{black}{(}\quad ?\quad ) \\ & = \color{Cerulean}{6 x y ^ { 2} }\color{black}{ (} 2 x y + 1 ) \end{aligned}\)

Ми бачимо, що розподільна властивість дозволяє записати многочлен\(12x^{2}y^{3} +  6xy^{2}\) як добуток двох факторів\(6xy^{2}\) і\((2xy+1)\). Відзначимо, що в даному випадку\(6x^{2}y\) є GCF з членів многочлена.

\(\operatorname { GCF } \left( 12 x ^ { 2 } y ^ { 3 } , 6 x y ^ { 2 } \right) = 6 x y ^ { 2 }\)

Факторинг найбільшого загального фактора (GCF) ¹⁰ полінома передбачає переписування його як добутку, де коефіцієнт є GCF всіх його термінів.

\(\left. \begin{array} { c } { 8 x ^ { 3 } + 4 x ^ { 2 } - 16 x = \color{Cerulean}{4 x} \color{black}{\left( 2 x ^ { 2 } + x - 4 \right) }} \\ { 9 a b ^ { 2 } - 18 a ^ { 2 } b - 3 a b =\color{Cerulean}{ 3 a b}\color{black}{ (} 3 b - 6 a - 1 ) } \end{array} \right\} \quad \color{Cerulean}{Factoring\:out\:the\:GCF}\)

Щоб зарахувати GCF полінома, спочатку визначаємо ЗКФ всіх його членів. Потім ми можемо розділити кожен член многочлена на цей фактор як засіб для визначення коефіцієнта, що залишився після застосування розподільної властивості у зворотному напрямку.

Приклад\(\PageIndex{3}\)

Фактор з GCF:\(18x^{7}−30x^{5}+6x^{3}\).

Рішення

У цьому випадку\(GCF(18, 30, 6) = 6\), і загальним змінним коефіцієнтом з найменшим показником є\(x^{3}\). ЗКФ многочлена є\(6x^{3}\).

\(18 x ^ { 7 } - 30 x ^ { 5 } + 6 x ^ { 3 } = \color{Cerulean}{6 x ^ { 3} }\color{black}{ (} \quad ?\quad )\)

Відсутній фактор можна знайти, розділивши кожен член вихідного виразу на GCF.

\(\frac { 18 x ^ { 7 } } { \color{Cerulean}{6 x ^ { 3} } } \color{black}{=} 3 x ^ { 4 } \quad \frac { - 30 x ^ { 5 } } { \color{Cerulean}{6 x ^ { 3} } } \color{black}{=} - 5 x ^ { 2 } \quad \frac { + 6 x ^ { 3 } } {\color{Cerulean}{ 6 x ^ { 3} } } \color{black}{=} + 1\)

Застосовуйте розподільну властивість (навпаки), використовуючи терміни, знайдені в попередньому кроці.

\(18 x ^ { 7 } - 30 x ^ { 5 } + 6 x ^ { 3 } = \color{Cerulean}{6 x ^ { 3} }\color{black}{ \left( 3 x ^ { 4 } - 5 x ^ { 2 } + 1 \right)}\)

Якщо ГКФ збігається з одним з термінів, то після того, як буде враховано ЗКФ,\(1\) залишиться постійний термін. Важливість запам'ятовування постійного терміна стає зрозумілою при виконанні перевірки з використанням розподільного властивості.

\(\begin{aligned} \color{Cerulean}{6 x ^ { 3} }\color{black}{ \left( 3 x ^ { 4 } - 5 x ^ { 2 } + 1 \right)} & = \color{Cerulean}{6 x ^ { 3} }\color{black}{ \cdot} 3 x ^ { 4 } - \color{Cerulean}{6 x ^ { 3} }\color{black}{ \cdot} 5 x ^ { 2 } +\color{Cerulean}{ 6 x ^ { 3} } \color{black}{\cdot} 1 \\ & = 18 x ^ { 7 } - 30 x ^ { 5 } + 6 x ^ { 3 } \quad\color{Cerulean}{✓}\end{aligned}\)

Відповідь

\(6 x ^ { 3 } \left( 3 x ^ { 4 } - 5 x ^ { 2 } + 1 \right)\)

Приклад\(\PageIndex{4}\)

Фактор з GCF:\(27x^{5}y^{5}z+54x^{5}yz−63x^{3}y^{4}\).

Рішення

GCF термінів є\(9x^{3}y\). Останній термін не має змінного коефіцієнта\(z\), і тому\(z\) не може бути частиною найбільшого спільного фактора. Якщо розділити кожен член на\(9x^{3}y\), то отримаємо

\(\frac { 27 x ^ { 5 } y ^ { 5 } z } { \color{Cerulean}{9 x ^ { 3 } y} }\color{black}{ =} 3 x ^ { 2 } y ^ { 4 } z \quad \frac { 54 x ^ { 5 } y z } { \color{Cerulean}{9 x ^ { 3 } y} }\color{black}{ =} 6 x ^ { 2 } z \quad \frac { - 63 x ^ { 3 } y ^ { 4 } } { \color{Cerulean}{9 x ^ { 3 } y} }\color{black}{ =} - 7 y ^ { 3 }\)

і може написати

\(\begin{aligned} 27 x ^ { 5 } y ^ { 5 } z + 54 x ^ { 5 } y z - 63 x ^ { 3 } y ^ { 4 } & = \color{Cerulean}{9 x ^ { 3 } y}\color{black}{ (} \quad ?\quad ) \\ & = 9 x ^ { 3 } y \left( 3 x ^ { 2 } y ^ { 4 } z + 6 x ^ { 2 } z - 7 y ^ { 3 } \right) \end{aligned}\)

Відповідь:

\(9 x ^ { 3 } y \left( 3 x ^ { 2 } y ^ { 4 } z + 6 x ^ { 2 } z - 7 y ^ { 3 } \right)\)

Вправа\(\PageIndex{1}\)

Фактор з GCF:\(12 x ^ { 3 } y ^ { 4 } - 6 x ^ { 2 } y ^ { 3 } - 3 x y ^ { 2 }\)

Відповідь

\(3 x y ^ { 2 } \left( 4 x ^ { 2 } y ^ { 2 } - 2 x y - 1 \right)\)

www.youtube.com/В/ФРНЛ

Звичайно, не кожен многочлен з цілими коефіцієнтами може бути врахований як добуток поліномів з цілими коефіцієнтами, відмінними від самого\(1\) і самого. Якщо це так, то ми говоримо, що це простий многочлен ¹¹. Наприклад, лінійний коефіцієнт, такий як\(10x−9\) простий. Однак його можна врахувати наступним чином:

\(10 x - 9 = x \left( 10 - \frac { 9 } { x } \right) \quad \text { or } \quad 10 x - 9 = 5 \left( 2 x - \frac { 9 } { 5 } \right)\)

Якщо x враховано, результуючий коефіцієнт не є поліномом. Якщо будь-яка константа буде врахована, результуючий множник поліномів не матиме цілочисельних коефіцієнтів. Крім того, деякі лінійні фактори не є простими. Наприклад,

\(5x−10=5(x−2)\)

Загалом, будь-який лінійний множник виду\(ax+b\), де\(a\) і\(b\) є відносно простими цілими числами, є простим.

Факторинг за групуванням

У цьому розділі ми окреслимо методику факторингу поліномів з чотирма долями. Спочатку перегляньте попередній приклад, де терміни мають загальний біноміальний фактор.

Приклад\(\PageIndex{5}\)

Фактор:\(7x(3x−2)−(3x−2)\).

Рішення

Почніть з переписування другого члена\(−(3x−2)\) як\(−1(3x−2)\). Далі розгляньте\((3x−2)\) як загальний біноміальний фактор і перерахуйте його наступним чином:

\(\begin{aligned} 7 x ( 3 x - 2 ) - ( 3 x - 2 ) & = 7 x \color{Cerulean}{( 3 x - 2 )}\color{black}{ -} 1 \color{Cerulean}{( 3 x - 2 )} \\ & =\color{Cerulean}{ ( 3 x - 2 )}\color{black}{ (}\quad ?\quad ) \\ & = ( 3 x - 2 ) ( 7 x - 1 ) \end{aligned}\)

Відповідь:

\((3x−2)(7x−1)\)

Факторинг шляхом групування ¹² - це метод, який дозволяє нам множити поліноми з чотирма добутками у добуток біноміалів. Це передбачає проміжний крок, де буде врахований загальний біноміальний фактор. Наприклад, ми хочемо врахувати

\(3x^{3}−12x^{2}+2x−8\)

Почніть з групування перших двох термінів і двох останніх членів. Потім перерахуйте GCF кожної групи:

Малюнок\(\PageIndex{1}\)

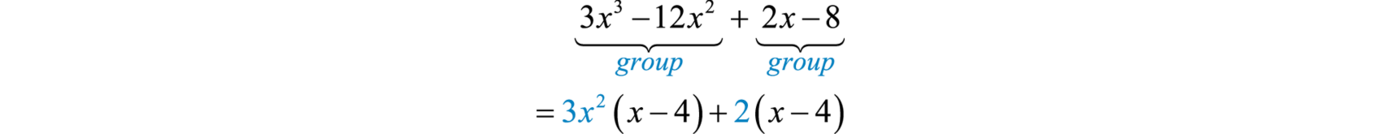
У такому вигляді многочлен є біном із загальним біноміальним фактором,\((x−4)\).

\(\begin{array} { c } { = ( x - 4 ) ( \quad?\quad ) } \\ { = ( x - 4 ) \left( \color{Cerulean}{3 x ^ { 2 } + 2} \right) } \end{array}\)

Тому

\(3 x ^ { 3 } - 12 x ^ { 2 } + 2 x - 8 = ( x - 4 ) \left( 3 x ^ { 2 } + 2 \right)\)

Ми можемо перевірити, перемноживши.

\(\begin{aligned} ( x - 4 ) \left( 3 x ^ { 2 } + 2 \right) & = 3 x ^ { 3 } + 2 x - 12 x ^ { 2 } - 8 \\ & = 3 x ^ { 3 } - 12 x ^ { 2 } + 2 x - 8 \end{aligned} \:\:\color{Cerulean}{✓}\)

Приклад\(\PageIndex{6}\)

Фактор за групуванням\(24a^{4}−18a^{3}−20a+15\).

Рішення

GCF для першої групи є\(6a^{3}\). Ми повинні вибрати\(5\) або\(−5\) вивести з другої групи.

Малюнок\(\PageIndex{2}\)

Факторинг\(+5\) не призводить до загального біноміального фактора. Якщо ми вирішимо враховувати\(−5\), то отримаємо загальний біноміальний коефіцієнт і можемо продовжити. Зауважимо, що при факторингу негативного числа ми змінюємо ознаки факторних термінів.

Малюнок\(\PageIndex{3}\)

Відповідь

\((4a−3)(6a^{3}−5)\). Перевірте, множивши; це залишається читачеві як вправу.

Іноді ми повинні спочатку переставити терміни, щоб отримати загальний фактор.

Приклад\(\PageIndex{7}\)

Фактор\(ab -2a^{2}b + a^{3} -2b^{2}\).

Рішення

Просто факторинг GCF з першої групи і останньої групи не дає загального біноміального фактора.

Малюнок\(\PageIndex{4}\)

Ми повинні переставляти терміни, шукаючи групування, яке створює загальний фактор. У цьому прикладі ми маємо працездатну групування, якщо ми переключаємо терміни\(a^{3}\) і\(ab\).

Малюнок\(\PageIndex{5}\)

Відповідь

\(( a - 2 b ) \left( a ^ { 2 } + b \right)\)

Вправа\(\PageIndex{2}\)

Фактор\(x ^ { 3 } - x ^ { 2 } y - x y + y ^ { 2 }\).

Відповідь

\(( x - y ) \left( x ^ { 2 } - y \right)\)

www.youtube.com/В/ЕДПАОЗ 0ТРС

Не всі факторні чотиричленні поліноми можуть бути враховані за допомогою цієї методики. Наприклад,

\(3x^{3}+5x^{2}−x+2\)

Цей чотиричленний многочлен не може бути згрупований жодним чином, щоб створити загальний біноміальний фактор. Незважаючи на це, многочлен не є простим і може бути записаний як добуток многочленів. Вона може бути врахована наступним чином:

\(3x^{3}+5x^{2}−x+2=(x+2)(3x^{2}−x+1)\)

Факторинг таких поліномів - це те, що ми навчимося робити, рухаючись далі в нашому вивченні алгебри. Наразі ми обмежимо нашу спробу множити чотиричленні поліноми використанням фактора методом групування.

Факторинг Спеціальні Біноміали

Біноміал - це многочлен з двома долями. Почнемо зі спеціального біноміала, званого різницею квадратів ¹³:

\(a^{2}−b^{2}=(a+b)(a−b)\)

Щоб перевірити наведену вище формулу, помножте.

\(  \begin{aligned} ( a + b ) ( a - b ) & = a ^ { 2 } - a b + b a - b ^ { 2 } \\ & = a ^ { 2 } \color{red}{- a b + a b}\color{black}{ -} b ^ { 2 } \\ & = a ^ { 2 } - b ^ { 2 } \end{aligned}\)

Цю формулу ми використовуємо для множення певних спеціальних біноміалів.

Приклад\(\PageIndex{8}\)

Фактор\(x^{2}-9y^{2}\).

Рішення

Визначте біноміал як різницю квадратів і визначте квадратні множники кожного члена.

Малюнок\(\PageIndex{6}\)

Тут ми можемо написати

\(x ^ { 2 } - 9 y ^ { 2 } = ( \color{Cerulean}{x}\color{black}{ )} ^ { 2 } - ( \color{Cerulean}{3 y}\color{black}{ )} ^ { 2 }\)

Підставляємо в різницю квадратів формулу де\(a=x\) і\(b=3y\).

\(\begin{array} { c } { a ^ { 2 } - b ^ { 2 } = ( a + b ) ( a - b ) } \\ {\quad\quad\quad\quad \color{Cerulean}{\downarrow\quad\downarrow\quad\:\downarrow\quad\downarrow} } \\ { x ^ { 2 } - 9 y ^ { 2 } = ( x + 3 y ) ( x - 3 y ) } \end{array}\)

Помножте, щоб перевірити:

\(\begin{aligned} ( x + 3 y ) ( x - 3 y ) & = x ^ { 2 } - 3 x y + 3 y x - 9 y ^ { 2 } \\ & = x ^ { 2 } - 3 x y + 3 x y - 9 y ^ { 2 } \\ & = x ^ { 2 } - 9 y ^ { 2 }\:\:\color{Cerulean}{✓} \end{aligned}\)

Відповідь

\(( x + 3 y ) ( x - 3 y )\)

Приклад\(\PageIndex{9}\)

Фактор:\(x ^ { 2 } - ( 2 x - 1 ) ^ { 2 }\).

Рішення

Спочатку визначте цей вираз як різницю квадратів.

\(x ^ { 2 } - ( 2 x - 1 ) ^ { 2 } = ( \color{Cerulean}{x}\color{black}{ )} ^ { 2 } - ( \color{Cerulean}{2 x - 1}\color{black}{ )} ^ { 2 }\)

Використовують\(a=x\) і\(b=2x−1\) в формулі для різниці квадратів і потім спрощують.

\(a ^ { 2 } - b ^ { 2 } = ( a + b ) ( a - b )\)

\(\begin{aligned} x ^ { 2 } - ( 2 x - 1 ) ^ { 2 } & = [ x + ( 2 x - 1 ) ] [ x - ( 2 x - 1 ) ] \\ & = ( x + 2 x - 1 ) ( x - 2 x + 1 ) \\ & = ( 3 x - 1 ) ( - x + 1 ) \end{aligned}\)

Відповідь

\((3x−1)(−x+1)\)

Задано будь-яке дійсне число\(b\), многочлен форми\(x^{2}+b^{2}\) є простим. Крім того, сума квадратів ¹⁴\(a^{2}+b^{2}\) не має загального факторного еквівалента. Слід подбати про те, щоб не переплутати це з ідеальним квадратним триноміалом.

\(\begin{aligned} ( a + b ) ^ { 2 } & = ( a + b ) ( a + b ) \\ & = a ^ { 2 } + a b + b a + b ^ { 2 } \\ & = a ^ { 2 } + 2 a b + b ^ { 2 } \end{aligned}\)

Тому

\((a+b)^{2}≠a^{2}+b^{2}\)

Наприклад, сума квадратів біноміальної\(x^{2}+9\) є простим. Два інших спеціальних бінома, що представляють інтерес, це сума ¹⁵ і різниця кубів ¹⁶:

\(\begin{aligned} a ^ { 3 } + b ^ { 3 } & = ( a + b ) \left( a ^ { 2 } - a b + b ^ { 2 } \right) \\ a ^ { 3 } - b ^ { 3 } & = ( a - b ) \left( a ^ { 2 } + a b + b ^ { 2 } \right) \end{aligned}\)

Ми можемо перевірити ці формули, множивши.

\(\begin{aligned} ( a + b ) \left( a ^ { 2 } - a b + b ^ { 2 } \right) & = a ^ { 3 } - a ^ { 2 } b + a b ^ { 2 } + a ^ { 2 } b - a b ^ { 2 } + b ^ { 3 } \\ & = a ^ { 3 } + b ^ { 3 } \end{aligned} \:\:\color{Cerulean}{✓}\)

\(\begin{aligned} ( a - b ) \left( a ^ { 2 } + a b + b ^ { 2 } \right) & = a ^ { 3 } + a ^ { 2 } b + a b ^ { 2 } - a ^ { 2 } b - a b ^ { 2 } - b ^ { 3 } \\ & = a ^ { 3 } - b ^ { 3 } \end{aligned}\:\:\color{Cerulean}{✓}\)

Процес факторингу сум і різниць кубів дуже схожий на процес різниці квадратів. Спочатку визначаємо,\(a\)\(b\) а потім підставляємо у відповідну формулу. Окремі формули для суми та різниці кубів дозволяють завжди\(b\) вибирати\(a\) і бути позитивними.

Приклад\(\PageIndex{10}\)

Фактор\(x^{3}-8y^{3}\).

Рішення

По-перше, визначте цей біноміал як різницю кубів.

Малюнок\(\PageIndex{7}\)

Далі визначте, що відбувається в кубі.

\(x ^ { 3 } - 8 y ^ { 3 } = ( \color{Cerulean}{x}\color{black}{ )} ^ { 3 } - ( \color{Cerulean}{2 y}\color{black}{ )} ^ { 3 }\)

В даному випадку\(a=x\) і\(b=2y\). Підставляємо в різницю кубиків формулу.

\(\begin{aligned} a ^ { 3 } + b ^ { 3 } = ( a\:\: - b \:\:) \left( a ^ { 2 }\:\: + a\: \cdot\: b\:\:\: + b ^ { 2 } \right)\:\:\:\: \\ \color{Cerulean}{\downarrow\quad\:\:\:\downarrow\quad\:\:\downarrow\:\:\:\quad\:\:\downarrow\quad\downarrow\quad\:\:\:\:\:\downarrow\quad\:\:\:} \\ x ^ { 3 } - 8 y ^ { 3 } = ( x - 2 y ) \left( ( x ) ^ { 2 } + x \cdot 2 y + ( 2 y ) ^ { 2 } \right) \\ = ( x - 2 y ) \left( x ^ { 2 } + 2 x y + 4 y ^ { 2 } \right) \end{aligned}\)

Ми можемо перевірити цю факторизацію шляхом множення.

\(\begin{aligned} ( x - 2 y ) \left( x ^ { 2 } + 2 x y + 4 y ^ { 2 } \right) & = x ^ { 3 } + 2 x ^ { 2 } y + 4 x y ^ { 2 } - 2 x ^ { 2 } y - 4 x y ^ { 2 } - 8 y ^ { 3 } \\ & = x ^ { 3 } \color{red}{+ 2 x ^ { 2 } y}\color{OliveGreen}{ + 4 x y ^ { 2 }}\color{red}{ - 2 x ^ { 2 } y}\color{OliveGreen}{ - 4 x y ^ { 2} }\color{black}{ - 8 y ^ { 3} } \\ & = x ^ { 3 } - 8 y ^ { 3 } \end{aligned}\:\:\color{Cerulean}{✓}\)

Відповідь

\(( x - 2 y ) \left( x ^ { 2 } + 2 x y + 4 y ^ { 2 } \right)\)

Може бути так, що терміни біноміала мають загальний фактор. Якщо це так, буде важко визначити його як спеціальний біноміал, поки ми вперше не перерахуємо GCF.

Приклад\(\PageIndex{11}\)

Фактор:\(81 x ^ { 4 } y + 3 x y ^ { 4 }\).

Рішення

Терміни не ідеальні квадрати або ідеальні кубики. Однак зауважте, що вони мають загальний фактор. По-перше, фактор з GCF,\(3xy\).

\(81 x ^ { 4 } y + 3 x y ^ { 4 } = 3 x y \left( 27 x ^ { 3 } + y ^ { 3 } \right)\)

Отриманий біноміальний коефіцієнт являє собою суму кубів з\(a=3x\) і\(b=y\).

\(\begin{aligned} 81 x ^ { 4 } y + 3 x y ^ { 4 } & = 3 x y \left( 27 x ^ { 3 } + y ^ { 3 } \right) \\ & = 3 x y ( 3 x + y ) \left( 9 x ^ { 2 } - 3 x y + y ^ { 2 } \right) \end{aligned}\)

Відповідь

\(3 x y ( 3 x + y ) \left( 9 x ^ { 2 } - 3 x y + y ^ { 2 } \right)\)

Коли ступінь спеціального біноміала перевищує два, нам може знадобитися застосувати формули кілька разів, щоб отримати повну факторизацію. Поліном повністю враховується ¹⁷, коли він простий або записується як добуток простих многочленів.

Приклад\(\PageIndex{12}\)

Фактор повністю\(x ^ { 4 } - 81 y ^ { 4 }\).

Рішення

По-перше, визначте, що знаходиться в квадраті.

\(x ^ { 4 } - 81 y ^ { 4 } = (\:\: ) ^ { 2 } - (\:\: ) ^ { 2 }\)

Для цього слід згадати правило потужності для експонентів,\((x^{m})^{n}=x^{mn}\). Коли експоненти піднімаються до степеня, помножте їх. Маючи це на увазі, ми знаходимо

\(x ^ { 4 } - 81 y ^ { 4 } = \left( \color{Cerulean}{x ^ { 2} } \right) ^ { 2 } - \left(\color{Cerulean}{ 9 y ^ { 2} } \right) ^ { 2 }\)

Тому\(a=x^{2}\) і\(b=9y^{2}\). Підставляємо в формулу різниці квадратів.

\(x ^ { 4 } - 81 y ^ { 4 } = \left( x ^ { 2 } + 9 y ^ { 2 } \right) \left( x ^ { 2 } - 9 y ^ { 2 } \right)\)

На цьому етапі зверніть увагу, що коефіцієнт сам по собі\((x^{2}−9y^{2})\) є різницею двох квадратів і, таким чином, може бути додатково врахований за допомогою\(a=x^{2}\) і\(b=3y\). Коефіцієнт\((x^{2}+9y^{2})\) є простим і не може бути врахований за допомогою дійсних чисел.

\(\begin{aligned} x ^ { 4 } - 81 y ^ { 4 } & = \left( x ^ { 2 } + 9 y ^ { 2 } \right) \left( x ^ { 2 } - 9 y ^ { 2 } \right) \\ & = \left( x ^ { 2 } + 9 y ^ { 2 } \right) ( x + 3 y ) ( x - 3 y ) \end{aligned}\)

Відповідь

\(\left( x ^ { 2 } + 9 y ^ { 2 } \right) ( x + 3 y ) ( x - 3 y )\)

При факторингу завжди шукайте результуючі фактори для подальшого фактору.

Приклад\(\PageIndex{13}\)

Фактор повністю\(64 x ^ { 6 } - y ^ { 6 }\).

Рішення

Цей біноміал є одночасно різницею квадратів і різницею кубів.

\(\begin{array} { l } { 64 x ^ { 6 } - y ^ { 6 } = \left( \color{Cerulean}{4 x ^ { 2} } \right) ^ { 3 } - \left( \color{Cerulean}{y ^ { 2} } \right) ^ { 3 } \quad\color{Cerulean} { Difference\: of\: cubes } } \\ { 64 x ^ { 6 } - y ^ { 6 } = \left( \color{Cerulean}{8 x ^ { 3} } \right) ^ { 2 } - \left( \color{Cerulean}{y ^ { 3} } \right) ^ { 2 } \quad \color{Cerulean} { Difference\: of\: squares } } \end{array}\)

При зіткненні з біноміалом, який є різницею як квадратів, так і кубів, як це є, візьміть за правило, щоб коефіцієнт спочатку використовуючи різницю квадратів. Тому\(a=8x^{3}\) і\(b=y^{3}\). Підставляємо в різницю квадратів формулу.

\(64 x ^ { 6 } - y ^ { 6 } = \left( 8 x ^ { 3 } + y ^ { 3 } \right) \left( 8 x ^ { 3 } - y ^ { 3 } \right)\)

Отримані два біноміальних множника є сумою і різницею кубів. Кожен може бути врахований далі. Тому у нас є

Малюнок\(\PageIndex{8}\)

Триноміальні фактори є простими, а вираз повністю враховано.

Відповідь

\(( 2 x + y ) \left( 4 x ^ { 2 } - 2 x y + y ^ { 2 } \right) ( 2 x - y ) \left( 4 x ^ { 2 } + 2 x y + y ^ { 2 } \right)\)

Як вправу, спочатку врахуйте попередній приклад як різницю кубів, а потім порівняйте результати. Чому, на вашу думку, ми беремо за правило спочатку коефіцієнт, використовуючи різницю квадратів?

Вправа\(\PageIndex{3}\)

Фактор:\(a ^ { 6 } b ^ { 6 } - 1\)

Відповідь

\(( a b + 1 ) \left( a ^ { 2 } b ^ { 2 } - a b + 1 \right) ( a b - 1 ) \left( a ^ { 2 } b ^ { 2 } + a b + 1 \right)\)

www.youtube.com/В/OZZXRFB7АПО

Ключові винос

• ГКФ двох і більше мономов - добуток ГКФ коефіцієнтів і загальних змінних коефіцієнтів з найменшою потужністю.
• Якщо члени многочлена мають найбільший спільний фактор, то враховують, що GCF використовує розподільну властивість. Розділіть кожен член многочлена на ЗКФ, щоб визначити члени залишився коефіцієнта.
• Деякі чотиричленні многочлени можуть бути враховані шляхом групування перших двох членів і двох останніх членів. Фактор з GCF кожної групи, а потім вивести загальний біноміальний фактор.
• При факторингу шляхом групування іноді доводиться переставляти терміни, щоб знайти загальний біноміальний коефіцієнт. Після факторингу GCF, інші біноміальні фактори повинні бути однаковими, щоб техніка працювала.
• При факторингу спеціальних біноміалів першим кроком є визначення його як суми або різниці. Після того, як ми ідентифікуємо біном, ми потім визначаємо значення,\(a\)\(b\) а потім підставляємо у відповідну формулу.
• Якщо біноміал - це і різниця квадратів і кубів, то спочатку множьте його як різницю квадратів.

Вправа\(\PageIndex{4}\)

Визначте ЗКФ заданих виразів.

1. \(9 x ^ { 5 } , 27 x ^ { 2 } , 15 x ^ { 7 }\)
2. \(20 y ^ { 4 } , 12 y ^ { 7 } , 16 y ^ { 3 }\)
3. \(50 x ^ { 2 } y ^ { 3 } , 35 x y ^ { 3 } , 10 x ^ { 3 } y ^ { 2 }\)
4. \(12 x ^ { 7 } y ^ { 2 } , 36 x ^ { 4 } y ^ { 2 } , 18 x ^ { 3 } y\)
5. \(15 a ^ { 7 } b ^ { 2 } c ^ { 5 } , 75 a ^ { 7 } b ^ { 3 } c , 45 a b ^ { 4 } c ^ { 3 }\)
6. \(12 a ^ { 6 } b ^ { 3 } c ^ { 2 } , 48 a b c ^ { 3 } , 125 a ^ { 2 } b ^ { 3 } c\)
7. \(60 x ^ { 2 } ( 2 x - 1 ) ^ { 3 } , 42 x ( 2 x - 1 ) ^ { 3 } , 6 x ^ { 3 } ( 2 x - 1 )\)
8. \(14 y ^ { 5 } ( y - 8 ) ^ { 2 } , 28 y ^ { 2 } ( y - 8 ) , 35 y ( y - 8 ) ^ { 3 }\)
9. \(10 a ^ { 2 } b ^ { 3 } ( a + b ) ^ { 5 } , 48 a ^ { 5 } b ^ { 2 } ( a + b ) ^ { 2 } , 26 a b ^ { 5 } ( a + b ) ^ { 3 }\)
10. \(45 a b ^ { 7 } ( a - b ) ^ { 7 } , 36 a ^ { 2 } b ^ { 2 } ( a - b ) ^ { 3 } , 63 a ^ { 4 } b ^ { 3 } ( a - b ) ^ { 2 }\)

Відповідь

1. \(3x^{2}\)

3. \(5xy^{2}\)

5. \(15ab^{2}c\)

7. \(6x(2x-1)\)

9. \(2 a b ^ { 2 } ( a + b ) ^ { 2 }\)

Вправа\(\PageIndex{5}\)

Визначте відсутній фактор.

1. \(18 x ^ { 4 } - 6 x ^ { 3 } + 2 x ^ { 2 } = 2 x ^ { 2 } ( \:\:?\:\: )\)
2. \(6 x ^ { 5 } - 9 x ^ { 3 } - 3 x = 3 x ( \:\:?\:\: )\)
3. \(- 10 y ^ { 6 } + 6 y ^ { 4 } - 4 y ^ { 2 } = - 2 y ^ { 2 } ( \:\:?\:\: )\)
4. \(- 27 y ^ { 9 } - 9 y ^ { 6 } + 3 y ^ { 3 } = - 3 y ^ { 3 } ( \:\:?\:\: )\)
5. \(12 x ^ { 3 } y ^ { 2 } - 8 x ^ { 2 } y ^ { 3 } + 8 x y = 4 x y ( \:\:?\:\: )\)
6. \(10 x ^ { 4 } y ^ { 3 } - 50 x ^ { 3 } y ^ { 2 } + 15 x ^ { 2 } y ^ { 2 } = 5 x y ( \:\:?\:\: )\)
7. \(14 a ^ { 4 } b ^ { 5 } - 21 a ^ { 3 } b ^ { 4 } - 7 a ^ { 2 } b ^ { 3 } = 7 a ^ { 2 } b ^ { 3 } ( \:\:?\:\: )\)
8. \(15 a ^ { 5 } b ^ { 4 } + 9 a ^ { 4 } b ^ { 2 } - 3 a ^ { 2 } b = 3 a ^ { 2 } b (\:\: ?\:\: )\)
9. \(x ^ { 3 n } + x ^ { 2 n } + x ^ { n } = x ^ { n } ( \:\:?\:\: )\)
10. \(y ^ { 4 n } + y ^ { 3 n } - y ^ { 2 n } = y ^ { 2 n } ( \:\:?\:\: )\)

Відповідь

1. \(\left( 9 x ^ { 2 } - 3 x + 1 \right)\)

3. \(\left( 5 y ^ { 4 } - 3 y ^ { 2 } + 2 \right)\)

5. \(\left( 3 x ^ { 2 } y - 2 x y ^ { 2 } + 2 \right)\)

7. \(\left( 2 a ^ { 2 } b ^ { 2 } - 3 a b - 1 \right)\)

9. \(\left( x ^ { 2 n } + x ^ { n } + 1 \right)\)

Вправа\(\PageIndex{6}\)

Фактор з GCF.

1. \(12 x ^ { 4 } - 16 x ^ { 3 } + 4 x ^ { 2 }\)
2. \(15 x ^ { 5 } - 10 x ^ { 4 } - 5 x ^ { 3 }\)
3. \(20 y ^ { 8 } + 28 y ^ { 6 } + 40 y ^ { 3 }\)
4. \(18 y ^ { 7 } - 24 y ^ { 5 } - 30 y ^ { 3 }\)
5. \(2 a ^ { 4 } b ^ { 3 } - 6 a ^ { 3 } b ^ { 2 } + 8 a ^ { 2 } b\)
6. \(28 a ^ { 3 } b ^ { 3 } - 21 a ^ { 2 } b ^ { 4 } - 14 a b ^ { 5 }\)
7. \(2 x ^ { 3 } y ^ { 5 } - 4 x ^ { 4 } y ^ { 4 } + x ^ { 2 } y ^ { 3 }\)
8. \(3 x ^ { 5 } y - 2 x ^ { 4 } y ^ { 2 } + x ^ { 3 } y ^ { 3 }\)
9. \(5 x ^ { 2 } ( 2 x + 3 ) - 3 ( 2 x + 3 )\)
10. \(y ^ { 2 } ( y - 1 ) + 9 ( y - 1 )\)
11. \(9 x ^ { 2 } ( 3 x - 1 ) + ( 3 x - 1 )\)
12. \(7 y ^ { 2 } ( 5 y + 2 ) - ( 5 y + 2 )\)
13. \(x ^ { 5 n } - x ^ { 3 n } + x ^ { n }\)
14. \(y ^ { 6 n } - y ^ { 3 n } - y ^ { 2 n }\)

Відповідь

1. \(4 x ^ { 2 } \left( 3 x ^ { 2 } - 4 x + 1 \right)\)

3. \(4 y ^ { 3 } \left( 5 y ^ { 5 } + 7 y ^ { 3 } + 10 \right)\)

5. \(2 a ^ { 2 } b \left( a ^ { 2 } b ^ { 2 } - 3 a b + 4 \right)\)

7. \(x ^ { 2 } y ^ { 3 } \left( 2 x y ^ { 2 } - 4 x ^ { 2 } y + 1 \right)\)

9. \(( 2 x + 3 ) \left( 5 x ^ { 2 } - 3 \right)\)

11. \(( 3 x - 1 ) \left( 9 x ^ { 2 } + 1 \right)\)

13. \(x ^ { n } \left( x ^ { 4 n } - x ^ { 2 n } + 1 \right)\)

Вправа\(\PageIndex{7}\)

Фактор за групуванням.

1. \(2 x ^ { 3 } + 3 x ^ { 2 } + 2 x + 3\)
2. \(5 x ^ { 3 } + 25 x ^ { 2 } + x + 5\)
3. \(6 x ^ { 3 } - 3 x ^ { 2 } + 4 x - 2\)
4. \(3 x ^ { 3 } - 2 x ^ { 2 } - 15 x + 10\)
5. \(x ^ { 3 } - x ^ { 2 } - 3 x + 3\)
6. \(6 x ^ { 3 } - 15 x ^ { 2 } - 2 x + 5\)
7. \(2 x ^ { 3 } + 7 x ^ { 2 } - 10 x - 35\)
8. \(3 x ^ { 3 } - x ^ { 2 } + 24 x - 8\)
9. \(14 y ^ { 4 } + 10 y ^ { 3 } - 7 y - 5\)
10. \(5 y ^ { 4 } + 2 y ^ { 3 } + 20 y + 8\)
11. \(x ^ { 4 n } + x ^ { 3 n } + 2 x ^ { n } + 2\)
12. \(x ^ { 5 n } + x ^ { 3 n } + 3 x ^ { 2 n } + 3\)
13. \(x ^ { 3 } - x ^ { 2 } y + x y ^ { 2 } - y ^ { 3 }\)
14. \(x ^ { 3 } + x ^ { 2 } y - 2 x y ^ { 2 } - 2 y ^ { 3 }\)
15. \(3 x ^ { 3 } y ^ { 2 } + 9 x ^ { 2 } y ^ { 3 } - x - 3 y\)
16. \(2 x ^ { 3 } y ^ { 3 } - x ^ { 2 } y ^ { 3 } + 2 x - y\)
17. \(a ^ { 2 } b - 4 a b ^ { 2 } - 3 a + 12 b\)
18. \(a ^ { 2 } b + 3 a b ^ { 2 } + 5 a + 15 b\)
19. \(a ^ { 4 } + a ^ { 2 } b ^ { 3 } + a ^ { 2 } b + b ^ { 4 }\)
20. \(a ^ { 3 } b + 2 a ^ { 2 } + 3 a b ^ { 4 } + 6 b ^ { 3 }\)
21. \(3 a x + 10 b y - 5 a y - 6 b x\)
22. \(a ^ { 2 } x - 5 b ^ { 2 } y - 5 a ^ { 2 } y + b ^ { 2 } x\)
23. \(x ^ { 4 } y ^ { 2 } - x ^ { 3 } y ^ { 3 } + x ^ { 2 } y ^ { 4 } - x y ^ { 5 }\)
24. \(2 x ^ { 5 } y ^ { 2 } + 4 x ^ { 4 } y ^ { 2 } + 18 x ^ { 3 } y + 36 x ^ { 2 } y\)
25. \(a ^ { 5 } b ^ { 2 } + a ^ { 4 } b ^ { 4 } + a ^ { 3 } b ^ { 3 } + a ^ { 2 } b ^ { 5 }\)
26. \(3 a ^ { 6 } b + 3 a ^ { 5 } b ^ { 2 } + 9 a ^ { 4 } b ^ { 2 } + 9 a ^ { 3 } b ^ { 3 }\)

Відповідь

1. \(( 2 x + 3 ) \left( x ^ { 2 } + 1 \right)\)

3. \(( 2 x - 1 ) \left( 3 x ^ { 2 } + 2 \right)\)

5. \(( x - 1 ) \left( x ^ { 2 } - 3 \right)\)

7. \(( 2 x + 7 ) \left( x ^ { 2 } - 5 \right)\)

9. \(( 7 y + 5 ) \left( 2 y ^ { 3 } - 1 \right)\)

11. \(\left( x ^ { n } + 1 \right) \left( x ^ { 3 n } + 2 \right)\)

13. \(( x - y ) \left( x ^ { 2 } + y ^ { 2 } \right)\)

15. \(( x + 3 y ) \left( 3 x ^ { 2 } y ^ { 2 } - 1 \right)\)

17. \(( a - 4 b ) ( a b - 3 )\)

19. \(\left( a ^ { 2 } + b \right) \left( a ^ { 2 } + b ^ { 3 } \right)\)

21. \(( a - 2 b ) ( 3 x - 5 y )\)

23. \(x y ^ { 2 } ( x - y ) \left( x ^ { 2 } + y ^ { 2 } \right)\)

25. \(a ^ { 2 } b ^ { 2 } \left( a ^ { 2 } + b \right) \left( a + b ^ { 2 } \right)\)

Вправа\(\PageIndex{8}\)

Фактор.

1. \(x^{2}-64\)
2. \(x^{2}-100\)
3. \(9-4y^{2}\)
4. \(25 - y^{2}\)
5. \(x ^ { 2 } - 81 y ^ { 2 }\)
6. \(x ^ { 2 } - 49 y ^ { 2 }\)
7. \(a ^ { 2 } b ^ { 2 } - 4\)
8. \(1 - 9 a ^ { 2 } b ^ { 2 }\)
9. \(a ^ { 2 } b ^ { 2 } - c ^ { 2 }\)
10. \(4 a ^ { 2 } - b ^ { 2 } c ^ { 2 }\)
11. \(x ^ { 4 } - 64\)
12. \(36 - y ^ { 4 }\)
13. \(( 2 x + 5 ) ^ { 2 } - x ^ { 2 }\)
14. \(( 3 x - 5 ) ^ { 2 } - x ^ { 2 }\)
15. \(y ^ { 2 } - ( y - 3 ) ^ { 2 }\)
16. \(y ^ { 2 } - ( 2 y + 1 ) ^ { 2 }\)
17. \(( 2 x + 5 ) ^ { 2 } - ( x - 3 ) ^ { 2 }\)
18. \(( 3 x - 1 ) ^ { 2 } - ( 2 x - 3 ) ^ { 2 }\)
19. \(x ^ { 4 } - 16\)
20. \(81 x ^ { 4 } - 1\)
21. \(x ^ { 4 } y ^ { 4 } - 1\)
22. \(x ^ { 4 } - y ^ { 4 }\)
23. \(x ^ { 8 } - y ^ { 8 }\)
24. \(y ^ { 8 } - 1\)
25. \(x ^ { 2 n } - y ^ { 2 n }\)
26. \(x ^ { 2 n } y ^ { 2 n } - 4\)
27. \(x ^ { 4 n } - y ^ { 4 n }\)
28. \(x ^ { 4 n } y ^ { 4 n } - 16\)
29. \(x ^ { 3 } - 27\)
30. \(8 x ^ { 3 } - 125\)
31. \(8 y ^ { 3 } + 27\)
32. \(64 x ^ { 3 } + 343\)
33. \(x ^ { 3 } - y ^ { 3 }\)
34. \(x ^ { 3 } + y ^ { 3 }\)
35. \(8 a ^ { 3 } b ^ { 3 } + 1\)
36. \(27 a ^ { 3 } - 8 b ^ { 3 }\)
37. \(x ^ { 3 } y ^ { 3 } - 125\)
38. \(216 x ^ { 3 } + y ^ { 3 }\)
39. \(x ^ { 3 } + ( x + 3 ) ^ { 3 }\)
40. \(y ^ { 3 } - ( 2 y - 1 ) ^ { 3 }\)
41. \(( 2 x + 1 ) ^ { 3 } - x ^ { 3 }\)
42. \(( 3 y - 5 ) ^ { 3 } - y ^ { 3 }\)
43. \(x ^ { 3 n } - y ^ { 3 n }\)
44. \(x ^ { 3 n } + y ^ { 3 n }\)
45. \(a ^ { 6 } + 64\)
46. \(64 a ^ { 6 } - 1\)
47. \(x ^ { 6 } - y ^ { 6 }\)
48. \(x ^ { 6 } + y ^ { 6 }\)
49. \(x ^ { 6 n } - y ^ { 6 n }\)
50. \(x ^ { 6 n } + y ^ { 6 n }\)
51. Враховуючи\(f (x) = 2x − 1\), показати, що\((f + f ) (x) = 2f (x)\).
52. Враховуючи\(f (x) = x^{2} − 3x + 2\), показати, що\((f + f ) (x) = 2f (x)\).
53. Враховуючи\(f (x) = mx + b\), показати, що\((f + f ) (x) = 2f (x)\).
54. Враховуючи\(f (x) = ax^{2} + bx + c\), показати, що\((f + f ) (x) = 2f (x)\).
55. Враховуючи\(f (x) = ax^{2} + bx + c\), показати, що\((f − f ) (x) = 0\).
56. Враховуючи\(f (x) = mx + b\), показати, що\((f − f ) (x) = 0\).

Відповідь

1. \(( x + 8 ) ( x - 8 )\)

3. \(( 3 + 2 y ) ( 3 - 2 y )\)

5. \(( x + 9 y ) ( x - 9 y )\)

7. \(( a b + 2 ) ( a b - 2 )\)

9. \(( a b + c ) ( a b - c )\)

11. \(\left( x ^ { 2 } + 8 \right) \left( x ^ { 2 } - 8 \right)\)

13. \(( 3 x + 5 ) ( x + 5 )\)

15. \(3 ( 2 y - 3 )\)

17. \(( 3 x + 2 ) ( x + 8 )\)

19. \(\left( x ^ { 2 } + 4 \right) ( x + 2 ) ( x - 2 )\)

21. \(\left( x ^ { 2 } y ^ { 2 } + 1 \right) ( x y + 1 ) ( x y - 1 )\)

23. \(\left( x ^ { 4 } + y ^ { 4 } \right) \left( x ^ { 2 } + y ^ { 2 } \right) ( x + y ) ( x - y )\)

25. \(\left( x ^ { n } + y ^ { n } \right) \left( x ^ { n } - y ^ { n } \right)\)

27. \(\left( x ^ { 2 n } + y ^ { 2 n } \right) \left( x ^ { n } + y ^ { n } \right) \left( x ^ { n } - y ^ { n } \right)\)

29. \(( x - 3 ) \left( x ^ { 2 } + 3 x + 9 \right)\)

31. \(( 2 y + 3 ) \left( 4 y ^ { 2 } - 6 y + 9 \right)\)

33. \(( x - y ) \left( x ^ { 2 } + x y + y ^ { 2 } \right)\)

35. \(( 2 a b + 1 ) \left( 4 a ^ { 2 } b ^ { 2 } - 2 a b + 1 \right)\)

37. \(( x y - 5 ) \left( x ^ { 2 } y ^ { 2 } + 5 x y + 25 \right)\)

39. \(( 2 x + 3 ) \left( x ^ { 2 } + 3 x + 9 \right)\)

41. \(( x + 1 ) \left( 7 x ^ { 2 } + 5 x + 1 \right)\)

43. \(\left( x ^ { n } - y ^ { n } \right) \left( x ^ { 2 n } + x ^ { n } y ^ { n } + y ^ { 2 n } \right)\)

45. \(\left( a ^ { 2 } + 4 \right) \left( a ^ { 4 } - 4 a ^ { 2 } + 16 \right)\)

47. \(( x + y ) \left( x ^ { 2 } - x y + y ^ { 2 } \right) ( x - y ) \left( x ^ { 2 } + x y + y ^ { 2 } \right)\)

49. \(\begin{array} { l } { \left( x ^ { n } + y ^ { n } \right) \left( x ^ { 2 n } - x ^ { n } y ^ { n } + y ^ { 2 n } \right) } { \times \left( x ^ { n } - y ^ { n } \right) \left( x ^ { 2 n } + x ^ { n } y ^ { n } + y ^ { 2 n } \right) } \end{array}\)

51. Відповідь може відрізнятися

53. Відповідь може відрізнятися

55. Відповідь може відрізнятися

Вправа\(\PageIndex{9}\)

1. Що можна сказати про ступінь множника многочлена? Наведемо приклад.
2. Якщо біноміал потрапляє в обидві категорії, різниця квадратів і різниця кубів, що краще використовувати для факторингу, і чому? Створіть приклад, який ілюструє цю ситуацію, і врахуйте її за допомогою обох формул.
3. Напишіть власні приклади для кожного з трьох спеціальних типів біноміальних. Фактор їх і поділіться своїми результатами.

Відповідь

1. Відповідь може відрізнятися

3. Відповідь може відрізнятися

Виноски

⁵ Процес написання числа або виразу як твір.

⁶ Будь-яка комбінація факторів, помножених разом, в результаті виходить твір.

⁷ Будь-яке з чисел або виразів, що утворюють твір.

⁸ Добуток загальних змінних факторів і ЗКФ коефіцієнтів.

⁹ Вирази, які не мають спільних факторів, крім\(1\).

¹⁰ Процес переписування полінома як добутку з використанням GCF всіх його термінів.

¹¹ Поліном з цілими коефіцієнтами, які не можуть бути враховані як добуток поліномів з цілими коефіцієнтами,\(1\) відмінними від самого себе.

¹² Методика факторингу поліномів з чотирма домірами.

¹³\(a ^ { 2 } - b ^ { 2 } = ( a + b ) ( a - b )\), де\(a\) і\(b\) представляють алгебраїчні вирази.

¹⁴\(a^{2} + b^{2}\), де\(a\) і\(b\) представляють алгебраїчні вирази. Це не має загального факторного еквівалента.

¹⁵\(a^{3} + b^{3} = (a+b)(a^{2} - ab + b^{2})\) де\(a\) і\(b\) представляють алгебраїчні вирази.

¹⁶\(a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})\) де\(a\) і\(b\) представляють алгебраїчні вирази.

¹⁷ Поліном, який є простим або записаним як добуток простих многочленів.