1.7: Розв'язування лінійних рівнянь

Last updated
Save as PDF

Page ID: 58244

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Використовуйте властивості рівності для розв'язання основних лінійних рівнянь.
Визначте та вирішуйте умовні лінійні рівняння, тотожності та протиріччя.
Очистити дроби з рівнянь.
Налаштуйте та вирішуйте лінійні рівняння.

Розв'язування основних лінійних рівнянь

Рівняння ¹²⁹ - це твердження, яке вказує на те, що два алгебраїчні вирази рівні. Лінійне рівняння з однією змінною ¹³⁰$x$, - це рівняння, яке можна записати в стандартному вигляді,$ax + b = 0$ де$a$ і$b$ є дійсними числами і$a ≠ 0$. Наприклад

$3 x - 12 = 0$

Рішення ¹³¹ до лінійного рівняння - це будь-яке значення, яке може замінити змінну для отримання істинного твердження. Змінна в лінійному рівнянні$3x − 12 = 0$ є$x$ і рішення є$x = 4$. Щоб перевірити це, підставити значення$4$ в for$x$ і перевірте, чи ви отримаєте true твердження.

$\begin{aligned} 3 x - 12 & = 0 \\ 3 ( \color{Cerulean}{4}\color{Black}{ )} - 12 & = 0 \\ 12 - 12 & = 0 \\ 0 & = 0 \:\: \color{Cerulean}{✓} \end{aligned}$

Крім того, коли рівняння дорівнює константі, ми можемо перевірити рішення, підставивши значення в змінну і показавши, що результат дорівнює цій константі. У цьому сенсі ми говоримо, що рішення «задовольняють рівнянню».

Приклад$\PageIndex{1}$:

Чи$a=−\frac{1}{2}$ є рішенням$−10a+5=25$?

Рішення

Нагадаємо, що при оцінці виразів хороша практика спочатку замінити всі змінні дужками, а потім підставити відповідні значення. Використовуючи дужки, ми уникаємо деяких поширених помилок при роботі з порядком операцій.

$- 10 a + 5 = - 10 ( \color{Cerulean}{- \frac { 1 } { 2 }} \color{Black}{ ) +} 5 = 5 + 5 = 10 \neq 25\:\: \color{red}{✗}$

Відповідь:

Ні,$a=−\frac{1}{2}$ не задовольняє рівняння.

Розробка методик розв'язання різних алгебраїчних рівнянь є однією з наших головних цілей в алгебрі. У цьому розділі розглядаються основні прийоми, що застосовуються для розв'язання лінійних рівнянь з однією змінною. Почнемо з визначення еквівалентних рівнянь ¹³² як рівнянь з однаковим набором розв'язків.

$\left. \begin{aligned} 3 x - 5 & = 16 \\ 3 x & = 21 \\ x & = 7 \end{aligned} \right\} \quad \color{Cerulean}{Equivalent \:equations}$

Тут ми бачимо, що три лінійні рівняння еквівалентні тому, що вони мають один і той же набір рішень, а саме,$\{7\}$. Для отримання еквівалентних рівнянь використовують наступні властивості рівності ¹³³. Дано алгебраїчні вирази$A$ і$B$, де$c$ є ненульовим числом:

Таблиця$\PageIndex{1}$
Додаткова властивість рівності:	Якщо$A=B$, то$A\color{Cerulean}{+c}\color{Black}{=} B\color{Cerulean}{+c}$
Віднімання властивості рівності:	Якщо$A=B$, то$A\color{Cerulean}{-c}\color{Black}{-}B\color{Cerulean}{-c}$
Властивість множення рівності:	Якщо$A=B$, то$\color{Cerulean}{c}\color{Black}{A}=\color{Cerulean}{c}\color{Black}{B}$
Поділ властивості рівності:	Якщо$A=B$, то$\frac{A}{\color{Cerulean}{c}}\color{Black}{=}\frac{B}{\color{Cerulean}{c}}$

Примітка

Обережно уникнути множення або ділення обох сторін$0$ рівняння на. Ділення на$0$ не визначено і множення обох сторін на$0$ результати в рівнянні$0 = 0$.

Вирішуємо алгебраїчні рівняння шляхом виділення змінної з коефіцієнтом 1. Якщо задано лінійне рівняння виду$ax + b = c$, то ми можемо вирішити його в два етапи. По-перше, використовуйте відповідну властивість рівності додавання або віднімання для виділення змінного члена. Далі виділяють змінну, використовуючи властивість рівності множення або ділення. Перевірка рішення в наступних прикладах залишається за читачем.

Приклад$\PageIndex{2}$:

Вирішити:$7x − 2 = 19$.

Рішення

$\begin{aligned} 7 x - 2 & = 19 \\ 7 x - 2 \color{Cerulean}{+ 2} & = 19 \color{Cerulean}{+ 2} \quad Add\: 2\: to\: both\: sides. \\ 7 x & = 21 \\ \frac { 7 x } { \color{Cerulean}{7} } & = \frac { 21 } { \color{Cerulean}{7} } \quad \color{Cerulean}{Divide\: both\: sides\: by\: 7.} \\ x & = 3 \end{aligned}$

Відповідь:

Рішення є$3$.

Приклад$\PageIndex{3}$:

Вирішити:$56 = 8 + 12y$.

Рішення

Коли жоден знак не передує терміну, він розуміється як позитивний. Іншими словами, подумайте про це як$56 = +8 + 12y$. Тому починаємо з віднімання$8$ по обидва боки знака рівності.

$\begin{aligned} 56 \color{Cerulean}{- 8} & = 8 + 12 y \color{Cerulean}{- 8} \\ 48 & = 12 y \\ \frac { 48 } { \color{Cerulean}{12} } & = \frac { 12 y } { \color{Cerulean}{12} } \\ 4 & = y \end{aligned}$

Не має значення, з якого боку ми вибираємо ізолювати змінну, оскільки симетрична властивість ¹³⁴ стверджує,$4 = y$ що еквівалентно$y = 4$.

Відповідь:

Рішення є$4$.

Приклад$\PageIndex{4}$:

Вирішити:$\frac { 5 } { 3 } x + 2 = - 8$.

Рішення

Виділіть змінний член, використовуючи властивість додавання рівності, а потім помножте обидві сторони рівняння на зворотну коефіцієнту$\frac{5}{3}$.

\ почати {вирівняні}\ розриву {5} {3} x + 2 & = - 8\\ розриву {5} {3} x + 2\ колір {- 2} & = - 8\ колір {- 2} {- 2}\ квадратний\ колір {Cerulean} {Відніміть\: 2\: на\: обидві\: сторони.}\\ frac {5} {3} x & = - 10\\\ колір {\ фрейк {3} {5}}\ колір {чорний} {\ cdot}\ frac {5} {3} x & =\ колір {Cerulean} {\ frac {3} {\ скасувати {5}}}\ колір {чорний} {\ cdot} (\ зміщення {-2} {\ скасувати {-10}})\ квадратний\ колір {Cerulean} {Множення\ :обидві\ :сторони\: на\:\ frac {3} {5}.}\\ 1x & = 3\ cdot (- 2)\\ x & = - 6\ кінець {вирівняний}

Відповідь:

Рішення є$−6$.

Підсумовуючи, щоб зберегти еквівалентні рівняння, ми повинні виконати одну і ту ж операцію з обох сторін рівняння.

Вправа$\PageIndex{1}$

Вирішити:$\frac { 2 } { 3 } x + \frac { 1 } { 2 } = - \frac { 5 } { 6 }$.

Відповідь

$x=-2$

www.youtube.com/В/КВККХС9АД6М

Загальні рекомендації щодо розв'язання лінійних рівнянь

Зазвичай лінійні рівняння не задаються в стандартному вигляді, і тому їх вирішення вимагає додаткових кроків. При вирішенні лінійних рівнянь мета полягає в тому, щоб визначити, яке значення, якщо воно є, дасть істинне твердження при підстановці в вихідне рівняння. Зробіть це, ізолюючи змінну за допомогою наступних кроків:

Крок 1: Спростити обидві сторони рівняння, використовуючи порядок операцій, і об'єднати всі подібні члени на одній стороні знака рівності.
Крок 2: Використовуйте відповідні властивості рівності, щоб об'єднати подібні терміни з протилежних сторін знака рівності. Мета полягає в тому, щоб отримати змінний член з одного боку рівняння і постійний член з іншого.
Крок 3: Розділіть або помножте за потребою, щоб ізолювати змінну.
Крок 4: Перевірте, чи вирішує відповідь вихідне рівняння.

Ми часто стикаємося з лінійними рівняннями, де вирази з кожного боку знака рівності можуть бути спрощені. Якщо це так, то краще спростити кожну сторону спочатку перед вирішенням. Зазвичай це передбачає об'єднання однієї сторони, як терміни.

Примітка

На даний момент в нашому вивченні алгебри використання властивостей рівності має здатися рутиною. Тому відображення цих кроків в цьому тексті, як правило, синім кольором, стає необов'язковим.

Приклад$\PageIndex{5}$:

Вирішити:$- 4 a + 2 - a = 1$.

Рішення

Спочатку з'єднайте подібні терміни з лівого боку знака рівності.

$\begin{aligned} - 4 a + 2 - a = 1 & \quad \color{Cerulean}{ Combine\: same-side\: like\: terms.} \\ - 5 a + 2 = 1 & \quad\color{Cerulean} { Subtract\: 2\: on\: both\: sides.} \\ - 5 a = - 1 & \quad\color{Cerulean} { Divide\: both\: sides\: by\: - 5.} \\ a = \frac { - 1 } { - 5 } = \frac { 1 } { 5 } \end{aligned}$

Завжди використовуйте вихідне рівняння, щоб перевірити, чи правильне рішення.

$\begin{aligned} - 4 a + 2 - a & = - 4 \left( \color{OliveGreen}{\frac { 1 } { 5 }} \right) + 2 - \color{OliveGreen}{\frac { 1 } { 5 }} \\ & = - \frac { 4 } { 5 } + \frac { 2 } { 1 } \cdot \color{Cerulean}{\frac { 5 } { 5 }}\color{Black}{ -} \frac { 1 } { 5 } \\ & = \frac { - 4 + 10 + 1 } { 5 } \\ & = \frac { 5 } { 5 } = 1 \:\:\color{Cerulean}{✓} \end{aligned}$

Відповідь:

Рішення є$\frac{1}{5}$.

З огляду на лінійне рівняння у вигляді$ax + b = cx + d$, ми починаємо процес розв'язання з об'єднання подібних членів з протилежних сторін знака рівності. Для цього використовуйте властивість додавання або віднімання рівності, щоб розмістити подібні терміни на одній стороні, щоб їх можна було об'єднати. У прикладах, які залишилися, чек залишається читачеві.

Приклад$\PageIndex{6}$:

Вирішити:$−2y − 3 = 5y + 11$.

Рішення

Відніміть з$5y$ обох сторін, щоб ми могли об'єднати терміни за участю y з лівого боку.

$\begin{array} { c } { - 2 y - 3 \color{Cerulean}{- 5 y}\color{Black}{ =} 5 y + 11 \color{Cerulean}{- 5 y} } \\ { - 7 y - 3 = 11 } \end{array}$

Звідси вирішуйте, використовуючи методи, розроблені раніше.

$\begin{aligned} - 7 y - 3 & = 11 \quad\color{Cerulean}{Add\: 3\: to\: both\: sides.} \\ - 7 y & = 14 \\ y & = \frac { 14 } { - 7 } \quad\color{Cerulean}{Divide\: both\: sides\: by\: -7.} \\ y & = - 2 \end{aligned}$

Відповідь:

Рішення є$−2$.

Рішення часто зажадає застосування розподільного майна.

Приклад$\PageIndex{7}$:

Вирішити:$- \frac { 1 } { 2 } ( 10 x - 2 ) + 3 = 7 ( 1 - 2 x )$.

Рішення

Спочатку спростіть лінійні вирази по обидва боки знака рівності.

$\begin{aligned} - \frac { 1 } { 2 } ( 10 x - 2 ) + 3 = 7 ( 1 - 2 x ) & \quad\color{Cerulean} { Distribute } \\ - 5 x + 1 + 3 = 7 - 14 x & \quad\color{Cerulean} { Combine\: same-side\: like\: terms. } \\ - 5 x + 4 = 7 - 14 x & \quad\color{Cerulean} { Combine\: opposite-side\: like\: terms. } \\ 9 x = 3 & \quad\color{Cerulean} { Solve. } \\ x = \frac { 3 } { 9 } = \frac { 1 } { 3 } \end{aligned}$

Відповідь:

Рішення є$\frac{1}{3}$.

Приклад$\PageIndex{8}$:

Вирішити:$5(3−a)−2(5−2a)=3$.

Рішення

Почніть з застосування розподільного властивості.

$\begin{aligned} 5 ( 3 - a ) - 2 ( 5 - 2 a ) & = 3 \\ 15 - 5 a - 10 + 4 a & = 3 \\ 5 - a & = 3 \\ - a & = - 2 \end{aligned}$

Тут ми вказуємо,$−a$ що еквівалентно$−1a$; отже, ми вирішили розділити обидві сторони рівняння на$−1$.

$\begin{array} { c } { - a = - 2 } \\ { \frac { - 1 a } { \color{Cerulean}{- 1} }\color{Black}{ =} \frac { - 2 } { \color{Cerulean}{- 1} } } \\ { a = 2 } \end{array}$

Як варіант, ми можемо помножити обидві сторони$−a=−2$ на негативну і досягти однакового результату.

$\begin{aligned} - a & = - 2 \\ \color{Cerulean}{( - 1 )}\color{Black}{ (} - a ) & = \color{Cerulean}{( - 1 )}\color{Black}{ (} - 2 ) \\ a & = 2 \end{aligned}$

Відповідь:

Рішення є$2$.

Вправа$\PageIndex{2}$

Вирішити:$6 - 3 ( 4 x - 1 ) = 4 x - 7$.

Відповідь

$x=1$

www.youtube.com/В/ІАЗРФЮ-О

Існує три різних типи рівнянь. До цього моменту ми розв'язували умовні рівняння ¹³⁵. Це рівняння, які вірні для певних значень. Ідентичність ¹³⁶ - це рівняння, яке вірно для всіх можливих значень змінної. Наприклад,

$x = x \quad\color{Cerulean}{Identity}$

має набір розв'язків, що складається з усіх дійсних чисел,$ℝ$. Протиріччя ¹³⁷ - це рівняння, яке ніколи не є істинним і, таким чином, не має розв'язків. Наприклад,

$x+1=x\quad\color{Cerulean}{Contradiction}$

не має рішення. Використовуємо порожній набір$Ø$, щоб вказати, що рішень немає.

Якщо кінцевим результатом розв'язання рівняння є істинне твердження, як$0 = 0$, то рівняння є тотожністю і будь-яке дійсне число - це рішення. Якщо рішення призводить до помилкового твердження, типу$0 = 1$, то рівняння є протиріччям і рішення немає.

Приклад$\PageIndex{9}$:

Вирішити:$4 (x + 5) + 6 = 2 (2x + 3)$.

Рішення

$\begin{aligned} 4 ( x + 5 ) + 6 & = 2 ( 2 x + 3 ) \\ 4 x + 20 + 6 & = 4 x + 6 \\ 4 x + 26 & = 4 x + 6 \\ 26 & = 6\:\: \color{red}{✗} \end{aligned}$

Розв'язування призводить до помилкового твердження; отже, рівняння є протиріччям і рішення не існує.

Відповідь:

$Ø$

Приклад$\PageIndex{10}$:

Вирішити:$3 (3y + 5) + 5 = 10 (y + 2) − y$.

Рішення

$\begin{aligned} 3 ( 3 y + 5 ) + 5 & = 10 ( y + 2 ) - y \\ 9 y + 15 + 5 & = 10 y + 20 - y \\ 9 y + 20 & = 9 y + 20 \\ 9 y & = 9 y \\ 0 & = 0 \:\:\color{Cerulean}{✓} \end{aligned}$

Розв'язування призводить до істинного твердження; отже, рівняння є ідентичністю, а будь-яке дійсне число - це рішення.

Відповідь:

$ℝ$

Коефіцієнти лінійних рівнянь можуть бути будь-якими дійсними числами, навіть десятковими і дроби. Коли це так, можна використовувати властивість множення рівності для очищення дробових коефіцієнтів і отримання цілих коефіцієнтів за один крок. Якщо задані дробові коефіцієнти, то помножте обидві сторони рівняння на найменш спільний кратний знаменникам (РК).

Приклад$\PageIndex{11}$:

Вирішити:$\frac { 1 } { 3 } x + \frac { 1 } { 5 } = \frac { 1 } { 5 } x - 1$.

Рішення

Очистіть дроби, множивши обидві сторони на найменш спільний кратний заданих знаменників. В даному випадку це$LCD (3, 5) = 15$.

$\begin{aligned} \color{Cerulean}{15}\color{Black}{ \cdot} \left( \frac { 1 } { 3 } x + \frac { 1 } { 5 } \right) & = \color{Cerulean}{15}\color{Black}{ \cdot} \left( \frac { 1 } { 5 } x - 1 \right) \quad \color{Cerulean}{Multiply\: both\: sides\: by\: 15.} \\ \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 3 } x + \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 5 } & = \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 5 } x - \color{Cerulean}{15}\color{Black}{ \cdot} 1\quad\color{Cerulean}{Simplify.} \\ 5 x + 3 & = 3 x - 15\quad\quad\quad\color{Cerulean}{Solve.} \\ 2 x & = - 18 \\ x & = \frac { - 18 } { 2 } = - 9 \end{aligned}$

Відповідь:

Рішення є$−9$.

Важливо знати, що ця методика працює лише для рівнянь. Не намагайтеся очищати дроби при спрощенні виразів. Як нагадування:

Таблиця$\PageIndex{2}$
Вираз	Рівняння
$\frac { 1 } { 2 } x + \frac { 5 } { 3 }$	$\frac { 1 } { 2 } x + \frac { 5 } { 3 }=0$

Спрощуємо вирази і вирішуємо рівняння. Якщо помножити вираз на$6$, ви зміните задачу. Однак, якщо помножити обидві сторони рівняння на$6$, ви отримаєте еквівалентне рівняння.

Таблиця$\PageIndex{3}$
Невірно	Правильно
$ \frac { 1 } { 2 } x + \frac { 5 } { 3 }$ $\begin{aligned} \neq & \color{red}{6 \cdot}\color{Black}{ \left( \frac { 1 } { 2 } x + \frac { 5 } { 3 } \right)} \\ = & 3 x + 10 \quad \color{red}{✗} \end{aligned}$	$\begin{aligned} \frac { 1 } { 2 } x + \frac { 5 } { 3 } & = 0 \\ \color{Cerulean}{6 \cdot}\color{Black}{ \left( \frac { 1 } { 2 } x + \frac { 5 } { 3 } \right)} & = \color{Cerulean}{6 \cdot}\color{Black}{ 0} \\ 3 x + 10 & = 0\quad\color{Cerulean}{✓} \end{aligned}$

Програми, що включають лінійні рівняння

Алгебра спрощує процес вирішення реальних завдань. Це робиться за допомогою букв для представлення невідомих, повторення задач у вигляді рівнянь та пропонуючи систематичні методи вирішення цих рівнянь. Для вирішення завдань, використовуючи алгебру, спочатку перекладіть формулювання задачі в математичні твердження, які описують зв'язки між заданою інформацією і невідомою. Зазвичай цей переклад на математичні твердження є складним кроком у процесі. Ключ до перекладу - уважно прочитати проблему і визначити певні ключові слова і фрази.

Таблиця$\PageIndex{4}$
Ключові слова	Переклад
Сума, збільшена на, більше, ніж, плюс, додана до, загальна	$+$
Різниця, зменшена на, віднімається від, менше, мінус	$-$
Твір, помножене на, разів, в два рази	$\cdot$
Коефіцієнт, розділений на, співвідношення, на	$÷$
Є, підсумок, результат	$=$

При перекладі пропозицій в математичні твердження обов'язково кілька разів прочитайте пропозицію і розібрати ключові слова і фрази. Важливо спочатку визначити змінну, «нехай x представляти...» і вказати словами, що таке невідома величина. Цей крок не тільки робить нашу роботу більш читабельною, але і змушує задуматися про те, що ми шукаємо.

Приклад$\PageIndex{12}$:

Коли$6$ віднімається з подвоєної суми$8$ числа і результат$5$. Знайдіть номер.

Рішення

Нехай n представляє невідоме число.

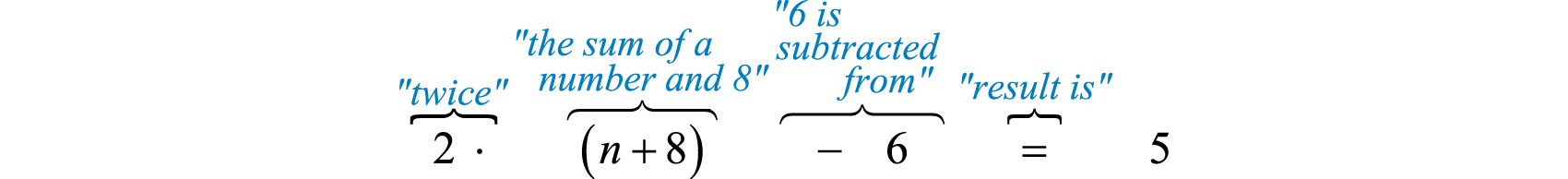
Щоб зрозуміти, чому ми включили дужки в набір, необхідно вивчити структуру наступних двох пропозицій і їх переклади:

Таблиця$\PageIndex{5}$
«удвічі більше суми числа і 8»	2 (н+8)
«сума подвоєного числа* і 8*»	2н+8

Ключовим було зосередитися на фразі «вдвічі більше суми», це спонукало нас згрупувати суму в дужках, а потім помножити на$2$. Після перекладу речення в математичне твердження ми потім вирішуємо.

$\begin{aligned} 2 ( n + 8 ) - 6 & = 5 \\ 2 n + 16 - 6 & = 5 \\ 2 n + 10 & = 5 \\ 2 n & = - 5 \\ n & = \frac { - 5 } { 2 } \end{aligned}$

Перевірте.

$\begin{aligned} 2 ( n + 8 ) - 6 & = 2 \left( \color{Cerulean}{- \frac { 5 } { 2 }}\color{Black}{ +} 8 \right) - 6 \\ & = 2 \left( \frac { 11 } { 2 } \right) - 6 \\ & = 11 - 6 \\ & = 5 \quad\color{Cerulean}{✓}\end{aligned}$

Відповідь:

Число є$−\frac{5}{2}$.

Далі слідують загальні рекомендації по налаштуванню та вирішенню проблем зі словами.

Крок 1: Прочитайте проблему кілька разів, визначте ключові слова та фрази та впорядкуйте задану інформацію.
Крок 2: Визначте змінні, призначивши букву або вираз невідомим величинам.
Крок 3: Перекладіть та налаштуйте алгебраїчне рівняння, яке моделює задачу.
Крок 4: Розв'яжіть отримане алгебраїчне рівняння.
Крок 5: Нарешті, дайте відповідь на питання у формі речення і переконайтеся, що це має сенс (перевірте його).

Наразі налаштуйте всі свої рівняння, використовуючи лише одну змінну. Уникайте двох змінних, шукаючи зв'язок між невідомими.

Приклад$\PageIndex{13}$:

Прямокутник має периметр вимірювальних$92$ метрів. Довжина в$2$ метри менше ширини в$3$ рази. Знайдіть розміри прямокутника.

Рішення

Речення «Довжина на 2 метри менше, ніж в 3 рази більше ширини» дає нам зв'язок між двома змінними.

$w$Дозволяти представляти ширину прямокутника.

$3w−2$Дозволяти представляти довжину.

Речення «Прямокутник має периметр розміром 92 метри» передбачає алгебраїчне налаштування. $92$Підставляємо периметр і$3w−2$ вираз довжини у відповідну формулу наступним чином:

$P = \quad2 l\:\:\:\:\: +\:\:\: 2 w$

$\color{Cerulean}{\downarrow} \quad\:\:\:\quad \color{Cerulean}{\downarrow}\quad\quad\quad\quad$

$\color{OliveGreen}{92}\color{Black}{ =} 2 (\color{OliveGreen}{ 3 w - 2}\color{Black}{ )} + 2 w$

Після того, як ви встановили алгебраїчне рівняння з однією змінною, вирішіть для ширини,$w$.

$\begin{array} { l } { 92 = 2 ( 3 w - 2 ) + 2 w \color{Cerulean}{ Distribute. } } \\ { 92 = 6 w - 4 + 2 w \quad\: \color{Cerulean} { Combine\: like\: terms. } } \\ { 92 = 8 w - 4 \quad\quad\quad\:\:\:\color{Cerulean} { Solve\: for\: w. } } \\ { 96 = 8 w } \\ { 12 = w } \end{array}$

Використовуйте$3w−2$, щоб знайти довжину.

$l = 3 w - 2 = 3 ( \color{OliveGreen}{12}\color{Black}{ )} - 2 = 36 - 2 = 34$

Для перевірки переконайтеся, що периметр дорівнює$92$ метрам.

$\begin{aligned} P & = 2 l + 2 w \\ & = 2 ( 34 ) + 2 ( 12 ) \\ & = 68 + 24 \\ & = 92 \end{aligned}$

Відповідь:

Прямокутник вимірює$12$$34$ метри за метрами.

Приклад$\PageIndex{14}$:

Враховуючи$4 \frac{3}{8}$ відсоткову річну процентну ставку, скільки часу знадобиться,$$2,500$$$437.50$ щоб дати прості відсотки?

Рішення

Нехай t представляє час, необхідний для заробітку$$437.50$ при$4 \frac{3}{8}$%. Організуйте інформацію, необхідну для використання формули для простого інтересу,$I=prt$.

Таблиця$\PageIndex{6}$
Надані відсотки за часовий період:	$I=$437.50$
Дано принципал:	$p=$2,500$
Задана ставка:	$r= 4 \frac{3}{8}$%$=4.375$%$=0.04375$

Далі підставляємо всі відомі величини в формулу і потім вирішуємо для єдиного невідомого, т.

$\begin{aligned} I & = p r t \\ \color{OliveGreen}{437.50} & \color{Black}{=} \color{OliveGreen}{2500}\color{Black}{ (}\color{OliveGreen}{ 0.04375}\color{Black}{ )} t \\ 437.50 & = 109.375 t \\ \frac{437.50}{\color{Cerulean}{109.375}} & \color{Black}{=} \frac { 109.375 t } { \color{Cerulean}{109.375} } \\ 4 & = t \end{aligned}$

Відповідь:

Потрібні$4$ роки, щоб$$2,500$ інвестувати під$4 \frac{3}{8}$%, щоб заробити$$437.50$ в простих відсотках.

Приклад$\PageIndex{15}$:

Сьюзен вклала свої загальні заощадження$$12,500$ на два рахунки, заробляючи прості відсотки. Її рахунок пайового фонду заробив$7$% минулого року, а її компакт-диск заробив$4.5$%. Якщо її загальний відсоток за рік був$$670$, скільки було на кожному рахунку?

Рішення

Відносини між двома невідомими є те, що вони загальні$$12,500$. Коли задіяна загальна сума, загальною методикою, яка використовується для уникнення двох змінних, є представлення другої невідомої як різниці загальної кількості та першої невідомої.

Нехай$x$ представляють суму, вкладену в ПІФ.

$12,500 − x$Дозволяти представляти решту суми, вкладеної в компакт-диск.

Організуйте дані.

Таблиця$\PageIndex{7}$
Відсотки, зароблені в ПІФ:	$\begin{aligned} I & = p r t \\ & = x \cdot 0.07 \cdot 1 \\ & = \color{OliveGreen}{0.07 x} \end{aligned}$
Відсотки, зароблені на компакт-диску:	$\begin{aligned} I & = p r t \\ & = ( 12,500 - x ) \cdot 0.045 \cdot 1 \\ & = \color{OliveGreen}{0.045 ( 12,500 - x )} \end{aligned}$
Загальний відсоток:	$\color{OliveGreen}{$670}$

Загальний відсоток - це сума відсотків, зароблених з кожного рахунку.

$\color{Cerulean}{mutual fund interest + CD interest = total interest}$

$ 0.07x + 0.045(12,500−x) = 670$

Це рівняння моделює задачу з однією змінною. Вирішити для$x$.

$\begin{aligned} 0.07 x + 0.045 ( 12,500 - x ) & = 670 \\ 0.07 x + 562.5 - 0.045 x & = 670 \\ 0.025 x + 562.5 & = 670 \\ 0.025 x & = 107.5 \\ x & = \frac { 107.5 } { 0.025 } \\ x & = 4,300 \end{aligned}$

Використовуйте$12,500−x$, щоб знайти суму на компакт-диску.

$12,500−x=12,500−\color{OliveGreen}{4,300}\color{Black}{=}8,200$

Відповідь:

Сьюзен інвестувала$$4,300$ на рівні$7$% в пайовий фонд і$$8,200$ під$4.5$% в компакт-диск.

Ключові виноси

Розв'язування загальних лінійних рівнянь передбачає виділення змінної$1$, з коефіцієнтом, з одного боку знака рівності. Для цього спочатку використовують відповідну властивість рівності додавання або віднімання, щоб виділити змінний член з одного боку знака рівності. Далі виділяють змінну, використовуючи властивість рівності множення або ділення. Нарешті, перевірте, чи вирішує ваше рішення вихідне рівняння.
Якщо рішення лінійного рівняння призводить до істинного твердження типу$0 = 0$, то рівняння є тотожністю, а набір розв'язків складається з усіх дійсних чисел,$ℝ$.
Якщо рішення лінійного рівняння призводить до помилкового твердження типу$0 = 5$, то рівняння є протиріччям і рішення немає,$Ø$.
Очистіть дроби, множивши обидві сторони рівняння на найменш спільний кратний усіх знаменників. Розподіліть і помножте всі члени на РК, щоб отримати еквівалентне рівняння з цілими коефіцієнтами.
Спростити процес вирішення реальних задач шляхом створення математичних моделей, що описують взаємозв'язок між невідомими. Використовуйте алгебру для вирішення отриманих рівнянь.

Вправа$\PageIndex{3}$

Визначте, чи є дане значення рішенням.

$−5x + 4 = −1 ; x = −1$
$4x − 3 = −7 ; x = −1$
$3y − 4 = 5; y = \frac{9}{3}$
$−2y + 7 = 12 ; y = −\frac{5}{2}$
$3a − 6 = 18 − a; a = −3$
$5 (2t − 1) = 2 − t; t = 2$
$ax − b = 0; x = \frac{b}{a}$
$ax + b = 2b; x = \frac{b}{a}$

Відповідь

1. Ні

3. Так

5. Ні

7. Так

Вправа$\PageIndex{4}$

Вирішити.

$5x − 3 = 27$
$6x − 7 = 47$
$4x + 13 = 35$
$6x − 9 = 18$
$9a + 10 = 10$
$5 − 3a = 5$
$−8t + 5 = 15$
$−9t + 12 = 33$
$\frac{2}{3} x + \frac{1}{2} = 1$
$\frac{3}{8} x + \frac{5}{4} = \frac{3}{2}$
$\frac{1 − 3y}{5} = 2$
$\frac{2 − 5y}{6} = −8$
$7 − y = 22$
$6 − y = 12$
Вирішити для$x: ax − b = c$
Вирішити для$x: ax + b = 0$

Відповідь

1. $6$

3. $\frac{11}{2}$

5. $0$

7. $−\frac{5}{4}$

9. $\frac{3}{4}$

11. $−3$

13. $−15$

15. $x = \frac{b+c}{a}$

Вправа$\PageIndex{5}$

Вирішити.

$6x − 5 + 2x = 19$
$7 − 2x + 9 = 24$
$12x − 2 − 9x = 5x + 8$
$16 − 3x − 22 = 8 − 4x$
$5y − 6 − 9y = 3 − 2y + 8$
$7 − 9y + 12 = 3y + 11 − 11y$
$3 + 3a − 11 = 5a − 8 − 2a$
$2 − 3a = 5a + 7 − 8a$
$\frac{1}{3} x −\frac{3}{2} + \frac{5}{2} x = \frac{5}{6} x + \frac{1}{4}$
$\frac{5}{8} + \frac{1}{5} x −\frac{3}{4} = \frac{3}{10} x − \frac{1}{4}$
$1.2x − 0.5 − 2.6x = 2 − 2.4x$
$1.59 − 3.87x = 3.48 − 4.1x − 0.51$
$5 − 10x = 2x + 8 − 12x$
$8x − 3 − 3x = 5x − 3$
$5 (y + 2) = 3 (2y − 1) + 10$
$7 (y − 3) = 4 (2y + 1) − 21$
$7 − 5 (3t − 9) = 22$
$10 − 5 (3t + 7) = 20$
$5 − 2x = 4 − 2 (x − 4)$
$2 (4x − 5) + 7x = 5 (3x − 2)$
$4 (4a − 1) = 5 (a − 3) + 2 (a − 2)$
$6 (2b − 1) + 24b = 8 (3b − 1)$
$\frac{2}{3} (x + 18) + 2 = \frac{1}{3} x − 13$
$\frac{2}{5} x − \frac{1}{2} (6x − 3) = \frac{4}{3}$
$1.2 (2x + 1) + 0.6x = 4x$
$6 + 0.5 (7x − 5) = 2.5x + 0.3$
$5 (y + 3) = 15 (y + 1) − 10y$
$3 (4 − y) − 2 (y + 7) = −5y$
$\frac{1}{5} (2a + 3) −\frac{1}{2} = \frac{1}{3} a + \frac{1}{10}$
$\frac{3}{2} a = \frac{3}{4} (1 + 2a) −\frac{1}{5} (a + 5)$
$6 − 3 (7x + 1) = 7 (4 − 3x)$
$6 (x − 6) − 3 (2x − 9) = −9$
$\frac{3}{4} (y − 2) + \frac{2}{3} (2y + 3) = 3$
$\frac{5}{4} − \frac{1}{2} (4y − 3) = \frac{2}{5} (y − 1)$
$−2 (3x + 1) − (x − 3) = −7x + 1$
$6 (2x + 1) − (10x + 9) = 0$
Вирішити для$w: P = 2l + 2w$
Вирішити для$a: P = a + b + c$
Вирішити для$t: D = rt$
Вирішити для$w: V = lwh$
Вирішити для$b: A = \frac{1}{2} bh$
Вирішити для$a:s = \frac{1}{2}at^{2}$
Вирішити для$a: A = \frac{1}{2}h (a + b)$
Вирішити для$h: V = \frac{1}{3}πr^{2}h$
Вирішити для$F: C = \frac{5}{9} (F − 32)$
Вирішити для$x: ax + b = c$

Відповідь

1. $3$

3. $−5$

5. $−\frac{17}{2}$

7. $ℝ$

9. $\frac{7}{8}$

11. $2.5$

13. $Ø$

15. $3$

17. $2$

19. $Ø$

21. $−\frac{5}{3}$

23. $−81$

25. $1.2$

27. $ℝ$

29. $0$

31. $Ø$

33. $\frac{6}{5}$

35. $ℝ$

37. $w = \frac{P − 2l}{2}$

39. $t = \frac{D}{r}$

41. $b = \frac{2A}{h}$

43. $a = \frac{2A}{h} − b$

45. $F = \frac{9}{5} C + 32$

Вправа$\PageIndex{6}$

Налаштуйте алгебраїчне рівняння, а потім вирішіть.

Проблеми з числом

Коли$3$ віднімається від суми числа і$10$ результат є$2$. Знайдіть номер.
Сума$3$ разів на число і$12$ дорівнює$3$. Знайдіть номер.
Тричі сума числа і$6$ дорівнює числу$5$ разів. Знайдіть номер.
Подвоєна сума числа і$4$ дорівнює сумі$3$ числа і дорівнює сумі числа і$1$. Знайдіть номер.
Більше ціле число$1$ більше, ніж$3$ в рази інше ціле. Якщо сума цілих чисел дорівнює$57$, знайдіть цілі числа.
Більше ціле число$5$ більше, ніж удвічі інше ціле число. Якщо сума цілих чисел дорівнює$83$, знайдіть цілі числа.
Одне ціле число$3$ менше, ніж двічі інше ціле число. Знайти цілі числа, якщо їх сума дорівнює$135$.
Одне ціле число$10$ менше, ніж$4$ інше ціле число. Знайти цілі числа, якщо їх сума дорівнює$100$.
Сума трьох послідовних цілих чисел дорівнює$339$. Знайти цілі числа.
Сума чотирьох послідовних цілих чисел дорівнює$130$. Знайти цілі числа.
Сума трьох послідовних парних чисел дорівнює$174$. Знайти цілі числа.
Сума чотирьох послідовних парних чисел дорівнює$116$. Знайти цілі числа.
Сума трьох послідовних непарних цілих чисел дорівнює$81$. Знайти цілі числа.
Сума чотирьох послідовних непарних цілих чисел дорівнює$176$. Знайти цілі числа.

Відповідь

1. $−5$

3. $9$

5. $14, 43$

7. $46, 89$

9. $112, 113, 114$

11. $56, 58, 60$

13. $25, 27, 29$

Вправа$\PageIndex{7}$

Проблеми геометрії

Довжина прямокутника на$5$ сантиметри менше, ніж в два рази більше його ширини. Якщо периметр дорівнює$134$ сантиметрам, знайдіть довжину і ширину.
Довжина прямокутника в$4$ сантиметри більше, ніж в$3$ рази більше його ширини. Якщо периметр дорівнює$64$ сантиметрам, знайдіть довжину і ширину.
Ширина прямокутника на половину менше його довжини. Якщо периметр вимірює$36$ дюйми, знайдіть розміри прямокутника.
Ширина прямокутника на$4$ дюйми менше його довжини. Якщо периметр вимірює$72$ дюйми, знайдіть розміри прямокутника.
Периметр квадрата дорівнює$48$ дюймам. Знайдіть довжину кожної сторони.
Периметр рівностороннього трикутника дорівнює$96$ дюймам. Знайдіть довжину кожної сторони.
Окружність кола вимірює$80π$ одиниці виміру. Знайдіть радіус.
Окружність кола вимірює$25$ сантиметри. Знайдіть радіус, округлений до найближчої сотої.

Відповідь

1. Ширина:$24$ сантиметри; довжина:$43$ сантиметри

3. Ширина:$6$ дюйми; довжина:$12$ дюйми

5. $12$дюймів

7. $40$одиниць

Вправа$\PageIndex{8}$

Прості проблеми з інтересами

За скільки років потрібно$$1,000$ вкладати під$5\frac{1}{2}$%, щоб заробити$$165$ на прості відсотки?
За скільки років потрібно$$20,000$ вкладати під$6\frac{1}{4}$%, щоб заробити$$3,125$ на прості відсотки?
За якою річною процентною ставкою$$6500$ необхідно інвестувати$2$ роками, щоб поступитися$$1,040$ в прості відсотки?
За якою річною процентною ставкою$$5,750$ необхідно інвестувати на$1$ рік, щоб поступитися$$333.50$ в прості відсотки?
Якщо прості відсотки, зароблені$5$ роками, були,$$1,860$ а річна процентна ставка становила$6$%, то що було основним?
Якщо прості відсотки, зароблені$2$ роками, були,$$543.75$ а річна процентна ставка становила$3\frac{3}{4}$%, то що було основним?
Скільки років знадобиться,$$600$ щоб подвоїти заробіток простих відсотків під$5$% річної ставки? (Підказка: Щоб подвоїти, інвестиції повинні заробляти$$600$ в простих відсотках.)
Скільки років знадобиться,$$10,000$ щоб подвоїти заробіток простих відсотків під$5$% річної ставки? (Підказка: Щоб подвоїти, інвестиції повинні заробляти$$10,000$ в простих відсотках.)
Джим інвестував$$4,200$ в два рахунки. Один рахунок заробляє$3$% простих відсотків, а інший заробляє$6$%. Якщо відсотки за$1$ роком були$$159$, скільки він вклав у кожен рахунок?
Джейн вклала$$6,500$ свої заощадження на два рахунки. Вона має частину його на компакт-диску під$5$% річних відсотків, а решта на ощадному рахунку, який заробляє$4$% річних відсотків. Якщо прості відсотки, зароблені з обох рахунків, припадають$$303$ на рік, то скільки у неї на кожному рахунку?
Хосе поклав торішній бонус$$8,400$ на два рахунки. Він інвестував частину в компакт-диск з$2.5$% річних відсотків, а решту - у фонд грошового ринку з$1.5$% річних відсотків. Його загальний інтерес за рік був$$198$. Скільки він вклав в кожен рахунок?
Мері вклала свої загальні заощадження$$3,300$ на два рахунки. Її рахунок пайового фонду заробив$6.2$% минулого року, а її компакт-диск заробив$2.4$%. Якщо її загальний відсоток за рік був$$124.80$, скільки було на кожному рахунку?
Аліса інвестує гроші на два рахунки, один з$3$ відсотками річних відсотків, а інший з$5$% річних відсотків. Вона вкладає$3$ рази стільки ж в рахунок з вищою прибутковістю, як і в нижчий прибутковий рахунок. Якщо її загальний відсоток за рік становить$$126$, скільки вона вклала в кожен рахунок?
Джеймс інвестував спадщину в двох окремих банках. Один банк запропонував$5\frac{1}{2}$% річної процентної ставки, а інший$6\frac{1}{4}$%. Він вклав в більш прибутковий банківський рахунок вдвічі більше, ніж в інший. Якщо його сумарний простий відсоток за$1$ рік був$$5,760$, то якою була сума його спадщини?

Відповідь

1. $3$років

3. $8$%

5. $$6,200$

7. $20$років

9. Він інвестував$$3,100$ по$3$% і$$1,100$ під$6$%.

11. Хосе інвестував$$7,200$ в компакт-диск і$$1,200$ в фонд грошового ринку.

13. Аліса інвестувала$$700$ в$3$% і$$2,100$ під$5$%.

Вправа$\PageIndex{9}$

Проблеми рівномірного руху

Якщо Джиму потрібні$1 \frac{1}{4}$ години, щоб проїхати$40$ милі, щоб працювати, то яка середня швидкість Джима?
Джил зайняв$3 \frac{1}{2}$ години, щоб проїхати$189$ милі додому від коледжу. Якою була її середня швидкість?
З якою швидкістю повинен їздити Джим, якщо він бажає проїхати$176$ милі в$2 \frac{3}{4}$ годинами?
Джеймс і Мартін змогли проїхати$1,140$ милі від Лос-Анджелеса до Сіетла. Якщо загальна поїздка зайняла$19$ години, то якою була їх середня швидкість?

Відповідь

1. $32$миль на годину

3. $64$миль на годину

Вправа$\PageIndex{10}$

Що розглядається як основна справа алгебри? Поясніть.
Яке походження слова алгебра?
Створіть власну ідентичність або протиріччя та поділіться нею на дошці обговорень. Надайте рішення та поясніть, як ви його знайшли.
Опублікуйте щось, що ви знайшли особливо корисним чи цікавим у цьому розділі. Поясніть чому.
Провести веб-пошук «рішення лінійних рівнянь». Поділіться посиланням на веб-сайт або відеоурок, який ви вважаєте корисним.

Відповідь

1. Відповідь може відрізнятися

3. Відповідь може відрізнятися

5. Відповідь може відрізнятися

Виноски

¹²⁹ Заява, що вказує на те, що два алгебраїчні вирази рівні.

¹³⁰ Рівняння, яке можна записати в стандартному вигляді$ax + b = 0$, де$a$ і$b$ є дійсними числами і$a ≠ 0$.

¹³¹ Будь-яке значення, яке може замінити змінну в рівнянні для отримання істинного твердження.

¹³² Рівняння з однаковим набором розв'язків.

¹³³ Властивості, які дозволяють отримати еквівалентні рівняння шляхом додавання, віднімання, множення та ділення обох сторін рівняння на ненульові дійсні числа.

¹³⁴ Дозволяє вирішувати для змінної по обидва боки знака рівності,$x = 5$ тому що еквівалентно$5 = x$.

¹³⁵ Рівняння, які вірні для певних значень.

¹³⁶ Рівняння, яке вірно для всіх можливих значень.

¹³⁷ Рівняння, яке ніколи не є істинним і не має рішення.

Додаткова властивість рівності:	Якщо\(A=B\), то\(A\color{Cerulean}{+c}\color{Black}{=} B\color{Cerulean}{+c}\)
Віднімання властивості рівності:	Якщо\(A=B\), то\(A\color{Cerulean}{-c}\color{Black}{-}B\color{Cerulean}{-c}\)
Властивість множення рівності:	Якщо\(A=B\), то\(\color{Cerulean}{c}\color{Black}{A}=\color{Cerulean}{c}\color{Black}{B}\)
Поділ властивості рівності:	Якщо\(A=B\), то\(\frac{A}{\color{Cerulean}{c}}\color{Black}{=}\frac{B}{\color{Cerulean}{c}}\)

Ключові слова	Переклад
Сума, збільшена на, більше, ніж, плюс, додана до, загальна	\(+\)
Різниця, зменшена на, віднімається від, менше, мінус	\(-\)
Твір, помножене на, разів, в два рази	\(\cdot\)
Коефіцієнт, розділений на, співвідношення, на	\(÷\)
Є, підсумок, результат	\(=\)

Надані відсотки за часовий період:	\(I=$437.50\)
Дано принципал:	\(p=$2,500\)
Задана ставка:	\(r= 4 \frac{3}{8}\)%\(=4.375\)%\(=0.04375\)

Відсотки, зароблені в ПІФ:	\(\begin{aligned} I & = p r t \\ & = x \cdot 0.07 \cdot 1 \\ & = \color{OliveGreen}{0.07 x} \end{aligned}\)
Відсотки, зароблені на компакт-диску:	\(\begin{aligned} I & = p r t \\ & = ( 12,500 - x ) \cdot 0.045 \cdot 1 \\ & = \color{OliveGreen}{0.045 ( 12,500 - x )} \end{aligned}\)
Загальний відсоток:	\(\color{OliveGreen}{$670}\)