1.6: Властивості дійсних чисел
- Page ID
- 59586
До кінця цього розділу ви зможете:
- Використовуйте комутативні та асоціативні властивості
- Використовуйте властивості ідентичності, оберненої та нульової
- Спрощення виразів за допомогою властивості розподілу
Використання комутативних та асоціативних властивостей
Порядок додавання двох чисел не впливає на результат. Якщо додати\(8+9\) або\(9+8\), результати однакові - вони обидва рівні 17. Отже,\(8+9=9+8\). Порядок, в якому ми додаємо, значення не має!
Аналогічно при множенні двох чисел порядок не впливає на результат. Якщо ми помножимо\(9·8\) або\(8·9\) результати однакові - вони обидва дорівнюють 72. Отже,\(9·8=8·9\). Порядок, в якому ми розмножуємо, значення не має! Ці приклади ілюструють Комутативне майно.
\[\begin{array}{lll} \textbf{of Addition} & \text{If }a \text{ and }b \text{are real numbers, then} & a+b=b+a. \\ \textbf{of Multiplication} & \text{If }a \text{ and }b \text{are real numbers, then} & a·b=b·a. \end{array} \]
При додаванні або множенні зміна порядку дає той же результат.
Комутативна власність має відношення до порядку. Віднімаємо\(9−8\) і\(8−9\), і бачимо, що\(9−8\neq 8−9\). Оскільки зміна порядку віднімання не дає однакового результату, ми знаємо, що віднімання не є комутативним.
Розподіл також не є комутативним. Так як\(12÷3\neq 3÷12\), зміна порядку поділу не дало такого ж результату. Комутативні властивості застосовуються тільки до додавання і множення!
- Додавання і множення є комутативними.
- Віднімання і ділення не є комутативними.
При складанні трьох чисел зміна угруповання чисел дає однаковий результат. Наприклад\((7+8)+2=7+(8+2)\), так як кожна сторона рівняння дорівнює 17.
Це справедливо і для множення. Наприклад\(\left(5·\frac{1}{3}\right)·3=5·\left(\frac{1}{3}·3\right)\), так як кожна сторона рівняння дорівнює 5.
Ці приклади ілюструють асоціативну властивість.
\[\begin{array}{lll} \textbf{of Addition} & \text{If }a,b, \text{ and }c \text{ are real numbers, then} & (a+b)+c=a+(b+c). \\ \textbf{of Multiplication} & \text{If }a,b,\text{ and }c \text{ are real numbers, then} & (a·b)·c=a·(b·c). \end{array} \]
При додаванні або множенні зміна угруповання дає той же результат.
Асоціативна властивість має відношення до групування. Якщо ми змінимо спосіб групування чисел, результат буде однаковим. Зверніть увагу, що це ті ж три числа в тому ж порядку - єдина різниця полягає в групуванні.
Ми побачили, що віднімання та поділ не були комутативними. Вони також не асоціативні.
\[\begin{array}{cc} (10−3)−2\neq 10−(3−2) & (24÷4)÷2\neq 24÷(4÷2) \\ 7−2\neq 10−1 & 6÷2\neq 24÷2 \\ 5\neq 9 & 3\neq 12 \end{array}\]
Спрощуючи вираз, завжди є гарною ідеєю планувати, якими будуть кроки. Для того, щоб об'єднати подібні терміни в наступному прикладі, ми будемо використовувати Commutative Property of addition, щоб написати подібні терміни разом.
Спростити:\(18p+6q+15p+5q\).
- Відповідь
-
\[\begin{array}{lc} \text{} & 18p+6q+15p+5q \\ \text{Use the Commutative Property of addition to} & 18p+15p+6q+5q \\ \text{reorder so that like terms are together.} & {} \\ \text{Add like terms.} & 33p+11q \end{array}\]
Спростити:\(23r+14s+9r+15s\).
- Відповідь
-
\(32r+29s\)
Спростити:\(37m+21n+4m−15n\).
- Відповідь
-
\(41m+6n\)
Коли нам доводиться спростити алгебраїчні вирази, ми часто можемо полегшити роботу, застосувавши спочатку Комутативну властивість або асоціативну властивість.
Спростити:\((\frac{5}{13}+\frac{3}{4})+\frac{1}{4}\).
- Відповідь
-
\( \begin{array}{lc} \text{} & (\frac{5}{13}+\frac{3}{4})+\frac{1}{4} \\ {\text{Notice that the last 2 terms have a common} \\ \text{denominator, so change the grouping.} } & \frac{5}{13}+(\frac{3}{4}+\frac{1}{4}) \\ \text{Add in parentheses first.} & \frac{5}{13}+(\frac{4}{4}) \\ \text{Simplify the fraction.} & \frac{5}{13}+1 \\ \text{Add.} & 1\frac{5}{13} \\ \text{Convert to an improper fraction.} & \frac{18}{13} \end{array}\)
Спростити:\((\frac{7}{15}+\frac{5}{8})+\frac{3}{8}.\)
- Відповідь
-
\(1 \frac{7}{15}\)
Спростити:\((\frac{2}{9}+\frac{7}{12})+\frac{5}{12}\).
- Відповідь
-
\(1\frac{2}{9}\)
Використання властивостей ідентичності, зворотного та нульового
Що відбувається, коли ми додаємо 0 до будь-якого числа? Додавання 0 не змінює значення. З цієї причини ми називаємо 0 аддитивної ідентичністю. Властивість Identity of Addition, яка стверджує, що для будь-якого реального числа\(a,a+0=a\) і\(0+a=a.\)
Що відбувається, коли ми помножимо будь-яке число на одиницю? Множення на 1 не змінює значення. Таким чином, ми називаємо 1 мультиплікативна ідентичність. Властивість ідентичності множення, яка стверджує, що для будь-якого дійсного числа\(a,a·1=a\) і\(1⋅a=a.\)
Ми підсумовуємо Властивості ідентичності тут.
\[\begin{array}{ll} \textbf{of Addition} \text{ For any real number }a:a+0=a & 0+a=a \\ \\ \\ \textbf{0} \text{ is the } \textbf{additive identity} \\ \textbf{of Multiplication} \text{ For any real number } a:a·1=a & 1·a=a \\ \\ \\ \textbf{1} \text{ is the } \textbf{multiplicative identity} \end{array}\]
Яке число, додане до 5, дає адитивну ідентичність, 0? Ми знаємо
.jpg)
Відсутнє число було протилежним числу!
\(−a\)Називаємо добавку, обернену\(a\). Протилежністю числу є його адитивна зворотна. Число і його протилежність додають до нуля, що є адитивною ідентичністю. Це призводить до зворотного властивості додавання, яке вказує на будь-яке дійсне число.\(a,a+(−a)=0.\)
Яке число, помножене на\(\frac{2}{3}\) дає мультиплікативну ідентичність, 1? Іншими словами,\(\frac{2}{3}\) раз, що призводить до 1? Ми знаємо
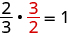
Відсутнє число було відповідним числом!
Ми\(\frac{1}{a}\) називаємо мультиплікативну обернену a. Зворотне число - це його мультиплікативний зворотний. Це призводить до оберненої властивості множення, яка стверджує, що для будь-якого дійсного числа\(a,a\neq 0,a·\frac{1}{a}=1.\)
Ми формально заявляємо зворотні властивості тут.
\[\begin{array}{lc} \textbf{of addition} \text{For any real number }a, & a+(−a)=0 \\ \;\;\;\; −a \text{ is the } \textbf{additive inverse }\text{ of }a & {} \\ \;\;\;\; \text{A number and its } \textit{opposite } \text{add to zero.} \\ \\ \\ \textbf{of multiplication } \text{For any real number }a,a\neq 0 & a·\dfrac{1}{a}=1 \\ \;\;\;\;\;\dfrac{1}{a} \text{ is the } \textbf{multiplicative inverse} \text{ of }a \\ \;\;\;\; \text{A number and its } \textit{reciprocal} \text{ multiply to one.} \end{array}\]
Властивість Identity додавання говорить, що коли ми додаємо 0 до будь-якого числа, результат - це те саме число. Що відбувається, коли ми помножимо число на 0? Множення на 0 робить добуток рівним нулю.
А як щодо поділу за участю нуля? Що таке\(0÷3\)? Подумайте про реальний приклад: якщо в банку печива немає печива і 3 людини повинні поділитися ними, скільки печива отримує кожна людина? Немає файлів cookie для спільного використання, тому кожна людина отримує 0 файлів cookie. Отже,\(0÷3=0.\)
Ми можемо перевірити ділення з відповідним фактом множення. Отже, ми знаємо,\(0÷3=0\) тому що\(0·3=0\).
Тепер подумайте про поділ на нуль. Який результат ділення 4 на 0? Подумайте про пов'язаний факт множення:

Чи є число, яке помножене на 0 дає 4? Оскільки будь-яке дійсне число, помножене на 0, дає 0, не існує реального числа, яке можна помножити на 0, щоб отримати 4. Ми робимо висновок, що відповіді немає,\(4÷0\) і тому ми говоримо, що поділ на 0 не визначено.
Підсумовуємо тут властивості нуля.
Множення на нуль: для будь-якого дійсного числа
\[a⋅0=0 \; \; \; 0⋅a=0 \; \; \; \; \text{The product of any number and 0 is 0.}\]
поділ на нуль: для будь-якого дійсного числа a,\(a\neq 0\)
\[\begin{array}{cl} \dfrac{0}{a}=0 & \text{Zero divided by any real number, except itself, is zero.} \\ \dfrac{a}{0} \text{ is undefined} & \text{Division by zero is undefined.} \end{array}\]
Тепер ми будемо практикувати використання властивостей тотожностей, зворотних і нульових для спрощення виразів.
Спростити:\(−84n+(−73n)+84n.\)
- Відповідь
-
\(\begin{array}{lc} \text{} & −84n+(−73n)+84n \\ \text{Notice that the first and third terms are} \\ \text{opposites; use the Commutative Property of} & −84n+84n+(−73n) \\ \text{addition to re-order the terms.} \\ \text{Add left to right.} & 0+(−73n) \\ \text{Add.} & −73n \end{array}\)
Спростити:\(−27a+(−48a)+27a\).
- Відповідь
-
\(−48a\)
Спростити:\(39x+(−92x)+(−39x)\).
- Відповідь
-
\(−92x\)
Тепер ми побачимо, як корисно розпізнавати взаємні дії. Перш ніж множити зліва направо, шукайте взаємні - їх продукт дорівнює 1.
Спростити:\(\frac{7}{15}⋅\frac{8}{23}⋅\frac{15}{7}\).
- Відповідь
-
\(\begin{array}{lc} \text{} & \frac{7}{15}⋅\frac{8}{23}⋅\frac{15}{7} \\ \text{Notice the first and third terms} \\ {\text{are reciprocals, so use the Commutative} \\ \text{Property of multiplication to re-order the} \\ \text{factors.}} & \frac{7}{15}·\frac{15}{7}·\frac{8}{23} \\ \text{Multiply left to right.} & 1·\frac{8}{23} \\ \text{Multiply.} & \frac{8}{23} \end{array}\)
Спростити:\(\frac{9}{16}⋅\frac{5}{49}⋅\frac{16}{9}\).
- Відповідь
-
\(\frac{5}{49}\)
Спростити:\(\frac{6}{17}⋅\frac{11}{25}⋅\frac{17}{6}\).
- Відповідь
-
\(\frac{11}{25}\)
Наступний приклад дає нам знати про різницю між діленням 0 на деяке число або деяке число ділиться на 0.
Спростити: a.\(\frac{0}{n+5}\), де\(n\neq −5\) б.\(\frac{10−3p}{0}\) де\(10−3p\neq 0.\)
- Відповідь
-
а.
\(\begin{array}{lc} {} & \dfrac{0}{n+5} \\ \text{Zero divided by any real number except itself is 0.} & 0 \end{array}\)
б.
\(\begin{array}{lc} {} & \dfrac{10−3p}{0} \\ \text{Division by 0 is undefined.} & \text{undefined} \end{array}\)
Спростити: а.\(\frac{0}{m+7}\), де\(m\neq −7\) б.\(\frac{18−6c}{0}\), де\(18−6c\neq 0\).
- Відповідь
-
а. 0
б. невизначено
Спростити: а.\(\frac{0}{d−4}\), де\(d\neq 4\) б.\(\frac{15−4q}{0}\), де\(15−4q\neq 0\).
- Відповідь
-
а. 0
б. невизначено
Спрощення виразів за допомогою властивості розподілу
Припустимо, що в кіно збираються троє друзів. Кожному з них потрібно $9.25 - це 9 доларів і 1 квартал - щоб оплатити свої квитки. Скільки грошей їм потрібно всім разом?
Можна подумати про доларах окремо від кварталів. Їм потрібно 3 рази $9 так $27 і 3 рази 1 квартал, так 75 центів. Всього їм потрібно $27,75. Якщо ви думаєте про те, щоб зробити математику таким чином, ви використовуєте розподільну властивість.
\(\begin{array}{lc} \text{If }a,b \text{,and }c \text{are real numbers, then} \; \; \; \; \; & a(b+c)=ab+ac \\ {} & (b+c)a=ba+ca \\ {} & a(b−c)=ab−ac \\{} & (b−c)a=ba−ca \end{array}\)
В алгебрі ми використовуємо властивість Distributive для видалення дужок, оскільки ми спрощуємо вирази.
Спростити:\(3(x+4)\).
- Відповідь
-
\(\begin{array} {} & 3(x+4) \\ \text{Distribute.} \; \; \; \; \; \; \; \; & 3·x+3·4 \\ \text{Multiply.} & 3x+12 \end{array}\)
Спростити:\(4(x+2)\).
- Відповідь
-
\(4x8\)
Спростити:\(6(x+7)\).
- Відповідь
-
\(6x42\)
Деякі студенти вважають корисним малювати стрілки, щоб нагадати їм, як використовувати розподільну властивість. Тоді перший крок у прикладі виглядатиме так:
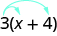
Спростити:\(8(\frac{3}{8}x+\frac{1}{4})\).
- Відповідь
-
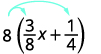
Розподілити. 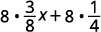
Помножити. 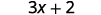
Спростити:\(6(\frac{5}{6}y+\frac{1}{2})\).
- Відповідь
-
\(5y+3\)
Спростити:\(12(\frac{1}{3}n+\frac{3}{4})\)
- Відповідь
-
\(4n+9\)
Використання розподільної властивості, як показано в наступному прикладі, буде дуже корисно, коли ми вирішуємо грошові додатки в наступних розділах.
Спростити:\(100(0.3+0.25q)\).
- Відповідь
-
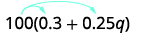
Розподілити. 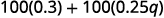
Помножити. 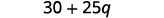
Спростити:\(100(0.7+0.15p).\)
- Відповідь
-
\(70+15p\)
Спростити:\(100(0.04+0.35d)\).
- Відповідь
-
\(4+35d\)
Коли ми розподіляємо негативне число, нам потрібно бути особливо обережними, щоб знаки були правильними!
Спростити:\(−11(4−3a).\)
- Відповідь
-
\(\begin{array}{lc} {} & −11(4−3a) \\ \text{Distribute. } \; \; \; \; \; \; \; \; \; \;& −11·4−(−11)·3a \\ \text{Multiply.} & −44−(−33a) \\ \text{Simplify.} & −44+33a \end{array}\)
Зверніть увагу, що ви також можете написати результат як\(33a−44.\) Чи знаєте ви чому?
Спростити:\(−5(2−3a)\).
- Відповідь
-
\(−10+15a\)
Спростити:\(−7(8−15y).\)
- Відповідь
-
\(−56+105y\)
У наступному прикладі ми покажемо, як використовувати властивість Distributive, щоб знайти протилежне виразу.
Спростити:\(−(y+5)\).
- Відповідь
-
\(\begin{array}{lc} {} & −(y+5) \\ \text{Multiplying by }−1 \text{ results in the opposite.}& −1(y+5) \\ \text{Distribute.} & −1·y+(−1)·5 \\ \text{Simplify.} & −y+(−5) \\ \text{Simplify.} & −y−5 \end{array} \)
Спростити:\(−(z−11)\).
- Відповідь
-
\(−z+11\)
Спростити:\(−(x−4)\).
- Відповідь
-
\(−x+4\)
Будуть випадки, коли нам потрібно буде використовувати розподільну властивість як частину порядку операцій. Почніть з погляду на дужки. Якщо вираз всередині дужок не можна спростити, наступним кроком буде множення за допомогою розподільної властивості, яка видаляє дужки. Наступні два приклади проілюструють це.
Спростити:\(8−2(x+3)\)
- Відповідь
-
Стежимо за порядком операцій. Множення відбувається перед відніманням, тому ми спочатку розподілимо 2, а потім віднімаємо.
\(\begin{array}{lc} {} & \text{8−2(x+3)} \\ \text{Distribute.} & 8−2·x−2·3 \\ \text{Multiply.} & 8−2x−6 \\ \text{Combine like terms.} &−2x+2 \end{array}\)
Спростити:\(9−3(x+2)\).
- Відповідь
-
\(3−3x\)
Спростити:\(7x−5(x+4)\).
- Відповідь
-
\(2x−20\)
Спростити:\(4(x−8)−(x+3)\).
- Відповідь
-
\(\begin{array}{lc} {} & 4(x−8)−(x+3) \\ \text{Distribute.} & 4x−32−x−3 \\ \text{Combine like terms.} & 3x−35 \end{array}\)
Спростити:\(6(x−9)−(x+12)\).
- Відповідь
-
\(5x−66\)
Спростити:\(8(x−1)−(x+5)\).
- Відповідь
-
\(7x−13\)
Усі властивості дійсних чисел, які ми використовували в цьому розділі, узагальнені тут.
| Комутативне майно
При додаванні або множенні зміна порядку дає той же результат \[\begin{array}{lll} \textbf{of Addition} & \text{If }a \text{ and }b \text{are real numbers, then} & a+b=b+a. \\ \textbf{of Multiplication} & \text{If }a \text{ and }b \text{are real numbers, then} & a·b=b·a. \end{array} \] |
| Асоціативна властивість
При додаванні або множенні зміна угруповання дає той же результат. \[\begin{array}{lll} \textbf{of Addition} & \text{If }a,b, \text{ and }c \text{ are real numbers, then} & (a+b)+c=a+(b+c). \\ \textbf{of Multiplication} & \text{If }a,b,\text{ and }c \text{ are real numbers, then} & (a·b)·c=a·(b·c). \end{array} \] |
| Розподільна власність
\[\begin{array}{lc} \text{If }a,b \text{,and }c \text{are real numbers, then} \; \; \; \; \; & a(b+c)=ab+ac \\ {} & (b+c)a=ba+ca \\ {} & a(b−c)=ab−ac \\{} & (b−c)a=ba−ca \end{array}\] |
| Ідентичність власності \[\begin{array}{ll} \textbf{of Addition} \text{ For any real number }a:a+0=a & 0+a=a \\ \;\;\;\; \textbf{0} \text{ is the } \textbf{additive identity} \\ \textbf{of Multiplication} \text{ For any real number } a:a·1=a & 1·a=a \\ \;\;\;\; \textbf{1} \text{ is the } \textbf{multiplicative identity} \end{array}\] |
| Зворотна властивість
\[\begin{array}{lc} \textbf{of addition } \text{For any real number }a, & a+(−a)=0 \\ \;\;\;\; −a \text{ is the } \textbf{additive inverse }\text{ of }a & {} \\ \;\;\;\; \text{A number and its } \textit{opposite } \text{add to zero.} \\ \\ \\ \textbf{of multiplication } \text{For any real number }a,a\neq 0 & a·\dfrac{1}{a}=1 \\ \;\;\;\;\;\dfrac{1}{a} \text{ is the } \textbf{multiplicative inverse} \text{ of }a \\ \;\;\;\; \text{A number and its } \textit{reciprocal} \text{ multiply to one.} \end{array}\] |
| Властивості нуля \[\begin{array}{lc} \text{For any real number }a, & a·0=0 \\ {} & 0·a=0 \\ \text{For any real number }a,a\neq 0, & \dfrac{0}{a}=0 \\ \text{For any real number }a, & \dfrac{a}{0} \text{ is undefined} \end{array}\] |
Ключові концепції
| Комутативне властивість При додаванні або множенні зміна порядку дає однаковий результат \[\begin{array}{lll} \textbf{of Addition} & \text{If }a \text{ and }b \text{are real numbers, then} & a+b=b+a. \\ \textbf{of Multiplication} & \text{If }a \text{ and }b \text{are real numbers, then} & a·b=b·a. \end{array} \] |
| Асоціативна властивість При додаванні або множенні зміна групування дає однаковий результат. \[\begin{array}{lll} \textbf{of Addition} & \text{If }a,b, \text{ and }c \text{ are real numbers, then} & (a+b)+c=a+(b+c). \\ \textbf{of Multiplication} & \text{If }a,b,\text{ and }c \text{ are real numbers, then} & (a·b)·c=a·(b·c). \end{array} \] |
| Розподільна власність
\[\begin{array}{lc} \text{If }a,b \text{,and }c \text{are real numbers, then} \; \; \; \; \; & a(b+c)=ab+ac \\ {} & (b+c)a=ba+ca \\ {} & a(b−c)=ab−ac \\{} & (b−c)a=ba−ca \end{array}\] |
| Ідентичність власності
\[\begin{array}{ll} \textbf{of Addition} \text{ For any real number }a:a+0=a & 0+a=a \\ \;\;\;\; \textbf{0} \text{ is the } \textbf{additive identity} \\ \textbf{of Multiplication} \text{ For any real number } a:a·1=a & 1·a=a \\ \;\;\;\; \textbf{1} \text{ is the } \textbf{multiplicative identity} \end{array}\] |
| Зворотна властивість
\[\begin{array}{lc} \textbf{of addition} \text{For any real number }a, & a+(−a)=0 \\ \;\;\;\; −a \text{ is the } \textbf{additive inverse }\text{ of }a & {} \\ \;\;\;\; \text{A number and its } \textit{opposite } \text{add to zero.} \\ \\ \\ \textbf{of multiplication } \text{For any real number }a,a\neq 0 & a·\dfrac{1}{a}=1 \\ \;\;\;\;\;\dfrac{1}{a} \text{ is the } \textbf{multiplicative inverse} \text{ of }a \\ \;\;\;\; \text{A number and its } \textit{reciprocal} \text{ multiply to one.} \end{array}\] |
| Властивості нуля
\[\begin{array}{lc} \text{For any real number }a, & a·0=0 \\ {} & 0·a=0 \\ \text{For any real number }a,a\neq 0, & \dfrac{0}{a}=0 \\ \text{For any real number }a, & \dfrac{a}{0} \text{ is undefined} \end{array}\] |
Глосарій
- адитивна ідентичність
- Число 0 є адитивним ідентифікатором, оскільки додавання 0 до будь-якого числа не змінює його значення.
- добавка обернена
- Протилежністю числу є його адитивна зворотна.
- мультиплікативна ідентичність
- Число 1 є мультиплікативною ідентичністю, оскільки множення 1 на будь-яке число не змінює його значення.
- мультиплікативний зворотний
- Зворотне число - це його мультиплікативний зворотний.
