Skip to main content
LibreTexts - Ukrayinska

6.6: Розділити многочлени

  1. Last updated
  2. Save as PDF
  • Page ID
    58962

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    До кінця цього розділу ви зможете:

    • Розділити многочлен на моном
    • Розділити многочлен на біноміал
    Примітка

    Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

    1. Додати:\(\dfrac{3}{d}+\dfrac{x}{d}\)
      Якщо ви пропустили цю проблему, перегляньте вправу 1.7.1.
    2. Спрощення:\(\dfrac{30 x y^{3}}{5 x y}\)
      Якщо ви пропустили цю проблему, перегляньте Вправу 6.5.37.
    3. Поєднуйте подібні терміни:\(8 a^{2}+12 a+1+3 a^{2}-5 a+4\)
      Якщо ви пропустили цю проблему, перегляньте Вправу 1.3.37.

    Розділити многочлен на мономіал

    В останньому розділі ви дізналися, як розділити мономіал на мономіал. Оскільки ви продовжуєте нарощувати свої знання про поліноми, наступна процедура полягає в тому, щоб розділити многочлен з двох або більше членів на мономіал.

    Метод, який ми будемо використовувати для поділу многочлена на мономіал, заснований на властивостях додавання дробів. Отже, ми почнемо з прикладу для перегляду додавання дробу.

    \(\begin{array}{ll}{\text { The sum, }} & {\dfrac{y}{5}+\dfrac{2}{5}} \\ {\text { simplifies to }} & {\dfrac{y+2}{5}}\end{array}\)

    Тепер ми зробимо це в зворотному порядку, щоб розділити один дріб на окремі дроби.

    Ми будемо стверджувати властивість додавання дробу тут так само, як ви дізналися його і навпаки.

    ДОДАВАННЯ ФРАКЦІЇ

    Якщо a, b і c - числа де\(c\neq 0\), то

    \[\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \quad \text { and } \quad \dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}\]

    Ми використовуємо форму зліва для додавання дробів і використовуємо форму праворуч, щоб розділити многочлен на моном.

    \(\begin{array}{ll}{\text { For example, }} & {\dfrac{y+2}{5}} \\ {\text { can be written }} & {\dfrac{y}{5}+\dfrac{2}{5}}\end{array}\)

    Цю форму додавання дробів ми використовуємо для поділу многочленів на мономи.

    ДІЛЕННЯ ПОЛІНОМА НА МОНОМІАЛ

    Щоб розділити многочлен на мономіал, розділіть кожен член многочлена на моном.

    Вправа\(\PageIndex{1}\)

    Знайдіть частку:\(\dfrac{7 y^{2}+21}{7}\)

    Відповідь

    \(\begin{array}{ll} & \dfrac{7 y^{2}+21}{7}\\\text{Divide each term of the numerator by the denominator.} & \dfrac{7 y^{2}}{7}+\dfrac{21}{7} \\ \text {Simplify each fraction. } & y^{2}+3 \end{array}\)

    Вправа\(\PageIndex{2}\)

    Знайдіть частку:\(\dfrac{8 z^{2}+24}{4}\)

    Відповідь

    \(2 z^{2}+6\)

    Вправа\(\PageIndex{3}\)

    Знайдіть частку:\(\dfrac{18 z^{2}-27}{9}\)

    Відповідь

    \(2 z^{2}-3\)

    Пам'ятайте, що поділ можна представити у вигляді дробу. Коли вас попросять розділити многочлен на мономіал і він вже не в дробовій формі, напишіть дріб з поліномом в чисельнику і моном в знаменнику.

    Вправа\(\PageIndex{4}\)

    Знайдіть частку:\(\left(18 x^{3}-36 x^{2}\right) \div 6 x\)

    Відповідь

    \(\begin{array}{ll} & \left(18 x^{3}-36 x^{2}\right) \div 6 x\\\text { Rewrite as a fraction. } & \dfrac{18 x^{3}-36 x^{2}}{6 x} \\ \text { Divide each term of the numerator by the denominator. }& \dfrac{18 x^{3}}{6 x}-\dfrac{36 x^{2}}{6 x}\\ \text { Simplify. } &3 x^{2}-6 x\end{array}\)

    Вправа\(\PageIndex{5}\)

    Знайдіть частку:\(\left(27 b^{3}-33 b^{2}\right) \div 3 b\)

    Відповідь

    \(9 b^{2}-11 b\)

    Вправа\(\PageIndex{6}\)

    Знайдіть частку:\(\left(25 y^{3}-55 y^{2}\right) \div 5 y\)

    Відповідь

    \(5 y^{2}-11 y\)

    Коли ми ділимося на негатив, ми повинні бути особливо обережними зі знаками.

    Вправа\(\PageIndex{7}\)

    Знайдіть частку:\(\dfrac{12 d^{2}-16 d}{-4}\)

    Відповідь

    \(\begin{array}{ll} &\dfrac{12 d^{2}-16 d}{-4}\\ \text { Divide each term of the numerator by the denominator. }& \dfrac{18 x^{3}-36 x^{2}}{6 x} \\ \text { Simplify. Remember, subtracting a negative is like adding a positive! }& -3 d^{2}+4 d\end{array}\)

    Вправа\(\PageIndex{8}\)

    Знайдіть частку:\(\dfrac{25 y^{2}-15 y}{-5}\)

    Відповідь

    \(-5 y^{2}+3 y\)

    Вправа\(\PageIndex{9}\)

    Знайдіть частку:\(\dfrac{42 b^{2}-18 b}{-6}\)

    Відповідь

    \(-7 b^{2}+3 b\)

    Вправа\(\PageIndex{10}\)

    Знайдіть частку:\(\dfrac{105 y^{5}+75 y^{3}}{5 y^{2}}\)

    Відповідь

    \(\begin{array}{ll} &\dfrac{105 y^{5}+75 y^{3}}{5 y^{2}}\\ \text { Separate the terms. }& \dfrac{105 y^{5}}{5 y^{2}}+\dfrac{75 y^{3}}{5 y^{2}}\\ \text { Simplify. }& 21 y^{3}+15 y\end{array}\)

    Вправа\(\PageIndex{11}\)

    Знайдіть частку:\(\dfrac{60 d^{7}+24 d^{5}}{4 d^{3}}\)

    Відповідь

    \(15 d^{4}+6 d^{2}\)

    Вправа\(\PageIndex{12}\)

    Знайдіть частку:\(\dfrac{216 p^{7}-48 p^{5}}{6 p^{3}}\)

    Відповідь

    \(36 p^{4}-8 p^{2}\)

    Вправа\(\PageIndex{13}\)

    Знайдіть частку:\(\left(15 x^{3} y-35 x y^{2}\right) \div(-5 x y)\)

    Відповідь

    \(\begin{array}{ll} &\left(15 x^{3} y-35 x y^{2}\right) \div(-5 x y)\\ \text { Rewrite as a fraction. }& \dfrac{15 x^{3} y-35 x y^{2}}{-5 x y}\\\text { Separate the terms. Be careful with the signs! }& \dfrac{15 x^{3} y}{-5 x y}-\dfrac{35 x y^{2}}{-5 x y}\\ \text { Simplify. } & -3 x^{2}+7 y\end{array}\)

    Вправа\(\PageIndex{14}\)

    Знайдіть частку:\(\left(32 a^{2} b-16 a b^{2}\right) \div(-8 a b)\)

    Відповідь

    \(-4 a+2 b\)

    Вправа\(\PageIndex{15}\)

    Знайдіть частку:\(\left(-48 a^{8} b^{4}-36 a^{6} b^{5}\right) \div\left(-6 a^{3} b^{3}\right)\)

    Відповідь

    \(8 a^{5} b+6 a^{3} b^{2}\)

    Вправа\(\PageIndex{13}\)

    Знайдіть частку:\(\dfrac{36 x^{3} y^{2}+27 x^{2} y^{2}-9 x^{2} y^{3}}{9 x^{2} y}\)

    Відповідь

    \(\begin{array}{ll} &\dfrac{36 x^{3} y^{2}+27 x^{2} y^{2}-9 x^{2} y^{3}}{9 x^{2} y}\\\text { Separate the terms. }& \dfrac{36 x^{3} y^{2}}{9 x^{2} y}+\dfrac{27 x^{2} y^{2}}{9 x^{2} y}-\dfrac{9 x^{2} y^{3}}{9 x^{2} y}\\ \text { Simplify. } & 4 x y+3 y-y^{2}\end{array}\)

    Вправа\(\PageIndex{14}\)

    Знайдіть частку:\(\dfrac{40 x^{3} y^{2}+24 x^{2} y^{2}-16 x^{2} y^{3}}{8 x^{2} y}\)

    Відповідь

    \(5 x y+3 y-2 y^{2}\)

    Вправа\(\PageIndex{15}\)

    Знайдіть частку:\(\dfrac{35 a^{4} b^{2}+14 a^{4} b^{3}-42 a^{2} b^{4}}{7 a^{2} b^{2}}\)

    Відповідь

    \(5 a^{2}+2 a^{2} b-6 b^{2}\)

    Вправа\(\PageIndex{16}\)

    Знайдіть частку:\(\dfrac{10 x^{2}+5 x-20}{5 x}\)

    Відповідь

    \(\begin{array}{ll}&\dfrac{10 x^{2}+5 x-20}{5x}\\\text { Separate the terms. }& \dfrac{10 x^{2}}{5 x}+\dfrac{5 x}{5 x}-\dfrac{20}{5 x}\\ \text { Simplify. } &2 x+1-\dfrac{4}{x}\end{array}\)

    Вправа\(\PageIndex{17}\)

    Знайдіть частку:\(\dfrac{18 c^{2}+6 c-9}{6 c}\)

    Відповідь

    \(3 c+1-\dfrac{3}{2 c}\)

    Вправа\(\PageIndex{18}\)

    Знайдіть частку:\(\dfrac{10 d^{2}-5 d-2}{5 d}\)

    Відповідь

    \(2 d-1-\dfrac{2}{5 d}\)

    Розділити многочлен на біноміал

    Щоб розділити многочлен на біноміал, ми дотримуємося процедури, дуже схожою на довге ділення чисел. Отже, давайте уважно розглянемо кроки, які ми робимо, коли ми ділимо 3-значне число, 875, на 2-значне число, 25.

    Пишемо довгий поділ 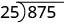Довгий поділ 875 на 25.
    Ділимо перші дві цифри, 87, на 25. 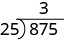25 вписується в 87 три рази. 3 написано над другою цифрою 875 в довгій ділильної дужці.
    Множимо 3 рази 25 і пишемо твір під 87. 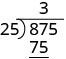Твір 3 і 25 дорівнює 75, що написано під першими двома цифрами 875 в довгій ділильної дужці.
    Тепер віднімаємо 75 з 87. 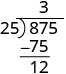87 мінус 75 дорівнює 12, що написано під 75.
    Потім збиваємо третю цифру дивіденду, 5. 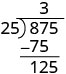5 в 875 збивається поруч з 12, роблячи 125.
    Повторіть процес, розділивши 25 на 125. 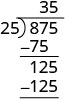25 вписується в 125 п'ять разів. 5 написано праворуч від 3 зверху довгою дужки поділу. 5 разів 25 дорівнює 125. 125 мінус 125 дорівнює нулю. Існує нульовий залишок, тому 25 вписується в 125 рівно п'ять разів. 875 ділиться на 25 дорівнює 35.

    Перевіряємо ділення множенням частки на дільник.

    Якщо ми зробили поділ правильно, продукт повинен дорівнювати дивідендам.

    \[\begin{array}{l}{35 \cdot 25} \\ {875}\checkmark\end{array}\]

    Тепер розділимо тріноміал на біноміал. Коли ви читаєте приклад, зверніть увагу, наскільки кроки схожі на числовий приклад вище.

    Вправа\(\PageIndex{19}\)

    Знайдіть частку:\(\left(x^{2}+9 x+20\right) \div(x+5)\)

    Відповідь
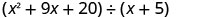
      Триноміал, х у квадраті плюс 9 х плюс 20, розділений на біноміал, х плюс 5.
    Напишіть це як довгу проблему поділу.  
    Переконайтеся, що дивіденди в стандартній формі. 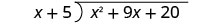Довге поділ х в квадраті плюс 9 х плюс 20 на х плюс 5
    Розділіть x 2 на x. Це може допомогти запитати себе: «Що мені потрібно помножити x на, щоб отримати x 2?»  
    Помістіть відповідь, x, у частку над терміном x. 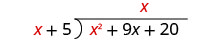х вписується в х квадрат х разів. х пишеться над другим терміном x в квадраті плюс 9 х плюс 20 у довгій дужці поділу.
    Помножте x раз x + 5. Вибудовуйте подібні умови під дивідендами. 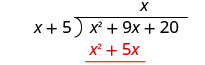Твір х і х плюс 5 х квадрат плюс 5 х, що написано нижче перших двох членів х в квадраті плюс 9x плюс 20 в довгій дужці поділу.
    Відніміть х 2 + 5 х з х 2 + 9 х.  
    Можливо, вам буде легше змінити знаки, а потім додати.
    Потім збити останній термін, 20.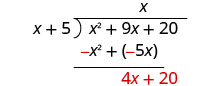    		 Сума х в квадраті плюс 9 х і негативний х квадрат плюс негативний 5 х 4 х, що написано під негативним 5 х Третій член в х квадрат плюс 9 х плюс 20 збивається поруч з 4 х, що робить 4 х плюс 20.
    Розділіть 4 x на x. Це може допомогти запитати себе: «Що мені потрібно
    помножити x на, щоб отримати 4 х?»    		  
    Поставте відповідь, 4, в частку над постійним терміном. 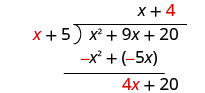4 х ділиться на х дорівнює 4. Плюс 4 написано на верхній частині довгою дужки поділу, поруч з х і вище 20 в х квадрат плюс 9 х плюс 20.
    Помножте 4 рази х + 5. 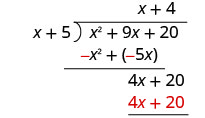х плюс 5 разів 4 це 4 х плюс 20, що написано під першими 4 х плюс 20.
    Відніміть 4 х + 20 з 4 х + 20. 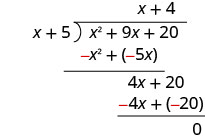4 х плюс 20 мінус 4 х плюс 20 дорівнює 0. Залишок 0. Х в квадраті плюс 9 х плюс 20 ділиться на х плюс 5 дорівнює х плюс 4.
    Перевірка:  
    Помножте частку на дільник.  
    (х + 4) (х + 5)  
    Ви повинні отримати дивіденди.  
    х 2 + 9 х + 20 ✓
    Вправа\(\PageIndex{20}\)

    Знайдіть частку:\(\left(y^{2}+10 y+21\right) \div(y+3)\)

    Відповідь

    y+7

    Вправа\(\PageIndex{21}\)

    Знайдіть частку:\(\left(m^{2}+9 m+20\right) \div(m+4)\)

    Відповідь

    м+5

    Коли дільник має знак віднімання, ми повинні бути особливо обережними, коли множимо частковий частковий, а потім віднімаємо. Може бути безпечніше показати, що ми змінюємо знаки, а потім додаємо.

    Вправа\(\PageIndex{22}\)

    Знайдіть частку:\(\left(2 x^{2}-5 x-3\right) \div(x-3)\)

    Відповідь
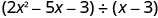
      Триноміал, 2 х квадрат мінус 5 х мінус 3, розділений на біноміал, х мінус 3.
    Напишіть це як довгу проблему поділу.  
    Переконайтеся, що дивіденди в стандартній формі. 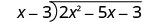Довге поділ 2 х в квадраті мінус 5 х мінус 3 на х мінус 3.
    Розділіть 2 х 2 на х.
    Помістіть відповідь, 2 x, у частку над терміном x.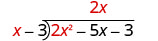    		 x вписується в 2 х квадрат 2 х разів. 2 х записується над другим терміном 2 х квадрат мінус 5 х мінус 3 в довгій дужці поділу.
    Помножте 2 x на x − 3. Вибудовуйте подібні умови під дивідендами. 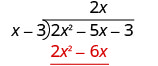Твір 2 х і х мінус 3 дорівнює 2 х в квадраті мінус 6 х, який записаний нижче перших двох членів 2 х квадрат мінус 5 х мінус 3 в довгій дужці поділу.
    Відняти 2 х 2 − 6 х з 2 х 2 − 5 х.
    Змініть знаки, а потім додайте.
    Потім збиваємо останній термін.    		 Сума 2 х в квадраті мінус 5 х і негативних 2 х в квадраті плюс 6 х, яка записана під 6 х Третій член в 2 х квадрат мінус 5 х мінус 3 збивається поруч з х, роблячи х мінус 3.
    Розділіть x на x.
    Поставте відповідь, 1, в частку над постійним терміном.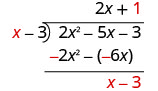    		 Плюс 1 написано на верхній частині довгою дужки поділу, поруч з 2 х і вище мінус 3 в 2 х квадрат мінус 5 х мінус 3.
    Помножте 1 раз x − 3. 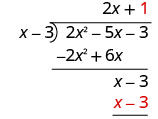х мінус 3 рази 1 х мінус 3, який пишеться під першим х мінус 3.
    Відніміть x − 3 від x − 3 шляхом зміни знаків та додавання. 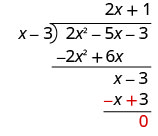Біноміальний х мінус 3 мінус біноміальний від'ємний х плюс 3 дорівнює 0. Залишок 0. 2 х в квадраті мінус 5 х мінус 3 ділиться на х мінус 3 дорівнює 2 х плюс 1.
    Щоб перевірити, помножте (x − 3) (2 x + 1).  
    Результат має бути 2 x 2 − 5 x − 3.
    Вправа\(\PageIndex{23}\)

    Знайдіть частку:\(\left(2 x^{2}-3 x-20\right) \div(x-4)\)

    Відповідь

    2х+5

    Вправа\(\PageIndex{24}\)

    Знайдіть частку:\(\left(3 x^{2}-16 x-12\right) \div(x-6)\)

    Відповідь

    3х+2

    Коли ми розділили 875 на 25, у нас не було залишку. Але іноді ділення чисел залишає залишок. Те ж саме відбувається, коли ми ділимо многочлени. У Вправи\(\PageIndex{25}\) ми будемо мати поділ, який залишає залишок. Запишемо залишок у вигляді дробу з дільником як знаменником.

    Вправа\(\PageIndex{25}\)

    Знайдіть частку:\(\left(x^{3}-x^{2}+x+4\right) \div(x+1)\)

    Відповідь
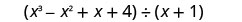
      Многочлен, х в кубі мінус х квадрат плюс х плюс 4, розділений на інший многочлен, х плюс 1.
    Напишіть це як довгу проблему поділу.  
    Переконайтеся, що дивіденди в стандартній формі. 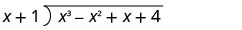Довге поділ х в кубі мінус х квадрат плюс х плюс 4 на х плюс 1.
    Розділіть x 3 на x.
    Помістіть відповідь, x 2, у частку над терміном x 2.
    Помножте x 2 рази x + 1. Вибудовуйте подібні умови під дивідендами.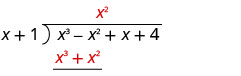    		 x вписується в х квадрат х разів. х пишеться над другим терміном х кубічних мінус х квадрат плюс х плюс 4 у довгій дужці поділу.
    Відніміть x 3+ x 2 від x 3 − x 2 шляхом зміни знаків та додавання.
    Потім збийте наступний термін.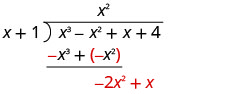    		 Сума х в кубі мінус х квадрат і негативний х кубічний плюс негативний х квадрат є від'ємним 2 х квадрат, який написаний під негативним x квадратом. Наступний термін в х кубі мінус х квадрат плюс х плюс 4 збивається поруч з негативним 2 х квадрат, що робить негативний 2 х квадрат плюс х.
    Розділіть −2 x 2 на x.
    Помістіть відповідь, −2 x, у частку над терміном x.
    Помножте −2 x на x + 1. Вибудовуйте подібні умови під дивідендами.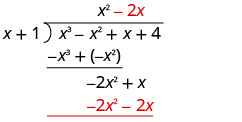    		 Мінус 2 х написано на верхній частині довгою дужки поділу, поруч з х в квадраті і вище х в кубі мінус х квадрат плюс х плюс 4. Негативний 2 х в квадраті мінус 2 х записується під негативним 2 х в квадраті плюс х.
    Відніміть −2 x 2 − 2 x від −2 x 2 + x шляхом зміни знаків та додавання.
    Потім збиваємо останній термін.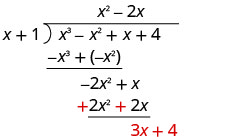    		 Сума негативних 2 х в квадраті плюс х і 2 х в квадраті плюс 2 х вважається 3 х Останній термін в х кубі мінус х квадрат плюс х плюс 4 збивається вниз, роблячи 3 х плюс 4.
    Розділіть 3 x на x.
    Поставте відповідь, 3, в частку над постійним терміном.
    Помножте 3 рази x + 1. Вибудовуйте подібні умови під дивідендами.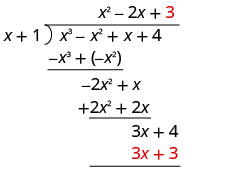    		 Плюс 3 написано на верхній частині довгою дужки поділу, над 4 в х куб мінус х квадрат плюс х плюс 4. 3 х плюс 3 написано під 3 х плюс 4.
    Відніміть 3 х + 3 з 3 х + 4, змінивши знаки і додаючи.
    Запишіть залишок у вигляді дробу з дільником як знаменником.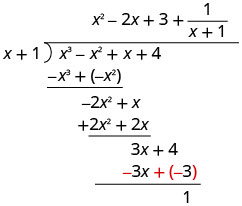    		 Сума 3 х плюс 4 і негативних 3 х плюс негативний 3 дорівнює 1. Таким чином, многочлен х в кубі мінус х квадрат плюс х плюс 4, розділений на біноміал х плюс 1, дорівнює x у квадраті мінус 2 х плюс дріб 1 над x плюс 1.
    Щоб перевірити, помножити\((x+1)\left(x^{2}-2 x+3+\dfrac{1}{x+1}\right)\)
    Результат повинен бути\(x^{3}-x^{2}+x+4\)
    Вправа\(\PageIndex{26}\)

    Знайдіть частку:\(\left(x^{3}+5 x^{2}+8 x+6\right) \div(x+2)\)

    Відповідь

    \(x^{2}+3 x+2+\dfrac{2}{x+2}\)

    Вправа\(\PageIndex{27}\)

    Знайдіть частку:\(\left(2 x^{3}+8 x^{2}+x-8\right) \div(x+1)\)

    Відповідь

    \(2 x^{2}+6 x-5-\dfrac{3}{x+1}\)

    Озирніться назад на дивіденди в Приклад , Приклад та Приклад. Терміни писалися в порядку убування ступенів, і відсутніх ступенів не було. Дивіденд у прикладі буде\(x^{4}-x^{2}+5 x-2\). У ньому відсутній\(x^{3}\) термін. Ми додамо в\(0x^{3}\) якості заповнювача.

    Вправа\(\PageIndex{28}\)

    Знайдіть частку:\(\left(x^{4}-x^{2}+5 x-2\right) \div(x+2)\)

    Відповідь

    Зверніть увагу, що в дивіденді немає\(x^{3}\) терміну. Ми додамо\(0x^{3}\) як заповнювач.

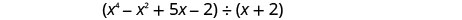
      Многочлен, х до четвертого степеня мінус х в квадраті мінус 5 х мінус 2, розділений на інший многочлен, х плюс 2.
    Напишіть це як довгу проблему поділу. Переконайтеся, що дивіденди в стандартній формі з заповнювачами для відсутніх термінів. 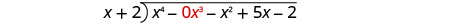Довге поділ х на четверту потужність плюс 0 х в кубі мінус х в квадраті мінус 5 х мінус 2 на х плюс 2.
    Розділіть x 4 на x.
    Помістіть відповідь, x 3, у частку над терміном x 3.
    Помножте x 3 рази x + 2. Вибудовуйте подібні терміни.
    Відніміть, а потім збийте наступний термін.    		 x cubed пишеться на верхній частині довгою дужки поділу над кубовим терміном x у дивіденді. Нижче перших двох членів дивіденду х до четвертої степені плюс 2 х куб віднімається, щоб дати від'ємний 2 х куб мінус х квадрат. Примітка поруч із розділом гласить: «Можливо, буде корисно змінити знаки та додати».
    Розділіть −2 x 3 на x.
    Помістіть відповідь, −2 x 2, у частку над числом x 2.
    Помножте −2 x 2 рази x + 1. Вибудовуйте подібні терміни.
    Відніміть і збийте наступний термін.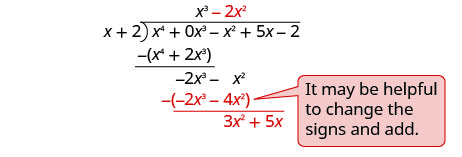    		 х кубічний мінус 2 х квадрат написано на верхній частині довгою дужки поділу. У нижній частині довгого поділу негативний 2 х куб мінус 4 х квадрат віднімається, щоб дати 3 х в квадраті плюс 5 х Примітка гласить: «Може бути корисно змінити знаки і додати».
    Розділіть 3 х 2 на х.
    Помістіть відповідь, 3 x, у частку над терміном x.
    Помножте 3 x рази x + 1. Вибудовуйте подібні терміни.
    Відніміть і збийте наступний термін.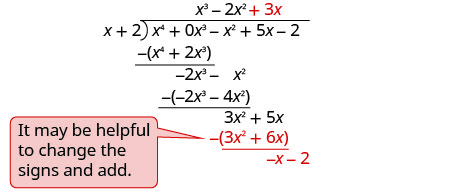    		 x в кубі мінус 2 х в квадраті плюс 3 х написано на верхній частині довгою дужки поділу. У нижній частині довгого поділу 3 х в квадраті плюс 6 х віднімається, щоб дати від'ємний х мінус 2. У примітці написано: «Можливо, буде корисно змінити знаки та додати».
    Розділити − x на x.
    Поставте відповідь, −1, у частку над постійним терміном.
    Помножте −1 раз x + 1. Вибудовуйте подібні терміни.
    Змінити знаки, додати.    		 х куб мінус 2 х квадрат плюс 3 х мінус 1 написано на верхній частині довгою дужки поділу. У нижній частині довгого ділення від'ємний х мінус 2 віднімаємо, щоб дати 0. У примітці написано: «Можливо, буде корисно змінити знаки та додати». Многочлен х до четвертої степені мінус х у квадраті плюс 5 х мінус 2, розділений на біном x плюс 2 дорівнює многочлену x в кубі мінус 2 x в квадраті плюс 3 х мінус 1.
    Щоб перевірити, помножте\((x+2)\left(x^{3}-2 x^{2}+3 x-1\right)\)  
    Результат повинен бути\(x^{4}-x^{2}+5 x-2\)
    Вправа\(\PageIndex{29}\)

    Знайдіть частку:\(\left(x^{3}+3 x+14\right) \div(x+2)\)

    Відповідь

    \(x^{2}-2 x+7\)

    Вправа\(\PageIndex{30}\)

    Знайдіть частку:\(\left(x^{4}-3 x^{3}-1000\right) \div(x+5)\)

    Відповідь

    \(x^{3}-8 x^{2}+40 x-200\)

    У Вправи\(\PageIndex{31}\) ми розділимо на\(2a−3\). Коли ми ділимо, нам доведеться розглянути константи, а також змінні.

    Вправа\(\PageIndex{31}\)

    Знайдіть частку:\(\left(8 a^{3}+27\right) \div(2 a+3)\)

    Відповідь

    Цього разу ми покажемо поділ всього за один крок. Нам потрібно додати два заповнювачі для того, щоб розділити.

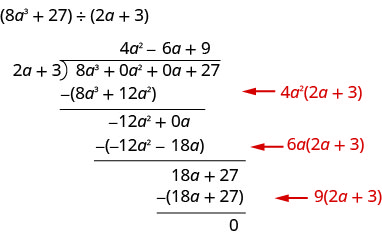
    На малюнку показано довге поділ 8 куб плюс 27 на 2 плюс 3. У довгій дужці ділення заповнювачі 0 a в квадраті та 0 a додаються до многочлена. На першому рядку під дивідендом 8 віднімається куб плюс 12 квадрат. Праворуч стрілка вказує на те, що це значення прийшло з множення 4 a в квадраті на 2 плюс 3. Віднімання дає негативний 12 квадрат плюс 0 a. З цього негативного 12 віднімається квадрат мінус 18 a. Праворуч стрілка вказує на те, що це значення прийшло з множення 6 a на 2 плюс 3. Віднімання дають 18 плюс 27. З цього 18 віднімається плюс 27. Праворуч стрілка вказує на те, що це значення прийшло з множення 9 на 2 плюс 3. Результат - 0.

    Щоб перевірити, помножте\((2 a+3)\left(4 a^{2}-6 a+9\right)\)

    Результат повинен бути\(8 a^{3}+27\)

    Вправа\(\PageIndex{32}\)

    Знайдіть частку:\(\left(x^{3}-64\right) \div(x-4)\)

    Відповідь

    \(x^{2}+4 x+16\)

    Вправа\(\PageIndex{33}\)

    Знайдіть частку:\(\left(125 x^{3}-8\right) \div(5 x-2)\)

    Відповідь

    \(25 x^{2}+10 x+4\)

    Примітка

    Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з діленням поліномів:

    • Розділити многочлен на мономіал
    • Розділити многочлен на мономіал 2
    • Розділити многочлен на біноміальний

    Ключові концепції

    • Додавання дробу
      • Якщо a, b і c - числа де\(c\neq 0\), то
        \(\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c}\) і\(\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}\)
    • Ділення многочлена на мономіал
      • Щоб розділити многочлен на мономіал, розділіть кожен член многочлена на моном.