6.7: Цілочисельні показники та наукові позначення
- Page ID
- 58965
До кінця цього розділу ви зможете:
- Використовуйте визначення негативного показника
- Спрощення виразів з цілими показниками
- Перетворення з десяткових позначень в наукові
- Перетворення наукового позначення в десяткову форму
- Множення і ділення за допомогою наукових позначень
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Яке місце має 6 в числі 64891?
Якщо ви пропустили цю проблему, перегляньте Вправа 1.2.1. - Назва десяткового числа: 0.0012.
Якщо ви пропустили цю проблему, перегляньте Вправа 1.8.1. - Відніміть: 5− (−3).
Якщо ви пропустили цю проблему, перегляньте Вправа 1.4.33.
Використання визначення негативного показника
Ми побачили, що частка властивість для експонентів, введені раніше в цьому розділі, має дві форми залежно від того, чи є показник більше в чисельнику або знаменнику.
Якщо a - дійсне число\(a\neq0\), а m і n - цілі числа, то
\[\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \quad\]
і
\[\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}, n>m\]
Що робити, якщо ми просто віднімаємо експоненти незалежно від того, який більший?
Розглянемо\(\dfrac{x^{2}}{x^{5}}\).
Віднімаємо показник в знаменнику від показника в чисельнику.
\[\begin{array}{c}{\dfrac{x^{2}}{x^{5}}} \\ {x^{2-5}} \\ {x^{-3}}\end{array}\]
Ми також можемо спростити\(\dfrac{x^{2}}{x^{5}}\), розділивши загальні фактори:
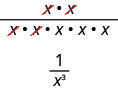
це означає, що\(x^{-3}=\dfrac{1}{x^{3}}\) і це призводить нас до визначення негативного показника.
Якщо n - ціле число і\(a\neq 0\), то\(a^{-n}=\dfrac{1}{a^{n}}\)
Негативний показник говорить нам, що ми можемо переписати вираз, взявши взаємну основу, а потім змінивши знак експоненти.
Будь-який вираз, що має негативні показники, не вважається в простій формі. Ми будемо використовувати визначення негативного показника та інші властивості експонент для написання виразу тільки з додатними показниками.
Наприклад, якщо після спрощення виразу ми закінчимо виразом\(x^{-3}\), ми зробимо ще один крок і напишемо\(\dfrac{1}{x^{3}}\). Відповідь вважається в найпростішій формі, коли він має тільки позитивні показники.
Спростити:
- \(4^{-2}\)
- \(10^{-3}\)
- Відповідь
-
- \(\begin{array}{ll}& 4^{-2} \\{\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}},} & {\dfrac{1}{4^{2}}} \\ {\text { Simplify. }} & \dfrac{1}{16} \end{array}\)
- \(\begin{array}{ll}& 10^{-3} \\{\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}},} & \dfrac{1}{10^{3}} \\ {\text { Simplify. }} & \dfrac{1}{1000}\end{array}\)
Спростити:
- \(2^{-3}\)
- \(10^{-7}\)
- Відповідь
-
- \(\dfrac{1}{8}\)
- \(\dfrac{1}{10^{7}}\)
Спростити:
- \(3^{-2}\)
- \(10^{-4}\)
- Відповідь
-
- \(\dfrac{1}{9}\)
- \(\dfrac{1}{10,000}\)
У\(\PageIndex{1}\) Вправі ми підняли ціле число до від'ємного показника. Що відбувається, коли ми піднімаємо дріб до негативного показника? Ми почнемо з дивлячись на те, що відбувається з дробу чильник якого один і чиїм знаменником є ціле число піднято до негативного показника.
\(\begin{array}{ll}& \dfrac{1}{a^{-n}}\\ {\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} } & \dfrac{1}{\dfrac{1}{a^{n}}} \\ {\text { Simplify the complex fraction. }} & 1 \cdot \dfrac{a^{n}}{1}\\ {\text { Multiply. }} & a^{n}\end{array}\)
Це призводить до властивості негативних показників.
Якщо n - ціле число and\(a\neq 0\), то\(\dfrac{1}{a^{-n}}=a^{n}\).
Спростити:
- \(\dfrac{1}{y^{-4}}\)
- \(\dfrac{1}{3^{-2}}\)
- Відповідь
-
- \(\begin{array} { ll } & \dfrac{1}{y^{-4}}\\ \text { Use the property of a negative exponent, } \dfrac{1}{a^{-n}}=a^{n} . & y^{4}\end{array}\)
- \(\begin{array} { ll } & \dfrac{1}{3^{-2}}\\ \text {Use the property of a negative exponent, } \dfrac{1}{a^{-n}}=a^{n} . & 3^{2} \\ \text{Simplify.}& 9\end{array}\)
Спростити:
- \(\dfrac{1}{p^{-8}}\)
- \(\dfrac{1}{4^{-3}}\)
- Відповідь
-
- \(p^{8}\)
- 64
Спростити:
- \(\dfrac{1}{q^{-7}}\)
- \(\dfrac{1}{2^{-4}}\)
- Відповідь
-
- \(q^{7}\)
- 16
Припустимо, тепер у нас є дріб, піднятий до негативного показника. Давайте використаємо наше визначення негативних показників, щоб привести нас до нової властивості.
\(\begin{array}{ll}& \left(\dfrac{3}{4}\right)^{-2}\\ {\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} } & \dfrac{1}{\left(\dfrac{3}{4}\right)^{2}} \\ {\text { Simplify the denominator. }} & \dfrac{1}{\dfrac{9}{16}}\\ {\text { Simplify the complex fraction.}} &\dfrac{16}{9}\\ \text { But we know that } \dfrac{16}{9} \text { is }\left(\dfrac{4}{3}\right)^{2} & \\ \text { This tells us that: } & \left(\dfrac{3}{4}\right)^{-2}=\left(\dfrac{4}{3}\right)^{2}\end{array}\)
Щоб отримати від початкового дробу, піднятого до негативного показника до кінцевого результату, ми взяли зворотну основу - фракцію - і змінили знак показника.
Це призводить нас до частки до властивості негативної влади.
Якщо\(a\) і\(b\) є дійсними числами,\(a \neq 0, b \neq 0,\) і\(n\) є цілим числом, то\(\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}\)
Спростити:
- \(\left(\dfrac{5}{7}\right)^{-2}\)
- \(\left(-\dfrac{2 x}{y}\right)^{-3}\)
- Відповідь
-
- \(\begin{array}{ll}& \left(\dfrac{5}{7}\right)^{-2}\\ \text { Use the Quotient to a Negative Exponent Property, }\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}& \\ \text { Take the reciprocal of the fraction and change the sign of the exponent. }&\left(\dfrac{7}{5}\right)^{2}\\ \text { Simplify. } & \dfrac{49}{25}\end{array}\)
- \(\begin{array}{ll}& \left(-\dfrac{2 x}{y}\right)^{-3}\\ \text { Use the Quotient to a Negative Exponent Property, }\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}& \\ \text { Take the reciprocal of the fraction and change the sign of the exponent. }&\left(-\dfrac{y}{2 x}\right)^{3}\\ \text { Simplify. } & -\dfrac{y^{3}}{8 x^{3}}\end{array}\)
Спростити:
- \(\left(\dfrac{2}{3}\right)^{-4}\)
- \(\left(-\dfrac{6 m}{n}\right)^{-2}\)
- Відповідь
-
- \(\dfrac{81}{16} \)
- \(\dfrac{n^{2}}{36 m^{2}}\)
Спростити:
- \(\left(\dfrac{3}{5}\right)^{-3}\)
- \(\left(-\dfrac{a}{2 b}\right)^{-4}\)
- Відповідь
-
- \(\dfrac{125}{27}\)
- \(\dfrac{16 b^{4}}{a^{4}}\)
Спрощуючи вираз з показниками, ми повинні бути обережними, щоб правильно визначити базу.
Спростити:
- \((-3)^{-2}\)
- \(-3^{-2}\)
- \(\left(-\dfrac{1}{3}\right)^{-2}\)
- \(-\left(\dfrac{1}{3}\right)^{-2}\)
- Відповідь
-
- Тут показник застосовується до основи −3. \(\begin{array}{ll} & (-3)^{-2}\\ {\text { Take the reciprocal of the base and change the sign of the exponent. }}& \dfrac{1}{(-3)^{-2}} \\ {\text { Simplify. }} & \dfrac{1}{9}\end{array}\)
- Вираз\(-3^{-2}\) означає «знайти протилежне\(3^{-2}\)». Тут показник застосовується до основи 3. \(\begin{array}{ll} &-3^{-2}\\ \text { Rewrite as a product with }-1&-1 \cdot 3^{-2}\\\text { Take the reciprocal of the base and change the sign of the exponent. } & -1 \cdot \dfrac{1}{3^{2}}\\ {\text { Simplify. }} & -\dfrac{1}{9}\end{array}\)
- Тут показник застосовується до бази\(\left(-\dfrac{1}{3}\right)\). \(\begin{array}{ll} &\left(-\dfrac{1}{3}\right)^{-2}\\ {\text { Take the reciprocal of the base and change the sign of the exponent. }}& \left(-\dfrac{3}{1}\right)^{2}\\ {\text { Simplify. }} & 9\end{array}\)
- Вираз\(-\left(\dfrac{1}{3}\right)^{-2}\) означає «знайти протилежне\(\left(\dfrac{1}{3}\right)^{-2}\)». Тут показник застосовується до бази\(\left(\dfrac{1}{3}\right)\). \(\begin{array}{ll} &-\left(\dfrac{1}{3}\right)^{-2}\\ \text { Rewrite as a product with }-1&-1 \cdot\left(\dfrac{1}{3}\right)^{-2}\\\text { Take the reciprocal of the base and change the sign of the exponent. } & -1 \cdot\left(\dfrac{3}{1}\right)^{2}\\ {\text { Simplify. }} & -9 \end{array}\)
Спростити:
- \((-5)^{-2}\)
- \(-5^{-2}\)
- \(\left(-\dfrac{1}{5}\right)^{-2}\)
- \(-\left(\dfrac{1}{5}\right)^{-2}\)
- Відповідь
-
- \(\dfrac{1}{25}\)
- \(-\dfrac{1}{25}\)
- 25
- −25
Спростити:
- \((-7)^{-2}\)
- \(-7^{-2}\)
- \(\left(-\dfrac{1}{7}\right)^{-2}\)
- \(-\left(\dfrac{1}{7}\right)^{-2}\)
- Відповідь
-
- \(\dfrac{1}{49}\)
- \(-\dfrac{1}{49}\)
- 49
- −49
Ми повинні бути обережними, щоб дотримуватися Порядку операцій. У наступному прикладі частини (a) і (b) виглядають аналогічно, але результати різні.
Спростити:
- 4\(\cdot 2^{-1}\)
- \((4 \cdot 2)^{-1}\)
- Відповідь
-
- \(\begin{array}{ll} \text { Do exponents before multiplication. }&4 \cdot 2^{-1}\\ \text { Use } a^{-n}=\dfrac{1}{a^{n}}&4 \cdot \dfrac{1}{2^{1}}\\ {\text { Simplify. }} & 2 \end{array}\)
- \(\begin{array}{ll} &(4 \cdot 2)^{-1}\\ \text { Simplify inside the parentheses first. }&(8)^{-1}\\ \text { Use } a^{-n}=\dfrac{1}{a^{n}} & \dfrac{1}{8^{1}}\\{\text { Simplify. }} & \dfrac{1}{8} \end{array}\)
Спростити:
- 6\(\cdot 3^{-1}\)
- \((6 \cdot 3)^{-1}\)
- Відповідь
-
- 2
- \(\dfrac{1}{18}\)
Спростити:
- 8\(\cdot 2^{-2}\)
- \((8 \cdot 2)^{-2}\)
- Відповідь
-
- 2
- \(\dfrac{1}{256}\)
Коли змінна піднімається до негативного показника, ми застосовуємо визначення так само, як і з числами. Будемо вважати, що всі змінні ненульові.
Спростити:
- \(x^{-6}\)
- \(\left(u^{4}\right)^{-3}\)
- Відповідь
-
- \(\begin{array}{ll} &x^{-6}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{x^{6}}\end{array}\)
- \(\begin{array}{ll} &\left(u^{4}\right)^{-3}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{\left(u^{4}\right)^{3}} \\ \text{ Simplify.} & \dfrac{1}{u^{12}}\end{array}\)
Спростити:
- \(y^{-7}\)
- \(\left(z^{3}\right)^{-5}\)
- Відповідь
-
- \(\dfrac{1}{y^{7}}\)
- \(\dfrac{1}{z^{15}}\)
Спростити:
- \(p^{-9}\)
- \(\left(q^{4}\right)^{-6}\)
- Відповідь
-
- \(\dfrac{1}{p^{9}}\)
- \(\dfrac{1}{q^{24}}\)
Коли є продукт і показник, ми повинні бути обережними, щоб застосувати показник до правильної кількості. Відповідно до Порядку операцій, ми спрощуємо вирази в дужках перед застосуванням показників. Ми побачимо, як це працює в наступному прикладі.
Спростити:
- 5\(y^{-1}\)
- \((5 y)^{-1}\)
- \((-5 y)^{-1}\)
- Відповідь
-
- \(\begin{array}{ll} &5 y^{-1}\\ \text { Notice the exponent applies to just the base y. }& \\ \text { Take the reciprocal of } y \text { and change the sign of the exponent. }&5 \cdot \dfrac{1}{y^{1}} \\ \text { Simplify. } & \dfrac{5}{y}\end{array}\)
- \(\begin{array}{ll} &(5 y)^{-1}\\\text { Here the parentheses make the exponent apply to the base } 5 y .& \\ \text { Take the reciprocal of } 5 y \text { and change the sign of the exponent. }&\dfrac{1}{(5 y)^{1}}\\ \text { Simplify. } &\dfrac{1}{5 y}\end{array}\)
- \(\begin{array}{ll} &(-5 y)^{-1}\\\text { The base here is }-5 y& \\ \text { Take the reciprocal of }-5 y \text { and change the sign of the exponent. }&\dfrac{1}{(-5 y)^{1}}\\ \text { Simplify. } &\dfrac{1}{-5 y}\\ \text { Use } \dfrac{a}{-b}=-\dfrac{a}{b} & -\dfrac{1}{5 y}\end{array}\)
Спростити:
- 8\(p^{-1}\)
- \((8 p)^{-1}\)
- \((-8 p)^{-1}\)
- Відповідь
-
- \(\dfrac{8}{p}\)
- \(\dfrac{1}{8 p}\)
- \(-\dfrac{1}{8 p}\)
Спростити:
- 11\(q^{-1}\)
- \((11 q)^{-1}-(11 q)^{-1}\)
- \((-11 q)^{-1}\)
- Відповідь
-
- \(\dfrac{11}{1 q}\)
- \(\dfrac{1}{11 q}-\dfrac{1}{11 q}\)
- \(-\dfrac{1}{11 q}\)
З від'ємними показниками правило частки потребує лише однієї форми\(\dfrac{a^{m}}{a^{n}}=a^{m-n},\) для\(a \neq 0\) 0. Коли показник у знаменнику більше показника в чисельнику, показник частки буде негативним.
Спрощення виразів з цілими показниками
Усі властивості експоненти, які ми розробили раніше в главі з цілими числовими показниками, також застосовуються до цілих показників. Ми повторюємо їх тут для довідки.
Якщо\(a\) і\(b\) є дійсними числами, а\(m\) і\(n\) цілими числами, то
\(\begin{array}{lrll}{\textbf { Product Property }}& a^{m} \cdot a^{n} &=&a^{m+n} \\ {\textbf { Power Property }} &\left(a^{m}\right)^{n} &=&a^{m \cdot n} \\ {\textbf { Product to a Power }} &(a b)^{m} &=&a^{m} b^{m} \\ {\textbf { Quotient Property }} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0 \\ {\textbf { Zero Exponent Property }}& a^{0} &= & 1, a \neq 0 \\ {\textbf { Quotient to a Power Property }} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \\ {\textbf { Properties of Negative Exponents }} & a^{-n} &=&\dfrac{1}{a^{n}} \text { and } \dfrac{1}{a^{-n}}=a^{n}\\ {\textbf { Quotient to a Negative Exponents }}& \left(\dfrac{a}{b}\right)^{-n} &=&\left(\dfrac{b}{a}\right)^{n} \\\end{array}\)
Спростити:
- \(x^{-4} \cdot x^{6}\)
- \(y^{-6} \cdot y^{4}\)
- \(z^{-5} \cdot z^{-3}\)
- Відповідь
-
- \(\begin{array}{ll}& x^{-4} \cdot x^{6} \\ \text { Use the Product Property, } a^{m} \cdot a^{n}=a^{m+n} & x^{-4+6} \\ \text { Simplify. } & x^{2} \end{array}\)
- \(\begin{array}{ll}& y^{-6} \cdot y^{4} \\ \text { Notice the same bases, so add the exponents. }& y^{-6+4}\\ \text { Simplify. } & y^{-2} \\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} & \dfrac{1}{y^{2}}\end{array}\)
- \(\begin{array}{ll}& z^{-5} \cdot z^{-3} \\ \text { Add the exponents, since the bases are the same. }& z^{-5-3}\\ \text { Simplify. } & z^{-8}\\ \text { Take the reciprocal and change the sign of the exponent, }& \dfrac{1}{z^{8}} \\ \text { using the definition of a negative exponent. }\end{array}\)
Спростити:
- \(x^{-3} \cdot x^{7}\)
- \(y^{-7} \cdot y^{2}\)
- \(z^{-4} \cdot z^{-5}\)
- Відповідь
-
- \(x^{4}\)
- \(\dfrac{1}{y^{5}}\)
- \(\dfrac{1}{z^{9}}\)
Спростити:
- \(a^{-1} \cdot a^{6}\)
- \(b^{-8} \cdot b^{4}\)
- \(c^{-8} \cdot c^{-7}\)
- Відповідь
-
- \(a^{5}\)
- \(\dfrac{1}{b^{4}}\)
- \(\dfrac{1}{c^{15}}\)
У наступних двох прикладах ми почнемо з використання Commutative Property, щоб згрупувати однакові змінні разом. Це полегшує ідентифікацію подібних баз перед використанням Product Property.
Спростити:\(\left(m^{4} n^{-3}\right)\left(m^{-5} n^{-2}\right)\)
- Відповідь
-
\(\begin{array}{ll}& \left(m^{4} n^{-3}\right)\left(m^{-5} n^{-2}\right) \\ \text { Use the Commutative Property to get like bases together. }& m^{4} m^{-5} \cdot n^{-2} n^{-3}\\ \text { Add the exponents for each base. }&m^{-1} \cdot n^{-5}\\ \text { Take reciprocals and change the signs of the exponents. }& \dfrac{1}{m^{1}} \cdot \dfrac{1}{n^{5}} \\ \text { Simplify. } & \dfrac{1}{m n^{5}}\end{array}\)
Спростити:\(\left(p^{6} q^{-2}\right)\left(p^{-9} q^{-1}\right)\)
- Відповідь
-
\(\frac{1}{p^3 q^3}\)
Спростити:\(\left(r^{5} s^{-3}\right)\left(r^{-7} s^{-5}\right)\)
- Відповідь
-
\(\frac{1}{r^2 s^8}\)
Якщо мономи мають числові коефіцієнти, множимо коефіцієнти, так само, як ми робили раніше.
Спростити:\(\left(2 x^{-6} y^{8}\right)\left(-5 x^{5} y^{-3}\right)\)
- Відповідь
-
\(\begin{array}{ll}& \left(2 x^{-6} y^{8}\right)\left(-5 x^{5} y^{-3}\right) \\ \text { Rewrite with the like bases together. }& 2(-5) \cdot\left(x^{-6} x^{5}\right) \cdot\left(y^{8} y^{-3}\right)\\ \text { Multiply the coefficients and add the exponents of each variable. }&-10 \cdot x^{-1} \cdot y^{5}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&-10 \cdot \dfrac{1}{x^{1}} \cdot y^{5} \\ \text { Simplify. } & \dfrac{-10 y^{5}}{x}\end{array}\)
Спростити:\(\left(3 u^{-5} v^{7}\right)\left(-4 u^{4} v^{-2}\right)\)
- Відповідь
-
\(-\frac{12v^5}{u}\)
Спростити:\(\left(-6 c^{-6} d^{4}\right)\left(-5 c^{-2} d^{-1}\right)\)
- Відповідь
-
\(\frac{30d^3}{c^8}\)
У наступних двох прикладах ми будемо використовувати властивість живлення та продукт до властивості живлення.
Спростити:\(\left(6 k^{3}\right)^{-2}\)
- Відповідь
-
\(\begin{array}{ll}&\left(6 k^{3}\right)^{-2}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{n} b^{m}&(6)^{-2}\left(k^{3}\right)^{-2}\\ \text { Use the Power Property, }\left(a^{m}\right)^{n}=a^{m \cdot n}&6^{-2} k^{-6}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{6^{2}} \cdot \dfrac{1}{k^{6}} \\ \text { Simplify. } & \dfrac{1}{36 k^{6}}\end{array}\)
Спростити:\(\left(-4 x^{4}\right)^{-2}\)
- Відповідь
-
\(\frac{1}{16x^8}\)
Спростити:\(\left(2 b^{3}\right)^{-4}\)
- Відповідь
-
\(\frac{1}{16b^{12}}\)
Спростити:\(\left(5 x^{-3}\right)^{2}\)
- Відповідь
-
\(\begin{array}{ll}&\left(5 x^{-3}\right)^{2}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{n} b^{m}&5^{2}\left(x^{-3}\right)^{2}\\ \begin{array}{l}{\text { Simplify } 5^{2} \text { and multiply the exponents of } x \text { using the Power }} \\ {\text { Property, }\left(a^{m}\right)^{n}=a^{m \cdot n} .}\end{array}&25 \cdot x^{-6}\\ \begin{array}{l}{\text { Rewrite } x^{-6} \text { by using the Definition of a Negative Exponent, }} \\ {\space a^{-n}=\dfrac{1}{a^{n}}}\end{array}&25 \cdot \dfrac{1}{x^{6}}\\ \text { Simplify. } & \dfrac{25}{x^{6}}\end{array}\)
Спростити:\(\left(8 a^{-4}\right)^{2}\)
- Відповідь
-
\(\frac{64}{a^8}\)
Спростити:\(\left(2 c^{-4}\right)^{3}\)
- Відповідь
-
\(\frac{8}{c^{12}}\)
Щоб спростити дріб, ми використовуємо властивість Коефіцієнт і віднімаємо показники.
Спростити:\(\dfrac{r^{5}}{r^{-4}}\)
- Відповідь
-
\(\begin{array}{l} & \dfrac{r^{5}}{r^{-4}}\\ {\text { Use the Quotient Property, } \dfrac{a^{n}}{a^{n}}=a^{m-n}} & r^{5-(-4)}\\ {\text { Simplify. }} & r^{9}\end{array}\)
Спростити:\(\dfrac{x^{8}}{x^{-3}}\)
- Відповідь
-
\(x^{11}\)
Спростити:\(\dfrac{y^{8}}{y^{-6}}\)
- Відповідь
-
\(y^{14}\)
Перетворити з десяткового позначення на наукові позначення
Пам'ятайте, що робота з місцем значення для цілих чисел і десяткових знаків? Наша система числення заснована на повноваженнях 10. Ми використовуємо десятки, сотні, тисячі тощо. Наші десяткові числа також засновані на степенях десятків - десятих, сотих, тисячних і так далі. Розглянемо цифри 4000 і 0,004. Ми знаємо, що 4 000 означає\(4 \times 1,000\) і 0,004 означає\(4 \times \dfrac{1}{1,000}\).
Якщо ми запишемо 1000 як ступінь десяти в експоненціальній формі, ми можемо переписати ці числа таким чином:
\[\begin{array}{ll}{4,000} & {0.004} \\ {4 \times 1,000} & {4 \times \dfrac{1}{1,000}} \\ {4 \times 10^{3}} & {4 \times \dfrac{1}{10^{3}}} \\ & {4 \times 10^{-3}}\end{array}\]
Коли число записується як добуток двох чисел, де перший множник - це число більше або дорівнює одиниці, але менше 10, а другий множник - це ступінь 10, написана в експоненціальній формі, воно, як кажуть, знаходиться в науковому позначенні.
Число виражається в науковому позначенні, коли воно має форму
\[a \times 10^{n} \text { where } 1 \leq a<10 \text { and } n \text { is an integer }\]
У науковому позначенні прийнято використовувати як знак\(\times\) множення, хоча ми уникаємо використання цього знака в інших місцях алгебри.
Якщо ми подивимося на те, що сталося з десятковою крапкою, ми можемо побачити метод легко перетворити з десяткового позначення в наукові позначення.
В обох випадках десяткова кома була переміщена на 3 місця, щоб отримати перший множник між 1 і 10.
\(\begin{array}{ll}{\text { The power of } 10 \text { is positive when the number is larger than } 1 :} & {4,000=4 \times 10^{3}} \\ {\text { The power of } 10 \text { is negative when the number is between } 0 \text { and } 1 :} & {0.004=4 \times 10^{-3}} \end{array}\)
Напишіть в науковому позначенні: 37000.
- Відповідь
-
Напишіть в науковій позначенні: 96000.
- Відповідь
-
\(9.6 \times 10^{4}\)
Напишіть в науковій позначенні: 48300.
- Відповідь
-
\(4.83 \times 10^{4}\)
- Крок 1. Перемістіть десяткову крапку так, щоб перший множник був більшим або дорівнював 1, але менше 10.
- Крок 2. Підрахуйте кількість десяткових знаків, n, щоб десяткова крапка була переміщена.
- Крок 3. Напишіть число у вигляді добутку зі степеню 10.
Якщо початковий номер:- більше 1, потужність 10 складе 10 п.
- між 0 і 1, потужність 10 буде дорівнює 10 −n.
- Крок 4. Перевірте.
Напишіть в науковому позначенні: 0.0052.
- Відповідь
-
Початкове число, 0.0052, знаходиться між 0 і 1, тому ми матимемо негативну силу 10.
Перемістіть десяткову крапку, щоб отримати 5,2, число від 1 до 10. Підрахуйте кількість знаків після коми, в яку була переміщена точка. Пишіть як продукт потужністю 10. Перевірте. \(\begin{array}{l}{5.2 \times 10^{-3}} \\ {5.2 \times \dfrac{1}{10^{3}}} \\ {5.2 \times \dfrac{1}{1000}} \\ {5.2 \times 0.001}\end{array}\) 0,0052
Напишіть в наукових позначеннях: 0.0078
- Відповідь
-
\(7.8 \times 10^{-3}\)
Напишіть в наукових позначеннях: 0.0129
- Відповідь
-
\(1.29 \times 10^{-2}\)
Перетворити наукове позначення на десяткову форму
Як ми можемо перетворити з наукового позначення в десяткову форму? Давайте розглянемо два числа, написані в науковому позначенні, і подивимося.
\[\begin{array}{cc}{9.12 \times 10^{4}} & {9.12 \times 10^{-4}} \\ {9.12 \times 10,000} & {9.12 \times 0.0001} \\ {91,200} & {0.000912}\end{array}\]
Якщо ми подивимося на розташування десяткової крапки, ми можемо побачити простий метод перетворення числа з наукового позначення в десяткову форму.
\[9.12 \times 10^{4}=91,200 \quad 9.12 \times 10^{-4}=0.000912\]
В обох випадках десяткова крапка перемістилася на 4 місця. Коли показник був додатним, десяткова кома переміщається вправо. Коли показник був від'ємним, десяткова крапка переміщається вліво.
Перетворити на десяткову форму:\(6.2 \times 10^{3}\)
- Відповідь
-
Перетворити на десяткову форму:\(1.3 \times 10^{3}\)
- Відповідь
-
\(1,300\)
Перетворити на десяткову форму:\(9.25 \times 10^{4}\)
- Відповідь
-
\(92,500\)
Кроки підсумовані нижче.
Перетворіть наукові позначення в десяткову форму.
Щоб перетворити наукові позначення в десяткову форму:
- Крок 1. Визначте показник\(n\), на коефіцієнт\(10\).
- Крок 2. Перемістіть\(n\) десяткові розряди, при необхідності додаючи нулі.
- Якщо показник позитивний, перемістіть знаки після\(n\) коми вправо.
- Якщо показник від'ємний, перемістіть знаки після\(|n|\) коми вліво.
- Крок 3. Перевірте.
Перетворити на десяткову форму:\(8.9\times 10^{-2}\)
- Відповідь
-
Визначте показник\(n\), на коефіцієнт\(10\). Оскільки показник від'ємний, перемістіть десяткову крапку на 2 розряди вліво. Додайте нулі, якщо потрібно для заповнювачів.
Перетворити на десяткову форму:\(1.2 \times 10^{-4}\)
- Відповідь
-
\(0.00012\)
Перетворити на десяткову форму:\(7.5 \times 10^{-2}\)
- Відповідь
-
\(0.075\)
Множення та ділення за допомогою наукових позначень
Астрономи використовують дуже великі числа для опису відстаней у Всесвіті та епохи зірок і планет. Хіміки використовують дуже малі числа для опису розміру атома або заряду на електроні. Коли вчені виконують розрахунки з дуже великими або дуже маленькими числами, вони використовують наукові позначення. Наукові позначення забезпечують спосіб проведення обчислень без написання безлічі нулів. Ми побачимо, як Властивості експонентів використовуються для множення та ділення чисел у наукових позначеннях.
Помножити. Напишіть відповіді в десятковій формі:\(\left(4 \times 10^{5}\right)\left(2 \times 10^{-7}\right)\)
- Відповідь
-
\(\begin{array}{ll} & \left(4 \times 10^{5}\right)\left(2 \times 10^{-7}\right)\\\text { Use the Commutative Property to rearrange the factors. }& 4 \cdot 2 \cdot 10^{5} \cdot 10^{-7} \\ \text{ Multiply.} & 8 \times 10^{-2} \\ \text { Change to decimal form by moving the decimal two places left. } & 0.08\end{array}\)
Помножити\((3\times 10^{6})(2\times 10^{-8})\). Напишіть відповіді в десятковій формі.
- Відповідь
-
\(0.06\)
Помножити\(\left(3 \times 10^{-2}\right)\left(3 \times 10^{-1}\right)\). Напишіть відповіді в десятковій формі.
- Відповідь
-
\(0.009\)
Розділити. Напишіть відповіді в десятковій формі:\(\dfrac{9 \times 10^{3}}{3 \times 10^{-2}}\)
- Відповідь
-
\(\begin{array}{ll} & \dfrac{9 \times 10^{3}}{3 \times 10^{-2}}\\\text { Separate the factors, rewriting as the product of two fractions. }& \dfrac{9}{3} \times \dfrac{10^{3}}{10^{-2}}\\ \text{ Divide.} & 3 \times 10^{5} \\ \text { Change to decimal form by moving the decimal five places right. } & 300000\end{array}\)
Розділіть\(\dfrac{8 \times 10^{4}}{2 \times 10^{-1}} .\) Запишіть відповіді в десятковій формі.
- Відповідь
-
\(400,000\)
Розділіть\(\dfrac{8 \times 10^{2}}{4 \times 10^{-2}} .\) Запишіть відповіді в десятковій формі.
- Відповідь
-
\(20,000\)
Отримайте доступ до цих онлайн-ресурсів для додаткового навчання та практики з цілими показниками та науковими позначеннями:
- Негативні експоненти
- Наукові позначення
- Наукові позначення 2
Ключові концепції
- Властивість негативних показників
- Якщо\(n\) є натуральним числом і\(a \ne 0\), то\(\dfrac{1}{a^{−n}}=a^n\)
- Якщо\(n\) є натуральним числом і\(a \ne 0\), то\(\dfrac{1}{a^{−n}}=a^n\)
- Коефіцієнт до негативного показника
- Якщо\(a\) і\(b\) є дійсними числами,\(b \ne 0\) і\(n\) є цілим числом, то\(\left(\dfrac{a}{b}\right)^{−n}=\left(\dfrac{b}{a}\right)^n\)
- Якщо\(a\) і\(b\) є дійсними числами,\(b \ne 0\) і\(n\) є цілим числом, то\(\left(\dfrac{a}{b}\right)^{−n}=\left(\dfrac{b}{a}\right)^n\)
- Щоб перетворити наукові позначення в десяткову форму:
- Визначте показник,\(n\) на коефіцієнт\(10\).
- Перемістіть\(n\) десяткові розряди, при необхідності додаючи нулі.
- Якщо показник позитивний, перемістіть знаки після\(n\) коми вправо.
- Якщо показник від'ємний, перемістіть знаки після\(|n|\) коми вліво.
- Перевірте.
- Щоб перетворити десяткове число в наукові позначення:
- Перемістіть десяткову крапку так, щоб перший множник був більшим або рівним,\(1\) але менше\(10\).
- Підрахуйте кількість десяткових знаків,\(n\) щоб десяткова крапка була переміщена.
- Напишіть число як добуток з силою\(10\). Якщо початковий номер:
- більше\(1\), ніж, сила\(10\) буде\(10^n\)
- між\(0\) і\(1\), сила\(10\) буде\(10^{−n}\)
- Перевірте.
Глосарій
- негативний показник
- Якщо\(n\) є натуральним числом and\(a \neq 0\), то\(a^{-n}=\dfrac{1}{a^{n}}\).
- наукові позначення
- Число виражається в науковому позначенні, коли воно має вигляд\(a \times 10^{n}\) де\(a \geq 1\) і a<10 і\(n\) є цілим числом.
